New criteria for the oscillation of a class of third-order quasilinear delay differential equations

1.   Introduction

This study focuses on the asymptotic and oscillatory characteristics of solutions to a class of third-order delay differential equations of the form:

where $\varrho$ represents the ratio of two odd positive integers, and the following conditions are satisfied:

$\textbf{(H} _{1})$ $r\in C^{1}\left(\left[ \top _{0}, \infty \right), \mathbb{R} \right)$, $r\left(\top \right) > 0$ and

$(\textbf{H} _{2})$ $\tau _{i}\in C^{1}\left(\left[ \top _{0}, \infty \right), \mathbb{R} \right), \Theta _{i}\in C^{1}\left(\left[ \top _{0}, \infty \right), \mathbb{R} \right),$ $\Theta _{i}\left(\top \right) > 0$ does not vanish eventually, $\tau ^{\prime }\left(\top \right) > 0, \tau (\top)\leq \tau _{i}\left(\top \right) \leq \top$, and $\lim_{\top \rightarrow \infty }\tau _{i}\left(\top \right) = \infty,$ $i = 1, 2, .., k.$

Definition 1.1. The function $\digamma \in C^{1}\left(\left[ t_{\digamma }, \infty \right), \mathbb{R} \right),$ $t_{\digamma }\geq \top _{0},$ is called a solution of (1.1), if it verifies $\digamma ^{\prime }, r\left(\digamma ^{\prime \prime }\right) ^{\varrho }\in C^{1}\left(\left[ \top _{0}, \infty \right), \mathbb{R} \right)$ and satisfies (1.1) on $\left[ t_{\digamma }, \infty \right).$ We only consider those solutions of (1.1) which exist on some half-line $\left[ t_{\digamma }, \infty \right)$ and satisfy

for any $t\geq t_{\digamma }$.

Definition 1.2. A solution of (1.1) is called oscillatory if it is neither eventually positive nor eventually negative. Otherwise, the solution is called non-oscillatory. The equation is called oscillatory if all its solutions are oscillatory.

Remark 1.1. Note that if $\digamma$ is a solution of (1.1), then $-\digamma$ is also a solution of (1.1). Therefore, when analyzing nonoscillatory solutions of (1.1), it is sufficient to focus on the eventually positive ones.

Advanced differential equations are essential tools in mathematical modeling, playing a fundamental role in understanding complex phenomena across various fields, including biomathematics. This discipline addresses the mathematical applications in biology based on the use of mathematical models to comprehend vital processes and interactions within biological systems.

Differential equations provide the ideal framework for describing dynamic changes in living organisms. They allow researchers to model the behavior of different biological systems, such as disease spread, ecological interactions, population dynamics, and genetic processes. Advanced differential equations, including those involving partial equations, offer powerful tools for analyzing complex phenomena involving multiple variables ^[1,2,3]. Models based on differential equations are crucial for understanding how biological systems respond to external variables and how these changes can affect the health and sustainability of living organisms. For instance, differential equations are used to describe the spread of infectious diseases, providing insight into how infections are transmitted among individuals of how infections transmit among individuals and the impact of various factors such as social distancing and vaccination. Furthermore, the connection between differential equations and biomathematics opens new avenues for scientific research. By developing accurate mathematical models, researchers can test biological hypotheses, analyze experimental data, and gain new insights into complex biological processes ^[4,5,6].

Oscillation theory, central to many scientific fields such as physics and chemistry, has its roots in the study of motion and the effects of forces. Over centuries, it has evolved to incorporate complex mathematical concepts, enabling the analysis of dynamic systems across diverse domains, including engineering and quantum mechanics. In the seventeenth century, the pioneering works of Galileo Galilei and Isaac Newton contributed to a deeper understanding of the concepts of motion and acceleration, laying the foundation for the theory of oscillation. By the nineteenth century, scientists such as James Clerk Maxwell and Pierre-Simon Laplace developed advanced mathematical models, resulting in widespread applications in the fields of thermodynamics and wave theory^[7,8,9]. With the advent of the twentieth century, the scope of the theory of oscillation expanded to include new fields such as quantum theory and relativity, where the concepts of oscillation became fundamental to understanding the behavior of particles at atomic and subatomic levels, enabling scientists to explore natural phenomena in greater depth. Today, oscillation theory remains a vital area of research, providing insights into intricate systems and fostering innovative solutions to challenging problems. Through the study of oscillations, we can understand complex systems and develop innovative solutions to intricate problems, making it an exciting and significant area of research in the present day ^[10,11,12].

On the other hand, oscillation theory plays a crucial role in understanding dynamic processes in chemistry and biology, where periodic fluctuations govern numerous natural and synthetic systems. In chemistry, oscillatory reactions such as the Belousov-Zhabotinsky reaction exemplify nonlinear chemical dynamics, providing insight into reaction-diffusion mechanisms and self-organization phenomena. In biological systems, oscillatory behaviors are fundamental to circadian rhythms, metabolic cycles, and neural activity, where feedback loops and regulatory networks maintain homeostasis and adaptive responses. The study of these oscillatory systems not only advances theoretical models but also informs practical applications, including drug delivery, synthetic biology, and bioengineering ^[13,14,15].

The qualitative analysis of differential equations of the form (1.1), including their applications and generalizations, has become a subject of significant interest.

Remark 1.2. In this context, we say that Eq (1.1) verifies the property $M$ if every nonoscillatory solution $F > 0$ belongs to $C_{3}$ in Lemma 2.1.

1.1.   Motivation

Several studies have explored the oscillatory behavior of solutions to third-order differential equations, focusing on establishing sufficient conditions for oscillation and non-oscillation. For instance, Fahd et al. in ^[16] investigated some asymptotic properties for the neutral differential equation

where $\varrho > 1$,

and

They established sufficient conditions guaranteeing that every solution of the preceding equations either exhibits oscillatory behavior or converges to zero.

In 2023, the authors in ^[17] investigated the asymptotic properties of the third-order delay differential equations

where $\sigma \in C\left(\left[ \top _{0}, \infty \right), \mathbb{R} \right),$

and (1.2) holds. They derived conditions that establish the convergence criteria for all nonoscillatory solutions approaching zero.

Almarri in ^[18] introduced new criteria for oscillation of third-order delay differential equations of the form

where $\sigma \in C^{1}\left(\left[ \top _{0}, \infty \right), \mathbb{R} \right),$ and (1.2) holds.

Previous studies in this field can be referenced, such as ^[19,20,21] and the cited references. Most of the previous studies have addressed the oscillation of the solutions of Eq (1.1) under the condition $\Pi \left(\top _{0}\right) = \infty.$ In this paper, we discuss in detail several results related to Eq (1.1) under the condition $\Pi \left(\top _{0}\right) < \infty$. In [22, Theorem 1], a particular criterion was obtained using an effective and novel technique based on the reduction of equation

to a first-order Riccati-type inequality.

Theorem 1.1. [22, Theorem 1] Suppose that

If, also,

and

for some $\ell$ and $k$ $\in \left(0, 1\right)$, and $t_{\ell }\geq \top _{0},$ $\top _{2}\geq t_{\ell }$ and $\top _{3}\geq \top _{0}$, then (1.3) is oscillatory or all its solutions satisfy

Furthermore, in [23, Theorem 3], the authors established certain oscillation criteria for Eq (1.3) by reducing its order from a third-order equation to a first-order equation and then applying the comparison principle. They obtained the following theorem:

Theorem 1.2. [23, Theorem 3.1] Suppose that there exist nondecreasing functions $\Psi _{1}\left(\top \right)$ and $\Psi _{2}\left(\top \right) \in C^{1}\left([\top _{0}, \infty), \mathbb{R} \right)$ such that

If

and

for any $t\geq \top _{0}$,

then (1.3) is oscillatory.

As we find, the authors in [24, Corollary 1] studied the equation

and, using the principles of comparison with the first-order delay differential equation, they obtained the following result:

Theorem 1.3. [24, Corollary 1] Suppose that there exist nondecreasing functions $\Psi _{1}, \Omega \in C^{1}\left([\top _{0}, \infty), \mathbb{R} \right)$ such that

If

and

for all $\top _{2} > \top _{1}\geq \top _{0},$

then (1.11) is oscillatory.

It is clear that Theorems 1.2 and 1.3 rely on three independent conditions that exclude all non-oscillatory solutions belonging to (C$_{1}-$C$_{3}$), ensuring the oscillation of all solutions to the Eqs (1.3) and (1.11). The results of these theorems depend heavily on the appropriateness of the auxiliary functions involved in the conditions of the (lim inf) type, which makes the application of these conditions somewhat complex.

In Theorem 1.1, it is observed that the non-oscillatory solutions belonging to cases C$_{1}$ and C$_{2}$ are excluded by conditions (1.6) and (1.5), while condition (1.4) ensures that any non-oscillatory solution belonging to case C$_{3}$ tends to zero.

All the results above share the common requirement of adhering to three independent conditions to ensure the exclusion of any non-oscillatory solutions, thereby guaranteeing the oscillation of the studied equations.

This paper aims to establish new oscillation criteria for Eq (1.1) that complement, improve, and simplify the existing results, including Theorems 1.1–1.3. By reducing the number of required conditions and constraints, our results provide a more streamlined approach to ensuring the oscillation of Eq (1.1).

2.   Main results

We begin by introducing the classification of the derivatives of the solution and then introduce the absence of solutions belonging to C$_{1}$. As will be shown later, this condition is also encompassed by those that rule out solutions belonging to C$_{2}$. In addition, we present theories that guarantee the oscillation of the solutions of the Eq (1.1) or their approximation to zero.

Lemma 2.1. Assume that $\digamma > 0$ is a solution of (1.1). Then $\digamma$ belongs to one of the following sets:

Proof. Let $\digamma$ be a non-oscillatory solution of (1.1). Without loss of generality, we may suppose that $\digamma$ is positive. From (1.1), we see that

Scince $\Theta _{i}\left(\top \right),$ $\digamma ^{\varrho }\left(\tau _{i}\left(\top \right) \right) > 0$, then

Hence, $\digamma ^{\prime }\left(\top \right)$ and $\digamma ^{\prime \prime }\left(\top \right)$ are of one sign eventually, which implies the stated result. □

Lemma 2.2. Assume that $\digamma > 0$ is a solution of (1.1). If

then C$_{1} = \Phi.$

Proof. To proceed with a proof by contradiction, assume that $\digamma$ belongs to C$_{1}$ and $\digamma (\tau (\top) > 0$ for $\top \geq \top _{1}$, $\top _{1}\in \lbrack \top _{0}, \infty)$. Since $\digamma ^{\prime \prime } > 0$, we note that $c: = \digamma ^{\prime }\left(\top _{1}\right) \leq \digamma ^{\prime }\left(\top \right)$. Therefore,

and

Integrating (1.1) from $\top _{2}$ to $\top$ and using (2.1), we have

which is a contradiction. The proof is complete. □

Lemma 2.3. Assume that $\digamma > 0$ is a positive increasing solution of (1.1)$.$ If

then $\digamma$ belongs to C$_{2}$ for $\top \geq \top _{1}$, moreover,

(a) $\left(\digamma \left(\top \right) /\top \right) ^{\prime } < 0,$ $\lim_{\top \rightarrow \infty }\digamma \left(\top \right) /\top = \digamma ^{\prime }\left(\top \right) = 0,$ and

(b) $\left(\digamma ^{\prime }\left(\top \right) /\Pi \left(\top \right) \right) ^{\prime } > 0$ and

Proof. Let $\digamma$ be increasing: From Lemma 2.1, $\digamma$ belongs to C$_{1}$ or C$_{2}$ for $\top \geq \top _{1}$, $\top _{1}\in \lbrack \top _{0}, \infty)$, that is, $\digamma \left(\tau _{i}\left(\top \right) \right)$ is positive for $\top \geq \top _{1}$. Since $\Pi \left(\top _{0}\right) < \infty$, (2.4) leads to (2.1). Thus, from Lemma 2.2, $\digamma$ belongs to C$_{2}$ for $\top \geq \top _{1}$.

Since $\left(\digamma ^{\prime }\left(\top \right) \right) ^{\prime } < 0$, we see that $\lim_{\top \rightarrow \infty }\digamma ^{\prime }\left(\top \right) \geq \lambda = 0$. If $\digamma ^{\prime }\left(\top \right) \geq \lambda > 0$ for $\top \geq \top _{1}$, following a similar approach in the proof of Lemma 2.2, we obtain (2.3). From $r\left(\top \right) \left(\digamma ^{\prime \prime }\left(\top \right) \right) ^{\varrho } < 0$, we obtain

Integrating (2.6) from $\top _{2}$ to $\top$, we obtain

which leads to a contradiction, and thus, $\lambda = 0$. By using l'Hospital's Rule, we note that

Thus,

From (2.7), we obtain

That is,

which yields

Now, it is clear that

and hence,

The proof is complete. □

We can now move forward by introducing several straightforward criteria for property $M$ for (1.1).

Theorem 2.1. If

then $\digamma \in$C$_{3}$.

Proof. To proceed with a proof by contradiction, assume that $\digamma$ belongs to C$_{1}$ or C$_{2}$ for $\top \geq \top _{1}$. Since $\digamma ^{\prime } > 0$, there is a $\top _{2}\geq \top _{1}$ such that $\ell : = \digamma \left(\top _{1}\right) \leq \digamma \left(\top \right)$ for $\top \geq \top _{2}$. From (1.1), we have

Since $\Pi \left(\top _{0}\right) < \infty$, from (2.8) we arrive at

If $\digamma$ belongs to C$_{1}$, then according to (2.10) $r\left(\top \right) \left(\digamma ^{\prime \prime }\left(\top \right) \right) ^{\varrho }$ is not positive, and thus we lead to a contradiction. Assume that $\digamma$ belongs to C$_{2}$. Using the property $r\left(\top \right) \left(\digamma ^{\prime \prime }\left(\top \right) \right) ^{\varrho } < 0$ in (2.9), we see that

Integrating the above inequality from $\top _{2}$ to $\top$, we obtain

which contradicts $\digamma ^{\prime }\left(\top \right) > 0$. The proof is complete. □

Theorem 2.2. If

then $\digamma \in$C$_{3}.$

Proof. To proceed with a proof by contradiction, assume that $\digamma$ belongs to C$_{1}$ or C$_{2}$ for $\top \geq \top _{1}$. It is clear that for (2.12) to be valid, it is essential that (2.4) is true. From Lemma 2.3, we note that $\digamma$ belongs to C$_{2}$ and properties (a) and (b) are satisfied for $\top _{1}\leq \top _{2}\leq \top.$ Thus,

From (1.1), obtain

Integrating (2.13) from $\top _{2}$ to $\top$ and using $\digamma ^{\prime } < 0$, we get

Now, setting $x\left(\top \right) : = \digamma ^{\prime }\left(\top \right) > 0,$ we find

Thus, by [25, Theorem 2.1.1], (2.15) does not have a positive solution, contradicting our original assumption. The proof is complete. □

A principle like the one we used in the proof of Theorem 2.2 always requires $\tau \left(\top \right) < \top$. The results presented in the sequel, however, apply also in the case when $\tau \left(\top \right) = \top$.

Theorem 2.3. Assume that (2.4) holds. If

then $\digamma \in$C$_{3}.$

Proof. To proceed with a proof by contradiction, assume that $\digamma$ belongs to C$_{1}$ or C$_{2}$ for $\top \geq \top _{1}$. We see that $\lim_{\top \rightarrow \infty }\Pi \left(\top \right) = 0$ is satisfied. According to $\Pi \left(\top _{0}\right) < \infty$, and (2.16), this implies (2.1). By Lemma 2.3, we obtain that $\digamma$ belongs to C$_{2}$ and satisfies properties $(a)$ and $(b)$ for $\top _{1}\leq$ $\top _{2}\leq \top$.

Proceeding similarly as in Theorem 2.2, we obtain (2.14). Using the monotonicity of $r\left(\top \right) \left(\digamma ^{\prime \prime }\left(\top \right) \right) ^{\varrho }$ and property (b) in (2.14), we find that

that is,

This contradicts (2.16), and the proof is complete. □

Theorem 2.4. Suppose that (2.4) holds. If there is a function $\rho \in C^{1}\left([\top _{0}, \infty), \left(0, \infty \right) \right),$ $\rho ^{\prime }\geq 0$ such that

for any $\Upsilon \in \lbrack \top _{0}, \infty)$, then $\digamma \in$C$_{3}$.

Proof. To proceed with a proof by contradiction, assume that $\digamma$ belongs to C$_{1}$ or C$_{2}$ for $\top \geq \top _{1}$. From Lemma 2.3, we see that $\digamma$ belongs to C$_{2}$ and satisfies properties (a) and (b) for $\top _{1}\leq$ $\top _{2}\leq \top$. Define the following function $w > 0$ as

We have that

Integrating (1.1) from $\top _{2}$ to $\top$ and taking into account that $\left(\digamma \left(\tau \left(\top \right) \right) /\tau \left(\top \right) \right) ^{\prime } < 0$, we have

Using the fact that $\lim_{\top \rightarrow \infty }$ $\digamma \left(\top \right) /\top = 0$, we obtain

From (2.19) and (2.20), we obtain

that is,

Using (2.21) and (2.18), we have

Integrating (2.22) from $\top _{3}$ to $\top$, we find

which is a contradiction. The proof is complete. □

Corollary 2.1. Suppose that (2.4) holds. If

for any $\Upsilon \in \lbrack \top _{0}, \infty)$, then $\digamma \in$C$_{3}$.

Proof. Taking $\rho \left(\top \right) = 1/\Pi \left(\top \right)$, the results follows directly □

Theorem 2.5. Suppose that (2.4) holds. If there is a function $\delta \in C^{1}\left([\top _{0}, \infty), \left(0, \infty \right) \right)$ such that

for any $\Upsilon \in \lbrack \top _{0}, \infty)$, then $\digamma \in$C$_{3}$.

Proof. To proceed with a proof by contradiction, assume that $\digamma$ belongs to C$_{1}$ or C$_{2}$. From Lemma 2.3, we see that $\digamma$ belongs to C $_{2}$ and the properties $(a)$ and $(b)$ are satisfied for $\top _{1}\leq \top _{2}\leq \top$. Using Lemma 2.3, we obtain

Define the following function as

From (2.25), we note that $\theta \geq 0$ on $[\top _{1}, \infty)$. Differentiating (2.25) and using (1.1), we obtain

Using that $\digamma ^{\prime }\left(\top \right) +\Pi \left(\top \right) r^{1l\varrho }\left(\top \right) \digamma ^{\prime \prime }\left(\top \right) \geq 0$ in (2.26)$,$ we obtain

In view of [26, Lemma 2.3], we find that

using the above inequality with

in (2.27), we obtain that

Integrating (2.29) from $\top _{2}$ to $\top$, we arrive at

From (2.25), we obtain

We note that (2.24) leads to

Substituting (2.31) into (2.30), we obtain

which is a contradiction to (2.23). The proof is complete. □

Remark 2.1. We note that upon closer examination it becomes apparent that condition (1.6) of Theorem 1.1 is unnecessary.

Theorem 2.6. If (1.5) holds for $0 < k < 1$and $\top _{3}\geq \top _{0}$, then $\digamma \in$C$_{3}$.

Proof. In view of [22, Theorem 1], we note that (1.6) and (1.5) exclude solutions belonging to C$_{1}$ and C$_{2}$, respectively. We find that for (1.5) to be satisfied, the following equation must be satisfied:

which according to $\Pi \left(\top _{0}\right) < \infty$ implies (2.1). By Lemma 2.2, the class of solutions belonging to C$_{1}$ is empty. □

Remark 2.2. Considering the proof of Theorem 1.1, we observe that by utilizing the property

condition (2.4) was established to exclude any solutions belonging to the class C$_{2}$. Furthermore, by employing property (2.5) from Lemma 2.3, we can obtain a stronger result in Theorem 2.6 with $k = 1.$

Lemma 2.4. Suppose that $\digamma > 0$ is a solution of (1.1) belonging to C$_{3}$. If

or

then $\digamma$ satisfies (1.7).

Proof. Let $\digamma \left(\tau _{i}\left(\top \right) \right) > 0$ for some $\top _{1}\in \lbrack \top _{0}, \infty)$ and $\top \geq \top _{1}$. Since $\digamma ^{\prime } < 0$, there is a finite limit $\lim_{\top \rightarrow \infty }\digamma \left(\top \right) = \lambda \geq 0$. Let $\lambda > 0$. Integrating (1.1) from $\top _{1}$ to $\top$ and using (2.34), we obtain

which is a contradiction. Therefore, $\lim_{\top \rightarrow \infty }\digamma \left(\top \right) = 0$. To demonstrate that the same conclusion is valid in the case where

the reader is directed to ^[22]HY__HY, Theorem 1]. The proof is complete. □

By combining the results in Theorems 2.1–2.5 with the results in Lemma 2.4, we obtain new results that guarantee that the solutions of (1.1) are oscillatory or satisfy (1.7).

Theorem 2.7. If (2.8) is satisfied, then (1.1) is oscillatory or its solution satisfies (1.7).

Proof. Since $\Pi \left(\top _{0}\right) < \infty,$ and from (2.8), we see that (2.34) is satisfied. □

Theorem 2.8. If (2.12) and either (2.34) or (2.35) are satisfied, then (1.1) is oscillatory or its solution satisfies (1.7).

Theorem 2.9. If (2.4), (2.16), and either (2.34) or (2.35) are satisfied, then (1.1) is oscillatory or its solution satisfies (1.7).

Theorem 2.10. Assume that (2.4) holds. If there is a function $\rho \in C^{1}\left([\top _{0}, \infty), \left(0, \infty \right) \right)$ with $\rho ^{\prime }\geq 0$ such that (2.17) holds and either (2.34) or (2.35) is satisfied, then (1.1) is oscillatory or its solution satisfies (1.7).

Theorem 2.11. Assume that (2.4) holds. If there is a function $\delta \in C^{1}\left([\top _{0}, \infty), \left(0, \infty \right) \right)$ such that (2.23) holds and either (2.34) or (2.35) is satisfied, then (1.1) is oscillatory or its solution satisfies (1.7).

Now, we establish the following theorem, which guarantees the exclusion of non-oscillatory solutions belongs to C$_{3}$. Then, we present the theorem that ensures the oscillation of all solutions of Eq (1.1).

Theorem 2.12. Suppose that $\digamma > 0$ is a solution of (1.1). If

where

then C$_{3} = \Phi$.

Proof. Let $\tau \left(\top \right) \geq \top _{1}$ for some $\top _{1}\in \lbrack \top _{0}, \infty)$ and $\top \geq \top _{1}$. By the monotonicity of $r\left(\top \right) \left(\digamma ^{\prime \prime }\left(\top \right) \right) ^{\varrho }$, we have

Integrating (2.37) from $u$ to $v$ in $u$, we obtain

Integrating (1.1) from $\tau \left(\top \right)$ to $\top$ and from (2.38) with $u = \tau \left(s\right)$ and $v = \tau \left(\top \right)$, we obtain

This contradiction ends the proof. □

By combining the results in Theorems 2.1–2.6 with the results in Lemma 2.4, we obtain new results that guarantee that all solutions of (1.1) are oscillatory.

Theorem 2.13. Suppose that all conditions in Theorem 2.1, Theorem 2.2, Theorem 2.3, Theorem 2.4, Theorem 2.5, or Theorem 2.6 and (2.36) are satisfied. Then (1.1) is oscillatory.

3.   Example

Example 3.1. Consider the differential equation

where $0 < \lambda < 1$ and $\Theta _{0}$ is positive.

Applying the previous results to Eq (3.1), we conclude that

– Since (2.8) is not satisfied, Theorem 2.1 is inapplicable.

– Theorem 2.2 implies

– Theorem 2.3 implies

– (Corollary 2.1) implies

- Also, Theorem 2.5 with $\rho \left(\top \right) = \tau \left(\top \right) \Pi \left(\top \right)$ implies (3.3), and Theorem 2.6 implies (3.4).

Note that conditions (2.34) and (2.35) in Lemma 2.4 are satisfied. Therefore, we can say that the solutions of Eq (3.1) are either oscillatory or tend to zero if one of the conditions (3.2)–(3.4) is satisfied.

Now, we use Theorem 2.12 to exclude any positive decreasing solutions of (3.1), which implies

Using Theorem 2.13, we see that all solutions of (3.1) are oscillatory if one of the conditions (3.2)–(3.4) and (3.5) hold.

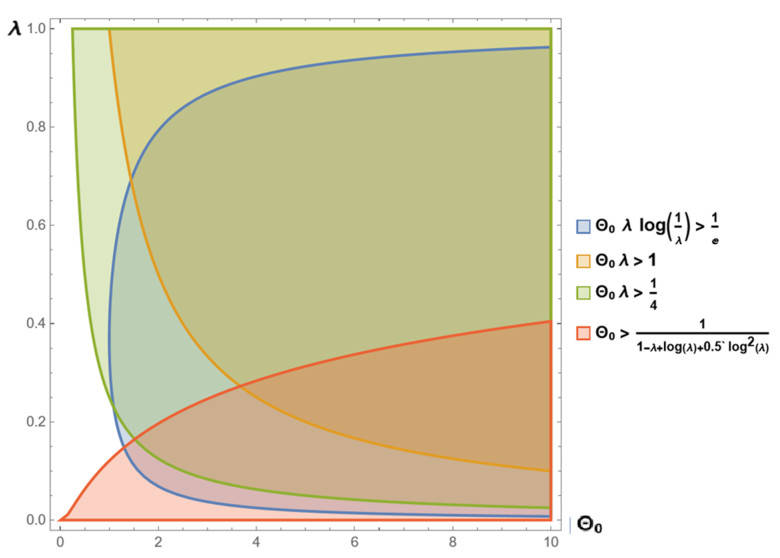
Remark 3.1. In view of Figure 1, we note that condition (3.4) is less stringent than conditions (3.2) and (3.3), allowing greater flexibility in the permissible values for $\lambda$ and $\Theta _{0}$. This implies a broader range of application and parameter adjustment. Also,

(1) when the values of $\lambda$ are small, condition (3.2) is the most efficient condition.

(2) when the values of $\lambda$ are large, condition (3.4) is the most efficient condition.

Example 3.2

$\top \geq 1,$ where $\Theta _{0} > 0$. Applying the previous results to the Eq (3.6), we obtain

– Theorem 2.2 implies

– Theorem 2.3 implies

– (Corollary 2.1) implies

According to Theorem 2.12, we see that the following condition

exclude any positive decreasing solutions of (3.1). Thus, by Theorem 2.13, that is, all solutions of (3.6) are oscillatory if one of the conditions (3.7)–(3.9) and (3.10) hold.

Remark 3.2. In view of the previous example, we note that according to (1.4), Theorem 1.1 is not applicable.

4.   Conclusions

This paper establishes several new oscillation results for (1.1). These results enhance, complete, and simplify the existing ones (e.g., Theorems 1.2 and 1.1). Initially, we provide multiple criteria to ensure the absence of any non-oscillatory solutions belonging to either class C$_{1}$ or C$_{2}$. Notably, Theorems 2.1 and 2.2 require only a single condition, compared to the multiple conditions necessary in Theorems 1.2 and 1.1. We also demonstrate that Condition (1.6) is unnecessary in Theorem 1.1. Furthermore, we present more general results to ensure no non-oscillatory solutions belong to class C$_{1}$ or C$_{2}$. Subsequently, we derived criteria ensuring that the solutions to (1.1) are either oscillatory or tend to zero by integrating previous results with Lemma 2.4.

Additionally, we provided a new condition to exclude any non-oscillatory solution belonging to class C$_{3}$ and expanded condition (1.4) to encompass the Euler equation

while Theorem 1.1 fails to apply due to (4.1). By combining all the above results with Theorem 2.12, we establish criteria that ensure the oscillation of all solutions to Eq (1.1).

Author contributions

Z.A., H.R. and B.Q.: Conceptualization; Z.A., B.Q. and A.A.: Methodology; Z.A., B.Q. and A.A.: Validation; Z.A., B.Q. and A.A.: Investigation; B.Q. and Z.A.: Resources; Z.A., B.Q., I.F.B.S. and A.A.: Data curation; Z.A., A.A., I.F.B.S., H.R. and B.Q.: Writing-original draft preparation; B.Q., Z.A., I.F.B.S., A.A. and H.R.: Writing-review and editing; Z.A., A.A. and B.Q.: Visualization; A.A., H.R., Z.A. and B.Q.: Supervision; B.Q.: Project administration. All authors have read and agreed to the published version of the manuscript.

Use of Generative-AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors acknowledge the Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2025R518), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding

This research was funded by Researchers Supporting Project number (PNURSP2025R518), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare no conflicts of interest.