New refinements of Becker-Stark inequality

1.   Introduction

It is known in the literature that, for $x\in(0, \pi/2)$, the inequality

was first established by Becker and Stark ^[6]. This is always known as Becker-Stark inequality, which has attracted much interest many researchers and has been generalized in many different ways; see ^{[7,8,10,13,17,26,27,28]} and the references therein. The importance of Becker-Stark inequality is to find the bounds for $\tan x/x$, which are the rational functions with the same order of infinity near $\pi/2$. In particular, the first of the notable refinements is given by Zhu [27,Theorem 1.3], who proved that, for $x\in(0, \pi/2)$,

As a matter of fact, Zhu [27,Theorem 1.4] gives a general refinement of the Becker-Stark inequality. In view of

the left-hand side of (1.1) becomes a good approximate of $\tan x/x$ near $\pi/2$. Motivated by this remark, Zhu [28,Theorem 3] gives a refinement of (1.1), for $x\in(0, \pi/2)$,

where $-(\pi^2-9)/(6\pi^4)$ and $-(10-\pi^2)/\pi^4$ are the best constants. Further, Debnath et al. ^[13] present two estimates of $\tan x/x$ near $\pi/2$ but not in the whole interval $(0, \pi/2)$; more precisely, the following inequalities hold true

for $x\in(0.373, \pi/2)$ and

for $x\in(0, 301, \pi/2)$. Recently, alternative good improvements can be found in [10,Equation (2.11)] and [4,Theorem 2.1], where they establish the inequalities

and

for $x\in(0, \pi/2)$, where the second inequality had been improved by Zhu ^[29] to the following inequality

for $x\in(0, \pi/2)$ with the best constants $\frac{(240-17\pi^2)\pi^2}{45}$ and $\frac{(240-17\pi^2)1024}{\pi^4(17\pi^2-120)}$. It is observed that all the above improvements keep the structure of the Becker-Stark inequality, that is to say, the denominator of their approximate functions is $\pi^2-4x^2$.

Very recently, Wu and Bercu ^[18] approximated $\tan x/x$ by utilizing the cosine polynomials due to the property of even function, and established the inequalities

for $x\in(0, \pi/2)$. Clearly, inequality (1.3) has broken the structure of the Becker-Stark inequality, which leads to the left-hand side of (1.3) being just a bounded function.

The main objective of this paper is to provide new lower and upper bounds for $\tan x/x$ whose forms preserve the structure of the Becker-Stark inequality and numerator is a polynomial of $\sin^2x$. More precisely, we transform the function $(\pi^2-4x^2)\tan x/x$ into the ratio of two hypergeometric functions by changing a variable $t = \sin^2x$ and use the first few terms of the series expansion to approximate the objective function. This method, as a practice toy, can be used to reprove the Becker-Stark inequality. The importance of our findings is not only illustrated by giving some new refinements of inequality (1.1), but also by the fact that the method can be extended to generalized trigonometric functions.

The rest of this paper is organized as follows: In this section, we give an introduction and highlight the relevant previous results. Section 2 consists of some basic knowledge and two lemmas, and is devoted to the proof of the main result. Diverse complements are offered in Section 3, including a comparison of the obtained bounds by graphical analysis, a conjecture raised from the main result, and a $p$-analogue of Becker-Stark inequality.

2.   Main results and proofs

2.1.   Preliminaries and lemmas

In this section, we first introduce some basic knowledge and present two lemmas that are used to prove the main result.

Definition 2.1. For real numbers $a, b$, and $c$ with $-c\notin\mathbb{N}\cup\{0\}$, the Gaussian hypergeometric function is defined as

for $x\in(-1, 1)$, where $(a)_n = a(a+1)\cdots(a+n-1) = \Gamma(a+n)/\Gamma(a)$ denotes the Pochhammer symbol or the shifted factorial function for $n\in\mathbb{N}$. In particular, $(a)_0 = 1$ for $a\neq0$. Here $\Gamma(x) = \int_0^\infty t^{x-1}e^{-t}dt$ is the classical Euler gamma function ^[21,23].

Recall that the hypergeometric function $F(a, b;c; x)$ has the following properties:

Property 2.1. A simple derivative formula

Property 2.2. The behavior of hypergeometric function $F(a, b;c; x)$ near $x = 1$ satisfies the following situations:

$\diamond$ $c > a+b$ (cf. [16,p. 49])

$\diamond$ $c = a+b$ (cf. [1,15.3.10]), the Ramanujan's asymptotic formula

$\diamond$ $c < a+b$ (cf. [15,(1.2)]), as $x\to1$,

where $B(a, b) = [\Gamma(a)\Gamma(b)]/\Gamma(a+b)$, $R(a, b) = -2\gamma-\psi(a)-\psi(b)$, $\psi(x) = \Gamma'(x)/\Gamma(x)$ and $\gamma$ is the beta function, the Ramanujan constant, the psi function, and the Euler-Mascheroni constant.

In a particular case of $a, b, c$, the inverse trigonometric tangent function can be represented by hypergeometric function.

Property 2.3. (see [1,15.1.5])

Remark 2.1. The second equality of (2.4) can be obtained from the transformation formula $F(a, b;c; z) = (1-z)^{-a}F(a, c-b; c;z/(z-1))$ (c.f. [1,15.3.4]), and also coincides with the case of $p = 2$ in [3,Lemma 1].

Property 2.4. (see [31,(3.6)]) An identity

As is known, a real function $\varphi$ is said to be absolutely monotonic on the interval $I$ if the $k$th derivative of $\varphi$, denoted by $\varphi^{(k)}(x)$, exists and is non-negative for each $k\geq0$ and $x\in I$. In other words, if $\varphi$ can be expressed as a power series on $I$, then all coefficients are non-negative. In particular, a special power series, roughly speaking, whose coefficients are first negative and then positive is said to be a negative-positive type series, of which the name was first proposed formally in ^[25] although this type of special series has been studied extensively in the literature ^[11,22,30].

Definition 2.2. A power series $S(x)$ given by

is called a "Negative-Positive type" (or "NP type" for short) power series, if its coefficients $a_k$ for $k\geq0$ satisfy

(i) $a_k\geq0$ for all $k\geq0$;

(ii) There exist at least two integers $0\leq k_1\leq m$ and $k_2\geq m+1$ such that $a_{k_1}, a_{k_2}\neq 0$.

Correspondingly, $S(x)$ is called a "Positive-Negative type" (or "PN type" for short) power series if $-S(x)$ is a Negative-Positive type power series.

The following lemma is a simple and efficient tool to determine the sign of an NP (or PN) type power series, which has been proved in ^[22,24].

Lemma 2.1. Let $S(x)$ be a Negative-Positive type power series converging on the interval $(0, R)$. Then

(i) if $S(R^-)\leq0$, then $S(x) < 0$ for all $x\in(0, R)$;

(ii) if $S(R^-) > 0$, then there is a unique $\tilde{x}\in(0, R)$ such that $S(x) < 0$ for $x\in(0, \tilde{x})$ and $S(x) > 0$ for $x\in(\tilde{x}, R)$.

As a consequence, for a PN-type power series, the inequalities of $(i)$ and $(ii)$ are reversed.

We provide a power series expansion of $\left[F(a, b;a+b+1/2)\right]^2$ in the following lemma, which has been demonstrated in [19,Example 14.11] (see also ^[9]).

Lemma 2.2. For $c = a+b+1/2$, it holds that

In particular, we have

2.2.   Statement of Theorem 2.1

Let $t = \sin^2x$ for $x\in(0, \pi/2)$, and then $t\in(0, 1)$. This gives $\tan^2x = t/(1-t)$, which by (2.4) is equivalent to

By (2.7), it can be rewritten as

where

by (2.5) and (2.6). Here, $u_n$ and $v_n$ are given by

Moreover, by (2.1), we have

Suppose that $\alpha_n$ is the Maclaurin's coefficients of $\pi^2-f(t)/g(t)$, that is,

then it follows from (2.9) and (2.10) that

which deduces $\alpha_1 = 4-\pi^2/3$ and the recurrence relation

Before stating Theorem 2.1, we can compute a finite number of $\alpha_n$ by (2.12), which are listed numerically in Table 1. Table 1 illustrates that $\alpha_n > 0$ for $1\leq n\leq30$. Although we only know a finite $\alpha_n > 0$, it still encourages us to prove the following theorem. These evidence demonstrate that Theorem 2.1 is valid in the case of $2\leq N\leq 28.$

Theorem 2.1. Let $\alpha_n$ be defined as in (2.12). If there exists an integer $N\geq2$ such that $\alpha_n > 0$ for $1\leq n\leq N+2$, then the double inequality

holds for all $x\in(0, \pi/2)$ with the best constants $\alpha_{N}$ and $\widetilde{\alpha}_N$, where

2.3.   Proofs

Proof of Theorem 2.1. In order to obtain inequality (2.13), it suffices to show that

for $x\in(0, \pi/2)$, which by (2.7) and (2.8) is equivalent to

for $t\in(0, 1)$.

In terms of power series, by (2.9) and (2.10), we can rewrite $\phi_1(t)$ and $\phi_2(t)$ as

where

(i) To prove $\phi_1(t) > 0$ for $t\in(0, 1)$.

We first assert that if $\tau_n\leq0$ for $n\geq N+1$, then $\tau_{n+1} < 0$. To confirm this, if $\tau_n\leq0$ for $n\geq N+1$, that is,

then we deduce by (2.18) that

for $n\geq N+1$, where the last inequality follows from

for $1\leq k\leq N$. This confirms the truth of the assertion.

We now complete the proof in the following two steps:

Step 1: We prove $\tau_{N+1} > 0$. Otherwise, we see from the above assertion that $\tau_n < 0$ for $n\geq N+2$.

This, together with (2.16) implies that $\phi_1(t) < 0$ for $t\in(0, 1)$. On the other hand, it follows from (2.14) and $\alpha_{N+1} > 0$ that

for $t\in(0, \epsilon_1)$ with a sufficiently small $\epsilon_1 > 0$, which is a contradiction.

Step 2: There are only two situations:

(a) If all $\tau_n > 0$ for $n\geq N+1$, then $\phi_1(t) > 0$ for $t\in(0, 1)$ by (2.16).

(b) If there exists an integer $m\geq N+2$ such that $\tau_m\leq0$, we may assume that $\tau_m$ is the first non-positive term. Then the above assertion tells us that $\tau_n > 0$ for $N+1\leq n\leq m-1$ and $\tau_n\leq0$ for $n\geq m$. That is to say, $\phi_1(t)$ is a PN-type power series on $(0, 1)$. Combining this with Lemma 2.1 and $\phi_1(1^-) = 0$, it follows that $\phi_1(t) > 0$ for $t\in(0, 1)$.

(ii) To prove $\phi_2(t) < 0$ for $t\in(0, 1)$.

Due to $\alpha_{N+2} > 0$, by repeating the above steps, it can also be shown that

by (2.11), which gives $\widetilde{\alpha}_N\geq\alpha_N+\alpha_{N+1} > \alpha_{N}$. Observe that $v_n/v_{n-1} = 1-3/(3+2n) < 1$, that is to say, $v_n$ is strictly decreasing for $n\geq0$. According to this, with $\widetilde{\alpha}_N > 0$ and $\alpha_k > 0$ ($1\leq k\leq N+1$), it follows that

for $n\geq N+1$. If $\widetilde{\tau}_N-\widetilde{\alpha}_N\geq0$, then $\phi_2(t) > 0$ for $t\in(0, 1)$ by (2.17). This, together with (2.15), implies that

for $t\in(0, \epsilon_2)$ with a sufficiently small $\epsilon_2 > 0$. This contradicts $\phi_2(t) > 0$ for $t\in(0, 1)$ and thereby $\widetilde{\tau}_N-\widetilde{\alpha}_N < 0$. According to (2.17), we conclude that $\phi_2(t)$ is an NP-type power series on $(0, 1)$ and so $\phi_2(t) < 0$ for $t\in(0, 1)$ by Lemma 2.1 and $\phi_2(1^-) = 0$.

In this end, the optimality of constants follows from

and

This completes the proof of Theorem 2.1. □

Remark 2.2. It is worth pointing out that the numerator of (2.13) is just a $N$-order polynomial of $\sin^2x$, but the condition of Theorem 2.1 still requires $\alpha_{N+1} > 0$ and $\alpha_{N+2} > 0$. This is mainly used to determine the sign of the first terms of the power series in (2.16) and (2.17). As a fact to remember, if a specific integer $N\geq2$ is given, then it can be directly verified the sign of $\tau_{N+1}$ and $\widetilde{\tau}_N-\widetilde{\alpha}_N$ without the conditions that $\alpha_{N+1} > 0$ and $\alpha_{N+2} > 0$.

Remark 2.3. Inequality (2.13) can provide better bounds for larger $N$. First, our remark is obvious on the right side of (2.13). To see the left side, it suffices to verify from $\widetilde{\alpha}_{N+1} > 0$ that

Remark 2.4. It is worth noting that it can be seen from the left side of (2.13) that $N$ must be greater than or equal to 2. Now we can extend the range of $N$ to $N\geq1$. Indeed, due to $\widetilde{\alpha}_{N+1} = \widetilde{\alpha}_N-\alpha_N$, we can rewrite as

This, together with (2.13), gives

holds for all $x\in(0, \pi/2)$.

Taking $N = 1$ into (2.19), we obtain

Corollary 2.1. For all $x\in(0, \pi/2)$, it holds

with the sharp constants $\pi^2-8$ and $4-\pi^2/3$.

Proof. The sharp constants follow from

and

by (2.11). □

Taking $N = 2$ into Theorem 2.1, we obtain

Corollary 2.2. For all $x\in(0, \pi/2)$, it holds

where the constants $\frac{4(\pi^2-9)}{3}$ and $\frac{120-11\pi^2}{45}$ are sharp.

Remark 2.5. Remark 2.3 enables us to know that the inequality (2.21) is better than inequality (2.20). Further, it is easy to see that inequality (2.20) is better than (1.1). In conclusion, inequality (2.13) completely improves the Becker-Stark inequality. As a matter of fact, Corollaries 2.1 and 2.2 can also be obtained through the method used in ^[5,14].

3.   Complements

In this section, we provide a graphical analysis of the obtained bounds, give a conjecture and propose a $p$-analogue of Becker-Stark inequality.

3.1.   Graphical analysis

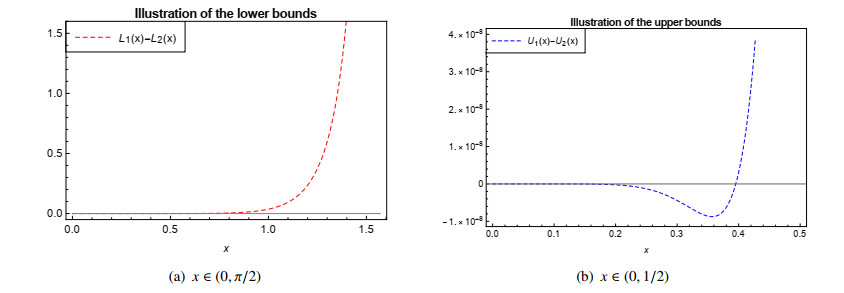
We now provide a graphical analysis of the lower bounds of Theorem 2.1 ($N = 5$) and (1.3) by distinguishing lower bounds.

By (2.12), we can compute the first few $\alpha_n$ as follows:

We denote by $L_j(x)$ and $U_j(x)$ ($j = 1, 2$) the lower and upper bounds of Theorem 2.1 $(N = 5)$ and (1.3), respectively, as follows:

Figure 1 presents the graph of the functions $L_1(x)$ and $L_2(x)$ for $x\in(0, \pi/2)$. An immediate remark arising from Figure 1(a) is that the lower bound of Theorem 2.1 ($N = 5$) is better than (1.3). Figure 1(b) illustrates that the upper bound of Theorem 2.1 ($N = 5$) is better than the one of (1.3) near at $x = 0$.

3.2.   A conjecture

From Table 1, it can be seen that $\alpha_n > 0$ for $1\leq n\leq 30$. This allows us to pose the following conjecture:

Conjecture 3.1. Let $f(t)$ and $g(t)$ be defined as in (2.9) and (2.10) respectively. Then $\pi^2-f(t)/g(t)$ is absolute monotonic on $(0, 1)$.

Remark 3.1. If Conjecture 3.1 can be confirmed, then inequality (2.13) can be directly derived from Conjecture 3.1. However, the advantage of Theorem 2.1 is that we only need to know a finite number of $\alpha_n > 0$ to prove inequality (2.13).

3.3.   $p$-analogue of Becker-Stark inequality

For $p > 1$, the generalized sine function $\sin_p$ is the eigenfunction of the one-dimensional $p$-Laplacian problem ^[12]

which is also the inverse function of $\arcsin_p: (0, 1)\mapsto(0, \pi_p/2)$ defined as

where

In this case, $\sin_px$ is defined on the interval $[0, \pi_p/2]$ and can be extended to the whole $\mathbb{R}$ by symmetry and periodicity. Define $\cos_p:\mathbb{R}\mapsto\mathbb{R}$ by

In particular, it holds

which leads to

Similar to the classical trigonometric function, one can define the generalized tangent function

It is natural to ask whether the $p$-analogue of the Becker–Stark inequality holds for $x\in(0, \pi_p/2)$. Observed that

which allows us to pose the following problem:

Problem 3.1. To determine the range of $p$ in $[2, \infty)$ (resp. $(1, 2)$) such that the inequality

holds for $x\in(0, \pi_p/2)$.

Remark 3.2. Inequality (3.1) can be viewed as the $p$-analogue of Becker-Stark inequality. Our method in this paper reveals that it only needs to study a ratio of two hypergeometric functions by changing the variable $t = \sin_p^px$ in (3.1).

4.   Conclusions

In this paper, from the viewpoint of hypergeometric function, we study the well-known Becker-Stark inequality by changing a variable $t = \sin^2x$. Our main result is to approximate the function $\pi-[(\pi^2-4x^2)\tan x]/x$ by the first few terms of the Taylor series, even if we only know finitely many positive coefficients. In particular, the double inequality

holds for $x\in(0, \pi/2)$, which improves Becker-Stark inequality (1.1).

Author contributions

Suxia Wang: Conceptualisation, writing – original draft, formal analysis; Tiehong Zhao: Writing – review & editing, supervision, validation. All authors have read and approved the final version of the manuscript for publication.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors would like to thank the anonymous referees for their valuable comments and suggestions, which led to considerable improvement of the article.

This research was supported by the Natural Science Research Project of Colleges and Universities in Anhui Province (2022AH051588, 2023AH051549), the Natural Science Research Project of Huainan Normal University (2022XJZD031) and the National Natural Science Foundation of China (11971142).

Conflict of interest

The authors declare that there are no conflicts of interest regarding the publication of this paper.