An age-structured SIPC model of cervical cancer with immunotherapy

1.   Introduction

Cervical cancer is a type of cancer that can be prevented with screening and vaccines. However, it is still a significant type of cancer for women. Even though surgery, chemotherapy, and radiation provide the potential for survival, the side effects will burden the patient, such as the appearance of secondary infections, anemia, hair loss, skin rashes, and diarrhea ^[1].

Like other cancer cells, cervical cancer cells are camouflaged to trick the T-cells so that they cannot recognize the presence of the cancer cells. Typically, the cells undergo a cyclic process that stimulates immune cells by strengthening and expanding the response of T-cells. Simultaneously, this process also considers the inhibiting factors that limit immunity and thus prevent autoimmunity. This cyclic process is known as the cancer-immunity cycle ^[2]. The cancer-immunity cycle can be divided into seven main steps. The first step is the antigen release from cancer cells. The second one involves the antigen being transported to T-cells. In the third step, the T-cells become active and initiate the immune system's fight against the cancer cells. The four-next steps involve active T-cells passing through the blood vessels to find cancer cells, infiltrate, recognize the cancer cells due to the generated antigens, and kill cancer cells. Identification of T-cell inhibitory signals by cancer cells drives the development of immunotherapy.

Immunotherapy treats the cancer cells by stimulating the immune response, where the immunotherapy drugs will block the cancer cells from deactivating T-cells. There are several types of immunotherapy, i.e., immune checkpoint inhibitors, T-cell transfer therapy, monoclonal antibodies, treatment vaccines, and immune system modulators. The T-cell transfer therapy has three approaches, i.e., the use of tumor-infiltrating lymphocytes, chimeric antigen receptor T-cells, and engineered T-cell receptor T cells ^[3]. These procedures entail harvesting the immune cells, multiplying vast numbers of them ex vivo, and then returning the cells to the host via a vein needle.

In terms of mathematical models, cervical cancer growth models have been developed with several approaches. The development of cervical cancer at the tissue level can be modeled by a system of ordinary differential equations; see ^[4,5,6]. In those cases, the cell population was divided into susceptible, infected, precancer, cancer cells, and the virus population. Since HPV infects cells within a specific age interval, the cervical cancer cell model can be described as age-structured; see ^[7,8,9,10]. The authors of ^[7] described the dynamics between age- and time-dependent cell population and the time-dependent free-floating virus population. Age-structured cervical cancer cell models have been developed and analyzed by numerically modeling the solution behavior ^[8,10].

In fact, viruses that have entered the tissue will be reproduced by infected cells; after that, the infected cells release the virus particles into the extracellular environment, and the virus has the ability to infect the surrounding susceptible cells ^[11]. Therefore, the authors of ^[9] reconsidered the appearance of the free-floating virus compartment and proposed a new parameter to represent the infection rate of the viruses, called the force of infection. However, the authors of ^[7,9] considered the interaction between cells without treatment, which is important for the control of cancer cells in the tissue.

Meanwhile, cancer models with immunotherapy and involve the use of systems of ordinary differential equations have been discussed in ^[12,13,14]. The authors of ^[12] incorporated immunotherapy by applying a constant number to represent how the cytokine interleukin-2 boosts the immune system to fight tumors. A mathematical analysis considering immune checkpoint inhibitors has been studied and described in ^[13]. Moreover, a group of scholars have modeled immunotherapy by using a perturbation term to take into account the protein fluctuations in the cells ^[14].

Due to the fact that the role of the E2F1 gene is to preserve the code of proteins, E2F1 regulates cell cycle progression through the $G_1$-to-$S$ transition of the cell cycle, where HPV damages cells when cells are in this phase. E2F1 also plays an important role in DNA repair and apoptosis ^[15]. On the other hand, the administration of immunotherapy can activate the enhancer of zeste homolog 2 (EZH2) as a tumor suppressor gene. EZH2 and E2F1 can induce apoptosis in the abnormal cells ^[16]. Thus, the immunotherapy process works when the cells are in a specific phase of their life. Therefore, in our model, immunotherapy is considered as age-dependent.

In this paper, we introduce a new mathematical model for cervical cancer that includes an age-structured immunotherapy program. We have extended the investigations in ^[9] by adding an immunotherapy term. According to the authors of ^[4], the precancerous cells can be controlled when the lesions become precancerous. Hence, we chose to apply the immunotherapy term to the precancerous cells. Motivated by the results in ^[14,17], since the levels of stimulation and inhibition of T-cells fluctuate throughout the cell cycle, we assume that the interaction between the T-cells and the precancerous cells can be represented by a periodic function with a small amplitude.

Due to the addition of the immunotherapy term, the discussion on an endemic steady-state solution draws attention to the Riccati differential equation. The characteristics of the Riccati differential equation are as follows: the coefficient of the dependent variable is a function of the independent variable, and the highest power of the dependent variable is two. There are some methods for solving the Riccati differential equation. In ^[18], the Riccati equation was converted into a differential equation of the second order with variable coefficients. Commonly, the general solutions of the second order differential equation with variable coefficients can be calculated by applying a reduction of order, a change of independent variables, and an undetermined coefficient method. The restrictive conditions in ^[19,20] showed that the method can only be used in some instances. The authors of ^[21] provided another alternative for solving the second-order differential equation with variable coefficients by using an integral series. Apart from the existing procedures, we can solve the Riccati case in this study by manipulating the algebra such that the equation becomes linear-differential.

Remarkable mathematical models can make contributions toward reducing abnormal cells in the tissue. It is promising to use age-dependent treatment to interact with age-dependent abnormal cells. Therefore, in this article, there are three main findings, as follows. The first one is a new mathematical model that contains the force of infection that represents the infection rate of the free-floating viruses. Second, the mathematical model considers the age-dependency of immunotherapy. Third, through theoretical and numerical analysis, we have drawn some conclusions, i.e., the infection rate plays an important role in reducing precancerous cells when no immunotherapy exists; the higher the infection rate, the more immunotherapy that is needed; and the best time to apply immunotherapy is the initial cell cycle phase.

We present the content of this work as follows. Section 2 describes a new age-structured mathematical model of cervical cancer that incorporates a force of infection parameter and age-dependent immunotherapy. Section 3 shows that the solution exists and is unique. Detailed steps for obtaining the basic reproduction numbers are presented in Section 4. This value is important as a threshold to analyze the stability of infection-free and endemic steady-state solutions. In Section 5, we provide numerical simulations to verify the results in Section 4. Finally, we give a concluding remark in the last section.

2.   Formulation of the model

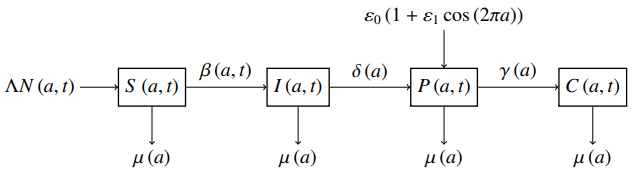
The progression of cervical cancer occurs as follows: HPV infecting susceptible cells, the transformation of infected cells to precancerous cells, and the formation of cancer. For background information regarding the interaction of cells at specific ages and with time-dependency, recall the model in ^[9]. The susceptible cells, infectious cells, precancerous cells, and cancer cells at age $a$ and time $t$ are respectively denoted by $S(a, t)$, $I(a, t), P(a, t)$, and $C(a, t)$. The notation $N(a, t)$ expresses the total population of cells at age $a$ and time $t$ in the cervical tissue. In this paper, the age of a cell that can be infected by the virus or become abnormal is denoted by $a_1$, and the maximum cell's age is $a_\sigma$.

Infected cells will keep producing viruses, and then infect susceptible cells around them. Therefore, we use the force of infection parameter, instead of applying a virus compartment as in ^[4,7]. This parameter is denoted by $\beta(a, t)$, which represents the infection rate of a susceptible cell due to the virus; it is as follows:

where $b \in \left[a_{1}, a_{\sigma}\right]$, $\lambda(a)$ denotes the innate susceptibility of susceptible cells at age $a$, and $h(b)$ represents the innate ability of infected and cancer cells to infect at age $b$. The infection rate of susceptible cells at age $a$ due to interaction with infected cells and cancer cells at age $b$ is denoted by the product of $\lambda(a)h(b)$.

We have extended the model in ^[9] by adding an immunotherapy parameter. The precancerous phase can regress with proper immunotherapy and return to the infected phase. In this model, the immunotherapy term was designed to depend on cell age to determine the appropriate cell age for drug administration. This study is focused on analyzing a cervical cancer model with immunotherapy. Immunotherapy works against abnormal cells by stimulating the immune response system. In this case, the immunotherapy drugs will activate T-cells. When T-cells are activated, they undergo proliferation to generate more T-cells. On the other side, the authors of ^[4] suggested reducing the risk of cervical cancer by making cells stay longer in the precancerous phase. In the precancerous phase, it is easier for cells to regress and prevent them from becoming cancer cells by increasing the body's immunity. Hence, we have added a new parameter to show the immunotherapy process that affects the reduction of precancerous cells. The dividing T-cells will be more controlled and become active against precancerous cells.

Note that ${\varepsilon}_{0}$ represents the rate of T-cell division after being stimulated by immunotherapy drugs. The interaction between T-cells and precancerous cells was set to fluctuate according to ${\varepsilon}_{1}$. We write ${\varepsilon}_{0}\left(1+ {\varepsilon}_{1}\cos \left(2\pi a \right)\right)$, where ${\varepsilon}_{0} > 0$ and $0 < {\varepsilon}_{1} \ll 1$. If $\varepsilon_{0} > 0$ and $\varepsilon_1 = 0$, the treatment is constant since the rate of T-cell division is comparable to that for precancerous cells. Furthermore, $\delta(a)$ denotes the age-dependent rate of progression from infected to precancerous, $\gamma(a)$ denotes the age-dependent rate of progression from precancerous to cancer, and $\mu(a)$ denotes the age-dependent death rate of each type of cell. Because of the cell division, we denote $\Lambda N(a, t)$ as the density of new susceptible cells.

Considering that the infection rate of HPV is based on cell age, the growth of the susceptible, the infected, the precancerous, and the cancer cell densities also depend on cell age. Moreover, the immunotherapy term and death rate of each cell type depend on the age of the cell as well. Thus, the densities of susceptible, infected, precancerous, and cancer cells are considered in terms of age and time. Figure 1 illustrates the interaction between the densities of susceptible, infected, precancerous, and cancer cells.

A mathematical model of cervical cancer progression that includes age-dependent immunotherapy can be formulated as a nonlinear system of partial differential equations as follows:

where the boundary and initial conditions are as follows:

The analysis of System (2.2) is complicated since there is a term that contains $N(a, t)$. Dividing each of the variables $S(a, t), I(a, t), P(a, t)$, and $C(a, t)$ by the corresponding total population $N(a, t)$ will transform System (2.2) into a non-dimensional system. It is important to simplify the analysis of the model, so we can remove the total population $N(a, t)$ on the first line of System (2.2). Therefore, we use the following coordinate transformation to remove $N(a, t)$ from the system:

where $s\left(a, t\right)+i\left(a, t\right)+p\left(a, t\right)+c\left(a, t\right) = 1$. By applying the transformations of (2.4) to the force of infection parameter (2.1), we acquire

If the transformations of (2.4) is substituted into System (2.2) and the boundary-initial conditions of (2.3), we obtain

and the boundary-initial values are given by

As we know, $N(a, t) = S(a, t)+I(a, t)+P(a, t)+C(a, t)$. Hence, System (2.2) analysis appears complex since the first equation of System (2.2) contains the dependent variables $S(a, t), I(a, t), P(a, t)$, and $C(a, t)$. Using the transformations of (2.4), we can obtain System (2.6), which no longer contains $N(a, t)$; thus, the analysis of System (2.6) is obviously preferable. In the next section, we discuss the existence and uniqueness of solutions, as well as the steady-state solutions of System (2.6) and their stability. By applying System (2.6), we can obtain two types of steady-state conditions, i.e., infection-free and endemic. The local stability of the steady-state can be determined by using the perturbation approach and solving integral equations. Some numerical simulations are also presented in this paper to illustrate the behavior of the solutions.

3.   Existence and uniqueness of the solutions

In this section, we will discuss whether the solution of System (2.6) exists and is unique. We use Banach spaces, which possess a complete norm. It implies that every Cauchy sequence in the space converges to a unique limit in the same space. This property allows for the development of many important theorems for partial differential equations. We explore the existence and uniqueness of the solutions of System (2.6) by using the techniques given in ^[22,23]. Let the Banach space $\mathbf{Y} = L^{1}(a_1, a_\sigma) \times L^{1}(a_1, a_\sigma) \times L^{1}(a_1, a_\sigma) \times L^{1}(a_1, a_\sigma)$, which is the set of Lebesgue integral functions that are endowed with the norm

where $\mathbf{X}(a) = (X_1(a), X_2(a), X_3(a), X_4(a))^T \in \mathbf{Y}$. In this study, $L^1$ is applied since it can be interpreted as the total population. Transform System (2.6) into an abstract Cauchy problem by moving the derivative term for age $a$ on the left-hand side of System (2.6) to the right-hand side such that the independent variable $a$ is considered to be in the function space. Introducing $\check{s}(a, t) = s(a, t)-1$ into the transformed System (2.6) gives

The associated boundary and initial conditions are as follows: $\check{s}\left({{a}_{1}}, t \right) = 0, i\left({{a}_{1}}, t \right) = 0, p\left({{a}_{1}}, t \right) = 0, c\left({{a}_{1}}, t \right) = 0, \check{s}\left(a, 0 \right) = {{s}_{0}}\left(a \right)-1, i\left(a, 0 \right) = {{i}_{0}}\left(a \right), p\left(a, 0 \right) = {{p}_{0}}\left(a \right), c\left(a, 0 \right) = {{c}_{0}}\left(a \right)$. For convenience, we denote $\bar{\varepsilon}(a) = \varepsilon_0 (1+\varepsilon_1\cos(2\pi a))$. Suppose that the linear operator $A$ is defined by

and the domain of $\mathbf{X}(a)$ as follows:

Let $G:\mathbf{Y}\to \mathbf{Y}$ be a nonlinear operator defined by

where $Z$ is a bounded linear operator on $L^1 (a_1, a_\sigma)$ that is defined by

If $x(t) = (\check{s}(\cdot, t), i(\cdot, t), p(\cdot, t), c(\cdot, t))^T \in \mathbf{Y}$, then System (3.1) can be written as a Cauchy problem:

where $x_0(a) = (s_0(a)-1, i_0(a), p_0(a), c_0(a))$. According to the work in ^[23], we have the following results.

Lemma 3.1. The operator $A$ generates a $C_0$ semigroup $e^{At}$.

Definition 3.1. ^[24] Let $\mathbf{Y}$ be a Banach space and $\mathbf{V}$ be an open set in $\mathbf{Y}$. An operator $G:\mathbf{V} \to \mathbf{Y}$ is Fréchet-differentiable at $\mathbf{X} \in \mathbf{V}$ if there exists $G_1$ such that

Lemma 3.2. Let $G$ be as shown in (3.3). Then, $G$ is Fréchet-differentiable on $\mathbf{Y}$.

Lemma 3.3. For each $x_0 \in \mathbf{Y}$, there exists a maximal interval of existence $[0, t_0)$ and a unique continuous (mild) solution $t\to x(t, x_0)$ from $[0, t_0)$ to $\mathbf{Y}$ for (2.6) such that

Proof of Lemmas 3.1–3.3 can be achieved by using the Hille-Yosida theorem and the Gâteaux derivative, which can be seen in ^{[23,24,25,26]}. Next, a unique global classical solution of (3.4) can be derived by applying the following theorem. Let $\Delta = \left\lbrace (\check{s}, i, p, c) \in \mathbf{Y}:\check{s} \ge -1, i, p, c \ge 0\right\rbrace$ and $\Delta_0 = \left\lbrace (\check{s}, i, p, c) \in \mathbf{Y}:-1 \le \check{s} \le 0, 0 \le i, p, c \le 1\right\rbrace$.

Theorem 3.1. The mild solution $x(t) \in \Delta$ of (3.4) where $x_0 \in \Delta$, enters into $\Delta_0$ in finite time, and $\Delta_0$ is positively invariant.

Generally, to prove Theorem 3.1, the first step is to find solutions $s(a, t), p(a, t), c(a, t)$ for System (2.6) by taking into account the characteristic equation. The next step is to transform $i(a, t)$ in System (3.1) into the Cauchy problem. Therefore, (3.4) or, equivalently, the initial-boundary value problem given by System (2.6) has a unique positive global solution on $\mathbf{Y}$ with respect to the positive initial value in $D(A) \cap \Delta$.

4.   Steady-state solutions and their stability

4.1.   Infection-free steady-state solution

This subsection will discuss an infection-free steady-state solution, i.e., no virus infection in the cell population. Let $(\hat{s}^*\left(a\right), \hat{i}^*\left(a\right), \hat{p}^*\left(a\right), \hat{c}^*\left(a\right))$ be the steady-state solution of System (2.6); then, we have

where

In the case of the absence of infection, the infection-free steady-state solution is $E_{0} = \left(1, 0, 0, 0 \right)$.

The coefficient of the left hand side derivative with respect to $a$ of System (2.6) is a diagonal matrix; then, System (2.6) is a hyperbolic system of partial differential equations ^[27]. Therefore, we apply a perturbation technique to analyze the stability of the infection-free steady-state solution, that is, $(\tilde{s}(a)e^{\xi t}, \tilde{i}(a)e^{\xi t}, \tilde{p}(a)e^{\xi t}, \tilde{c}(a)e^{\xi t})$ near the steady-state solution $E_0$, i.e.,

where $\xi$ is a real or complex number, and

By substituting (4.3) and (4.4) into System (2.6), it follows that $(\tilde{s}(a), \tilde{i}(a), \tilde{p}(a), \tilde{c}(a))$ will satisfy the conditions of the following linearized system:

The value of $U$ in (4.4) is obtained by solving System (4.5). Considering System (4.5), we get

Substituting (4.7) and (4.9) into $U$, we have

We can rewrite (4.10) by applying $U = U\hat{Q}(\xi)$, where

Note that $U = U\hat{Q}(\xi)$ is equivalent to $U(1-\hat{Q}(\xi)) = 0$. The solution of this equation is $U = 0$ or

Solution $U = 0$ shows the existence of the infection-free steady-state solution. Meanwhile, $\hat{Q}(\xi) = 1$ corresponds to the characteristic equation. Considering (4.11), we have

Now, we will show the relationship between $\xi$ and $\hat{Q}(0)$ to determine the conditions of $\xi$ that satisfy (4.12).

Lemma 4.1. Let $\xi$ satisfy $\hat{Q}\left(\xi \right) = 1$.

(1) If $\hat{Q}(0) > 1$, then $\xi > 0$,

(2) If $\hat{Q}(0) < 1$, then $\xi < 0$.

We use the reductio ad absurdum method to prove Lemma 4.1. By using Lemma 4.1, we show that the threshold criterion of $\hat{Q}(\xi) = 1$ is valid, and we can define the basic reproduction number as follows:

See ^[28,29] for the detailed method. Biologically, the value of $R_0$ represents the average number of secondary infections by HPV that are produced by one single infected cell or cancer cell during the period of infection, assuming that all other cells in the population are uninfected.

4.2.   Local stability analysis for infection-free steady-state solutions

The first step in analyzing the stability of an infection-free steady-state solution is to show that (4.12) has only one real solution.

Lemma 4.2. If $0 < {\varepsilon}_{1} \ll 1$, $\varepsilon_{0}, \xi, \Lambda > 0$, and the functions $h(a), \lambda(a), \delta(a), \gamma(a)$ are continuous, positive and defined in $a_1 < \tau < w < \nu < b < a_\sigma$, then $\hat{Q}'\left(\xi \right) < 0$, $\lim\limits_{\xi \to \infty } \hat{Q}\left(\xi \right) = 0$, and $\lim\limits_{\xi \to -\infty} \hat{Q}\left(\xi \right) = \infty$.

Proof. Let $\xi$ be a real number; then, we obtain

where $\tau < b$. Furthermore, $\lim\limits_{\xi \to \infty} \hat{Q}\left(\xi \right) = 0$ and $\lim\limits_{\xi \to -\infty} \hat{Q}\left(\xi \right) = \infty$.

According to Lemma 4.2, the function $\hat{Q}\left(\xi\right)$ is decreasing monotonically. It implies that the characteristic Eq (4.12) has a real solution and it is unique, denoted by $\xi^*$. Next, we will show that (4.12) has a dominant root, where the real part of the other roots are smaller than $\xi^*$.

Lemma 4.3. If $\xi^*$ is the root of (4.12), then $\xi^*$ is the dominant root.

Proof. Suppose that ${{\xi }^{**}} = x+iy$ is a complex root of (4.12); hence, $\xi^{**}$ satisfies (4.12). Then

By equating the real and imaginary parts, we observe that

According to Lemma 4.2, for ${\hat{Q}}'\left(\xi \right) < 0$, we acquire that $\hat{Q}\left({{\xi }^{*}} \right) \le \hat{Q }\left(\operatorname{Re}{{\xi }^{**}} \right)$. Therefore, we obtain that $\operatorname{Re}{{\xi }^{**}} \le {{\xi }^{*}}$.

Theorem 4.1. The infection-free steady-state solution $E_{0} = \left(1, 0, 0, 0 \right)$ is locally asymptotically stable if $R_{0} < 1$, and it is unstable if $R_{0} > 1$.

Proof. If $R_{0} > 1$, according to Lemma 4.1, it follows that $\hat{Q}(0) > 1$. Considering Lemma 4.2, let the unique real value root of (4.12) be denoted as $\xi^*$, which further implies that ${\xi}^* > 0$. Since the characteristic equation has a positive root, the infection-free steady-state ($E_{0}$) is unstable.

On the other hand, if $R_{0} < 1$, it follows that $\hat{Q}(0) < 1$ according to Lemma 4.1, and the root of (4.12) is real and negative. Let us assume that the root of the characteristic equation is $\xi^*$. Then, we have that ${\xi}^* < 0$. Since, as per Lemma 4.3, ${\xi}^*$ is the dominant root of (4.12), the infection-free steady-state ($E_{0}$) is asymptotically stable.

4.3.   Global stability analysis for infection-free steady-state solutions

The term "clearance" is used when HPV can be eliminated from the tissue. This can be numerically modeled if the initial value of each subpopulation is in the basin of attraction at $E_{0}$. It means that a global stability analysis needs to be carried out around $E_0$ to determine the conditions that must be obtained for HPV clearance to occur.

In order to demonstrate the global stability of $E_{0}$, it suffices to show that, as time $t$ approaches infinity, $s\left(a, t\right)$ approaches 1, while $i\left(a, t\right)$, $p\left(a, t\right)$, and $c\left(a, t\right)$ all approach 0. Equation (2.5) can be rewritten as ${{\beta }^{*}}\left(a, t \right) = \lambda \left(a \right)B\left(t \right)$, where

Recall that we use $\bar{\varepsilon}(a) = \varepsilon_0 (1+\varepsilon_1\cos(2\pi a))$ for convenience. Considering (4.14), System (2.6) can be solved for $a < t$ as follows:

Substituting (4.16) and (4.18) at $E_0$ into (4.14), we obtain

Applying the supremum limit $t \to \infty$, we get

Let $V\left(a \right) = \lambda \left(a \right)\underset{t\to \infty }{\mathop{\lim \sup }}\, B\left(t \right)$; then,

where

By applying (4.19) and (4.20), we have

Given (4.13), we note that (4.21) is equivalent to $C_1\le C_1 R_0$. Hence, it can be rewritten as $C_1(1-R_0)\le 0$. We maintain the last inequality to show global stability around the infection-free steady-state through Theorem 4.2.

Theorem 4.2. If $R_{0} < 1$, then the infection-free steady-state $E_{0} = \left(1, 0, 0, 0 \right)$ is globally asymptotically stable.

Proof. Since $R_ 0 < 1$, for the inequality $C_ 1(1-R_ 0)\le 0$ to be satisfied, it must hold that $C_1 = 0$. It follows that $V\left(a \right) = 0$. As a consequence, we obtain that $\underset{t\to \infty }{\mathop{\lim \sup }}\, B\left(t \right) = 0$. Therefore, we acquire that at $E_0$, the $\lim\limits_{t\to \infty } i\left(a, t \right) = \lim\limits_{t\to \infty } p\left(a, t \right) = \lim\limits_{t\to \infty } c\left(a, t \right) = 0$ and $\lim\limits_{t\to \infty } s\left(a, t \right) = 1$, as required.

We have analyzed the stability when $J = 0$, that is, in an infection-free steady-state $(1, 0, 0, 0)$. This means that there are only susceptible cells in the tissue. We analyze the condition for $J > 0$ and its stability in the following subsections.

4.4.   Existence of endemic steady-state solution

The endemic steady-state solution is obtained by solving System (4.1). Let $E_1 = \left({{\hat{s}}^{*}}\left(a \right), {{\hat{i}}^{*}}\left(a \right), {{\hat{p}}^{*}}\left(a \right), {{\hat{c}}^{*}}\left(a \right) \right)$ be the endemic steady-state solution. System (4.1) can be considered as a system of first-order ordinary differential equations in $a$. Therefore, by multiplying each equation by a specific integration factor and performing simple algebraic calculations, we obtain the solution $E_1$ given by (4.22)–(4.25):

The solution of $E_1$ exists if ${{\hat{s}}^{*}}\left(a \right), {{\hat{i}}^{*}}\left(a \right), {{\hat{p}}^{*}}\left(a \right)$, and ${{\hat{c}}^{*}}\left(a \right)$ are positive. We can see that (4.22) is always positive. The solution $\hat{i}^*(a)$ in (4.23) is positive for $J$ that is positive. Moreover, $\hat{p}^*(a) > 0$ and $\hat{c}^*(a) > 0$ if $\hat{i}^*(a) > 0$. Therefore, it is necessary to find biologically meaningful conditions for the positive value of $J$. Now, substituting $\hat{i}^*(a)$ in (4.23) into $\hat{p}^*(a)$ in (4.24), we can substitute the resulting $\hat{p}^*(a)$ into $\hat{c}^*(a)$ in (4.25); then, (4.2) becomes as follows:

We denote that

Considering (4.26), (4.27) can be rewritten as $J = J\hat{Q}(J)$ or $J(1-\hat{Q}(J)) = 0$. Thus, we have that $J = 0$ or

Note that, using (4.27), we obtain

By applying (4.13), we can see that $\hat{Q}(0) = R_0$. On the other hand, since $\hat{i}^*(a)+\hat{c}^*(a) < 1$, then

If $\int\limits_{a_1}^{a_\sigma} h(b)db = h^+$, then $J\hat{Q}(J) < h^+$. In particular, if $J = h^+$, we have that $h^+\hat{Q}(h^+) < h^+$, which means that

The existence of a positive endemic steady-state can be summarized as follows. Since we require the necessary condition of existence of the endemic steady-state, we will determine the condition for $J$ to be positive. Considering (4.28), we have that $\hat{Q}(J) = 1$. It is noteworthy that $\hat{Q}(0) = R_0$ and the function $\hat{Q}(J)$ is monotonically decreasing. By (4.29), we find that $\hat{Q}(h^+) < 1$. Therefore, the equation $\hat{Q}(J) = 1$ will have a positive intersection if $\hat{Q}(0) = R_0$ is greater than 1. The proof of this condition is in Lemma 4.4, and we note that (4.29) is the inequality used to prove Lemma 4.4.

Lemma 4.4. If $R_0 > 1$, then the endemic steady-state exists.

Proof. Since $R_0 = \hat{Q}(0) > 1$, (4.29) states that $\hat{Q}(h^+) < 1$, and $\hat{Q}(J)$ is continuous, then the solution of (4.28) is $J > 0$. Furthermore, for $J > 0$, the solution that satisfies the steady-state system (4.1) is $({{\hat{s}}^{*}}\left(a \right), { {\hat{i}}^{*}}\left(a \right), {{\hat{p}}^{*}}\left(a \right), {{\hat{c}}^ {*}}\left(a \right))$, as given by (4.22)–(4.25).

4.5.   Local stability analysis for endemic steady-state solutions

Stability analysis will be discussed by using the perturbation approach and using the exponential solutions $(\tilde{s}^*(a)e^{\xi t}, \tilde{i}^*(a)e^{\xi t}, \tilde{p}^*(a)e^{\xi t}, \tilde{c}^*(a)e^{\xi t})$ near the steady-state solution $({{\hat{s}}^{*}}\left(a \right), {{\hat{i}}^{*}}\left(a \right), {{\hat{p}}^{*}}\left(a \right), {{\hat{c}}^{*}}\left(a \right))$, as follows:

where $({{\hat{s}}^{*}}\left(a \right), {{\hat{i}}^{*}}\left(a \right), {{\hat{p}}^{*}}\left(a \right), {{\hat{c}}^{*}}\left(a \right))$, as shown in Lemma 4.4. We obtain

where

Using (4.30)–(4.32), the functions $(\tilde{s}^*(a), \tilde{i}^*(a), \tilde{p}^*(a), \tilde{c}^*(a))$ will satisfy the conditions of the following linear system:

Since $U^* \ne 0$, to simplify the analysis, we can apply the following ratio:

Furthermore, (4.32) becomes

and we obtain the following system:

The solution of System (4.34) is given by

The value of $\bar{s}(a)$ is negative if ${{\varepsilon }_{0}}(1+{{\varepsilon }_{1}}\cos 2\pi a)\bar{p}(a) < \lambda (a)$. It can be interpreted that, if the immunotherapy treatment parameter is less than the virus infection parameter, then an endemic condition appears in the tissue. To simplify the function in subsequent calculations, (4.36) can be substituted into (4.37); we get

If we substitute the solutions of $\bar{i}(a)$ and $\bar{c}(a)$ into (4.33), we obtain $\bar{Q}(\xi)$ on the right-hand side of (4.33). Then, if we further substitute $\bar{s}(a)$ from (4.35) into $\bar{Q}(\xi)$, we obtain

If $\Psi (b, w) = {{e}^{-\int\limits_{w}^{b}{\left(\delta \left(j \right) \right)dj}}}-J\int\limits_{{{a}_{1}}}^{w}{\lambda (\tau){{e}^{-\int\limits_{\tau }^{w}{(\lambda (j)J-{{\varepsilon }_{0}}(1+{{\varepsilon }_{1}}\cos 2\pi j){{{\hat{p}}}^{*}}(j))dj}}}}{{e}^{-\int\limits_{\tau}^{b}{\delta \left(j \right)dj}}}d\tau$ and we let

and

then

Thus, $\bar{Q}(\xi)$ can be written as follows:

where

Lemma 4.5 proves that $\bar{Q}(\xi)$ is a monotonically decreasing function. We prove that the first derivative of $\bar{Q}(\xi)$ is negative, $\bar{Q}(\xi)$ goes to zero as $\xi$ tends to infinity, and $\bar{Q}(\xi)$ goes to infinity as $\xi$ tends to negative infinity.

Lemma 4.5. If $L_1(w) < 0$ and $F (b, w)\ge 0$, then ${\bar{Q}}'(\xi) < 0, \underset{\xi \to \infty }{\mathop{\lim }}\, \bar{Q}(\xi) = 0$, $\lim\limits_{\xi \to -\infty} \bar{Q}(\xi) = \infty$, and $\bar{Q}(0) < 1$.

Proof. We will prove the first statement. If $F(b, w)\ge 0$, then $\bar{Q}(\xi)\ge 0$ and

since $b > w$. For the second statement, it is easy to see that ${\bar{Q}}'(\xi) < 0, \underset{\xi \to \infty }{\mathop{\lim }}\, \bar{Q}(\xi) = 0,$ and $\lim\limits_{\xi \to -\infty} \bar{Q}(\xi) = \infty$. Now, we will prove that $\bar{Q(0)} < 1$. By applying (4.40), we have

Moreover, by applying (4.28), we notice that the two-first integrals are equal to one. Thus, $\bar{Q}(0)$ can be written as

Since $\bar{s}(a) < 0$ and $L_1(w) < 0$, then $\bar{Q}(0) < 1$.

Theorem 4.3. If $R_0 > 1$, then the endemic steady-state is locally asymptotically stable.

Proof. By applying Lemma 4.4, we found that the endemic steady-state exists for $R_0 > 1$. Lemma 4.5 guarantees that $\bar{Q}(\xi)$ is a monotonically decreasing function such that $\bar{Q}\left(\xi \right) = 1$ has a unique real root. On the other hand, considering Lemma 4.5, for $\bar{Q}(0) < 1$, we obtain $\xi < 0$ as the negative real root. The appearance of this negative real root means that the endemic steady-state of System (2.6) is locally asymptotically stable.

5.   Numerical simulation for fixed values of parameters

In this simulation, we investigate the model in a constant scenario. This indicates that all parameters have fixed values. We used the parameter values shown in the Table 1. In this case, different values of $h$ produce different values of $R_0$. Recall that $h$ denotes the infection rate associated with susceptible cells being transformed to infected cells; the larger the value of $h$, the larger the value of $R_0$.

Figures 2a and 2b align with Theorem 4.1, which states that the solution is an infection-free steady-state solution if $R_0 < 1$. According to Figures 2c and 2d, the solution tends to the endemic steady-state solution if $R_0 > 1$, which is in line with Theorem 4.3. In this work, immunotherapy was applied as the treatment to reduce precancerous cells to control the endemic condition. In Figure 3, the graph for $\varepsilon_{0} = 0$ illustrates the density of precancerous cells when no immunotherapy treatment has been given. When the cell age is between 0 and 10, there is a significant increase in the density of precancerous cells. This is consistent with the fact that HPV will damage cells when cells are in the initial phase of their cycle, namely, between the $G_1$ and $S$ phases ^[32].

For this reason, it is hoped that immunotherapy can suppress the growth of precancerous cells. According to the Lemma 4.4, an endemic steady-state condition is defined if $R_0 > 1$. Furthermore, according to Theorem 4.3, the endemic steady-state conditions are locally asymptotically stable. It can be interpreted analytically that precancerous cells are still present in the cervical tissue. Figure 3 shows that precancerous cells are still present when $\varepsilon_{0} = 0.0801$. However, the density is less than the case without therapy. When $\varepsilon_{0} = 0.09$ (larger than before), the density of precancerous cells decrease even more. The precancerous cell population remains in cervical tissue, as indicated for $\varepsilon_{0} = 0.123$. Precancerous cells are not entirely eliminated since the $R_0$ value is still larger than one.

Moreover, as $h$ increases, more susceptible cells become infected. Thus, it can be seen in Figure 4a that a larger $\varepsilon_0$ is required through greater T-cell proliferation. If the infection rate for susceptible cells is $h = 0.5625$ and the effects of immunotherapy on T-cell proliferation is represented by $\varepsilon_{0} = 0.0179$, then the infected, precancerous, and cancerous cells decrease rapidly, as shown in Figure 4b.

When $R_0 = 1$, the dynamical behavior is related to the characteristic root, which has a value of zero. However, working directly with $R_0$ can be complicated, so it is straightforward to observe the parameters that form $R_0$. In this case, we chose to use the parameter $h$ to form $R_0$ and then determine the value of $h^*$ that makes $R_0 = 1$. On the other hand, the characteristic root is correlated with $J$ in (4.2). If $J = 0$, then the system is in an infection-free steady-state condition, while, if $J > 0$, the system is in an endemic steady-state condition. To illustrate, we have provided Figure 5, which shows that $h^* = 0.079$ results in $R_0 = 1$. We also show in Figure 6 that a value of $h$ less than or more than $h^*$ causes the behavior of precancerous and cancer cells to change significantly.

6.   Concluding remarks

We propose a new mathematical model of age-structured development of cervical cancer cells. We consider an age-dependent immunotherapy treatment for the precancerous cell population. Regarding the basic reproduction number, we have examined the existence and stability of the infection-free and endemic steady-states. Determination of the basic reproduction number in this work began by proofing Lemma 4.1. Lemma 4.1 provides some insights into the threshold value of the basic reproduction number, which is important for the stability analysis of the model.

The value of $R_0 = 1$, as shown in Figure 5, can be observed as a bifurcation point since it marks the boundary between two distinct behaviors. It could happen due to the changes in stability. For this value of $R_0$, we will have a degenerate case in which linearization near the infection-free steady-state condition yields a characteristic equation with a zero root. Intuitively, the endemic steady-state is forwardly bifurcating from the infection-free steady-state at $R_0 = 1$; see ^[23,33].

The results of the theoretical analysis and numerical simulation of the model suggest that immunotherapy is more effective in the initial precancerous phase. Significant changes in precancerous cell population behavior occur when the cell age is between 0 to 10. This means that the simulation results provide valuable insights into the behavior of precancerous cells and the effectiveness of immunotherapy in the early phase of its cycle, namely, the $G_1$-to-$S$ phase.

In a previous model ^[14], the effects of representing immunotherapy treatment as a periodic function were examined. However, the model did not specifically provide the therapy based on cell age. On the other hand, the models in ^[7,9] were related to age structure, but the authors did not discuss the provision of therapy. In contrast, in this research, we indicate that administering therapy based on cell age is a promising approach that can lead to more optimal results. This study clearly demonstrates the potential benefits of administering therapy based on cell age, especially in the early phase. Therefore, if immunotherapy drugs are given when precancerous cells are in this phase, there is a high probability of success of immunotherapy. One way to see if a cell is in a particular phase of its cycle is to employ flow cytometry, which uses light scattering.

However, our work does not take into account some considerable findings, i.e., optimal control, cervical cancer metastasis condition, and uniform persistence analysis. The concept of persistence in dynamical systems is of significant importance; see ^[34]. Persistence is referred to as the long-term survival of some or all system components when predicting the behavior of systems. Although we have not addressed this here, it could be addressed in future research.

Moreover, in this research, immunotherapy term involved the assumption of T-cells as immune cells. Naturally, T-cells have the ability to remember past infection by pathogens upon subsequent exposures. On the other hand, by allowing the derivative order to be a non-integer value, fractional derivatives can capture the influence of past states and events on the current state of the system. Therefore, fractional derivatives can be used to model the dynamics of immune cells, including the memory response; see ^[35,36] for detailed explanations. Hence, for further research, the HPV infection model with immunotherapy can be developed with fractional derivatives.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The first author would like to express gratitude to the Indonesian Endowment Fund for Education (LPDP) Indonesia for awarding the Doctoral scholarship. All authors extend their appreciation to Universitas Gadjah Mada for partially funding this work through "Rekognisi Tugas Akhir" 2023, with the assignment letter number 5075/UN1.P.II/Dit-Lit/PT.01.01/2023.

Conflict of interest

The authors declare that they have no conflict of interest.