Existence, and Ulam's types stability of higher-order fractional Langevin equations on a star graph

1.   Introduction

A chaotic system is a complex nonlinear dynamical system characterized by high dynamic complexity. It possesses excellent characteristics such as sensitivity to initial values, ergodicity, non-periodicity, long-term unpredictability and pseudo-randomness. These attributes have led to the wide application of chaos theory across various disciplines and fields for a long time ^[1,2], including physics ^[3,4,5], mathematics ^[6,7,8], engineering ^[9,10,11], economics ^[12,13,14] and computer science ^[15,16]. Besides, due to its natural resemblance to confusion and diffusion in cryptography, the application of chaos to encryption algorithms was proposed by Mathews ^[17] in 1989. Numerous chaos-based encryption algorithms have been developed and popularized since then ^[18,19,20].

There are currently two primary methods to realize chaotic systems. One is simulated chaotic systems ^[21], i.e., continuous chaotic systems implemented on analog circuits and modeled by ordinary differential equations. The performance of such simulations can be more susceptible to environmental factors, potentially leading to instability and slow responsiveness. The second method is realization on finite precision devices, such as computers, where chaotic systems can be described by discrete iterative equations, known as digital chaotic maps. However, this approach has a limitation due to the confined state space of finite-precision devices. During the realization of a chaotic map, motion trajectories will eventually enter a loop, leading to a significant weakening of various chaotic properties. This phenomenon, known as chaotic dynamic degradation, renders the degraded chaotic map unsuitable for designing cryptosystems. To address the issue of degradation in digital chaotic map dynamics, researchers have proposed numerous different methods ^[8,22].

Nowadays, there are several effective approaches to address the issue of degradation. Primarily, it is very effective to increase the precision of the device ^[23]. Greater precision implies that the simulation of the chaotic map is more fitting, making it harder to degenerate into loops. However, the need for high-precision equipment can lead to higher implementation costs, and it is also not easy to control the trajectory cycle of the chaotic map. The second approach to address degradation is to increase the dimensionality ^[21,24]. High-dimensional chaotic maps typically offer better resistance to chaotic dynamics degradation compared to their low-dimensional counterparts, thanks to their inherent dimensional and complexity advantages. In ^[24], a method for constructing an N-dimensional chaotic system is introduced. This method uses a one-dimensional chaotic map as the foundational seed to generate chaotic maps of any dimension. One of its key benefits is its resistance to transmission noise. Meanwhile, ^[21] introduces a 3-dimensional logistic map. This map is combined with the analog-digital hybrid chaotic (ADHC) system to counteract the degradation of dynamics. However, solutions for high-dimensional chaotic maps tend to be specialized for specific chaotic maps. Consequently, this method is less universal and challenging to apply to chaotic maps outside of a specific set. As a third approach, some researchers suggest using feedback control ^[3,25] to address the degradation of chaotic dynamics. The core principle of this approach involves adding a state feedback control function to the original chaotic map. In ^[3], a solution is presented using an enhanced minimal antithetic integral feedback controller (AIFC) scheme. This solution aims to determine if sustained non-periodic oscillations can coexist when such a regulator circuit implements Robust perfect adaptation (RPA). However, even with feedback control, the chaotic map remains deterministic. As a result, this method might not be sufficiently effective in rectifying the degradation of chaotic dynamics. Another approach to address this bottleneck is introducing external perturbations, as suggested in ^[26,27,28]. In ^[28], new chaotic system trajectories were derived from the trajectory errors of three chaotic systems with distinct initial values, making it challenging for attackers to decipher. However, in related studies where perturbation sources are essential, these new systems tend to be dominated by the perturbation sources. Introducing additional perturbation sources also results in a rise in application costs. Finally, coupling chaotic systems to delay the degradation is also an effective method, such as the methods in ^[29,30,31], where new chaotic models are derived by coupling multiple chaotic maps. However, while simply coupling the chaotic system does increase its complexity, it doesn't address the chaotic degradation that arises due to the condition x_p = x_q within the constraints of finite precision.

After evaluating the strengths and weaknesses of the aforementioned methods, this paper introduces a digital chaotic map model that employs both delayed feedback and coupling to enhance the chaotic dynamics in the face of finite precision. This model, called the delayed exponent coupled chaotic map (DECCM), amalgamates the benefits of both strategies. It's versatile enough to be expanded beyond two dimensions and can incorporate any one-dimensional map as the seed to produce a novel chaotic map. This sets it apart from some recent solutions that restrict either the dimensionality or the types of mappings, as seen in ^[30,32]. Importantly, our model preserves the phase space of the seed map. This indicates that in contrast to methods in ^[21,24], our approach isn't aimed at diminishing the dynamics of the original chaotic map by introducing a new stochastic source. Instead, we seek to improve them. And after various experimental results, it has been proved that the proposed scheme effectively improves the dynamic degradation observed in chaotic maps with lower precision. Here are the main innovations of this paper:

(1) The proposed model effectively addresses the degradation of chaotic dynamics caused by implementing a chaotic map on finite precision devices. Both the number of iterations before first entering a cycle and the period of the cycle substantially outperform other leading remedial schemes. Even if a sub-dimension is caught in a cycle it has little effect on the other sub-dimensions.

(2) The scheme demonstrates broad applicability as it can extend any number of one-dimensional maps into delayed coupled maps of higher dimensions, while maintaining excellent characteristics of chaotic dynamics.

(3) The ability of the scheme to maintain fairly stable high entropy values at all precision implies its excellent stochasticity.

The remainder of this article is organized as follows: In Section 2, we introduce the proposed generalized model DECCM aimed at mitigating the degradation of chaotic dynamics. Section 3 showcases the advantages of DECCM by contrasting it with alternative solutions using various tests, including trajectories and sensitivity analysis, period analysis, bifurcation diagrams, phase space, lyapunov exponent, entropy analysis, auto-correlation analysis and correlation dimension, among others. To demonstrate the applicability of DECCM to different seed mappings, Section 4 provides a new 3D chaotic map as an example; the new system also undergoes the same tests detailed in Section 3. We conclude the paper in Section 5, summarizing our findings and discussing potential directions for future research.

2.   A novel N-dimensional delayed exponent coupled chaotic map

The mathematical model of a chaotic map can be described as:

where x_i denotes the state variable, r is the control coefficient, f is the iterative function. With appropriate selection of control coefficient r, the map f will be chaotic, with rich dynamic behaviors and high sequence complexity. However, once the map f is realized on a finite precision device, it will suffer dynamical degradation, the mathematical model of which can be written as:

Here, FL[] is the precision function that limits the state space. With the control of function FL[], the trajectory of map f will enter a cycle inevitably, and its dynamical charactersitics will deteriorate rapidly. Thus, this kind of digital chaotic map cannot be regarded as mathematical chaos anymore, which is not suitable for cryptographic applications. Therefore, in order to reduce the dynamical degradation of the digital chaotic map, in this section, a delayed exponent coupling chaotic map is proposed.

The tendency of a chaotic map to enter a cycle stems from the possibility of encountering x_p = x_q (0 < p < q < M, M is the length of the chaotic map) during the iteration of the mapping with limited precision. When this occurs, and other parameters remain unchanged, the system inevitably falls into a loop. To counteract this, we initially introduce a delayed feedback term k × x_i-1 to Eq (2). This ensures that if x_p = x_q arises, the delayed term will make the necessary corrections to prevent the system from looping. The mathematical representation is detailed below:

Subsequently, we expand the Eq (3) to two dimensions to augment the system's complexity and dynamics. To prevent the system from converging after numerous iterations, we incorporate the exponential function e^x, known for its divergent nature, to couple with the other dimension. At the same time, the other dimension is also added with the delay feedback term. Concurrently, we employ the modulus function mod to ensure the entire system remains bounded. The comprehensive system can be articulated as:

Now, we can advance to extending the system across N dimensions to get the generalized model called the delayed exponent coupled chaotic map, whose mathematical model can be written as:

Here, ${x}_{i}^{\left(j\right)}$ denotes the state variable of sub-map j, 1 < j ≤ N, and i is the iterative step. k₁, k₂, ..., k_N are the control coefficients. And f_j can be chosen to be any one-dimensional map. In this model, the delayed state of sub-map j+1 is coupled to the sub-map j. The e exponent function ${e}^{{x}_{i-1}^{j+1}}$ is used to make the system diverge and the modular function mod is to make the system bounded. Both divergence and boundedness can make the system present complex chaotic behavior. In order to further improve its chaotic characteristics and reduce the dynamical degradation, a linear delayed feedback control function ${k}_{j}\times \left({x}_{i-1}^{\left(j\right)}+{x}_{i-1}^{\left(j-1\right)}\right)$ is used in this model.

This delayed exponent coupled chaotic map has good dynamical properties, its output sequence has high complexity, and it is able to reduce dynamical degradation even with a low computing precision. A series of numerical experiments will be provided in the next section to prove the effectiveness of this new chaotic model.

3.   A two-dimensionality example of the DECCM

Theoretically, the DECCM is valid for any dimension with N ≧ 2. In this section, the dimension N is selected to be 2 as an example of DECCM, whose mathematical models are described in Eq (6).

In order to demonstrate the validity of the DECCM, we select f₁ and f₂ as the logistic map, the mathematical model of which can be described as Eq (7). Then various tests are performed to verify its dynamic behavior. If no additional explanation is stated, the initial values, parameters and the computing precision p are selected as x₀ = 0.2147, x₁ = 0.3257, y₀ = 0.2579, y₁ = 0.6547, k₁ = 0.4, k₂ = 0.8, r₁ = 3.99, r₂ = 3.98 and p = 2^-12.

In addition, to enable a visual comparison, some of the test results will be compared with a logistic map having limited precision. The mathematical model for this comparison is expressed as

where the initial value and parameters are chosen as x₀ = 0.12567, r = 3.98, respectively, if no additional explanation is stated.

3.1.   Trajectories and sensitivity analysis

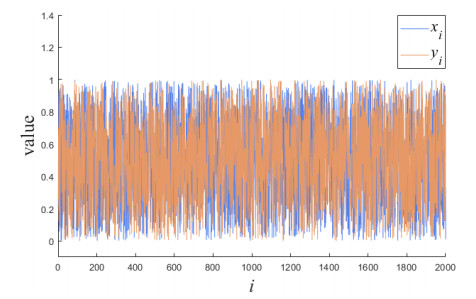
Trajectory diagrams offer a straightforward insight into the traversal characteristics of chaotic systems and the presence or absence of cycles. The trajectory plotted in Figure 1 illustrates that the x and y dimensional variables in Eq (6) all follow highly random trajectories, with no discernible cyclic structure. Figure 2(a) shows that in the precision limit of the 2^-12 case the logistic map falls into a loop after only about 50 iterations. In contrast, Figure 2(b) demonstrates that our scheme avoids entering the loop even after 5000 iterations. These experiments imply that our method effectively mitigates the degradation of the dynamics resulting from limited precision. We will conduct more detailed experiments in the period analysis section later on.

Sensitivity to the key (initial condition) is a characteristic of an ideal chaotic system, implying that even a minor change in the initial parameters can result in a substantial deviation in the chaotic trajectory. In this case, we opt to alter the initial conditions by 2^-12 to observe the changes in the x-dimensional trajectory. As shown in Figure 3, this slight error in the initial values leads to a divergence from the original trajectory after only a a small number of iterations. This indicates that the model is highly sensitive to initial conditions and is unpredictable in the long term.

3.2.   Period analysis

Currently, when using computers to simulate chaotic systems, the limited precision of the hardware may cause chaotic simulations to enter cycles, leading to a degradation in their chaotic dynamics. When evaluating the periodicity of a digital map, two aspects must be considered: the number of iterations required to first enter the cycle, and the length of the cycle once it has been entered. In this experiment, the length of each generated sequence is set to 200,000 of Eqs (6) and (7). Then we select a random set of 200 secret keys (initial conditions) within the parameter range and sequentially adjust the precision limit from 2^-6 to 2^-16. This adjustment will be used to compute both the average number of iterations required for the first entry into the period and the average length of the cycle period. The results are presented in Table 1. It can be seen that the number of iterations and the period length required for both chaotic systems to enter the cycle for the first time are enhanced with the increase in precision, which proves the effect of precision on the degradation of the dynamics of chaotic systems. Specifically, the number of iterations required for Eq (6) to enter the cycle for the first time is much larger than that of the logistic map, and this difference grows almost exponentially. Moreover, the magnitude of Eq (6)'s cycle period is also significantly larger than that of the logistic map. It's worth mentioning that this method starts to fail to detect loops at precision greater than 2^-15. This requirement for less precision contrasts with the precision 2^-20 required by ^[26] and the precision 2^-36 required by ^[30]. These results highlight DECCM's significant effect on mitigating the degradation of chaotic dynamics.

3.3.   Bifurcation diagram

The bifurcation diagram illustrates the relationship between chaotic properties and control parameters. It enables the analysis of how system performance changes with parameters, particularly highlighting the abrupt alterations in system behavior under critical parameters. Figure 4 displays the bifurcation diagrams of the x-dimensional variables in response to the changes in k₁ and k₂. It demonstrates that even when k₁ and k₂ are selected within a broad parameter range [0, 20], there is no non-chaotic domain in Eq (6). This confirms that the chaotic properties of the DECCM are sufficiently stable.

3.4.   Phase space

A strange attractor represents a set of values to which a system tends to evolve. In chaotic systems, strange attractors often manifest, and they are characterized by fractal structures. The strange attractors of Eqs (6) and (7) are evident in the phase space plotted in Figure 5 (with the precision limited as 2^-12 and 2^-30). In Figure 5(f), the phase space graph of the high precision limited logistic map displays a distinct inverted U-shape, but it is not very obvious at low precision. Figure 5(a) and (b) show that it does not completely destroy the phase space structure of logistic map, but has some visualization structure similar to it. In addition, the phase space of Eq (6) is much more widely distributed, encompassing almost the entire region, regardless of the precision. The results of this experiment show that the system does not completely destroy the chaotic attractor of the original mapping and exhibits a characteristic chaotic fractal structure.

3.5.   Lyapunov exponent

In practical terms, the Lyapunov Exponent (LE) can serve as an indicator to ascertain whether a system is chaotic ^[33]. A chaotic system exhibits at least one positive LE, distinguishing it from other stochastic systems. Additionally, the larger the LE value, the more pronounced the chaotic characteristics become. We have configured the parameters k₁ and r in Eqs (6) and (7) to fall within the range of (0, 4], with a step size of 0.1 for the LE analysis. It can be seen that in Fig. 6, over the entire parameter range, the LE of the logistic map is positive when r is approximately greater than 3.57. On the contrary, the result illustrates that even when the parameter k₁ is varied across a broad range, our scheme consistently yields positive LE values. In comparison, our scheme has better chaotic performance over a wider range. This serves as sufficient evidence to validate the excellent chaotic characteristics of DECCM.

Furthermore, we compare the x-dimensional LEs of Eq (6) with the 2D Logistic-Sine map (initial value is set as x₀ = 0.2147, y₀ = 0.2579, p₁ = p₂ = 50) in ^[21] and 3D logistic map (initial value is set as x₀ = 0.1, y₀ = 0.2, z₀ = 0.3, x₁ = 0.2, y₁ = 0.2, z₁ = 0.2, a = 1, b = 2.5, c = 4, λ = 1, ρ = 2, σ = 3) in ^[24] for improving chaotic degradation of logistic maps at different precision (2^-6 to 2^-14). It can be seen from Figure 7 that the LE of Eq (6) is not only quite competitive, but even superior to the other remedies when compared to the other schemes (^[21] and ^[24]). This is particularly noticeable at lower precision levels, where Eq (6), with its higher LE, underscores its effectiveness in improving chaotic dynamics degradation.

3.6.   Entropy analysis

Approximate entropy (ApEn) is one of the metrics utilized to gauge the complexity of a time series. A larger ApEn value signifies that the chaotically generated orbits are more intricate, possessing more repetitive structures and exhibiting stronger nonlinear dynamics. Permutation entropy (PE) is a statistical measure that quantifies the complexity of a time series. Different from other measures that focus on the distance between vectors, PE is based on the ordering or displacement of values in a time series rather than the distance between vectors. As such, PE contributes to an understanding of chaotic behavior. Figure 8(a) and (b) show that as k₁ and k₂ are varied in the range [0, 10], the ApEn and PE values of the equation (6) are both positive and essentially stabilized at 1.67 and 0.98, respectively, except for some few cases when k₁ or k₂ = 0. Compared to the logistic map in Figure 8(c) where the entropy values have positive values only in very small intervals, Eq (6) exhibits better chaotic behavior over a larger range of parameters.

Figure 9 also compares the ApEn and PE of various remedies under different precision constraints with that of our scheme. Results indicate that at different precisions (2^-6~2^-18), not only does the ApEn of Eq (6) remain essentially unaffected by changes in computational precision and remain very stable, it also consistently outperforms both ^[30] and ^[31]. In particular, at lower precisions, the PE of Eq (6) is notably higher than that of the model presented in ^[24,30,31]. The results consistently demonstrate that, irrespective of variations in computational precision, our proposed scheme maintains a stable performance, with its ApEn and PE values consistently surpassing those of other comparative methods. This underscores the robustness of our model, emphasizing its superior chaotic behavior and its ability to sustain its unpredictability in comparison to other established methods. These outcomes suggest that our scheme effectively improves the degradation of chaotic dynamics and consistently maintains robust stochastic and dynamic characteristics, even at lower computational precisions.

3.7.   Auto-correlation analysis

The auto-correlation analysis measures the correlation between two-time points in a sequence and is commonly employed to identify periodicity or repetition within the sequence. In the case of a sequence generated by a chaotic system, the auto-correlation should diminish quickly with increasing state intervals. As depicted in Figure 10, the auto-correlation value of Eq (6) is at its peak for the sequence when the interval is 0. As the time interval increases, the value of auto-correlation diminishes swiftly, approaching 0. These findings suggest that the chaotic sequences produced by Eq (6) possess a significant degree of independence, thereby ensuring a high level of randomness.

3.8.   Correlation dimension

The correlation dimension is a common metric used to describe the geometry of strange attractors in chaotic systems and to quantify the self-similarity of chaotic attractors. It serves as a parameter that characterizes the complexity of fractal structures. In this test, we modify the values of k₁, k₂ and k₃ in Eq (6) to observe changes in the correlation dimension and compare it with the original logistic map. Figure 11 reveals that regardless of how the parameters k₁ and k₂ are varied, the correlation dimension of our approach essentially stabilizes around 1.88, which is much larger than that of the logistic map. This observation indicates that the system maintains robustness over a fairly extensive range of parameters, thereby showcasing the favorable chaotic properties of this scheme.

4.   A three-dimensionality example of DECCM and its performance analysis

In the preceding section, to examine the diverse dynamics of the DECCM, we expanded the model to two dimensions and selected two logistic maps as the seed mappings. In this section, to validate the DECCM's generalizability, we expand the model to three dimensions and select three different seed mappings to construct a new chaotic map, 3D logistic-Tent-Sine map (3D-LTS-M). We then assess their performance through a series of experiments.

4.1.   3D logistic-tent-sine map

When we set the dimension in Eq (5) to 3 and select the seed mapping f₁, f₂ and f₃ as the logistic map, tent map and sinusoidal system, respectively, the mathematical model can be described as:

where min function takes the minimum value. If not otherwise specified, the initial parameters are chosen as x₀ = 0.2147, x₁ = 0.3257, y₀ = 0.2579, y₁ = 0.6547, z₀ = 0.0148, z₁ = 0.1356, k₁ = 0.8267, k₂ = 0.5998, k₃ = 0.3141, r = 3.99, u = 1.99, v = 1 and p = 2^-12.

4.2.   Performance analysis of examples

We run performance tests on 3D-LTS-M given in the previous section to demonstrate the model's generalizability. These tests also underscore the model's versatility, its efficacy in mitigating the dynamic degradation of chaotic systems with limited precision and its other dynamic attributes. For ease of visualization, the x-dimension is chosen as the default for experimental observation unless otherwise specified.

4.2.1.   Trajectories and sensitivity analysis

In Figure 12, the x-dimensional iterative trajectories of Eq (8) are presented. Notably, throughout the 10000 iterations, none show signs of degenerating into a cycle even under the precision limit of 2^-8. To further assess their dynamical behavior, we minutely adjusted the initial value k₁ of 3D-LTS-M by a deviation of 2^-12 and plotted the resulting trajectories alongside their original counterparts (with the original trajectories depicted in blue and the modified ones in green) in Figure 13. Remarkably, the motion trajectories of all three dimensions began diverging from their original paths within just 10 iterations. These findings underscore the efficacy of DECCM in curtailing the degradation of chaotic dynamics, all the while preserving its inherent sensitivity to initial conditions.

4.2.2.   Period analysis

In this section, we randomly chose 200 sets of initial conditions for the logistic map, tent map, sine map and Eq (8). Subsequently, we calculated the average number of iterations required for these chaotic maps to enter a cycle for the first time under varying precision (2^-6 ~ 2^-15) constraints and the average value of their cycle periods. Table 2 displays the average number of iterations needed for each chaotic map to enter a cycle for the first time. It's evident that the values for Eq (8) are significantly higher than these seed mappings under arbitrary precision constraints. The enhanced chaotic map effectively delays the average number of iterations needed to enter a cycle initially. Moreover, Table 3 also indicates that the cycle period of 3D-LTS-M surpasses the value of its seed mapping cycle at all precision. After entering the cycle period, the period for Eq (8) increases more rapidly compared to the logistic map, tent map and sine map as precision improves. This further validates the scheme's efficacy in extending the cycle period under precision constraints. Furthermore, Tables 2 and 3 compare the period analysis of the digital logistic map in Eq (8) and ^[26,30,31] at various precisions. The tables demonstrate that, in terms of delaying the entry into a cycle and the cycle length, 3D-LTS-M consistently outperforms ^[30,31] across whatever low or high precision thresholds. Equation (8)-x is also comparable to ^[26] at precision less than 8 and exceeds ^[26] with increasing precision. Additionally, the cycle duration is superior compared to other methods and simultaneously increases as the precision improves. This signifies that even when entering cycles simultaneously, 3D-LTS-M demonstrates enhanced and more secure dynamical characteristics compared to these other methods. The experimental results underscore the substantial efficacy of the proposed scheme in addressing the degradation of chaotic dynamics, particularly when the chaotic map is implemented on hardware with constrained computational precision.

It's noteworthy to observe from the table that the z-dimensional sequence of Eq (8) has never entered a period. This suggests that the chaotic map crafted using DECCM exhibits remarkable stability and robustness. This robustness is evident in the fact that even if certain sub-dimensional mappings descend into a cycle due to precision constraints, other dimensional mappings can sustain for prolonged durations without becoming cyclic, thereby preserving superior chaotic dynamic properties.

4.2.3.   Bifurcation diagram

The bifurcation diagram visually illustrates the route of a chaotic system as it multiplies its cycles toward chaos. It offers a graphic representation of the system's dynamic behavior in response to parameter variations. A complex, densely branched structure within the diagram typically signifies chaotic behavior.

In this study, we set the parameters of 3D-LTS-M such that k₁ = k₂ = k₃ = k. Subsequently, we observe the bifurcation diagram by adjusting the value of parameter k. As depicted in Figure 14, there's a consistent absence of non-chaotic regions and periodic windows throughout the entire parameter space. The bifurcation diagram encompasses nearly the entire space, irrespective of how these parameters fluctuate within the (0, 5] interval. This underscores the robust chaotic characteristics of the model. Remarkably, the parameter k is confined to the (0, 5] range in this experiment, but the range of the parameter in practical applications is much larger than this.

4.2.4.   Phase space

In Figure 15, we present the phase spaces of the three seed mappings at varying computational precisions, providing a visual insight into their singular attractors. Specifically, the digital phase spaces for the logistic map, tent map and sinusoidal system at computational precisions of 2^-12 and 2^-30 are depicted. It is evident from the figure that the phase space of the original digital chaotic map is significantly influenced by precision. At lower precisions, its structural clarity is somewhat diminished.

On the other hand, Figure 16 showcases the phase space of 3D-LTS-M at the same precisions of 2^-12 and 2^-30. From this figure, one can observe that the phase space of the new map, across different precision levels, not only retains elements of the structure of the original seed mapping but also disperses it across a broader area. This not only reaffirms the intent of DECCM to enhance the dynamical properties of the original chaotic map but also underscores that it does not arbitrarily create an entirely novel system. Moreover, while compensating for its shortcomings, the wider phase space implies more complex chaotic properties, increasing the robustness against space decomposition.

4.2.5.   Lyapunov exponent

Figure 17 shows the LEs of Eq (8) at different precision levels. It shows that 3D-LTS-M remains quite stable even at all computational precision and is always greater than 0. This emphasizes the effectiveness of DECCM in mitigating the degradation of the digital chaotic map while keeping the chaotic features at any computational precision.

4.2.6.   Entropy analysis

In this section, we change two parameters of k₁, k₂ and k₃ in Eq (8) as variables. We then compute the ApEn and PE of Eq (8), showcasing the results in Figures 18 and 19, respectively. The data suggests that both ApEn and PE values for 3D-LTS-M consistently remain positive, registering higher values across all parameter ranges. In addition, except for a few cases when k₁, k₂ or k₃ = 0, the entropy values are quite stable and their visual representations remain within a stable plane. These findings effectively demonstrate that the chaotic dynamics of Eq (8) is largely independent of the choice of parameters. These stable high entropy values show the intricate complexity of the random sequences spawned by Eq (8), highlighting their inherent unpredictability. Such results demonstrate the superior long-term unpredictability of the chaotic nature of DECCM.

In addition, Figure 20(a) and (b) illustrate the ApEn and PE values of Eq (8) in comparison to its seed mappings at various computational precisions. From the observations, it is evident that 3D-LTS-M consistently upholds a stable, elevated level for both entropy values across both low and high precision ranges, settling approximately around 1.62 and 0.98, respectively. These values are significantly higher compared to those of several seed mappings. These findings affirm the potency of DECCM in addressing and ameliorating the degradation issues inherent in numerical chaotic dynamics.

4.2.7.   Auto-correlation analysis

In Figure 21, subfigures (a), (b) and (c) depict the x-dimensional, y-dimensional and z-dimensional auto-correlation values for Eq (8), respectively. Like for Eq (6), auto-correlation peaks exclusively when the interval is zero. Meanwhile, as the time interval expands, the auto-correlation value swiftly drops to zero. This indicates that the DECCM is sufficient to improve any one-dimensional mapping into which it is substituted to have significant independence and to improve its stochasticity.

4.2.8.   Correlation dimension

In this section, we assess the correlation dimension of various chaotic maps at a fixed computational precision limit of 2^-12 and set the parameters of 3D-LTS-M such that k₁ = k₂ = k₃ = k. The domain of parameter k is defined from 0 to 10 with an increment of 0.25. The results, presented in Figure 22, reveal that both the logistic and tent maps experience a swift decline to 0 in their correlation dimension when their parameters exceed values of 4 and 2, respectively. Moreover, the correlation dimension for the sine map remains below 0.3 across the entire parameter range. When looking at the correlation dimension of Eq (8), one can see that across an extensive parameter range, all three dimensions of Eq (8) distinctly exhibit higher correlation dimensions and remain around 1.97. This underlines that chaotic maps fashioned using DECCM are endowed with a richer fractal structure across a broad swath of parameters.

5.   Conclusions

Chaotic systems, due to their sensitivity to initial values, long-term unpredictability and other commendable properties, have found applications across a variety of disciplines. However, the limited precision of hardware devices poses a challenge. When simulating chaotic systems with these constraints, we encounter state space limitations, causing motion trajectories to eventually cycle, thereby leading to a decline in the digital chaotic map's intrinsic properties. Consequently, such degraded systems become less suited for many disciplines. In response, we introduce the DECCM model in this paper, which can improve the dynamics degradation of any one-dimensional digital chaotic map, and not only generalize M seed mappings to N dimensions and maintain good dynamic properties, but also effectively solve the chaotic dynamics degradation problem that occurs when the original low-dimensional maps are simulated on finite precision devices. Periodicity, a primary factor contributing to chaotic degradation, is a significant concern in our approach. With DECCM, the number of iterations before entering a period and the period length substantially surpass those of the original seed mappings and some other state-of-the-art remedies. Further experiments confirm the enhanced complexity and chaotic attributes of the improved chaotic map. However, the adaptability of DECCM to high-dimensional chaotic systems requires further exploration, which will be the focus of our upcoming research.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by National Natural Science Foundation of China (62262039); Outstanding Youth Foundation of Jiangxi Province (20212ACB212006); Key Project of Jiangxi Provincial Natural Science Foundation (20232ACB202009).

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.