Separable algebras in multitensor C$^*$-categories are unitarizable

1.   Introduction

1.1.   Motivation and literature survey

Infection with the Hepatitis C virus (HCV) is a major global health concern and a substantial contributor to liver cirrhosis, liver cancer, and chronic liver disease. Chronic HCV infection is believed to be the primary cause of chronic liver disease, which can progress to serious complications such as primary hepatocellular carcinoma (HCC) or cirrhosis. In severe cases, this progression necessitates liver transplantation or can lead to death in some individuals. According to recent data, it is estimated that between $130$ and $170$ million people worldwide are living with chronic HCV infections, highlighting the extensive reach and impact of this virus on global health. The discovery of HCV marked a significant milestone in medical research. It was only in $1989$ that the cause of HCV was discovered using modern genome sequencing and molecular cloning techniques, which allowed for the identification of previously uncharacterized non-$B$ and non-$A$ Hepatitis viruses. As an RNA virus belonging to the Flaviviridae family, HCV is characterized by a limited host population, primarily humans. The HCV has a single-stranded RNA genome approximately $10,000$ nucleotides in length, comprising both structural and non-structural protein-coding regions. Two envelope proteins, $E_1$ and $E_2$, are crucial components of the virus, with the $\frac{E_2}{N S_1}$ region containing a hypervariable area that is key to the virus's ability to evade the host immune system. While structural proteins form the virus's outer shell, non-structural proteins are essential for viral replication. Diagnosing HCV infection involves a multi-step process. The standard method begins with checking for antibodies to detect the presence of the virus. This is followed by measuring HCV RNA levels to confirm active infection and monitor the virus's presence over time. These tests are critical in diagnosing HCV and guiding treatment plans. Following infection, the half-life of infected cells varies significantly, with rates ranging from $1.7$ to $70$ days. This variability suggests that effective treatment requires high doses of interferon-alpha $(\mathrm{IFN}-\alpha)$, between $3$ and $15$ million international units (mIU) per day, to hasten the death of infected cells during early viral load measurements. This dosing strategy aligns with current recommendations for overcoming HCV infection, aiming to reduce viral load and promote recovery. One of the challenges in treating HCV is the virus's rapid mutation rate and high turnover of HCV RNA molecules, which presents an opportunity for early eradication if addressed promptly. Despite advances in treatment, there is currently no vaccine available to protect against HCV infection. However, early intervention with antiviral therapies can significantly improve outcomes. Administering interferon (IFN) in the early stages of treatment, particularly within $89$ days of infection, has been shown to increase the sustained viral response (SVR) rate. Combining ribavirin with IFN therapy results in an SVR rate exceeding $50\%$ during the chronic phase, providing a substantial benefit to patients. Research into the antiviral effects of IFN has revealed that hepatocytes persistently infected with HCV respond to IIFN-$\alpha$ treatment by exhibiting enhanced antiviral activity and inhibition of host RNA translation. Several HCV proteins have been identified as regulators of the IFN response pathway, suggesting a complex interaction between the virus and host immune responses. Understanding these interactions is crucial for developing more effective treatments and overcoming the challenges posed by the virus's ability to evade immune defenses ^[1]. In recent years, researchers have turned their attention to the dynamical analysis of HCV models, seeking to understand the virus's behavior and its impact on infected populations. Mathematical modeling of HCV infection dynamics has become an essential tool in this effort, providing insights into the factors influencing infection spread, treatment efficacy, and disease progression. By incorporating elements of chaos and bifurcation theory, these models offer a deeper understanding of the complex dynamics underlying HCV infections. Discrete models of HCV dynamics, in particular, have garnered interest due to their ability to capture the non-linear behaviors and chaotic patterns observed in the progression of HCV infections. These models examine the local dynamics of the virus, shedding light on how small changes in parameters or initial conditions can lead to significant variations in disease outcomes. By exploring the potential for chaos and bifurcations, researchers aim to identify critical thresholds and tipping points that influence the course of infection and response to treatment. For instance, Li et al. ^[2] have examined the behavior of the following chronic HCV model:

where $T$, $T_1$, $V$, $D$, $D_1$, $C$ are healthy hepatocytes, infected hepatocytes, free virus, non-activated DC, activated DC, and cross-presentation CTL, respectively. Moreover, $r$, $K$, $\kappa$, $\beta_1$, $d_1$, $\gamma$, $\lambda$, $\delta_1$, $\delta_2$, $\eta$, $\beta_3$, $\mu$ are all positive parameters. Rihan et al. ^[3] have investigated bifurcation scenarios of the following HCV model:

where $H$, $I$, $V$ represent the concentration of uninfected, infected hepatocytes, and free HCV cells, respectively, $s$, $\kappa_1$ denote uninfected and infected hepatocytes and the rest are parameters that cause the production or death of hepatocytes. Nangue ^[4] has examined global dynamics of the HCV model:

where $V$, $I$, and $T$ respectively denote free virus, infected, and target uninfected cells. Moreover, $\lambda$, $d$, $\delta$, $\beta$, $p$, $s$, $c$, $\epsilon$, $\eta$ are all positive parameters that represent production and death rate of $T$, $I$, and $V$ cells. Ahmed et al. ^[5] have investigated global dynamics of the HCV model:

where $B$, $\mu$ describe birth and death rates, respectively, and $k$, $b$, $\sigma_1$, $\sigma_2$, $\delta$ are positive parameters. Ntaganda ^[6] has explored the global dynamics of the HCV model:

where $I$ and $H$ stand for infected and uninfected hepatocytes, respectively, at time $t$, $\alpha$ and $\beta$ are model's constants, and $f$, $g$ are functions to be found. Sun et al. ^[7] have explored the dynamics of disease spreading on networks using reaction-diffusion systems. They focused on understanding how diseases propagate through different network structures, analyzing the impact of network topology on the spread and control of infectious diseases. The study employed mathematical modeling to describe disease transmission processes, incorporating elements such as diffusion rates, infection rates, and network connections. The authors used simulations to investigate various scenarios and parameters, revealing complex patterns of disease spread that were highly sensitive to network configurations. Their findings indicated that network heterogeneity played a crucial role in determining the speed and extent of disease outbreaks. They demonstrated that nodes with high connectivity significantly influenced the overall dynamics, often acting as super-spreaders within the network. The authors also analyzed the effectiveness of different intervention strategies, such as targeted vaccinations and quarantine measures, in mitigating disease spread. They concluded that understanding the interplay between network structure and disease dynamics is essential for designing effective public health interventions. Furthermore, their work contributed to the field by providing insights into the mechanisms of disease spread in networked environments and highlighting the importance of considering network characteristics in epidemic modeling and control. RabieiMotlagh and Soleimani ^[8] investigated the impact of mutations on the stochastic dynamics of infectious diseases using a probability-based approach. They developed a mathematical model to analyze how mutations in pathogens can influence the spread and control of infectious diseases. The authors incorporated mutation effects into a stochastic framework, allowing them to examine the probabilistic behavior of disease transmission under various scenarios. By doing so, they aimed to understand better the role of genetic changes in pathogens and their implications for disease dynamics and public health interventions. The study utilized a combination of analytical and computational methods to explore the dynamics of mutated pathogens in a population. The authors considered different types of mutations, including beneficial, neutral, and deleterious, and examined their effects on the basic reproduction number and disease prevalence. They found that mutations could lead to significant changes in disease dynamics, potentially increasing the difficulty of controlling outbreaks. The model also highlighted the importance of considering stochasticity in disease modeling, as random events can significantly impact the outcomes of infectious disease spread. They also conducted several simulations to validate their model and demonstrate its applicability to real-world scenarios. They showed that mutations could lead to increased variability in disease outcomes, with some scenarios resulting in more severe outbreaks than others. The authors also explored the effects of vaccination and other control measures, finding that their effectiveness could be compromised by the presence of mutations. Their work underscored the need for adaptive strategies in public health responses to infectious diseases, considering the potential for rapid genetic changes in pathogens. Overall, the study provided valuable insights into the complex interplay between mutations and stochastic dynamics in infectious disease modeling. The authors emphasized the importance of integrating genetic factors into epidemiological models to improve predictions and inform public health strategies. Their findings suggested that traditional deterministic models might underestimate the impact of mutations and stochastic events, leading to less effective control measures. By incorporating a probabilistic approach, RabieiMotlagh and Soleimani offered a more comprehensive framework for understanding and managing infectious diseases in the face of evolving pathogens. For further results, we direct the reader to the work of eminent mathematicians ^{[9,10,11,12,13]} and references cited therein.

1.2.   Mathematical formulation

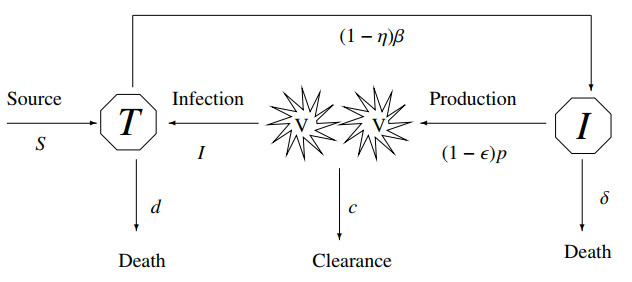
Mathematical modeling of the Hepatitis C virus (HCV) is crucial for understanding the complex dynamics of this persistent infection. HCV affects millions of people worldwide and poses significant challenges to public health due to its high mutation rate and diverse disease progression patterns. Mathematical models provide a powerful framework for analyzing these complexities by allowing researchers to simulate the interactions between the virus, host immune responses, and treatment interventions. By capturing the non-linear behaviors and potential for chaos inherent in HCV dynamics, these models help identify critical factors influencing disease spread and treatment efficacy. This approach enables the prediction of outbreak scenarios, the optimization of therapeutic strategies, and the development of more effective public health policies. Through mathematical modeling, we can gain valuable insights into HCV's behavior, ultimately paving the way for better management and control of this global health threat. So, hereafter, we will reformulate the mathematical modeling of the continuous HCV model. Based on Figure 1, the model's equation for continuous-time HCV model takes the following form ^[1] :

where $V$, $I$, and $T$ respectively denote free virus, infected, and target uninfected cells. Moreover, $T$ cells are created and destroyed at rates $s$ and $d$; $I$ cells are destroyed at a rate $\delta$; $\beta$ represents de novo infection; $p$ denotes viral production; and $c$ represents the clearance per virion of $V$ cells. Additionally, the model's therapeutic effect of IFN treatment included preventing the production of virion and reducing the number of new infections denoted by $1-\epsilon$ and $1-\eta$, respectively. Furthermore, for the specific range of parameters $d, s, \beta, \eta, \epsilon, p, c$, and $\delta$, we refer the reader to ^[1] and literature cited therein. It is important to mention that discrete-time models driven by difference equations are preferred to continuous ones in populations with non-overlapping generations. Discrete models can also produce effective computational results for numerical simulations. For instance, the continuous-time HCV model, which is depicted in (1.6), by Euler-forward formula, becomes:

where $h$ is the integral step size.

1.3.   Main contribution

In this paper, our key findings include:

● Mathematical formulation of the discrete Hepatitis C virus model (1.7).

● Existence of steady states of discrete HCV model.

● Construction of basic reproduction number by next-generation approach.

● Local dynamics at steady states of the HCV model.

● Bifurcation analysis at steady states.

● Study of chaos by state feedback method.

● Numerical verification of theoretical results.

1.4.   Paper layout

This paper is organized as follows. The existence of steady states and the linearized form of discrete HCV model (1.7) is studied in Section 2. We study the basic reproduction number by next-generation matrix in Section 3, whereas local stability at steady states is studied in Section 4. The detailed bifurcation analysis at steady states is given in Section 5. In Section 6, we study chaos control, whereas theoretical results are verified numerically in Section 7. Finally, a brief conclusion is given in Section 8.

2.   Existence of steady states and linearized form

In this section, we study the existence of steady states and linearized form of discrete HCV model (1.7). To do this, we first need to point out the steady states of the discrete HCV model (1.7).

Lemma 2.1. The following statements hold for HCV model's steady states:

(ⅰ) Discrete HCV model (1.7) has uninfected steady state (USS) $\left(\frac{s}{d}, 0, 0\right)\ \forall\ d, s, \beta, \eta, \epsilon, h, p, c, \delta$;

(ⅱ) Model (1.7) has infected steady state (ISS) $\left(\frac{\delta c}{p \beta (1 -\epsilon) (1-\eta)}, \frac{s p \beta (1 - \epsilon) (1-\eta) - d c \delta}{p \beta \delta(1 -\epsilon) (1-\eta)}, \frac{s p \beta (1 - \epsilon) (1- \eta) - d c \delta}{c \beta \delta(1 - \eta)} \right)$ if $s > \frac{d c \delta}{p\beta(1-\epsilon)(1-\eta)}$ with $\epsilon, \eta < 1$.

Proof. The point $(T, I, V)$ is a steady state of discrete HCV model (1.7) if

Since system (2.1) obviously satisfies if $(T, I, V) = \left(\frac{s}{d}, 0, 0\right)$, and therefore $\forall\ d, s, \beta, \eta, \epsilon, h, p, c, \delta$, the discrete HCV model (1.7) has USS $\left(\frac{s}{d}, 0, 0\right)$. In order to find ISS, from (2.1), one has

The system's third equation (2.2) yields

Using (2.3) into system's second equation (2.2), we get

Using (2.3) and (2.4) into system's first equation (2.2), we get

Finally, using (2.5) into (2.3), one gets

Equations (2.4), (2.5), and (2.6) then imply that if $s > \frac{d c \delta}{p\beta(1-\epsilon)(1-\eta)}$ with $\epsilon, \eta < 1$, then the HCV model (1.7) has ISS $\left(\frac{\delta c}{p \beta (1 -\epsilon) (1-\eta)}, \frac{s p \beta (1 - \epsilon) (1-\eta) - d c \delta}{p \beta \delta(1 -\epsilon) (1-\eta)}, \frac{s p \beta (1 - \epsilon) (1- \eta) - d c \delta}{c \beta \delta(1 - \eta)} \right)$. □

Now, variational matrix $J|_{(T, I, V)}$ evaluated at $(T, I, V)$ under the map $(f, g, w)\mapsto (T_{t+1}, I_{t+1}, V_{t+1})$ is

where

3.   Basic reproduction number

Based on the existing theory ^{[14,15,16,17]}, we aim to calculate the basic reproduction number for discrete HCV model (1.7) by the next-generation approach. The next-generation matrix for the understudied HCV model (1.7) can be performed as follows:

where corresponding variational matrices at USS are, respectively,

Further, the simple calculation yields that $\hat{F}|_{\mathrm{USS}}\hat{H}^{-1}|_{\mathrm{USS}} = \left(\begin{array}{ccc} \frac{sp\beta(1-\eta)(1-\epsilon)}{d\delta c} & \frac{s\beta(1-\eta)}{dc}\\ 0 & 0 \end{array} \right)$ has dominant eigenvalue $\frac{s p\beta(1-\epsilon)(1-\eta)}{d c \delta}$, which is the required basic reproduction number, that is, $\mathcal{R}_0: = \frac{s p\beta(1-\epsilon)(1-\eta)}{d c \delta}$.

4.   Stability analysis

Here, local stability at steady states is studied by stability theory ^{[18,19,20,21,22]}. At USS, (2.7) becomes

with

where

Theorem 4.1. If $\Delta < 0$, then USS is a

$(i)$ stable focus if

$(ii)$ unstable focus if

$(iii)$ saddle focus if

or

$(iv)$ non-hyperbolic if

or

Proof. By stability theory, if $|\lambda_1| = |1-d h| < 1$ and $|\lambda_{2, 3}| = \left|\frac{2-h(c+\delta)\pm \sqrt{\Delta}}{2}\right| < 1$, that is, $d < \frac{2}{h}$ and $d < \frac{h(1-\epsilon)(1-\eta)\beta ps}{c\delta h-c-\delta}$, then USS is a stable focus. Alternately, USS is a stable focus if $0 < d < \min\ \left\{\frac{2}{h}, \frac{h(1-\epsilon)(1-\eta)\beta ps}{c\delta h-c-\delta}\right\}$. Similarly, is is also easy to obtain that USS is unstable focus if $d > \max\ \left\{\frac{2}{h}, \frac{h(1-\epsilon)(1-\eta)\beta ps}{c\delta h-c-\delta}\right\}$, saddle focus if $\frac{2}{h} < d < \frac{h(1-\epsilon)(1-\eta)\beta ps}{c\delta h-c-\delta}$ or $\frac{h(1-\epsilon)(1-\eta)\beta ps}{c\delta h-c-\delta} < d < \frac{2}{h}$, and non-hyperbolic if $d = \frac{2}{h}$ or $d = \frac{h(1-\epsilon)(1-\eta)\beta ps}{c\delta h-c-\delta}$. □

Theorem 4.2. If $\Delta > 0$, then USS is a

$(i)$ stable node if

$(ii)$ unstable node if

$(iii)$ saddle node if

or

$(iv)$ non-hyperbolic if

or

or

Proof. It is the same as the proof of Theorem 4.1. □

Finally, at ISS, Eq (2.7) gives

with

where

Based on Theorem 1.4 of ^[19], the local dynamics at ISS of HCV model (1.7) is given by

Theorem 4.3. ISS of HCV model (1.7) is a sink if

5.   Bifurcation analysis

Hereafter, we examine local bifurcations at USS and ISS of HCV model (1.7) by bifurcation theory ^[23,24,25].

5.1.   Neimark-Sacker bifurcation at USS if $\Delta < 0$

If (4.9) holds, then from (4.2) together with (4.3), one gets $|\lambda_{2, 3}|_{(4.9)} = 1$ but $\lambda_1|_{(4.9)} = 1- \frac{h^2(1-\epsilon)(1-\eta)\beta ps}{c\delta h-c-\delta} \ne 1\ \mathrm {or}\ -1$, and hence at USS, the HCV model (1.7) may undergo Neimark-Sacker bifurcation if $\mathfrak{L} = (d, s, \beta, \eta, \epsilon, h, p, c, \delta)$ crosses the curve:

Hereafter, it is proved that at USS, HCV model (1.7) undergoes Neimark-Sacker bifurcation if $\mathfrak{L}\in N|_{\mathrm{USS}}$, where $d$ is associated with the bifurcation parameter. It is noted that the HCV model (1.7) takes the following form:

if $u_t = T_t-\frac{s}{d}$, $v_t = I_t$ and $w_t = V_t$. Additionally, if $\mathfrak{L}\in N|_{\mathrm{USS}}$ where (4.9) holds, then roots of $J|_{\mathrm{USS}}$ satisfying $|\lambda_{2, 3}|_{(4.9)} = 1$ and $\frac{d}{d d}\left(\left|\lambda_{2, 3}\right|\right)|_{(4.9)} = \frac{(\delta+c-\delta h c)^2}{2p\beta s(1-\epsilon)(1-\eta)}\not = 0$ and moreover, the calculation yields $\lambda^m_{2, 3}\neq 1$ where $m = 1, \cdots, 4$. Now, if

then HCV model (5.2) becomes

where

Now, the center manifold $W^C(0)$ for HCV model (5.4) is

where

From (5.7) and (5.8), HCV model (5.4) becomes

where after calculation, one gets

Therefore, discrete HCV model (5.4) restricted to $W^C(0)$ is

where

Now, at USS, HCV model (5.11) undergoes Neimark-Sacker bifurcation if discriminatory quantity, that is, $\sigma\not = 0$ ^[26,27]:

where

Moreover, the calculation yields

The above analysis yields the following result:

Theorem 5.1. If $\sigma\neq0$, then at USS, the HCV model (5.11) undergoes Neimark-Sacker bifurcation as $\mathfrak{L}\in N|_{\mathrm{USS}}$. In addition, Neimark-Sacker bifurcation is supercritical (subcritical) if $\sigma < 0 \ (\sigma > 0)$.

5.2.   Period-doubling and fold bifurcations at USS if $\Delta > 0$

If (4.14) holds, then $\lambda_1|_{(4.14)} = -1$ but $\lambda_{2, 3}|_{(4.14)} = \frac{2-h(c+\delta)\pm h\sqrt{(c-\delta)^2+2h p\beta s(1-\epsilon)(1-\eta)}}{2}$, and hence at USS, HCV model (1.7) may undergo period-doubling bifurcation if

On the other hand, at USS, HCV model (1.7) is invariant with respect to $I = V = 0$ and so one has

From (5.17), one has

Now if $d = d^* = \frac{2}{h}$, $T = T^* = \frac{s}{d}$ then $f_T|_{d = d^* = \frac{2}{h}, \ T = T^* = \frac{s}{d}} = -1$, $f_d|_{d = d^* = \frac{2}{h}, \ T = T^* = \frac{s}{d}} = -\frac{h^2 s}{2}\neq0$ and $f_{TT}|_{d = d^* = \frac{2}{h}, \ T = T^* = \frac{s}{d}} = 0$. Since $f_{TT}|_{d = d^* = \frac{2}{h}, \ T = T^* = \frac{s}{d}} = 0$ fail to satisfy non-degenerate condition, and so has the following result ^[28,29,30]:

Theorem 5.2. At USS, no period-doubling bifurcation occurs for discrete HCV model (1.7) if $\mathfrak{L}\in F|_{\mathrm{USS}}$.

Next, if (4.15) holds, then $\lambda_2|_{(4.15)} = 1$ but $\lambda_{1, 3}|_{(4.15)} = 1- \frac{h(1-\epsilon)(1-\eta)p\beta s}{\delta c}, \ 1-h\left(\delta+c\right)\ne 1\ \mathrm {or }\ -1$, and hence at USS, the HCV model (1.7) may undergo fold bifurcation if

It is recalled that if $d = d^* = \frac{(1-\epsilon)(1-\eta)p\beta s}{\delta c}$ and $T = T^* = \frac{s}{d}$, then from (5.18) the calculation yields $f_d|_{d = d^* = \frac{(1-\epsilon)(1-\eta)p\beta s}{\delta c}, \ T = T^* = \frac{s}{d}} = -\frac{h \delta c}{(1-\epsilon)(1-\eta)p\beta }\neq0$, $f_T|_{d = d^* = \frac{(1-\epsilon)(1-\eta)p\beta s}{\delta c}, \ T = T^* = \frac{s}{d}} = 1-h\left(\frac{(1-\epsilon)(1-\eta)p\beta s}{\delta c}\right) \ne 1$ and $f_{TT}|_{d = d^* = \frac{(1-\epsilon)(1-\eta)p\beta s}{\delta c}, \ T = T^* = \frac{s}{d}} = 0$ which fail to satisfy non-degenerate condition, and so has the following result:

Theorem 5.3. At USS, no fold bifurcation occurs for discrete HCV model (1.7) if $\mathfrak{L}\in \breve{F}|_{\mathrm{USS}}$.

Finally, if (4.16) holds, then $\lambda_2|_{(4.16)} = -1$ but $\lambda_{1, 3}|_{(4.16)} = 1- \frac{h^3(1-\epsilon)(1-\eta)p\beta s}{4-2\delta h-2hc+h^2 \delta c}, \ 3-h \left(c+\delta\right)\ne 1\ \mathrm {or }\ -1$, and hence at USS, the HCV model (1.7) may undergo period-doubling bifurcation if

Based on this computation, one has the following result:

Theorem 5.4. At USS, no period-doubling bifurcation occurs for discrete HCV model (1.7) if $\mathfrak{L}\in \hat{F}|_{\mathrm{USS}}$.

Proof. Same as the proof of Theorems 5.2 and 5.3. □

5.3.   Bifurcations at ISS

The occurrence of bifurcations at ISS will be studied in this section by explicit criterion ^{[31,32,33,34]}.

Theorem 5.5. If

then at ISS, discrete HCV model (1.7) undergoes N-S bifurcation at $d_0$ where $d_0$ is the real root of $1 - \varsigma_2(d) + \varsigma_3(d)(\varsigma_1(d) - \varsigma_3(d)) = 0$.

Proof. For $n = 3$, the explicit criterion yields

and

□

Theorem 5.6. If

then at ISS, discrete HCV model (1.7) undergoes P-D bifurcation at $d_0$ where $d_0$ is the real root of $1- \varsigma_1(d)+\varsigma_2(d) - \varsigma_3(d) = 0$.

Proof. For $n = 3$, the explicit criterion yields

and

□

6.   Chaos control

Chaos control plays a significant role in the study and application of complex dynamical systems, including biological models such as the discrete HCV model. In these contexts, chaos refers to a system's sensitive dependence on initial conditions, leading to seemingly random and unpredictable behavior over time. Although chaotic behavior can be fascinating and informative about a system's dynamics, it can also be undesirable, especially in practical applications where stability and predictability are necessary. The primary role of chaos control is to regulate and stabilize chaotic systems to achieve desired behaviors and outcomes. This is particularly important in fields like biology, engineering, and economics, where chaotic dynamics can lead to adverse effects or inefficiencies. By applying control methods, researchers can guide the system towards stable periodic orbits or fixed points, thereby reducing or eliminating chaotic behavior. In the context of biological models, such as the discrete HCV model, chaos control can help understand how to stabilize the spread of a virus or disease. For example, controlling chaotic dynamics might involve adjusting treatment parameters or other factors in the model to maintain an uninfected steady state or a manageable level of infection. This can be crucial for developing strategies to manage diseases effectively and prevent outbreaks. Various techniques are employed for chaos control, including feedback control, adaptive control, and parameter adjustments. Feedback control involves using real-time information about the system's state to make small adjustments that keep the system in a desired behavior. Adaptive control techniques adjust parameters dynamically based on the system's current state and desired outcomes. Parameter adjustments involve fine-tuning specific model parameters to transition the system from chaotic to stable behavior. So, in this section, we explore chaos in discrete HCV model (1.7) by existing theory ^[35,36]. By utilizing feedback control strategy, HCV model (1.7) becomes

where $\varrho$ is considered as a control parameter. Moreover, $J|_{\mathrm{ISS}}$ at ISS for controlled HCV model (6.1) is

with

where

Finally, the dynamics of controlled HCV model (6.1) at ISS can be stated as follows:

Lemma 6.1. If

then ISS of controlled HCV model (6.1) is a sink where $\varsigma_i^{*}\ (i = 1, 2, 3)$ are expressed in (6.4).

7.   Numerical simulations

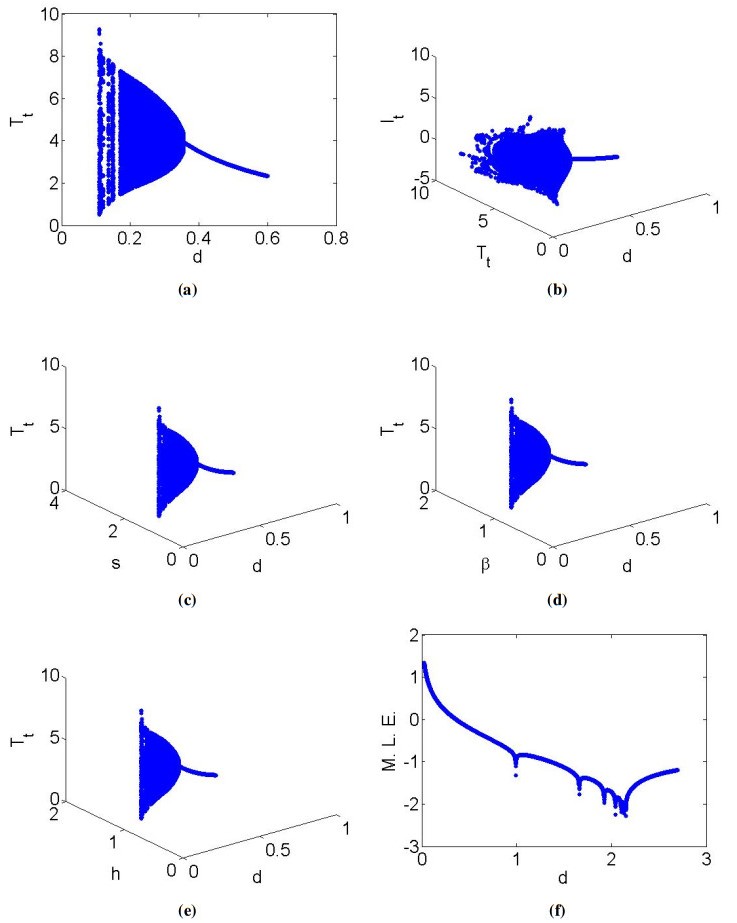
Example 7.1. If $s = 1.4$, $\beta = 1$, $\eta = 2$, $\epsilon = 0.23$, $h = 0.444$, $p = 2$, $c = 1$, and $\delta = 3$, then from (4.9), one gets $d = 0.3587946026986506$, where model's uninfected steady state is $\mathrm{USS} = \left(3.901953901953902, 0, 0\right)$. Further, if $\left(d, s, \beta, \eta, \epsilon, h, p, c, \delta \right) = \left(0.3587946026986506, 1.4, 1, 2, 0.23, 0.444, 2, 1, 3\right)$, then from (4.1), one has

with

From (7.2), one has $\lambda_1 = 0.8406951964017991$ and $\lambda_{2, 3} = 0.11199999999999999\pm 0.9937082066683358 \iota$ with $|\lambda_{2, 3}| = 1$ and so, $\left(d, \ s, \beta, \eta, \epsilon, \ h, \ p, \ c, \delta \right) = \left(0.3587946026986506, 1.4, 1, 2, 0.23, 0.444, 2, 1, 3\right) \in \mathcal{N}|_{\mathrm{USS}} = (3.901953901953902, 0, 0)$, which implies that eigenvalues criterion holds for the appearance of N-S bifurcation at $\mathrm{USS}$ of HCV model (1.7). In order to prove this fact, hereafter, we will prove the discriminatory quantity that is depicted in (5.13), that is, $\sigma < 0$. For instance, if $s = 1.4$, $\beta = 1$, $\eta = 2$, $\epsilon = 0.23$, $h = 0.444$, $p = 2$, $c = 1$, $\delta = 3$, $d = 0.3587946026986506$, then from (5.5) and (5.6) one gets:

Using (7.3) in (5.15), we get

Lastly, using (7.4) along with $\lambda, \bar{\lambda} = 0.285547487081691 \pm 0.9082322117438064 \iota$ into (5.13) we get $\sigma = -0.877578212800106 < 0$. This implies that at USS, discrete HCV model (1.7) must undergo supercritical N-S bifurcation where maximum Lyapunov exponent and bifurcation diagrams are drawn in Figure 2.

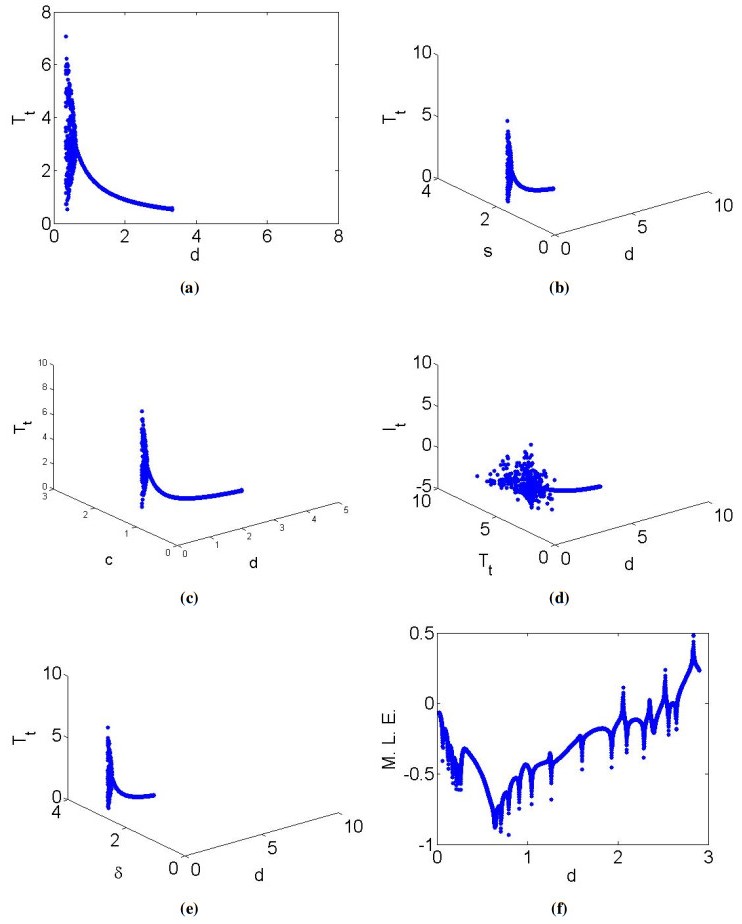
Example 7.2. If $s = 1.8$, $\beta = 7.09$, $\eta = 0.567$, $\epsilon = 0.554$, $h = 0.6$, $p = 0.7$, $c = 1.037$, $\delta = 2.8082$, then from the first equation of (5.21), one of the real roots of $1 - \varsigma_2(d) + \varsigma_3(d)\left(\varsigma_1(d) - \varsigma_3(d)\right) = 0$ is $d = 5.947904220066088$. Therefore, at $\left(d, \ s, \ \beta, \ \eta, \ h, \ p, \ c, \ \delta\right) = \left(5.947904220066088, 1.85, 7.09, 0.567, 0.554, 0.7, 1.037, 2.808\right)$ model (1.7) has steady-state solution ISS and moreover, from (4.17), we have

with

where $\lambda_1 = 2.3198112564498503$ and $|\lambda_{2, 3}| = |-0.592625573703747 \pm 0.8054780750537566 \iota| = 1$ that fulfills eigenvalues criterion for the appearance of Neimark-Sacker bifurcation at ISS of HCV model (1.7). Additionally, from (5.21), we get

Further, $\cos\frac{2\pi}{l} = -0.5926255737037465$ gives $l = \pm2.8493738112285323$, and hence, by explicit criterion, N-S bifurcation exists at ISS where maximum Lyapunov exponent and N-S bifurcation diagrams are drawn in Figure 3.

Example 7.3. If $s = 2.00065$, $\beta = 9.09$, $\eta = 0.341$, $\epsilon = 0.344$, $h = 0.444$, $p = 0.7$, $c = 1.437$, $\delta = 3.0082$, then from the fifth equation of (5.23), the one real root of $1-\varsigma_1(d)+\varsigma_2(d)-\varsigma_3(d) = 0$ is $d = 1.0733956213777098$ where model's infected steady state is $\mathrm{ISS} = \left(1.571492446363595, 0.10432048701721004, 0.0333360943899115\right)$. Further, if $\left(d, s, \beta, \eta, \epsilon, h, p, c, \delta \right) = \left(1.0733956213777098, 2.00065, 9.09, 0.341, 0.344, 0.444, 0.7, 1.437, 3.0082\right)$ then from (4.17), we have

with

where $\lambda_1 = -1$ and $\lambda_{2, 3} = 0.5439114359500233, 0.9171681765826085 \neq \pm1$ that fulfills eigenvalues criterion for the appearance of P-D bifurcation at $\mathrm{ISS}$ of HCV model (1.7). Additionally, from (5.23), one gets

This implies that at ISS, discrete HCV model (1.7) must undergo P-D bifurcation where maximum Lyapunov exponent and P-D bifurcation diagrams are drawn in Figure 4.

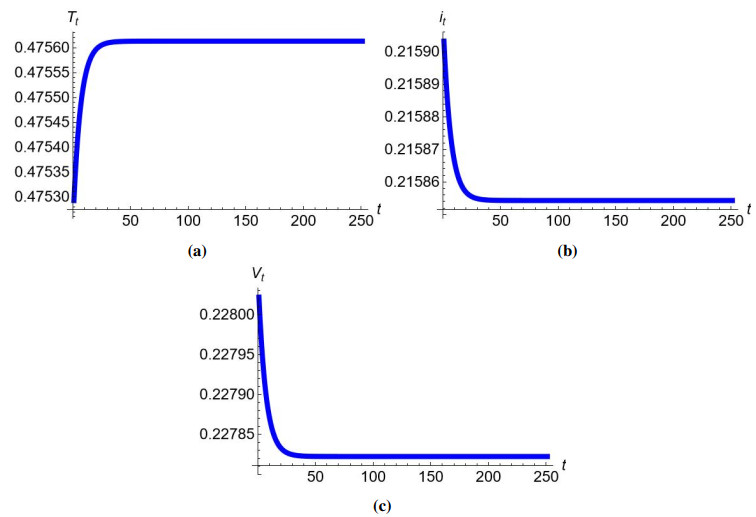
Example 7.4. If $s = 2.00065$, $\beta = 9.09$, $\eta = 0.341$, $\epsilon = 0.344$, $h = 0.444$, $p = 0.7$, $c = 1.437$, $\delta = 3.0082$, $\varrho = 0.001$, and $d = 1.0734$, then from (6.5), one has $|\varsigma_1^{*}+\varsigma_3^{*}| = 0.9276491817948008 < 1+\varsigma_2^{*} = 1.9601656901999216$, $|\varsigma_1^{*}-3\varsigma_3^{*}| = 0.9266290952538755 < 3-\varsigma_2^{*} = 3.9601656901999216$ and ${\varsigma_3^{*}}^2+\varsigma_2^{*}-\varsigma_3^{*}\varsigma_1^{*} = -0.960402130739115 < 1$, which implies that ISS of a controlled discrete HCV model (6.1) is a sink (see Figure 5).

Remark 7.1. It is important to remark that when selecting parameters for numerical simulations, especially in the context of studying complex phenomena like bifurcations and Lyapunov exponents in the discrete HCV model, it is essential to base these choices on both theoretical insights and empirical data. The parameters used in the model should reflect biologically realistic values, obtained either from experimental observations or the existing literature, to ensure that the simulation outcomes are relevant to the real-world dynamics of HCV infection. Parameters like infection rates, recovery rates, and viral reproduction numbers must be carefully considered, as they directly impact the stability and behavior of the model's steady states. For instance, when analyzing Neimark-Sacker bifurcation diagrams, it is crucial to explore a range of parameter values to identify the onset of bifurcations, where a stable fixed point becomes unstable and leads to quasi-periodic behavior. Similarly, in studying period-doubling bifurcations along with the maximum Lyapunov exponent for the infected steady state, varying parameters such as the viral production rate and immune response rate can provide insights into how the system transitions from stable to chaotic dynamics. This involves systematically adjusting parameters and observing changes in the bifurcation structure and Lyapunov exponents, which measure the sensitivity of the system to initial conditions. Moreover, parameters should be chosen to reflect different scenarios, such as varying levels of immune response or treatment effectiveness, to capture a comprehensive picture of the system's dynamics. Sensitivity analysis can be a valuable tool in this context, helping identify which parameters have the most significant impact on the system's behavior. Ultimately, the goal of selecting parameters in numerical simulations is to balance biological realism with the need to explore the mathematical properties of the model, thereby gaining deeper insights into the mechanisms driving the complex dynamics of HCV infection.

8.   Conclusions

In this study, we thoroughly examined the dynamical characteristics of a discrete Hepatitis C virus (HCV) model, focusing on both the uninfected steady state (USS) and the infected steady state (ISS). We proved that $\forall\ d$, $s$, $\beta$, $\eta$, $\epsilon$, $h$, $p$, $c$, $\delta$, discrete HCV model (1.7) has USS $\left(\frac{s}{d}, 0, 0\right)$ and ISS $\left(\frac{\delta c}{p \beta (1 -\epsilon) (1-\eta)}, \frac{s p \beta (1 - \epsilon) (1-\eta) - d c \delta}{p \beta \delta(1 -\epsilon) (1-\eta)}, \frac{s p \beta (1 - \epsilon) (1- \eta) - d c \delta}{c \beta \delta(1 - \eta)} \right)$ if $s > \frac{d c \delta}{p\beta(1-\epsilon)(1-\eta)}$ with $\epsilon, \eta < 1$. Through local dynamics analysis, we discovered that USS is a stable focus if $0 < d < \min\ \left\{\frac{2}{h}, \frac{h(1-\epsilon)(1-\eta)\beta ps}{c\delta h-c-\delta}\right\}$, unstable focus if $d > \max\ \left\{\frac{2}{h}, \frac{h(1-\epsilon)(1-\eta)\beta ps}{c\delta h-c-\delta}\right\}$, saddle focus if $\frac{2}{h} < d < \frac{h(1-\epsilon)(1-\eta)\beta ps}{c\delta h-c-\delta}$ or $\frac{h(1-\epsilon)(1-\eta)\beta ps}{c\delta h-c-\delta} < d < \frac{2}{h}$, and non-hyperbolic if $d = \frac{2}{h}$ or $d = \frac{h(1-\epsilon)(1-\eta)\beta ps}{c\delta h-c-\delta}$. Also, USS is a stable node if $\frac{(1-\epsilon)(1-\eta)p\beta s}{\delta c} < d < \min\ \left\{\frac{h^2 (1-\epsilon)(1-\eta)p\beta s}{4-2\delta h-2hc+h^2 \delta c}, \frac{2}{h}\right\}$, an unstable node if $\max\ \left\{\frac{h^2 (1-\epsilon)(1-\eta)p\beta s}{4-2\delta h-2hc+h^2 \delta c}, \frac{2}{h}\right\} < d < \frac{(1-\epsilon)(1-\eta)p\beta s}{\delta c}$, saddle node if $\frac{h^2 (1-\epsilon)(1-\eta)p\beta s}{4-2\delta h-2hc+h^2 \delta c} < d < \min\ \left\{\frac{h^2 (1-\epsilon)(1-\eta)p\beta s}{4-2\delta h-2hc+h^2 \delta c}, \frac{2}{h}\right\}$ or $\max\ \left\{\frac{(1-\epsilon)(1-\eta)p\beta s}{\delta c}, \frac{2}{h}\right\} < d < \frac{h^2 (1-\epsilon)(1-\eta)p\beta s}{4-2\delta h-2hc+h^2 \delta c}$, non-hyperbolic if $d = \frac{2}{h}$ or $d = \frac{(1-\epsilon)(1-\eta)p\beta s}{\delta c}$ or $d = \frac{h^2 (1-\epsilon)(1-\eta)p\beta s}{4-2\delta h-2hc+h^2 \delta c}$, and ISS is a sink if $|\varsigma_1 + \varsigma_3| < 1+\varsigma_2$, $|\varsigma_1 -3 \varsigma_3| < 3 -\varsigma_2$, $\varsigma^2_3 +\varsigma_2 -\varsigma_3 \varsigma_1 < 1$ where $\varsigma_1, \varsigma_2$ and $\varsigma_3$ are depicted in (4.19). These findings highlight the intricate behavior of the system, such as transitions between stability and instability, depending on the value of $d$ relative to other parameters. Further, our analysis revealed the existence of bifurcations at USS and ISS; we first identified bifurcation sets for understudied model (i) Neimark-Sacker bifurcation set $N|_{\mathrm{USS}}: = \left\{\mathfrak{L}: \Delta < 0 \ \mathrm{and}\ d = \frac{h(1-\epsilon)(1-\eta)\beta ps}{c\delta h-c-\delta}\right\}$, (ii) period-doubling bifurcation set $F|_{\mathrm{USS}}: = \left\{\mathfrak{L}: \Delta > 0 \ \mathrm{and}\ d = \frac{2}{h}\right\}$, $\hat{F}|_{\mathrm{USS}}: = \left\{\mathfrak{L}: \Delta > 0 \ \mathrm{and}\ d = \frac{h^2 (1-\epsilon)(1-\eta)p\beta s}{4-2\delta h-2hc+h^2 \delta c}\right\}$, and (iii) fold bifurcation set $\breve{F}|_{\mathrm{USS}}: = \left\{\mathfrak{L}: \Delta > 0 \ \mathrm{and}\ d = \frac{(1-\epsilon)(1-\eta)p\beta s}{\delta c}\right\}$. We then presented the detailed bifurcation analysis at USS of HCV model (1.7). In addition, we also gave the N-S and P-D bifurcations at ISS by explicit criterion. The identification of these bifurcation sets enhances our understanding of how changes in parameters can induce shifts in system dynamics, which is crucial for devising effective control strategies. Moreover, we explored the role of chaos control using feedback strategies to manage the chaotic dynamics often present in such models. This aspect of the study underscores the potential for practical applications, where controlling chaos can lead to more stable outcomes, such as suppressing the spread of infection or maintaining manageable levels of the virus. In contrast to existing literature, our study offers a comprehensive exploration of local dynamics of the HCV model, incorporating a robust bifurcation analysis that parallels theoretical predictions with numerical simulations. While previous studies have often focused on specific aspects of HCV dynamics, our work integrates these components into a cohesive framework, providing insights that can inform future research and application in disease management. Through comparison with similar models, our findings confirm and extend the understanding of viral dynamics, contributing to the broader field of infectious disease modeling by offering novel perspectives on control strategies and system behavior. Finally, the theoretical results were validated numerically, demonstrating the model's capacity to accurately capture complex dynamics and providing a solid foundation for future explorations into the control and management of HCV and similar infectious diseases.

Author contributions

Abdul Qadeer Khan: Conceptualization, formal analysis, investigation, methodology, resources, software, supervision, validation, visualization, writing original draft, writing review & editing; Ayesha Yaqoob: formal analysis, investigation, software, writing original draft, writing review & editing; Ateq Alsaadi: conceptualization, funding acquisition, resources, writing original draft, writing review & editing. All authors have read and approved the final version of the manuscript for publication.

Acknowledgements

The authors extend their appreciation to Taif University, Saudi Arabia, for supporting this work through project number (TU-DSPP-2024-259).

Conflict of interest

The authors declare that they have no conflict of interest.