The uniformly continuous theorem of fractal interpolation surface function and its proof

1.   Introduction

As a new branch of research in mathematics and physics, fractal geometry was proposed by American mathematician Mandlebrot in the 1960s and 1970s ^[1,2,3,4,5]. In nature and society, rather irregular phenomena and things are studied in fractal geometry. Because extremely irregular things and phenomena are ubiquitous in nature and society, fractal geometry is applied in almost every field, such as, chemistry, physics, biology, engineering mechanics, geology, economics, anthropology, sociology, and so on ^[6,7,8,9,10]. With the development of fractals, many new fractal research methods have also emerged. First, in aspect of fractal theoretical research methods, on the one hand, there is the fractal dimension method, which describes the roughness of extremely irregular curves and surfaces in nature ^[11,12]. On the other hand, an iterated functional system generated by affine mapping can produce a unique attractor, which has fractal self similar property and other fractal properties. This fractal theory was first proposed by American mathematicians Barnsley and Massopust in the 1980s and 1990s ^{[13,14,15,16,17]}. The self similar property of fractal can be applied in describing highly irregular shapes in nature, for example, the irregular shapes of galaxies, clouds, leaves, flowers, mountains, torrents of water, and much else. The advantage of the research method is that as long as a small amount of data information is obtained, the picture shape can be iterated through self similar property. For example, as long as three pairs of interpolation data points' cartesian coordinates are obtained, the curve shape can be iterated by the fractal interpolation curve by three iterations. (refer to: Figure 1). Of course, these fractal graphics are drawn by a computer program. Second, a multi-fractal method describes the state in which the multi-fractal spectrum and generalized fractal dimension change with a probability factor. The multi-fractal method is widely applied in studying thin film growth in material science ^[18,19,20]. Finally, the theory of fractal interpolation curves on the two-dimensional plane is extended to that of fractal interpolation surfaces in the three-dimensional space ^{[21,22,23,24]}. Some properties of fractal interpolation surfaces in three-dimensional space need to be researched. For example, the uniform continuity of a fractal interpolation surface will be researched in the following content of the paper.

The proof of the uniform continuity theorem of fractal interpolation surface can be proven rigorously by the accumulation principle on the two-dimensional plane and the uniform continuity definition of a function of two variables in the three-dimensional space in the paper.

2.   Major concepts and lemmas

Definition 1. ^[25,26] Let $E$ and $A(x, y)$ be a set of planar points and a point on the plane, respectively. $A(x, y)$ is called accumulation point if, for any nonempty neighborhood region ${ \cup ^o}(A)$ of $A$, there is always a point in $E$, where $A(x, y)$ belongs to $E$ or $A(x, y)$ does not belong to $E$.

Definition 2. ^[25,26] Let $f$ be a function of two variables defined on a plane set $D$. There is a point $({x_0}, {y_0}) \in D$. The $f$ is called continuous function at the point $({x_0}, {y_0}) \in D$ if, for any given number $\varepsilon > 0$, there is a real number $\delta > 0$ so that

as long as $d((x, y), ({x_0}, {y_0})) < \delta$ for all $(x, y) \in D$.

Definition 3. ^[25,26] Let $f$ be a function of two variables defined on a plane set $D$. The $f$ is called uniformly continuous function on the set $D$ if, for any given number $\varepsilon > 0$, there exists $\delta = \delta (\varepsilon ) > 0$, such that

for any point $(x', y'), (x'', y'') \in D$, as long as $d((x', y'), (x'', y'')) < \delta$.

Definition 4 ^[27,28] Let $I = [a, b]$ and $J = [c, d]$ be two closed intervals. Construct a planar rectangular closed region $D = I \times J = \left\{ {(x, y)|a \leqslant x \leqslant b, c \leqslant y \leqslant d} \right\}$. Divide $D$ into grids in steps of $\Delta x$ and $\Delta y$. The segmentation points are as follows:

The spacial coordinate data $({x_i}, {y_i}, {z_{i, j}})$($i = 0, 1, \cdots N;j = 0, 1, \cdots , M$) on a set of grid points are given. The function of two variables $f:D \to R$ is called fractal interpolation function of two variables if it satisfies:

The following discuss is based on spacial region $K = D \times [{h_1}, {h_2}]$$( - \infty < {h_1} < {h_2} < + \infty )$. The special distance $d(({x_1}, {y_1}, {z_1}), ({x_2}, {y_2}, {z_2})) = \max \left\{ {\left| {{x_1} - {x_2}} \right|, \left| {{y_1} - {y_2}} \right|, \left| {{z_1} - {z_2}} \right|} \right\}$ is defined, for any points $({x_1}, {y_1}, {z_1}), ({x_2}, {y_2}, {z_2}) \in K$.

Denote ${I_n} = [{x_{n - 1}}, {x_n}]$, ${J_m} = [{y_{m - 1}}, {y_m}]$, ${D_{n, m}} = {I_n} \times {J_m}$, $(n \in \left\{ {1, \cdots N} \right\};m \in \left\{ {1, \cdots , M} \right\})$. Define ${\Phi _n}:I \to {I_n}, {\Psi _m}:J \to {J_m}$ be contraction mapping and satisfy:

and

where ${x_1}, {x_2} \in I$, ${y_1}, {y_2} \in J$, $0 \leqslant {k_1} < 1$, $0 \leqslant {k_2} < 1$.

Define the two mappings ${L_{n, m}}:D \to {R^2}$ and ${L_{n, m}}(x, y) = ({\Phi _n}(x), {\Psi _m}(y))$ that are contraction mappings. The mapping ${F_{n, m}}:D \to \left[ {{h_1}, {h_2}} \right]$ is continuous and satisfies:

For any points $({x_1}, {y_1}), ({x_2}, {y_2}) \in D$, $({z_1}, {z_2}) \in [{h_1}, {h_2}]$, $n \in \left\{ {1, 2, \cdots N} \right\};m \in \left\{ {1, 2, \cdots , M} \right\}$, and $0 \leqslant {k_3} < 1$, the following formula is correct

Lemma 1. ^[25,26] If $E$ is a bounded infinite set of planar points, there is at least one accumulation point in $E$ on the plane ${R^2}$.

Lemma 2. ^[25,26] If the sequence $\left\{ {{P_n}({x_n}, {y_n})} \right\}$ of planar points is infinite and bounded, there exists a convergent subsequence $\left\{ {{P_{{n_k}}}({x_{{n_k}}}, {y_{{n_k}}})} \right\}$ of $\left\{ {{P_n}({x_n}, {y_n})} \right\}$.

Lemma 3. ^[27,28] Let the mapping ${\Phi _n}$ defined by Definition 5 above be a affine mapping, ${\Phi _n}(x) = {a_n}x + {b_n}$, from the Eq (5) above,

So, the two coefficients ${a_n}$ and ${b_n}$ can be solved. The following equation can be obtained

So,

Let the mapping ${\Psi _m}(y)$ defined by Definition 5 above be a affine mapping, ${\Psi _m}(y) = {c_m}y + {d_m}$ according to the Eq (5) above, the following equations can be obtained

From the equations above, ${c_m}$ and ${d_m}$ can be solved.

So,

Let

according to the Eq (7), the following system of equations can be obtained

Let ${s_{n, m}}$ be free parameter and satisfies $0 \leqslant {s_{n, m}} < 1$, which is called vertical ratio factor. The every coefficient of the system of equations above can be solved.

where $n \in \left\{ {1, \cdots , N} \right\}$, $m \in \left\{ {1, \cdots , M} \right\}$.

Lemma 4 ^[27,28] For the interpolation function system defined above from Eq (4) to Eq (17), there exists a unique attractor $G = \left\{ {\left. {(x, y, f(x, y))} \right|(x, y) \in D} \right\}$ and it is a graph of continuous function $f$, which satisfies:

According to the principle of fractal interpolation on closed rectangular region, the following analytic function of self affine two variables fractal interpolation function can be solved.

where

The coefficients ${e_{n, m}}$, ${f_{n, m}}$, ${g_{n, m}}$, ${k_{n, m}}$ of Eq (19) can be solved by Eq (17) and the coefficient ${s_{n, m}}$ is vertical compress ratio factor, which is artificially given according to roughness of fractal interpolation surface.

3.   Uniform continuity of fractal interpolation surface on a closed rectangular area

Theorem. If the fractal interpolation surface function $f(x, y)$ defined by Eq (19) above is a continuous function on a closed rectangular area $D = [a, b] \times [c, d]$. Then $f(x, y)$ is uniformly continuous function on $D$.

Proof: Here the contradiction proof method can be used. Suppose that $f(x, y)$ is continuous on closed rectangular region $D$, but it is not uniformly continuous on $D$. That is to say, $\exists {\varepsilon _0} > 0, \forall \delta > 0, \exists P(x, y), Q(x', y') \in D,$ and $d(P, Q) < \delta$, but

Because $D$ is a bounded closed domain, from Lemmas 2 and 3, there is a convergent subsequence $\left\{ {{P_{{n_k}}}\left( {{x_{{n_k}}}, {y_{{n_k}}}} \right)} \right\} \subseteq D$, and let

According to the hypothesis condition of contradiction proof method above, there exists points sequence $\left\{ {{Q_{{n_k}}}\left( {{{x'}_{{n_k}}}, {{y'}_{{n_k}}}} \right)} \right\}$ with the same subscript as $\left\{ {{P_{{n_k}}}\left( {{x_{{n_k}}}, {y_{{n_k}}}} \right)} \right\}$ and satisfies:

On the one hand,

The following Eq (30) is correct.

which repeats the steps of Eq (29).

To sum up, Eq (25)

can be arbitrarily positive small and tend to zero. In other words,

However, according to the not uniform continuity definition and the inequalities of limits, the following inequality is right.

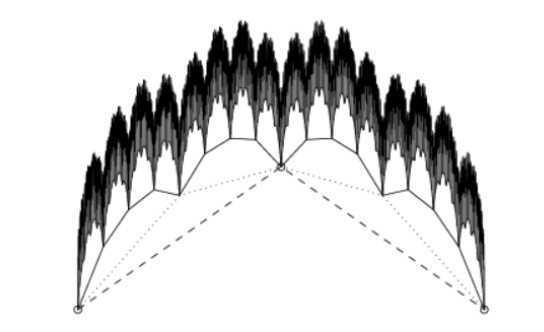
It is very obvious that there is a contradiction between Eqs (32) and (33), which indicates that the previous negative hypothesis is incorrect. Thus, the conclusion above indicates that fractal interpolation surface on a closed rectangular region is uniformly continuous through the proof from Eq (25) to Eq (31) by the definition of uniform continuity. A uniformly continuous fractal interpolation surface on a rectangle can be drawn by a computer program (refer to: Figure 2).

4.   Conclusions

First, the definition and relational theorems of fractal interpolation surface function are expounded. Second, the definition and theorem of accumulation point are introduced. Finally, the contradiction proof method and accumulation principle are applied to prove the uniform continuity of fractal interpolation surface function on a closed rectangular area.

In the future, on the one hand, research will be conducted on the variation of uniformly continuous fractal surface. On the other hand, the study of the relationship between the morphology differences of rock fracture surfaces and the fracture mechanics mechanisms of uniformly continuous fractal surfaces will continue.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was funded by "Funding for school-level research projects of Yancheng Institute of Technology", project grant number "xjr2022041". This research was funded by the National Natural Science Foundation of China (Grant No. 72243005), Qing Lan Project of Jiangsu Province (2021), and the Special Science and Technology Innovation Program for Carbon Peak and Carbon Neutralization of Jiangsu Province (Grant No. BE2022612).

Conflict of interest

The authors declare no conflicts of interest.