Positive periodic solution for enterprise cluster model with feedback controls and time-varying delays on time scales

1.   Introduction

An ecosystem is a sustainable system, and the coexistence of species is one of its essential attributes. Similarly, in the business world, competition and coexistence among enterprises are also crucial for their sustainable development. In recent years, the use of ecological theory and dynamical system methods to study clusters has gradually attracted the attention of a large number of researchers. In ^[1], the authors considered the following autonomous model:

where $u_1$ and $u_2$ represent the output of two enterprises $A$ and $B$, respectively; $a_1$ and $a_2$ are the intrinsic growth of two enterprises; $b_{ij}(i, j = 1, 2)$ represents the load capacity of enterprises $A$ and $B$; $c_{i}(i = 1, 2)$ denotes the initial production of enterprises $A$ and $B$. Considering the impact of time delay, the following model can be obtained:

where $\tau_i\; (i = 1, 2, 3, 4)$ is a constant delay. Liang, Xu, and Tang ^[2,3] studied dynamic behaviours (including stability and Hopf bifurcation) for system (1.2). For more results about competition models, see ^[4,5,6].

Due to the fact that the external development environment of enterprise clusters is constantly changing over time, and the internal architecture of the enterprise clusters is also changing over time, a coefficient of variation system can more accurately depict the actual situation. Muhammadhaji and Nureji ^[7] studied the competition and cooperation model of enterprises with variable coefficients

where $a_i(t), \; b_{ij}(t)$, and $c_i(t)$ are continuous functions on $\mathbb{R}, \; i, j = 1, 2$. Using the Lyapunov function method and useful inequality techniques, several conditions on the dynamic behaviours of system (1.3) have been obtained. Xu and Shao ^[8] investigated a competition and corporation impulsive model with variable coefficients and obtained the uniqueness and global attractivity of the positive periodic solution by using the continuation theorem of coincidence degree theory and the Lyapunov functional method.

Feedback control has been widely applied in many fields, including economics, physics, biology, neural networks, and so on. In order to maintain the continuous stability and accuracy of the system, it is necessary to effectively monitor the system and use feedback control to adjust its state. Feedback control helps to correct errors and deviations, ensuring that the system is in a stable operating state. In short, for a complex system, an efficient feedback control system is the foundation for ensuring long-term stable operation of the system. In recent years, Muhammadhaji and Maimaiti ^[9] studied a non-autonomous competition and cooperation model of two enterprises with discrete feedback controls and constant delays as follows:

where $v_1$ and $v_2$ denote the indirect feedback control variables, and $f_i$ and $e_i$ (i = 1, 2) are feedback control coefficients. Lu, Lian, and Li ^[10] studied dynamic properties for a discrete competition model of with multiple delays and feedback controls. Xu and Li ^[11] considered almost periodic solution problems for a competition and cooperation model of two enterprises with time-varying delays and feedback controls.

The dynamic system on a time scale can unify discrete and continuous equations, which is currently a hot research. However, the enterprise cluster model on time scales is rarely studied. To the best of our knowledge, we only found that an enterprise cluster model based on with feedback controls on time scales $\mathbb{T}$ has been studied in ^[12] as follows:

The authors proposed new criteria for analyzing the permanence, periodic solution, and global attractiveness of system (1.5). Motivated by the above work, we consider the following enterprise cluster model with feedback controls and time-varying delays on time scale $\mathbb{T}$:

where $-a_1, -a_2, \alpha_1, \alpha_2\in\mathcal{R}^+$ with $a_1(t), a_2(t)\geq0, \; \alpha_1(t), \alpha_2(t)\leq0$ for all $t\in \mathbb{T}$; for $i, j = 1, 2$ and $k = 1, 2, \cdots, 8$, $a_i, \alpha_i, c_i, d_i, e_i, b_{ij}, \tau_k$ are continuous $\omega$-periodic functions with $c_i, d_i, e_i, b_{ij}, \tau_k\geq0$. $\mathbb{T}$ denotes a periodic time scale which has the subspace topology inherited from the standard topology on $\mathbb{R}$.

We list the main contributions of this paper as follows:

(1) We first study a class of enterprise cluster model with feedback controls and time-varying delays on time scales. The model in the present paper is different than the model in ^[12], and when $\mathbb{T} = \mathbb{R}$ and the delays are constants in system (1.6), system (1.6) can be changed into system (1.4). Since the model of this paper is based on the theory of time scales, which unifies discrete and continuous systems, the results of this article have wider applicability than those of references ^[8,9,10,11].

(2) We develop the fixed-point theorem of $k$-set contraction operators for studying dynamic systems on time scales.

(3) For obtaining the existence of positive periodic solutions to system (1.6), we construct a proper cone by using periodic time scale theory.

The remainder of this paper is organized as follows: Section 2 gives some preliminaries. In Section 3, some sufficient conditions for the existence of positive periodic solutions of system (1.6) are obtained. In Section 4, two examples are given to show the effectiveness of the main results in this paper. Finally, some conclusions and discussions are given.

2.   Preliminaries

A time scale $\mathbb{T}$ is a closed subset of $\mathbb{R}.$ For $t\in\mathbb{T},$ the forward jump operator $\sigma$ and backward jump operator $\rho$ are respectively defined by

The forward graininess $\mu:\mathbb{T}\rightarrow [0, \infty)$ is defined by $\mu(t) = \sigma(t)-t$. $\mathcal {R}$ and $\mathcal {R}^+$ denote all regressive $rd$-continuous functions and positive regressive $rd$-continuous functions, respectively.

Definition 2.1. ^[19] A function $U:\mathbb{T}_k\rightarrow \mathbb{R}$ is a delta-antiderivative of $U:\mathbb{T}_k\rightarrow \mathbb{R}$ if $U^\Delta = u$ holds for $t\in\mathbb{T}_k$. Then, define the integral of $u$ by

Lemma 2.1.^[19] Let $p, q\in\mathcal {R}.$ Then,

$(1) \; {e}_0(t, s)\equiv1$ and ${e}_p(t, t)\equiv1;$

$(2) \; {e}_p(\rho(t), s) = (1-\mu(t)p(t)){e}_p(t, s);$

$(3) \; {e}_p(t, s) = \frac{1}{{e}_p(s, t)} = e_{\ominus p}(s, t);$

$(4) \; {e}_p(t, s){e}_p(s, r) = {e}_p(t, r);$

$(5) \; {e}_p(t, s){e}_q(t, s) = {e}_{p\oplus q}(t, s).$

Definition 2.2. ^[20] A time scale $\mathbb{T}$ is periodic if there is $k > 0$ for each $t\in\mathbb{T}$ such that $t\pm k\in\mathbb{T}$. For $\mathbb{T}\neq\mathbb{R}$, the period of the time scale is the smallest positive $k$.

Definition 2.3. ^[20] Let $\mathbb{T}\neq\mathbb{R}$ be a periodic time scale with the period $k$. The function $\psi:\mathbb{T}\rightarrow \mathbb{R}$ is periodic with period $\tau$ if there exists a natural number $n$ such that $\tau = nk, \; \psi(t\pm\tau) = \psi(t)$ for all $t\in\mathbb{T}$. When $\mathbb{T} = \mathbb{R}$, $\psi$ is a periodic function if $\tau$ is the smallest positive number such that $\psi(t\pm\tau) = \psi(t)$.

Let $\mathcal{B}$ be a Banach space. For a bounded subset $E\subset\mathcal{B}$, the Kuratowski measure of non-compactness can be defined by

where $diam(E_i)$ denotes the diameter of the set $E_i$. Let $\mathcal{B}$ and $\mathcal{D}$ be two Banach spaces and $\Omega$ be a bounded open subset of $\mathcal{B}$. A continuous and bounded map $\phi:\overline{\Omega}\longrightarrow\mathcal{D}$ is called $k$-set contractive if for any bounded set $C\subset\Omega$ we have

where $k\geq0$ is a constant. If $0\leq k < 1,$ the mapping $\phi$ is called strict-set-contractive.

Lemma 2.2. ^[21] Let $P$ be a cone of the real Banach space $X$ and $P_{r, R} = \{u\in P:r\leq||u||\leq R\}$ with $R > r > 0$. Assume that $\Psi:P_{r, R}\rightarrow P$ is strict-set-contractive such that one of the following two conditions is satisfied:

(1) $(\Psi u\nleq u$ for all $u\in P, \; ||u|| = r)$ and $(\Psi u\ngeq u$ for all $u\in P, \; ||u|| = R)$;

(2) $(\Psi u\ngeq u$ for all $u\in P, \; ||u|| = r)$ and $(\Psi u\nleq u$ for all $u\in P, \; ||u|| = R)$.

Then, $\Psi$ has at least one fixed point in $P_{r, R}$.

Let $C_\omega$ be a $\omega$-periodic continuous function space. Let

where $u_1, u_2, v_1, v_2\in C_\omega$. $X$ has the following norm:

where $|f|_0 = \max_{t\in\mathbb{T}}|f(t)|$. Thus, $X$ is a Banach space. Define the cone $P$ in $X$ by

where $y = (y_1, \cdots, y_4)^T, \; \rho > 0$ is a given constant. Throughout this paper, we need the following notations:

Throughout this paper, we assume:

(H$_1$) $e_{\ominus(-a_1)}(t, t-\omega) > 1, \; e_{\ominus(-a_2)}(t, t-\omega), \; e_{\ominus(\alpha_1)}(t, t-\omega) > 1$ and $e_{\ominus(\alpha_2)}(t, t-\omega) > 1$ for all $t\in[0, \omega]_\mathbb{T}$.

Lemma 2.3. System (1.6) exists a periodic solution $x = (u_1, u_2, v_1, v_2)^T\in X$ if only if

Proof. The proof of Lemma 2.3 is similar to the proof of Lemma 2.3 in ^[22]. For the convenience of the readers, we provide its details. Let $x = (u_1, u_2, v_1, v_2)^T\in X$ be a periodic solution of system (1.6). Rewrite the first equation of system (1.6) in the form:

Multiplying both sides of (2.5) by $e_{-a_1}(t, 0)$ and integrating them from $t-\omega$ to $t$, we get

Dividing both sides of (2.6) by $e_{-a_1}(t, 0)$, we get

Similar to the above proof, we obtain that Eqs (2.2)–(2.4) hold. Hence, the proof is completed.

Let the mapping $\Psi:P\rightarrow P$ by

where

Lemma 2.4. Assume that (H$_1$) holds. Then, $\Psi:P\rightarrow P$ is well defined.

Proof. For each $x = (u_1, u_2, v_1, v_2)^T\in P$ and $t\in \mathbb{T}$, by (2.7) we have

Letting $\eta = s-\omega$ in (2.11), in view of the periodicity of $b_{11}, \; b_{12}, \; \tau_1, \; \tau_2, \; \tau_3, c_2$, and $d_1$, we have

From the periodicity of $a_1$ and the properties of $e_p(t, s)$, we have

Thus, by (2.12) we have $(\Psi u_1)(t+\omega) = (\Psi u_1)(t)$. Similar to the above proof, we also have

From ^[22], it is easy to see that $e_{\ominus(-a_1)}(t, t-\omega), \; e_{\ominus(-a_2)}(t, t-\omega), \; e_{\ominus(\alpha_1)}(t, t-\omega)$, and $e_{\ominus(\alpha_2)}(t, t-\omega)$ are independent on $t$. By (2.7), we get

and

It follows from (2.13) and (2.14) that

Similar to the above proof, from (2.8)–(2.10), we have

From (2.15)–(2.18), we have

Hence, $\Psi x\in P$.

Lemma 2.5. Assume that (H$_1$) holds. If $\Lambda < 1$, then $\Psi:\Gamma_R\cap P\rightarrow P$ is strict-set-contractive, where $\Gamma_R = \{x\in X:||x|| < R\}$,

Proof. From Lemma 2.4, it is easy to see that $\Psi$ is continuous and bounded on $\Gamma_R$. Let $U\subset\Gamma_R$ and $\gamma = \alpha_{X}(U)$. For any sufficiently small positive number $\varepsilon$, there is a finite family of subsets $\{U_i\}$ such that $U = \cup_iU_i$ and $\mathrm{diam}U_i\leq\gamma+\varepsilon$. Thus,

where $x = (u_1, u_2, v_1, v_2)^T, \; \tilde{x} = (\tilde{u}_1, \tilde{u}_2, \tilde{v}_1, \tilde{v}_2)^T.$ For each $x, \tilde{x}\in U$ and $t\in[0, \omega]_\mathbb{T}$, we have

Therefore, we have

Since $\varepsilon$ is arbitrarily small and $\Lambda < 1$, we have

and $\Psi$ is strict-set-contractive on $P\cup\Gamma_R$.

3.   Existence of positive periodic solution

In this section, we need the following assumption:

(H$_2$) There exist constants $r$ and $R$ with $0 < r < R$ such that

and

Theorem 3.1. Suppose that all conditions of Lemma 2.5 and assumption (H$_2$) hold. Then, system (1.6) has at least one positive $\omega$-periodic solution.

Proof. We will use Lemma 2.2 for studying the existence of positive $\omega$-periodic solutions to system (1.6). Let $\Gamma_{R, r} = \{x\in P:r < ||x|| < R\}$. In view of Lemma 2.3, it is easy to see that if there exists $x^*\in P$ such that $\Psi x^* = x^*$, then $x^*$ is a positive $\omega$-periodic solution of system (1.6). Since all conditions of Lemma 2.5 hold, we know that $\Psi:\Gamma_{R, r}\cap P\rightarrow P$ is strict-set-contractive. Now, we show that condition (1) or (2) of Lemma 2.2 holds. For each $x = (u_1, u_2, v_1, v_2)^T\in \Gamma_{R, r}$, we first show that $\Psi x\ngeq x$ for $||x|| = r$. Otherwise, there exists $x = (u_1, u_2, v_1, v_2)^T\in \Gamma_{R, r}$ with $||x|| = r$ such that $\Psi x\geq x$. Thus, $\Psi x- x\in\Gamma_{R, r}$ which implies that

and

In addition, for $t\in[0, \omega]_\mathbb{T}$ we have

From (3.1) and (3.4)–(3.7), we have

(3.3) and (3.8) are contradictory. Next, we show that $\Psi x\nleq x$ for all $x\in\Gamma_{R, r}$ and $||x|| = R$. Otherwise, there exists $x = (u_1, u_2, v_1, v_2)^T\in \Gamma_{R, r}$ with $||x|| = R$ such that $\Psi x\leq x$. Thus, $x-\Psi x\in\Gamma_{R, r}$ which implies that

From (3.9), for $t\in[0, \omega]_\mathbb{T}$, we have

which implies

which implies

which implies

which implies

From (3.10)–(3.13), we have

which is a contradiction to (3.2). Applying Lemma 2.2, we obtain that $\Psi$ has at least one nonzero fixed point in $\Gamma_{R, r}$. Hence, system (1.6) has at least one positive $\omega$-periodic solution.

4.   Numerical examples

Example 4.1. When $\mathbb{T} = \mathbb{R}$, consider the following system:

where

Then, we get

Choosing $R = 0.1, \; r = 0.01,$ we get

and

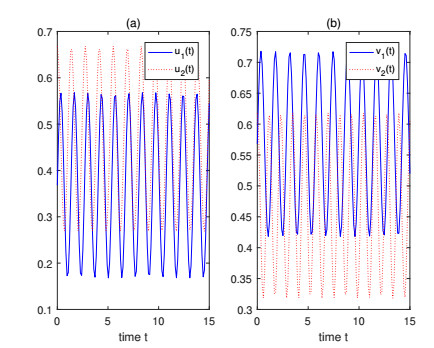
One can see that all conditions of Theorem 3.1 hold. Hence, system (4.1) has at least one positive $\omega$-periodic solution. Figure 1 shows periodicity of the solution to system (4.1).

Example 4.2. When $\mathbb{T} = \mathbb{Z}$, consider the following system:

where

Then, we get

Choosing $R = 10^{-3}, \; r = 10^{-4},$ we get

and

Thus, all conditions of Theorem 3.1 hold. It follows that system (4.2) has at least one positive $\omega$-periodic solution. Figure 2 shows the periodicity of the solution to system (4.2).

5.   Conclusions

In this paper, the issues of the existence of positive periodic solution to a class of enterprise cluster models with feedback controls and time-varying delays on time scales have been studied. Based on the theory of time scales, the fixed point theorem of strict-set-contraction, and under some conditions, we showed that system (1.6) has at least one positive periodic solution. Two examples with their respective computer simulations are given to illustrate the effectiveness of the obtained results. This article develops the corresponding results in ^[12] in two aspects. On the one hand, the model studied in this article is a generalization of classic enterprise cluster models. But, the model in ^[12] has exponential function terms. Hence, the model in this article can better characterize the enterprise cluster model. On the other hand, the research method of this article is different from that of ^[12]. The research method in this paper can be applied to the study of the existence and dynamical behaviors of positive periodic solutions or almost-periodic solutions for neutral-type enterprise cluster models.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work is supported by the Doctor Training Program of Jiyang College, Zhejiang Agriculture and Forestry University (RC2022D03).

Conflict of interest

The authors confirm that they have no conflict of interest in this paper.