The defined contribution pension plan after retirement under the criterion of a revised loss considering the economic situation

1.   Introduction

According to the ways of deposit and payment, the pension plan can be divided into the type of defined benefit (DB) and the type of defined contribution (DC). DB is a pension plan that determines the pension deposit according to the fixed wage, and the risk is borne by the insurance company; DC is a pension plan with a fixed contribution, but the pension income can be adjusted by the risk capital market, and the longevity risk is borne by the policyholder. Driven by the dual purpose of benefiting the insured and the insurance company, the pension plan domestically and abroad is gradually dominated by DC. From its birth, many studies have been conducted on the DC pension plan, such as literature ^{[1,2,3,4,5,6,7,8,9,10,11,12,13]}.

The pension plan can be divided into the accumulative stage of the premium before retirement and the pension income stage after retirement. In the post-retirement stage, by paying a pension, the social instability caused by numerous unemployed retirees can be avoided, thus ensuring economic stability and sustainable social development. Moreover, in this stage, due to the continuous issue, the balance of pension fund accounts gradually decreases. To protect the terminal wealth of the insurance company (the terminal surplus of the account is not lower than the established balance), it is necessary to improve the optimal allocation of risk assets after retirement. At present, most studies focus on the post-retirement stage, such as the literature ^{[1,2,3,4,5,7,8,9,10,11,12,13]}; however, relatively few relevant studies focus on the post-retirement stage, and only a small number of scholars have considered this aspect, such as the literature ^[6], which also investigated the whole stage before and after retirement. In these studies, the research work is generally conducted based on two common optimization criteria: One is the utility function criteria, such as the literature ^{[1,2,3,4,6,9,12,13]}, and the other is the mean-variance criterion, such as the literature ^[5,10,14]. The utility function is a relatively early optimization criterion, and its advantage is that the value function is easy to deduce and calculate mathematically; its disadvantage is that just considers the wealth level of the terminal time but ignores the risk in the investment process. The mean-variance criterion overcomes this drawback and considers both income and risk. Although this criterion considers return and risk, it pays only attention to the risk and returns at the terminal moment. However, due to the characteristics of people's livelihood and long-period investments, large losses of pension accounts should be avoided in the process of risk investment; in this case, the mean-variance criterion does have a good measurement effect.

In recent years, minimizing the expected square loss criterion has gradually become a new optimization criterion in pension planning research. In fact, minimizing the expectation of the difference between the actual and target wealth levels as an optimization criterion can better measure the pension account loss. This criterion was first introduced into pension plans by Habemans and Vigna ^[9]. Sun et al. ^[12] considered the problem of pre-retirement pension plans with random wage income, but similar to the literature ^[15], their study only involved risk-averse criteria, which is inconsistent with the current operating philosophy of earning preference of insurance companies. Then, Vigna and Habemans ^[14] investigated the multidimensional asset pension plan based on different risk measures with the expectation square loss criterion. Sun et al. ^[10] proposed a loss recovery criterion with loss aversion and surplus preference. It uses a positive penalty factor to hedge the part above the expected level of wealth as profit and takes the part below the expected level of wealth as a risk and punishes it again. When the penalty factor is equal to zero, the criterion is the general expected square loss criterion, and the fund manager is risk-aversion; when the penalty factor is larger than zero, the fund manager is surplus preference. Although Sun et al. ^[11] avoided the disadvantage of taking the part that exceeds the expected level of wealth as a risk, their study considered the pension plan in the pre-retirement stage like many other studies.

To improve the pension benefits of retirees and effectively enhance the quality of pension work, more attention should be paid to the post-retirement stage pension plan. Furthermore, with the deepening of social development, people's living standards are constantly improving, there are an increasing number of longevity people, and pension treatment after retirement has received wide attention. Chen et al. ^[12] studied the problem of DC pension plan before and after retirement, but they considered the utility of wealth in the end; Dong and Zheng ^[13] studied the same problem of short-selling and portfolio constraints after retirement, but they regarded managers as conservative based on the general criterion of expectation squared loss.

Seeking benefits and avoiding losses is a business philosophy generally followed by pension fund managers. Based on this concept, the management strategy of surplus preference has become the management method commonly adopted by insurance companies. With the changes in the global economic situation, especially the impact of the global COVID-19, the great changes in the economic situation also significantly affect people's pension levels.

Inspired by the above literature and analysis, this paper investigates the optimal asset allocation of DC pension, which is affected by the economic situation after retirement under the modified criterion of quadratic loss that considers surplus preference and risk aversion. In the following, this criterion is referred to as the criterion of modified quadratic loss. Assuming that retirees' pension payment rate conforms to the drift-diffusion model and insurance companies invest in risk-free assets and risky assets respectively. The closed forms of the optimal time-consistent investment strategy and the value function are obtained by following the stochastic dynamic programming principle and using the method of optimal control. Finally, the sensitivity of key parameters is analyzed. The innovations of this paper are as follows:

(1) Different from many studies in recent years such as ^{[1,2,3,4,5,7,8,9,10,11,12,13]}, which consider only the pension accumulation stage, i.e., the optimal pension plan before retirement, we investigate the optimal asset allocation of DC pension in the post-retirement stage.

(2) By introducing the penalty coefficient, the general criterion of quadratic loss is supplemented with the criterion of modified quadratic loss that combines surplus preference and risk aversion. In this way, the part exceeding the investment target is truly identified as profit rather than risk, and the part below the investment target continues to be regarded as a risk, thereby overcoming the risk defect that the literature ^[13,14,15] cannot fully identify.

(3) The impact of the overall economic situation on the expected rate of pension payment is considered, and the impact of the overall economic situation on the optimal asset allocation of the pension is analyzed, and the rationality of the model is verified.

2.   The model assumption

In this paper, it is assumed that all stochastic processes are defined on the complete probability space ${{(\Omega , \{ }}{\mathcal{F}_t}{{\text{\} }}_{t \in [0, T]}}{\text{, P)}}$, the ${\rm{ \mathsf{ σ} }}$-filtration flow ${\{ {\mathcal{F}_t}\} _{0 \leqslant t \leqslant T}}$ is complete and right continuous, and ${{\text{\{ }}{\mathcal{F}_t}{\text{\} }}_{t \in [0, T]}}$ denotes the sum of all market information at time t, and all stochastic processes are adaptation processes in the complete probability space. $T$ is a limited time, which represents the investment time of the pension and the benefit time of the participant's pension. Continuous trading is permitted, and assets can be arbitrarily divided, with no friction, self-financing, and no arbitrage.

In this paper, we consider that the pension fund manager runs the pension account of the participant based on the asset portfolio at the time of the participant's retirement t = 0(year) and t = T(years) to minimize the loss at the investment moment. The following introduces the price process, wealth process, and loss function of investment assets, respectively.

Pension fund managers of insurance companies take out a certain proportion $\pi (t, x)$ of their wealth from the participants' pension accounts to invest in risky assets (such as stock), whose price $P(t)$ can be described by the diffusion process $dP(t) = P(t)(\mu dt + \sigma d{B_1}(t))$, where $\mu$ denotes the expected yield of unit risk assets, $\sigma$ represents the price volatility of unit risk assets, ${B_1}(t)$ is a standard Brown motion and represents the random factors affecting the price of risky assets. The insurance company uses the rest of the pension accounts to invest in risk-free assets (such as the bank account), whose price ${P_0}(t)$ is modeled by $d{P_0}(t) = {P_0}(t){r_0}dt$, where ${r_0}$ denotes the rate of risk-free interest. This paper assumes that the rate of pension payment for participants after retirement satisfies the following diffusion process

where $({\mu _b} + \xi {r_0})$ represents the rate of pension payment, ${\mu _b}$ denotes the basic growth rate of the pension payment, $\xi {r_0}$ represents the rate of pension payment relevant to the overall economic situation, and $\xi ( > 0)$ is the coefficient of growth rate related to the overall economic situation, and ${\sigma _b}$ represents the volatility of the pension payment. When the economic situation is good, $\xi$ has a large value, and when the economic situation is poor, $\xi$ has a small value. One-dimensional standard Brownian motion ${B_2}(t)$ represents the random factors affecting the pension payment rate. Obviously, the rate of DC pension payment is closely related to the capital market. We assume that the covariance $\langle d{B_1}(t), d{B_2}(t)\rangle = \rho dt$ and $\rho > 0$ is the correlation coefficient of the pension payment rate and risk capital market.

Let the wealth level of pension accounts at time t be $X(t)$, which can be derived from the above assumptions

where ${x_0}$ represents the wealth of pension account at the retirement time $t{\text{ = 0}}$.

Definition 1. Let $\pi (t, x)$ be the existence and uniqueness solution to Eq (1). If $\pi (t, x)$ is ${{\text{\{ }}{{\text{F}}_t}{\text{\} }}_{t \in [0, T]}}$ predictable, and $E[\int_0^\infty {{\pi ^2}(t, x)dt} ] < \infty a.e$ for all $x \in {R^ + }$, then $\pi (t, x)$ is called an admissible strategy, and all admission strategies are called the admissible strategy set.

Definition 2. $R(t, {X^\pi }(t)) = {(G(t) - X(t))^2} + \eta (G(t) - X(t))$ is called the function of modified quadratic loss, where $G(t)$ represents the expected level of the wealth of pension accounts at time t, $\eta ( \geqslant 0)$ represents the modified factor, and $G(t) - X(t)$ represents the deviation between the expected level of account wealth and the actual level of account wealth.

Let $\eta > 0$. When the level of actual account wealth $X(t)$ exceeds the level of expected account wealth $G(t)$, the modified factor $\eta$ in the function of modified quadratic loss is to reduce the degree of misjudging the gain as the loss, and it can compensate for the loss of ${(G(t) - X(t))^2}$ to a certain extent; when the wealth of actual account wealth $X(t)$ is smaller than the expected wealth level $G(t)$, the modified factor compensates for the extent of the loss. If $\eta = 0$, it is the function of quadratic loss in the literature ^[7]. Obviously, this paper improves on the loss function in the literature ^[7,14,15,16]. Therefore, according to the relationship between the modified factor $\eta$ and 0, pension fund managers can be divided into the type of risk aversion ($\eta = 0$) and surplus preference ($\eta > 0$). Here, we conduct a comparative study on the two types of managers.

Definition 3. For $\forall \pi \in \Pi$, ${J^\pi }(t, x, l) = E[R(T, {X^\pi }(T))\left| {X(t)} \right. = x, L(t) = l]$ is called the function of preference, and $V(t, x, l) = \mathop {\min }\limits_{\pi \in \Pi } {J^\pi }(t, x, l)$ is also called the value function or the function of minimum loss.

Therefore, the problem investigated in this paper can be transformed into the stochastic optimal control problem as follows:

3.   Solution to the problem

The differential operator of the value function $V(t, x, l)$ is

Using the stochastic optimal control principle, problem (2) can be transformed into the following HJB equation:

To solve Eq (3), the test theorem is given below.

Theorem 1 (test theorem). If the function $H(t, x, l) \in {C^{1, 2, 2}}([0, T] \times {R^ + } \times {R^ + })$ is the solution to Eq (3) and satisfies the boundary condition $H(T, X(T), L(T)) = R(T, X(T))$, then $H(t, x, l) \leqslant J(t, x, l)$. Furthermore, if ${\pi ^ * } \in \Pi$ exists and ${\pi ^ * } \in \arg \mathop {\min }\limits_{\pi \in \Pi } {\mathcal{A}^\pi }V(t.x, l)$, then $H(t, x, l) = V(t, x, l)$ for $\forall t \in [0, T]$.

Proof. Combining the properties of the local martingale, we have

For each $s \in [t, T]$, applying the ${\text{It}}\hat {\text{o}}$ formula of the diffusion process to $H(t, x, l)$ and then integrating it again yields

Taking the conditional expectation on both sides of the above formula and then

From the HJB Eq (3), for every $\pi \in \Pi$, $s \in [t, T]$, the following inequality holds.

Furthermore

then

when $\pi = {\pi ^ * } \in \arg \mathop {\min }\limits_{\pi \in \Pi } {\mathcal{A}^\pi }V(t.x, l)$, $E[\int_t^T {{\mathcal{A}^{{\pi ^ * }}}} H(s, X(s), L(s))ds\left| {{\mathcal{F}_t}} \right.] = 0$. This implies that

By the definition of $V(t, x, l)$, we have

Therefore, according to Definition 3, if ${\pi ^ * } \in \Pi$ exists, and ${\pi ^ * } \in \arg \mathop {\min }\limits_{\pi \in \Pi } {\mathcal{A}^\pi }V(t.x, l)$, then ${J^{{\pi ^ * }}}(t, x, l) = V(t, x, l)$ for $\forall t \in [0, T]$. That is, $H(t, x, l) = V(t, x, l)$, and ${\pi ^ * }$ is the optimal strategy for the optimal control problem (2).

Then, Eq (3) is solved.

Suppose that the solution to Eq (3) is in the following form

Combined with the boundary conditions of Eq (3), we have

Taking the partial derivative for $V(t, x, l)$, we have

Substituting the above partial derivatives into Eq (3) respectively and using the first-order optimal condition, we have

Then, substituting ${\pi ^ * }(t, x)$ into Eq (3) yields

From the arbitrariness of $x$ and $l$, the following differential equations can be obtained

To simplify the solution to the above differential equations, the following substitution is performed first:

Let ${\hat \mu _b} = {\mu _b} + \xi {r_0}$, ${K_1} = {r_0} - \frac{{{{(\mu - {r_0})}^2}}}{{{\sigma ^2}}}$, ${K_2} = {r_0} - \frac{{{{(\mu - {r_0})}^2}}}{{{\sigma ^2}}} - \rho {\sigma _b}\frac{{\mu - {r_0}}}{\sigma }$, and ${K_3} = {r_0} + \rho {\sigma _b}\frac{{\mu - {r_0}}}{\sigma }$.

Finally, we have

Thus, substituting ${A_1}(t)$, ${A_2}(t)$, ${A_3}(t)$, ${A_4}(t)$, ${A_5}(t)$ and ${A_6}(t)$ into Eqs (6) and (4), a closed-form solution of the time-consistent optimal investment strategy

and a closed-form analytic solution of value function can be obtained

where ${A_1}(t)$, ${A_2}(t)$, ${A_3}(t)$, ${A_4}(t)$, ${A_5}(t)$ and ${A_6}(t)$ are described above.

4.   Mathematical and numerical analysis

After calculation, it can be obtained

It can be seen that the time-consistent optimal investment strategy ${\pi ^ * }(t, x)$ is an increasing function of the growth rate coefficient related to the overall economic situation $\xi$. This demonstrates that the overall economic situation is improving, and the pension managers tend to risk capital investment; otherwise, under a poor overall economic situation, the pension fund managers will reduce risk capital investment, which is consistent with the practical management philosophy. In addition, the rate of basic growth for the pension fund ${\mu _b}$ has increased, and the risk capital investment ${\pi ^ * }(t, x)$ has also increased. This is because the more the level of the pension decreases, the more the surplus level of the account needs to be increased by increasing risky investments.

At the beginning of the pension plan (t = 0), two numerical examples are taken to analyze the influence of several key parameters on the optimal investment strategy ${\pi ^ * }(t, x)$ and the function of minimum loss $V(t, x, l)$, explain the economic significance, and verify the rationality of the model and the results.

According to the third set of China Personal Insurance Industry Experience Life Table (2010–2013) issued by the China Insurance Regulatory Commission on December 28, 2016, the life expectancy for males is 79.7 years old, while that for females is 83.7 years old. Now, seven years have passed, and considering the continuous improvement of the people's living standards in our country, the current average remaining life can be taken as 85 years old; that is, to retire at the age of 60, and to enjoy pension benefits with T = 25 years.

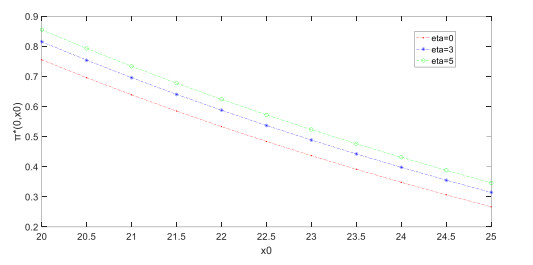
Numerical examples 1. Let the time of retirement be $t{\text{ = 0}}$ year and the stopping time of investment be $T{\text{ = 25}}$ years. Moreover, let the wealth of the pension fund account at the beginning of retirement be ${x_0}{\text{ = 20}}$ thousand yuan, the risk-free rate of interest be ${r_0}{\text{ = 0}}{\text{.03}}$, the return rate of the risk assets be $\mu {\text{ = 0}}{\text{.3}}$, the volatility of the risky assets be $\sigma {\text{ = 0}}{\text{.4}}$, the basic growth rate of the pension payment be ${\mu _b}{\text{ = 0}}{\text{.015}}$, the coefficient of growth rate related to the overall economic situation be $\xi {\text{ = 0}}{\text{.7}}$, the volatility of the pension payment be ${\sigma _b}{\text{ = 0}}{\text{.02}}$, the rate of the first pension payment after retirement be ${l_0}{\text{ = 1}}$ ten thousand yuan/year, the correlation coefficient of the pension payment rate and risk capital market be $\rho {\text{ = 0}}{\text{.3}}$, and the terminal target for the pension fund account be $G(T){\text{ = 6}}$ ten thousand yuan. At retirement time $t{\text{ = 0}}$, the relationship between the wealth of the pension fund account, the penalty coefficient $\eta$, and the optimal investment strategy ${\pi ^ * }(0, {x_0})$ can be obtained using the $Matlab$ software, which is shown in Figure 1.

As illustrated in Figure 1:

1) The optimal investment strategy ${\pi ^ * }(0, {x_0})$ is a monotonous decreasing function of the initial wealth ${x_0}$ at retirement time, which indicates that the more sufficient the pension fund account reserves, the less the proportion of investment to risk capital, and the better the terminal target of the pension fund account can be realized, which is consistent with people's basic understanding.

2) When $\eta = 0$, i.e., when the fund managers are risk-averse, the optimal investment strategy ${\pi ^ * }(0, {x_0})$ reaches the minimum value; the larger the penalty coefficient $\eta$, the greater the optimal investment strategy ${\pi ^ * }(0, {x_0})$. This is because when the wealth exceeds the target level of investment, the surplus is correctly identified as profitable, and at this point, the fund managers are surplus-preferring, the attitude towards investment will become more proactive; if the wealth does not reach the target level of investment, the risk can be correctly identified and punished. Thus, under a more accurate criterion of the risk, the fund managers should change their attitude of investment from conservative to active: by increasing the investment in risky assets, the investment targets can be achieved as soon as possible, which will increase the surplus level and thus the level of pension payments for beneficiaries.

Numerical examples 2. Let the time of retirement be $t{\text{ = 0}}$ year and the stopping time of investment be $T{\text{ = 25}}$ years. Furthermore, let the wealth of the pension fund account at the beginning of retirement be ${x_0}{\text{ = 20}}$ thousand yuan, the rate of risk-free interest be ${r_0}{\text{ = 0}}{\text{.03}}$, the return rate of the risk assets be $\mu {\text{ = 0}}{\text{.3}}$, the volatility of the risky assets be $\sigma {\text{ = 0}}{\text{.4}}$, the basic growth rate of the pension payment be ${\mu _b}{\text{ = 0}}{\text{.015}}$, the coefficient of growth rate related to the overall economic situation be $\xi {\text{ = 0}}{\text{.7}}$, the volatility of the pension payment be ${\sigma _b}{\text{ = 0}}{\text{.02}}$, the correlation coefficient of the pension payment rate and risk capital market be $\rho {\text{ = 0}}{\text{.3}}$, and the terminal target of the pension fund account be $G(T){\text{ = 1}}$ ten thousand yuan. At retirement time $t{\text{ = 0}}$, the relationship between the penalty coefficient $\eta$, the rate of first pension payment ${l_0}$, and the function of minimum loss $v(0, {x_0}, {l_0})$ can be obtained using MATLAB software, which is shown in Figure 2.

It can be seen from Figure 2:

1) When $\eta = 0$, i.e., when the fund manager is risk-aversion, the function of minimum loss $v(0, {x_0}, {l_0})$ reaches the maximum value, and with the increase of penalty coefficient $\eta$, i.e., the fund manager is surplus-preferring, the function of minimum loss $v(0, {x_0}, {l_0})$ decreases; this shows that the function of minimum loss under the criterion of surplus-preferring and risk-aversion can identify investment risks more correctly than the function of general loss.

2) The higher the rate of pension payment ${l_0}$, the greater the function of minimum loss $v(0, {x_0}, {l_0})$. This indicates that a greater rate of pension payment will lead to a large loss of the pension fund account, which is consistent with the general empirical understanding, so choosing an appropriate payment rate is crucial for risky control.

From the above two examples, it can be seen that the risk measured by the function of minimum loss under the general criterion of quadratic loss is too large, and the investment of venture capital is too small. Therefore, the general criterion of quadratic loss cannot fully improve the wealth level of pension fund accounts. Moreover, under the criterion of modified quadratic loss, due to the correct identification of profit and risk, the measurement of risk is reduced, and the wealth level of pension fund accounts can be enhanced by increasing the investment amount of risk capital and utilizing the income of the risk capital market.

5.   Conclusions

In this paper, a criterion of modified quadratic loss that combines surplus-preferring and risk-aversion is considered, and under this criterion, the optimal pension plan affected by the economic situation after retirement is investigated. This criterion optimizes the general criterion of quadratic loss, which considers not only the interests of insurance companies but also the interests of pension participants, so it can more accurately identify risks and benefits. Under this criterion, with more accurate identification of risk, the fund managers prefer to increase the investment of risk assets to better achieve the expected goals of investment and better provide payment of pension for retirees. Thus, the investment attitude of the fund managers has changed from conservative to active; furthermore, the rate of pension payment should be set appropriately; otherwise, insurance companies will have a large loss, which is not conducive to stable operation. Though the rate of pension payment should not be too high, under normal circumstances, some of the insurance companies will pay the terminal part of the pension fund account as the death benefit to the beneficiaries of the participants.

Certainly, the criterion used in this paper has certain defects. For instance, the penalty coefficient $\eta$ is too large, which makes the risk of measurement too small and is not conducive to risk management. Also, the active attitude of investment may cause improper investment of risky assets and bring greater risks of operation to the insurance companies. Therefore, the loss function as a risk criterion is not perfect, and future work should consider the bankruptcy probability criterion, the utility function criterion, or other criteria.

Revised sentence: Moreover, using the penalty coefficient to depict the economic state does not have sufficient accuracy. Recently, He et al. ^{[16,17,18,19]} proposed a stochastic volatility model with Markov modulation that can accurately capture the impact of diverse market economic states on risk asset prices. However, integrating this model into the DC pension problem increases the complexity of obtaining the closed solution to the value function in the HJB equation. Therefore, finding a way to overcome this challenge and derive an analytical solution to the value function under this model is a crucial focus of future research.

Use of AI tools declaration

We have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

Z. Sun was partially supported by the Humanities and Social Sciences Research Project of the Ministry of Education of China (No.21XJC910001). The author is grateful to the anonymous referees for their valuable comments and suggestions.

Conflict of interest

The authors declare no conflicts of interest.