Stress boundary layers for the Giesekus fluid at the static contact line in extrudate swell

1.   Introduction

The stress singularity at a static contact line is a longstanding challenge for models of viscoelastic liquids. This phenomenon occurs when a fluid interface separates from a solid surface, such as during polymer extrusion where the fluid exits a channel (in applications termed a die). This situation is particularly significant for viscoelastic liquids because the diameter of the emerging jet is often several times larger than the channel, leading to extrudate swell (histroically termed die-swell). A critical aspect is that the fluid flow traverses the contact line at the solid/air junction. The abrupt change in boundary conditions, from no-slip on the solid channel wall to no-shear on the free surface outside the die, creates a singularity in the fluid stress field when the angle of fluid separation is sufficiently large. This stress singularity presents issues for Newtonian fluids ^[1,2,3], but is particularly problematic for viscoelastic fluids due to the profound effects of their memory properties on flow behavior ^[4,5]. This situation should be contrasted with edge flow ^[6] or rivulet flow ^[7,8,9], where the fluid flow is parallel to the contact line.

Extrusion is important in the polymer processing industry, where it is used for the manufacturing of many plastic pipe and profile products ^[10,11]. The polymers used typically possess a macromolecular structure with long chains of repeating units. They are processed in a molten state, exhibiting very high viscosity and shear-thinning behavior (due to the alignment and disentanglement of the polymer chains with increasing shear-rate). In addition, they display elasticity, which is responsible for effects such as stress relaxation and normal stress differences ^[12,13,14]. Normal stress differences contribute to flow instabilities ^[15,16,17] and extrudate swelling ^[18]. The latter phenomenon is particularly striking in polymers, where a significant increase in cross-sectional area occurs ^[4,5,19].

The extrudate swell problem is not only relevant for industrial applications but also serves as a crucial computational test for viscoelastic fluids with free surfaces. It is a benchmark problem in computational rheology ^[20]. During the transition from fully-developed flow within the die to plug flow outside, the fluid jet swells due to stress relaxation at the surface. The maximum cross-sectional area of the jet is usually reached a few die-diameters downstream from the die exit. The behaviors of polymeric and Newtonian jets differ significantly ^[19]. For polymer melts and solutions, which are highly viscous and involve moderate velocities, the flow is primarily in the Stokes regime rather than at high Reynolds numbers. Polymeric jets show a substantial increase in the swelling ratio, where the dimension of the extrudate is seen experimentally as two to three times that of the die ^{[21,22,23,24,25]}. This constrasts with Newtonian jets, where the swelling ratio is only 1.1 to 1.2 ^{[26,27,28,29,30]}. As the Reynolds number increases, the swelling ratio for polymeric jets also increases, while for Newtonian jets, it decreases, leading to contraction at $\text{Re} > 16$. Higher Reynolds numbers are achievable experimentally for Newtonian fluids compared to polymeric fluids, which are limited to moderate flow rates due to instability and melt fracture at high extrusion rates ^[17]. This confines polymeric fluid dynamics to a low Reynolds number regime, where the swelling ratio increases with flow rate, and inertia effects are negligible.

As the polymeric fluid exits the die, the polymer free surface is assumed to remain attached to the die exit. This forms a three-phase contact point/line among two immiscible fluids and a solid. The interface shape evolves from this tri-junction until, in the absence of streamwise normal stresses, the polymer reaches its final thickness. Analyzing and simulating flows involving such contact points or lines is challenging due to a singularity in the rate-of-deformation and stress tensors. This singularity results from the change in boundary conditions from no-slip along the die wall to no-shear on the polymer free surface. The trijunction is usually modeled as a sharp corner with a fixed or static contact point/line ^[31], contrasting with moving contact lines in liquid/fluid/solid systems. Such singularities raise questions about the well-posedness of the mathematical problem, troublesome even for Newtonian flows and particularly acute for viscoelastic fluids. The physics near a contact line remains unclear and has been studied from both molecular and continuum perspectives ^{[32,33,34,35,36]}. At the continuum level, the presence of a stress singularity at the contact line suggests a breakdown of the theory, leading some researchers to introduce slip along the die-wall boundary in this vicinity. This approach has been used in both Newtonian cases ^{[32,37,38,39,40,41]} and polymer models ^[42]. The origin of such slip may be attributed to true slip at the molecular level or apparent slip on a macroscopic scale due to microscopic phenomena ^[43], such as surface roughness or the presence of a lower viscosity gas in surface grooves. Introducing wall slip significantly alters the local stress behavior, making it difficult to determine behavior in the no-slip case, even when slip effects are minor. In the no-slip case, the stress singularity is physically acceptable if integrable, ensuring a finite total force on the solid upstream die wall.

Numerous constitutive equations have been developed to relate stress and strain rates in polymer flows ^[44]. The Giesekus model, is based on the concept of a deformation dependent tensorial mobility for the polymer molecules ^[45]. It enables a qualitative description of a number of well-known properties of viscoelastic fluids, namely shear thinning, nonzero second normal stress coefficient and stress overshoot in transient shear flows ^[44,46,47].

This study continues the investigation into the stress singularity at the separation point for the Giesekus viscoelastic fluid. Currently, little is known about the behavior of this model near such points, unlike Newtonian viscous fluids ^[48]. Understanding these singularities tests the well-posedness of the constitutive equations and can improve numerical scheme convergence, similar to the Newtonian case ^[1,2]. Preliminary findings on this problem were presented in ^[49], where the stress singularity was identified. However, the approach relied on order-of-magnitude estimates along streamlines without detailed examination of their mathematical solutions. Here, we address this issue by providing boundary layer solutions and setting the results on a more rigorous footing through matched asymptotic analysis. The key to this approach is aligning the polymer extra-stress tensor along streamlines, which reformulates the constitutive equations along their characteristics and enables the correct stress information to be transmitted between the different asymptotic regions. The analysis is able to quantify the effect of the singularity on the free-surface for the Giesekus model, which has been a key unknown for viscoelastic liquids ^[5]. The approach extends the results of the simpler stick-slip problem ^[50] and the asymptotic structure parallels that of the simplified Phan-Thien-Tanner (sPTT) model in ^[51], although the details of the boundary layers are very different.

2.   Problem formulation and governing equations

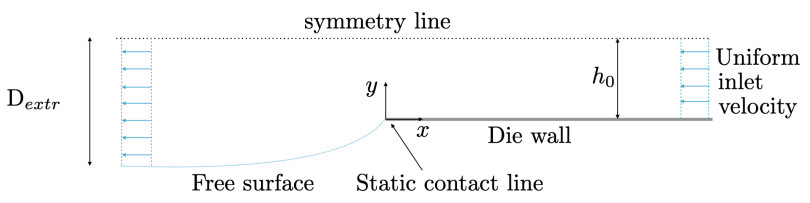
We present here the geometry, summarized in Figure 1, and the dimensionless governing equations. The dimensional model is given in ^[49]. The velocity, pressure and extra-stress fields satisfy the conservation equations

where the total extra-stress $\mathbf{T} = \beta \mathbf{T}^s + (1-\beta) \mathbf{T}^p$ has a Newtonian solvent component $\mathbf{T}^s = 2\mathbf{D}$ and the polymer extra-stress satisfies the Giesekus constitutive equation

with the upper convected derivative of stress and the rate of strain terms being

The main dimensionless parameters are the Weissenberg number $\text{Wi}\ge 0$, the solvent viscosity fraction $\beta \in[0, 1]$ and the mobility factor $\kappa \in[0, 1]$. Realistic behavior of the model is usually obtained for $0 < \kappa < 0.5$ ^[12,52]. The analysis will be confined to the die exit, the local coordinate system for which at the lower die-wall is depicted in Figure 2. As boundary conditions, we have no-slip on the die-wall, whilst on the free-surface of the emerging jet we have the kinematic (or no-flux) condition, together with the tangential and normal stress balance presented as

where $C_a$ is the capillary number, $p_a$ the external atmospheric pressure (taken as datum and thus set to zero), $\mathbf{m}$ unit tangent and $\mathbf{n}$ unit normal to the free surface.

The separation angle $\alpha$ is a parameter of the problem, its physical range of interest being between $\pi/2$ and ${3 \pi}/{2}$. It is determined by the global flow rather than the normal stress condition in (2.4), which specifies the free-surface curvature. The influence of surface tension is thus primarily on the shape of the free-surface and not the singularity, as explained in ^[53].

The formulation of the problem that we adopt is one where the velocity field (and an orthogonal vector) are used to span the polymer stress field. This idea was first suggested by Renardy ^[54,55] as an approach to dealing with situations where the stress field encounters a geometrical singularity, such as at sharp corners. The mathematical basis for doing this, is that the polymer stress is then aligned with the streamlines of the flow, which are characteristics of the constitutive equations ^[56,57,58]. To achieve this, we write the polymer stress in the form

where

and $T_{uu}$, $T_{uw}, T_{ww}$ are the natural stress components. The component form of the Giesekus constitutive equation then gives the natural stress equations

These equations are in their steady form, which is the regime we investigate for the asymptotics. The unsteady version is required for full numerical simulations that we present in Section 4, a version of which can be found in ^[59].

3.   Matched asymptotics

The goal is to determine the asymptotic behavior of the velocity and stress variables as the radial distance to the contact line vanishes. This asymptotic limit is inherently nonuniform and requires consideration of a three-region structure, summarized in Figure 3. It comprises narrow stress boundary layers for the polymer at both the die wall and free-surface linked through an outer (also termed core) region in which the solvent stress dominates. We approach the problem using the method of matched asymptotic expansions, with emphasis on deriving systematically the boundary layer equations and providing their solutions. We pose the problem in the sector $0 < r < \infty, 0 < \theta < \alpha$, with $\alpha\in [\pi/2, 3\pi/2]$. In this geometry, the problem is self-similar with no inherent length scale, so that we may take $\text{Wi} = 1$ without loss of generality. The asymptotic results we derive will hold for any positive value of the Weissenberg number. However the Weissenberg number will influence the length scale on which the asymptotics dominate and we discuss this further in Section 5 using the numerical results in Section 4.

3.1.   The outer or core solution

The outer region is near to the separation point at the die exit, but still away from both the solid and free surfaces. The main behavior that identifies it, is that the solvent stress dominates the polymeric stress in this region, so that

with both possessing singular behavior. In fact, Renardy ^[60] argues that this will be the case for most flows of interest where the Weissenberg number is large. Here the presence of the stress singularity, means that the "local" Weissenberg number is infinite, taken as the product of the shear rate (which goes infinite at the singularity) and the relaxation time. Thus many of the features of high Weissenberg number flows will manifest themselves in this problem, despite the actual Weissenberg number being unity, purely because of the singularity. In addition to (3.1), a further example will be the presence of the wall boundary layer being the same equations as those found for high Weissenberg numbers ^[61].

We now summarize the main results for this region from ^[49]. This gives the outer region a Newtonian balance $\mathbf{T} \sim \beta \mathbf{T}^s$ for the stress, and the momentum equation reduces to Stokes flow,

for which there are well-known separable solutions ^[48]. Using a stream function, these may be written as

where $C_0$ is an arbitrary constant and expressions for the angular functions $f_0(\theta)$ and $g_0(\theta)$ can be found in ^[49] or ^[51].

The leading eigenvalue $\lambda_0$ depends on the separation angle $\alpha$, and satisfies the transcendental equation

A discussion on its behavior and the key angles is given in ^[53]. The stress singularity at the separation point is present for separation angles between $129^o$ and $270^o$, with the swelling range greater than $180^o$ being of relevance for viscoelastic fluids.

This Newtonian flow field in the core region gives order of magnitude estimates as

Using these orders of magnitude along with the assumption in (3.1) implies the dominance of the upper convected derivative in the polymeric stress equation resulting in

The natural stress equations at leading order reduce to

provided

which can be subsequently verified. At leading order, the natural stress variables are constant along streamlines, so that the asymptotic solution for the polymer stress in this region is

The first term is the well-known stretching solution and is an exact solution to (3.6). For convenience, power law forms are adopted for the stream function behavior of the natural stress variables,

where $C_1, C_2, C_3$ are arbitrary constants and the exponents

are determined by matching to the boundary layer behavior at the die wall (considered next). Initially, these exponents have to be carried through the analysis, but will be assumed known here for conciseness of exposition. Consequently, the singularity of the polymer stress is determined as

which is subdominant to the solvent stress in (3.5), for all separation angles of interest (i.e., $1/3 < \lambda_0 < 1$). The required assumptions (3.1) and (3.8) can now be verified to hold for this asymptotic behavior. We remark that the presence of the solvent viscosity $\beta > 0$ is needed for this behavior, which no longer holds when $\beta$ vanishes.

The behavior in (3.9) is not uniformly valid around the corner, but rather breaks down near the die wall and free surface. The reasons are different for the two locations. In the die wall case, the omission in (3.6) of the quadratic stress and rate-of-strain terms prevents the recovery of the necessary viscometric stress behavior associated with shear flow at the die wall. For the free-surface, it is only the quadratic stress terms that are required.

Using local Cartesian coordinates $x\sim r, y\sim r\theta$ as shown in Figure 2, we have the limiting behavior

At the free-surface, using Cartesian coordinates $x'\sim-r, y'\sim r(\alpha-\theta)$ as orientated in Figure 2, we have the limiting behaviors

where the constant

is positive for all angles of interest. Although the natural stress $T_{uu}$ is unbounded at the free-surface, this also translates into the leading-order Cartesian normal stress $T_{11}^p = T_{uu}u^2$ being unbounded. A narrow region at the free-surface, a stress boundary layer, is thus needed to arrest its growth. We note that the leading order polymer shear stress $T_{12}^p = T_{uu}uv$ does vanish at the free-surface.

3.2.   The stress boundary layer at the die wall

An inner region is now sought at the die wall. To compare terms systematically, we introduce an artificial small parameter $\epsilon > 0$ through the scaling

and consider $\bar{X} = O(1)$. The equations below are derived for the asymptotic limit $\epsilon \to 0$ and formal expansions are unnecessary since we deal with the leading order terms only. The introduction of this parameter allows us to perform a coordinate expansion of our system of equations in the neighborhood of the wall near to the singularity. Since the parameter $\epsilon$ is not present in the original system, it scales from the solution we derive. Physically it represents the length scale on which the small $\epsilon$ asymptotic behavior near to the singularity emerges. Estimates for it can be determined from numerical solution of the full problem presented in Section 4 and we discuss this in Section 5. The distinction between coordinate and parameter expansions goes back to ^[62,63], and the use of an artificial parameter is mentioned in the classic texts of ^[64,65,66].

The limiting behaviors in (3.13) and dominant balance in the polymer stress equations (2.7), when taken together determine the following scalings

where the boundary layer variables are denoted by bars. The Cartesian components of the solvent stresses follow from the stream function as

where

The scalings for the Cartesian components of the polymer extra-stresses may be determined from (2.5) as

where

at leading order in $\epsilon$. In the scalings of the total extra-stress components, the normal 11 component of the solvent and polymer stresses are comparable in this boundary layer, whilst the remaining polymer components remain subdominant to their solvent counterparts. The momentum equation for this inner region, $\bar{X} = O(1)$ and $\bar{Y} = O(1)$, reduces to

at leading order. These imply that the stream function, solvent stresses and pressure remain unchanged at this order through this boundary layer with the explicit solution

after matching to (3.13), which also givens the form of the pressure.

The leading order boundary layer equations for the polymer natural stresses are

with the parameter

We note that these are the same wall boundary layer equations obtained in the high Weissenberg limit ^[61], and, is a consequence of the singularity inducing high Weissenberg behavior locally in the fluid. We complete their statement, with viscometric stress behavior at the die wall

and outer matching conditions

We remark that the viscometric wall behavior (3.28) can be written in the more familiar Cartesian stress components using the component form of (2.5), which gives

Introducing the shear rate $\dot{\gamma} = \partial \bar{u}/\partial \bar{Y} = 2\kappa C_0 \bar{X}^{\lambda_0-1}$, we have

on the wall, which is the high shear rate viscometric behavior appropriate for the Giesekus model ^[61].

The governing equations (3.24)–(3.26), together with (3.28) and (3.29) possess a similarity solution in the form

the resultant set of ODEs being

with

and the scaled far-field constants

are introduced for convenience. The choice of upper sign in (3.31)–(3.35) occurs for the case $C_0 < 0$ corresponding to flow toward the singularity and is relevant to the extrudate swell situation. For completeness, the lower sign choice corresponds to the case $C_0 > 0$ and flow away from the singularity, which we simply record and don't pursue further here, as it would correspond to the reverse situation of the fluid entering the channel.

The nonlinear third-order system of Eqs (3.31)–(3.33) can be solved as an initial value problem with (3.34) posed as initial data and (3.35) to be determined. As implementation, we used MATLAB solver ode15s on the interval $[\xi_0, \xi_{\infty}]$ with $\xi_0 = 10^{-6}$ and $\xi_{\infty}\geq 10^{10}$ being sufficiently large to ensure convergence to (3.35). Figure 4 presents scaled profiles for $\alpha = 7\pi/6\approx 210^o$, which we take as a representative case. The variation of the far-field constants with selected separation angles are given in Table 1.

3.3.   The stress boundary layer at the free-surface

To derive the asymptotics at the free-surface, we follow the same approach used at the die-wall and introduce an artificial small parameter $\epsilon$ through the scaling $x' = \epsilon \bar{X}$ and consider $\bar{X} = O(1)$. The limiting behavior (3.14) and dominant balance in (2.7), determine the scalings for the other variables as

where $\delta = \epsilon^{\frac{(1-\lambda_0^2)}{(\lambda_0+3)} + 1}$ and we again use bars for the boundary layer (or inner) variables. The leading order polymer natural stress equations are now

which we note are similar to the die wall boundary layer equations, although crucially missing the $\nabla \cdot \mathbf{w}$ terms, since these are small near the slip surface. From (3.14), these require the outer matching conditions

Similar to the die-wall boundary layer, it may be verified that the stream function and pressure remain unchanged from the their limiting outer behaviors in (3.14). In $\bar{X} < 0, \bar{Y} = O(1)$, we thus have

For this given stream function, the nonlinear polymer stress equations (3.38)–(3.40) possess an exact solution. It may be compactly written in the following similarity form

with

The constants of integration have been determined by matching to the limiting outer behavior (3.14). On the free-surface the stresses are now bounded, the recovery of the quadratic stress terms in this boundary layer, being able to arrest the stress growth from the outer region.

For comparison with the solvent stresses, we record the Cartesian components of the polymer extra-stresses, namely,

where

are the leading order expressions and follow from (2.5). The Cartesian components of the solvent extra-stresses may be deduced from the stream function as

with

However, the solvent shear stress vanishes for the stream function (3.42) and its scaling has to be determined from the correction term to the stream function in the outer region, which can be shown to be of size $O(\delta^3\epsilon^{\lambda_0-2})$. Solving for the next term of the stream function provides for unnecessary details and we suffice with recording the scalings for the total extra-stresses in this region as

Only the polymer normal extra-stress $T_{22}^p$ is subdominant to its solvent counterpart. On the free surface $\bar{Y} = 0$, we obtain elongational behavior for the polymer stress in the form

where $\dot{e} = \frac{\partial u_0}{\partial \bar{X}}$ is the elongational rate.

We may now determine the shape of the free-surface using the normal stress condition in (2.4). Introducing the scaled free-surface $h(x') = \epsilon^{\lambda_0+1} H(\bar{X})$, and using the pressure (3.42) and normal total extra-stress (3.49), both evaluated on $y' = \bar{Y} = 0$, the normal stress condition gives

where $g_0(\alpha) = 1/\sin((1-\lambda_0)\alpha)$ and $C_{\alpha}$ as given in (3.15). Integrating then gives the position of the free-surface as

or equivalently

for small negative $x'$. We note that the constant $k$ vanishes in the "stick-slip" planar flow case $\alpha = 180^o, \lambda_0 = 0.5$ and may be verified to be positive for larger separation angles of interest up until $\alpha = 270^o$. The main conclusion is that it is the solvent stress and pressure that determine the shape of the free-surface at the die exit for the Giesekus model, rather than the polymer stress. As such, the curvature of the free-surface (3.51) is that expected of Newtonian flow and its form is consistent with that conjectured in ^[38] and discussed in ^[67]. The singularity is solvent dominated and influences the free-surface through the angle of separation, which is determined by the global flow dynamics within the channel.

4.   Numerical simulation results

We present here further comparisons between the numerical results of the full extradute-swell problem and the theoretical asymptotic behaviors. Initial comparisons were made in ^[49] for parameter values of $Wi = 1, \beta = 0.5$, indicating that the postulated asymtptoics are borne out in the numerical computations. Here we give comparisons for higher Weissenberg numbers, which not only give larger swelling ratios but supports the persistence of the singularity over greater parameter values.

For the numerical simulation of planar extrusion, we use the volume of fluid method in the rheoTool toolbox ^[68] of OpenFOAM. Details of the scheme are given in ^[69] and we use the same implementation specifics (mesh details and solver tolerances for convergence) as given in ^[49]. The natural stress formulation of the Giesekus constitutive equations were used, rather than rheoTool's default Cartesian stresses. This gave more stable results and allowed attainment of higher Weissenberg numbers. We focus on the parameter case $\beta = 0.5$, with two values of the mobility factor $\kappa = 0.1$ and $0.25$ and the selected Weissenberg numbers in the range $1$ to $10$. The Reynolds number is fixed at $10^{-2}$ and all results are in the absence of surface tension. The separation angle is estimated as the angle of the tangent to the free-surface at the die wall contact point. Its values are recorded in Table 2, along with the consequent Newtonian eigenvalue calculated from (3.4). Also recorded are the final and maximum extrudate-swell ratios $D_{extr}/h$ and $D_{max}/h_0$ respectively. The difference in these values illustrate the secondary shrinkage of the extrudate after its initial swell, which is more pronounced with increasing Weissenberg number and smaller mobility factor (the Oldroyd-B model being obtained as $\kappa$ vanishes). Further, these swell ratios appear consistent with the rheotool M3 values reported in ^[69] for Weissenberg numbers up to $6$ (the upper limit of their results). Figures 5 and 6 show the radial behaviors of the velocity components, pressure and natural stresses along three fixed angles (as orientated in Figure 2) in the parameter cases $\text{Wi} = 5, \beta = 0.5$ and $\kappa = 0.25$ or $0.1$. The velocities and natural stresses converge to their theoretical behaviors along all three rays, confirming the assumption leading to (3.2) that the velocity field is Newtonian-like near the singularity. The rapid convergence of the natural stresses is noteworthy. The pressure converges notably slower and is clearly affected whether the ray to the contact point is inside or outside the channel. For comparison with Figure 6, in Figure 7 we include the equivalent plots for larger Weissenberg number $\text{Wi} = 10$ with $\beta = 0.5, \kappa = 0.1$. Similar trends and rate of convergences are observed, confirming the theoretical asymptotics at this higher Weissenberg number.

5.   Conclusions

The details of the matched asymptotic expansion approach for the contact line singularity occurring in extrudate swell have been provided here for the Giesekus model. Similar to the simplified PTT model ^[49,51], the solvent stress dominates the polymer stress, except in boundary layers at both the die wall and the free-surface. The solution has been detailed here for these narrow regions. In both boundary layers, the polymer and solvent stresses are comparable and are required for the polymer stress to adjust either to the no-slip condition on the die wall or the zero shear stress on the free-surface.

We may compare the boundary layer thicknesses at the die wall and free-surface. These are given by the $y$ scaling in (3.17) and $y'$ scaling in (3.37), which we denote as

The free-surface boundary layer is thicker than that at the die wall for $\lambda_0 < 1$, correpsonding to all separation angles greater than $129^o$. This should be contrasted to the sPTT model where the free-surface boundary becomes thinner than that at the die wall for separation angles greater than $199.2^o$. The narrowest values of the boundary layers occurs when $\lambda_0 = 1/3$ corresponds to the $270^o$ angle of separation, when we have

These are smaller than the corresponding values in the sPTT case ^[51].

We have demonstrated the validity of the main asymptotic result (3.9) through its comparison with full numerical simulations of the problem in Section 4. As such, we may use this comparison to now estimate the length scales on which the asymptotics emerge. Figures 5–7 suggest the estimate $\epsilon = 10^{-2}$ as an approximate upper bound on the distance on which the singularity asymptotics and numerical solution agree. We note that this value is limited by the velocity and solvent stresses, the convergence of the polymer stresses being on larger length scales that increase with the Weissenberg number (the polymer results in ^[49] indicate $\epsilon = 10^{-2}$ for Wi$= 1$ whilst here in Figure 7 it extends up to $\epsilon = 10^{-0.5}$ for Wi = $10$). On the length scale at which the solvent singularity emerges around $10^{-2}$, the narrowest boundary layer thickness using (5.1) is $\delta_{wall}\approx 2\times 10^{-3}$. Numerical grids far finer than this would be required to adequately resolve the boundary layers. This shows the extent of the challenges in performing accurate numerical simulations for these models.

The analysis has also elucidated the influence of the stress singularity on the free-surface. The shape of the free-surface local to the singularity is given by (3.51), which shows that it is primarily influenced by the Newtonian eigenvalue. Thus it is the solvent stress rather than the polymer stress that determines the curvature of the surface. However, the polymer stress does play a role in determining the separation angle of the surface, attributed to the relaxation of the normal polymer stresses ^[19]. It is this influence that allows the Giesekus model to attain far higher swelling ratios than Newtonian fluids due to its larger separation angles.

The asymptotic structure presented here, is valid for the wide parameter ranges $\beta\in(0, 1]$ and $\kappa > 0$. However, if either the solvent viscosity vanishes, $\beta = 0$, or the mobility factor vanishes, $\kappa = 0$, then the nature of the singularity changes. These cases require separate consideration and results are currently outstanding. In the polymer melt case $\beta = 0$, the Newtonian velocity field is lost and a decoupling of the velocity and pressure fields from the polymer stress no longer occurs. Simulation results have been obtained for this case in extrudate swell ^[70], although no investigation on the nature of the singularity has been undertaken. When the mobility factor vanishes, we obtain the Oldroyd-B model for which the solvent stress no longer dominates the polymer stress. Whether this model is well-posed in this geometry is an outstanding issue, due to its unbounded stresses at finite strain rates in elongational flow ^[12]. Notwithstanding these isolated parameter cases, the asymptotic results presented here are expected to hold for all positive Weissenberg numbers.

Author contributions

J. D. Evans: Conceptualization, writing-original draft preparation, formal analysis, software, reviewing and editing; M. L. Evans: Formal analysis and software. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

This work was supported by Sun Chemical Ltd and University of Bath scholarship, and FAPESP-SPRINT grant no. 2018/22242-0. The authors declare that they have no conflict of interest.

Conflict of interest

The authors declare no conflicts of interest.