Novel linguistic $ q $-rung orthopair fuzzy Aczel-Alsina aggregation operators for group decision-making with applications

Ghous Ali; Kholood Alsager; Asad Ali; Ghous Ali; Kholood Alsager; Asad Ali

doi:10.3934/math.20241551

AIMS Mathematics

2024, Volume 9, Issue 11: 32328-32365. doi: 10.3934/math.20241551

Previous Article Next Article

Research article Topical Sections

Novel linguistic $q$ -rung orthopair fuzzy Aczel-Alsina aggregation operators for group decision-making with applications

Ghous Ali ^{1
,
,},
Kholood Alsager ^{2
,
,},
Asad Ali ¹

1.
Department of Mathematics, Division of Science & Technology, University of Education, Lahore, Pakistan
2.
Department of Mathematics, College of Science, Qasim University, Buraydah, Saudi Arabia

Received: 17 September 2024 Revised: 30 October 2024 Accepted: 05 November 2024 Published: 15 November 2024
MSC : 03E72, 91B06

In this article, we presented two novel approaches for group decision-making (GDM) that were derived from the initiated linguistic $q$ -rung orthopair fuzzy Aczel-Alsina weighted arithmetic (L $q$ -ROFAAWA) aggregation operator (AgOp) using linguistic $q$ -rung orthopair fuzzy numbers (L $q$ -ROFNs). To introduce these GDM techniques, we first defined new operational laws for L $q$ -ROFNs based on Aczel-Alsina $t$ -norm and $t$ -conorm. The developed scalar multiplication and addition operations of L $q$ -ROFNs addressed the limitations of operations when $q = 1$ . The first proposed GDM methodology assumed that both experts' weights and attribute weights were fully known, while the second technique assumed that both sets of weights were entirely unknown. We also discussed properties of L $q$ -ROFNs under the L $q$ -ROFAAWA operators, such as idempotency, boundedness, and monotonicity. Furthermore, we solved problems related to environmental and economic issues, such as ranking countries by air pollution, selecting the best company for bank investments, and choosing the best electric vehicle design. Finally, we validated the proposed GDM approaches using three validity tests and performed a sensitivity analysis to compare them with preexisting models.

Keywords:

linguistic $q$ -rung orthopair fuzzy set,
aggregation operator,
Aczel-Alsina $t$ -norm,
air pollution,
sensitivity analysis,
decision-making

Citation: Ghous Ali, Kholood Alsager, Asad Ali. Novel linguistic $q$ -rung orthopair fuzzy Aczel-Alsina aggregation operators for group decision-making with applications[J]. AIMS Mathematics, 2024, 9(11): 32328-32365. doi: 10.3934/math.20241551

Related Papers:

[1]	K. Jeganathan, S. Selvakumar, N. Anbazhagan, S. Amutha, Porpattama Hammachukiattikul . Stochastic modeling on M/M/1/N inventory system with queue-dependent service rate and retrial facility. AIMS Mathematics, 2021, 6(7): 7386-7420. doi: 10.3934/math.2021433
[2]	Zhen Wang, Liwei Liu, Yuanfu Shao, Yiqiang Q. Zhao . Joining strategies under two kinds of games for a multiple vacations retrial queue with $N$ -policy and breakdowns. AIMS Mathematics, 2021, 6(8): 9075-9099. doi: 10.3934/math.2021527
[3]	Linhong Li, Wei Xu, Zhen Wang, Liwei Liu . Improving efficiency of the queueing system with two types of customers by service decomposition. AIMS Mathematics, 2023, 8(11): 25382-25408. doi: 10.3934/math.20231295
[4]	Bharathy Shanmugam, Mookkaiyah Chandran Saravanarajan . Unreliable retrial queueing system with working vacation. AIMS Mathematics, 2023, 8(10): 24196-24224. doi: 10.3934/math.20231234
[5]	Shaojun Lan, Yinghui Tang . An unreliable discrete-time retrial queue with probabilistic preemptive priority, balking customers and replacements of repair times. AIMS Mathematics, 2020, 5(5): 4322-4344. doi: 10.3934/math.2020276
[6]	Ciro D'Apice, Alexander Dudin, Sergei Dudin, Rosanna Manzo . Analysis of a multi-server retrial queue with a varying finite number of sources. AIMS Mathematics, 2024, 9(12): 33365-33385. doi: 10.3934/math.20241592
[7]	Messaoud Bounkhel, Lotfi Tadj . Model predictive control based integration of pricing and production planning. AIMS Mathematics, 2024, 9(1): 2282-2307. doi: 10.3934/math.2024113
[8]	Avijit Duary, Md. Al-Amin Khan, Sayan Pani, Ali Akbar Shaikh, Ibrahim M. Hezam, Adel Fahad Alrasheedi, Jeonghwan Gwak . Inventory model with nonlinear price-dependent demand for non-instantaneous decaying items via advance payment and installment facility. AIMS Mathematics, 2022, 7(11): 19794-19821. doi: 10.3934/math.20221085
[9]	Mengrao Ma, Linmin Hu, Yuyu Wang, Fang Luo . Discrete-time stochastic modeling and optimization for reliability systems with retrial and cold standbys. AIMS Mathematics, 2024, 9(7): 19692-19717. doi: 10.3934/math.2024961
[10]	Rubén Blancas-Rivera, Hugo Cruz-Suárez, Gustavo Portillo-Ramírez, Ruy López-Ríos . $(s, S)$ Inventory policies for stochastic controlled system of Lindley-type with lost-sales. AIMS Mathematics, 2023, 8(8): 19546-19565. doi: 10.3934/math.2023997

Abstract

1. Introduction

In this paper, we consider a make-to-stock retrial queueing system. Customers are served immediately if the system contains only products or the production server is idle upon their arrival; if the production server is busy, the customer enters a retrial queue. After the completion of service, the server searches for a customer from the retrial queue. This model reduces the cost of waiting for customers and improves the benefit to producers.

A considerable amount of research has thus been devoted to the production inventory retrial queueing system. Jose and Nair ^[8] examined a retrial queueing system for a production inventory under dynamic rates of production. They obtained the relevant performance measures by using the geometric matrix method based on two models, and numerically compared their expected cost functions. Jeganathan et al. ^[6] verified its performance by using a geometric matrix solution, and obtained the optimal inventory level through numerical simulations of a retrial inventory system. Shajin and Krishnamoorthy ^[16] investigated a retrial production inventory system with the $(s, S)$ replenishment policy. They obtained the relevant performance measures and the optimal $(s, S)$ by using numerical simulations. In the context of an inventory retrial queueing system with multiple servers and multiple server vacations, Jose and Beena ^[7] obtained the performance measures of a system with two servers under the $(s, S)$ policy, while Jeganathan et al. ^[5] studied its performance measures and the expected cost function. They also analyzed the performance measures and the optimal inventory level based on numerical calculations. Other studies in the area have been conducted by Reiyas and Jeganathan ^[15], and Jose and Reshmi ^[9].

Although many scholars have researched retrial queueing systems for the production inventory, most of them have examined the relevant performance measures and the optimal inventory levels under different policies, while few researchers have considered models of the production inventory with strategic customers and their influence on the optimal inventory level. Customers join the system if their individual utilities are positive, and otherwise give up trying to join it. However, every customer is influenced by other customers and seeks to attain a Nash equilibrium. $\ddot{O}$ z and Karaesmen ^[14] examined the optimal inventory level with strategic customers in unobservable cases. Li, Guo, Li and Song ^[11] studied the equilibrium strategies of customers and determined the optimal control values in an inventory system by using a negative queueing system. Zhang and Wang ^[22] considered a queueing system for the production inventory with a dynamic rate of production. They obtained the individual equilibrium states and the optimum cost in cases of observable as well as unobservable inventories.

Many researchers have investigated the individual and social strategic behaviors of customers in the traditional queueing system. Economous and Kanta ^[3] obtained the equilibrium strategies of customers and the socially optimal strategies in unobservable as well as observable cases in a retrial queueing system. Zhang ^[21] extended this model to a queueing system with server vacations. Wang and Zhang ^[18] extended it to a queueing system with dynamic rates of retrial. Wang, Zhang, and Huang ^[20] subsequently investigated a retrial queueing system with the N-policy. In this model, when the server was in dormant state, it did not offer any service to the customers and would not be activated until the number of customers in the wait list (retrial orbit) reached to a given threshold length $N$ $(N \geq 1)$ . Wang, Liu and Zhao ^[19] subsequently investigated the model developed by Zhang and Huang ^[20] in case of multiple server vacations. Kerner and Shmuel-Bittner ^[10] researched the strategic behaviors of customers in a hybrid retrial queueing system. Other research in the area includes work by Li and Wang ^[12], Shi and Liu ^[17], Zhang and Wang ^[23], Gao, Wang, and Dong ^[4], and Do, Van Do, and Melikov ^[2].

In this study, we examine a make-to-stock queueing system with a constant retrial rate by using a double-ended queue. When the queue length is negative, the system contains only products and customers immediately take unit productions. When the queue length is positive, customers are waiting in the retrial queue. Customers arriving the system in this case find that the stock is empty and the server is busy, and then decide whether to leave their contact information or balk.

The remainder of this paper is organized as follows: In Section 2, we describe a make-to-stock retrial double-ended queueing system. Sections 3 and 4 contain discussions of the equilibrium strategies and the expected cost functions of the entire system in the observable and fully observable cases. In Section 5, we analyze the equilibrium strategies of the customers as well as their expected cost functions, and obtain the optimal inventory levels for these two cases based on numerical experiments. Section 6 summarizes the conclusions of this study.

2. Model description

We discuss a single-server make-to-stock queueing system with no waiting space. Customers arrive according to a Poisson process at rate $\lambda$ . The time taken by a production server to manufacture a unit product follows an exponential distribution with rate $\mu$ . We assume that a customer takes a unit of the product once service to them has been completed. When a customer arrives, there are products in the inventory, and they take one away immediately. If the production server is serving a customer, we say that it is busy, and is otherwise idle. In order to reduce the waiting time, we stipulate that customers will not wait in the system if the production server is found to be busy. In this case, they leave their contact information and join a retrial queue according to a first-come first-serve strategy. After completion of service, the customer leaves the system and the production server searches for the next customer in the retrial queue. The search time follows an exponential distribution with rate $\alpha$ . When a new customer arrives during the search period, the production server stops searching and serves the new customer immediately. The server stops producing when the inventory level reaches $N$ . The inter-arrival times of customers, and the times required for production and for the server to search for customers are mutually independent. Economou and Kanta ^[3] have investigated this model when $N = 0$ .

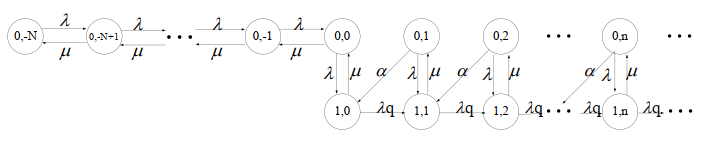
$I(t)$ represents the state of the production server. $I(t) = 0$ means that the production server is idle while $I(t) = 1$ means that it is busy. $N(t)$ represents the number of customers or production units. $N(t) = -n < 0$ means that there are $n$ units of inventory, $N(t) = n > 0$ means that there are $n$ customers in the retrial queue, and $N(t) = 0$ means that there is neither a customer nor inventory in the system. $(I(t), N(t))$ constitutes a two-dimensional continuous-time Markov chain in state space $\{(i, n): i = 0, 1; n = -N, -N+1, \cdots, 0, 1, \cdots\}$ .

A customer purchases a production unit at price $f_1$ , makes a profit $R$ , and incurs a waiting cost $C_1$ per unit time. The production server obtains benefit $f_1$ when a customer purchases a production unit, and needs to pay the inventory cost $C_2$ per unit time.

3. The observable case

Arriving customers can observe the state of the production server in the observable case. In this case, the strategy of the customer is represented by their probability of joining the queue. When a customer finds the production server busy, they decide to join the retrial queue with probability $q$ and balk with probability $1 -q$ . When they find the production server idle, they are served immediately. Therefore, the probability of a customer joining the queue is one in this case.

Following Economou and Kanta ^[3], we obtain the stable condition for a make-to-stock system through Lemma 3.1.

Lemma 3.1. (^[3], Proposition 3.1) The necessary and sufficient conditions for the stability of the system are

$\begin{eqnarray*} \rho_1 : = \frac{\lambda q (\lambda + \alpha)}{\mu \alpha} < 1. \end{eqnarray*}$

Let $\pi_{i, j}$ be the steady distribution of state $(i, j)$ . We denote the partial generation function by $P_0(s) = \sum_{i = 0}^{\infty} \pi_{0, i} s^i$ and $P_1(s) = \sum_{i = 0}^{\infty} \pi_{1, i}s^i$ . We now study the steady distribution in the almost observable case by using Lemma 3.1.

Lemma 3.2. The steady distribution is given as follows:

$\begin{eqnarray*} \label{lem3.1} &&\pi_{0,-N} = \frac{(1 - \rho_1)(1 - \rho)}{1 - \rho_1 + \rho_1 \rho^N - q \rho^{N+1} + q \rho^{N + 2} - \rho^{N + 2}};\\ &&\pi_{0,i} = \rho^{i + N}\pi_{0,-N}, \qquad -N+1 \leq i \leq 0;\\ &&P_0(1) = \frac{1 - q \rho}{1 - \rho_1} \rho^N \pi_{0,-N};\\ &&P_1(1) = \frac{\rho}{1 - \rho_1} \rho^N \pi_{0,-N}, \end{eqnarray*}$

where $\rho = \frac{\lambda}{\mu}$ .

Proof. We can obtain the balanced equations from Figure 1.

$\begin{eqnarray} \lambda\pi_{0,-N} & = & \mu \pi_{0,-N+1}; \end{eqnarray}$

(3.1)

$\begin{eqnarray} (\lambda + \mu) \pi_{0,i} & = & \lambda \pi_{0,i-1} + \mu \pi_{0,i+1}, \quad -N + 1 \leq i \leq -2; \end{eqnarray}$

(3.2)

$\begin{eqnarray} (\lambda + \mu) \pi_{0,-1} & = & \lambda \pi_{0,-2} + \mu \pi_{0,0}; \end{eqnarray}$

(3.3)

$\begin{eqnarray} (\lambda + \mu) \pi_{0,0} & = & \lambda \pi_{0,-1} + \mu \pi_{1,0}; \end{eqnarray}$

(3.4)

$\begin{eqnarray} (\lambda + \alpha) \pi_{0,i} & = & \mu \pi_{1,i}, \qquad \qquad i \geq 1; \end{eqnarray}$

(3.5)

$\begin{eqnarray} (\lambda q + \mu)\pi_{1,0} & = & \lambda \pi_{0,0} + \alpha \pi_{0,1}; \end{eqnarray}$

(3.6)

$\begin{eqnarray} (\lambda q + \mu) \pi_{1,i} & = & \lambda \pi_{0,i} + \lambda q \pi_{1,i-1} + \alpha \pi_{0, i+1}, \quad i \geq 1. \end{eqnarray}$

(3.7)

Figure 1. State transition diagram for the observable case.

DownLoad: Full-Size Img PowerPoint

By (3.1), (3.2) and (3.3), we have

$\begin{eqnarray*} \pi_{0,i} & = & \rho^{i + N} \pi_{0,-N}, -N + 1\leq i \leq -1, \\ \pi_{0,0} & = & \rho^N \pi_{0,-N}. \end{eqnarray*}$

Multiply by $s^i$ on both sides of (3.5) and (3.7), and summing up, we obtain

$\begin{eqnarray*} (\lambda + \alpha) \sum\limits_{i = 1}^{\infty}\pi_{0,i}s^i & = & \mu \sum\limits_{i = 1}^{\infty}\pi_{1,i}s^i; \label{un-gene-1}\\ (\lambda q + \mu) \sum\limits_{i = 1}^{\infty}\pi_{1,i}s^i & = & \lambda \sum\limits_{i = 1}^{\infty}\pi_{0,i}s^i + \lambda q s \sum\limits_{i = 1}^{\infty}\pi_{1,i-1}s^{i-1} + \frac{\alpha}{s} \sum\limits_{i = 1}^{\infty}\pi_{0, i + 1}s^{i+1}. \label{un-gene-2} \end{eqnarray*}$

Therefore, together with (3.4) and (3.6), we have

$\begin{eqnarray*} (\lambda + \alpha) P_0(s) & = & \alpha \pi_{0,0} + \mu P_1(s), \\ (\lambda q + \mu) P_1(s) & = & \lambda P_0(s) + \lambda q s P_1(s) + \frac{\alpha}{s} P_0(s) - \frac{\alpha}{s} \pi_{0,0}, \end{eqnarray*}$

which yields

$\begin{eqnarray*} P_0(s) & = & \frac{\lambda q \alpha s - \alpha \mu}{\lambda q (\lambda + \alpha)s - \alpha \mu} \pi_{0,0} = \frac{1 - \rho q s}{1 - \rho_1 s} \pi_{0,0},\\ P_1(s) & = & \frac{\alpha \lambda}{\alpha \mu - \lambda q (\lambda + \alpha)s} \pi_{0,0} = \frac{\rho}{1 - \rho_1 s} \pi_{0,0}. \end{eqnarray*}$

By the normalized condition,

$\begin{eqnarray*} \sum\limits_{i = -N}^{-1}\pi_{0,i} + \sum\limits_{ i = 0}^{\infty} (\pi_{0,i} + \pi_{1,i}) = 1, \end{eqnarray*}$

we obtain

$\begin{eqnarray*} \pi_{0,-N} = \frac{(1 - \rho_1)(1 - \rho)}{1 - \rho_1 + \rho_1 \rho^N - q \rho^{N+1} + q \rho^{N + 2} - \rho^{N + 2}}. \end{eqnarray*}$

□

By using the method developed in ^[3], we can obtain the mean waiting time of a customer who finds upon arrival that the state of the system is $(1, j)$ .

$\begin{equation} T(1,j) = (j+1) \frac{\lambda+\alpha+\mu}{\mu \alpha} +\frac{1}{\mu}. \end{equation}$

(3.8)

The mean waiting time of a customer when they find the production server to be busy upon arrival can be given by

$\begin{eqnarray*} E (W_c | I(t) = 1) & = & \sum\limits_{j = 0}^{+ \infty} \frac{\pi_{1,j}}{P_1(1)} T(1,j) = \frac{\lambda+\alpha+\mu}{\mu \alpha}\bigg(\frac{\frac{\rho \rho_1 \pi_{0,0}}{(1-\rho_1)^2}}{\frac{\rho \pi_{0,0}}{1-\rho_1}} +1 \bigg) + \frac{1}{\mu}\\ & = &\frac{\lambda + \alpha + \mu}{\mu \alpha (1- \rho_1)} + \frac{1}{\mu}. \end{eqnarray*}$

Therefore, the utility of a customer in the almost observable case is

$\begin{eqnarray*} U_c(q) & = & R -f_1 - C_1 E(W_c|I(t) = 1 ) = R - f_1 - C_1 \bigg\{ \frac{\lambda + \alpha + \mu}{\mu \alpha(1- \rho_1)} + \frac{1}{\mu} \bigg\}. \end{eqnarray*}$

The equilibrium strategy of a customer in the almost observable case is specified by the joining probability. When the server is found to be busy, the customer decides to join the system with probability $q_e$ or to balk with probability $1 - q_e$ . $q_e$ is also called the equilibrium joining strategy. If the server is found to be idle, the customer joins the system, and their probability of joining is one.

When the production server is found to be busy in the observable case, the customer's strategy can be given as follows:

Theorem 3.1. When the production server is found to be busy in the observable case, the strategy of a customer is given as follows:

$\begin{eqnarray*} q_e = \left\{ \begin{array}{ll} 0, & if \; R < f_1 + C_1 \big\{ \frac{\lambda + \alpha + \mu}{\mu \alpha} + \frac{1}{\mu} \big\} ;\\ q_e^*, & if \; f_1 + C_1 \big\{ \frac{\lambda + \alpha + \mu}{\mu \alpha} + \frac{1}{\mu} \big\} < R < f_1 + C_1 \big\{ \frac{\lambda + \alpha + \mu}{\mu \alpha} \frac{1}{1- \rho^*} + \frac{1}{\mu} \big\} ;\\ 1, & if \; R > f_1 + C_1 \big\{ \frac{\lambda + \alpha + \mu}{\mu \alpha} \frac{1}{1- \rho^*} + \frac{1}{\mu} \big\}. , \end{array} \right. \end{eqnarray*}$

where

$\begin{eqnarray*} q_e^* = \frac{h- 1}{h\rho^*}, \rho^* = \frac{\lambda(\lambda+\alpha)}{\mu \alpha}, h = \bigg[\frac{R - f_1}{C_1} - \frac{1}{\mu} \bigg] \frac{\mu \alpha}{\lambda + \alpha + \mu}. \end{eqnarray*}$

Proof. We can then easily observe that $U_c(q)$ increases with $q$ .

(1) If $R < f_1 + C_1 \big\{ \frac{\lambda + \alpha + \mu}{\mu \alpha} + \frac{1}{\mu} \big\}$ , then $U_c(q) < 0$ . Therefore, in this case, the best choice for an arriving customer is to balk, thus $q_e = 0$ .

(2) If $f_1 + C_1 \big\{ \frac{\lambda + \alpha + \mu}{\mu \alpha} + \frac{1}{\mu} \big\} < R < f_1 + C_1 \big\{ \frac{\lambda + \alpha + \mu}{\mu \alpha} \frac{1}{1- \rho^*} + \frac{1}{\mu} \big\}$ , then there exists a unique solution $q_e^*$ for $U_c(q) = 0$ . $q_e^*$ is the equilibrium joining strategy of the customer.

(3) If $R > f_1 + C_1 \big\{ \frac{\lambda + \alpha + \mu}{\mu \alpha} \frac{1}{1- \rho^*} + \frac{1}{\mu} \big\}$ , then $U_c(q) > 0$ . Thus, an arriving customer's choice is to join the queue, such that $q_e = 1$ . □

We now calculate the mean cost function of the entire system.

When the queue length is negative upon a customer's arrival, their waiting time is zero; thus, the mean queue length of customers $E N_c$ is

$\begin{eqnarray*} E N_c & = & \lambda P_0(1) \frac{1}{\mu} + \lambda q P_1(1) E (W_c | I(t) = 1)\\ & = & \frac{\rho (1-q\rho)}{1-\rho_1}\pi_{0,0} + \lambda q \frac{\rho}{1-\rho_1}\pi_{0,0} \bigg\{ \frac{\lambda + \alpha + \mu }{\mu \alpha(1- \rho_1)} + \frac{1}{\mu} \bigg\}\\ & = & \frac{\rho}{1-\rho_1} \pi_{0,0} + \frac{\rho^2 q}{(1-\rho_1)^2}\frac{\lambda +\alpha +\mu}{\alpha} \pi_{0,0}. \end{eqnarray*}$

The expected inventory level $E N_{p}$ is

$\begin{equation*} E N_{p} = \sum\limits_{i = -1}^{-N}(-i)\pi_{0,i} = \pi_{0,-N}\frac{(\rho^{N+1} -\rho-N(\rho-1))}{(1-\rho)^2}. \end{equation*}$

The expected cost function of the entire system $S(N)$ is

$\begin{eqnarray*} S(N) & = & C_1 E N_c + C_2 E N_p\\ & = &C_1 \frac{\rho}{1-\rho_1} \pi_{0,0} + C_1 \frac{\rho^2 q}{(1-\rho_1)^2}\frac{\lambda +\alpha +\mu}{\alpha} \pi_{0,0} + C_2 \pi_{0,-N}\frac{(\rho^{N+1} -\rho-N(\rho-1))}{(1- \rho)^2}\\ & = & C_1 \frac{\rho^{N+1}}{1-\rho_1}\pi_{0,-N}+ C_1 \frac{\rho^{2+N} q}{(1-\rho_1)^2}\frac{\lambda +\alpha +\mu}{\alpha} \pi_{0,-N}+C_2 \frac{(\rho^{N+1} -\rho-N(\rho-1))}{(1-\rho)^2}\pi_{0,-N}. \end{eqnarray*}$

This function $S(N)$ is related to the equilibrium strategy of the customer $q_{e}^{*}$ . However, from Theorem 3.1, we know that the expression of $q_{e}^*$ does not contain $N$ . We thus use $q$ instead of $q_{e}^*$ . Our objective is to minimize the above function to obtain the optimal inventory level. However, the expected cost function is complex, because of which we analyze it by using numerical calculations.

4. Fully observable case

In this section, we study the fully observable case. In this case, customers have all the information regarding the system, then, their equilibrium strategies can be represented by the threshold $n_{e}$ . When the production server is found to be idle, an arriving customer is served at once.

Let $n$ be the threshold. When the production server is found to be busy, customers enter the retrial queue if $N(t) \leq n$ , and otherwise balk.

By using the method applied by Economou and Kanta ^[3], we obtain the waiting time for a customer $EW_c^{ob}(n)$ when they arrive in the system, and there are $n$ customers in the retrial queue.

$EW_c^{ob}(n) = n \frac{\lambda + \alpha + \mu}{\mu \alpha} + \frac{1}{\mu}.$

The utility of a customer who is in the $n$ th position of the retrial queue is

$\begin{equation*} U_{c}^{ob}(n) = R - f_1 - C_1 E W_c^{ob}(n-1). \end{equation*}$

We can then obtain the equilibrium strategies of customers $n_e$ , where this satisfies

$\begin{eqnarray*} n_e = \bigg[ \frac{(R- f_1)\mu \alpha}{C_1(\lambda + \alpha + \mu)} +1 \bigg], \end{eqnarray*}$

which satisfies

$\begin{eqnarray*} \left\{ \begin{array}{ll} U_{c}^{ob}(n_e) \geq 0;\\ U_{c}^{ob}(n_e + 1) < 0. \end{array} \right. \end{eqnarray*}$

From the above function, we know that $n_e$ is increasing because $\mu$ , $\alpha$ , and $R$ are increasing. On the contrary, $n_e$ is decreasing because $\lambda$ and $C_1$ are increasing.

Let $\pi_{i, j}^{ob}$ be the steady distribution of state $(i, j)$ in the fully observable case. To obtain the relevant performance measures, we investigate the steady distribution in the fully observable case as shown in Figure 2. See the following Lemma 4.1.

Figure 2. State transition diagram for the fully observable case.

DownLoad: Full-Size Img PowerPoint

Lemma 4.1. The steady distribution in the fully observable case is given as follows:

$\begin{eqnarray*} &&\pi_{0,i}^{ob} = \rho^{i + N} \pi_{0,-N}^{ob}, -N + 1 \leq i \leq 0,\\ &&\pi_{0,i}^{ob} = \beta \rho_2^i\rho \pi_{0,0}^{ob} , 1 \leq i \leq n,\\ &&\pi_{1,i}^{ob} = \rho_2^i\rho \pi_{0,0}^{ob}, 0 \leq i \leq n,\\ &&\pi_{0,-N}^{ob} = \frac{(1 - \rho)(1 - \rho_2)}{(1 - \rho^{N+2})(1 - \rho_2) + (\beta+1) \rho_2 \rho^{N+1} (1 - \rho_2^n)(1 - \rho)}, \end{eqnarray*}$

where $\beta = \frac{\mu}{\lambda + \alpha}$ , $\rho_2 = \frac{\lambda(\lambda+\alpha)}{\mu \alpha}$ .

Proof. The balance equations in the fully observable case are given as follows.

$\begin{eqnarray} \lambda \pi_{0,-N}^{ob} & = & \mu \pi_{0,-N + 1}^{ob}; \end{eqnarray}$

(4.1)

$\begin{eqnarray} (\lambda + \mu) \pi_{0,i}^{ob} & = & \lambda \pi_{0,i -1}^{ob} + \mu \pi_{0,i+1}^{ob}, \quad -N + 1 \leq i \leq -1; \end{eqnarray}$

(4.2)

$\begin{eqnarray} (\lambda + \mu) \pi_{0,0}^{ob} & = & \lambda \pi_{0,-1}^{ob} + \mu \pi_{1,0}^{ob}; \end{eqnarray}$

(4.3)

$\begin{eqnarray} (\lambda + \alpha) \pi_{0,i}^{ob} & = & \mu \pi_{1,i}^{ob}, \quad \qquad \qquad \qquad 1 \leq i \leq n; \end{eqnarray}$

(4.4)

$\begin{eqnarray} (\lambda + \mu) \pi_{1,0}^{ob} & = & \lambda \pi_{0,0}^{ob} + \alpha \pi_{0,1}^{ob}; \end{eqnarray}$

(4.5)

$\begin{eqnarray} (\lambda + \mu)\pi_{1,i}^{ob} & = & \lambda \pi_{1, i-1}^{ob} + \lambda \pi_{0,i}^{ob} + \alpha \pi_{0,i+1}^{ob}, \quad 1 \leq i \leq n-1; \end{eqnarray}$

(4.6)

$\begin{eqnarray} \mu \pi_{1,n}^{ob} & = & \lambda \pi_{1, n-1}^{ob} + \lambda \pi_{0,n}^{ob}. \end{eqnarray}$

(4.7)

Substituting (4.4) into (4.6) and (4.7), we obtain

$\begin{eqnarray*} &&\pi_{1, n}^{ob} = \rho_2 \pi_{1, n-1}^{ob};\\ &&(\lambda + \mu) \pi_{1,i}^{ob} = \lambda \pi_{1, i-1}^{ob} + \frac{\lambda \mu}{\alpha + \lambda}\pi_{1,i}^{ob} + \frac{\alpha \mu}{\alpha + \lambda} \pi_{1,i+1}^{ob} \quad 1 \leq i \leq n -1. \end{eqnarray*}$

Therefore, we have

$\begin{equation} \pi_{1,i}^{ob} = \rho_2^i\rho \pi_{0,0}^{ob}, 1 \leq i \leq n. \end{equation}$

(4.8)

Substituting (4.8) into (4.4), we get

$\begin{align*} \pi_{0,i}^{ob} = \beta \pi_{1,i}^{ob} = \beta \rho_2^i\rho \pi_{0,0}^{ob} , 1 \leq i \leq n. \end{align*}$

By (4.1), (4.2) and (4.3), we obtain

$\begin{eqnarray*} &&\pi_{0,i}^{ob} = \rho^{i + N} \pi_{0,-N}^{ob}, -N + 1 \leq i \leq -1,\\ &&\pi_{0,0}^{ob} = \rho^N \pi_{0,-N}^{ob}, \pi_{1,0}^{ob} = \rho \pi_{0,0}^{ob}. \end{eqnarray*}$

By the normalized condition,

$\begin{align*} \sum\limits_{i = -N}^{-1} \pi_{0,i}^{ob} + \sum\limits_{i = 0}^{n} (\pi_{0,i}^{ob} + \pi_{1,i}^{ob}) = 1, \end{align*}$

we get

$\begin{eqnarray*} \pi_{0,-N}^{ob} = \frac{(1 - \rho)(1 - \rho_2)}{(1 - \rho^{N+2})(1 - \rho_2) + (\beta+1) \rho_2 \rho^{N+1} (1 - \rho_2^n)(1 - \rho)}. \end{eqnarray*}$

□

To obtain the expected cost function of the entire system, we first give the expected queue length of customers and the expected inventory level.

According to Little's law, the expected queue length of customers is $E N_c^{ob} = \lambda_{e} E W_{c}^{ob}$ , where

$\lambda_{e} = \lambda \big(1- \pi_{1,n}^{ob} -\sum\limits_{i = -N}^{-1} \pi_{0,i}^{ob}\big) = \lambda \pi_{0,0}^{ob}\frac{(1-\rho_2+\beta\rho\rho_2- \beta \rho\rho_2^{n}+\rho(1-\rho_2^n))}{1-\rho_2},$

represents the effective rate of arrival of customers when the queue length is nonnegative, and $E W_{c}^{ob}$ is the mean waiting time of a customer. When the customer arrive at the system, the state is $(0, i), i\geq 0$ , and the waiting time is $1/\mu$ . When the customer arrive at the system, the state is $(1, i)$ , and the waiting time is $\frac{1}{\mu}+ (i+1) \frac{\lambda +\alpha + \mu}{\mu \alpha}$ . Therefore, we obtain

$\begin{eqnarray*} E W_{c}^{ob} & = & \sum\limits_{i = 0}^{n} \frac{\pi_{o,i}^{ob}}{1- \pi_{1,n}^{ob} -\sum_{i = -N}^{-1} \pi_{0,i}^{ob}} \frac{1}{\mu} + \sum\limits_{i = 0}^{n-1} \frac{\pi_{1,i}^{ob}}{1-\pi_{1,n}^{ob} -\sum_{i = -N}^{-1} \pi_{0,i}^{ob}} \bigg(\frac{1}{\mu} +(i+1) \frac{\lambda +\alpha +\mu}{\mu \alpha}\bigg). \end{eqnarray*}$

Therefore, the mean queue length of customers is

$\begin{eqnarray*} E N_c^{ob}& = & \lambda_{e} E W_{c}^{ob} = \lambda_{e} \frac{1}{\mu} + \sum\limits_{i = 0}^{n-1}\pi_{1,i}^{ob}\cdot(i+1) \frac{\lambda +\alpha +\mu}{\mu \alpha}\\ & = & \lambda_{e} \frac{1}{\mu} + \frac{\lambda +\alpha +\mu}{\mu \alpha} \bigg( \frac{\rho_2 (1-\rho_2^{n-1} -(n-1)\rho_2^{n-1} (1-\rho_2))}{(1-\rho_2)^2}\rho \pi_{0,0}^{ob} + \frac{1-\rho_2^n}{1-\rho_2} \rho \pi_{0,0}^{ob} \bigg)\\ & = & \lambda_{e} \frac{1}{\mu}+ \pi_{0,-N}^{ob} \frac{\rho^{N+1}(1-(n+1)\rho_2^{n} +n \rho_2^{n+1})}{(1-\rho_2)^2} \frac{\lambda +\alpha +\mu}{\mu \alpha}. \end{eqnarray*}$

The expected inventory level $E N_{p}^{ob}$ is

$\begin{eqnarray*} E N_{p}^{ob} = \sum\limits_{i = -1}^{-N}(-i)\pi_{0,i}^{ob} = \pi_{0,-N}^{ob}\frac{(\rho^{N+1} -\rho-N(\rho- 1))}{(1-\rho)^2}. \end{eqnarray*}$

We can then obtain the expected cost function of the entire system $S_{ob} (N)$ .

$\begin{eqnarray*} S_{ob} (N) & = & C_1 E N_{c}^{ob} + C_2 E N_{p}^{ob}\\ & = & C_1 \lambda_{e} \frac{1}{\mu}+ C_1 \pi_{0,-N}^{ob} \frac{\rho^{N+1} (1-(n+1)\rho_2^{n} +n \rho_2^{n+1})}{(1-\rho_2)^2}\frac{\lambda +\alpha +\mu}{\mu \alpha} \\ &+& C_2 \pi_{0,-N}^{ob}\frac{(\rho^{N+1} -\rho-N(\rho- 1))}{(1-\rho)^2}. \end{eqnarray*}$

Because the expression of $S_{ob}(N)$ is complex, we determine the optimal inventory level by using numerical calculations.

5. Numerical experiments

We investigate the equilibrium strategies of customers and the expected cost functions in two cases through numerical experiments. First, we show how the parameters (such as the rates of customer arrival $\lambda$ , production $\mu$ , and retrial $\alpha$ ) influence the equilibrium strategies of the customers in two cases $q_e^*, n_e^*$ . Second, we analyze the expected cost functions in the two cases ( $S(N), S_{ob}(N)$ ) under the influence of the parameters of the system ( $\lambda, \mu, \alpha$ ). Finally, we obtain the optimal inventory level $N$ based on values of the expected cost functions in two cases.

We assume that the profit from a customer's purchase of a production unit is $R = 15$ , the cost of purchasing a production unit is $f_1 = 5$ , the customers' unit waiting cost is $C_1 = 3$ , and the cost of inventory for production in unit time is $C_2 = 1$ .

5.1. Equilibrium strategies of customers

As shown in , the equilibrium strategies of the customers decrease as $\lambda$ increases in both cases. When more customers arrive at the system, their waiting time increases such that many customers are unwilling to enter the system. The customers' strategies are increasing for $\mu$ in the two cases presented in because a reduction in the production time reduces the customer's waiting time. We know from that the equilibrium strategies of the customers are increasing for $\alpha$ in the two cases. This means that the customers are likely to receive service with a reduction in their waiting time.

Table 1. Equilibrium strategies in the observable and fully observable case for

$\mu = 15$ ,

$\alpha = 4$ .

$\lambda$	$5.7$	$5.8$	$5.9$	$6$	$7$	$8$	$10$	$12$	$14$
$q_e^*$	$0.95$	$0.92$	$0.89$	$0.87$	$0.68$	$0.54$	$0.37$	$0.26$	$0.20$
$n_e^*$	$9$	$9$	$9$	$9$	$8$	$8$	$7$	$7$	$7$

| Show Table

DownLoad: CSV

Table 2. Equilibrium strategies in the observable and fully observable case for

$\lambda = 15$ ,

$\alpha = 6$ .

$\mu$	$20$	$21$	$22$	$25$	$28$	$34$	$40$	$44$	$50$
$q_e^*$	$0.34$	$0.36$	$0.38$	$0.43$	$0.48$	$0.59$	$0.70$	$0.78$	$0.88$
$n_e^*$	$10$	$11$	$11$	$11$	$12$	$13$	$14$	$14$	$15$

| Show Table

DownLoad: CSV

Table 3. Equilibrium strategies in the observable and fully observable cases for

$\lambda = 15$ ,

$\mu = 40$ .

$\alpha$	$3$	$4$	$4.5$	$5$	$6$	$7$	$8$	$9$	$9.5$
$q_e^*$	$0.38$	$0.5$	$0.55$	$0.61$	$0.70$	$0.79$	$0.87$	$0.95$	$0.98$
$n_e^*$	$7$	$10$	$11$	$12$	$14$	$16$	$17$	$19$	$20$

| Show Table

DownLoad: CSV

In summary, we know that the equilibrium strategies of the customers decrease as $\lambda$ increases, and increase with $\mu$ and $\lambda$ in two cases. These results are understandable.

5.2. The expected cost function of the system

We can determine from the left side of that the expected cost function of the entire system is a concave function of $\lambda$ in both cases. As $\lambda$ increases, so does the speed at which products are taken from the inventory to reduce the cost of inventory. However, when $\lambda$ increases to a fixed value, the waiting time for customers increases such that the expected cost of the entire system increases. The right side of illustrates that the expected cost function of the entire system decreases with respect to $\mu$ in both cases. When $\mu > 1.5$ , the mean cost of the system does not change by much. The waiting cost of the customers is very short when $\mu$ is large, while the cost of inventory of products remains almost unchanged. Thus, the mean cost of the entire system tends to be stable.

Figure 3. Left: The expected cost functions of entire system in two cases vs.

$\lambda$ for

$\mu = 1$ ,

$q = 0.9$ ,

$\alpha = 4$ ,

$N = 4$ ,

$n = 5$ ; Right: The expected cost functions of entire system in two cases vs.

$\mu$ for

$\lambda = 0.8$ ,

$q = 0.9$ ,

$\alpha = 4$ ,

$N = 4$ ,

$n = 5$ .

DownLoad: Full-Size Img PowerPoint

The left side of indicates that the expected cost of the system decreases and tends to stabilize as $\alpha$ increases in both cases. This implies that when $\alpha$ increases to a certain level, the expected waiting cost of customers changes by little, such that the cost of the entire system tends toward a constant value.

Figure 4. Left: The expected cost functions of entire system in two cases vs.

$\alpha$ for

$\lambda = 2$ ,

$\mu = 4$ ,

$n = 5$ ,

$N = 5$ ,

$q = 0.9$ ; Right: The expected cost functions of entire system in two cases vs.

$N$ for

$\lambda = 2$ ,

$\mu = 4$ ,

$\alpha = 3$ ,

$n = 5$ ,

$q = 0.9$ .

DownLoad: Full-Size Img PowerPoint

The right side of illustrates that the expected cost functions of the entire system are concave functions with respect to $N$ in the two cases considered. Thus, there exists an optimal inventory level in our model. This level is $1$ in the observable case, and $2$ in the fully observable case. These results provide a sound basis for production managers to plan the levels of their inventory.

Because the expected waiting cost increases with $q$ and $n$ , the expected cost functions of the entire system are an increasing function of $q$ and $n$ in both cases, respectively—see Figure 5.

Figure 5. Left: The expected cost function of entire system in the observable case vs.

$q$ for

$\lambda = 0.8$ ,

$\mu = 1$ ,

$\alpha = 4$ ,

$N = 5$ ; Right: The expected cost function of entire system in the fully observable case vs.

$n$ for

$\lambda = 0.8$ ,

$\mu = 1$ ,

$\alpha = 4$ ,

$N = 5$ .

DownLoad: Full-Size Img PowerPoint

6. Conclusions

In this paper, we considered a make-to-stock retrial double-ended queueing system. When customers find that the production server is busy upon their arrival, they decide whether to join the system or to balk. We discussed the equilibrium strategies of the customers and the expected cost functions of the system in two cases. Furthermore, we examined the equilibrium strategies of the customers and the expected cost functions, and calculated the optimal inventory levels under two states of information based on numerical experiments. We also obtained the optimal inventory levels for the two cases through simulations. Our results here provide a basis for managers to make decisions to optimize their inventories.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This article has been partially supported by the National natural Science Foundation of China (Grants no.11901186, 12271062), the Social Science Foundation of Hunan Province (No. 19YBQ113), Scientific Research Foundation of Hunan Education Department (No. 23A0679) and Natural Science Foundation of Hunan Province (No. 2021JJ41088).

Conflict of interest

The authors declare no conflict of interest in this paper.

References

[1]	L. A. Zadeh, Fuzzy sets, Information and Control, 8 (1965), 338–353. https://doi.org/10.1016/S0019-9958(65)90241-X doi: 10.1016/S0019-9958(65)90241-X
[2]	R. E. Bellman, L. A. Zadeh, Decision-making in a fuzzy environment, Manage. Sci., 17 (1970), 141–164. https://doi.org/10.1287/mnsc.17.4.B141 doi: 10.1287/mnsc.17.4.B141
[3]	Z. Pawlak, Rough sets, International Journal of Computer and Information Sciences, 11 (1982), 341–356. https://doi.org/10.1007/BF01001956 doi: 10.1007/BF01001956
[4]	J. Q. Wang, X. H. Zhang, Q. Shen, Choquet-like integrals with rough attribute fuzzy measures for data-driven decision-making, IEEE T. Fuzzy Syst., 32 (2024), 2825–2836. https://doi.org/10.1109/TFUZZ.2024.3363415 doi: 10.1109/TFUZZ.2024.3363415
[5]	J. Q. Wang, X. H. Zhang, Intuitionistic fuzzy granular matrix: novel calculation approaches for intuitionistic, fuzzy covering-based rough sets, Axioms, 13 (2024), 411. https://doi.org/10.3390/axioms13060411 doi: 10.3390/axioms13060411
[6]	K. T. Atanassov, Intuitionistic fuzzy sets, Fuzzy Set. Syst., 20 (1986), 87–96. https://doi.org/10.1016/S0165-0114(86)80034-3 doi: 10.1016/S0165-0114(86)80034-3
[7]	R. R. Yager, Pythagorean fuzzy subsets, 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Edmonton, AB, Canada, 2013, 57–61. https://doi.org/10.1109/IFSA-NAFIPS.2013.6608375
[8]	R. R. Yager, Generalized orthopair fuzzy sets, IEEE T. Fuzzy Syst., 25 (2017), 1222–1230. https://doi.org/10.1109/TFUZZ.2016.2604005 doi: 10.1109/TFUZZ.2016.2604005
[9]	L. A. Zadeh, The concept of a linguistic variable and its application to approximate reasoning–I, Inform. Sciences, 8 (1975), 199–249. https://doi.org/10.1016/0020-0255(75)90036-5 doi: 10.1016/0020-0255(75)90036-5
[10]	Z. C. Chen, P. H. Liu, Z. Pei, An approach to multiple attribute group decision making based on linguistic intuitionistic fuzzy numbers, Int. J. Comput. Int. Sys., 8 (2015), 747–760. https://doi.org/10.1080/18756891.2015.1061394 doi: 10.1080/18756891.2015.1061394
[11]	M. Akram, S. Naz, T. Abbas, Complex $q$ -rung orthopair fuzzy 2-tuple linguistic group decision-making framework with Muirhead mean operators, Artif. Intell. Rev., 56 (2023), 10227–10274. https://doi.org/10.1007/s10462-023-10408-4 doi: 10.1007/s10462-023-10408-4
[12]	M. Akram, N. Ramzan, A. Luqman, G. Santos-García, An integrated MULTIMOORA method with 2-tuple linguistic Fermatean fuzzy sets: Urban quality of life selection application, AIMS Mathematics, 8 (2023), 2798–2828. https://doi.org/10.3934/math.2023147 doi: 10.3934/math.2023147
[13]	M. R. Seikh, U. Mandal, Interval-valued Fermatean fuzzy Dombi aggregation operators and SWARA based PROMETHEE II method to bio-medical waste management, Expert Syst. Appl., 226 (2023), 120082. https://doi.org/10.1016/j.eswa.2023.120082 doi: 10.1016/j.eswa.2023.120082
[14]	P. D. Liu, X. X. Liu, G. Y. Ma, Z. L. Liang, C. H. Wang, F. E. Alsaadi, A multi-attribute group decision-making method based on linguistic intuitionistic fuzzy numbers and Dempster-Shafer evidence theory, Int. J. Inf. Tech. Decis., 19 (2020), 499–524. https://doi.org/10.1142/S0219622020500042 doi: 10.1142/S0219622020500042
[15]	R. P. Yuan, J. Tang, F. Y. Meng, Linguistic intuitionistic fuzzy group decision making based on aggregation operators, Int. J. Fuzzy Syst., 21 (2019), 407–420. https://doi.org/10.1007/s40815-018-0582-4 doi: 10.1007/s40815-018-0582-4
[16]	X. J. Gou, X. R. Xu, F. M. Deng, W. Zhou, E. Herrera-Viedma, Medical health resources allocation evaluation in public health emergencies by an improved ORESTE method with linguistic preference orderings, Fuzzy Optim. Decis. Making, 23 (2024), 1–27. https://doi.org/10.1007/s10700-023-09409-3 doi: 10.1007/s10700-023-09409-3
[17]	X. T. Cheng, K. Zhang, T. Wu, Z. S. Xu, X. J. Gou, An opinions-updating model for large-scale group decision-making driven by autonomous learning, Inform. Sciences, 662 (2024), 120238. https://doi.org/10.1016/j.ins.2024.120238 doi: 10.1016/j.ins.2024.120238
[18]	M. R. Seikh, U. Mandal, $q$ -Rung orthopair fuzzy Archimedean aggregation operators: application in the site selection for software operating units, Symmetry, 15 (2023), 1680. https://doi.org/10.3390/sym15091680 doi: 10.3390/sym15091680
[19]	M. R. Seikh, U. Mandal, Q-Rung orthopair fuzzy Frank aggregation operators and its application in multiple attribute decision-making with unknown attribute weights, Granul. Comput., 7 (2022), 709–730. https://doi.org/10.1007/s41066-021-00290-2 doi: 10.1007/s41066-021-00290-2
[20]	H. Garg, K. Kumar, Group decision making approach based on possibility degree measures and the linguistic intuitionistic fuzzy aggregation operators using Einstein norm operations, J. Mult.-Valued Log. S., 31 (2018), 175–209.
[21]	H. Garg, K. Kumar, Some aggregation operators for linguistic intuitionistic fuzzy set and its application to group decision-making process using the set pair analysis, Arab. J. Sci. Eng., 43 (2018), 3213–3227. https://doi.org/10.1007/s13369-017-2986-0 doi: 10.1007/s13369-017-2986-0
[22]	H. Garg, T. Mahmood, U. U. Rehman, G. N. Nguyen, Multi-attribute decision-making approach based on Aczel-Alsina power aggregation operators under bipolar fuzzy information and its application to quantum computing, Alex. Eng. J., 82 (2023), 248–259. https://doi.org/10.1016/j.aej.2023.09.073 doi: 10.1016/j.aej.2023.09.073
[23]	K. Kumar, S. M. Chen, Group decision making based on improved linguistic interval-valued Atanassov intuitionistic fuzzy weighted averaging aggregation operator of linguistic interval-valued Atanassov intuitionistic fuzzy numbers, Inform. Sciences, 607 (2022), 884–900. https://doi.org/10.1016/j.ins.2022.05.082 doi: 10.1016/j.ins.2022.05.082
[24]	K. Kumar, S. M. Chen, Multiple attribute group decision making based on advanced linguistic intuitionistic fuzzy weighted averaging aggregation operator of linguistic intuitionistic fuzzy numbers, Inform. Sciences, 587 (2022), 813–824. https://doi.org/10.1016/j.ins.2021.11.014 doi: 10.1016/j.ins.2021.11.014
[25]	Y. Liu, G. W. Wei, H. B. Liu, L. Xu, Group decision making for internet public opinion emergency based upon linguistic intuitionistic fuzzy information, Int. J. Mach. Learn. & Cyber., 13 (2022), 579–594. https://doi.org/10.1007/s13042-020-01262-9
[26]	X. J. Gou, Z. S. Xu, H. C. Liao, F. Herrera, Probabilistic double hierarchy linguistic term set and its use in designing an improved VIKOR method: The application in smart healthcare, J. Oper. Res. Soc., 72 (2021), 2611–2630. https://doi.org/10.1080/01605682.2020.1806741 doi: 10.1080/01605682.2020.1806741
[27]	J. Tang, F. Y. Meng, Linguistic intuitionistic fuzzy Hamacher aggregation operators and their application to group decision making, Granul. Comput., 4 (2019), 109–124. https://doi.org/10.1007/s41066-018-0089-2 doi: 10.1007/s41066-018-0089-2
[28]	K. Kumar, S. M. Chen, Group decision making based on linguistic intuitionistic fuzzy Yager weighted arithmetic aggregation operator of linguistic intuitionistic fuzzy numbers, Inform. Sciences, 647 (2023), 119228. https://doi.org/10.1016/j.ins.2023.119228 doi: 10.1016/j.ins.2023.119228
[29]	R. Verma, N. Agarwal, Multiple attribute group decision-making based on generalized aggregation operators under linguistic interval-valued Pythagorean fuzzy environment, Granul. Comput., 7 (2022), 591–632. https://doi.org/10.1007/s41066-021-00286-y doi: 10.1007/s41066-021-00286-y
[30]	A. Fahmi, S. Abdullah, F. Amin, Aggregation operators on cubic linguistic hesitant fuzzy numbers and their application in group decision-making, Granul. Comput., 6 (2021), 303–320. https://doi.org/10.1007/s41066-019-00188-0 doi: 10.1007/s41066-019-00188-0
[31]	K. Kumar, S. M. Chen, Multiattribute decision making based on q-rung orthopair fuzzy Yager prioritized weighted arithmetic aggregation operator of q-rung orthopair fuzzy numbers, Inform. Sciences, 657 (2024), 119984. https://doi.org/10.1016/j.ins.2023.119984 doi: 10.1016/j.ins.2023.119984
[32]	X. T. Cheng, Z. S. Xu, X. J. Gou, A large-scale group decision-making model considering risk attitudes and dynamically changing roles, Expert Syst. Appl., 245 (2024), 123017. https://doi.org/10.1016/j.eswa.2023.123017 doi: 10.1016/j.eswa.2023.123017
[33]	F. X. Jin, F. Wang, K. Zhao, H. T. Chen, J. L. G. Guirao, The method of judging satisfactory consistency of linguistic judgment matrix based on adjacency matrix and 3-loop matrix, AIMS Mathematics, 9 (2024), 18944–18967. https://doi.org/10.3934/math.2024922 doi: 10.3934/math.2024922
[34]	M. W. Lin, X. M. Li, L. F. Chen, Linguistic q‐rung orthopair fuzzy sets and their interactional partitioned Heronian mean aggregation operators, Int. J. Intell. Syst., 35 (2019), 217–249. https://doi.org/10.1002/int.22136 doi: 10.1002/int.22136
[35]	P. D. Liu, W. Q. Liu, Multiple-attribute group decision-making based on power Bonferroni operators of linguistic q-rung orthopair fuzzy numbers, Int. J. Intell. Syst., 34 (2018), 652–689. https://doi.org/10.1002/int.22071 doi: 10.1002/int.22071
[36]	P. D. Liu, W. Q. Liu, Multiple‐attribute group decision‐making method of linguistic $q$ ‐rung orthopair fuzzy power Muirhead mean operators based on entropy weight, Int. J. Intell. Syst., 34 (2019), 1755–1794. https://doi.org/10.1002/int.22114 doi: 10.1002/int.22114
[37]	M. J. Ranjan, B. P. Kumar, T. D. Bhavani, A. V. Padmavathi, V. Bakka, Probabilistic linguistic q-rung orthopair fuzzy Archimedean aggregation operators for group decision-making, Decision Making: Applications in Management and Engineering, 6 (2023), 639–667. https://doi.org/10.31181/dmame622023527 doi: 10.31181/dmame622023527
[38]	H. J. Wang, Y. Liu, Y. Rong, Group decision making approach based on linguistic q-rung orthopair fuzzy generalized shapley bi-direction Choquet-copula operators, Granul. Comput., 8 (2023), 1837–1856. https://doi.org/10.1007/s41066-023-00404-y doi: 10.1007/s41066-023-00404-y
[39]	G. Ali, M. Afzal, M. Asif, A. Shazad, Attribute reduction approaches under interval-valued q-rung orthopair fuzzy soft framework, Appl. Intell., 52 (2022), 8975–9000. https://doi.org/10.1007/s10489-021-02853-x doi: 10.1007/s10489-021-02853-x
[40]	N. Deb, A. Sarkar, A. Biswas, Linguistic q-rung orthopair fuzzy prioritized aggregation operators based on Hamacher t-norm and t-conorm and their applications to multicriteria group decision making, Arch. Control Sci., 32 (2022), 451–484. https://doi.org/10.24425/acs.2022.141720 doi: 10.24425/acs.2022.141720
[41]	P. D. Liu, S. Naz, M. Akram, M. Muzammal, Group decision-making analysis based on linguistic $q$ -rung orthopair fuzzy generalized point weighted aggregation operators, Int. J. Mach. Learn. & Cyber., 13 (2022), 883–906. https://doi.org/10.1007/s13042-021-01425-2
[42]	M. Akram, S. Naz, S. A. Edalatpanah, R. Mehreen, Group decision-making framework under linguistic $q$ -rung orthopair fuzzy Einstein models, Soft Comput., 25 (2021), 10309–10334. https://doi.org/10.1007/s00500-021-05771-9 doi: 10.1007/s00500-021-05771-9
[43]	C. Jana, M. Dobrodolac, V. Simic, M. Pal, B. Sarkar, Ž. Stević, Evaluation of sustainable strategies for urban parcel delivery: Linguistic $q$ -rung orthopair fuzzy Choquet integral approach, Eng. Appl. Artif. Intel., 126 (2023), 106811. https://doi.org/10.1016/j.engappai.2023.106811 doi: 10.1016/j.engappai.2023.106811
[44]	S. Naz, M. Akram, A. Shafiq, K. Akhtar, Optimal airport selection utilizing power Muirhead mean based group decision model with 2-tuple linguistic q-rung orthopair fuzzy information, Int. J. Mach. Learn. & Cyber., 15 (2024), 303–340. https://doi.org/10.1007/s13042-023-01911-9
[45]	J. Aczél, C. Alsina, Characterizations of some classes of quasilinear functions with applications to triangular norms and to synthesizing judgements, Aeq. Math., 25 (1982), 313–315. https://doi.org/10.1007/BF02189626 doi: 10.1007/BF02189626
[46]	F. Farahbod, M. Efekhari, Comparison of different t-norm operators in classification problems, 2012, arXiv: 1208.1955. https://doi.org/10.48550/arXiv.1208.1955
[47]	M. Tahir, Azam, U. ur Rehman, J. Ahmmad, Prioritization and selection of operating system by employing geometric aggregation operators based on Aczel-Alsina t-norm and t-conorm in the environment of bipolar complex fuzzy set, AIMS Mathematics, 8 (2023), 25220–25248. https://doi.org/10.3934/math.20231286 doi: 10.3934/math.20231286
[48]	M. Tahir, Z. Ali, Multi-attribute decision-making methods based on Aczel-Alsina power aggregation operators for managing complex intuitionistic fuzzy sets, Comp. Appl. Math., 42 (2023), 87. https://doi.org/10.1007/s40314-023-02204-1 doi: 10.1007/s40314-023-02204-1
[49]	H. Garg, Tehreem, G. N. Nguyen, T. Alballa, H. A. E. W. Khalifa, Choquet integral-based Aczel–Alsina aggregation operators for interval-valued intuitionistic fuzzy information and their application to human activity recognition, Symmetry, 15 (2023), 1438. https://doi.org/10.3390/sym15071438 doi: 10.3390/sym15071438
[50]	P. D. Liu, Z. Ali, T. Mahmood, Y. S. Geng, Prioritized aggregation operators for complex intuitionistic fuzzy sets based on Aczel-Alsina t-norm and t-conorm and their applications in decision-making, Int. J. Fuzzy Syst., 25 (2023), 2590–2608. https://doi.org/10.1007/s40815-023-01541-x doi: 10.1007/s40815-023-01541-x
[51]	Z. U. Rehman, G. Ali, M. Asif, Y. F. Chen, M. Z. U. Abidin, Identification of desalination and wind power plants sites using $m$ -polar fuzzy Aczel-Alsina aggregation information, Sci. Rep., 14 (2024), 409. https://doi.org/10.1038/s41598-023-50397-6 doi: 10.1038/s41598-023-50397-6
[52]	G. Ali, A. Farooq, M. M. A. Al-Shamiri, Novel multiple criteria decision-making analysis under $m$ -polar fuzzy aggregation operators with application, Math. Biosci. Eng., 20 (2023), 3566–3593. https://doi.org/10.3934/mbe.2023166 doi: 10.3934/mbe.2023166
[53]	A. Ali, K. Ullah, A. Hussain. An approach to multi-attribute decision-making based on intuitionistic fuzzy soft information and Aczel-Alsina operational laws, Journal of Decision Analytics and Intelligent Computing, 3 (2023), 80–89. https://doi.org/10.31181/jdaic10006062023a doi: 10.31181/jdaic10006062023a
[54]	M. Akram, K. Ullah, G. Cirovic, D Pamucar, Algorithm for energy resource selection using priority degree-based aggregation operators with generalized orthopair fuzzy information and Aczel-Alsina aggregation operators, Energies, 16 (2023), 2816. https://doi.org/10.3390/en16062816 doi: 10.3390/en16062816
[55]	X. M. Shi, Z. Ali, T. Mahmood, P. D. Liu, Power aggregation operators of interval-valued Atanassov-intuitionistic fuzzy sets based on Aczel-Alsina t-norm and t-conorm and their applications in decision making, Int. J. Comput. Intell. Syst., 16 (2023), 43. https://doi.org/10.1007/s44196-023-00208-7 doi: 10.1007/s44196-023-00208-7
[56]	M. M. A. Al-Shamiri, A. Farooq, M. Nabeel, G. Ali, D. Pamucar, Integrating TOPSIS and ELECTRE-I methods with cubic m-polar fuzzy sets and its application to the diagnosis of psychiatric disorders, AIMS Mathematics, 8 (2023), 11875–11915. https://doi.org/10.3934/math.2023601 doi: 10.3934/math.2023601
[57]	P. D. Liu, P. Wang, Some improved linguistic intuitionistic fuzzy aggregation operators and their applications to multiple-attribute decision making, Int. J. Inf. Tech. Decis., 16 (2017), 817–850. https://doi.org/10.1142/S0219622017500110 doi: 10.1142/S0219622017500110
[58]	R. Verma, J. M. Merigo, Multiple attribute group decision making based on 2-dimension linguistic intuitionistic fuzzy aggregation operators, Soft Comput., 24 (2020), 17377–17400. https://doi.org/10.1007/s00500-020-05026-z doi: 10.1007/s00500-020-05026-z
[59]	Z. S. Xu, A method based on linguistic aggregation operators for group decision making with linguistic preference relations, Inform. Sciences, 166 (2004), 19–30. https://doi.org/10.1016/j.ins.2003.10.006 doi: 10.1016/j.ins.2003.10.006
[60]	M. R. Khan, K. Ullah, H. Karamti, Q. Khan, T. Mahmood, Multi-attribute group decision-making based on q-rung orthopair fuzzy Aczel-Alsina power aggregation operators, Eng. Appl. Artif. Intel., 126 (2023), 106629. https://doi.org/10.1016/j.engappai.2023.106629 doi: 10.1016/j.engappai.2023.106629
[61]	M. R. Seikh, U. Mandal, Multiple attribute group decision making based on quasirung orthopair fuzzy sets: Application to electric vehicle charging station site selection problem, Eng. Appl. Artif. Intel., 115 (2022), 105299. https://doi.org/10.1016/j.engappai.2022.105299 doi: 10.1016/j.engappai.2022.105299
[62]	M. R. Seikh, U. Mandal, Multiple attribute decision-making based on 3, 4-quasirung fuzzy sets, Granul. Comput., 7 (2022), 965–978, https://doi.org/10.1007/s41066-021-00308-9 doi: 10.1007/s41066-021-00308-9

Reader Comments

Your name:*

Email:*
© 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

AIMS Mathematics

1.8 3.4

Metrics

Article views(675) PDF downloads(35) Cited by(0)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

AIMS Mathematics

Novel linguistic $q$ -rung orthopair fuzzy Aczel-Alsina aggregation operators for group decision-making with applications

Related Papers:

Abstract

1. Introduction

2. Model description

3. The observable case

4. Fully observable case

5. Numerical experiments

5.1. Equilibrium strategies of customers

5.2. The expected cost function of the system

6. Conclusions

Use of AI tools declaration

Acknowledgments

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Catalog

Abstract

1. Introduction

2. Model description

3. The observable case

4. Fully observable case

5. Numerical experiments

5.1. Equilibrium strategies of customers

5.2. The expected cost function of the system

6. Conclusions

Use of AI tools declaration

Acknowledgments

Conflict of interest

References

AIMS Mathematics

Novel linguistic q q -rung orthopair fuzzy Aczel-Alsina aggregation operators for group decision-making with applications

Related Papers:

Abstract

1. Introduction

2. Model description

3. The observable case

4. Fully observable case

5. Numerical experiments

5.1. Equilibrium strategies of customers

5.2. The expected cost function of the system

6. Conclusions

Use of AI tools declaration

Acknowledgments

Conflict of interest

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

1. Introduction

2. Model description

3. The observable case

4. Fully observable case

5. Numerical experiments

5.1. Equilibrium strategies of customers

5.2. The expected cost function of the system

6. Conclusions

Use of AI tools declaration

Acknowledgments

Conflict of interest

References

Novel linguistic $q$ -rung orthopair fuzzy Aczel-Alsina aggregation operators for group decision-making with applications