An analysis of fractional integral calculus and inequalities by means of coordinated center-radius order relations

1.   Introduction

In reality to show fractional order demeanor which can change with time and space in case of large number of physical processes. The operations of differentiation and integration of fractional order are authorized by fractional calculus. The fractional order may be taken on imaginary and real values. The theory of fuzzy sets is continuously drawing the attention of researchers towards itself due to its rich application in many fields including mechanics, electrical, engineering, processing signals, thermal system, robotics and control, signal processing and many other fields. Therefore, it has been notice that it is the centre of increasing interest of researcher during past few years.

Differential equations are effective tools for describing a wide range of phenomena in modern-world problems. There has been meaningful progress in the study of different classes of differential equations. Traditional integer-order derivatives have recently lost popularity in recent decades in favor of fractional-order derivatives. This is because a variety of mathematical models for current issues involving fractional-order derivatives have been investigated, and their findings have been considerable. In contrast to integer-order derivatives, which are local operators, noninteger-order derivatives have the advantage of being global operators that yield precise and consistent results. Numerous classes of differential equations have been reorganized and constructed in terms of fractional-order derivatives as a result of these great benefits. We discuss some issues where fractional-order derivatives are excellent resources, such as models of global population growth, issues involving blood alcohol content, video tape models, etc. Similarly, fractional-order derivatives ^[3,4] are used in fields such as electrodynamics, fluid dynamics, fluid mechanics, and so on, see ^[1,2].

One of the major classes of differential equations is the class of implicit differential equations. These equations are useful in the management and economic sciences. The differential equations in the equilibrium state are typical of the implicit type in economic difficulties. Related to this, we can use implicit functions to explore important aspects of most real-world graphs or surface geometry.

Differential equations with impulsive conditions, on the other hand, are important in almost every branch of science. Dynamical systems with impulsive phenomena are used in physics, biology, economics, engineering, and other fields. See ^[5,6,7] for more information on how to model procedures with discontinuous jumps and disruptions using differential equations with impulsive conditions. Although impulsive differential equations have received considerable attention, it is worth noting that many aspects of these equations remain to be studied and explored. Delay differential equations can take many different forms. Pantograph differential equations, also known as proportional delay differential equations, are one type. These equations are significant because they can be used to simulate a wide range of issues in fields like population studies, physics, chemistry, economics, infectious diseases, biology, medicine, physiological and pharmaceutical kinetics, chemical kinetics, light absorption by interstellar matter, navigational control of ships and airplanes, electronic systems, electrodynamics, quantum mechanics, and more.

The pantograph equation is the most effective form of delay differential equations; these equations have gotten a lot of attention because of the numerous applications in which they appear ^[8,9,10]. Recently many of the existence-uniqueness of solutions for different classes of fractional pantograph equations, see, for instance, ^[11,12,13]. Also, we refer to the articles ^[14,15] and the references therein for a rigorous inspection of the Ulam-stability of fractional pantograph differential equations ^[16,17]. Balachandran et al. ^[18], Hashemi et al. ^[19] and Alzabut et al. ^[20] worked on the fractional pantograph equations. Abbas et al. ^[21,22] solve ordinary differential equations. Niazi et al.^[23], Iqbal et al. ^[24], Shafqat et al. ^[25,26], Alnahdi ^[27], Khan et al. ^[28], Boulares et al. ^[29] and Abuasbeh et al. ^[30,31,32] existence-uniqueness of the fuzzy fractional evolution equations were investigated. M. Houas ^[33] worked on the existence and Ulam stability of solution for FPDEs with two Caputo-hadamard type derivatives:

where $0 < \alpha, \beta \leq 1, _H^cD^{\alpha}, _H^cD^{\beta}$ are Caputo-Hadamard fractional derivatives and $f:[1, \Im] \times {\bf{R^m}} \times {\bf{R^m}} \rightarrow {\bf{R^m}}$, is given continuous function.

We discuss the existence-uniqueness and Ulam-stability of solutions for the FOPDEs with Caputo fractional derivatives in light of the mentioned research:

where $1 < \varpi, \varrho \leq 2, ^{c}D^{\varpi}, ^{c}D^{\varrho}$ denote the Caputo fractional derivatives, $\varpi-1 > 0, A$ is real constant, $\psi, f:[1, 2] \times {\bf{R^m}} \times {\bf{R^m}} \times {\bf{R^m}} \rightarrow {\bf{R^m}}$, $x : \mathcal{C}(0, 1) \cap L^1(0, 1)$ and $\|x\| = \sup_{\omega \in \Im}|x(\omega)|$ are given continuous functions. The goal of this work is to investigate the existence, uniqueness and Ulam-Hyers-Rassias stability of results to fractional integral pantograph differential equations. Some scholars discovered FDE results in the literature, although the vast majority of them were differential equations of the first order. We discovered the results for Caputo derivatives of order $(1, 2)$ in our research. Stability, as a part of differential equation theory, is vital in both theory and application. As a result, stability is a key subject of study for researchers, and research papers on stability for FDE have been published in the last two decades, for example, essential conditions for solution stability and asymptotic stability of FDEs. We use fractional integral pantograph differential equations and apply them on various kinds of fractional derivatives and studied the existence and stability of Ulam-Hyers. Pantograph equations also play a pivotal role in pure and applied mathematics and physics. Motivated by their significance, a ton of scientists generalized these equations into different types and presented the solvability aspect of such problems both numerically and theoretically; for additional subtleties. The remaining of this paper is as below. In Section 2, we discuss and outline that are the most important features. The existence-uniqueness of the solution is demonstrated in Section 3. Section 4 investigates the Ulam-Hyers-Rassias stability (UHRS) of the solution. In addition, an example is presented in Section 5 and applications in Section 6. Finally, in Section 6, a conclusion is given.

2.   Preliminaries

The operator $^{c}D^{\varpi}$ is the fractional derivative in the sense of Caputo ^[34,35], defined by

and the RL fractional integral ^[34,35] of order $\varpi > 0$, denoted by

The following lemmas are required.

Lemma 2.1. ^[35,36] Assume $\varpi > \varrho > 0$ and $\varphi \in L^1([a, b])$. Then $D^{\varsigma}I^{\varpi}\varphi(\omega = I^{\varpi-\varrho}\varphi(\omega), \; \omega \in [\ell, \hbar]$.

Lemma 2.2. ^[35,36] For $\varpi > 0$ and $\sigma > -1$, we have

In particular, for $x = 0$ and $\sigma > -1$, we have

We also require the below lemmas.

Lemma 2.3. ^[36] Suppose $\varrho > 0$ and $x \in C(0, 1) \cap L^1(0, 1)$. Then the fractional differential equation $^{RL}D^{\varrho}u(\omega) = 0$ has a unique solution

where $c_\jmath \in {\bf{R^m}}, \; \jmath = 1, 2, ..., n, \; n = [\varrho]+1$.

Lemma 2.4. ^[36] Let $\varrho > 0$. Then for $x \in \mathcal{C}(0, 1) \cap L^1(0, 1)$ and $^{RL}D^{\varrho}x \in \mathcal{C}(0, 1)\cap L^1(0, 1)$, we have

where $c_\jmath \in {\bf{R^m}}, \jmath = 1, 2, ..., n$ and $n-1 < \varrho < n$.

Lemma 2.5. ^[36] For $\vartheta > 0$, the general solution of the fractional differential equation $^{c}D^{\vartheta}u(\omega) = 0$ is given by

where $c_\jmath \in {\bf{R^m}}, \jmath = 0, 1, 2, ..., n-1, n = [\vartheta]+1$.

Lemma 2.6. ^[36] Assume $\varpi > 0$. Then

for some $c_\jmath \in {\bf{R^m}}, \jmath = 0, 1, 2, ..., n-1, n-1 < \varpi < n$.

Lemma 2.7. ^[37] Let $O: {\mathcal{E}} \rightarrow {\mathcal{E}}$ be a completely continuous operator (that is, a compact map that is constrained to any bounded set in ${\mathcal{E}}$). For some $0 < \rho < 1\}$, let $\Theta(O) = \{x \in {\mathcal{E}}: x = {\rho}O(x)$. The set $\Theta(O)$ is then either unbounded or has at least one fixed point.

Assume $\mathcal{W} = \mathcal{C}([0, 1], {\bf{R^m}})$ denote the Banach space of continuous functions with the norm $||u||$ from $[0, 1]$ to ${\bf{R^m}}$, where $||x|| = \sup_{\omega \in [0, \Im]}|x(\omega)|$.

In this section, we will look at the UH and UHRS for the fractional problem 1.1. We examine the following inequalities for $\omega \in [0, 1]$:

and

Definition 2.1. The problem 1.1 is UHS if a real number $\eta_{\varphi, \phi_\jmath} > 0(\jmath = 1, ..., m)$ exists such that for each $\varsigma > 0$ and for each solution $v \in \mathcal{W}$ of the inequality 2.1, there exists a solution $u \in \mathcal{W}$ of the problem 1.1:

Definition 2.2. The problem 1.1 is UHRS with respect to $g \in \mathcal{C}([0, 1], {\bf{R^m_+}})$ if there exists a real number $\eta_{\varphi, \phi_\jmath} > 0 (\jmath = 1, ..., m)$ such that for each $\varsigma > 0$ and for each solution $v \in \mathcal{W}$ of the inequality 2.2, there exists a solution $u \in \mathcal{W}$ of problem 1.1 with

Remark 2.8. If and only if there exists a function $\mathcal{F}:[0, 1] \rightarrow {\bf{R^m}}$, a function $v \in \mathcal{W}$ is a solution of the inequality 2.1 as

and

3.   Existence and uniqueness of solution

Lemma 3.1. Consider the fractional problem with $h(\omega) \in \mathcal{C}([0, 1], {\bf{R^m}})$,

with the condition

Then,

Proof. Using Lemma 2.4,

where $c_1 \in {\bf{R^m}}$. Now, by Lemma 2.6, we have

where $c_2 \in {\bf{R^m}}$. By using 3.2, we get

and

Substituting the value of $c_1$ and $c_2$ in 3.6 yields the solution 3.4. We define

We require the following conditions for the detail:

$(\mathcal{C}_1) : \varphi, \phi_\jmath:[0, 1] \times {\bf{R^m}} \times {\bf{R^m}} \rightarrow {\bf{R^m}}, \jmath = 1, ..., m,$ are continuous functions and there exist a constants $\kappa_\jmath > 0, (\jmath = 1, ..., m+1)$ such that for all $\omega \in [0, 1]$ and $x_\imath, y_\imath \in {\bf{R^m}}, \imath = 1, 2.$

$(\mathcal{C}_2) : \psi : \mathcal{C}([0, 1], {\bf{R^m}}) \rightarrow {\bf{R^m}}$ is continuous function with $\psi(0) = 0$ and there exists a constant $\omega > 0$,

Using BFPT, we will develop a special remedy for the FPE (1).

Theorem 3.2. Suppose that $(\mathcal{C}_1)$ and $(\mathcal{C}_2)$ hold. If

where $\kappa = \max\{\kappa_\jmath, \jmath = 1, 2, ..., m+1\}$, then fractional problem 1.1 has a unique solution on ^[1,2].

Proof. Assume that $L_1 = \max\{L_\jmath:\jmath = 1, 2, ..., m+1\}$, where $L_\jmath$ are finite numbers given by $\sup_{\omega \in [0, 1]}|\varphi(\omega, 0, 0)|$ and $L_{\jmath+1} = \sup_{\omega \in [0, 1]}|\varphi_\jmath(\omega, 0, 0)|$. Define

we show that $\mathcal{Q}\mathfrak{B}_r \subset \mathfrak{B}_r$, where $\mathfrak{B}_r = \{u \in \mathcal{W} : \|u\| \leq r\}$. For $u \in \mathfrak{B}_r$ and by $(\mathcal{C}_1)$ and $(\mathcal{C}_2)$,

and

Using 3.8 and 3.9,

By $(\mathcal{C}_1)$ and $(\mathcal{C}_2)$, we can write

Thus

This implies that $\mathcal{Q}\mathfrak{B}_r \subset \mathfrak{B}_r$. Now we have $u, v \in \mathfrak{B}_r$ and all $\omega \in [0, \Im]$,

So, according to $(\mathcal{C}_1)$ and $(\mathcal{C}_2)$, we get

We can see from 3.7 that $\mathcal{Q}$ is a contractive operator. As a result the BFPT, has a fixed point that is a solution of 1.1.

By Lemma 3.1, we demonstrate the existence of solutions to the FPE 1.1 in the below result.

For the forthcoming result, we need to provide the below conditions:

$(\mathcal{C}_3) : \varphi, \phi_\jmath:[0, 1] \times {\bf{R^m}} \times {\bf{R^m}} \rightarrow {\bf{R^m}}, \jmath = 1, ..., m$, are continuous and there exist real constants $b_\jmath, d_\jmath \geq 0$ and $a_\jmath > 0, \jmath = 1, ..., m+1$ such that for any $x_1, y_1 \in {\bf{R^m}}$, we have

$(\mathcal{C}_4) : \psi : \mathcal{C}([0, 1], {\bf{R^m}}) \rightarrow {\bf{R^m}}$ is continuous function with $\psi(0) = 0$ and there exists constant $\varsigma > 0$ such that

Theorem 3.3. Suppose that the conditions $(\mathcal{C}_3)$ and $(\mathcal{C}_4)$ are satisfied. If the inequality

at least one solution to the 1.1 problem can be found in ^[1,2].

Proof. In the first step, we demonstrate the complete continuity of the operator $\mathcal{Q}:\mathcal{W} \rightarrow \mathcal{W}$. It follows that the operator $\mathcal{Q}$ is continuous because the functions $\varphi, \phi_\jmath(\jmath = 1, ..., m)$ and $\psi_\jmath$ are continuous.

Assume $\Omega \in \mathcal{W}$ be bounded. Then there exist positive constants $M_\jmath, (\jmath = 1, ..., m+1)$ such that $|\varphi(\omega, x, y)| \leq M_1, |\phi_i(\omega, x, y)| \leq M_{\jmath+1}$, for each $x, y \in \Omega$ and constants $\Pi$ such that $|\psi(x)| \leq \Pi$ for all $x \in \mathcal{C}([0, 1], {\bf{R^m}})$. Then we have for any $x \in \Omega$, we have

which assumes that

As a result of the preceding inequality, the operator $\mathcal{Q}$ is uniformly bounded.

Following that, $\mathcal{Q}$ is an equicontinuous set of $\mathcal{W}$. Assume, $\omega_1, \omega_2 \in (0, 1]$ be replaced by $\omega_1 < \omega_2$. Then,

Hence, we obtain

According to the above inequality, we can state that $\|\mathcal{Q}x(\omega_2)-\mathcal{Q}x(\omega_1)\| \rightarrow 0$ as $\omega_2-\omega_1 \rightarrow 0$. By applying the Arzela-Ascoli theorem, $\mathcal{Q}: \mathcal{W} \rightarrow \mathcal{W}$ is completely continuous.

Finally, we demonstrate that the $\Theta$ set defined by

is bounded. Suppose $x \in \Theta$, then $x = \rho{\mathcal{Q}(x)}$. For each $\omega \in [0, 1]$,

Then

Hence

which implies that

This demonstrates that $\Theta$ is bounded. As a result, according to Lemma 2.7, operator O has at least one fixed point. As a result, there is at least one solution to the fractional pantograph problem 1.1 on $[1, 2]$. The proof is finally completed.

4.   Ulam-Hyers-Rassias stability

In this portion, we will look at the problem's UH and UHRS 1.1.

Theorem 4.1. If conditions $(C_1)$ and $(C_2)$ are satisfied and also

Then the problem 1.1 is UHS, and thus generalized UHS.

Proof. Presume that $x \in \mathcal{W}$ is the only solution to the issue and that $y \in \mathcal{W}$ is a solution to the inequality 2.1:

Using Eq 4.2, we can write

The inequality 1.1 has now been integrated, and we have

For any $\omega \in [0, 1]$, we have

where

and

then

According to $(\mathcal{C}_1)$, we get

This leads to

which indicates

Also, one can see that

Thus, we obtain the inequality

Problem 1.1 is UHS, we conclude.

Theorem 4.2. If conditions $(\mathcal{C}_1), (\mathcal{C}_2)$ and 3.10 are satisfied. Suppose there exists $\Lambda_g > 0$,

for all $\omega \in [0, 1]$, where $g \in \mathcal{C}([0, 1], {\bf{R^m_+}})$ is increasing. The problem 1.1 then becomes UHRS concerning $g$.

Proof. Assume $y \in \mathcal{W}$ be a solution to the inequality 2.2, and also presume $x \in \mathcal{W}$ be the unique solution to the problem:

We obtain by integrating the inequality 2.2:

In addition, we have

which implies that

Hence

This implies

Then, for each $\omega \in [0, 1]$, there is

As a result, we conclude that problem 1.1 has UHRS.

5.   Example

We will use the below example to demonstrate our main points.

Example 5.1. Assume the Caputo-type fractional pantograph equation

We have $\alpha \in \frac{5}{2}, \beta = \frac{3}{2}, \lambda = \frac{1}{2}$ and $\Im = e$. On the other hand,

For $\omega \in [0, \Im]$ and $(u_1, v_1)$ and $(u_2, v_2) \in {\bf{R^m}}$,

Hence, the condition $(H_1)$ holds with $K = \frac{2}{17}e^5$. Thus conditions

are satisfied. According to Theorem 3.2, the problem 5.1 has a unique solution on $[1, e]$, and according to Theorem 4.1, fractional problem 5.1 is UH stable.

6.   Applications

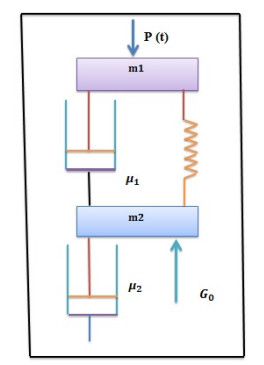
Pantograph is a linkage constituting of five link connected with pin joints to form revolute pairs. It is connected in a manner based on parallelograms so that the movement of one point, in tracing an image, produces identical movements by second point. A pantograph is used to reproduce to an enlarged or a reduced scale and as exactly as possible the path described by a given point. Pantograph equation is one of the most prominent delay differential equation that play a significant role in mathematical physics. This equation exists in several branches of pure and applied mathematics including dynamical systems, control system, probability, number theory, quantum mechanics, electrodynamics. In particular, Taylor and Ockendon formulated such type of equation to describe how to receive electric current from the pantograph of an electric locomotive. Figure 1 displays the pantograph model.

7.   Conclusions

In this work, we have explained the existence-uniqueness and Ulam-type stability of solutions for FOPDEs with fractional Caputo derivative. We have established the existence-uniqueness results applying the BFPT and Leray-Schauder's alternative. Moreover, the UHS and the UHRS have been discussed. To illustrate the theoretical results we have given an example. Future work may also involve generalizing other tasks, adding observability, and developing the concept that was introduced in this mission. This is a fertile field with numerous research initiatives that have the potential to produce a wide range of theories and applications.

Acknowledgements

The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University of funding this work through Small Groups (Project under grant number (1/350/43)).

Conflict of interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper