Linguistics complex intuitionistic fuzzy aggregation operators and their applications to plastic waste management approach selection

1.   Introduction

In everyday life, complications in systems are growing; therefore, the executives and decision makers are facing difficulties for achieving the best option from a set of possibilities. Many organizations found difficulties in setting motivational goals and removing opinion complications. It is difficult to obtain single objectives to summarize but not impossible. Different organizations have numerous objectives and are facing many uncertainties, ambiguities, and vagueness in the data regarding the solution of practical problems, which restricts the decision makers to get the reliable and applicable technique to find the finest option.

The crisp and classical methods could not always be effective for solving the problems of decision making with regard to ambiguous and uncertain data; thus, fuzzy set, as characterized by Zadeh ^[1] in 1965, are used to deal with these situations. Fuzzy sets part of degree having a place to [0, 1]. Fuzzy sets have been generally utilized in choice investigation, financial matters, hazard evaluation, and expectation, particularly in the design and administration areas. Allehiany et al. ^[2] developed a Bio-inspired numerical analysis of COVID-19 with fuzzy parameters. Talpur et al. ^[3] wrote comprehensive review of deep neuro-fuzzy system architectures and their optimization methods. Moreover the fuzzy sets theory and logic are powerful tools to represent reasoning with uncertain information; however, but traditional fuzzy sets are restricted to express membership degrees in terms of real numbers between 0 and 1. Deabes and Amin ^[4] suggested an image reconstruction algorithm based on a PSO-tuned fuzzy inference system for electrical capacitance tomography. Zadeh ^[5] also presented an idea about linguistics fuzzy sets in 1975 and valuable contribution in linguistic variables by allowing fuzzy sets in natural language terms like "high", "medium", and "low". This makes fuzzy sets more interpretable and intuitive, particularly in areas where humans naturally express uncertainty using language. In 1986, Atanassov ^[6] presented IFSs (intuitionistic fuzzy sets) by adding non-membership degrees with the membership degrees, with a more nuanced uncertainty representation. The work of Huimin ^[7] on applications of linguistic intuitionistic fuzzy sets in multi-attribute group decision-making (MAGDM) appeared in 2014; before that, Ramík et al. ^[8] introduced complex fuzzy sets in 2000 to expand upon traditional fuzzy sets by integrating complex numbers as relationship degrees. This permits the inclusion of data regarding phase and magnitude, which can be valued to represent oscillatory or periodic phenomena. Wan et al. ^[9] proposed an innovative use of intuitionistic fuzzy reference evaluations to expand the best-worst technique. Dai ^[10] provided a remarkable extension in the work of Ramík et al. ^[8] linguistic complex fuzzy sets. Bio et al. ^[11] marvelous work in the domain aggregation operators of the linguistic interval-valued intuitionistic fuzzy sets based on Hamacher's extended t-norm and s-norm along with their applications. These two concepts formed a unique section of fuzzy set, titled as "LIFSs" (linguistic intuitionistic fuzzy sets), which offered an influential context for dealing with complex and uncertain information in various fields of life. Zenga et al. ^[12] introduced a new operator with an application in intuitionistic fuzzy sets for the decision making process.

Wan et al. ^[13] worked on Group decision-making via intuitionistic fuzzy preference relations: Theory and methodology. Rahman et al. ^[14] launched a specific process for multi group decisions-making by introducing geometric operators of aggregation with applications on the basis of Pythagorean fuzzy Einstein operators. Yang et al. ^[15] wrote a remark on using Pythagorean fuzzy sets to extend the "technique for order of peference by similarity to ideal solution" for multiple criteria decision-making. Yager et al. ^[16], presented procedures for decision making by relating complex numbers with Pythagorean membership degrees. Phong et al. ^[17] worked on picture linguistic numbers for multiple decision making criteria. Wei ^[18], worked on decision-making process by focusing on picture fuzzy sets based on Hamacher's operators for aggregation with applications. Garg ^[19] pointed out Einstein operations in decision-making regarding Pythagorean fuzzy information. Ashraf et al. ^[20] formulated different approaches in decision-making issues using the environment of picture fuzzy sets. Wang et al. ^[21] first focused on geometric operators for aggregation in picture fuzzy environment in the domain of decision making process; second, Wang et al. ^[22] also gave attention to the decision-making process, especially for incomplete specific information regarding weights, and their concepts were based on Atanassov's intuitionistic fuzzy sets. Gautam et al. ^[23] used technique for order of peference by similarity to ideal solution in intuitionistic fuzzy sets. Deschrijver ^[24], in the domain of the decision-making procedure, represented t-norms and t-conorms of intuitionistic fuzzy sets. Zeng ^[25] made relationships between Intuitionistic fuzzy sets and distance operator of ordered weight, and Ye ^[26] researched the connection of intuitionistic fuzzy set's applications with cosine similarity measures ^[27]. Selecting a location for a solar power plant was done using a combined methodology for difficult homogeneous multi-attribute collaborative decision-making. In the proposed research study, novel decisions-making approaches based on linguistics complex intuitionistic fuzzy aggregation operators and their applications will be a valuable outcome of the applications of fuzzy sets, knowledge, logic, and theory. Garg et al. ^[28], used set pair analysis in the group decision-making process with special reference to operators for aggregation and applications in the intuitionistic fuzzy set. Tang et al. ^[29] worked on Hamacher's aggregation operators in the linguistic intuitionistic fuzzy environment. At first, Liu et al. ^[30] worked for a decision-making process by focusing on applications of the linguistic intuitionistic fuzzy sets; second, Liu et al. ^[31] introduced some improved aggregation operators in the same domain along with applications for decision-making to multiple attributes. Xu ^[32] introduced linguistic aggregation operators with preference to linguistic relations. Xu's ^[33] work was also decision-making process related to the approaches to ungroup linguistic environment based on aggregation operators of the linguistic intuitionistic fuzzy sets. Abrar Hussain et al. ^[34] developed the Sugano-Weber triangular norm-based $q$-rung orthopair fuzzy information approach to solar panel selection decision-making. Wan et al. ^[35] presented a brand-new intuitionistic fuzzy best-worst technique that uses intuitionistic fuzzy preference relations for group decision-making. Dong et al. ^[36] provided an additively consistent interval-valued intuitionistic fuzzy best-worst technique. Wan et al. ^[37] outlined a comprehensive approach for complex heterogeneous multi-attribute group decision-making and its use in the site selection of solar power plants. Wan et al. ^[38] developed a heterogeneous multi-criterion group decision-making process based on trapezoidal clouds for the selection of multi modal transport paths for containers. Wang et al. ^[39] contributed to the use of complex intuitionistic fuzzy Dombi prioritized aggregation operators for robust green supplier selection. Hussain et al. ^[40] contributed to the creation of an intelligent decision support system for real-world applications and Spherical fuzzy Sugino-Weber aggregation operators. Wang et al. ^[41] illustrated the use of fuzzy Dombi prioritization and complex intuitionistic aggregation operations for robust green supplier selection. Asif et al. ^[42] specified Hamacher aggregation operators for Pythagorean fuzzy sets and their use in problems involving several attributes for decision-making. Kannan et al. ^[43] undertook work on the linear Diophantine fuzzy CODAS method for the Logistic specialist selection, an advanced kind of fuzzy-based decision-making. Imran et al. ^[44] described an Aczel-Alsina Bonferroni means and interval-valued intuitionistic fuzzy information-based multi-criteria group decision-making.

For this study, linguistic complex intuitionistic fuzzy sets (LCIFSs) are on the extension of linguistic intuitionistic fuzzy sets into the complex domain to enable a more nuanced illustration of ambiguity and uncertainty in linguistic terms. LCIFSs are an association of linguistic variables with complex-valued relationship degrees to provide a powerful structure for reasoning and representing the complex, oscillatory, and ambiguous data in various real-world applications.

The major objectives are listed in the following points:

(1) To define the basic concept of LCIFSs and to explore basic operation laws of LCIFSs.

(2) To develop the basic results of LCIFSs and explore associated properties.

(3) To propose aggregation operators based on linguistic complex intuitionistic fuzzy operation laws.

(4) To develop a new multi-attribute group decision-making approach to solve a decision making problem.

(5) To generalize the existing notions to some advanced ideas and make them applicable in real life problems.

(6) To develop new results and notions, discuss their applications, and compare the results obtained with the existing theory.

This research article is organized as follows: In Section 2, we present preliminaries consist of some basic definitions, such as fuzzy sets, linguistic terms, complex fuzzy sets, linguistic intuitionistic fuzzy sets, linguistic intuitionistic fuzzy variables (LIFVs), and score functions. In Section 3, a new concept of LCIFSs, is introduced, which contains definitions as well as linguistic complex intuitionistic fuzzy aggregation operators and applications for LCIFSs, where method of normal distribution are used to determine the weights of linguistic complex intuitionistic fuzzy ordered weighted averaging (LCIFOWA) and linguistic complex intuitionistic fuzzy ordered weighted geometric (LCIFOWG). In Section 4, the operators and applications are used to solve problems of MAGDM. In Section 5, numerical analysis of decision-making problems has been illustrated. Finally, we conclude the study in Section 6.

2.   Preliminaries

Definition 2.1. ^[1] Assume that $A$ is a set that is not empty. Then, the fuzzy set $X$ in $A$ is defined as:

The membership function of $A$ is denoted by $s_{a(x)}$ in this case. i.e., $s_{a(x)}$: $A\rightarrow \lbrack 0, 1]$ represents the degree of membership function of $A$.

Definition 2.2. ^[11] Let

be a finite linguistic term where $a_{t}$ has the following properties:

ⅰ) The ordered set: $a_{j}\geq a_{k}$ iff $j\geq k$;

ⅱ) $N\left(a_{j}\right) = a_{t-j}$;

ⅲ) $Max\left(a_{j}, a_{k}\right) = a_{\max \left(j, k\right) }$;

ⅳ) $Min\left(a_{j}, a_{k}\right) = a_{\min \left(j, k\right) }$.

The Linguistic fuzzy set approach depends on fuzzy logic and fuzzy sets theory. Here, variables represent the linguistic terms. Every linguistic term is differentiated by a unique meaning and label.

The meaning and label stands for the fuzzy subset and the sentence of a language, respectively.

Definition 2.3. ^[5] Assume that $A$ is a set that is not empty. Then, IFS $X$ in $A$ is defined as:

such that; $s_{a}$: $A\rightarrow \lbrack 0, 1]$ and $r_{a}$: $A\rightarrow \lbrack 0, 1]$ indicate the level of membership and non-membership of "$a$" in $X$, respectively, for all any $a\in A,$

Definition 2.4. ^[8] Let $A$ be a universal set then complex fuzzy set $X$ is defined as:

where $S_{x(a)}\in \lbrack 0, 1];$ and $w_{x(a)}\in \lbrack 0, 2\pi].$

Definition 2.5. ^[7] Let $A$ be universal set which is finite and

be an ongoing collection of linguistic value set. A LIFS $X$ in $A$ is defined as,

where $s_{l(a)}; s_{m(a)}\in S^{\circ }$ define the term's linguistic membership and non-membership degrees $a$ to $X$, respectively. For any $a\in A$, the condition

is every time satisfied. $\psi (a)$ stands for degree of linguistic indeterminacy $a$ to

Obviously, if

then $\left(LIFS\right)X$ contains the lowest degree of linguistic indeterminacy, so

which shows that the degree of membership $\left(a\text{ to }X\right)$ can be expressed a unique linguistic value, and $X(LIFS)$ has been reduced into a linguistic variable. Inversely, if

then $\left(LIFS\right)X$ has the largest degree of linguistic indeterminacy,

As with IFS, the $\left(LIFS\right)X(a)$ can be converted into an interval of linguistic variable $[s_{l}(a), s_{t-m}(a)]$. This indicates that the terms' maximum and minimum linguistic membership degrees $a$ to $X$ are $s_{t-m}$ and $s_{l}$, respectively. Linguistic intuitionistic fuzzy values "LIFVs" are the unique element that both "LIFS " $X$ and $Y$ are supposed to have for notational simplicity, meaning the pairs

and

For comparability of any two LIFVs, the score and the accuracy functions could be defined as under:

Definition 2.6. ^[7] Let

and

be two LIFVs, with

Then, score function of $X$ could be defined as,

and accuracy function of $X$ could be defined as,

If

and

which implies

2.1.   LCIFS

The following is a presentation of the LCIFS.

Definition 2.7. Let $A$ be a finite universal set,

where $\check{S}$ a continuous linguist value set. Then,

where $s_{x(a)}, s_{y(a)}\in \lbrack 0, 1]$ and $w_{x(a)}, w_{y(a)}\in \lbrack 0, 2\pi]$ called linguistic complex intuitionistic set, i.e., fuzzy.

Definition 2.8. Let $A$ be a finite universal set and

a continuous complex linguistic term set $X$. Then, LCIFS $X$ in $A$ is given as,

where $s_{l\left(a\right) }e^{iw_{l\left(a\right) }}, s_{m\left(a\right) }e^{iw_{m\left(a\right) }}\in S$ stands for the degrees of linguistic complex membership and nonmembership of $X$ to $A$, respectively. For any $a\in A$, the condition

is usually satisfied. $\Omega \left(a\right)$ is defined as the degree of linguistic complex indeterminacy of $A$ in $X$, such that

of course, if

then $\left(\text{LCIFS} \right)$ $X$ possesses the smallest degree of linguistic complex indeterminacy, $\Omega \left(a\right) = 0,$ which shows that the membership degree of $A$ to $X$ with precision can be presented with a unique linguistic complex value and $\left(\text{LCIFS}\right)$ $X$ is decreased to a linguistic complex variable. Conversely, if

then $\left(\text{ LCIFS}\right)$ $X$ possesses the largest degree of linguistic complex indeterminacy,

Similar to ICFS, the $\left(\text{LCIFS}\right)$ $X\left(a\right)$ can be transformed into a linguistic complex variable interval $[s_{l}\left(a\right) e^{iw_{l}\left(a\right) }, s_{t-m}\left(a\right) e^{iw_{t-m}\left(a\right) }]$. This suggests that the items at $X$ have both maximum and minimum linguistic complex membership degrees $s_{t-m}e^{iw_{t-m}}$ and $s_{l}e^{iw_{l}}$ respectively.

For conceptual simplicity, we assume both $\left(\text{LCIFS}\right)$ $A$ and $B,$ which consist only unique element, and stand for linguistic complex intuitionistic fuzzy values (LCIFVs), that is, if

and

For comparability, for any two LCIFVs, the functions for accuracy and score could be described as follows:

Definition 2.9. Let

and

be two LCIFVs, with

Then, the score function of $X$ is determined as,

Then, the accuracy function is as follows:

Thus, the ranking procedure can be applied to $X$ and $Y,$ as follows:

(1) If $E\left(X\right) > E\left(Y\right),$ then $X > Y;$

(2) If $E\left(X\right) = E\left(Y\right)$ and

$(a)\ F\left(X\right) = F\left(Y\right),$ then $X = Y;$

$(b)\ F\left(X\right) > F\left(Y\right),$ then $X > Y;$

$(c)\ F\left(X\right) < F\left(Y\right),$ then $X < Y.$ It is obvious that,

This implies

3.   Aggregation operators for LCIFSs

Definition 3.1. If

and

be two LCIFSs where $a, b\in X$, $s_{l}, s_{m, }s_{p, }s_{q} \in \left[0, 1\right]$ and $w_{l}, w_{m}, w_{p}, w_{q}\in \left[0, 2\pi \right],$ then $A = B$ iff

and

(1) $A\cap B = \{\min \left(s_{l}e^{iw_{l}}, s_{p}e^{iw_{p}}\right), \max \left(s_{m}e^{iw_{m}}, s_{q}e^{iw_{q}}\right) \}.$

(2) $A\cup B = \left\{ \max \left(s_{l}e^{iw_{l}}, s_{p}e^{iw_{p}}\right), \min \left(s_{m}e^{iw_{m}}, s_{q}e^{iw_{q}}\right) \right\}.$

(3) $A^{c} = \left(s_{m}e^{iw_{m}}, s_{l}e^{iw_{l}}\right),$ where $A^{c}$ is complement of $A.$

We ascertain the following parameters of operation for linguistic complex terms, which are induced by the $t$-co-norm and the $t$-norm.

Definition 3.2. Assume any two terms of the linguistic complex. Assume any two terms of the linguistic complex, that is $s_{\alpha }e^{iw_{\alpha }}, s_{\beta }e^{iw_{\beta }}\in S^{\circ },$ where

the additive and multiplicative operation can be defined as, {}

The $t$-norm and $t$-conorm can be represented by $\Upsilon (\alpha /t, \beta /t)$ and $(\alpha /t, \beta /t)$, respectively. Since $\left(\alpha /t, \beta /t\right)$, $\Upsilon \left(\alpha /t, \beta /t\right) \in \left[0, 1\right],$ we have $t\left(\alpha /t, \beta /t\right), t\Upsilon \left(\alpha /t, \beta /t\right) \in \left[0, t\right].$

This implies that the, results of operation are identical to the linguistic complex values set $S^{\circ }$ in the original sense; that is, $s_{t\left(\alpha /t, \beta /t\right) }, s_{t\Upsilon \left(\alpha /t, \beta /t\right) }\in S^{\circ }.$ Additionally, we can clearly state that based on the monotonicity of the $t$-norm and $t$-conorm, the terms of function $t\left(\alpha /t, \beta /t\right)$ and $t\Upsilon \left(\alpha /t, \beta /t\right)$ monotonically increase with the increase of the values of $\alpha$ and $\beta,$ which shows the obtained operational results.

Then$,$ $S_{\zeta \left(\alpha /t, \beta /t\right) \text{ }}$ and $T_{\zeta \left(\alpha /t, \beta /t\right) }$ into (3.1) and (3.2) respectively, so we obtain

and

Example 3.1. Let

applying (3.3) and (3.4) we obtain

and

thus

and

Alternatively, if we take the operational laws of the previous definition, then we have

The cardinality of subscripts $s_{10}$ and $s_{24}$ is larger than the cardinality of linguistic complex value set. Furthermore, if we accept the discrete term set $S$to continuous

where $r\left(r > t\right)$ is sufficiently large positive integer, there is a question (unavoidable) for how to define the semantics for $s_{24}e^{iw_{24}}$ and $s_{10}e^{iw_{10}}$ "clearly" $s_{24}e^{iw_{24}}$ and $s_{10}e^{iw_{10}}$ have distinct meanings in various linguistic complex term set $S^{\circ }$ that have various cardinalities. If we use the most common method

For

then,

these observations contradict the facts that may be hard to apply. We can conquer the limitation that the subscripts of the linguistic complex variables are of larger cardinality than the linguistic complex term set $S^{\circ }$. We can achieve outcomes that agree with our intuition.

Definition 3.3. Let

and

be two linguistic complex intuitionistic fuzzy values, where

and

with $\lambda \succ 0.$ Now,

Some examples of $\lambda A$ and $A^{\lambda \text{ }}$are obtained as given below:

If

then,

Therefore

If

If $\lambda \rightarrow \infty$ then,

Theorem 3.1. Let

and

be two linguistic complex intuitionistic fuzzy values, where

with $\lambda, \lambda _{1}, \lambda _{2}\succ 0.$ Now,

(1) $\lambda \left(A\oplus B\right) = \lambda A\oplus \lambda B$;

(2) $\lambda _{1}A\oplus \lambda _{2}B = (\lambda _{1}+\lambda _{2})A$;

(3) $A^{\lambda }\otimes B^{\lambda } = (A\otimes B)^{\lambda }$;

(4) $A^{\lambda _{1}}\otimes A^{\lambda _{2}} = A^{\lambda _{1+}\lambda _{2}}$.

Proof. (1) We have

we obtain

Similarly

So we have$,$

So we get

thus we have

If

and

which finalizes the theorem's proof generated by complex intuitionistic fuzzy aggregation operators. □

Next, we define some aggregation operators for LCIFVs.

Definition 3.4.

is a finite set of LCIFVs. Than, the linguistic complex intuitionistic fuzzy weighted averaging (LCIFWA) operator is defined as

where

is the weight vector of $A_{\iota }(\iota = 1, 2, 3, ..., n),$ with, $\varpi _{\iota }\in \left[0, 1\right]$ and

in spatial, and if

then the $\left(\text{LCIFWA}\right)$ operator is simplified to a linguistic complex intuitionistic averaging $\left(\text{LCIFA}\right)$ operator, so that

Now, we get some properties of the (LCIFWA) operator.

Theorem 3.2. Let

be a set of LCIFV, where

is the weight vector of $A_{\iota }(\iota = 1, 2, 3, ..., n),$ with, $\varpi _{\iota }\in \left[0, 1\right]$ and

Then, we have

Idempotency. Let $A_{\iota }(\iota = 1, 2, 3, ..., n),$ where all $A_{\iota }$ are equal then,

Monotonicity. Let

be a set of LCIFV if

and

for any $\iota.$ Then, $LCIFWA\left(A_{1}, A_{2}, ..., A_{n}\right)$ for any $\varpi.$

Boundary. Let

be a set of LCIFVs. Then,

Proof. (1) Since,

for any $\iota$ then

(2) If

then for any $l_{\iota }^{\circ }\succeq l_{\iota }$ for any $\iota$. We have

Similarly, when

$\forall \iota,$ we have

According to (3), we obtain

that is

(3) Since

and

$\forall$ any $\iota,$ then, by the monotonocity of we can get

□

Definition 3.5. Let

is a finite set of LCIFV. Then, the LCIFOWA operator is defined as where

is the ith largest of $A_{1}, A_{2}, ..., A_{n}$ and

is the associated weight vector of $A_{\left(\iota \right) }\left(\iota = 1, 2, 3, ..., n\right)$, with $\varpi _{\iota }\in \left[0, 1\right]$ and

We get some properties of the LCIFOWA operator.

Theorem 3.3. Let

be a set of LCIFVs. Then,

is the associated weight vector of $A_{\left(\iota \right) }\left(\iota = 1, 2, 3, ..., n\right)$, with $\varpi _{\iota }\in \left[0, 1\right]$ and

Then, one can be expressed as

Idempotency. If $A_{\iota }(\iota = 1, 2, 3, ..., n)$ where $A_{\iota }$ are equal

Then,

Monotonocity. Let

be a set of LCIFVs. If

and

for any $\iota$. Then,

for any $\varpi.$

Boundary. Let

be a set of LCIFVs. Then,

Definition 3.6. Let

a set of LCIFVs. Then, the linguistic complex intuitionistic fuzzy weighted geometric (LCIFWG) operator is defined as

where the weight vector

of $A_{\left(\iota \right) }\left(\iota = 1, 2, 3, ..., n\right)$, with $\varpi _{\iota }\in \left[0, 1\right]$ and

Theorem 3.4. Let

be a set of LCIFVs. Here

is the weight vector of $A_{\left(\iota \right) }\left(\iota = 1, 2, 3, ..., n\right)$, with $\varpi _{\iota }\in \left[0, 1 \right]$ and

so we have the following:

Idempotency. If all $A_{\iota }(\iota = 1, 2, 3, ..., n)$ are equal

Then,

Monotonicity. Let

be a set of LCIFVs. If

and

for all $\iota.$ Then,

for any $\varpi.$

Boundary. Let

be a set of LCIFVs. If

and

for all $\iota.$Then,

Definition 3.7. Let

a finite set of LCIFV. Then, the LCIFOWG operator is defined as,

Theorem 3.5. Let

be a set of LCIFVs. Where

where, weight vector of $A_{\left(\iota \right) }\left(\iota = 1, 2, 3, ..., n\right)$, with $\varpi _{\iota }\in \left[0, 1 \right]$ and

Then, we get the following:

Idempotency. If all $A_{\iota }(\iota = 1, 2, 3, ..., n)$ are equal then,

$\forall \iota.$ Then,

Monotonicity. Let

be a set of LCIFVs. If

and

Then,

Boundary. Let

be a set of LCIFVs. If

and

Then,

Leema 3.1. Let

be a set of LCIFVs. Where the weight vector

is of $A_{\left(\iota \right) }\left(\iota = 1, 2, 3, ..., n\right)$, with $\varpi _{\iota }\in \left[0, 1\right]$ and

then, by lemma we have

with equality if and only if $l_{1} = l_{2} = ... = l_{n}$, that is

with equality if and only if $m_{1} = m_{2} = ... = m_{n}$, that is

with equality if and only if $m_{1} = m_{2} = ... = m_{n}$

consequently, we get

with equality if and only if $m_{1} = m_{2} = ... = m_{n};$ that is

with equality if and only if $A_{1} = A_{2} = ... = A_{n};$ that is, on the base of above property. We can drive the following results of LCIFOWA and LCIFOWG.

Theorem 3.7. Let

be a set of LCIFVs. Here the weight vector

of $A_{\left(\iota \right) }\left(\iota = 1, 2, 3, ..., n\right)$, with $\varpi _{\iota }\in \left[0, 1 \right]$ and $\sum_{\iota = 1}^{n}\varpi _{\iota } = 1,$ then one has the following:

(1) If $\varpi = (1, 0, ..., 0)^{T},$ then

(2) If $\varpi = (0, 0, ..., 1)^{T}$, then

(3) If $\varpi _{\iota } = 1$ and $\varpi _{j} = 0$ for $j\neq \iota$ than

where

is the largest of $A_{1}, A_{2}, A_{3}, ...$.

Example 3.2. Let

and

be LCIFVs, which are derived from

and let

be the weight vector of $A_{\iota }(\iota = 1, 2, 3, 4).$

so,

We get the following values of score function and accuracy function

Since

and, then

Assume that $\varpi = (0.155, 0.345, 0.345, 0.155)^{T}$, which are determined by the normal distribution, is the associated weight vector of $A(\iota)$. So, we have.

It is easy to see that

4.   MAGDM method with linguistic complex intuitionistic fuzzy information

A technique for handling MAGDM numerical problems is described below, wherein the weight vector of the attributes is identified and the attribute performance values are represented as LCIFVs.

Let the set of alternatives

with the set of attributes

where the weight vector is

with $\varpi _{\iota }\in \lbrack 0, 1]$ and

Suppose

be set of the decision makers, and

be the decision matrix, where

represents the preference value that decision-makers provide in the form of LCIFV. $D_{K}$ for alternative $A_{\iota }$ w. r. to attribute $C_{J}$ and

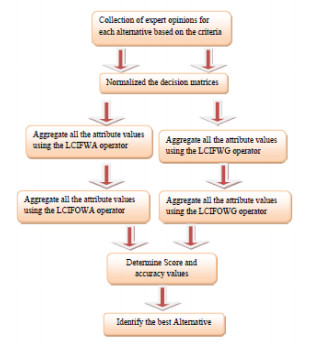
The suggested method could be explained as under:

Step 1. Make LCIF decision matrix $R_{K} = (r_{ij}^{k})_{r \times c}$.

Step 2. Normalized the decision matrix.

Step 3. Apply the LCIFOWA or LCIFOWG operator to obtain the aggregated decision matrix: $R = (r_{ij})_{r\times c}$

where the LCIFOWA and LCIFOWG weights are calculated by the method of normal distribution.

Step 4. The LCIFWA or LCIFWG operator determines the collective preference values (overall) $r_{\iota }$ for each option $A_{\iota }$ $(\iota = 1, 2, ..., r)$ after aggregating $r_{ij}(j = 1, 2, ..., c)$.

Step 5. Arrange the alternatives according to $r_{\iota }.$

In Figure 1, we represent the algorithm.

4.1.   Numerical example

Plastic's low price, effectiveness, and adaptability have made plastic the object of choice in today's world. However, plastic waste remains a huge ecological problem, especially in underdeveloped nations, such as Pakistan, where there is no established system for collecting and recycling this type of trash. Toxic compounds from plastic garbage can leach into the ground and water, and ingested plastic by livestock can make its way up the food cycle and endanger humans. In this section, we cover the level of plastic pollution in Pakistan as well as possible technological alternatives to this issue. In Pakistan, a growing country home to nearly 220 million people, plastic trash is now an ecological problem because of inadequate waste collection and disposal infrastructure. An estimated 20 million tons of solid trash are produced yearly in Pakistan, with 5%–10% of that being plastic, according to United Nations development program (UNDP) research. Furthermore, according to a 2018 worldwide fund for nature (WWF) report, Pakistan ranks as one of the top 10 countries for plastic waste, with around 90% of plastic trash being disposed of in an unsuitable manner. The health and ecological consequences of Pakistan's plastic pollution crisis are substantial. Accumulated plastic trash pollutes air, soil, and water, which can have devastating long-term effects on ecosystems. In the monsoon season, the plastic trash often jams gutters and waterways, causing flooding. Air pollution is partly caused by inhaling pollutants into the air from the combustion of plastic trash. Human health is also seriously threatened by the plastic waste challenge. Toxic substances from plastic debris that leach into the environment and water can make their way into the food chain. Furthermore, plastic trash can serve as an attractive target for pests and disease-transmitting vectors. Pakistan's plastic waste is a complicated issue that needs to be addressed from many angles. Some possible scientific approaches to Pakistan's plastic waste challenge are outlined.

Pakistan's plastic waste is a most complicated issue that needs to be addressed at different angles, and some viable scientific approaches for Pakistan's plastic waste challenge are as follows: $A_{1}$ is recycling, $A_{2}$ is a collection of plastic from desert locations, $A_{3}$ is replacement of plastic with glass biodegradable materials and jute, and $A_{4}$ is the disposal of plastic in the ocean. Experts select numerous criteria $c_{1};$ social benefits, $c_{2};$ environmental impact, $c_{3};$ operational cost and $c_{4};$ effectiveness. The weight vector is

Consequently, specialists are asked to provide their choices for each option for each attribute using the linguistic set which is described in the following:

Step 1. Decision makers construct their evaluation terms and prepare the LCIF decision matrix

which have been represented in the above mentioned Tables 1–3.

Step 2. Science all the attributes are benefit type, the normalization is not required.

Step 3. To determine the collective $\left(\text{overall }\right)$ preference values $r_{\iota }$ for each alternative $A_{\iota }(\iota = 1, ..., 4)$, aggregate $r_{ij}(j = 1, ..., 4).$ This may be done using the LCIFWA or LCIFWG operator with the experts weight vector $\epsilon = (0.243, 0.514, 0.243)^{T}$, as indicated in Tables 4 and 5.

Step 4. In this step, we apply the LCIFOWA and LCIFOWG operators, and obtain the alternative values given in Table 6.

Step 5. In this step, we find the score values and ranking of the alternatives from Table 7.

In Figure 2, we represent the ranking of the alternatives based on Table 7.

5.   Comparison analysis and other methods

MAGDM is commonly used in LIFVs, and due to its prominence, MAGDM methods are also utilized here the newly introduced LCIFVs. We solve the same example in the case of LIFVs as well as in LCIFVs. A comparison of both examples are presented for observation and explanation using the other MAGDM methods, including the LCIFWA, LCIFOWA and the LCIFWG, and LCIFOWG. The comparison results are shown in Table 6. A handling method for MAGDM problems by some aggregation operators of linguistic intuitionistic fuzzy sets are shown in Table 8.

Step 6. In this step, we find the score values of the alternatives from Table 9.

By comparing Tablse 6 and 7, based on the methods used, we get the same kind of $A_{4} > A_{1} > A_{2} > A_{3}$. However, in practical applications, comparison, the ranking result of using the LCIFWA, LCIFOWA and LCIFOWG, LCIFWG, LIFOWA, LIFWA and LIFOWG, LIFWG operators, the ranking results have not changed. Therefore, the proposed new methods can overcome the drawbacks of the LIFWA, LIFOWA operators, and the LIFWG, LIFOWG operators. Then, new introduced operators are more suitable than the previous because the new operators have a vast range but the already prevailing operators have limited use.

In Figure 3, we show the ranking of Table 9.

6.   Conclusions

The Linguistic intuitionistic fuzzy set is proposed by combining the concepts of linguistic variables and intuitionistic fuzzy sets. Its prominent operators are LIFWG, LIFOWG, and LIFWA, with LIFOWA in the MAGDM method. The use of these concepts, operators, and applications in decision-making issues were limited just to linguistic terms and intuitionistic fuzzy sets and have limited scope. In this paper, we tried to extend the prevailing methods, strategies, operators, and applications for a vast range and up to complex variables. New introduced concepts is LCIFs, its operators, LCIFWG, LCIFOWG, and LCIFWA, with LCIFOWA in the MAGDM method, and the mentioned procedure, operators, applications, and numerical analysis are evidence that the new introduced operators and applications cover a vast range and provide novel ideas to give the proper solutions of the problems in decision-making where data is ambiguous and uncertain. These new introduced methods are very useful in MAGDM methods.

In the future, we will extend this concept to Dombi operation, Hamacher operation, and Frank operations.

Author contributions

Sumaira Yasmin: write the original manuscript; Muhammad Qiyas: supervised; Lazim Abdullah: formal analysis; Muhammad Naeem: review and funding. All authors have read and agreed to the published version of the manuscript.

Acknowledgments

The authors extend their appreciation to the Deanship for Research and Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number: IFP22UQU4310396DSR080.

Conflict of interest

The authors certify that with regard to this publication, there are no conflicts of interest.