1.
Basic concepts and introduction
For n,q∈R with q≠1, the quantum number (q-number) defined by Jackson is
We note a relation as limq→1[n]q=n. Also, we call [k]q the q-integer for k∈Z; see [1,2,3].
With the advent of quantum numbers, new research in many areas of mathematics such as series, differential equations, and calculus has exploded; see [4,5,6,7]. For example, different types of trigonometric functions and hyperbolic functions defined by Duran et al. [8] bring generalized properties of different types of trigonometric functions and hyperbolic functions. In [4], Bangerezako combined q-number in an optimal control problem, making the q-Euler Lagrange equation, q-optimal control, and the q-Hamilton system q-Hamilton Pontriaguine system. These studies have resulted in several researches combined with quantum numbers in the application field.
Let n,j be non-negative integers with j≤n. Then, the q-Gaussian binomial coefficients is
We note [0]q!=1, [n]q!=[n]q[n−1]q⋯[2]q[1]q. The q-Gaussian binomial coefficients that are appeared in the q-Taylor formula of xn with x=1 become the ordinary binomials coefficients when q→1. We can check some properties of these coefficients in Sections 5 and 6 of [3].
The following two quantum derivatives
are called the q-derivative Dq and h-derivative Dh of the function f(ϱ), respectively. We note limq→1Dqf(ϱ)=limh→0Dhf(ϱ)=df(ϱ)dϱ if f(ϱ) is differentiable, see [3].
Since 2010, mathematicians have tried to introduce a new concept involving the properties of two kinds of quantum numbers. Benaoum [9] found (q,h)-Newton's binomial formula and its properties. Also, Cermak and Nechvatal studied a (q,h)-version of the fractional calculus in [10]. In 2019, the generalization of the quantum Taylor formula and quantum binomial is made by Silindir and Yantir [11]. We are well aware that one of the ways available for solving linear differential equations with specific integral equations is Laplace transformation. In [12], we can find the (q,h)-Laplace transformation, which is made by Rahmat and is a generalized type for classical Laplace transformation.
A two-parameter time scale Tq,h was introduced as follows:
Definition 1.1. [10,11] Let f:Tq,h→R be any function. Thus, the delta (q,h)-derivative of f Dq,h(f) is defined by
From the above definition, we can see several properties as follows:
(i) For ϱ∈Tq,h, Dq,hf(ϱ)=0 if and only if f(ϱ) is a constant;
(ii) Dq,hf(ϱ)=Dq,hg(ϱ) for all ϱ∈Tq,h if and only if f(ϱ)=g(ϱ)+c with some constant c;
(iii) for ϱ∈Tq,h, Dq,hf(ϱ)=c1 if and only if f(ϱ)=c1ϱ+c2, where c1 and c2 are constant.
In Definition 1.1, we can see that Dq,h(f), the delta (q,h)-derivative of f, reduces to Dq(f), the q-derivative of f for h→0 and reduces to Dh(f), the h-derivative of f for q→1. In addition, we can find the product rule and quotient rule for the delta (q,h)-derivative.
Let f,g be arbitrary functions.
Definition 1.2. [9,11] The generalized quantum binomial (ϱ−x0)nq,h is defined by
where x0∈R.
Definition 1.3. [11] The generalized quantum exponential function expq,h(αϱ) is defined as
where α is an arbitrary non-zero constant.
We remark that expq,h(0)=1. The generalized quantum exponential function expq,h(αϱ) reduces to the quantum exponential function eq(ϱ) as α=1 with h→0, see [3]. Similarly, expq,h(αϱ) becomes the h-exponential function e1,h(ϱ)=(1+h)ϱh as α=1 with q→1, see [3].
From now on, we briefly check the Genocchi polynomials. Classic orthogonal polynomials such as Chebyshev's and Laguerre's polynomials give us many possibilities. The Genocchi polynomials are polynomials that are helpful because they have fewer terms and coefficients than other polynomials in the process of approximating function.
Definition 1.4. [13] The quantum Genocchi numbers Gω,q and polynomials Gω,q(ϱ) are defined as
From Definition 1.4, we can see that Gω,q and Gω,q(ϱ) go to Genocchi numbers Gω and polynomials Gω(ϱ) as q→1, respectively.
Definition 1.5. [14] The degenerate Genocchi numbers Gω(h) and polynomials Gω(ϱ:h) are defined as
If h→0 in Definition 1.5, then we find that Gω(h) and Gω(ϱ:h) become Genocchi numbers and polynomials, respectively.
Based on the classical Genocchi numbers and polynomials, Isah and Phang[15] studied the Genocchi wavelet-like operational matrix of fractional order derivative and observed some numerical examples. In [16], we can see that wavelets are mathematical tools that can be used to extract information from audio signals and images as well as other various types of data. Also, Genocchi wavelets (GWs) can be said to be very useful among these wavelets. The approximation of the solution by using polynomials is used to solve the fractional differential equations (FDEs) and variable-orders differential equations. This technique reduces the differential equations to a system of algebraic equations. The operational matrix of Caputo fractional derivative and integration have been developed for some types of polynomials, such as Chebyshev, Legendre, and Genocchi polynomials; see [17].
The application of Genocchi numbers and polynomials as above motivated us to do new research; see [18]. When the degenerate polynomials defined by L. Calitz are combined with quantum numbers, many mathematicians wondered how Genocchi polynomials are defined and what properties are associated with them.
An important objective of this paper is to construct a new type of Genocchi polynomials containing the properties of quantum Genocchi and degenerate Genocchi polynomials and to find the difference equations related to them. This paper is structured as follows: In Section 2, we construct a new degenerate quantum Genocchi (DQG) polynomials and obtain several types of difference equations for these polynomials by using (q,h)-derivative. Section 3 shows expanded difference equations using classical Genocchi, quantum Genocchi, and degenerate Genocchi polynomials. Section 4 presents the structures of the approximate roots of DQG polynomials that are solutions of the difference equations obtained in the previous section. Also, through numerical experiments, we can guess the characteristics of DQG polynomials.
2.
Difference equations for DQG polynomials
We construct a new type of the DQG polynomials using the degenerate quantum exponential function in this section. We find several relations, a basic q-difference equation, and a basic symmetric property of the q-difference equation for DQG polynomials.
The degenerate quantum exponential function eq,h(ϱ:ϑ) is defined by
where (ϱ)ωq,h=ϱ(ϱ−h)(ϱ−[2]qh)⋯(ϱ−[ω−1]qh).
From the degenerate quantum exponential function eq,h(ϱ:ϑ), we note
where eh(ϱ:ϑ) is the h-exponential function (or degenerate exponential function) and eq(ϑϱ) is the quantum exponential function (or q-exponential function).
From Eq (2.1), we define a new type of Genocchi polynomials.
Definition 2.1. The DQG polynomials Gω,q(ϱ:h) are defined by
Replacing ϱ=0 for Definition 2.1, we note
where Gω,q(h) is the DQG numbers. Given the appropriate conditions for Definition 2.1, we can find several relations of various Genocchi polynomials as follows.
Case 1. We find the quantum Genocchi numbers Gω,q and polynomials Gω,q(ϱ) when h→0 in Gω,q(h) and Gω,q(ϱ:h) as follows:
Case 2. We can see the degenerate Genocchi numbers Gω(h) and polynomials Gω(ϱ:h) when q→1 in Gω,q(h) and Gω,q(ϱ:h) as follows:
where Gω(h)=Gω(0:h).
Case 3. We have the Genocchi numbers Gω and polynomials Gω(ϱ) as q→1 with h→0 in Gω,q(h) and Gω,q(ϱ:h) as follows:
Based on the various cases above, we can represent the diagram for the polynomial as follows:
Theorem 2.2. Let h∈N with |q|<1. Then, we obtain
Proof. To find a relation of DQG numbers Gω,q(h) and polynomials Gω,q(ϱ:h), we use the generating function of DQG polynomials as
We derive the required result applying the coefficient comparison method in the above equation. □
Corollary 2.3. We have the following relations from Theorem 2.2:
(i) Setting q→1, we have
(ii) Putting h→0, we have
Theorem 2.4. Let h be a non-negative integer with h≠0 and |q|<1. Then, we obtain
Proof. Applying (q,h)-derivative in Eq (2.1) eq,h(ϱ:t), we find
By using mathematical induction, we investigate
Using Eq (2.3) in the generating function of the DQG polynomials Gω,q(ϱ:h), we find
From Eq (2.4), we obtain a relation of D(k)q,hGω,q(ϱ:h) and Gω,q(ϱ:h) as
Hence, we find the desired result at once. □
Corollary 2.5. We have the following relations given the appropriate conditions for Theorem 2.4.
(i) For q→1, we obtain
(ii) For h→0, we obtain
Theorem 2.6. A solution of the following difference equation
is the DQG polynomials.
Proof. Here, we find the basic type of difference equation, which is related to DQG polynomials. Suppose eq,h(1:ϑ)≠−1 in the generating function of the DQG polynomials. Then, we find
The right-hand side of Eq (2.5) changes to
while the left-hand side becomes
Hence, we derive the following equation.
Using Theorem 2.4 in Eq (2.6), we have
The above equation allows us to complete the proof. □
For example, we can consider the first-order Bernoulli equation as Dq,hy+p(x)y−g(x)ym=0. When m=0 in the Bernoulli equation above and considering Theorem 2.6, the following first-order (q,h)-difference equation can be expressed in Bernoulli equation form, and its solution is a DQG polynomials,
Corollary 2.7. From Theorem 2.6, we have:
(i) As q→1, one holds
(ii) As h→0, one holds
Theorem 2.8. For |q|<1 with a,b≠0, we derive a basic symmetry relation for difference equation as
Proof. From Eq (2.1), we find a relation
Considering eq,h(abϱ:ϑ)=eq,a−1h(bϱ:aϑ), we suppose form A as follows:
From form A, we can derive
and
Comparing the coefficients of both sides in Eqs (2.7) and (2.8), we obtain
Using Theorem 2.4 in Gω−k,q(bϱ:a−1h) and Gω−k,q(aϱ:b−1h), we can note
Replacing Eq (2.9) with Eq (2.10), we have
From Eq (2.11), we complete the proof of Theorem 2.8. □
Corollary 2.9. From Theorem 2.8, we hold that:
(i) For q→1, it satisfies the following
(ii) For h→0, it satisfies the following
3.
Several relations of DQG polynomials and other polynomials
In Section 3, we investigate several difference equations combining Genocchi polynomials and quantum Genocchi polynomials using Theorem 2.4. Using Gω(h), we obtain another symmetric property for the difference equation, which is related to the degenerate quantum Genocchi polynomials Gω(ϱ:h).
Theorem 3.1. DQG polynomials are a solution for the following difference equation:
where Gω is the Genocchi numbers and Gω(ϱ) is the Genocchi polynomials.
Proof. Using Gω,q(ϱ:h) from Definition 2.1, Genocchi numbers Gω and polynomials Gω(ϱ), we have
From Eq (3.1), we find
If we compare the coefficients of both sides in Eq (3.2), then we find
Replacing D(k)q,hGω,q(ϱ:h) instead of Gω−k,q(ϱ:h) in Eq (3.3), we obtain
Through Eq (3.4), we find the desired result. □
Corollary 3.2. From Theorem 3.1, we have the following relations:
(i) For q→1, it satisfies the following
(ii) For h→0, it satisfies the following
Theorem 3.3. For |q|<1 and ω∈N, a solution of the following difference equation
is represented by the DQG polynomials.
Proof. The generating function of the DQG polynomials Gω,q(ϱ:h) can be expressed as:
Following a procedure similar to the process used for the proof of Theorem 3.1 in Eq (3.5), we finish the proof of Theorem 3.3. □
Corollary 3.4. As h→0 in Theorem 3.3, one holds
Theorem 3.5. For |q|<1 with α,β≠0, we derive
Proof. To obtain another symmetric difference equation that is related to DQG polynomials, we suppose form B as follows:
From form B, we have
and
From the same way as proving Theorem 2.8, we find as follows:
Using Theorem 2.4 in Eq (3.6), we obtain
From Eq (3.7), we complete the proof of Theorem 3.5. □
Corollary 3.6. Considering α=1 in Theorem 3.5, we have
4.
Structures and movement of approximate roots of DQG polynomials
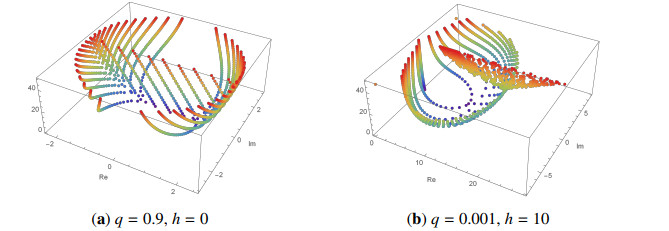
In this section, we look for approximate roots of DQG polynomials. Using Mathematica, the range of approximate roots was calculated to 16 decimal places. Based on the approximate roots of these polynomials, we can estimate several properties of DQG polynomials.
We recall that the DQG polynomials become quantum Genocchi polynomials as h→0 and become degenerate Genocchi polynomials for q→1. Let 0≤n≤50.
Then, Figure 1 shows approximate roots of DQG polynomials under conditions (a) q=0.9 and h=0, (b) q=0.001 and h=10. In Figure 1, as the value of n is smaller, approximate roots are expressed as blue dots, and approximate roots appear as red dots when n=50. Figure 1(a) is similar to quantum Genocchi polynomials because of the condition of h, and Figure 2(b) shows positions of approximate roots of DQG polynomials.
Several DQG polynomials Gω,q(ϱ:h) are provided below:
Figure 2 shows an interesting phenomenon related to Figure 1(b). Figure 2(a) shows the distribution of approximate roots when h=0, Figure 2(b) shows the distribution of approximate roots when h=5, and Figure 2(c) shows the distribution of approximate roots when h=10 under 0≤n≤50 and q=0.9. The x-axis represents the imaginary axis, and the y-axis represents the value of n. In Figure 2, we realize that as the value of h increases, the number of approximate roots decreases. In other words, comparing Figures 2(a–c), we can see that the number of approximate roots in Figure 2(c) is reduced.
Based on Figure 2, we can find the values of approximate roots as shown in Table 1 by dividing the real and imaginary roots. Table 1 shows the number of real roots among approximate roots of DQG polynomials.
Table 1 shows the number of real roots among approximate roots that change according to the value of h. At this time, the value of q is fixed at 0.9. In Table 1, we can see that the number of real roots increases as the values of h and n increase. From Figures 1 and 2, and Table 1, the following guesses can be obtained.
Conjecture 4.1. In the DQG polynomials Gω,0.9(ϱ:h), the number of real approximation roots increases as ω increases for h=10 and q=0.9.
5.
Conclusions
We defined DQG polynomials and found various forms of related differential equations. Based on these differential equations, we were able to verify the differential equations of various polynomials and also confirmed their symmetric properties. Furthermore, we showed the structure of approximate roots of DQS polynomials that have differential equations as solutions, and also estimated about the approximate roots. The results presented in this paper will be helpful in understanding quantum numbers and degenerate polynomials, and will serve as a foundation for constructing new polynomials.
Author contributions
Jung Yoog Kang: Software, writing-original draft, writing-review & editing, conceptualization, methodology; Cheon Seoung Ryoo: Supervision, validation, data curation, software, writing-review & editing. All authors equally contributed to this manuscript. All authors have read and approved the final version of the manuscript for publication.
Conflict of interest
The authors declare that there is no conflict of interest. Cheon Seoung Ryoo is the Guest Editor of special issue "Advances in Polynomials and Special Functions" for AIMS Mathematics. Cheon Seoung Ryoo was not involved in the editorial review and the decision to publish this article.









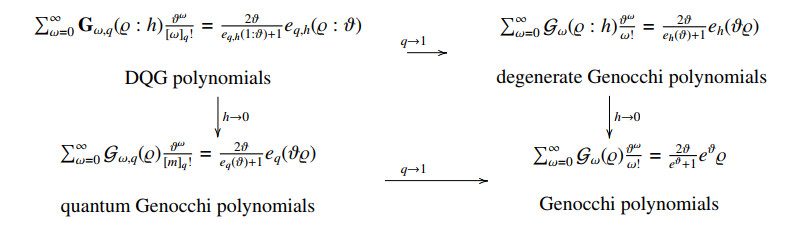
 DownLoad:
DownLoad:





