Discrete Hepatitis C virus model with local dynamics, chaos and bifurcations

1.   Introduction

In numerous broad fields of study, optimization is a useful strategy when choosing the most beneficial choice from a range of options is essential. These broad fields include computer science, applied mathematics, engineering, and management science, as discussed by Deb ^[1], Goldberg ^[2], Michalewicz, and Arabas ^[3]. Effective crossover operators are essential for solving complicated problems with genetic algorithms (GA), especially for addressing information technology (IT) outsourcing schedule concerns. Traditional crossover approaches frequently struggle to balance exploration and exploitation F Lu ^[4]. Complex systems, such as IT outsourcing timetables, have become increasingly difficult to manage in an era of globalization due to inherent risks and uncertainties. Just as supply chain optimization entails resolving multi-echelon difficulties and decreasing costs using advanced heuristics, improving IT outsourcing schedules necessitates sophisticated methodologies to efficiently manage numerous risks Nahangi and Awwad ^[5]. In computing and engineering, the aim is to maximize system or application performance while minimizing runtime and resource consumption as much as possible Chu and Beasley ^[6]. Decisions are made by creating optimization models containing the problem's core and then applying mathematical approaches to address these models Wasserkrug et al ^[7]. Optimization algorithms for unconstrained issues typically employ gradient information to locate the optimal solution. As such, the gradient-based optimization method can solve objective functions with non-differentiable components Ahmadianfar et al. ^[8]. Deterministic approaches are a type of local optimization where the search process and its outcome primarily depend on an initial guess. Several population-based stochastic techniques, including particle swarm optimization (PSO), simulated annealing (SA), GAs, and others, have been created and are employed to address optimization issues with constraints, as discussed in Eberhart et al. ^[9], Kirkpatrick et al. ^[10] and Deb ^[3].

The guided random search approaches comprise all of these optimization techniques Goldberg and Deb ^[11]. GAs are based on Charles Darwin's principle that only the offspring of the fittest parents can survive Holland ^[12]. GA is a reliable and effective evolutionary search technique for locating the best potential solutions to complicated multi-modal situations De-Jong ^[13]. Natural phenomena suggest that genetic inheritance is stored in chromosomes composed of genes Haq et al. ^[14]. As the mutation operator aids in preserving population diversity and preventing premature convergence, the crossover operator uses genetic information from different chromosomes to explore new search spaces Haq et al. ^[15]. The continuous search space is changed into a discrete one using a binary-coded scheme, where the string length is determined by the separation between two adjacent grids. Under a small number of decision variables, binary encoding performs well and requires less precision for the solutions Katoch et al. ^[16]. However, when high precision is needed to solve multi-dimensional optimization problems, binary encoding schemes perform unsatisfactorily Haq et al. ^[15]. The concept of real encoding first surfaced in the early 1990s, when a vector of real-coded GA was used to represent a chromosome Wright ^[17].

The crossover and mutation operators both have a big effect on how well GAs perform. As a result, a lot of research is focused on improving these operators' performance. Laplace crossover (LX) is used to locate the offspring and is linked with a Laplace probability distribution Deep et al. ^[18]. Therefore, the two offspring generated by the LX operator are symmetrical in terms of their parental position and did not automatically locate close to the better of the two parents. To create a simulated binary crossover (SBX), Deb et al. ^[19] modified a single-point binary crossover. When two parents are chosen, SBX produces two offspring. These offspring are positioned in a straight line that is connected to their parents. The main drawback of SBX is that it is unable to control the size of the parameter value adaptively. Essentially, the crossover operator uses the current population information to guide the search in the other search space. In this context, the crossover operator is essential to exploring the unique aspect of GA Naqvi et al. ^[20].

2.   Crossover operators used in the previous studies

2.1.   LX

At first, Deep and Thakur ^[18] proposed a self-parent-centric crossover operator based on the Laplace distribution. This is the Laplace distribution's distribution function:

where, respectively, a and b represent the location and shape parameters for Laplace distribution. Utilizing LX, from two parents ${y}^{\left(1\right)} = \left({y}_{1}^{\left(1\right)}, {y}_{2}^{\left(1\right)}, {y}_{3}^{\left(1\right)}, \dots, {y}_{n}^{\left(1\right)}\right)$ and ${y}^{\left(2\right)} = \left({y}_{1}^{\left(2\right)}, {y}_{2}^{\left(2\right)}, {y}_{3}^{\left(2\right)}, \dots, {y}_{n}^{\left(2\right)}\right)$, two offspring, ϑ = (ϑ1, ϑ2, ϑ3, …, ϑn) and τ = (τ1, τ2, τ3, ..., τn.

2.2.   Double Pareto crossover (DPX)

Based on the double Pareto probability distribution; the double Pareto crossover (DPX) is a parent-centric operator Thakur ^[21]. The distribution function of the double Pareto distribution, which this crossover operator uses, is given as

The Double Pareto probability distribution has two parameters, i.e., $\mathrm{a}$ & $\mathrm{b}$, where $\mathrm{a}$ belongs to a real number and b is greater than zero. Here $\mathrm{a}$ = location parameter and $\mathrm{b}$ = scale parameter of the double Pareto probability distribution.

2.3.   Fisk crossover (FX)

The Fisk crossover (FX) is a parent-centric crossover operator using a log-logistic distribution ul Haq et al. ^[22]. The FX operator uses the cumulative distribution function of the log-logistics distribution, as shown below:

where β > 0 and α > 0 are scale and shape parameters respectively.

2.4.   Logistic crossover (LogX)

This specific operator is proposed by Naqvi et al. ^[20], which is based on logistic distribution. The cumulative distribution function (CDF) of the logistic distribution is given as

where α > 0 and s > 0 are location and scale parameters respectively.

2.5.   SBX

The SBX is a real-coded crossover operator, which was first proposed by Deb and Agarwal ^[19]. The binary transformation to continuous search space is one of its special features. Following are the steps for generating offspring, ϑ = (ϑ1, ϑ2, ϑ3, …, ϑn) by two parents ${y}^{\left(1\right)} = \left({y}_{1}^{\left(1\right)}, {y}_{2}^{\left(1\right)}, {y}_{3}^{\left(1\right)}, \dots, {y}_{n}^{\left(1\right)}\right)$ and ${y}^{\left(2\right)} = \left({y}_{1}^{\left(2\right)}, {y}_{2}^{\left(2\right)}, {y}_{3}^{\left(2\right)}, \dots, {y}_{n}^{\left(2\right)}\right)$ are as follows:

1^st step: Generate a random number ɛi between zero and one.

2^nd step: Then, obtain a parameter β_i as:

where the distribution index is denoted by ${n}_{c}$ and ${n}_{c}$ ∈ [0, ∞].

Thus, both parents ${y}^{\left(1\right)} = \left({y}_{1}^{\left(1\right)}, {y}_{2}^{\left(1\right)}, {y}_{3}^{\left(1\right)}, \dots, {y}_{n}^{\left(1\right)}\right)$ and ${y}^{\left(2\right)} = \left({y}_{1}^{\left(2\right)}, {y}_{2}^{\left(2\right)}, {y}_{3}^{\left(2\right)}, \dots, {y}_{n}^{\left(2\right)}\right),$ and an offspring $\mathrm{\vartheta } = \mathrm{ }(\mathrm{\vartheta }1, \mathrm{\vartheta }2, \mathrm{\vartheta }3, \dots, \mathrm{\vartheta }\mathrm{n})$ is produced in the following Eq (6):

3.   Proposed real-coded crossover operators

By taking a balanced approach to exploration and exploitation, the GX (Gumbel-based) and RX (Rayleigh-based) crossover operators will improve the performance of GAs. The Gumbel distribution, which is well-known for modeling extreme values, is utilized by the GX operator to enhance the algorithm's exploratory power. The GX operator lets the algorithm escape local optima and fully search the solution space by producing offspring with features that can differ greatly from the parent population. This makes the method especially useful in complicated or misleading landscapes. Conversely, the RX operator, derived from the Rayleigh distribution, highlights moderate deviations and helps refine the search in areas of potential interest, hence improving exploitation.

3.1.   First proposed real-coded crossover operator based on Gumbel distribution

Extreme value distributions are frequently modeled by using the Gumbel distribution, especially when a set of random variables has maximum or minimum values Gumbel ^[23]. The Gumbel distribution is appropriate for modeling extreme events because it exhibits heavy tails, and a bell-shaped, double-exponential probability function describes it. The maximum or minimum of an objective function is a common problem in optimization. Modeling the distribution of extreme values with the Gumbel distribution gives statistical insight into and ability to predict rare but important events. So in optimization theory, Gumbel distribution plays an important role. It is favored for capturing extreme values in extremely complex and multimodal scenarios where extreme events are extremely important Kamel et al. ^[24]. The decision is based on the optimization problem and the particular features of the data. The GX operator has been proposed here. The density function of the Gumbel distribution is as follows:

where the location parameter is $\mu$ and the scale parameter is $\beta$.

The cumulative distribution function of Gumbel distribution is as follows:

Main steps for generating two offspring, ϑ = (ϑ1, ϑ2, ϑ3, …, ϑn) and τ = (τ1, τ2, τ3, ..., τn) by two parents ${y}^{\left(1\right)} = \left({y}_{1}^{\left(1\right)}, {y}_{2}^{\left(1\right)}, {y}_{3}^{\left(1\right)}, \dots, {y}_{n}^{\left(1\right)}\right)$ and ${y}^{\left(2\right)} = \left({y}_{1}^{\left(2\right)}, {y}_{2}^{\left(2\right)}, {y}_{3}^{\left(2\right)}, \dots, {y}_{n}^{\left(2\right)}\right),$ are as follows:

1^st step: Random number ɛ_i is generated in between zero and one.

2^nd step: The Gumbel distribution function is inverted to obtain the parameter βi, which is obtained by equating the randomly generated number ɛ to the area under the curve from −∞ to βi.

3^rd step: The generation of offspring is based on the following Eqs (14) and (15):

and

3.2.   Second proposed real-coded crossover operator based on Rayleigh distribution

A continuous probability distribution for random variables with nonnegative values is called the Rayleigh distribution. The distribution of a two-dimensional vector's magnitude is modeled using the Rayleigh distribution Grimmett & Stirzaker ^[25]. Rayleigh distribution describes the distribution of vector magnitudes rather than being specifically made for modeling extremes. In optimization theory, the Rayleigh distribution is important, especially in cases where squared magnitudes or the magnitudes of two-dimensional vector components are essential. Depending on the unique characteristics of the optimization problem and the type of data being modeled, the Rayleigh or Gumbel distributions can be very important in optimization theory. Each of the distributions is useful in various situations and has advantages of its own. The crossover operator RX, which is based on Rayleigh distribution, has also been proposed in this study. The density function of the Rayleigh distribution is as follows:

where the distribution's scale parameter is 𝝈.

The cumulative distribution function of Rayleigh distribution is as follows:

Prerequisite steps for generating two offspring, ϑ = (ϑ1, ϑ2, ϑ3, …, ϑn) and τ = (τ1, τ2, τ3, ..., τn) by two parents ${y}^{\left(1\right)} = \left({y}_{1}^{\left(1\right)}, {y}_{2}^{\left(1\right)}, {y}_{3}^{\left(1\right)}, \dots, {y}_{n}^{\left(1\right)}\right)$ and ${y}^{\left(2\right)} = \left({y}_{1}^{\left(2\right)}, {y}_{2}^{\left(2\right)}, {y}_{3}^{\left(2\right)}, \dots, {y}_{n}^{\left(2\right)}\right),$ are as follows:

1^st step: Begin with generating random number ɛ_i in between zero and one.

2^nd step: Calculating a parameter β_i, which follows Rayleigh distribution, by inverting the distribution function of Rayleigh distribution as follows:

3^rd step: Offspring are generated by using the following Eqs (22) and (23):

and

4.   Experimental setup

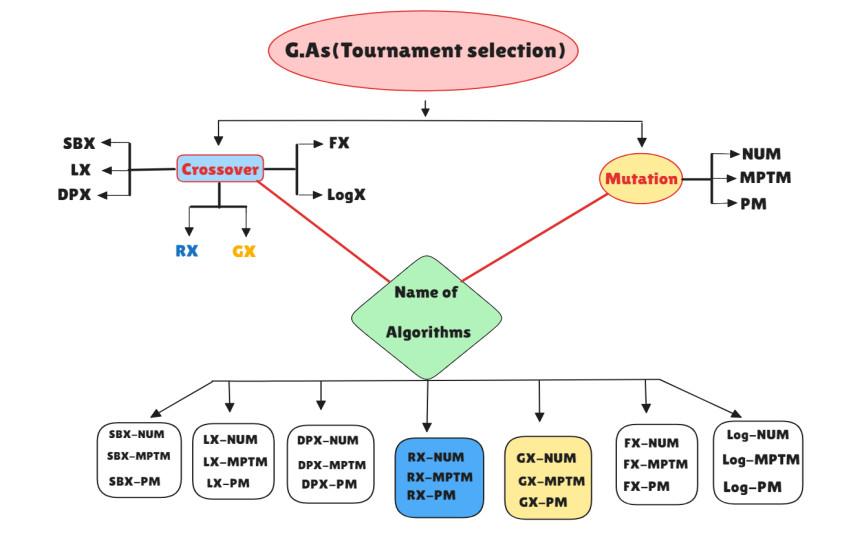
A set of benchmark test problems has been used to assess the performance of novel crossover operators. The two novel parent-centric crossovers GX and RX improve genetic process performance that is closely compared to considered real-coded operators, such as LX, DPX, and SBX. Along with nonuniform mutation (NUM), Makinen, Periaux, and Toivanen mutation (MPTM), and power mutation (PM), these seven crossover operators (LX, DPX, SBX, FX, LogX, RX, and GX) have been utilized for evaluating the global optimal performance. The population size has been set to be three hundred and thirty independent runs performed to obtain the simulated results. The selection criteria used by all GAs is tournament selection. Size-one elitism refers to the idea that the most esteemed individuals are retained in the present generation. Final results are considered in terms of mean values, standard deviation, and average execution time. The algorithm stops after five hundred generations. Trial runs and screening experimentation have produced the most optimal outcome for the GA process. Final parametric values are displayed in Figure 1, which summarizes a simulated analysis of fifteen algorithmic combinations and their corresponding crossover and mutation probabilities.

4.1.   Test problems

Benchmark functions are authentic tools used to assess the effectiveness of real-coded algorithms in optimization problems. In this study, we take a set of fifteen well-known benchmark functions with different complexity levels. This set of benchmark functions also has different levels of multimodality. The search technique that efficiently eliminates local optima and continues its journey to find global optima is considered an efficient search technique for optimization problems because it does not stick at local optima Mahajan et al. ^[26]. Table 1 details fifteen benchmark functions used in this study to judge the efficiency of proposed evolutionary methods.

5.   Results and discussion

Our primary contribution to this research effort is the introduction of two novel real-coded crossover operators such as GX and RX. The main objective is to assess the proposed crossover operators' performance in light of the simulation results. As GX-NUM, RX-NUM, GX-MPTM, RX-MPTM, GX-PM, and RX-PM are the proposed operators that are compared to other crossover operators, such as LX-NUM, DPX-NUM, SBX-NUM, FX-NUM, LogX-NUM LX-MPTM, DPX-MPTM, SBX-MPTM, FX-MPTM, LogX-MPTM, LX-PM, DPX-PM, SBX-PM, FX-PM, and LogX-PM.

Based on the results presented in Table 2, GX-NUM performs extremely efficiently against almost all other real-coded operators having the least mean value in all benchmark functions except 'Neumair'. The empirical results also indicate that other novel operators i.e. RX-NUM did not perform well. This suggests that GX-NUM has a clear-cut dominant capacity for handling selection pressure and population diversity as compared to RX-NUM and other considered operators. According to Table 3, the results show that GX-MPTM performs distinctly as compared to RX-MPTM and other considered operators under many benchmark functions. Similarly from Table 4, GX-PM can also efficiently handle the selection pressure and population diversity. This all suggests that the Gumbel distribution outperformed in terms of efficiently handling selection pressure, and preservation of population diversity than the Rayleigh distribution in the search for global maxima.

6.   Performance index

The behavior of several controlled stochastic search techniques was carefully examined by using the performance index (PI) in Figures 2–4. It is an approach that is frequently used to compare various heuristic algorithms Ul Haq et al. ^[22]. The equation that follows provides the mathematical derivation of PI:

where

${\vartheta }_{1}{\eta }_{1}^{i}$ = $\frac{{M}^{i}}{{m}^{i}}$, ${\vartheta }_{2}{\eta }_{2}^{i}$ = $\frac{{S}^{i}}{{s}^{i}}$ and ${\vartheta }_{3}{\eta }_{3}^{i}$ = $\frac{{C}^{i}}{{c}^{i}}$ for $i = \mathrm{1, 2}, 3, \dots, {N}_{q}$.

Three statistics were taken into consideration, with weights as ${\vartheta }_{1}$, ${\vartheta }_{2}$, and ${\vartheta }_{3}$ respectively (${\sum }_{i = 1}^{3}{\vartheta }_{i} = 1$ and 0 ≤ ${\vartheta }_{i}$ ≥1). Hence PI is the function of ${\vartheta }_{i}$, for making a clear visualization of all seven algorithms and avoiding overlapping. Two terms in PI expression are given equal weights at a time, thus PI becomes a function of a single variable. Following are the three resulting cases:

1) ${\vartheta }_{1} = weight\left(w\right)$, ${\vartheta }_{2} = {\vartheta }_{3} = 0.5(1-weight\left(w\right))$,

2) ${\vartheta }_{2} = weight\left(w\right)$, ${\vartheta }_{1} = {\vartheta }_{3} = 0.5(1-weight\left(w\right))$,

3) ${\vartheta }_{3} = weight\left(w\right)$, ${\vartheta }_{1} = {\vartheta }_{2} = 0.5(1-weight\left(w\right))$,

where for all cases $0\le weight\left(w\right)\le 1$.

When a line chart exhibits a consistent upward trending line above all other real-coded operators, it indicates in the form of a plotted metric line, and the corresponding crossover operator is outperforming the others. Here in Figures 2–4, we can observe that the line of novel crossover operator GX is initially below the line of considered crossover operator DPX, but it continuously rises and outperforms all. This increasing trend indicates a convergence toward the global solution for the proposed crossover operator (GX). The novel crossover operator (GX) allows for finding global solutions more successfully as the algorithm develops its search. Examine the rate at which each operator converges. It is possible to argue that the novel crossover (GX) is more efficient because it produces better results more quickly. Thus, in the context of the obtained optimum mean values in fifteen benchmark functions, seven real-coded crossover operators and three mutation operators are visually compared in Figure 5.

The first proposed crossover operator (GX) shows considerable dominance with 87% in NUM, 60% in MPTM, and 80% in PM mutation. But in the same visual representation, the second novel crossover operator (RX) shows limited performance.

7.   Multi-criteria decision-making technique

The process of finding and selecting the best option from multiple options by considering the decision maker's expectations is known as decision-making. The diversity of benchmarks used to evaluate the solutions makes the decision-making process the most challenging. Therefore, the term multi-criteria decision-making (MCDM) describes decision-making when faced with several, frequently opposing criteria.

7.1.   VIKOR method

Several strategies for MCDM, including VlseKriterijuska Optimizacija I Komoromisno Resenje (VIKOR) mean "multi-criteria optimization and compromise solution". Opricovic developed the main VIKOR research in a 1979 PhD dissertation and subsequently in an application in 1980 Mardani et al. ^[27], Zheng and Wang ^[28]. The VIKOR approach is necessary to create the appropriate evaluation or decision matrix, which displays how well the crossover operators perform on several test problems. Let, X_ij represent the performance measure of the i^th alternative (crossover operators) for the j^th criterion (test problems). The Lp-metric used as an aggregating function in a compromise programming technique, is then utilized to build the multi-criteria measure for compromise ranking Zeleny ^[29].

where ${w}_{j}$ denotes weights for j^th criteria, M is the number of criteria (test problems), and N is the number of alternatives (crossover operators). Applying the VIKOR approach, values of sum (Si) and maximum row (Ri) are first calculated for each crossover operator that is considered for a v = 0.5. The appropriate values of least quantity (Qi)are subsequently determined in Tables 5, 7, and 9 for each case of mutations (NUM, MPTM, and PM), respectively. Furthermore, Tables 6 and 8 demonstrate that as the v values change, the rankings of the crossover operators (alternatives) with the highest and lowest rankings remain unchanged, and moderate changes in the intermediate ranking order in Table 6 are observed. In Table 10, variation is observed in the best-ranked positions, but GX crossover operators hold the best ranking position.

8.   Conclusions

This study introduces two novel crossover operators, the GX operator and the RX operator. In comparison with three existing real-coded algorithms (LX, DPX, and SBX), the performance of GX and RX are evaluated to assess their effectiveness. Furthermore, six new algorithmic combinations, GX-NUM, GX-MPTM, GX-PM, RX-NUM, RX-MPTM, and RX-PM, are proposed by integrating GX and RX with three mutation operators (NUM, MPTM, and PM).

In terms of algorithmic procedures, tournament selection is employed during the reproduction phase, while a simulation-based approach is utilized to analyze the efficacy of the algorithms. A comprehensive evaluation uses fifteen benchmark functions sourced from existing literature to authenticate the performance of the novel algorithms introduced in this study. The comparison metrics encompass mean value, standard deviation, and execution time (measured in seconds) to gauge the efficiency of each algorithm.

Empirical findings, graphical representations of performance indices, and the MCDC VIKOR method indicate that GX outperforms RX and other operators. Notably, the real-coded crossover operator GX enhances the performance of the GA by fine-balancing population diversity and selection pressure. Consequently, GX exhibits significant potential in tackling increasingly complex optimization challenges compared to the existing real-coded operators. Moreover, future work should concentrate on several important areas, including evaluating these operators in practical settings, investigating their efficacy in dynamic and multi-objective scenarios, and extending their applicability to other optimization procedures. Furthermore, it's critical to improve the operators' effectiveness and adaptability across a range of problem kinds. However, this study has certain limitations, such as the scope of the benchmark functions utilized and the need for a broader variety of performance indicators. Addressing these constraints and introducing more evaluation criteria will result in a more comprehensive understanding of the operators' capabilities, paving the way for future breakthroughs in optimization techniques.

Author contributions

Jalal-ud-Din: Conceptualization, writing original draft, writing and editing, formal analysis, software; Ehtasham-ul-Haq: Conceptualization, investigation, methodology, supervision; Ibrahim M. Almanjahie: Investigation, resources; Ishfaq Ahmad: Data curation, formal analysis, validation. All authors have read and approved the final version of the manuscript for publication.

Data availability

The data used to support the findings of this study are available from the corresponding author upon request.

Acknowledgments

The authors thank and extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through a Large Research Project under grant number RGP2/338/45.

Conflict of interest

The authors declare that they have no conflicts of interest.