Recognition of the symplectic simple group $PSp_4(p)$ by the order and degree prime-power graph

1.   Introduction

Throughout the following, all groups are assumed to be finite, and all characters are complex characters. Let $G$ be a group, then $\operatorname{Irr}(G)$ denotes the set of all irreducible characters of $G$, and $\operatorname{cd}(G)$ denotes the set of all irreducible character degrees of $G$. For a positive integer $n$, we use $\pi(n)$ to denote the set of all prime divisors of $n$. For convenience, we write $\pi(G) = \pi(|G|)$, and $\rho(G) = \bigcup_{\chi\in \mathrm{Irr}(G)} \pi(\chi(1))$. For a prime $p$, the $p$-part of $n$, denoted by $n_p$, is the maximum power of $p$ such that $n_p \mid n$. CFSG is the abbreviation for the Classification Theorem of Finite Simple Groups.

The set $\operatorname{cd}(G)$ is very important for studying $G$. Many results have been obtained about the relationship between the set $\operatorname{cd}(G)$ and the structure of $G$. This paper's primary focus centers on finite non-abelian simple groups. In 2000, Huppert proposed a conjecture: "If $S$ is a non-abelian simple group such that $\operatorname{cd}(G) = \operatorname{cd}(M)$, then $G \cong$ $M \times A$, where $A$ is an abelian group" (see ^[1]). Currently, this conjecture has not been fully proven. If Huppert's conjecture proves valid, it would follow naturally that all finite non-abelian simple groups could be uniquely determined by their orders and sets of irreducible character degrees. Interestingly, provided $|G| = |M|$ and fewer numbers in $\operatorname{cd}(G)$ require consideration, one can still deduce the same conclusion more efficiently. Researchers have shown that certain simple groups can be uniquely determined by their orders and at most three distinct irreducible character degrees (see ^[2,3,4,5,6] etc.).

Other researchers have studied the structure of a finite group with the character degree graph $\Delta(G)$. The vertex set of $\Delta(G)$ is $\rho(G)$. In $\Delta(G)$, two vertices are joined by an edge if the product of them divides some number in $\operatorname{cd}(G)$. The character degree graph has been widely studied, for example, in ^[7]. Clearly, $\Delta(G)$ contains much less information of $\operatorname{cd}(G)$. An interesting fact is that some simple groups (not all) can be uniquely determined by their orders and degree graphs.

In ^[8], Khosravi et al. proved that $A_5$, $A_6$, $A_7$, $A_8$, $L_3(3)$, $L_3(4)$, $L_2(64)$, $L_2(q)$ (where $q$ is an odd prime or a square of an odd prime, and $q \geqslant 5$), and $L_2\left(2^\alpha\right)$ (where $\alpha$ is a positive integer such that $2^\alpha-1$ or $2^\alpha+1$ is a prime) can be uniquely determined by their orders and character degree graphs. However, in ^[9] Heydari and Ahanjideh gave a counter example of this characterization, that is, $M_{12}$ and $A_4 \times M_{11}$ have the same order and character degree graph. To overcome this shortcoming, Chao Qin and Guiyun Chen defined a new graph by using the information of $\mathrm{cd}(\mathrm{G})$ in ^[10], which is called the degree prime-power graph $\Gamma(G)$.

Definition. For every $p \in \rho(G)$, let $p^{e_p(G)} = \max \left\{\chi(1)_p \mid \chi \in \operatorname{Irr}(G)\right\}$ and $V(G) = \left\{p^{e_p(G)} \mid p \in \rho(G)\right\}$. Define the degree prime-power graph $\Gamma(G)$ of $G$ as follows: $V(G)$ is the vertex set, and there is an edge between distinct numbers $x, y \in V(G)$ if $x y$ divides some integer in $\operatorname{cd}(G)$. Denote the edge between distinct numbers $x, y \in V(G)$ by $x \sim y$, and the set of all edges of $\Gamma(G)$ by $E(G)$.

Chen, Qin, Wang and et al. have proven that the group $M_{12}$ can be uniquely determined by its order and degree prime-power graph. They have also shown that all sporadic simple groups, $PSL_2(p)$, $PSL_2(p-1)$ (where $p$ is a Fermat prime), $PSL_2(p^2)$, and $PSL_2(p^3)$ can be uniquely determined by their orders and degree prime-power graphs (see ^{[10,11,12,13]}). In this paper, we continue this investigation for the symplectic simple group $PSp_4(p)$. The following theorem is our main result.

Main Theorem. Let $p$ be an odd prime, then $G \cong PSp_4(p)$ if and only if $|G| = \left|PSp_4(p)\right|$ and $\Gamma(G) =$ $\Gamma\big(PSp_4(p)\big)$.

2.   The degree prime-power graph of $PSp_{4}(p)$ when $p$ is an odd prime

In this section, we present the degree prime-power graph of $PSp_{4}(p)$ when $p$ is an odd prime, along with an important proposition.

By Atlas ^[14] and Magma, we obtain the order and the degree prime-power graph of $PSp_{4}(p)$ when $p = 3, 5, 7$ (see Table 1).

If $p > 7$, then the order of $PSp_4(p)$ is

The character degrees of $PSp_4(p)$ were determined by Shahabi and Mohtadifar in ^[15], that is

where $\epsilon = (-1)^{(p-1) / 2}$. We see that $PSp_4(p)$ has irreducible characters of the following degrees:

Note that

and we have $|PSp_4(p)|_2 = \left(\left(p-1\right)^2\left(p+1\right)^2\right)_2$, moreover, $2^{e_2(PSp_4(p))} = |PSp_4(p)|_2$ by (2.1). Similarly, for every $r\in\rho(PSp_4(p)) = \pi(PSp_4(p))$, one has

That means the vertex set of $\Gamma(PSp_4(p))$ is

Observing $\operatorname{cd}(PSp_4(p))$, the edges of $\Gamma(PSp_4(p))$ can be described as

(1) $p^4$ is an isolated vertex,

(2) let $r_1$, $r_2\in\pi\big(PSp_4(p)\big)\setminus \{2, \; p\}$. From (2.1) there is an edge

(3) for every $r\in\pi\left(\left(p-1\right)^2\left(p+1\right)^2 \right)\setminus \{2\}$, there is an edge $|PSp_4(p)|_{2}\sim |PSp_4(p)|_{r}$,

(4) for every $r\in\pi\left(\frac{(p+1)^2}{2}\right)$, there is not an edge $|PSp_4(p)|_{2}\sim |PSp_4(p)|_{r}$.

Apart from the above cases, the following holds.

Proposition 2.1. If $p\geqslant 7$ and $r\in\pi(PSp_4(p))\setminus \{p, 3\}$, then there is always an edge $|PSp_4(p)|_3\sim|PSp_4(p)|_r$ in $\Gamma(PSp_4(p))$.

Proof. By the above statements about $\Gamma(PSp_4(p))$, we only need to prove

This is trivial, because we can obtain $3\, \big|\, (p-1)(p+1)$ by $3\nmid p$. □

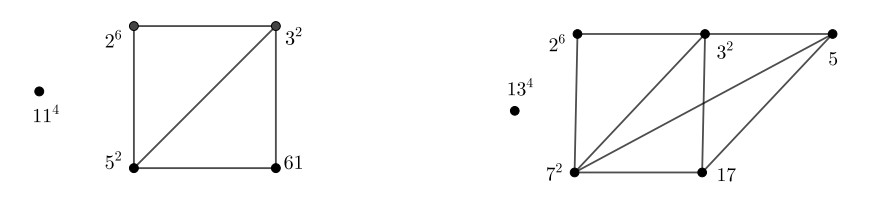
Example. The orders of $PSp_4(11)$ and $PSp_4(13)$ respectively are

Using the description above, we obtain the degree prime-power graphs of $PSp_{4}(11)$ and $PSp_4(13)$ (see Figure 1).

3.   The subnormal series of a non-solvable group

In this section, we study a subnormal chain of non-solvable groups through some lemmas. These lemmas will play an important role in the proof of the main theorem.

Lemma 3.1. [10,Lemma 2.5] Let $G$ be a non-solvable group. If $T / S$ is a non-abelian chief factor of $G$, then there is a normal series $1 \leq H < K \leq G$ such that $K / H \cong T / S$ and $G / K\, \lesssim \, \operatorname{Out}(T / S)$.

Lemma 3.2. [10,Corollary 2.1] Let $G$ be a non-solvable group. Then there is a subnormal series

such that $G_{2 k}$ is solvable, $G_{2 i-1} / G_{2 i}$ is a non-abelian chief factor of $G_{2 i-2}$, and

for each $1 \leqslant i \leqslant k$.

For convenience, we denote the subnormal series in Lemma 3.2 by $sn_{2k}$, or $sn_{2k}^H$ if the subnormal subgroups in the series are written as $H_i$, and denote the $j$-th term in $sn_{2k}$ by $sn_{2k}(j)$, where $0\leqslant j\leqslant 2k$. Generally, $sn_{2k}$ is not unique for $G$.

Lemma 3.3. Let $G$ be a finite non-solvable group, and $M$ be a non-abelian composition factor of $G$. If, for any $sn_{2k}$ and any $1\leqslant i\leqslant k$, the quotient group $sn_{2k}(2i-2)/ sn_{2k}(2i-1)$ does not have a non-abelian composition factor which is isomorphic to $M$, then there exists a subnormal series

such that $H_{2 t-1}/H_{2 t}\cong M^m$ for some integer $m$.

Proof. If $M$ is the unique (up to an isomorphism) non-abelian composition factor of $G$. By Lemma 3.2, the conclusion is obvious. Now suppose that the non-abelian composition factor of $G$ is not unique (up to an isomorphism).

Assume $M_1$ is a non-abelian composition factor of $G$ and $M_1$ is not isomorphic to $M$. Suppose $T/K$ is a non-abelian chief factor of $G$ and $T/K\cong M_1^{m_1}$. By Lemma 3.1, there is a normal series

such that $H_1/H_2\cong T/K\cong M_1^{m_1}$ and $H_0/H_1\lesssim \operatorname{Out}(H_1/H_2)$. By this assumption, $M$ is not a non-abelian composition factor of $H_0/H_1$. Then, $M$ is a non-abelian composition factor of $H_2$.

If $M$ is the unique (up to an isomorphism) non-abelian composition factor of $H_2$, then the conclusion holds by Lemma 3.2. If $M$ is not unique (up to an isomorphism) non-abelian composition factor of $H_2$, then we assume that $M_2$ is a non-abelian composition factor of $H_2$ and $M_2$ is not isomorphic to $M$. Similar to the above reason, there is a normal series

such that $H_3/H_4\cong M_2^{m_2}$ is a non-abelian chief factor of $H_2$, and $H_2/H_3\lesssim \operatorname{Out}(H_3/H_4)$. By this assumption, $M$ is a non-abelian composition factor of $H_4$.

Repeating the above process, we obtain a subnormal series

such that

(1) $M$ is the unique (up to an isomorphism) non-abelian composition factor of $H_{2r}$;

(2) $H_{2i-1}/H_{2i}\cong M_i^{m_i}$ is a non-abelian chief factor of $H_{2i-2}$, and $H_{2 i-2} / H_{2 i-1}\, \lesssim \, \operatorname{Out}\left(H_{2 i-1} / H_{2 i}\right)$ where $M_i$ is not isomorphic to $M$ and $i = 1$, $\cdots$, $r$.

By Lemma 3.2, there is a subnormal series

such that $H_{2t}$ is solvable, $H_{2 i-1} / H_{2 i}\cong M^{m_i}$ is a non-abelian chief factor of $H_{2 i-2}$, and $H_{2 i-2} / H_{2 i-1}\, \lesssim \, \operatorname{Out}\left(H_{2 i-1} / H_{2 i}\right)$ for each $r+1 \leqslant i \leqslant t$. Therefore, the proof is complete by (3.3) and (3.4). □

Lemma 3.4. Let $G$ be a group, and $p$ be an odd prime. Suppose that

(1) $|G|\leqslant p^{10}$, and

(2) $G$ has a non-abelian composition factor $M$ satisfying $p\, \big|\, |M|$.

Then, there exists a subnormal series $sn_{2k}$ such that

where $m$ is an integer. Specifically, if $sn_{2k}(2k) = 1$, then there exists a subnormal subgroup of $G$ which is isomorphic to $M$.

Proof. By Lemma 3.3, we only need to prove that for any ${sn}_{2t}^H$ and any $1\leqslant i\leqslant t$ the quotient group ${sn} _{2t}^H(2i-2)/ {sn}_{2t}^H(2i-1)$ does not have a non-abelian composition factor which is isomorphic to $M$.

Otherwise, suppose there is a ${sn}_{2t}^H$ such that ${sn} _{2t}^H(2i-2)/ {sn}_{2t}^H(2i-1)$ has a non-abelian composition factor which is isomorphic to $M$ for some $1\leqslant i\leqslant t$. Note that ${sn} _{2t}^H(2i-1)/ {sn}_{2t}^H(2i)$ is a non-abelian chief factor of ${sn} _{2t}^H(2i-2)$, and it is a direct product of isomorphic non-abelian simple groups. Let

where $M_1$ is a non-abelian simple group. Hence, we have

For convenience, denote ${sn} _{2t}^H(2i-2)/ {sn}_{2t}^H(2i-1)$ as $K$, then $K\lesssim \operatorname{Out}\left(M_1 \right)\wr S_{m}$. Without loss of generality, assume $K\leqslant \operatorname{Out}\left(M_1 \right)\wr S_{m}$. Then

Since $M_1$ is a non-abelian simple group, we know $\left(\text{Out}(M_1)\right)^m$ is solvable. So, $K\cap\left(\text{Out}(M_1)\right)^m$ is solvable. Because $K = {sn} _{2t}^H(2i-2)/{sn}_{2t}^H(2i-1)$ has a non-abelian composition factor which is isomorphic to $M$, we have

Hence, $p\, \Big|\, |S_m|$ and $p\leqslant m$. Therefore

This is a contradiction, because $p^{10}\geqslant 60^p$ is impossible. □

4.   The proof of the main theorem

For the main theorem, the necessity is obvious. It is enough to prove the sufficiency. To achieve this, we need the following series of lemmas.

Lemma 4.1. Let $G$ be a finite group and $K$ be a subnormal subgroup of $G$. If $V(G) = \big\{\, |G|_p\, \big|\, p\in\pi(G)\big\}$, then the following statements hold.

(1) $G$ is non-solvable.

(2) Every minimal subnormal subgroup of $G$ is a non-abelian simple group.

(3) $1$ is the unique solvable subnormal subgroup of $G$. Furthermore, for any $sn_{2k}$, we have $sn_{2k}(2k) = 1$.

(4) If $K\neq1$, then $V(K) = \big\{\, |K|_p\, \big|\, p\in\pi(K)\big\}$.

(5) If there are $p, r\in \pi(K)$ such that $|G|_p\sim |G|_r$ is an edge of $\Gamma(G)$, then $|K|_p\sim |K|_r$ is an edge of $\Gamma(K)$.

Proof. Statements (1) and (2) are Lemma 2.2 in ^[10]. Statement (3) is a corollary of (2).

For (4) and (5), without loss of generality we suppose $K$ is a normal subgroup of $G$. Suppose that $\chi\in\operatorname{Irr}(G)$ such that $\chi(1)_p = |G|_p$ where $p\in\pi(K)$. Let $\theta\in \operatorname{Irr}(K)$ be a constituent of $\chi_K$. Using Corollary 11.29 in ^[16], we have $\frac{\chi(1)}{\theta(1)}\, \Big|\, |G/K|$. Furthermore,

Then, $\theta(1)_p = |K|_p$ by $\chi(1)_p = |G|_p$. Hence, $|K|_p\in V(K)$. This means statement (4) holds.

Let $p, r\in \pi(K)$ such that $|G|_p\sim |G|_r$ is an edge of $\Gamma(G)$, then there exists $\chi\in\operatorname{Irr}(G)$ satisfying $(|G|_p\cdot |G|_r)\Big|\chi(1)$. If $\phi\in \operatorname{Irr}(K)$ is a constituent of $\chi_K$, then $\frac{\chi(1)}{\theta(1)}\, \Big|\, |G/K|$ by Corollary 11.29 in ^[16]. Hence, $(|K|_p\cdot |K|_r)\Big|\phi(1)$, i.e., $|K|_p\sim |K|_r$ is an edge of $\Gamma(K)$. Statement (5) holds. □

Lemma 4.2. The following statements about the exceptional group of Lie type ${ }^2 B_2\left(2^{2 n+1}\right)$ ($n\geqslant 1$) hold.

(1) ${ }^2 B_2\left(2^{2 n+1}\right)$ is the only simple group whose order is prime to $3$.

(2) Let $p\geqslant 5$ be a prime. If

then $n = 1$ and $p = 13$.

Proof. (1) Obviously, for any alternating group $A_n$ ($n \geqslant 5$), its order is divisible by $3$. According to Atlas ^[14], any sporadic simple group's order is divisible by 3 as well as the order of ${}^2F_4(2)^\prime$.

If $M$ is a simple group of Lie type over $GF(q)$ with $M \neq {}^2F_4(2)^{\prime}$ and ${ }^2 B_2\left(2^{2 n+1}\right)$ ($n\geqslant 1$), then $q(q^2-1)\, \big|\, |M|$. Notice that $3\, \big|\, q(q^2-1)$, and we have $3\, \big|\, |M|$.

The order of ${ }^2 B_2\left(2^{2 n+1}\right)$ is

Since

the order of ${ }^2 B_2\left(2^{2 n+1}\right)$ is not divisible by $3$. This completes the proof of (1) by CFSG.

(2) Suppose

It is not hard to prove that $q^2+1 = a b$, $\left(q^2+1, q-1\right) = 1$, and $(a, b) = 1$. Hence,

By $p\, \Big|\, |{ }^2 B_2\left(2^{2 n+1}\right)|$, we have

From $|{ }^2 B_2\left(2^{2 n+1}\right)|\, \Big|\, |PSp_4(p)|$, it follows that $q^2\, \Big|\, (p+1)^2(p-1)^2$, i.e., $q\, \big|\, (p+1)(p-1)$. Since $\bigl(p+1, p-1\bigr) = 2$, we get

(i) If $p\, \big|\, (q-1)$ and $q\, \big|\, 2(p+\epsilon_1)$, then there are positive integers $k$ and $m$ such that

It follows that

Hence $p\, \big|\, -m+2\epsilon_1$.

If $-m+2\epsilon_1 = 0$, then $m = 2$ and $\epsilon_1 = 1$, moreover, $q = p+1$, i.e., $p = q-1$. Therefore,

By $|{ }^2 B_2\left(2^{2 n+1}\right)|\, \Big|\, |PSp_4(p)|$, we obtain

A short calculation reveals that

Then, $\left(q^2+1, q-2\right)\Big|5$ and $\left(q^2+1, q^2-2q+2 \right) = \left(q^2+1, q-1\right) = 1$. Consequently, by (4.1) we know that $q^2+1\, \Big|\, (q-2)^2$, and $q^2+1$ is a power of $5$. This leads to $\pi\left(|{ }^2 B_2\left(2^{2 n+1}\right)|\right) = \{2, 5, p\}$. This is a contradiction, because $|{ }^2 B_2\left(2^{2 n+1}\right)|$ is not a $K_3$-simple group, where the so-called $K_3$-simple group is a non-abelian simple group with only three prime factors of its order.

Now we assume $-m+2\epsilon_1\neq0$. By $p\, \big|\, -m+2\epsilon_1$, it follows that $m\geqslant p+2\epsilon_1\geqslant3$. Then, $2(p+\epsilon_1) = mq\geqslant3(pk+1)$, i.e., $0 < (3k-2)p\leqslant 2\epsilon_1-3 < 0$. This is a contradiction.

(ii) If $p\, \big|\, q+\epsilon_2\sqrt{2q}+1$ and $q\, \big|\, 2(p+\epsilon_1)$, then there exist positive integers $k$ and $m$ such that

Then, $2(q+\epsilon_2\sqrt{2q}+1) = 2pk = (qm-2\epsilon_1)k$. Substituting $q = 2^{2n+1}$ into this equation yields

If $1+\epsilon_1k = 0$, then $k = 1$, $\epsilon_1 = -1$ and $2^{n}+\epsilon_2-2^{n-1}m = 0$, i.e., $\epsilon_2 = 2^{n-1}m-2^{n}$. It follows that $n = 1$ and $m = \epsilon_2+2 = 1$ or $3$. Therefore, $q = 2^{2n+1} = 8$ and $2(p-1) = 8m = 8$ or $24$, by (4.2). This means that $p = 5$ or $13$.

If $1+\epsilon_1k\neq0$, then $2^{n+1}\, \big|\, 1+\epsilon_1k$ by (4.3). We conclude that $k\geqslant 2^{n+1}-\epsilon_1$. Therefore,

By $q = 2^{2n+1}$, the above inequality can be rewritten as

Dividing both sides of this inequality by $2^{n+1}$, we get

which implies that $(2^{n+1}-\epsilon_1)m\leqslant 2+\frac{2}{2^{n-1}} \leqslant 4$. This means $2^{n+1}-\epsilon_1\leqslant 4$, moreover,

Therefore, $q = 2^{2n+1} = 8$. By $p\, \big|\, q+\epsilon_2\sqrt{2q}+1$, we obtain that $p\, \big|\, q^2+1$. Then, $p = 5$ or $13$.

Because $|{ }^2 B_2\left(8\right)| = 8^2(8^2+1)(8-1) = 2^6\cdot(5\cdot13)\cdot7$, $|PSp_4(5)| = 2^6 \cdot 3^2 \cdot 5^4 \cdot 13$, $|PSp_4(13)|$ = $13^4 \cdot \left(2^6\cdot 3^2\cdot 7^2\right)\cdot 5\cdot 17$, and $|{ }^2 B_2\left(2^{2 n+1}\right)|\, \Big|\, |PSp_4(p)|$, we obtain that $p$ can only be $13$. □

Lemma 4.3. If $M$ is a simple group of Lie type over $GF(q)$, where $q = p^f$, then $|M|_p$ is an isolated vertex in $\Gamma(M)$.

Proof. If $M$ is a simple group of Lie type over some $GF(q)$ with $M \neq {}^2F_4(2)^{\prime}$, the result can be obtained directly by Lemma 2.4 in ^[17]. If $M = {}^2F_4(2)^{\prime}$, then $|M|_2 = 2^{11}$ is an isolated vertex in $\Gamma(S)$ by the character table of ${}^2F_4(2)^{\prime}$ in ^[14]. □

Lemma 4.4. Let $G$ be a group, and $p\geqslant 7$ be an odd prime. If

then the following statements hold.

(1) Let $M$ be a simple group of Lie type over $GF(q)$ where $q = r^f$. If $p\, \big|\, |M|$ and $M$ is a subnormal subgroup of $G$, then $r = p$ or $M\cong ^2B_2(8)$.

(2) If $T$ is a non-abelian composition factor of $G$, then $p\, \nmid\, |\operatorname{Out}(T)$.

(3) For any $sn_{2k}$ and any $1\leqslant i\leqslant k$, the order of $\operatorname{Out}\left(sn_{2k}(2i-1)/ sn_{2k}(2i)\right)$ is not divisible by $p$, and $p\, \nmid\, |sn_{2k}(2i-2)/ sn_{2k}(2i-1)|$.

Proof. (1) By the assumption, the vertex set of $\Gamma(G)$ is $V(G) = \{|G|_t\, |\, t\in\pi(G)\}$. Then, $V(M) = \{|M|_t\, |\, t\in\pi(M)\}$ by Lemma 4.1(4).

First, we suppose that $r\neq p$ and $M$ is not isomorphic to ${ }^2 B_2\left(2^{2 n+1}\right)$ ($n\geqslant 1$).

If $r = 3$, then there exists an edge $|G|_2\sim |G |_3$ by Proposition 2.1. Because $M$ is not isomorphic to ${ }^2 B_2\left(2^{2 n+1}\right)$, we know $3\, \big|\, |M|$ and $|M|_3\sim|M|_2$ is an edge of $\Gamma(M)$ by Lemma 4.1(5). This is a contradiction, because $|M|_r$ is an isolated vertex in $\Gamma(M)$ by Lemma 4.3.

If $r\neq 3$, then there exists an edge $|G|_r\sim |G |_3$ by Proposition 2.1. We can obtain a contradiction using the same method as before.

Second, assume $r\neq p$ and $M$ is isomorphic to ${ }^2 B_2\left(2^{2 n+1}\right)$ ($n\geqslant 1$). By Lemma 4.2(2), we see that $M$ is isomorphic to ${ }^2 B_2\left(8\right)$ and $p = 13$. This completes the proof of (1).

(2) Assume $T$ is a non-abelian composition factor of $G$, and $p\, \big|\, |\operatorname{Out}(T)$. Since $p$ is an odd prime, $T$ is not isomorphic to an alternating group, one of $26$ sporadic simple groups or the Tits simple group $^2F_4(2)^\prime$, because the outer automorphism groups of these simple groups are $1$, $C_2$, or $C_2\times C_2$. By CFSG, $T$ is a simple group of Lie type over some $GF(q)$ except $^2F_4(2)^\prime$, where $q = r^f$, and $r$ is a prime. Therefore, $|\operatorname{Out(T)}| = dfg$ where $d$, $f$, and $g$ are the orders of diagonal, field, and graph automorphisms of $T$, respectively. By Table 5 in ^[14], we know that $g\, \big|\, 6$, so $p\, \nmid\, g$. Therefore, if $p\big| |Out(T)|$, then $p\, \big|\, d$ or $p\, \big|\, f$.

If $p\, \big|\, d$, then $T$ is isomorphic to $A_n(q)$ or ${}^2A_n(q)$ (i.e., $PSL_{n+1}(q)$ or $PSU_{n+1}(q)$) by Table 5 in ^[14]. Assume $T\cong A_n(q)$, then $d = (n+1, q-1)$ and

Hence, $n+1\geqslant p\geqslant 7$, $p\, \big|\, q-1$, and $p\, \big|\, |T|$. By Lemma 3.4 and Lemma 4.1(3), there exists a subnormal subgroup $K\trianglelefteq \trianglelefteq G$ such that $K\cong T \cong A_n(q)$. It follows that $q = p^f$ by (1). It contradicts to $p\, \big|\, q-1$. Using the same method, one can demonstrate that $T\ncong{}^2A_n(q)$.

Now, we assume $p\, \big|\, f$. It follows that $q = r^{kp}\geqslant 2^p\geqslant 2^7$. If $T$ is not isomorphic to $A_1(q)$, then one can obtain

by observing the order of a simple group of Lie type over $GF(q)$. Hence,

This implies $p\leqslant 5$ by Maple. This contradicts $p\geqslant 7$.

If $T$ is isomorphic to $A_1(q)$, then $|T| = \frac{1}{(2, q-1)}q(q^2-1)$. When $p\geqslant 7$, one can obtain the following inequality by Maple:

However, since $(2, q-1)\leqslant 2$ and $q = r^{kp}$, we have

By inequalities (4.4) and (4.5), one can see that $r^k = 2$, i.e., $q = 2^p$. Then, $|T| = \frac{1}{(2, 2^p-1)}2^p(2^{2p}$$-1) =$$2^p(2^{2p}-1)$. Using Maple to solve the inequality $|G|\geqslant |T|$, we conclude that $p\leqslant 11$, i.e., $p = 7$ or $11$. If $p = 7$, then $|T| = 2^7\cdot3\cdot43\cdot127$ and $|G| = 2^8 \cdot 3^2 \cdot 5^4 \cdot 7^4$. This is a contradiction to $|T|\, \big|\, |G|$. If $p = 11$, then $|T| = 2^{11}\cdot3\cdot23\cdot89\cdot683$ and $|G| = 11^4 \cdot\left(2^6 \cdot 3^2 \cdot 5^2\right) \cdot 61$. This is a contradiction. Therefore, $f$ is not divisible by $p$ when $p\geqslant7$. This completes the proof of (2).

(3) Suppose that there exists an $sn_{2k}$ and $i$ such that

Notice that ${sn} _{2k}(2i-1)/ {sn}_{2k}(2i)$ is a non-abelian chief factor of ${sn} _{2k}(2i-2)$, and we have

where $T$ is a non-abelian composition factor of $G$, and ${sn} _{2k}(2i-1)/ {sn}_{2k}(2i)$ is a direct product of $m$ copies of $T$. By the proof of Lemma 3.4, we know $p\, \nmid\, |S_m|$. Hence, $p\, \big|\, |\operatorname{Out}(T)|$. However, this is impossible by (2). Therefore, statement (3) is proved. □

Now we can present a proof of the main theorem based on the above lemmas.

Proof of Main Theorem. Obviously, it is enough to prove the sufficiency. We first prove the sufficiency when $p = 5$. If $p = 5$, then $|G| = |PSp_4(5)| = 2^6 \cdot 3^2 \cdot 5^4 \cdot 13$ and $\Gamma(G) = \Gamma(PSp_4(5))$. Hence,

By Lemma 4.1, $G$ is non-solvable and every minimal subnormal subgroup of $G$ is a non-abelian simple group. Let $N$ be a minimal normal subgroup of $G$. Then, $N$ is a direct product of isomorphic non-abelian simple groups. It is enough to prove $N\cong PSp_4(5)$. By $|N|\, \big|\, |G|$, we know that $N$ is isomorphic to one of $A_5$, $A_5\times A_5$, $A_6$, $PSL_3(3)$, $PSL_2(25)$, $PSU_3(4)$, $PSp_4(5)$ by ^[14]. If $N$ is isomorphic to one of $A_5$, $A_5\times A_5$, $A_6$, $PSL_3(3)$, $PSU_3(4)$, then $|N|_2\sim|N|_3$ is not an edge of $\Gamma(N)$ by checking their character table in ^[14]. However, there exists an edge $|N|_2\sim|N|_3$ in $\Gamma(N)$ by Lemma 4.1(5). This is a contradiction. If $N\cong PSL_2(25)$, then

By $|N| = |PSL_2(25)| = 2^3\cdot3\cdot5^2\cdot13$ and $\operatorname{Out}(PSL_2(25))\cong C_2\times C_2$, we have $|C_G(N)| = 2^\alpha \cdot3\cdot5^2$, where $\alpha = 1$, $2$, or $3$. Notice that $C_G(N)\vartriangleleft G$, and we know there exists a minimal subnormal subgroup of $G$, denoted by $T$, such that $T\leqslant C_G(N)$. Hence, $T$ is isomorphic to $A_5$. By Lemma 4.1(5), there exists an edge $|T|_2\sim|T|_3$ in $\Gamma(T)$, a contradiction. Therefore, $N\cong PSp_4(5)$, moreover, $G\cong PSp_4(5)$.

When $p \geqslant 7$, we will discuss all non-abelian composition factors of $G$ whose order can be divisible by $p$, covering all possible cases. Our proof for this purpose will consist of $5$ steps. Now, assume that $T$ is a non-abelian composition factor of $G$ satisfying $p\, \big|\, |T|$.

Step 1. Give information about the degree-power graph $\Gamma(T)$.

By Lemma 4.1(3) and Lemma 3.4, there exists a subnormal subgroup of $G$ which is isomorphic to $T$. Let $r\in\pi(T)\setminus\{p, 3\}$. Then there is an edge $|T|_3\sim|T|_r$ in $\Gamma(T)$, by Lemma 4.1(5) and Proposition 2.1.

Step 2. Prove $T$ is not isomorphic to an alternating group $A_n$.

On the contrary, $T$ is isomorphic to an alternating group $A_n$. By $p\, \big|\, |T|$, we know $p\leqslant n$, moreover, $\frac{p!}{2}\, \big|\, |T|$. Notice that $|T|\, \big|\, |G|$, and we see that

By $\left(\frac{p+1}{e} \right)^p < p!$ ($e$ is the natural constant), the following inequality holds:

Using Maple, it implies $p\leqslant13$. If $p = 13$, then $p! = 2^{10}\cdot3^5\cdot 5^2\cdot7\cdot11\cdot13$, $p^4(p^2-1)(p^4-1) = 2^7\cdot3^2\cdot5\cdot7^2\cdot13^4\cdot17$. This contradicts $p!\, \big|\, p^4(p^2-1)(p^4-1)$. If $p = 11$, then $p! = 2^{8}\cdot3^4\cdot 5^2\cdot7\cdot11$, $p^4(p^2-1)(p^4-1) = 2^7\cdot3^2\cdot5^2\cdot11^4\cdot61$, a contradiction. If $p = 7$, then $|G| = 2^8 \cdot 3^2 \cdot 5^4 \cdot 7^4$. Therefore, $T$ only is isomorphic to $A_7$ or $A_8$ by $|T|\, \big|\, |G|$. Observing the character tables of $A_7$ and $A_8$ in ^[14], there is not an edge $|T|_2\sim |T|_3$ of $\Gamma(T)$. However, $|T|_2\sim |T|_3$ should be an edge of $\Gamma(T)$ by {Step 1.} This is a contradiction.

Step 3. Prove $T$ is not isomorphic to any sporadic simple group.

We assume that $T$ is isomorphic to one of following simple groups:

Observing the degree prime-power graphs of the above $23$ sporadic simple groups in ^[11], there is not an edge $|T|_2\sim|T|_3$ in $\Gamma(T)$. This is a contradiction, by Step 1. Next, we analyze the remaining three sporadic simple groups: $O^{\prime}N$, $Ly$, $J_4$.

If $T$ is isomorphic to $O^{\prime}N$, then $\pi(T) = \{2, 3, 5, 7, 11, 19, 31\}$. By Step 1, for every $r\in\pi(T)\setminus\{p, 3\}$, there is an edge $|T|_3\sim|T|_r$ in $\Gamma(T)$. This indicates that there are at least $5$ edges at vertex $|T|_3$. However, by the character table of $O^{\prime}N$, we know there are only $3$ edges at vertex $|T|_3$, i.e., $|T|_3\sim|T|_2$, $|T|_3\sim|T|_5$ and $|T|_3\sim|T|_{31}$. This is a contradiction. Using the same method, one can obtain a contradiction when $T$ is isomorphic to $Ly$.

If $T\cong J_4$, then $|T| = 2^{21} \cdot 3^3 \cdot 5 \cdot 7 \cdot 11^3 \cdot 23 \cdot 29 \cdot 31 \cdot 37 \cdot 43$. Since $p\, \Big|\, |T|$, we obtain $p =$$7$, $11$, $23$, $29$, $31$, $37$ or $43$. Through calculations using the Magma, we have $|PSp_4(p)|_2\Big| 2^{13}$ when $p\in \{7, 11, 23, 29, 31, 37, 43\}$. This contradicts $|T|\, \Big|\, |PSp_4(p)|$.

Therefore, $T$ is not isomorphic to any sporadic simple group.

Step 4. Prove $T$ is isomorphic to one of $A_1(p^3)( = PSL_2(p^3))$, $A_2(p)( = PSL_3(p))$, ${}^2A_2(p)( = PSU_3(p))$, and $B_2(p)( = PSp_4(p))$.

By Steps 2 and 3, $T$ is a simple group of Lie type over some $GF(q)$ where $q = r^f$. Hence, by Lemma 4.4(1), we know $r = p$ or $T\cong {}^2B_2(8)$.

Assume $T\ncong {}^2B_2(8)$, then $r = p\geqslant7$. Since $|G|_p = p^4$, we can obtain that $T$ is isomorphic to one of

Notice that

By ^[18], the degrees of $A_1(p)$ and $A_1(p^2)$ are

respectively.

If $T\cong A_1(p^2)$, then we can obtain that $|T|_3\sim |T|_s$ is not an edge of $\Gamma(T)$ for every $s\in\pi(\frac{p^2+1}{2})$, because $3\, \big|\, (p^2-1)$ and $(p^2-1, p^2+1) = 2$. By Step 1, this is a contradiction.

If $T\cong A_1(p)$ and $\frac{p-1}{2}$ is an even number, then $\epsilon = -1$ and $\operatorname{cd}(T) = \{1, p, \frac{p+1}{2}, p-1, p+1\}$ where $\frac{p+1}{2} = \frac{p-1}{2}+1$ is an odd number. Hence, for every $s\in\pi(\frac{p+1}{2})$ and $t\in\pi(p-1)$ there is not an edge $|T|_s\sim|T|_t$ in $\Gamma(T)$. Since $s$, $t\in \pi\left((p-1)^2(p+1)^2\right)$ and $PSp_4(p)$ has an irreducible character of degree $(p-1)^2(p+1)^2$, then $|G|_s\sim |G|_t$ is an edge of $\Gamma(G)$. By Step 1, $T$ is isomorphic to a subnormal subgroup of $G$. Hence, $|T|_s\sim|T|_t$ is an edge of $\Gamma(T)$ by Lemma 4.1(5). So, it is a contradiction. Using the same method, there is a contradiction when $\frac{p-1}{2}$ is an odd number.

If $T\cong A_1(p^4)$, then $|T| > |G|$ obviously. This is a contradiction.

Assume $T\cong{}^2B_2(8)$, then $p = 13$ by Lemma 4.2. Hence, $|T| = 2^6\cdot5\cdot7\cdot13$ and $|G| = |PSp_4(13)|$ = $13^4 \cdot \left(2^6\cdot 3^2\cdot 7^2\right)\cdot 5\cdot 17$. Observing $|T|_2 = |G|_2$, we can conclude that $G$ has only one non-abelian composition factor. By Lemma 3.2 and 4.1(2), there is a subnormal series

such that $G_1/G_2\cong T$ and $G_0/G_1 \, \lesssim \, \operatorname{Out}\left(T\right)$. This will lead to a contradiction. Since the outer automorphism group is $C_3$, we obtain $|G| = |G_1/G_2|\cdot|G_0/G_1|\leqslant |T|\cdot |C_3| = 2^6\cdot5\cdot7\cdot13\cdot 3$. That is impossible.

Based on the above discussion, $T$ is isomorphic to one of $A_1(p^3)( = PSL_2(p^3))$, $A_2(p)( = PSL_3(p))$, ${}^2A_2(p)( = PSU_3(p))$, and $B_2(p)( = PSp_4(p))$.

Step 5. Prove $G$ is isomorphic to $PSp_4(p)$.

Take a subnormal series $sn_k^{G}$

By Lemmas 4.1(3) and 4.4(3), we have $G_{2k} = 1$ and $p\nmid |G_{2i-2}/G_{2i-1}|$ where $i = 1$, $2$, $\cdots$, $k$. It follows that

Notice that every $G_{2i-1}/G_{2i}$ is a product of isomorphic non-abelian simple groups, and we assume that the direct product factor of $G_{2i-1}/G_{2i}$ is $T_i$ for $i = 1, 2, \cdots, k$. Then there exists a $T_{j_1}$ such that its order is divisible by $p$. By Step 4, $T_{j_1}$ is isomorphic to one of $PSL_2(p^3)$, $PSL_3(p)$, $PSU_3(p)$, and $PSp_4(p)$. We claim $T_{j_1}$ is isomorphic to $PSp_4(p)$. Otherwise, $T_{j_1}$ is isomorphic to $PSL_2(p^3)$, $PSL_3(p)$, or $PSU_3(p)$. Then $|T_{j_1}|_p = p^3$, moreover $G_{2j_1-1}/G_{2j_1}\cong T_{j_1}$ by $|G|_p = p^4$. Hence, there is a $T_{j_2}$ such that its order is divisible by $p$, and $|T_{j_2}|_p$ can only be $p^1$. This contradicts the result in {Step 4}. Therefore, $G$ has a non-abelian composition factor that is isomorphic to $PSp_4(p)$. This means $G\cong PSp_4(p)$. This completes the proof of Main Theorem. □

5.   Conclusions

We have primarily investigated whether the symplectic simple group $PSp_4(p)$ can be uniquely determined by its order and degree prime-power graph. In the main theorem, we provide a positive answer to this question. In Lemma 3.3, a sufficient condition for adjusting the positions of specific non-abelian composition factors in the subnormal series $sn_{2k}$ is provided. This condition plays a crucial role in the proof of the main theorem. We believe that this condition is valuable for studying the characterization of more non-abelian simple groups. Based on the results of this paper and ^{[10,11,12,13]}, we conjecture that most non-abelian simple groups can be uniquely determined by their orders and degree prime-power graphs.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the Doctoral Through Train Scientific Research Project of Chongqing (No. sl202100000324), Guangxi Natural Science Foundation (No. 2022GXNSFBA035572), Scientific and Technological Research Program of Chongqing Municipal Education Commission (No. KJQN202300846) and National Natural Science Foundation of China (Nos. 12301021 and 12071376).

Conflict of interest

The authors declare no conflicts of interest.