Boosting task scheduling in IoT environments using an improved golden jackal optimization and artificial hummingbird algorithm

1.   Introduction

Working with large amounts of data is one of the main challenges we face today. With the rise of social networks and rapid technological advances, we must develop tools that allow us to work with so much information. At this point the use of tensor products comes into play, since their use reduces the number of and speed up the operations to be carried out. Proof of this is the recent article ^[1], where tensor products are used to speed up the calculation of matrix products. Other articles that exemplify the goodness of this operation include ^[2], where the solution of 2, 3-dimensional optimal control problems with spectral fractional Laplacian-type operators is studied, and ^[3], where high-order problems are studied through the use of proper generalized decomposition methods.

When we try to solve a linear system of the form $A \mathbf{x} = \mathbf{b}$, in addition to the classical methods, there are methods based on tensors that can be more efficient ^[4], since the classical methods face the problem of the curse of dimensionality, which makes them lose effectiveness as the size of the problem increases. The tensor methods look for the solution in separated form, that is, as the tensor combination

where $\mathbf{x}_i^j \in {\mathbb{R}}^{N_i}$, $d$ is the dimension of the problem, and $\otimes$ is the Kronecker product as reviewed in the next Section. The main family of methods that solves this problem is proper generalized decomposition family ^[5], and it is based on the greedy rank-one update (GROU) algorithm ^[6,7]. This algorithm calculates the solution of the linear system $A \mathbf{x} = \mathbf{b}$ in separated form and, for this, in each iteration, it updates the approximation of the solution with the term resulting from minimizing the remaining residue. Furthermore, there are certain square matrices for which the GROU algorithm improves their convergence i.e., matrices of the form

where $\mathrm{id}_{N_k}$ is the identity matrix of size $N_k \times N_k,$ and $A_{k} \in {\mathbb{R}}^{N_k \times N_k},$ for $1 \leq k \leq d$. These matrices are called Laplacian-like matrices, due to their relationship with the Laplace operator written as

It is not easy to decide when a given matrix $A$ can be represented in that form. To do this, we can use some of the previously results obtained by the authors of ^[8]. In this paper, we prove that the set of Laplacian-like matrices is a linear subspace for the space of square matrices with a particular decomposition of its dimension. Moreover, we provide a greedy algorithm that provides the best Laplacian approximation $L_A,$ for a given matrix $A,$ as well its residue, $R_A = A-L_A.$ However, an iterative algorithm it is not useful enough against a direct solution algorithm. The main goal of this paper is to provide a direct algorithm that allows one to construct the best Laplacian-like approximation by using only a particular block decomposition of the matrix $A.$ It can be considered as a pre-processing procedure that allows one to represent a given matrix in its best Laplacian-like form, and if the residual is equal to zero, we definitively have its Laplacian-like representation form. Hence, we efficiently use the GROU algorithm to solve the high-dimensional linear system associated with the matrix $A.$

We remark that, by using the decomposition $A = L_A + R_A,$ we can rewrite the linear system as $(L_A + R_A) \mathbf{x} = \mathbf{b}$, and when the value of the remainder is small, we can approximate the solution of the system $\mathbf{x}^*$ by using the solution of the Laplacian system $\mathbf{x}_L$. This fact is specially interesting in the case of the discretization of some partial differential equations. We also study the Laplacian decomposition of the matrix that comes from the discretization of a general second order partial differential equation of the form

with homogeneous boundary conditions. Besides, to compare different numerical methods to solve partial differential equations, we consider two particular cases: the Helmholtz equation, which solves an eigenvalue problem for the Laplace operator. Furthermore, to illustrate that it is not necessary to be limited to the second order, we also consider the 4th order Swift-Hohenberg equation

This equation is noted for its pattern-forming behavior, and it was derived from the equations for thermal convection ^[9].

The paper is organized as follows. We begin by recalling some preliminary definition and results used throughout the paper in Section 2. Section 3 is devoted to the statement and the proof of the main result of this paper, which allow one to construct explicitly the best approximation of a given matrix to the linear space of Laplacian-like matrices. After that, in Section 4, we discuss how we applied this result to compute the best Laplacian approximation for the discretization of a second order partial differential equations without mixing derivatives. Finally, some numerical examples are given in Section 5.

2.   Preliminary definitions and results

First at all we introduce some notations that we use throughout the paper. We denote by $\mathbb{R}^{N \times M},$ the set of $N \times M$-matrices and by $A^T$ the transpose of a given matrix $A.$ As usual we use

to denote the Euclidean inner product in $\mathbb{R}^N,$ and its corresponding $2$-norm, by $\| \mathbf{x}\|_2 = \| \mathbf{x}\|_{\mathbb{R}^N} = \langle \mathbf{x}, \mathbf{x}\rangle_2^{1/2}.$

Given a sequence $\{\mathbf{u}_j\}_{j = 0}^{\infty} \subset \mathbb{R}^N,$ we say that a vector $\mathbf{u} \in \mathbb{R}^N$ can be written as

if and only if

in the $\| \cdot \|_2$-topology.

The Kronecker product of two matrices $A \in \mathbb{R}^{N_1 \times M_1}$ and $B \in \mathbb{R}^{N_2 \times M_2}$ is defined by

We can see some of the well-known properties of the Kronecker product in ^[7].

As we already said, we are interested solving the high-dimensional linear system $A \mathbf{x} = \mathbf{b}$ obtained from a discretization of a partial differential equation. We are interested in solving it by using a tensor-based algorithm; so, we are going to look for an approximation of the solution in separated form. To see this, we assume that the coefficient matrix $A$ is a $(N_1 \cdots N_d) \times (N_1 \cdots N_d)$-dimensional invertible matrix for some $N_1, \cdots, N_d \in {\mathbb{N}}.$ Next, we look for an approximation (of rank $n$) of $A^{-1} \mathbf{b}$ of the form

To do this, given $\mathbf{x} \in \mathbb{R}^{N_1\cdots N_d},$ we say that $\mathbf{x} \in \mathcal{R}_1 = \mathcal{R}_1(N_1, N_2, \ldots, N_d)$ if $\mathbf{x} = \mathbf{x}_1 \otimes \mathbf{x}_2 \otimes \cdots \otimes \mathbf{x}_d,$ where $\mathbf{x}_i \in \mathbb{R}^{N_i}$ for $i = 1, \ldots, d.$ For $n \ge 2,$ we define, inductively, that $\mathcal{R}_{n} = \mathcal{R}_n(N_1, N_2, \ldots, N_d) = \mathcal{R}_{n-1} + \mathcal{R}_{1},$ that is,

Note that $\mathcal{R}_{n} \subset \mathcal{R}_{n+1}$ for all $n \ge 1.$

To perform (2.1), what we will do is minimize the difference

that is, solve the problem

Here, $\|\cdot \|_2$ is the 2-norm, or the Frobenius norm, defined by

Unfortunately, from Proposition 4.1(a) of ^[10], we have that the set $\mathcal{R}_{n}$ is not necessarily (or even usually) closed for each $n \ge 2.$ In consequence, no best rank-n approximation exists, that is, (2.2) has no solution. However, from Proposition 4.2 of ^[10] it follows that $\mathcal{R}_{1}$ is a closed set in any norm-topology. This fact allows us to introduce the following algorithm.

The GROU algorithm is an iterative method to solve linear systems of the form $A \mathbf{x} = \mathbf{b}$ by using only rank-one updates. Thus, given $A \in \mathrm{GL}(\mathbb{R}^{N\times N})$ with $N = N_1 \cdots N_d$, and $\mathbf{b}\in \mathbb{R}^N,$ we can obtain an approximation of the form

for some $n \geq 1,$ and $\mathbf{x}_i^j \in {\mathbb{R}}^{N_i}$ for $i = 1, 2, \ldots, d$ and $j = 1, 2, \ldots, n$ ^[7]. We proceed with the following iterative procedure (see algorithm 1 below): let $\mathbf{u}_0 = \mathbf{y}_0 = 0$, and, for each $n \geq 1,$ take

Since $\mathbf{u}_n \approx A^{-1} \mathbf{b},$ we can define the $\mathrm{rank}_{\otimes}$ for $A^{-1} \mathbf{b}$ obtained by the GROU Algorithm as

The next result, presented in ^[7], gives the convergence of the sequence $\{ \mathbf{u}_n\}_{n \ge 0}$ to the solution $A^{-1} \mathbf{b}$ of the linear system.

Theorem 2.1. Let $\mathbf{b} \in \mathbb{R}^{N_1\cdots N_d}$ and $A \in \mathbb{R}^{N_1\cdots N_d \times N_1\cdots N_d}$ be an invertible matrix. Then, by using the iterative scheme described by (2.3) and (2.4), we obtain that the sequence $\{\|\mathbf{r}_{n}\|_2\}_{n = 0}^{ \mathrm{rank}_{\otimes} (A^{-1} \mathbf{b})}$ is strictly decreasing and

Note that the updates in the previous scheme works under the assumption that, in line 5 of algorithm 1, we have a way to obtain

To compute $\mathbf{y},$ we can use an alternating least squares (ALS) approach (see ^[7,11]).

The idea below the ALS strategy to solve (2.6) is as follows: for each $1 \le k \le d,$ we proceed as follows. Assume that the values $\mathbf{x}_1, \ldots, \mathbf{x}_{k-1}, \mathbf{x}_{k+1}, \ldots, \mathbf{x}_d$ are given. Then, we look for the unknown $\mathbf{x}_k$, satisfying

where we can write

In consequence, by using a least squares approach ^[11], we can obtain $\mathbf{x}_k$ by solving the following $N_k \times N_k$-dimensional linear system:

where

and

Clearly,

holds for all $\mathbf{z}_k \in \mathbb{R}^{N_k \times N_k}.$ However, it is well known (see Section 4 in ^[11]) that the performance of the ALS strategy can be improved (see Algorithm 2 below) when the shape of the matrix $A^TA \in \mathbb{R}^{N \times N},$ with $N = N_1 \dots N_d$, can be written in the form

where $\bigotimes_{j = 1}^d A_j^{(i)} = A_1^{(i)} \otimes \cdots \otimes A_d^{(i)};$ here, $A_j^{(i)} \in \mathbb{R}^{N_j \times N_j}$ for $1 \le j \le d$ and $1 \le i \le r.$ In particular, when the matrix $A$ is given by

then the matrix $A^TA$ can be easily written in the form of (2.8). These matrices were introduced in ^[8] as Laplacian-like matrices since they can be easily related to the classical Laplacian operator ^[2,12]. The next section will be devoted to the study of this class of matrices.

3.   On the best Laplacian matrix approximation

As we said in the introduction, the proper orthogonal decomposition is a popular numerical strategy in the engineering process to solve high-dimensional problems. It is based on the GROU algorithms (2.3) and (2.4), and it can be considered as a tensor-based decomposition algorithm.

There is a particular type of matrices to solve high-dimensional linear systems for which these methods work particularly well, i.e., those that satisfy the property (2.8). To this end, we introduce the following definition.

Definition 3.1. Given a matrix $A \in \mathbb{R}^{N \times N},$ where $N = N_1\cdots N_d,$ we say that $A$ is a Laplacian-like matrix if there exist matrices $A_i \in \mathbb{R}^{N_i \times N_i}$ for $1 \le i \le d$ be such that

where $\mathrm{id}_{N_j}$ is the identity matrix of size $N_j \times N_j.$

It is not difficult to see that the set of Laplacian-like matrices is a linear subspace $\mathbb{R}^{N \times N}$ of matrices satisfying the property (2.8). From now on, we will denote by $\mathcal{L}\left(\mathbb{R}^{N \times N}\right)$ the subspace of Laplacian-like matrices in $\mathbb{R}^{N \times N}$ for a fixed decomposition of $N = N_1\cdots N_d$.

Now, given a matrix $A \in \mathbb{R}^{N \times N},$ our goal is to solve the following optimization problem:

Clearly, if we denote by $\Pi_{\mathcal{L}\left(\mathbb{R}^{N \times N}\right)}$ the orthogonal projection onto the linear subspace $\mathcal{L}\left(\mathbb{R}^{N \times N}\right),$ then $L_A: = \Pi_{\mathcal{L}\left(\mathbb{R}^{N \times N}\right)}(A)$ is the solution of (3.2). Observe that $\|A - L_A\|_2 = 0$ if and only if $A \in \mathcal{L}\left(\mathbb{R}^{N \times N}\right).$

We are interested in trying to achieve a structure similar to (3.1) to study the matrices of large-dimensional problems. We search an algorithm that allows one to construct, for a given matrix $A,$ its Laplacian-like best approximation $L_A.$

To do this, we will use the following theorem, which describes a particular decomposition of the space of matrices $\mathbb{R}^{N \times N}.$ Observe that the linear subspace $\mathrm{span}\{ \mathrm{id}_{N}\}$ in $\mathbb{R}^{N \times N}$ has, as the orthogonal space, the following null trace matrices:

with respect to the inner product $\langle A, B \rangle_{\mathbb{R}^{N \times N}} = \mathrm{tr}(A^TB).$

Theorem 3.2. Consider $\left(\mathbb{R}^{N \times N}, \|\cdot\|_2\right)$ as a Hilbert space where $N = N_1 \cdots N_d.$ Then, there exists a decomposition

where $\mathfrak{h}_N = \mathrm{span}\{ \mathrm{id}_{N}\}^{\bot}$ is the orthogonal complement of the linear subspace generated by the identity matrix. Moreover,

where $\Delta = \mathfrak{h}_N \cap \mathcal{L}(\mathbb{R}^{N \times N}).$ Furthermore, $\mathcal{L}(\mathbb{R}^{N \times N})^{\bot}$ is a subspace of $\mathfrak{h}_N$ and

Proof. It follows from Lemma 3.1, Theorem 3.1 and Theorem 3.2 in ^[8]. □

The above theorem allows us to compute the projection of matrix $A$ onto $\mathcal{L}(\mathbb{R}^{N \times N})$ as follows. Denote by $\Pi_i$ the orthogonal projection of $\mathbb{R}^{N \times N}$ onto the linear subspace

for $1 \le i \le d.$ Thus, $\sum_{i = 1}^k \Pi_i$ is the orthogonal projection of $\mathbb{R}^{N \times N}$ onto the linear subspace $\Delta.$ In consequence, by using (3.3), we have

If we further analyze (3.4), we observe that the second term on the left is of the form

and that it has only $(N_1^2+\cdots+N_d^2-d)$-degrees of freedom (recall that $\dim \mathrm{span}\{ \mathrm{id}_{N_i}\}^{\bot} = N_i^2 -1).$ In addition, due to the tensor structure of the products, the unknowns $x_l$ of $X_k$ are distributed in the form of a block so that we can calculate which will be the entries of the matrix $A$ that we can approximate. Therefore, to obtain the value of each $x_l,$ we only need to calculate which is the value that best approximates the entries $(i, j)$ of the original matrix that are in the same position as $x_l$.

In our next result, we will see how to carry out this procedure. To do this, we make the following observation. Given a matrix $A = (a_{i, j}) \in \mathbb{R}^{KL \times KL}$ for some integers $K, L > 1,$ we can write $A$ as a matrix block:

where the block $A_{i, j}^{(K, L)} \in \mathbb{R}^{K \times K}$ for $1 \le i, j \le L$ is given by

Moreover,

Observe that $K$ and $L$ can be easily interchanged. To simplify the notation, from now on given $N = N_1N_2\cdots N_d,$ we denote it by $N_{[k]} = N_1 \cdots N_{k-1} N_{k+1} \cdots N_d$ for each $1 \le k \le d.$

Theorem 3.3. Let $A \in \mathbb{R}^{N \times N},$ with $N = N_1 \cdots N_d.$ For each fixed $1 \le k \le d,$ consider the linear function $P_k:\mathbb{R}^{N_k \times N_k} \longrightarrow \mathbb{R}^{N \times N}$ given by

Then, the solution of the minimization problem

is given by

Proof. First, let us observe that $\mathrm{id}_{N_1} \otimes \cdots \otimes \mathrm{id}_{N_k} = \mathrm{id}_{N_1 \cdots N_k};$ so, we can find three different situations in the calculation of the projections:

(1). $P_1(A) = X_1 \otimes \mathrm{id}_{N_{[1]}}$; in this case,

(2). $P_d(X_d) = \mathrm{id}_{N_{[d]}} \otimes X_d$; in this case,

where $O_d$ denotes the zero matrix in $\mathbb{R}^{N_d \times N_d}.$

(3). $P_i(X_i) = \mathrm{id}_{N_1\cdots N_{i-1}} \otimes X_i \otimes \mathrm{id}_{N_{i+1}\cdots N_d}$ for $i = 2, \dots, d-1;$ in this case, for a fixed $2 \le i \le d-1,$ we write $N_{\ell} = N_1\cdots N_{i-1}$ and $N_{r} = N_{i+1}\cdots N_d.$ Thus,

In either case, a difference of the form

must be minimized. To this end, we will consider each case $A$ as a block matrix $A \in \mathbb{R}^{KL \times KL}$ in the form of (3.5).

Case 1: For $P_1(X_1),$ we take $K = N_{[1]}$ and $L = N_1;$ hence,

In this situation, we have

hence, we wish for each $1 \le i \text{ and } j \le N_{1}$ to yield

Thus, it is not difficult to see that

for $1 \le i, j \le N_{1}.$

Case 2: For $P_d(X_d),$ we take $K = N_{d}$ and $L = N_{[d]};$ hence,

Now, we have

Thus, $X_d \in \mathbb{R}^{N_{d} \times N_{d}}$ minimizes $\|A-P_d(X_d)\|_{_{\mathbb{R}^{N \times N}}}^2$ if and only if

In consequence,

Case 3: For $P_i(X_i),$ we take $K = N_iN_{r}$ and $L = N_{\ell};$ hence,

In this case,

so we need to solve the following problem:

Since $X \otimes \mathrm{id}_{N_{r}} \in \mathbb{R}^{N_i \times N_i} \otimes \mathrm{span}\{ \mathrm{id}_{N_{r}}\},$ we can write (3.7) as

Observe that

To simplify the notation, we write $\mathcal{U}: = \mathbb{R}^{N_i \times N_i} \otimes \mathrm{span}\{ \mathrm{id}_{N_{r}}\}$. Then, we have the following orthogonal decomposition, $\mathbb{R}^{N_iN_r \times N_iN_r} = \mathcal{U} \oplus \mathcal{U}^{\bot}.$ Denote by $\Pi_{\mathcal{U}}$ the orthogonal projection onto the linear subspace $\mathcal{U}.$ Then, for each $Z \in \mathcal{U},$ we have

because $(\mathrm{id}-\Pi_{\mathcal{U}})(A_{n, n}^{(K, L)}) \in \mathcal{U}^{\bot}$ and $\Pi_{\mathcal{U}}(A_{n, n}^{(K, L)}) - Z \in \mathcal{U}.$ In consequence, the process of solving (3.8) is equivalent that for solving the following optimization problem:

Thus,

that is, $Z^* = \Pi_{\mathcal{U}}(A^*);$ hence,

Proceeding in a similar way as in Case 1, we obtain

for $1 \le u, v \le N_{i}.$ This concludes the proof of the theorem. □

To conclude, we obtain the following useful corollary.

Corollary 3.4. Let $A \in \mathbb{R}^{N \times N},$ with $N = N_1 \cdots N_d.$ For each fixed $1 \le k \le d,$ consider the linear function $P_k:\mathbb{R}^{N_k \times N_k} \longrightarrow \mathbb{R}^{N \times N}$ given by

For each $1 \le k \le d,$ let $X_k \in \mathbb{R}^{N_k \times N_k}$ be the solution of the optimization problem (3.6). Then,

Proof. Observe that, for $1 \le k \le d,$ the matrix $X_k$ satisfies

where

is a linear subspace of $\mathbb{R}^{N \times N}$ that is linearly isomorphic to $\mathbb{R}^{N_k \times N_K}.$ Since $\mathbb{R}^{N_k \times N_k} = \mathrm{span}\{ \mathrm{id}_{N_k}\} \oplus \mathrm{span}\{ \mathrm{id}_{N_k}\}^{\bot},$ then

hence

We can conclude that $\Pi_k(A) = P_k\left(X_k - \frac{ \mathrm{tr}(X_k)}{N_k} \mathrm{id}_{N_k}\right);$ recall that $\Pi_k$ is the orthogonal projection of $\mathbb{R}^{N \times N}$ onto the linear subspace

From (3.4), the corollary is proved. □

4.   The best Laplacian approximation for the discretization of second-order partial differential equations without mixing derivatives

In this section, we consider the general equation of a generic second-order partial differential equation without mixing derivatives with homogeneous boundary conditions. More precisely, let

We discretize (4.1) with the help of the following derivative approximations:

and

for $i = 1, \dots, N$ and $j = 1, \dots, M.$ From (4.2), we have that $\mathbf{u}(x, y_0) = \mathbf{u}(x, y_{M+1}) = \mathbf{u}(x_0, y) = \mathbf{u}(x_{N+1}, y) = 0$ for all $0 \le x \le 1$ and $0 \le y \le 1.$

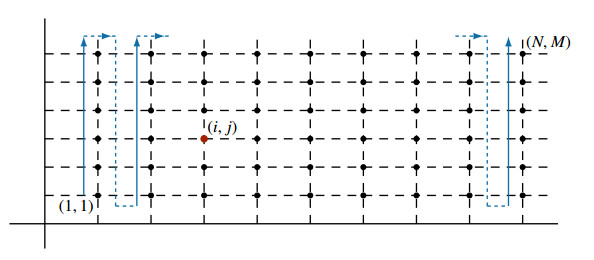
Next, in order to obtain a linear system, we put $\mathbf{u}_{\ell} : = \mathbf{u}(x_i, y_j)$ and $\mathbf{f}_{\ell}: = \mathbf{f}(x_i, y_j),$ where $\ell: = (i-1)M+j$ for $1 \le i \le N$ and $1 \le j \le M.$ In this way, the represented mesh is traversed as shown in Figure 1, and the elements $U = (\mathbf{u}_{\ell})_{\ell = 1}^{MN}$ and $F = \{ \mathbf{f}_{\ell}\}_{\ell = 1}^{MN}$ are column vectors. It allows us to represent (4.1) and (4.2) as the linear system $AF = U$, where $A$ is the $MN \times MN$-block matrix

for $T \in \mathbb{R}^{M \times M},$ given by

and $D_1, D_2 \in \mathbb{R}^{M \times M}$ are the diagonal matrices:

In this case, $\mathrm{tr}(A) = NM(2\mu h^2k^2-4\alpha k^2-4\beta h^2);$ so, instead of looking for $L_A,$ as in (3.10), we will look for $L_{\hat{A}},$ where

has a null trace. Proceeding according to Theorem 3.3 for sizes $N_1 = N$ and $N_2 = M$, we obtain the following decomposition:

and

We remark that $\mathrm{tr}(X_1) = \mathrm{tr}(X_2) = 0.$ Moreover, the residual of the approximation $L_{\hat{A}}$ of $\hat{A}$ is $\| \hat{A} - L_{\hat{A}} \| = 0.$ In consequence, we can write the original matrix $A$ as

Recall that the first term is

hence, $A$ can be written as

where

is an $N \times N$-matrix and

is a $M \times M$-matrix.

Now, we can use this representation of $A$ to implement the GROU Algorithm 1, together with the ALS strategy given by Algorithm 2, to solve the following linear system:

This study can be extended to high-dimensional equations, as occurs in ^[8] with the three-dimensional Poisson equation.

5.   Numerical examples

Next, we are going to consider some particular equations to analyze their numerical behavior. In all cases, the characteristics of the computer used are as follows: 11th Gen Intel$^{(R)}$ Core$^{(TM)}$ i7-11370H @ 3.30GHz, RAM 16 GB, 64-bit operating system; and, Matlab version R2021b ^[13].

5.1.   The Helmholtz equation

Let us consider the particular case of the second-order partial differential equation with $\alpha = \beta = 1$, $\mu = c^2$ and $\mathbf{f} = 0$, that is,

This is the 2D-Helmholtz equation. To obtain the linear system associated with the discrete problem, we need some boundary conditions; for example,

and

This initial value problem has a closed solution for $\omega = \dfrac{c}{\sqrt{2}},$

From the above operations, and by taking $h = k$ for simplicity, we can write the matrix of the discrete linear system associated with the equation of Helmholtz as

or, equivalently,

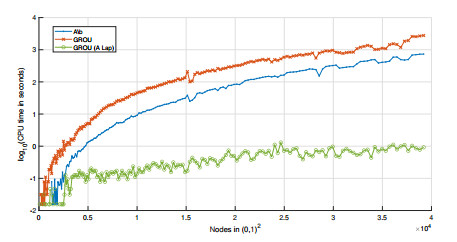
If we solve this linear system $A \mathbf{u}_l = \hat{\mathbf{f}}_{l}$ for the case $c = \sqrt{2}$, $L = T = ,$ and with $N = M$, we obtain the temporary results shown in Figure 2. To carry out this experiment, we have used the following parameter values: for the GROU Algorithm 1: $\texttt{tol} = 2.2204e-16$; $\varepsilon = 2.2204e-16$; $\texttt{rank_max} = 10$; ($\texttt{iter-max} = 5$ and $\varepsilon = 2.2204e-16$ were used to perform Algorithm 2); and, the number of nodes in $(0, 1)^2$ (that is, the number of rows or columns of the matrix $A$) was increased from $10^2$ to $200^2$.

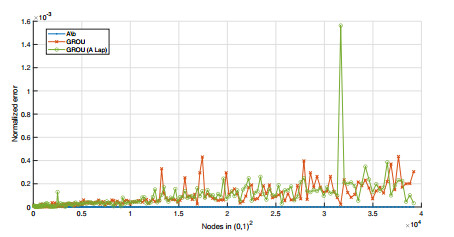
To measure the goodness of the approximations obtained, we calculated the normalized errors, that is, the value of the difference, in absolute value, of the results obtained and the real solution, between the length of the solution, i.e.,

for the different approximations obtained. The values of these errors were of the order of $10^{-4}$ and can be seen in Figure 3.

5.2.   The Swift-Hohenberg equation

Now, let us consider the partial differential equation of order four:

with the boundary conditions

and

For $k = \sqrt{1+\sqrt{\varepsilon-1}}$ $L = 2\pi/k$, the initial value problem (5.1)–(5.3) has the following as a solution:

If we discretize the problem described by (5.1)–(5.3) as in the previous example with the same step size for both variables, $h$, we obtain a linear system of the form $A \mathbf{u}_{l} = \hat{\mathbf{f}}_{l}$, where $A$, in Laplacian-like form, is the matrix

and $l = (i-1)M+j$ is the order established for the indices, with $1 \leq i \leq N$ and $1 \leq j \leq M$.

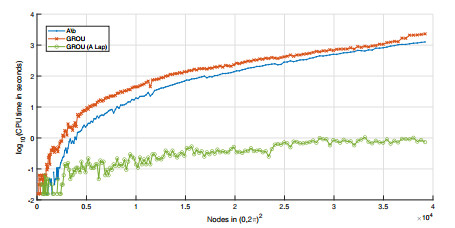
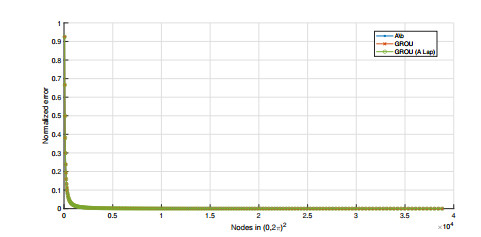
To perform a numerical experiment, we set $\varepsilon = 2$, $L = T = 2\pi$ and the same number of points for the two variables. At this point, we can solve the linear system associated with the Swift-Hohenberg discrete problem by using our tools: the Matlab command $A\backslash b$, the GROU Algorithm 1, and the GROU Algorithm 1, together with the ALS Algorithm 2 with $A$ written in Laplacian-like form. In this case, we used the following parameter values in the algorithms: $\texttt{tol} = 2.2204e-16$; $\varepsilon = 2.2204e-16$; $\texttt{rank_max} = 10$ for the GROU Algorithm 1, with $\texttt{iter-max} = 5$ for the ALS step; and, the number of nodes in $(0, 2\pi)^2$ was increased from $10^2$ to $200^2$. Figure 4 shows the results obtained.

Again, we calculated the normalized errors to estimate the goodness of the approximations, the results of which are shown in Figure 5.

6.   Conclusions

In this work, we have studied the Laplacian decomposition algorithm, which, given any square matrix, calculates its best Laplacian approximation. Furthermore, in Theorem 3.3, we have shown how it is implemented optimally.

For us, the greatest interest in this algorithm lies in the computational improvement of combining it with the GROU Algorithm 1 to solve linear systems through the discretization of a partial derivative equation. Said improvement can be seen in the different numerical examples shown, where we have compared this procedure with the standard resolution of Matlab by means of the instruction $A\backslash b.$

This proposal is a new way of dealing with certain large-scale problems, where classical methods prove to be more inefficient.

Use of AI tools declaration

The authors declare that they have not used artificial intelligence tools in the creation of this article.

Acknowledgments

J. A. Conejero acknowledges funding from grant PID2021-124618NB-C21, funded by MCIN/AEI/ 10.13039/501100011033, and by "ERDF: A way of making Europe", by the "European Union"; M. Mora-Jiménez was supported by the Generalitat Valenciana and the European Social Fund under grant number ACIF/2020/269; A. Falcó was supported by the MICIN grant number RTI2018-093521-B-C32 and Universidad CEU Cardenal Herrera under grant number INDI22/15.

Conflict of interest

The authors declare that they no have conflicts of interest.