1.
Introduction
Rice is a staple food for human consumption, especially Asians. Therefore, the production, consumption, and commerce of rice mostly occur in Asia. However, only 6% of rice is exported, and the remainder is consumed within the country. Unfortunately, sometimes the rice production does not meet the domestic demand since rice plants are infected with diseases. Brown spot disease is quite common that decreases the rice yield. It is caused by the spread of fungus called Bipolaris oryzae (Helminthosporium oryzae Breda de Haan.).
Every stage of the rice plant's life cycle makes it susceptible to numerous plant diseases. Diseases have the potential to lower rice crop production overall and in terms of quality. It is generally recognized that the pathogen can harm plants throughout several phases of storage, seed germination and seedling establishment, growth, and reproductive phase. One of fungal diseases infects rice is brown spot disease. Brown spot disease is a plant disease caused by a fungus that can reduce rice yield from around 4% to 52%. The disease disperses by letting the spore flow along with the wind and falls into the spikelet or seed. Consequently, the rice is damaged. Besides, the disease also leaves spots on rice seeds and causes low yield. In addition, if the infected seed is planted, the paddy field will be infected. The disease can be transmitted through seed and air, which are called seed-borne, and air-borne. Moreover, the fungus can live in the uncared field and poor soil. This means that the disease can invade the paddy field if it is not eradicated. Based on the problem, farmers need to control the disease by applying chemical substance, for example fungicide [1]. However, the chemical affects the environment and humans. Therefore, the strategy of controlling the spreading of disease is necessary.
Fungicide is a chemical that is used to restrain the growth of fungus spores. However, the fungicide not only affects the fungus spores but also affects agriculture products. There are three types of fungicide including: chemical fungicide, botanical fungicide, and biocontrol fungicide [8]. Since the chemical fungicide affects the environment and is poisonous to humans, fungicide containing natural extract such as botanical and biocontrol fungicide should be used. In the sense of fungus elimination, the botanical fungicide has higher performance than biocontrol fungicide. The mathematical model is a tool that can describe the spreading of disease that leads to the disease control strategy [9,10,11,12]. For example, the epidemiology mathematical model which considers the botanical fungicide is developed for controlling plant disease and preventive treatments of plants [7,13].
The SIR model [18,19,20], which has three compartment subclasses: susceptible, infected, and removed, is the general form of the epidemiological model. Mckendrick [21] proposed a fundamental model of SIR transmission in 1927. Song and Takeuchi used natural birth and death rates to study population dynamics. The plant population is separated into five compartments: susceptible, exposed, infected, post-infectious (removed), and protected with curative and preventive therapy, according to a mathematical model created and examined by Savary et al. [22]. The SIP model, or maize plant disease model, was presented by Windarto et al. [4].
In SIX model [2] studies the dynamics of susceptible plant population infected plant population pathogen population which in the actual situation that plants must be protected from fungus. This research selected the SIX model as a base for development using the real situation. Then, SIXP model was developed to match the situation we are interested in by adding protected plant populations denoted by P. After that, we analyzed the stability of the model developed for leaf brown spot disease with a standard incidence rate [15]. Then, we discussed the optimal control of fungicide to prevent the spread. Some numerical examples compare SIX model and SIXP model.
2.
Materials and methods
The proposed model is particularly well suited for describing diseases such as two infections in leaf brown spot disease and analysis the proposed model.
2.1. The proposed model
The proposed model is developed based on the SIX model [2], which is the mathematical model of the spreading of leaf brown spot disease in rice. We consider the effect of leaf brown spot disease on the rice population dynamics and add the rice population stage that are retreated with the botanical fungicide to protect them from the disease.
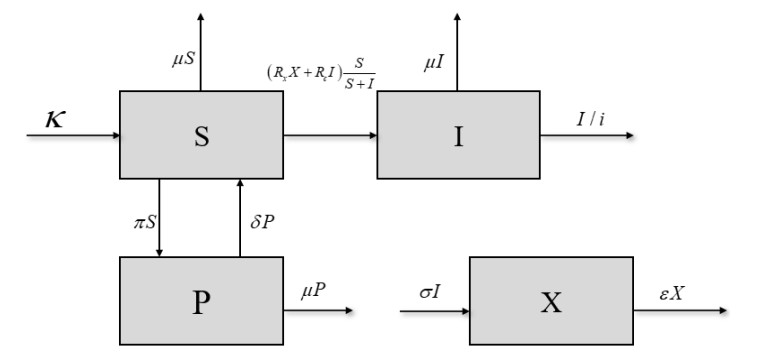
In this model, there are two types of population including plant population and pathogen population X. The plant population is classified into three categories: susceptible plant populations S, infected plant populations I, and protected plant populations P. The interaction between all populations is shown in Figure 1.
The compartment model can be written as the following system:
The feasible region of the system in Eqs (1)–(4) is
The parameters in Eqs (1)–(4) are positive. The meaning of the parameters is presented in Table 1.
2.2. Analysis of the model
The proposed model gives two equilibrium points, namely pathogen-free equilibrium (E0) and pathogen equilibrium (E1). The notation of pathogen-free equilibrium point is expressed by
Another equilibrium point is E1(S∗c,I∗c,X∗c,P∗c), which is pathogen equilibrium, where
2.2.1. Basic reproduction number
The basic reproduction number (R0) is the number of secondarily infected plants that infect from only one initial infected plant. The value of R0 can calculates by the technique of Van Den Driessche and Watmough [16]
The dominant eigen value gives us R0,
2.2.2. Stability analysis
The systems of equations from model could determine the stability of their equilibrium points.
By substituting all parameters in the systems and found all equilibrium points. Then, linearizing the system at each equilibrium point and considering the stability of the system at the point.
Theorem 2.1. The pathogen-free equilibrium E0(κ(δ+μ)μ(δ+μ+π),0,0,κπμ(δ+μ+π)) of the system (1)–(4) is locally asymptotically stable when the basic reproduction number is less than one, and otherwise is unstable.
Proof. To show that the system of Eqs (1)–(4) is locally asymptotically stable, the Jacobian matrix is used to evaluate the pathogen-free equilibrium E0 as shown by
The eigenvalues of J(E0) are obtained by solving det(J(E0)−λI)=0. We receive the eigenvalues of J(E0) from the following characteristic equation
where
The eigenvalues of the Jacobian matrix for the pathogen-free equilibrium can be computed as
It is obvious that all these eigenvalues are negative when ε > Rc.
By using the Routh-Hurwitz theorem [17], all eigenvalues are negative or complex eigenvalues with negative real part if and only if R0=(Rxσi+Rcεi)ε(1+μi)<1. Thus, the pathogen-free equilibrium point is locally asymptotically stable when the basic reproduction number is less than one.
Global stability of pathogen-free equilibrium is present in Theorem 2.2.
Theorem 2.2. The pathogen-free equilibrium E0 is globally asymptotically stable if R0>1, when I=0.
Proof. Let V is the Lyapunov function defined by
where, g(x)=x−1−lnx, which is positive function. Since I = 0, X = 0 then V≥0. We want to clarify that V is a positive function on the domain Ω.
The derivative of V respect to time evaluated at the solution of model in Eqs (1)–(4) is derived by
From the relation between arithmetic and geometric means 2−S0S−SS0<0.
Considering the second term, in the case that R0 = 1, we have ˙V<0 if and only if I = 0.
From Eq (3), I(t)=0 causes X→0 as t→∞. Then, by using X(t) = 0 in Eq (1), we find S(t)→κ(δ+μ)μ(δ+μ+π) as t→∞.
In addition, when R0<1, we obtain ˙V<0 if and only if
or I=0, which is the largest compact invariant set of Eqs (1)–(4). Then, by using LaSalle's invariant principle, we can conclude that every solution of the mathematical model in Eqs (1)–(4) with an initial value in Ω tends to the pathogen-free equilibrium.
The stability of the pathogen equilibrium is presented in Theorem 3.
Theorem 2.3. If R0>1, the pathogen equilibrium E1 is locally asymptotic stable
Proof. Let J(E1) be the Jacobian matrix in Eqs (1)–(4) derived from the pathogen equilibrium E1 is expressed by
and
where
Eigenvalues of J(E1) satisfy the following characteristic equation
where
where
The eigenvalues have a negative real part, so the equilibrium point is stable with the conditions below:
which are related to the condition of Routh Hurwitz. Thus, the pathogen equilibrium point is stable when R0=(Rxσi+Rcεi)ε(1+μi)>1.
At endemic equilibrium point [14] in theorem we use of compound matrix theorem in order to address dynamics stability issues that arose from the solution of nonlinear differential equations.
Theorem 2.4. Assume that R0>1 and ε > Rc, the pathogen equilibrium E1 is globally asymptotic stable.
Proof. We prove the global asymptotic stability of the model (1)–(4) with endemic equilibrium point, we consider the non-linear equations in the model (1)–(4) for which the Jacobian matrix at disease-endemic equilibrium points is:
Furthermore, the general form of third additive compound matrix J|1|, is given by
where
From matrices (9) and (10) implies that
where
Consider P(χ)=diag{P(t),X(t),I(t),S(t)}, the inverse of P(χ) is given as
the derivative with respect to time is
while
and
So that
From the system of equation, we obtain
Now, consequently we are to find ˉhi(t),i=1,2,3,4, by assuming that Mij are the entries of matrix M, such that
Now, in R4 we assume a vector (m1,m2,m3,m4). The Lozinskii measure l(M) is defined as l(M)=ˉhi(t), i=1,2,3,4. The integration of the Lozinskii measure l(M) and taking the limits as t→∞ lead to the following equations.
Now, the combination of inequalities from Eqs (12)–(15) and by the assumption ε > Rc, we can assert that
The system containing only four non-linear equations of model Eqs (1)–(4) is globally asymptotically stable around its interior equilibrium (S∗c,I∗c,X∗c,P∗c).
2.3. Sensitivity analysis
The basic parameters are carried on the sensitivity analysis. They are checked and identified the parameter that can impact the basic reproduction number. The sensitivity analysis is informed that each parameter's significance is disease transmission for control the spread of brown disease on leaf brown disease. The explicit expression of R0 is given by
Definition 2.1. The normalized forward sensitivity index of a variable, u, that depends differentiable on a parameter, p, is defined as:
The sensitivity indices of the basic reproductive number calculate by used parameters of endemic equilibrium point that are shown in Table 2 [2].
To consider the relationship between the primary infection (Rx) and the rate of and death rate of pathogen (ε), it was found that the basic reproductive number will increase when Rx increased at the tiny ε as shown in Figure 2a.
To consider the relationship between the rate of secondary infection (Rc) and the growth rate of pathogen (σ), it was found that the basic reproductive number will increase when Rc and σ increased as shown in Figure 2b.
To consider the relationship between the rate of secondary infection (Rc) and the primary infection (Rx), it was found that the basic reproductive number will increase when Rc increases. Despite the increase of Rx, the value of R0 marginally increased as shown in Figure 2c.
To consider the relationship between the natural death rate (μ) and rate of secondary infection (Rc), it was found that the basic reproductive number will increase when Rc and increased at the tiny μ as shown in Figure 2d.
2.4. Optimal control proble
The spreading of leaf brown spot disease is controlled by using the botanical fungicide. The goal is to decrease the amount of infected rice. Therefore, Pontryagin's principle, shown below, is used to control the number of rice [5,8,10]:
Where tf is the final time, A0 is balancing constant coefficients of the infected plant while A1 is weight coefficients for control measure and variable u(t) is the control variable of the preventive treatment. With the objective function J(u). The goal is to find the optimal control u∗(t) such that:
The state variable for the model
and the constraint:
The system should satisfy the condition:
We define Hamiltonian function as H=f(x,u,t)+λ'g(x,u,t), which equivalent to:
where λ1(t),λ2(t),λ3(t),λ4(t) are the co-state variable or the Lagrange multiplier of the optimization problem. The necessary conditions that an optimal control is archived, it must satisfy the following Pontryagin's principle:
● State equation:
● Co-state equation:
● Transversality conditions:
for t0≤t≤tf
● Stationer condition
then
Since 0≤u(t)≤1, then we get:
as the optimal control of the system.
3.
Results
In this section, we present some numerical simulations to ensure the analytic results by considering the pathogen-free and pathogen condition. For simulation that uses pathogen-free situation, the initial conditions using for calculation are denoted as S(0) = 200, I(0) = 400, X(0) = 400, P(0) = 0 and ε > Rc. Here, the proposed model is simulated from initial time to 140 days. The models were simulated by RK4 method with step size 0.01 which guaranteed the stability of the numerical solutions. The parameters and initial data in each case of simulation were shown in Table 3. There were two results of the simulation. The first results showed the dynamic model for pathogen-free. The second results showed dynamics model for the pathogen, was shown in Figures 3 and 4 respectively.
In case of the disease-free condition, the basic reproductive number is not greater than one that gives the disease-free equilibrium (E0), which is local asymptotically stable. The model is used the basic reproductive number about 0.8684. The simulation was shown the number of infectious, pathogen and susceptible sites decreased but the protected plant increased. The solution converges to the disease-free state, which means the infection and pathogen tend to zero when there is appropriate time as shown in Figure 3.
The model is used the basic reproductive number about 2.0236 in case of endemic condition, which is greater than one. So, it leads to the endemic equilibrium (E1) giving the global asymptotically stable when R0 is greater than 1. The simulation was shown that the infectious, pathogen and susceptible sites converged to the endemic equilibrium steady state when there is a suitable long time while the number of the protected plant increased. The solution curve tends to the endemic equilibrium as shown in Figure 4.
In Figures 5 and 6, the result of susceptible plant with control is lower than that without control because the susceptible site is moved to the protected site as shown in Figure 5. In the same way, the result of infected plant with control is lower than in case of without control because the infected site was protected by botanical fungicide as shown in Figure 6. Therefore, these results can be interpreted that the botanical fungicide can reduce the spread of leaf brown spot disease.
In Figure 7 show the proportion of fungicide used to protect plant from fungi. Here we choose A0=2,A1=5 using optimal control requires to maintain the control at 100% for 119 days before dropping to its lower bound. it appears that in the presence of fungicide control, susceptible plant and protected plant will grow more than without fungicide control.
4.
Discussion
In this paper, we have presented and analyzed a differential system of the SIXP model. The model has two equilibrium points. The disease-free equilibrium (E0) and endemic equilibrium (E1). It is found that R0<1 the disease-free equilibrium is locally asymptotically stable as guaranteed by Theorem 2.1. The Lyapunov function theory is used for disease-free equilibrium that is globally asymptotically stable if R0<1 the as guaranteed by Theorem 2.2. The epidemic equilibrium of the model is locally asymptotically stable when R0>1 as guaranteed by Theorem 2.3. The Lozinskii measure and additive compound Metrix Theorem is used to address dynamics stability issues that arose from the solution of nonlinear differential equations. If R0>1, the endemic equilibrium is globally asymptotic stable as guaranteed by Theorem 2.4.
5.
Conclusions
As a result, we discovered that the numerical simulation results verified the analytical findings of the propagation of the leaf brown spot disease in rice with standard incidence rate. The occurrence of brown spot illnesses in rice can be represented by the developed model. The endemic equilibrium and the disease-free equilibrium are the two equilibrium points in the SIXP models. Constructing a suitable Lyapunov function is observed that the global asymptotic stability of the disease-free equilibrium depends on the basic reproduction number (R0). If R0<1 the, then the endemic equilibrium is globally asymptotically stable by using the estimate of the Lozinskii measure applied to the systems. The sensitivity indices of the reproductive number and endemic equilibrium are determined and optimal control strategy. Parameters in the model illustrate that to reduce the spreading of leaf brown spot disease, the parameters Rc, Rx, i, σ must be reduced. In practice, botanical fungicide is one factor that can reduce the value of Rc, Rx, i, σ. The control plots we developed indicate that the site of susceptible and infected decreased in the optimality system. The results show that the modified model by considering the botanical fungicide can reduce the spreading of leaf brown spot disease. In addition, the numerical simulations were also to support the theoretical hypothesis and approach epidemic control. The study results suggest that the botanical fungicide can reduce the spreading of leaf brown spot disease.
Acknowledgments
The authors would like to express their gratitude to King Mongkut's University of Technology Thonburi, Thailand, for funding this research, the Science Achievement Scholarship of Thailand, Thailand Science Research and Innovation (TSRI) Basic Research Fund: Fiscal year 2022, and Ubon Ratchathani Rajabhat University, Thailand for supporting this research.
Conflict of interest
The authors declare no conflicts of interest.









 DownLoad:
DownLoad:











