Neighbor sum distinguishing total choice number of IC-planar graphs with restrictive conditions

1.   Introduction

Only simple graphs are considered in the paper. For any graph theory notation undefined here we follow ^[1].

Let $G = \big(V(G), E(G)\big)$ be a simple graph. For a vertex $u\in V(G)$, we denote the set of edges incident with $u$ by $E_{G}(u)$. The degree and the neighborhood of $u$ are denoted by $d_G(u)$ and $N_G(u)$, respectively. We use $\delta(G)$ and $\Delta(G)$ (or $\Delta$) to represent the minimum degree and the maximum degree of $G$, respectively.

Let $k\geq0$ be an integer and $T(G) = V(G)\cup E(G)$. A neighbor sum distinguishing (NSD) total coloring of $G$ is a mapping $\phi: T(G)\rightarrow \{1, 2, \cdots, k\}$ such that for any two adjacent or incident elements $z_{1}, z_{2}\in T(G)$, $\phi(z_{1})\neq \phi(z_{2})$ and for every edge $uv\in E(G)$, $\sum_{z\in E_{G}(u)\cup\{u\}}\phi(z)\neq\sum_{z\in E_{G}(v)\cup\{v\}}\phi(z)$. The NSD total chromatic number of $G$ is $\chi^{t}_{\Sigma}(G) = \min\{k\; |\mbox{ $G$ has an NSD $k$ -total coloring}\}$. In 2015, Pilśniak and Woźniak ^[2] introduced an important conjecture about the NSD total chromatic number as follows.

Conjecture 1.1. ^[2] For every graph $G$, $\chi^{t}_{\Sigma}(G)\leq \Delta(G)+3$.

Conjecture 1.1 was proved to hold for many special classes of graphs, such as complete graphs, bipartite graphs, subcubic graphs ^[2], planar graphs with $\Delta\geq10$ ^[3] and planar graphs with $\Delta\geq7$ but without five cycles ^[4] and so on.

In 2008, Alberson ^[5] introduced the concept of IC-planar graphs. A graph is called an IC-planar graph if the graph has a drawing in the plane such that each edge is crossed at most once and two pairs of crossing edges share no common end vertex.

Conjecture 1.1 also holds for some special IC-planar graphs, such as IC-planar graphs with $\Delta\geq12$ ^[6], IC-planar graphs with $\Delta\geq7$ but without triangles ^[7] and IC-planar graphs with $\Delta\geq10$ but without adjacent triangles ^[8].

A mapping $L$ of $G$ is called a $k$-list total assignment of $G$ if it assigns to each member $z\in T(G)$ a set $L(z)$ with $|L(z)| = k$. For a $k$-list total assignment $L$ of $G$, a mapping $\phi$ is called an NSD total $L$-coloring of $G$ if the $\phi$ is an NSD total coloring of $G$ and for each $z\in T(G)$, $\phi(z)\in L(z)$. The NSD total choice number of $G$ is $\rm{ch}_{\Sigma}^t(G) = \min\{k\; |\mbox{ $G$ has an NSD total $L$ -coloring for any $k$ -list total assignment $L$ }\}$.

Accordingly, the list version of Conjecture 1.1 is as follows.

Conjecture 1.2. ^[2] For every graph $G$, $\rm{ch}^{t}_{\Sigma}(G)\leq \Delta(G)+3$.

Obviously, Conjecture 1.2 implies Conjecture 1.1. Conjecture 1.2 was also shown to hold for many special classes of graphs, such as subcubic graphs ^[9,10], planar graphs with $\Delta\geq 13$ ^[11], planar graphs with $\Delta\geq 8$ but without adjacent triangles ^[12] and IC-planar graphs with $\Delta\geq 14$ ^[13] and so on. Zhang ^[14] considered any IC-planar graph without five cycles and obtained the following result.

Theorem 1.1. ^[14] For every IC-planar graph $G$ without five cycles,

There are many results of neighbor distinguishing coloring. However given this kind of result the case of a small $\Delta$ is interesting and difficult. For the results in this regard, see ^[9,10,15,16].

In this paper, we improve the result of Zhang ^[14] and obtain Theorem 1.2 as follows.

Theorem 1.2. Let $G$ be an IC-planar graph without five cycles. Then

2.   Preliminaries

Let $G$ be a simple graph. A vertex $u$ of $G$ is called an $\ell$-vertex ($\ell^{+}$-vertex, $\ell^{-}$-vertex) if $d_{G}(u) = \ell$ ($d_{G}(u)\geq\ell$, $d_{G}(u)\leq\ell$). We denote the number of $\ell$-vertex ($\ell^{+}$-vertex, $\ell^{-}$-vertex) adjacent to $u$ by $n_{G}^{\ell}(u)$ ($n_{G}^{\ell^{+}}(u)$, $n_{G}^{\ell^{-}}(u)$). A cycle of length $t$ (at least $t$, at most $t$) is called a $t$-cycle ($t^{+}$-cycle, $t^{-}$-cycle). In particular, a $(d_G(v_1), d_G(v_2), d_G(v_3))$-cycle is a $3$-cycle $v_1v_2v_3v_1$ when $d_G(v_1)\leq d_G(v_2)\leq d_G(v_3)$. Let $X$ be a subset of $T(G)$ and $\psi: X\rightarrow \mathbb{R}$ be a mapping. For every $u\in V(G)$, set

For any $k$-list total assignment $L$ of $G$ and every $z\in T(G)$, set

Lemma 2.1. ^[17] For an arbitrary field $\mathbb{F}$, let $P = P(x_{1}, \cdots, x_{n})$ be a polynomial in $\mathbb{F}[x_{1}, \dots, x_{n}]$ with degree $\deg(P) = \sum_{k = 1}^{n}i_{k}$, where $i_{k}\geq0$ is an integer. Assume that $c_{P}(x_{1}^{i_{1}}, \cdots, x_{n}^{i_{n}})$ is the coefficient of the monomial $x_{1}^{i_{1}}\dots x_{n}^{i_{n}}$ in $P$. If $S_{1}, \dots, S_{n}$ are subsets of \ $\mathbb{F}$ with $|S_{k}| > i_{k}$ and $c_{P}(x_{1}^{i_{1}}, \cdots, x_{n}^{i_{n}})\neq0$, then there are $s_{1}\in S_{1}, \dots, s_{n}\in S_{n}$ satisfying $P(s_{1}, \dots, s_{n})\neq 0$.

For finite real number sets $S_1, \cdots, S_m$, set

Lemma 2.2. ^[18] Let $m\ge 2$ be an integer and $S_1, \cdots, S_m$ be $m$ finite real number sets with $|S_i| = n_i$ and $n_1\ge \cdots \ge n_m.$ Set

If $n'_m > 0$, then

3.   Proof of Theorem 1.2

3.1.   Unavoidable configurations

Let $G$ be a counterexample to Theorem 1.2 with $E(G)$ being minimal. Set $k = \max\{\Delta(G)+3, 13\}$. Let $u$ be a $4^{-}$-vertex of $G$. For any $k$-list total assignment $L$, if $T(G)\setminus\{u\}$ exists a total coloring $\phi'$ such that for any adjacent or incident elements $z_1, z_2 \in T(G)\setminus\{u\}$, $\phi'(v_1)\neq\phi'(v_2)$; for any two adjacent vertices $v_{1}, v_2 \in V(G)\setminus\{u\}$, $m_{\phi'}(v_1)\neq m_{\phi'}(v_2)$ and for each $z \in T(G)\setminus\{u\}$, $\phi'(z)\in L(z)$, then there is a color in $L(u)$ to color $u$ so that the resulting coloring $\phi$ obtained from $\phi'$ is an NSD total $L$-coloring of $G$ since $|S_{\phi'}(u)|\geq k-2d_{G}(u)\geq5 > d_{G}(u)$, a contradiction. Thus, we will omit the colors of all $4^{-}$-vertices in the process of constructing an NSD total $L$-coloring of $G$ in the following.

Below, we discuss some local configurations of the counterexample $G$. Theorem 1.1 implies Claim 3.1.

Claim 3.1. $\Delta(G)\leq10$.

Claim 3.2. Let $u$ be an $\ell$-vertex of $G$. Then each one of the following statements holds.

(1) $n_{G}^{5^{-}}(u) = 0$ when $\ell\leq5$.

(2) $n_{G}^{4^{-}}(u)\leq\ell-6$ when $6\leq\ell\leq7$.

(3) $n_{G}^{3^{-}}(u)\leq\ell-6$ when $8\leq\ell\leq9$, furthermore, $n_{G}^{4^{-}}(u)\leq\ell-6$ when $n_{G}^{3^{-}}(u)\geq1$.

Proof. (1) Suppose to be contrary that the $5^-$-vertex $u$ is adjacent to one $5^-$-vertex $v$. Without loss of generality, set $d_{G}(u) = d_{G}(v) = 5$. For any $k$-list total assignment $L$ of $G$, $G'$ has an NSD total $L'$-coloring $\phi'$, where $G' = G-uv$ and $L'$ is the restriction of $L$ on $G'$. By erasing the colors on $u$ and $v$ from the coloring $\phi'$, we obtain the coloring $\phi''$. Then

Let $\phi$ be a mapping on $T(G)$ with $\phi(u) = x_1, \phi(v) = x_2, \phi(uv) = y_1$ and $\phi(z) = \phi''(z)$ for every $z\in T(G)\setminus\{u, v, uv\}$, and set

Then $\deg(P) = 12.$ Set

Then $\deg(P_{0}) = \deg(P) = 12$ and $c_{P}(P_{0}) = -20$ via MATHEMATICA. By Lemma 2.1, there are $s_{1}\in S_{\phi}(u), s_{2}\in S_{\phi}(v)$ and $s_{3}\in S_{\phi}(uv)$ such that $P(s_1, s_2, s_{3})\neq0$. Thus we can obtain an NSD total $L$-coloring $\phi$ of $G$ with $\phi(u) = s_1, \phi(v) = s_2, \phi(uv) = s_3$ and $\phi(z) = \phi''(z)$, a contradiction.

(2) and (3) Set $N_G^{4^{-}}(u) = \{v_1, \dots, v_{i}\}$ with $d_G(v_1)\leq \cdots \leq d_G(v_{i})\leq4$. Obviously, (2) and (3) hold when $N_G^{4^{-}}(u) = \emptyset$. Below, let $N_G^{4^{-}}(u)\neq\emptyset$. Set $G_{i}' = G-\{uv_1, \dots, uv_{i}\}$. For any $k$-list total assignment $L$ of $G$, $G_{i}'$ has an NSD total $L'$-coloring $\phi_{i}'$, where $L'$ is the restriction of $L$ on $G_{i}'$. By erasing the colors on $u, v_1, \dots, v_{i}$ from the coloring $\phi_{i}'$, we obtain the coloring $\phi_{i}''$. Then

Suppose that (2) is false. Note that $6\leq\ell\leq7.$ Fix $i = \ell-5$. Then

By lemma 2.2, we have

Suppose that (3) is false. Note that $8\leq\ell\leq9$. Fix $i = \ell-5$. Then $d_G(v_1)\leq3$ and

By lemma 2.2, we have

Under each of the above two assumptions, there are $s_1\in S_{\phi_i''}(u)$ to color $u$ and $s_{j+1}\in S_{\phi_i''}(uv_j)$ ($1\leq j\leq i$) to color $uv_j$ such that the resulting coloring $\phi$ obtained from $\phi_i''$ satisfies $m_{\phi}(u)\neq m_{\phi}(z)$ for each $z\in N_{G}(u)\setminus\{v_1, \dots, v_i\}$. Since $v_1, \dots, v_i$ are $4^-$-vertices, $\phi$ is an NSD total $L$-coloring of $G$, a contradiction.

With the similar proof to that of Claim 3.2 (1), we can obtain the below Claim 3.3.

Claim 3.3. Let $C$ be an $(\ell_1, \ell_2, \ell_3)$-cycle of $G$. Then $(\ell_1, \ell_2, \ell_3)\neq(5^{-}, 6^{-}, 6^{-})$.

Let $H$ be a graph obtained from $G$ by deleting all $2^-$-vertices. For each vertex $u\in V(H)$, we have

By Claim 3.2, the following Claim 3.4 is immediate.

Claim 3.4. Let $u$ be an $\ell$-vertex of $H$. Then each of the following statements holds.

$\rm(1)$ $\ell\geq 3$.

$\rm(2)$ $\ell = d_{G}(u)$ when $3\leq d_{G}(u)\leq 6$.

$\rm(3)$ $\ell\geq6$ when $d_{G}(u)\geq 7$.

$\rm(4)$ $n_{H}^{3}(u)+n_{H}^{4}(u)\leq\ell-6$ when $6\leq\ell\leq7$.

$\rm(5)$ $n_{H}^{3}(u)\leq\ell-6$ when $8\leq\ell\leq9$.

By Claims 3.2 and 3.3, we can directly obtain the below Claim 3.5.

Claim 3.5. Let $C$ be an $(\ell_1, \ell_2, \ell_3)$-cycle of $H$. Then

On a planar graph, if the boundary of a face is a $t$-cycle (resp., $t^+$-cycle, $t^-$-cycle, $(\ell_1, \ell_2, \ell_3)$-cycle), then the face is called a $t$-face (resp., $t^{+}$-face, $t^{-}$-face, $(\ell_1, \ell_2, \ell_3)$-face). A $3$-face with vertex set $\{v_1, v_2, v_3\}$ is denoted by $[v_1v_2v_3]$. A face is said to be incident with the vertices and edges in its boundary.

Through the rest, we assume that the counterexample $G$ is embedded on a plane with every edge crossed by at most one other edge and the minimal crossings. By turning all crossings of $G$ into new 4-vertices on the plane, we obtain a plane graph $G^{\times}$ called the associated plane graph of $G$. To make a difference, we call a vertex $u$ false vertex if $u\in V(G^{\times})\setminus V(G)$ and real vertex otherwise in $G^{\times}$. A face is called false face if it is incident with a false vertex and real face otherwise in $G^{\times}$.

Let $H^{\times}$ be the associated plane graph of $H$. For a vertex $u\in V(H)$, set

The follwing Claim 3.6 is immediate as $G$ (and thus $H$) is an IC-planar graph without 5-cycles.

Claim 3.6. Let $u$ be a real vertex of $H^{\times}$ with $d_{H^{\times}}(u)\geq4$. Then each of the following statements holds.

$\rm(1)$ $0\leq f_{\times}(u)\leq2$.

$\rm(2)$ $f_{t}(u)\leq\lfloor\frac{2d_{H^{\times}}(u)}{3}\rfloor$ if $u$ is not adjacent to any false $4$-vertex.

$\rm(3)$ $f_{t}(u)\leq\lfloor\frac{2d_{H^{\times}}(u)-3}{3}\rfloor$ if $u$ is adjacent to one false $4$-vertex and $d_{H^{\times}}(u)\in\{0, 2\}(\bmod3)$.

$\rm(4)$ $f_{t}(u)\leq\lfloor\frac{2d_{H^{\times}}(u)-3}{3}\rfloor$ if $f_{\times}(u) = 2$ and $d_{H^{\times}}(u)\equiv1(\bmod3)$; $f_{t}(u)\leq\lfloor\frac{2d_{H^{\times}}(u)-6}{3}\rfloor$ if $f_{\times}(u) = 2$ and $d_{H^{\times}}(u)\in\{0, 2\}(\bmod3)$.

$\rm(5)$ $f_{t}(u)\leq\lfloor\frac{2d_{H^{\times}}(u)-4}{3}\rfloor$ if $u$ is adjacent to one $4$-cycle in $H$.

Set

Claim 3.7. Let $f$ be a false $t$-face of $H^{\times}$. Then $n_{4^{\times}}(f)\leq\lfloor\frac{t}{3}\rfloor$.

3.2.   Discharging process

Let $\omega(H^{\times})$ be the number of connected components of $H^{\times}$. For every member $z\in V(H^{\times})\cup F(H^{\times})$, assign the weight $w(z) = d_{H^{\times}}(z)-4$. By Euler's formula, we have

In the following, we will apply the discharging method on $H^{\times}$ to prove that $H^{\times}$ (and thus $H$) does not exist. And so $G$ does not exist. To redistribute weights among vertices and faces, and keep the total weights unchanged, we design the discharging rules are as follows:

(R1) Every real $3$-vertex receives $\frac{1}{3}$ from its each neighbor.

(R2) Every false $3$-face receives $1$ from its incident false $4$-vertex.

(R3) Let $[v_{1}v_{2}v_{3}]$ be a real $(\ell_1, \ell_2, \ell_3)$-face in $H^{\times}$.

(R3.1) If $(\ell_1, \ell_2, \ell_3) = (3, 7^{+}, 7^{+})$ or $(4, 7^{+}, 7^{+})$, then $[v_{1}v_{2}v_{3}]$ receives $\frac{1}{2}$ from every incident real $7^{+}$-vertex.

(R3.2) If $(\ell_1, \ell_2, \ell_3) = (5^{+}, 6^{+}, 6^{+})$, then $[v_{1}v_{2}v_{3}]$ receives $\frac{1}{3}$ from every incident real $5^{+}$-vertex.

(R4) Every false $4$-vertex receives $1$ from its incident false $5^+$-face.

(R5) Let $z$ be a false $4$-vertex and $x$ be a neighbor of $z$ in $H^{\times}$.

(R5.1) Set $d_{H^{\times}}(x) = 6$. Then $z$ receives $2-\frac{1}{3}f_{t}(x)$.

(R5.2) Set $d_{H^{\times}}(x) = 7$. Then $z$ receives $\frac{8}{3}-\frac{1}{3}(f_{t}(x)+n_{H^{\times}}^{3}(x)).$

(R5.3) Set $d_{H^{\times}}(x) = 8$. Then $z$ receives $4-\frac{1}{2}f_{t}(x)-\frac{1}{3}n_{H^{\times}}^{3}(x)$.

(R5.4) Set $d_{H^{\times}}(x) = 9$. Then $z$ receives $5-\frac{1}{2}f_{t}(x)-\frac{1}{3}n_{H^{\times}}^{3}(x)$.

(R5.5) Set $d_{H^{\times}}(x) = 10$. Then $z$ receives $6-\max\{\frac{1}{2}f_{t}(x)+\frac{1}{3}n_{H^{\times}}^{3}(x)|\; f_{t}(z)\leq 6\; \mbox{and}f_{t}(x)+n_{H^{\times}}^{3}(x)\leq12\}$.

After redistributing weights by the discharging rules, we denote the new weight for each $z\in V(H^{\times})\cup F(H^{\times})$ by $w'(z)$. Since the total weights keep unchanged, we have

Thus, there is a nonempty set $Y\subseteq (V(H^{\times})\cup F(H^{\times}))$ such that for every element $z\in Y$, we have

In the following, we will prove that such $Y$ does not exist to obtain a contradiction.

Firstly, we choose arbitrarily an element $z$ from $F(H^{\times})$. If $z$ is a false $3$-face, then $w'(z) = 3-4+1 = 0$ by (R2) since each false $3$-face is incident with a false $4$-vertex. If $z$ is a real $3$-face, then $z$ is an $(\ell_1, \ell_2, \ell_3)$-face with $(\ell_1, \ell_2, \ell_3)\in\{(3, 7^{+}, 7^{+}), (4, 7^{+}, 7^{+}), (5^{+}, 6^{+}, 6^{+})\}$. Thus, by (R3), it is easy to verify $w'(z)\geq0$. If $z$ is a real $4^+$-face or a false $4$-face, then $w'(z)\geq0$ since no rule is applied to it. If $z$ is a false $t^+$-face with $t\geq5$, then $w'(z)\geq t-4-\lfloor\frac{t}{3}\rfloor\geq0$ by (R4) and Claim 3.7. Thus the nonempty set $Y\cap F(H^{\times}) = \emptyset.$

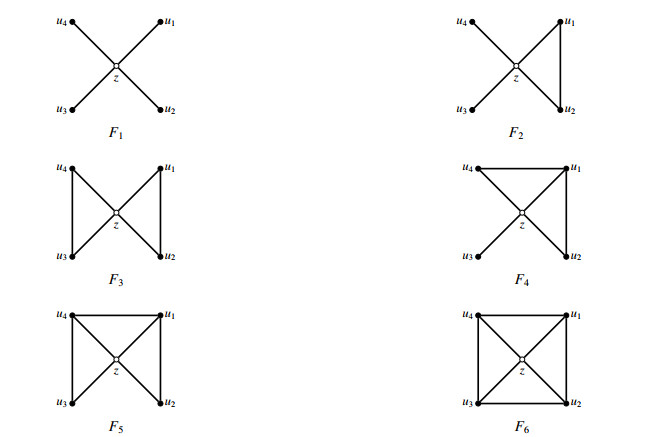
Next, we pick arbitrarily a false $4$-vertex $z$ from $V(H^{\times})\setminus V(H).$ Set $N_{H^{\times}}(z) = \{u_{1}, u_{2}, u_{3}, u_{4}\}$. Then, up to isomorphism, the configuration of the induced subgraph $H^{\times}[\{z\}\cup N_{H^{\times}}(z)]$ is one of six configurations in Figure 1. Note that $z$ is adjacent to at least two real $6^{+}$-vertices by Claims 3.2 and 3.4.

$(1)$ Let the configuration of $H^{\times}[\{z\}\cup N_{H^{\times}}(z)]$ be $F_{1}$ in Figure 1. Since $H$ is an IC-planar graph without $5$-cycles, $z$ is incident with at least two false $5^+$-faces in $H^{\times}$. Thus, $w'(z)\geq4-4+2-2\cdot\frac{1}{3} = \frac{4}{3} > 0$ by (R1) as $z$ is adjacent to at most two real $3$-vertices in $H^{\times}$.

$(2)$ Let the configuration of $H^{\times}[\{z\}\cup N_{H^{\times}}(z)]$ be $F_{2}$ in Figure 1. Since $H$ is an IC-planar graph without $5$-cycles, $z$ is incident with at least one false $5^+$-face $H^{\times}$. Thus, $w'(z)\geq4-4+1+2\times\min\{2-\frac{1}{3}\times3, \frac{8}{3}-\frac{1}{3}\times5, 4-\frac{1}{2}\times4-\frac{1}{3}\times2, 5-\frac{1}{2}\times5-\frac{1}{3}\times3, 6-\frac{1}{2}\times6-6\cdot\frac{1}{3}\}-1-\frac{1}{3}\times2 = \frac{4}{3} > 0$ by (R1), (R2), (R4), (R5) and Claims 3.1, 3.6 as $z$ is adjacent to at most two real $3$-vertices in $H^{\times}$.

$(3)$ Let the configuration of $H^{\times}[\{z\}\cup N_{H^{\times}}(z)]$ be $F_{3}$ in Figure 1. Then $w'(z)\geq4-4+2\times\min\{2-\frac{1}{3}\times2, \frac{8}{3}-\frac{1}{3}\times4, 4-\frac{1}{2}\times4-\frac{1}{3}\times2, 5-\frac{1}{2}\times4-\frac{1}{3}\times3, 6-\frac{1}{2}\times5-6\cdot\frac{1}{3}\}-2\times1-\frac{1}{3}\times2 = 0$ by (R1), (R2), (R5) and Claims 3.1, 3.6.

$(4)$ Let the configuration of $H^{\times}[\{z\}\cup N_{H^{\times}}(z)]$ be $F_{4}$ in Figure 1. Since $H$ is an IC-planar graph without $5$-cycles, $z$ is incident with two false $5^+$-faces in $H^{\times}$. Thus, $w'(z)\geq4-4+2\times1+2\times\min\{2-\frac{1}{3}\times3, \frac{8}{3}-\frac{1}{3}\times5, 4-\frac{1}{2}\times4-\frac{1}{3}\times2, 5-\frac{1}{2}\times5-\frac{1}{3}\times3, 6-\frac{1}{2}\times6-6\cdot\frac{1}{3}\}-2-\frac{1}{3}\times2 = \frac{4}{3} > 0$ by (R1), (R2), (R4), (R5) and Claims 3.1, 3.6.

$(5)$ Let the configuration of $H^{\times}[\{z\}\cup N_{H^{\times}}(z)]$ be $F_{5}$ in Figure 1. Since $H$ is an IC-planar graph without $5$-cycles, $z$ is incident with one false $5^+$-face in $H^{\times}$. Note that $u_i$ $(i = 1, 2, 3, 4)$ is incident with at least one $4$-cycle in $H$. Thus, $w'(z)\geq4-4+1+2\times\min\{2-\frac{1}{3}\times2, \frac{8}{3}-\frac{1}{3}\times4, 4-\frac{1}{2}\times4-\frac{1}{3}\times2, 5-\frac{1}{2}\times4-\frac{1}{3}\times3, 6-\frac{1}{2}\times5-6\cdot\frac{1}{3}\}-3-\frac{2}{3} = 0$ by (R1), (R2), (R4), (R5) and Claims 3.1, 3.6.

$(6)$ Let the configuration of $H^{\times}[\{z\}\cup N_{H^{\times}}(z)]$ be $F_{6}$ in Figure 1. Note that $z$ is adjacent to at least three real $6^+$-vertices and at most one real $3$-vertex by Claim 3.4.

$(6.1)$ Assume that $z$ is not adjacent to any real $3$-vertex. Then $w'(z)\geq4-4+3\times\min\{2-\frac{1}{3}\times2, \frac{8}{3}-\frac{1}{3}\times4, 4-\frac{1}{2}\times3-\frac{1}{3}\times2, 5-\frac{1}{2}\times4-\frac{1}{3}\times3, 6-\frac{1}{2}\times5-6\cdot\frac{1}{3}\}-4 = 0$ by (R2), (R5) and Claims 3.1, 3.6.

$(6.2)$ Assume that $z$ is adjacent to one real $3$-vertex. Then $z$ is adjacent to three real $7^+$-vertices by Claim 3.4. Set $d_{H^{\times}}(u_1) = 3$. If $d_{H^{\times}}(u_3) = 7$, then $u_3$ is not adjacent to any real $3$-vertex in $H^{\times}$ by Claim 3.4 since $u_3$ is adjacent to $u_1$ in $H$. Thus, $w'(z)\geq4-4+(\frac{8}{3}-\frac{1}{3}\times3)+2\times\min\{ \frac{8}{3}-\frac{1}{3}\times4, 4-\frac{1}{2}\times3-\frac{1}{3}\times2, 5-\frac{1}{2}\times4-\frac{1}{3}\times3, 6-\frac{1}{2}\times5-6\cdot\frac{1}{3}\}-4-\frac{1}{3} = 0$ by (R1), (R2), (R5) and Claims 3.1 and 3.6. If $8\leq d_{H^{\times}}(u_3)\leq9$, then $w'(z)\geq4-4+\min\{4-\frac{1}{2}\times3-\frac{1}{3}\times2, 5-\frac{1}{2}\times4-\frac{1}{3}\times3\}$+$2\times\min\{\frac{8}{3}-\frac{1}{3}\times4, 4-\frac{1}{2}\times3-\frac{1}{3}\times2, 5-\frac{1}{2}\times4-\frac{1}{3}\times3, 6-\frac{1}{2}\times5-6\cdot\frac{1}{3}\}-4-\frac{1}{3} = \frac{1}{6} > 0$ by (R1), (R2), (R5) and Claims 3.1 and 3.6. If $d_{H^{\times}}(u_3) = 10$, then $w'(z)\geq4-4+(6-\frac{1}{2}\times5-5\cdot\frac{1}{3})+2\times\min\{ \frac{8}{3}-\frac{1}{3}\times4, 4-\frac{1}{2}\times3-\frac{1}{3}\times2, 5-\frac{1}{2}\times4-\frac{1}{3}\times3, 6-\frac{1}{2}\times5-6\cdot\frac{1}{3}\}-4-\frac{1}{3} = 0$ by (R1), (R2), (R5) and Claims 3.1 and 3.6. By symmetry, we have $w'(z)\geq0$ when $d_{H^{\times}}(u_2) = 3$ or $d_{H^{\times}}(u_3) = 3$ or $d_{H^{\times}}(u_4) = 3$.

By the analysis above (1)–(6), the nonempty set $Y\cap (V(H^{\times})\setminus V(H)) = \emptyset.$

Finally, we choose arbitrarily a real vertex $z$ from $V(H)$. Note that $3\leq d_{H^{\times}}(z)\leq10$ by Claims 3.1 and 3.4. If $z$ is a real $3$-vertex, then $w'(z) = 3-4+3\times\frac{1}{3} = 0$ by (R1) since $z$ has three neighbors. If $z$ is a real $4$-vertex, then $w'(z) = 4-4 = 0$ since no rule is applied to it. If $z$ is a real $5$-vertex, then $f_t(z)\leq3$ and $n_{H^{\times}}^{3}(z)+n_{H^{\times}}^{4}(z) = 0$ by Claims 3.2, 3.4 and 3.6. Thus, $w'(z)\geq5-4-3\times\frac{1}{3} = 0$ by (R2). In the following, we consider that $z$ is a real $6^{+}$-vertex.

Assume that $z$ is not adjacent to any false $4$-vertex. Then $f_t(z)\leq\lfloor\frac{2d_{H^{\times}}(z)}{3}\rfloor$ by Claim 3.6. If $6\leq d_{H^{\times}}(z)\leq9$, then $w'(z)\geq d_{H^{\times}}(z)-4-(d_{H^{\times}}(z)-6)\times\frac{1}{3}-\lfloor\frac{2d_{H^{\times}}(z)}{3}\rfloor\times\frac{1}{2}\geq0$ by (R2) and Claims 3.4 and 3.6. If $d_{H^{\times}}(z) = 10$, then $w'(z)\geq d_{H^{\times}}(z)-4-\max\{\frac{1}{2}f_{t}(z)+\frac{1}{3}n_{H^{\times}}^{3}(z)| f_{t}(z)\leq 6\; \mbox{and} \; f_{t}(z)+n_{H^{\times}}^{3}(z)\leq13\}\geq\frac{2}{3}$ by Claim 3.6.

Assume that $z$ is adjacent to one false $4$-vertex. Note that $f_{t}(z)\leq 6\; \mbox{and} \; f_{t}(z)+n_{H^{\times}}^{3}(z)\leq12$ when $d_{H^{\times}}(z) = 10$. By (R3), (R5) and Claim 3.4, it is easy to verify $w'(z)\geq0.$ Thus, the nonempty set $Y\cap V(H) = \emptyset.$

By the analysis above, the nonempty set $Y\cap (V(H^{\times})\cup F(H^{\times})) = \emptyset$, This is a contradiction. The proof of Theorem 1.2 is completed.

4.   Conclusions

Graph coloring is one of the important research contents of graph theory. In recent years, neighbor distinguishing colorings have gradually become one of the research hotspots of graph coloring. The paper is devoted to the study of neighbor sum distinguishing list total coloring of graphs. We proved that $\rm{ch}^{t}_{\Sigma}(G)\leq \Delta(G)+3$ for every IC-planar graph with $\Delta\geq10$ but without $5$-cycles, which implies that Conjecture 1.2 holds for this class of graphs. There are many results about neighbor sum distinguishing list total coloring. According to currently known results, it yields a question for further research as follow:

Does Conjecture 1.2 hold for every IC-planar graph with $4\leq\Delta\leq9$ but without $5$-cycles?

Acknowledgments

This work was supported by Shangluo University Doctoral Initiation Fund Project (No. 21SKY108 and 22SKY112) and Shangluo University Key Disciplines Project, Discipline name: Mathematics.

Conflict of interest

All authors declare no conflicts of interest in this paper.