A new approximate method to the time fractional damped Burger equation

1.   Introduction

As we all know, complex natural phenomena are often characterized by nonlinear mathematical models. When dealing with specific nonlinear phenomena, it is often necessary to consider the initial value and boundary problems. This makes it difficult for us to find the exact solutions of this considered models ^[1,2,3,4,5]. In particular, this thing becomes more difficult to deal with the fractional differential equations. Therefore, in order to solve these problems, a lots of effective methods have been proposed ^{[6,7,8,9,10,11,12,13]}, such as the homotopy analysis method ^[6], the residual power series method ^[7], the Lie symmetry group method ^[8,9], the iterative reproducing kernel method ^[10] and the AAM ^[11], etc.

Here, we focus on the time fractional damped Burger equation ^[14] which reads,

with

where $p$ is a free constant.

The Burger's equation was used to express the shallow water wave phenomena. In 1915, Bateman H ^[15] proposed the one-dimensional nonlinear Burger's equation of integral order for the first time. Later, this equation was further studied by Burger JM ^[16]. In later days, many scholars applied various methods to handle Burger's-type model ^{[17,18,19,20,21]}. As feedback, exact solutions and approximate solutions of this Burger's equation, were obtained. For example, Guo T. et al. ^[17,18] utilized the BDF finite difference scheme to deal with the viscous Burger's equation. Inc ^[19] used an approximate approach to consider the space-time fractional Burger's equations. Peng X and Qiu W. et al.^[20,21] applied two different difference schemes to solve the mixed-type time fractional Burger's equation and the one-dimensional time fractional Burger's equation. The goal of this letter is to apply a new approximate method which is called the AAM to deal with the nonlinear time fractional damped Burger equation. Thus, approximate solution of this considered equation was obtained.

The plan of this article as follows: In Section 2, the definitions and properties of the Caputo fractional derivative were shown. The main steps, definitions and theorems of the AAM in Section 3, were expounded in detail. In Section 4, we apply the AAM to deal with the nonlinear time fractional damped Burger equation. Then, a new approximate solution of this researched model was yielded. In the last section of this paper, conclusions and discussions of full texts were given.

2.   Preliminaries

Before entering the discussion text, the definitions and properties of the Caputo fractional derivative in this section were shown ^[22,23].

Definition 2.1. ^[22,23] The Caputo fractional partial derivative of the order $\alpha > 0$ of the function $\Omega(\chi, \tau)$ with independent variables $\chi$ and $\tau$, is given by

Theorem 2.1. ^[22,23] For the Caputo fractional derivative operator $D_t^\alpha(\cdot)$, we have

and

3.   This idea of the AAM

This main idea and results of the AAM ^[11] in this section, were given. As the scope of applications of this method, we focus on this type fractional partial differential equations with initial values

where $L$ and $N$ are linear and nonlinear operators, respectively; and $\alpha$ is the fractional order of Caputo; and $\widetilde x = ({x_1}, {x_2}, ..., {x_n})\in R^n$.

In this section, the main results of this considered scheme ^[13] were shown.

Lemma 3.1. For $u(\widetilde x, t) = \sum\limits_{k = 0}^\infty {{l^k}{u_k}(\widetilde x, t)}$ with the parameter $l$, the linear operator $L(u)$ satisfies the following property:

Theorem 3.1. Let $u(x, t) = \sum\limits_{k = 0}^\infty {{u_k}(\widetilde x, t)}$. If considering ${u_\lambda}(\widetilde x, t) = \sum\limits_{k = 0}^\infty {{\lambda ^k}{u_k}(\widetilde x, t)}$ with the parameter $\lambda$, then the nonlinear operator $N({u_\lambda})$ satisfies the following property:

Remark 3.1. If we denote

then, Eq (3.3) becomes

Theorem 3.2. Let $n-1 < \alpha < n$, $f(\widetilde x, t)$ and ${f_i}(\widetilde x)$ from system (3.1a/b), then system (3.1a/b) admits at least a solution given by

where ${L_t^{(- \alpha)}({u_{(k - 1)}})}$ and ${E_{(k - 1)t}^{(- \alpha)}}$ are fractional partial integral of order $\alpha$ for ${L({u_{(k - 1)}})}$ and ${{E_{(k-1)}}}$.

Theorem 3.3. Let $B$ be a Banach space. Then, the series solution

converges to $S\in B$ for, if there exists $\gamma (0\leq \gamma < 1)$, such that

for $\forall n \in N$ and ${g_i}(\widetilde x)$ is initial value.

Theorem 3.4. The series solution

of the maximum absolute truncation error is

where the region ${(\widetilde x, t) \in \Omega }$.

In what follows, we apply the above definitions and theorems to deal with the nonlinear time fractional damped Burger equation.

4.   Approximate solution of the time fractional damped Burger equation

In this section, we applied the AAM to deal with the nonlinear time fractional damped Burger equation. Then, we yield a new approximate solution of this researched model.

First of all, this considered model with the initial condition was rewritten as the following form

When $\alpha = 1$, the exact solution with initial condition corresponding to

Equation (4.1a) was reexpressed as the form

where $N(u) = - u{u_x}$.

Now, we suppose that Eq (4.3) has a approximate solution of the form

For the sake of the solution to (4.3), we have

adjoint the initial condition given as

Further, considering Eq (4.5) has a solution of the form

Through Theorem 3.1 and initial condition (4.6), we have

Plugging (4.8) into (4.9) with (3.5), we have

We do the Eq (4.9) for the items with $\lambda$ equals the same power, get the following components:

where ${{E_{(k - 1)}}}$ have been known in (3.6).

From Eqs (4.4) and (4.7), we have

Further, one obtains

On the basis of the formula (4.10) with initial condition (4.12), we obtain a few components of form

Hence, Eq (4.1) has the third-order term approximate solution of the form

Remark 4.1. Reference ^[11] has given the approximate solution of some points and corresponding errors. It has been able to demonstrate the effectiveness and accuracy of this method. We won't repeat this work here.

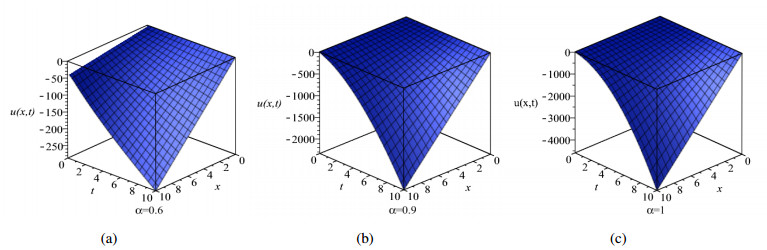
In order to better to state the fractional order values $\alpha$ how to effect the approximate solution (4.14), we plot two 3D-plots with the values $p = 1$ and $p = -1$ by Figures 1 and 2, respectively.

5.   Conclusions and discussions

In this article, we studied the model (4.1) which can be applied to show the shallow water wave phenomena. Here, we applied a new approximate method called the AAM to handle the nonlinear time fractional damped Burger equation. As a result, the approximate solution of model (4.1), was obtained. The result can be expressed by 3D-plots. We can see that this method is an effective tool to solve deal with other fractional differential equations.

Acknowledgments

This work is supported by the National Natural Science Foundations of China (No.62206297) and the Fundamental Research Funds for the Central Universities (No.2021QN1073).

Conflict of interest

No conflict of interest exits in the submission of this manuscript, and the manuscript is approved by all authors for publication.