A general chemostat model with second-order Poisson jumps: asymptotic properties and application to industrial waste-water treatment

1.   Introduction

1.1.   Research background and motivations

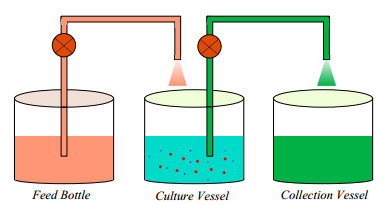
A chemostat (chemical environment that remains static) is a bioreactor in which fresh medium is continuously added, while culture fluid typically containing remaining nutrients, metabolic end products, and specific microorganisms is continuously removed to the same speed to absolutely keep the culture constant in volume. By adjusting the rate at which the medium is included to the bioreactor, the specific growth rate of the microorganism can be easily controlled within certain limits ^[1,2]. In industrial application, a standard chemostat is purely a laboratory instrument of three containers that function to multiply and increase microorganisms in an environment (see Figure 1). In its customary form, the outlet of the supply tank is the inlet of the culture vessel, while the outlet of the latter is the inlet of the collection bottle. The first vial contains all the nutritional needs that contribute to the development and reproduction of microorganisms. The content of this bowl is pumped into the 2nd at a constant rate. The microorganisms feed on the nutrients in the feeder and live in the culture vessel which is well agitated so that all organisms retain similar access to the nutrients ^[3]. The contents of the culture vessel are then pipetted into a third vessel containing the nutrient sources, bacteria and appendages produced by these microorganisms ^[4].

Broadly speaking, chemostats are the familiar representation of the natural biological competition that occurs when two or more groups compete for the same food supply ^[5]. It performs a crucial role in environmental modeling ^[1], interactions between populations ^[2] and other domains. To better characterize and describe the mechanism of a single-organism chemostat, we consider these two ordinary differential equations (ODEs):

where $N(t)$ and $M(t)$ are respectively the densities of nourishing elements and microbial organisms at time $t$. $N_{\star}$ is the alimentation flux rate, $\mathcal{Q}_0$ is the washout ratio for $N(t)$, $\mathcal{Q}_1$ is the elimination average combining alleviation ratio and bacterial death rate, $\Theta$ indicates the highest rate of nutrient depletion and also the rate of reproduction for $M(t)$, $\mathcal{G}$ refers to the functional response simulating nutrient utilization by bacteria. Generally, one can find in the literature several studies that have treated and analyzed chemostat systems with various shapes of $\mathcal{G}$ (uptake function). In Table 1, we assort some popular kinds of $\mathcal{G}$ and we offer some references for each case.

Fundamentally, uninterrupted environmental disturbances adversely affect microbiological cultures and inevitably make it difficult to predict their behavior and attitude ^{[16,17,18,19,20,21,22]}. In particular, in the chemostatic situation, even if the empirical results (typically observed according to theoretical standards) relatively resemble the asymptotic behavior of the deterministic model, we cannot ignore the variations that can naturally occur under the operational conditions ^{[23,24,25,26]}. Thus, some researchers have incorporated the effect of extrinsic fluctuations in chemostat systems by using white noises ^[27,28]. These systems are only probabilistic models with standard Brownian motions (SBMs) and therefore their solution is continuous ^{[29,30,31,32]}. Unluckily, this approach is not totally adequate to characterize some unforeseen external perturbations such as changes in lab conditions ^{[26,33,34,35,36,37]}. Hence, we will investigate to the Lévy effect which are known for their powerful ability to properly formulate the said randomness ^{[38,39,40,41,42]}. By taking into consideration this general frame, the authors in ^[26] integrated linear Lévy noises and the Michaelis-Menten response in the one-organism chemostat system which takes the following shape:

where $N(t^{-})$ and $M(t^{-})$ are respectively the left limits of $N(t)$ and $M(t)$. Let $\Omega^{\mathcal{E}, {\mathbb P}}\equiv(\Omega, \mathcal{E}, \{\mathcal{E}_t\}_{t\geq 0}, {\mathbb P})$ be a filtered probability space with $\{\mathcal{E}_t\}_{t\geq 0}$ satisfying the habitual conditions. For (1.1), ${\mathbb B}_{1}\equiv{\mathbb B}_{1}(t)$ and ${\mathbb B}_{2}\equiv{\mathbb B}_{2}(t)$ are independent SBMs defined on $\Omega^{\mathcal{E}, {\mathbb P}}$ with their associated intensities $\varrho_{11}, \; \varrho_{21} > 0$. $\mathbb{N}(\cdot, \cdot)$ is a Poisson random measure with finite characteristic measure $\chi(\cdot)$ on a measurable subset ${\mathcal H}$ of $(0, \infty)$, where $\chi({\mathcal H}) < \infty$. The associated compensated Poisson random measure ${\mathbb K}$ is expressed by

which is an $\{\mathcal{E}_t\}$-martingale. Furthermore, it is supposed that $\mathbb{N}$ is independent to SBMs ${\mathbb B}_1$, ${\mathbb B}_2$; and the functions $\kappa_{11}$, $\kappa_{21}$ are continuous on ${\mathcal H}$ such that $\kappa_{i1}(u) > -1$, $u\in{\mathcal H}$, $(i = 1, 2)$. In ^[26], the authors examined the leverage of the discrete-time delay and linear Lévy noises on the continuation and suppression of the single microorganism $M$. In a particular case, when $\kappa_{11}(u) = \kappa_{21}(u) = 0$, the authors in ^[20], studied the asymptotic behavior of a one organism in an irregular environment. They indicated that white noises have passive impacts on the organism perseverance.

When severely handling with chemostatic processes, other components must be taken into consideration, such as the acute sensitivity of microorganisms to nutrient concentrations and the mutual interference between chemostatic components ^[43,44,45]. Therefore, it should be stated that the choice of interaction function influences the prediction of behavior ^{[11,12,46,47]}. For this reason, this study puts forward a new chemostat model with an interaction function that takes into consideration many familiar interactions examples (Table 2). Hence, we formulate our system in the following structure:

We presume that the general interference response $\Phi\in \mathcal{C}^2({\mathbb R}_+\times{\mathbb R}_+, {\mathbb R}_+)$ verifies these hypotheses:

(a) $\Phi(0, M) = 0$, $\forall M\geq 0$.

(b) $\exists\mathfrak{A} > 0$ satisfying $\frac{\partial \Phi (N, M)}{\partial N}\leq \mathfrak{A}$, for all $N, M \geq 0$.

(c) $\Phi$ is increasing in $N$ and decreasing in $M$.

(d) $\Phi$ follows the uniformly continuous property at $M = 0$: $\underset{M\to 0}{\lim}\underset{N > 0}{\sup}\{|\Phi(N, M)-\Phi(N, 0)|\} = 0$.

The properties $(a)$, $(b)$, $(c)$ and $(d)$ are easily satisfied by the classic examples listed in the Table 2.

1.2.   Stochastic chemostat system with second order Poisson noises

Based on the fact that copious amounts of extrinsic fluctuations (physical conditions) can strongly affect chemostat dynamics, in this research we offer new insight into modeling these environmental complexities. Massive pollution, domestic and industrial sewage discharges, sudden climatic fluctuations, excessive temperatures and human intervention represent the frequent abrupt and unstable changes that affect ecological competition and lead to interruptions in the industrial chemostat process. For this cause, we aim to provide an alternative framework that adequately explains the said laboratory fluctuations ^[48,49]. Implementing Taylor expansion and second-order jumps, we suggest a highly perturbed model that extends the aforementioned studies and provides a general framework for randomness. This form of noise has not been addressed before in the literature due to a lack of modeling knowledge and some analytical complexities. So, the current study offers a major enhancement and generalization of the papers ^[20] and ^[26]. Explicitly, we presume the practical and real situation of the chemostat mechanism by assuming the nonlinearity of perturbations and raising the order of Lévy noises to the second one (quadratic) in the system (1.2) as follows:

where

Here, $\varrho_{11}$, $\varrho_{21}$ denote the white noise intensities of the first order (linear), and $\varrho_{12}$, $\varrho_{22}$ stand for that of the second order (quadratic). The Lévy intensities $\kappa_{11}(u)$, $\kappa_{21}(u)$, $\kappa_{12}(u)$, $\kappa_{22}(u)$ are positive and continuous functions.

Setting ${\mathbb R}_+^{2, \star} = \{(x, y):\; x > 0, y > 0\}$ and supposing that ${ }\int_{{\mathcal H}}\kappa^2_{k\ell}(u)\chi({{\rm{d}}} u) < \infty$; $k, \ell = 1, 2.$ By this assumption, and similar reasoning as in (^[33], Theorem 1), we deduce that for $\big(N(0), M(0)\big)\in{\mathbb R}_+^{2, \star}$, the corresponding solution $\big(N(t), M(t)\big)\in{\mathbb R}_+^{2, \star}$.

When analyzing a mathematical formulation that characterizes the long-run behavior of an organism, our main preoccupation is to know if it will end or will last. Since our stochastic model (1.3) is perturbed by a new version of perturbations, threshold analysis is considered an intriguing and important issue. Moreover, nonlinear random perturbations are a rich topic that arouses the interest of many researchers on account of their real-world significance and practicality ^{[22,50,51,52]}. As far as we know, there is no existing study that attempts to present and treat chemostat systems with quadratic Lévy noises and a general interference function. In this research, we adopt this general framework and we analyze the system (1.3) by discussing the stationarity and disappearance properties of $M$. So, our problematic is to find the sufficient and necessary condition for these two asymptotic characteristics. Technically, this study offers a new and general scope for treating perturbed models driven by quadratic Lévy jumps in biology. We present the sill among the ergodicity and disappearance of $M$ by the use of the probabilistic comparison theorem, the exponential inequality for martingales, the Feller property and other mathematical tools. The obtained threshold value $\mathfrak{C}^{\star}_0$ is regarded to be sufficient for having an excellent view of the long-time chemostat process. Specifically, if $\mathfrak{C}^{\star}_0 > 0$, we have the existence and uniqueness of an ergodic stationary distribution, while the extinction happens when $\mathfrak{C}^{\star}_0 < 0$.

The remaining parts of this research are ordered in the following arrangement: In Section 2, we present some long-run characteristics of an auxiliary chemostat equation with quadratic jumps, then we introduce the sill $\mathfrak{C}^{\star}_0$ of our model. In Section 3, we demonstrate that $\mathfrak{C}^{\star}_0$ is the real threshold of our system (1.3). In Section 4, we give an application of waste-water treatment to affirm and clarify our theoretical outcomes.

2.   Required results on the auxiliary chemostat equation with quadratic Lévy noises

This section is devoted to the dynamical analysis of a boundary chemostat equation in the case of $M(t) = 0$ (absence of the microorganism). Because of that reason, we utilize the following auxiliary equation with quadratic Lévy jumps:

Remark 2.1. For any positive initial value, Eq (2.1) has a solution which is: positive, unique and global ^[41].

Remark 2.2. Via the well-known probabilistic comparison theorem ^[53], one can infer that $\Psi(t)\geq N(t)$ for all $t\in[0, \infty)$ almost surely (abbreviated as a.s.).

To move forward, the next lemma is needed.

Lemma 2.1. The solution $\Psi$ of (2.1) satisfies two main results.

1) For all $p\in(0, 1]$, $\exists\tilde{\mathfrak{m}}$ independent of $\Psi(0)$ satisfying

2) $\Psi(t)$ has the unique ergodic stationary distribution $\pi^{\Psi}(\cdot)$, and

Proof. For the convenience of the reader, we split the proof into two stages.

Part I. We let the Lyapunov function

By Itô differential operator $\mathcal{L}V$ of (2.1), we get

Clearly, we have for all $0 < p\leq 1$, that

Then, $\mathcal{L}V(\Psi)\leq \underbrace{\mathcal{Q}_0(1+N_{\star})}_{ = v_2}(1+\Psi)^{p-1}-\underbrace{\mathcal{Q}_0}_{ = \frac{1}{p}v_1}(1+\Psi)^{p}$. Consequently

According to the proof of Lemma 2.3 in ^[54], we get

Part II. Based on the theory presented in ^[55], in order to check the ergodicity of $\Psi(t)$, it is enough to prove the existence of a non-negative function $V$ and $v_1, v_2 > 0$ such that

From the inequality (2.4), Theorem 6.3 in ^[55], and ergodic theorem ^[56], we deduce that $\Psi(t)$ has a unique ergodic stationary distribution (named as $\pi^{\Psi}$), and

To find this limit, we simply take the expectation on both sides of (2.1), then we have

Therefore

Consequently, we get

Remark 2.3. Lemma 2.1 plays an intrinsic role to substantiate the outcomes of this study.

Remark 2.4. Set $\varrho^{\star} = \max\big\{\varrho_{11}^2, \varrho_{21}^2\big\}$, $\kappa^{\star}(u) = \max \big\{\kappa_{11}(u), \kappa_{21}(u)\big\}$ and $\kappa_{\star}(u) = \min \big\{\kappa_{11}(u), \kappa_{21}(u)\big\}$. To highlight the value of the result (2.5), we compare it with that in ^[34]. According to ^[41], we can get the results in ^[34] without considering the following assumption:

which is widely used to demonstrate that

1) ${ }\underset{t\to\infty}{\lim}\frac{\Psi(t)}{t} = 0$ a.s.

2) ${ }\underset{t\to\infty}{\lim}\frac{1}{t}\int_0^t \Psi(s){{\rm{d}}} {\mathbb B}_1(s) = 0$, and ${ }\underset{t\to\infty}{\lim}\frac{1}{t}\int_0^t \Psi^2(s){{\rm{d}}} {\mathbb B}_1(s) = 0$ a.s.

3) ${ }\underset{t\to\infty}{\lim}\frac{1}{t}\int_0^t\int_{{\mathcal H}} \big(\kappa_{11} (u)\Psi(s^{-})+\kappa_{12}(u) \Psi^2(s^{-})\big){\mathbb K}({\rm{d}}s, {\rm{d}}u) = 0$ a.s.

In this study, we offer an alternative approach without any extra restrictions on parameters like (2.6).

Remark 2.5. Note that the result exhibited in Lemma 2.1 is a generalization of that presented in Remarks 2 and 3 of ^[41].

Remark 2.6. By using the properties of $\Phi$ and Lemma 2.1, we conclude that

By using Remark 2.6, the threshold value of (1.3) is given in the following structure

Remark 2.7. Note that in the case of the functional response type 1, the threshold is

Since the expression of $\pi^{\Psi}$ is unknown, Lemma 2.1 gives the exact value of the sill value which is presented as:

In the next part, we shall show that $\mathfrak{C}^{\star}_0$ is the sill among the stationarity and the disappearance of $M$.

3.   Threshold analysis of the perturbed system (1.3)

3.1.   The stationarity case

This subsection introduces a new approach to verify the stationarity (and of course the ergodic property) of our system. This method is presented by the following interesting lemma.

Lemma 3.1. [Limited possibilities lemma ^[57]] Consider a stochastic process $\mathcal{M}\in {\mathbb R}^n$ that satisfy the Feller property, then one of the following cases occurs: theexistence and uniqueness of an ergodic stationary distribution, or

where the supremum is taken over all initial distributions $\hat{\zeta}$ on ${\mathbb R}^n$ and ${\mathbb P}\big(x; s, {\mathbb D}\big)$ is the probability for $\mathcal{M}$ belongs to ${\mathbb D}$ with $\mathcal{M}(0) = x\in {\mathbb R}^n$.

Theorem 3.1. For any initial data $\big(N(0), M(0)\big)\in{\mathbb R}_+^{2, \star}$, if $\mathfrak{C}^{\star}_0 > 0$, the solution $\big(N(t), M(t)\big)$ to (1.3) has the ergodic property and admits a unique stationary distribution $\pi^{\star}(\cdot)$.

Proof. From (Lemma 3.2 ^[58]), we easily verify that the solution of (1.3) has the Feller property. The main purpose of next part is to prove that (3.1) is impossible. Via using Itô's formula, we have

Then, we get

On the other hand, we have

We combine (3.2) and (3.3), then

Choose a positive value $\mathfrak{s}$ verifying ${ }\mathfrak{s}\geq \frac{1}{\mathcal{Q}_1}\bigg(\frac{\mathfrak{A}^2\Theta^2}{\varrho_{11}\varrho_{12}}+\varrho_{21}\varrho_{22}+\int_{{\mathcal H}}\kappa_{22}(u)\chi({{\rm{d}}} u)\bigg)$, and define

Then, we have

By Itô's formula to $p^{-1}(1+N)^p$ and $p^{-1}M^p$ for $p\in(0, 1)$, gives

and

Consider the function $\widetilde{\mathcal{V}}(N(t), M(t)) = \mathfrak{D}\mathcal{V}(t)+\frac{(1+N(t))^p}{p}+\frac{M^p(t)}{p}$, where $\mathfrak{D} > 0$ is a sufficiently large number such that $-\mathfrak{D}\mathfrak{C}^{\star}_0+\mathfrak{B}\leq -2$, and

Since $\widetilde{\mathcal{V}}(N, M)$ gets the lower bound at $(\underline{N}, \underline{M})$ in ${\mathbb R}^2_+$, we let the Lyapunov function

Then, one can see that

We consider the following bounded domain

with $0 < \epsilon < 1$, $\epsilon_{\star} = \min\{\epsilon, \epsilon_0\}$ and $\epsilon_0$ will be accurately chosen in the following. In the set ${\mathbb R}^{2, \star}_{+}\setminus{\mathbb D}_{\epsilon, \epsilon_{\star}}$, let $\epsilon$ sufficiently small satisfying

where

Next, we split ${\mathbb R}^{2, \star}_{+}\setminus{\mathbb D}_{\epsilon, \epsilon_{\star}}$ into

Plainly, ${\mathbb D}_{\epsilon, \epsilon_{\star}}^c = {\mathbb R}^{2, \star}_{+}\setminus{\mathbb D}_{\epsilon, \epsilon_{\star}} = {\mathbb D}_{\epsilon, 1}\cup{\mathbb D}_{\epsilon_{\star}, 2}\cup{\mathbb D}_{\epsilon, 3}\cup{\mathbb D}_{\epsilon_{\star}, 4}$. Next, we check the inequality

First case. For any $(N, M)\in{\mathbb D}_{\epsilon, 1}$, we utilize $NM\leq \epsilon M\leq \epsilon(1+M^2)$ and (3.4) to obtain that

Second case. $\Phi(N(t), M(t))$ is uniformly continuous at $M = 0$. Hence, assumption $(d)$ implies that $\exists \epsilon_0 > 0$ satisfying $0 < M\leq\epsilon_0$,

Thus, if $M < \epsilon_{\star} = \min\{\epsilon, \epsilon_0\}$, $NM\leq \epsilon N\leq \epsilon (1+N^2)$, we get from (3.5) that

Third case. When $(N, M)\in{\mathbb D}_{\epsilon, 3}$, we use the classical inequality $NM\leq N^22^{-1}+M^22^{-1}$, then

that can be deduced by (3.6).

Fourth case. For any $(N, M)\in{\mathbb D}_{\epsilon_{\star}, 4}$, by the arguments in case 3, we obtain from (3.7)

Hence, (3.8) is obtained. Besides, we can prove that $\exists\tilde{\mathfrak{a}} > 0$ verifying $g(N, M)\leq \tilde{\mathfrak{a}}$, for all $(N, M)\in {\mathbb R}_+^{2, \star}$. Thus,

The ergodic property of $\Psi(t)$ gives

Therefore,

Which means

3.2.   The disappearance case

Theorem 3.2. Let $\big(N(t), M(t)\big)$ be the solution of (1.3) for $\big(N(0), M(0)\big)\in{\mathbb R}_+^{2, \star}$. If $\mathfrak{C}^{\star}_0 < 0$, then $\big(N(t), M(t)\big)$ follows:

which means that $M$ will exponentially extinct with probability 1. Moreover, $N(t)$ converges weakly to the stationary distribution $\pi^{\Psi}$ of $\Psi(t)$.

Proof. The proof is achieved through the following parts.

Part I. Itô's formula implies

From Remark (2.2), we obtain

We integrate from $0$ to $t$ and divide by $t$ on both sides of the last inequality, then

We let ${ }\mathcal{G}_1(t) = \int^t_0\varrho_{21}{{\rm{d}}} {\mathbb B}_2(s)$ and ${ }\mathcal{G}_2(t) = \int^t_0\int_{{\mathcal H}}\ln\big(1+\kappa_{21}(u)\big){\mathbb K}({\rm{d}}s, {\rm{d}}u)$. It is easy to show that their quadratic variations are given by

By employing the strong large numbers theorem for local martingales ^[59], we obtain

Now, we apply the exponential inequality for martingales described in ^[59], then

Borel-Cantelli Lemma ^[59] stated that for almost $\omega\in\Omega$, we have the existence of an integer $\mathfrak{n}_{\omega} > 0$ such that for all $n\geq \mathfrak{n}_{\omega}$, $t\in [\mathfrak{n}-1, \mathfrak{n})\subseteq {\mathbb R}_+$ a.s.,

Consequently, for all $\mathfrak{n}\geq \mathfrak{n}_{\omega}$, $t\in [\mathfrak{n}-1, \mathfrak{n})\subseteq {\mathbb R}_+$ a.s., we established that

We take the superior limit on both sides of the last result, then

Since the exponential extinction implies the stochastic extinction ^[59], so $\underset{t\to\infty}{\lim} M(t) = 0$ a.s. and the microorganism in the chemostat of (1.3) almost sure to be extinct.

Part II. From Part I, we deduce that for $\mathfrak{r} > 0$, $\exists\mathfrak{t}_0$ and $\Omega_{\mathfrak{r}}\subset\Omega$ verify ${\mathbb P}(\Omega_{\mathfrak{r}}) > 1-\mathfrak{r}$ and

Hence,

indicates that the distribution of $N(t)$ converges weakly to the $\pi^{\Psi}(\cdot)$. The proof of the extinction theorem is finished.

4.   Concrete example and discussion

Now, we give a real example of the stochastic model (1.3). Our fundamental purpose is to belay the accuracy of the obtained results and to highlight the complex long-run attitude of chemostat mechanisms. Lastly, we will give a short discussion about our outcomes.

4.1.   Numerical experiment: industrial waste-water treatment

Through waste-water handling, we can turn sewage into treated water that is reused in daily activities. In general, waste-water is full of bacterial contaminants, chemicals, and other toxins that can result from industrial production and standard human activities. Its treatment process aims to reduce pollutants to reasonable levels and make the water safe to discharge back into the environment. Figure 2 presents a classical configuration for a biological interaction that is used in the waste-water treatment. A detailed description can be found in ^[2].

Now, we investigate the bacteria reproduction in the waste-water treatment process by (1.3) with Beddington-DeAngelis interference function. Specifically, we suppose that the bacteria reproduction is presented by the $M$ equation, and reproduce through the consumption of a substrate species $N$. The purpose is to monitor the substrate and bacteria density of waste-water generated by industry activities. For this reason, we study the asymptotic dynamics of the model processed by Nguyen et al. in ^[60], that is

Here, we apply the algorithm presented in ^[61] to discretize (4.1). We consider the values listed in Tables 3 (obtained from ^[2]) and 4, we consider two different scenarios of waste-water operation under unexpected and higher order fluctuations.

4.2.   Scenario 1: extinction of bacteria

We take the values of the detreministc coefficients from Table 3 (column Scenario 1) and the values of noise intensities from Table 4 (column Scenario 1). By assuming that $\chi({\mathcal H}) = 1$ and for $T > 0$ sufficiently large, the sill $\mathfrak{C}^{\star}_0$ is calculated as follows:

From Theorem 3.2, we deduce that $M$ goes to extinction and $N$ persists almost surely. Figure 3 confirm this result.

4.3.   Scenario 2: permanence of bacteria

Let us choose the parameters from 5th column of Table 3 and 3rd column of Table 4. Then, we get

Hence, by Theorem 2.3 that there exists a unique ergodic stationary distribution of (4.1) (see Figure 4). This result indicates that the bacteria persists in the waste-water regulation process. We also sketch experimental two-dimensional density of $(N(t), M(t))$ in Figure 5.

To highlight the impact of second-order noise on the chaotic dynamics of the industrial chemostat, we merely present Figures 6. In the latter, we can clearly show that taking higher-order disturbances into account can radically alter the behavior asymptotic of microorganisms and can switch its persistence to its state of extinction. This means that a large amount of noise helps severely reduce the growth of bacteria and inhibit the chemostat process. In other words, at a given value of quadratic jump intensities, a dynamic bifurcation occurs and various scenarios can occur. Moreover, it can be deduced that loud noises have a negative impact on the dynamics of bacteria and the extinction time is proportional to the intensity values.

4.4.   Practical scenario: waste-water performance under wash-out condition

Determining the hydraulic retention time $\theta$ is an intrinsic factor for the operation of a waste-water treatment process. To accommodate the high hydraulic load, the station must control the wash-out time. In fact, sewage flow rates throughout the day have a large variance, and the drainage system must adjust this difference. If the residence time is less than a critical value, denoted by $\theta^{\star}_0$ (to find it, we solve the equation $\mathfrak{C}^{\star}_0(\theta) = 0$), then the sewage flow is too fast for bacteria to grow and increase, existing cells are flushed out rapidly than they can compound ^[60]. Consequently, the bacteria become extinct. From Figure 7, we conclude that $\mathfrak{C}^{\star}_0$ is an increasing function of $\theta$ and we have the result appearing in Table 5. Under specified conditions, controlling $\theta^{\star}_0$ is the theoretical approach to enable the plant to handle with the higher hydraulic loading and avoid the disappearance of bacteria (Scenario 1) under the faster flow of the untreated effluent.

5.   Conclusions and open questions

During this research, we have suggested and processed a novel shape of the chemostat model which joints two hypotheses: general interaction function and quadratic Lévy noises. This merger provides a comprehensive overview of the intermingling among organisms and nutrients in a highly perturbed environment. Then we have the following points:

$\star$ The investigated model has a threshold behavior using some dynamical properties of the Eq (2.1) perturbed by quadratic Lévy noises.

$\star$ By Theorem 3.1, have that the model has a stationarity and ergodicity point.

$\star$ In Theorem 3.2, the extinction scenario is investigated, also the weak convergence of nutrient distribution to that of the boundary auxiliary Eq (2.1).

$\star$ As a practical example, we have treated the waste-water operation under Lévy perturbations.

The strong point of this study is that we succeeded in obtaining the sufficient and necessary condition of the ergodicity and the extinction without imposing any additional hypotheses or constraints on the model parameters. As limitations of this study, we can mention the following two open problems:

$\star$ What happens in the case of $\mathfrak{C}^{\star}_0 = 0$?

$\star$ Can we give an analytical method to process the model (1.3) in the case of negative Lévy intensities?

We will do our best in the future to address these issues.

Acknowledgments

This work has been financed by the CEU San Pablo University, grant number MGI22AOQ.

Conflict of interest

The corresponding author states that there is no conflict of interest.