Improved wolf swarm optimization with deep-learning-based movement analysis and self-regulated human activity recognition

1.   Introduction

With the development of the times and the progress of science and technology, online games have become a new means of entertainment. While people enjoy the happiness brought by online games, more and more people are addicted to it, especially teenagers. On September 29, 2020, China Internet Network Information Center (CNNIC) released the 46th statistical report on China's Internet development in Beijing^[1]. By June 2020, the number of online game users has reached 540 million. The proportion of game addicts in China has reached 27.5%. Among them, 30.5 percent of teenagers are addicted to online games.

Teenagers are being in a critical period of growth and development, and their discrimination ability is not enough. Some bad information in the game will cause them to deviate from their values, and even lead to illegal acts such as theft and violence. At the same time, indulging in games consumes energy, delays studies, and also leads to mental decadence and physical weakness^[2]. Using medical methods, American scientists have found that the brain waves of internet addicts are exactly the same as those of drug addicts, which proved that online game addiction is indeed "internet opium" and "electronic heroin". Teenagers are obsessed with online games, which is tantamount to taking drugs^[3].

It is found that the lack of family education is the key factor of teenagers' online game addiction. Parents' neglect, rudeness, doting, excessive care and inability to take care of their children can lead to teenagers' over dependence on online games. In addition, single-parent families and left-behind children are more likely to indulge in online games^[4]. Therefore, family education plays a very key role in the growth of teenagers. And the online games have a strong infectious, because many games have such a setting: players need to form a team to enter the game, and there are rich returns by inviting new people to join the game^[5].

In recent years, the use of mathematical models to simulate infectious diseases has played an important role in analyzing disease control processes^[6,7,8,9]. Many scholars applied the research methods of infectious diseases to many other infectious problems, such as smoking, drinking, rumors, game addiction, etc^{[10,11,12,13,14,15,16,17,18,19,20,21,22,23]}. Sharomi ^[10] provided a rigorous mathematical study to assess the dynamics of smoking and its impact on community public health. The difference in transmission between light and heavy smokers was taken into account, and the incidence was $\frac{\beta(S_{1}+\psi S_{2})}{N}$. Huo et al. ^[11] proposed a new SAITS alcoholism model on networks, which divided alcoholism into mild alcoholism and severe alcoholism. The authors studied the dynamical properties of the unweighted network model, including the basic reproduction number, the existence and stability of the equilibria. Zhao et al. ^[12] discussed a new rumor-truth mixed propagation model and developed an isolation-conversion strategy to minimize the influence of rumor. Li and Guo ^[13] studied an online game addiction model with positive and negative media reports. The authors considered for the first time that the media have positive and negative effects in the process of game transmission, which is an important difference from the process of infectious disease transmission. Viriyapong and Sookpiam ^[14] established a deterministic online game addiction model based on the situation of teenagers' addiction in Thailand, and studied the dynamic properties of the model. Through the numerical simulation, it is concluded that the effectiveness of family education is an important factor to reduce the $R_{0}$, which is of great help to reduce the number of Thai children and adolescents with online game addiction.

In recent years, the optimal control theory is more and more widely used in infectious diseases dynamics^{[24,25,26,27,28]}. Khan et al. ^[18] developed and used a mathematical model to explore the effect of treatment on the dynamics of hepatitis B infection, and obtained the optimal control strategy by combining vaccine, isolation and treatment. Ullah et al. ^[19] established a deterministic model to study the dynamics and possible control of tuberculosis, estimated the parameter values of confirmed tuberculosis cases reported in Khyber Pakhtunkhwa, Pakistan from 2002 to 2017, and obtained a set of control measures that can be used to eliminate tuberculosis infection in the community. Pang et al. ^[20] proposed a new mathematical model without any control strategies to investigate the dynamic behaviors of smoking, applied a concrete example to calculate the incremental cost-effectiveness ratio and analyzed all possible combinations of two control measures.

In real life, in addition to family education, we also have means of isolation and treatment to reduce the number of teenagers addicted to games^[29,30]. Based on the investigation of the problems in reality and inspired by the above literature, we establish a new online game addiction model with considering family education. The following are the main differences between this paper and previous works.

(i) In order to escape from the unpleasant reality, the probability of falling into game addiction will be greater for teenagers who lack family education factors. Thus, in this paper the susceptible groups are divided into two categories: susceptible teenagers without family education $S_{1}$ and susceptible teenagers with family education $S_{2}$. Their infection rates are different when they come into contact with infected people. And the infected teenagers are also divided into two categories: game addicted teenagers without family education $I_{1}$ and game addicted teenagers with family education $I_{2}$. Their addiction degree and withdrawal ratio are different.

(ii) Different from the previous literatures, we not only consider the influence of family education on the problem of game addiction, but also take into account the important control means such as isolation and treatment of teenagers addicted to games in reality. This makes the analysis of game addiction more close to the objective reality.

(iii) We will not only make qualitative analysis on the model, but also make further quantitative simulation analysis on it. In order to find the optimal control strategy, we study the control results and cost-benefit analysis under different combination strategies.

The healthy growth of young people concerns the future of mankind. At present, the problem of adolescent game addiction has broken out in many parts of the world, and more and more scholars have begun to pay attention to this serious problem. The use of mathematical modeling to analyze adolescent addiction is an important method ^{[13,14,18,19,20,21,22,31]}. Inspired by references ^[14,31] and combined with the control strategies of game addiction, a new mathematical model of game addiction with considering family education is established in this paper.

The organizational structure of this rest work is as follows. The online game addiction model and its basic properties are shown in section 2. The basic reproduction number $R_{0}$ and the equilibria are given in section 3. The stability analysis of Addiction-Free Equilibrium is discussed in section 4. The optimal control problem is shown in section 5. The global sensitivity analysis is presented in section 6. Numerical simulation with detailed discussion is given in section 7. The results are summarized and possible suggestions and suggestions are given in section 8.

2.   The model formulation

2.1.   System description

In recent years, mathematical modeling method has gained wide attention, and it has been applied to explore the complex dynamics of some real world problems. These models can be used to develop appropriate control strategies to eradicate the disease. Some numerical simulations using these models can predict the spread of the disease. And the threshold of epidemic outbreak can also be obtained from the results of these simulations. The model of infectious disease based on fractional derivative is another effective method to study the dynamics of infectious disease. The mathematical model based on fractional differential equation has memory effect and non-local property, so we have a deeper understanding of the phenomenon. For more information, please refer to ^{[32,33,34,35,36]}.

As the lack of family education is crucial to the influence of teenagers' addiction to games, we further consider the factors of family education on the basis of literature ^[35]. The susceptible population was divided into those who lacked home schooling and those who did not. And among them, the proportion of addicted games is not the same.

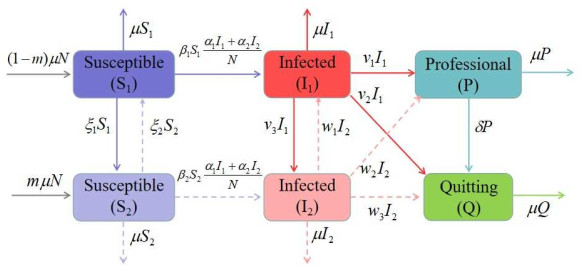
So we divide the total population into six compartments: namely the susceptible people with lack of family education ($S_{1}$), that is, people who lack family education and spend less than 5 hours on playing games every day^[31]. The susceptible people with normal family education ($S_{2}$), that is, people who have family education and spend less than 5 hours on playing games every day. The infected people with lack of family education ($I_{1}$), that is, people who lack family education and play games for more than 5 hours per day. The infected people with perfect family education ($I_{2}$), that is, people who have family education and play games for more than 5 hours per day. The professional people ($P$), that is, people who are E-sports players or engaged in game related career. The quitting people ($Q$), that is, people who are no longer addicted to online games. So we have

The population flow among those compartments is shown in Figure 1.

The transfer diagram leads to the following system of ordinary differential equations:

In system (2.2), $1-m$ denotes the proportion of teenagers who lack education from their families; $\mu$ is the natural birth rate and death rate; $\xi_{1}$ is the rate of progression to $S_{2}$ from $S_{1}$; $\xi_{2}$ is the rate of progression to $S_{1}$ from $S_{2}$; $\beta_{1}$ is the proportion of $S_{1}$ transformed into $I_{1}$ after contacting addicts; $\beta_{2}$ is the proportion of $S_{2}$ transformed into $I_{2}$ after contacting addicts; $\alpha_{1}$ is the transmission rate for contact with $I_{1}$; $\alpha_{2}$ is the transmission rate for contact with $I_{2}$; $v_{1}$ represents the proportion of $I_{1}$ who become $P$; $v_{2}$ represents the proportion of $I_{1}$ who become $Q$; $v_{3}$ represents the proportion of $I_{1}$ who become $I_{2}$; $w_{1}$ represents the proportion of $I_{2}$ who become $I_{1}$; $w_{2}$ represents the proportion of $I_{2}$ who become $P$; $w_{3}$ represents the proportion of $I_{2}$ who become $Q$; $\delta$ denotes the quitting rate of $P$;

2.2.   Nonnegativity and boundedness of solutions

From the practical point of view, we can know that the number of people in each warehouse is nonnegative. So we first prove that the solution is nonnegative. System (2.2) can be rewritten in the form of the following matrix

where $X = (S_{1}, S_{2}, I_{1}, I_{2}, P, Q)^\mathrm{T} \in R^{6}$ and G(X) is given by

So we have,

From the initial value of system (2.2) and the components of matrix G are nonnegative, we can know that all the solutions of the system are remaining in a positive region. Because of $\Sigma_{i = 1}^{6}G_{i}(x) = 0$, $N(t)$ is a constant denoted by $N$. We set

It is a positive invariant set of system (2.2). The dissipative and the global attractor are still in $\Omega$.

3.   The basic reproduction number and existence of addiction equilibrium

3.1.   The basic reproduction number

The basic reproduction number $R_{0}$ represents "the average number of new infections directly caused by an infected case during his entire infectious period, in a wholly susceptible population". It is a key concept in epidemiology, and is inarguably 'one of the foremost and most valuable ideas that mathematical thinking has brought to epidemic theory'^[37].

Obviously, system (2.2) has Addiction-Free Equilibrium, which is written down as the following

Next, we obtain the basic reproduction number $R_{0}$ by using the classical method of next generation matrix. (For details, please refer to reference ^[38]). Letting $x = (I_{1}, I_{2}, P, Q, S_{1}, S_{2})^\mathrm{T}$, then system (2.2) can be written as

where

The Jacobian matrices of ${\mathscr{F}}(x)$ and ${\mathscr{V}}(x)$ at the Addiction-Free Equilibrium $E_{0}$ are

where

Following Driessche et al.^[38], the basic reproduction number, denoted by $R_{0}$, is given by

where $\rho(A)$ denotes the spectral radius of a matrix A, $d_{1} = \mu+\xi_{1}+\xi_{2}$, $d_{2} = \mu-m\mu+\xi_{2}$, $d_{3} = \xi_{1}+m\mu$, $k_{3} = \mu+v_{1}+v_{2}+v_{3}$ and $k_{4} = \mu+w_{1}+w_{2}+w_{3}$.

3.2.   Existence of addiction equilibrium

The Addiction Equilibrium $E^{*} = (S_{1}^{*}, S_{2}^{*}, I_{1}^{*}, I_{2}^{*}, P^{*}, Q^{*})$ of system (2.2) is determined by equations:

where $k_{1} = \mu+\xi_{1}$, $k_{2} = \mu+\xi_{2}$, $k_{3} = \mu+v_{1}+v_{2}+v_{3}$, $k_{4} = \mu+w_{1}+w_{2}+w_{3}$ and $k_{5} = \delta+\mu$. By solving the equations, we have

where

Substituting the expression of $I_{1}^{*}$ and $I_{2}^{*}$ into $\lambda_{0}^{*}$, we get a quadratic equation after simplification.

where

We know $F_{1}$ is positive and $F_{3}$ is negative when $R_{0} > 1$. Combined with Theorem 2 in ^[40], we can get the following theorem.

Theorem 1. In the model (2.2), there exists an Addiction-Free Equilibrium $E_{0} = (\frac{N(-m\mu+\mu+\xi_{2})}{\mu+\xi_{1}+\xi_{2}}, \frac{N(\xi_{1}+\mu m)}{\mu+\xi_{1}+\xi_{2}}, 0, 0, 0, 0)$. And model (2) has:

(i) If $F_{3} < 0$, then model (2) has a unique Addiction Equilibrium if $R_{0} > 1$,

(ii) If $F_{2} < 0$, $F_{3} = 0$ or $(F_{2})^{2}-4F_{1}F_{3} = 0$, then model (2) has a unique Addiction Equilibrium,

(iii) If $F_{3} > 0$, $F_{2} < 0$ and $(F_{2})^{2}-4F_{1}F_{3} > 0$ then model (2) has two Addiction Equilibrium,

(iv) Otherwise no endemic equilibrium exists.

4.   Stability analysis of addiction-free equilibrium

We denote a vector $x = (I_{1}, I_{2}, P, Q, S_{1}, S_{2})^\mathrm{T}$ and

So the Jacobian matrix of $f(x)$ about vector $x$ is as the following:

Theorem 2. For the system (2.2), the Addiction-Free Equilibrium $E_{0}$ is Locally Asymptotically Stable (LAS) if $R_{0} < 1$.

Proof. Since

where

It is easily known that the eigenvalues of $J_{4}$ are $\lambda_{1} = -k_{5}, \ \ \lambda_{2} = \lambda_{3} = -\mu, \ \ \lambda_{4} = -k_{1}-\xi_{2}$ and they are all negative. The characteristic equation of characteristic matrix of $M$ is

where

and

Let's replace $R_{0}$ with the following shorthand.

Due to $0 < R_{0} < 1$, so we have

So the real part of all eigenvalues of $M$ are negative, the Addiction-Free Equilibrium (AFE) $E_{0}$ is LAS. The proof is completed.

Theorem 3. For the system (2.2), the Addiction-Free Equilibrium $E_{0}$ is Globally Asymptotically Stable (GAS) if $R_{0} < 1$.

Proof. We introduce the Lyapunov function V as follows:

So

Because $0 < R_{0} < 1$, we can obtain the conclusion that $V'(t)\leq 0$. Due to the LaSalles Invariance Principle^[39], the Addiction-Free Equilibrium $E_{0}$ is Globally Asymptotically Stable.

5.   Optimal control analysis

In order to explore how to better control or inhibit the problem of game addiction, we add three control means (family education $u_{1}$, isolation $u_{2}, u_{3}$, treatment $u_{4}, u_{5}$) on the basis of system (2.2), and get the following new state system.

where $\theta_{1}$ indicates the proportion of susceptible people in adolescence who lack family education are transformed into normal susceptible people under the communication and education of family members; $\theta_{2}$ and $\theta_{3}$ respectively indicate the proportion of addicts who lack family education and normal family addicts who quit the game through formal treatment. The control variables $U(t) = (u_{1}, u_{2}, u_{3}, u_{4}, u_{5})\in\Lambda$ are bounded and measured with

Our control goal is not only to minimize the number of game addicts, but also to keep the cost as low as possible. So we consider this objective function

where $A_{1}, A_{2}$ are the weight coefficients relate to addicts. The constants $B_{1}, B_{2}, B_{3}, B_{4}, B_{5}$ are the weight coefficients of the control variables $u_{1}, u_{2}, u_{3}, u_{4}$ and $u_{5}$. Thus we need to find the optimal control such that

Through the Pontryagin's maximum principle^[40], we consider the Hamiltonian function as follows

where $\lambda_{i}\ (i = 1, 2, 3, 4, 5, 6)$ are the adjoint variables that satisfy this following adjoint system.

The corresponding terminal condition of the above adjoint system is

and the optimal controls $u_{1}^{*}, u_{2}^{*}, u_{3}^{*}, u_{4}^{*}, u_{5}^{*}$ are given by

where

6.   Global sensitivity analysis

In this section, we will study global sensitivity analysis (SA) of the model's base reproduction number $R_{0}$ to identify those model parameters that have the greatest impact on disease dynamics. Global sensitivity analysis is used to quantify the uncertainty in a mathematical model. The most effective combination of methods is to quantify the sensitivity of the model parameters using numerical simulation results of Latin hypercube sampling (LHS) and partial rank correlation coefficient (PRCC). LHS is a layered sampling technique without substitution that allows efficient analysis of variations in each parameter within an uncertain range. PRCC measures the strength of the relationship between the output results and parameters of the model, and indicates the degree of influence of each parameter on the results. To generate the LHS matrix, all model parameters are uniformly distributed. Referring to relevant literatures^[13,14,31], we assume that the baseline values of all parameters are: $m = 0.8$, $\mu = 0.04$, $\xi_{1} = 0.05$, $\xi_{2} = 0.15$, $\beta_{1} = 0.7$, $\beta_{2} = 0.45$, $\alpha_{1} = 0.4$, $\alpha_{2} = 0.55$, $v_{1} = 0.05$, $v_{2} = 0.08$, $v_{3} = 0.05$, $w_{1} = 0.15$, $w_{2} = 0.15$, $w_{3} = 0.1$, $\delta = 0.25$. We then ran a total of 1,000 simulations. PRCC values and corresponding P-values of each parameter in $R_{0}$ of model (2.2) are shown in Figure 2 and Table 1.

The larger the absolute value of PRCC of the parameter is, the greater its influence on the basic regeneration number is. And $R_{0}$ is more sensitive to the parameter with smaller $p$ value. As can be seen from Figure 2, $\mu$, $\xi_{2}$, $\beta_{1}$, $v_{1}$ and $v_{3}$ have large positive PRCC values, while $\xi_{1}$, $\beta_{2}$, $\alpha_{1}$ and $w_{1}$ have large negative PRCC values. If we want to lower the $R_{0}$ value to control the spread of the game, we can lower the parameter with a positive PRCC value, or increase the parameter with a negative PRCC value.

Figures 3–9 show the influence of different model parameters on $R_{0}$ value. And we can see what happens to $R_{0}$ when the parameters change. In Figure 3 we can see that $R_{0}$ increases as $m$ and $\mu$ increase. In Figure 4 we can see that $R_{0}$ decreases as $\xi_{1}$ increases and increases as $\xi_{2}$ increases. In Figures 5 and 6, we can see that $R_{0}$ increases as $\beta_{1}$, $\beta_{2}$, $\alpha_{1}$ and $\alpha_{2}$ increases. In Figure 7 we can see that $R_{0}$ decreases as $v_{1}$ and $v_{2}$ increase. In Figure 8, we can see that $R_{0}$ decreases as $v_{3}$ increases and increases as $w_{1}$ increases. Figure 9 reflects that $R_{0}$ decreases with the increase of $w_{2}$ and $w_{3}$. All of this information tells us that we can control the spread of the game by taking corresponding measures in our lives.

7.   Comparison of different control strategies and cost-effectiveness analysis

7.1.   Different control strategies

In this section, we use the forward backward sweep method with the fourth order Runge-Kutta scheme to solve the above optimal system. The process of the algorithm is as follows: the first step is to guess a reasonable initial value of the control variable and use the fourth order Runge-Kutta method to solve the state system from front to back according to time. The second step is to solve the adjoint system forwards. The third step is to substitute the obtained state solution and adjoint solution into the expression of the control variables and update the value of the control variables by a convex combination. The fourth step is to continue the iteration with the new control variables until the two adjacent optimal solutions are close enough. For more details of the algorithm, please refer to ^[41,42,43].

In order to compare the effect of different control measures, we combine the three control measures and get the following control strategy.

Scenario 1: Single control strategies

  Strategy A: family education only ($u_{1}$).

  Strategy B: isolation only ($u_{2}, u_{3}$).

  Strategy C: treatment only ($u_{4}, u_{5}$).

Scenario 2: Double control strategies

  Strategy D: family education ($u_{1}$) + isolation ($u_{2}, u_{3}$).

  Strategy E: family education ($u_{1}$) + treatment ($u_{4}, u_{5}$).

  Strategy F: isolation ($u_{2}, u_{3}$) + treatment ($u_{4}, u_{5}$).

Scenario 3: Triple control strategies

  Strategy G: family education ($u_{1}$) + isolation ($u_{2}, u_{3}$) + treatment ($u_{4}, u_{5}$).

The main object of this study is 12–24 years old children and youth in Chinese mainland. According to some relevant statistics^[1], we choose the initial value of each warehouse as follows: $S_{1}(0) = 20$, $S_{2}(0) = 100$, $I_{1}(0) = 5$, $I_{2}(0) = 5$, $P(0) = 2$, $Q(0) = 6$(units in million). With the help of ^[13,14,31], other parameter values we selected are as follows: $m = 0.8$, $\mu = 0.04$, $\xi_{1} = 0.05$, $\xi_{2} = 0.15$, $\beta_{1} = 0.7$, $\beta_{2} = 0.45$, $\alpha_{1} = 0.4$, $\alpha_{2} = 0.55$, $v_{1} = 0.05$, $v_{2} = 0.08$, $v_{3} = 0.05$, $w_{1} = 0.15$, $w_{2} = 0.15$, $w_{3} = 0.1$, $\delta = 0.25$, $\theta_{1} = 0.6$, $\theta_{2} = 0.25$, $\theta_{3} = 0.5$. The weight coefficients of the objective function are as follows: $A_{1} = 30$, $A_{2} = 10$, $B_{1} = 1$, $B_{2} = 10$, $B_{3} = 10$, $B_{4} = 50$, $B_{5} = 50$. As many control measures are very difficult to achieve 100% in the actual implementation process, the control variable $u_{i}(t)$ $(i = 1, 2, 3, 4, 5)$ are subjected to the constraints^[44],

The implementation of the whole control measures is set at 100 days.

Scenario 1: Single control strategies

The population change diagram of $I_{1}$ and $I_{2}$ warehouses without control and strategy A, B and C in scenario 1 are shown in Figure 10. In Figure 10 (a), we can see that without the intervention of control measures, the addicts who lack family education $I_{1}$ will reach the peak in the following period of time, and then gradually tend to be stable. In strategy A, B and C, the number of addicts without family education is significantly reduced. Strategy A is the slowest and strategy C is the fastest. In Figure 10 (b), we can see that without the intervention of control measures, the addicts in normal families $I_{2}$ will gradually drop to a certain height and then remain stable. $I_{2}$ in strategy A, B and C will also decrease. Similar to Figure 2 (a), strategy A decreases the slowest and strategy C decreases the fastest.

The change of optimal control variables of each control strategy in scenario 1 are shown in Figure 11. In Figure 11 (a), we can see that in strategy A, the intensity of family education $u_{1}$ needs to be maintained at the maximum value of 0.8 from the beginning to the end. As can be seen from Figure 11 (b) and (c), the control intensity of $u_{2}$, $u_{3}$, $u_{4}$ and $u_{5}$ is maintained at the maximum intensity of 0.8 at the beginning, and then gradually decreases to 0 from the 38th day, the 18th day, the 16th day and the 6th day respectively.

From the comparison of strategy A, B, C and without control, we can see that the effect of using strategy A to control is not ideal, which is worse than using strategy B and strategy C. Therefore, we know that it is not enough to rely only on family education in controlling teenagers' game addiction.

As can be seen from the comparison results in Figure 10, when control measures are used alone, the most effective control measure is the treatment measure. With treatment, teenagers in $I_{1}$ and $I_{2}$ who are addicted to video games can be quickly brought back into normal life. In Figure 11 (c), the variation rules of control variables $u_{4}$ and $u_{5}$ in strategy C are shown. Compared with treatment $u_{5}$ for adolescents without lack of family education, treatment $u_{4}$ for adolescents without lack of family education should last longer at the maximum intensity of 0.8, and then gradually decrease.

Scenario 2: Double control strategies

Figure 12 (a) and (b) respectively show the number of game addicts without family education $I_{1}$ and the number of game addicts with family education $I_{2}$ of strategy D, E and F in scenario 2. These results are similar to those in strategy B and C, and are ideal.

Figure 13 (a) shows the changes in the control variables of strategy D. At the beginning, $u_{1}$, $u_{2}$ and $u_{3}$ kept at the level of 0.8, and then gradually decreased to 0 at the 43rd day, the 19th day and the 25th day, respectively. Figure 13 (b) shows the change of control variables of strategy E. At the beginning, $u_{1}$, $u_{4}$ and $u_{5}$ kept at the level of 0.8, and then gradually decreased to 0 at the 57th day, the 9th day and the 6th day, respectively. Figure 13 (c) shows the changes in the control variables of strategy F. $u_{2}$, $u_{3}$, $u_{4}$ and $u_{5}$ all kept at the level of 0.8 at the beginning, and then gradually decreased to 0 at the 20th, 7th, 6th and 3rd day, respectively.

As can be seen from the comparison results in Figure 12, when the two control measures are combined, the most effective control strategy is strategy F (isolation and treatment), which can rapidly reduce the number of people in $I_{1}$ and $I_{2}$. From Figure 13 (c), we can see how the strength of each control variable of policy F should change. It can be seen that the control variables $u_{2}$ and $u_{4}$ for adolescents with lack of family education will last longer and require greater intensity compared with $u_{3}$ and $u_{5}$. It also suggests that in the real world, isolation and treatment programs for gaming addicts should be developed quickly to help teens overcome their addiction.

Scenario 3: Triple control strategies

Figure 14 (a) and (b) respectively show the number of game addicts without family education $I_{1}$ and the number of game addicts with family education $I_{2}$ of strategy G in scenario 3. In Figure 15, the change process of the control variables of strategy G is shown. All the control variables $u_{1}$, $u_{2}$, $u_{3}$, $u_{4}$ and $u_{5}$ were kept at the maximum strength of 0.8 at the beginning, and then gradually decreased to 0 from the 25th day, the 9th day, the 11th day, the 6th day and the 3rd day respectively.

As can be seen from Figure 14, when strategy G is adopted, the number of people in compartment $I_{1}$ and $I_{2}$ will decrease rapidly to the end. This is a very desirable result. Figure 15 shows the change rules of each control variable. By comparing with Figure 13(c), we find that the additional control measure, family education $u_{1}$, needs to be implemented for a longer time and with a greater intensity. This mainly depends on the implementation of family education, which needs to invest a lot of manpower in a certain period of time and rebuild a harmonious family environment through effective communication.

What we are concerned about is that the number of addicts in the whole control process is as small as possible, but from the image, it is difficult to distinguish the total number of addicts under each strategy. Therefore, we need to further analyze and compare these control strategies from specific data.

7.2.   Cost-effectiveness analysis

Cost-effectiveness analysis is to evaluate the rationality of the strategy by calculating the incremental cost-effectiveness ratio (ICER) generated in the process of strategy implementation^[26,45]. The ICER of strategy A relative to strategy B is defined as follow.

where TC(B) denotes the total cost of strategy B in implementation, TA(B) indicates that the total number of averted infectious people in the implementation process of strategy B compared with that without control. The definition expression of the total cost (TC) is as follows

where $C_{1} = 2$, $C_{2} = 30$, $C_{3} = 20$, $C_{4} = 50$, $C_{5} = 40$ (unit: ＄). There are several underlying assumptions here.

(1) $C_{1}$ is the cost per person per day when family education $u_{1}$ measure is taken. When the family education measure $u_{1}$ is implemented, the cost consumed per person per day is $C_{1}$. It is worth noting that the implementation of family education will not only be applied in the addict without family education $I_{1}$, but also in the susceptible person without family education $S_{1}$. This will allow $S_{1}$ to be converted into $S_{2}$ as much as possible and reduce the number of people flowing into $I_{1}$. Family care mainly depends on the communication and understanding between the guardian and the teenagers, so the cost consumption here is relatively small. Let's take $C_{1}$ = 2.

(2) $C_{2}$ and $C_{3}$ represent the cost per person per day to isolate people in $I_{1}$ and $I_{2}$, respectively. The mechanics of game addiction are similar to those of drug addiction. Once the addict is separated from the internet, he will have obvious withdrawal reaction in a short time. In addition, teenagers are in adolescence, easy to appear rebellious psychology and behavior. Therefore, the cost of isolation measures will be relatively high, especially for addicts without family education. Through some social surveys, we assume the cost coefficient $C_{2} = 30$, $C_{3} = 20$.

(3) $C_{4}$ and $C_{5}$ represent pharmacological interventions for $I_{1}$ and $I_{2}$, respectively. The Chinese mainland now has more than 100 internet addiction treatment institutions^[31]. The clinic doctors and other professionals in the institution carry out comprehensive auxiliary treatment for game addicts, such as drug, physical and skill training. Institutions also set up learning rooms, libraries, painting rooms, gyms, karaoke rooms and so on, through a variety of courses to addiction patients' attention from online to offline, cultivate their various interests, from interaction with the game screen to interpersonal interaction in real life. The treatment cycle is usually 3 months. Through some statistical investigation, we assume that the cost coefficient $C_{4}$ = 50, $C_{5}$ = 40.

The definition expression of the total averted cases (TA) is as follows

where $I_{1}, I_{2}$ denote the addicts without and with family education of without control respectively, $\tilde{I_{1}}, \tilde{I_{2}}$ denote the addicts without and with family education of one strategy respectively. $\int_{0}^{t_{f}}(I_{1}+I_{2})dt$ is the total number of people infected (TI) in the whole process of without control. We show the value of infection averted ratio (IAR) and incremental cost-effectiveness ratio (ICER) under all control strategies (A to G) in Table 2.

From the ICER data in the last column of Table 2, we can know that ICER(F) = $1.7627$ is the smallest, which means that more people can avoid being addicted to the game with the least cost. When the policy budget is limited, we should choose strategy F as the optimal control strategy.

From the IAR data of each strategy in Table 2, we can see that strategy G has the largest proportion of avoiding being addicted to the game. When the policy budget is adequate, we should choose strategy G as the optimal control strategy from the perspective of people-oriented, so that as many people as possible can avoid being addicted to the game.

8.   Conclusions

The lack of family education has a great impact on Teenagers' game addiction. In this paper, a six dimensional nonlinear deterministic online game addiction model considering the impact of lack of family education on teenagers' game addiction was established. By the next generation matrix, we obtained the expression of the basic reproduction number $R_{0}$. Then some dynamic properties of the model were analyzed. In the analysis of optimal control theory, an optimal system with three control measures was established. Through the Pontryagin's maximum principle, we got the expression of the optimal control pairs.

In the numerical simulation, the combination of LHS and PRCC is used to perform global sensitivity analysis of the parameters in $R_{0}$, and the relationship between $R_{0}$ and all parameters is shown in the graph. We combined the three control measures (family education, isolation and treatment) and simulated the seven control strategies in three scenarios by using the forward backward sweep method with fourth order Runge-Kutta scheme. Then the cost-effectiveness analysis was carried out, and different optimal control strategies under different budget situations were determined through ICER and IAR data under different combination strategies.

Through the above analysis, we found that the combination of isolation and treatment was the optimal control strategy in the case of limited budget. When the budget was adequate, if the control measures of family education were added, more teenagers could avoid being addicted to online games.

Conflict of interest

The authors declare no conflict of interest.