A predictive neuro-computing approach for micro-polar nanofluid flow along rotating disk in the presence of magnetic field and partial slip

1.   Introduction

Neural networks are widely used in financial operations, trading, enterprise planning, product maintenance, and business analytics. Neural networks are also widely used in corporate applications such as marketing exploration and forecasting, risk assessment and fraud detection. In input multilayer neural networks, backpropagation is a popular learning mechanism. This approach has lately been employed by examiners to investigate heat transfer characteristics and also the fluid flow of non-Newtonian systems. Using neural networks, Shoaib et al. ^[1] examined the creation of entropy under the influence of magnetohydrodynamic and thermal radiation. Ullah et al. ^[2] used artificial neural networks with a Levenberg-Marquardt backpropagation approach to explore the influence of magnetic fields and Hall current on the flow of micropolar nanofluid between two rotating parallel plates. By combining the Levenberg-Marquardt with the backpropagated Neural Network, Zubair et al. ^[3] investigated the flow of silver-based Dihydrogen carbon nano-tubes between two stretchy coaxial disks. To examine the smoking model in this study, Shoaib et al. incorporated intelligent computing algorithms for entropy analysis in the fluid flow systems ^[4,5,6] and the epidemic model ^[7]. Aljohani et al. ^[8] investigate intelligent numerical computational models by including a Levenberg-Marquardt backpropagation-based on neural network to examine the magnetohydrodynamics of a third-grade fluid flow for wire coating assessment.

The micro-polar fluid is a liquid crystal or microbes such as blood or polymeric fluid. The micro-polar fluid flow is a dynamically oriented crystal particle motion that is easily narrated by the law of conservation momentum and mass. The constitutive relationship of fluid has characterized the micromotion, couple stress and spin inertia. The micro-polar fluid flow has a broader spectrum of features. The flow of micro-polar fluid has attracted the attention of many researchers, they developed different models to study the motion of the micro-polar fluids. These models and theories discussed micro-polar fluid motion from different aspects, such as Eringen ^[9] suggested a micro-polar fluid model. Ishak et al. ^[10] studied the flow of the boundary layer on the planer surface. Acharya et al. ^[11] investigate the effect of heat radiation on the Illustration of the Reynolds number on micropolar nanofluid flow through a permeable media. Ramesh et al. ^[12] examined the time-dependent squeezing flow of Casson-micropolar nanofluid with injection/suction and slip effects. Siddiqui et al. ^[13] examined Casson nanofluid MHD flow and heat transmission via a porous medium over a stretched sheet. Krishna et al. ^[14] investigated the effects of thermal radiation, chemical reaction, Hall, and ion slip on the MHD oscillatory rotational flow of a micro-polar liquid. Perdikis et al. ^[15] investigate the constant flow of a micropolar fluid through an immovable plate in the presence of radiation. Sandeep and Sulo-chana ^[16] explored the dual solution of magneto hydrodynamic micro-polar fluid flow and unsteady mixed convection along a stretching/shrink sheet in the existence of non-uniform heat source/sink. Nadeem et al. ^[17] are exploring the numerical consequences of Nanofluid micro-polar boundary layer flow. Similarly, Ali et al. ^[18] calculated the numerical consequences of the micro-polar fluid flow for the boundary layer over a cylinder.

Choi ^[19] introduces the nanofluid concept. Nanofluid has various characteristics and applications the researchers have been focusing on to explore the behavior of nanofluid from different aspects. Due to viscous behavior, the small size and higher thermal conductivity of Nanofluids (Nanometer sized metallic particle colloidal suspension) make them highly effective, they are attracting considerable attention due to their varied variety of applications in the field of biological science and engineering. Rashidi et al. ^[20] used the RK4 method to analyze the analytical and numerical solution of viscous water-based nanofluid with second-order slip condition in combination with the shooting iteration method. Hayat et al. ^[21] found a solution of Oldroyd-B Nano-fluid flow in the existence of heat generation/absorption past a stretched surface. Dhanai et al. ^[22] investigated Nanofluid the flow while identifying numerous Nanofluid flow solutions with mixed convection and slip effect. Koriko et al. ^[23] focused on the boundary layer flow of nanofluid in their study by using a horizontal surface. Mehmood et al. ^[24] applied Optimal Homotopy Analysis Method to study the flow of Oblique Jeffery nanofluid in the vicinity of a stagnation point. Hayat et al. ^[25] checked the nanofluid flow slip effects in the existence of magnetic field due to a rotating disk. ^[26] used the differential transformation method to analyze the time-dependent nanofluid flow between two parallel plates. Sandeep et al. ^[27] conducted their study on analyzing the increase or decrease in the rate of heat transfer of unsteady magneto hydrodynamics nanofluid flow. Furthered Sandeep study ^[28] by checking and investigating a thin flow of nanofluid under the action of magnetic field consisting of graphene Nanoparticles. Many other researchers have already conducted their studies on checking and investigating the effects of the flow of Nanofluid particles such as ^{[29,30,31,32,33,34,35]}.

The researchers are interested in studying the flow of fluid through a rotating disk due to its numerous applications in engineering and aeronautical sciences, such as thermal power generation systems, air cleaning machines, medical equipment, gas turbine rotors, crystal growth processes, computer storage devices, electronic crystal growth processes, devices, and numerous more ^[36,37,38]. Von Karman ^[39] is one of the popular researchers who conducted his research on fluid flow through a rotating disc, which has been regarded as pioneer contribution to this area of research. He applied the momentum-integral approach to conduct an analytical analysis of the resulting problem. Cochran ^[40] solved the von Karman problem asymptotically. Ackroyd ^[41] studied suction/injection effects and provided a series solution with exponentially decaying coefficients in the Von Karman problem. These solutions are based on the coefficients called exponentially decaying coefficients. Bashir et al. ^[42] examined the Thermophoresis phenomena in the radiative flow around a rotating disk vertical movement in a porous environment. Asymmetric laminar flow and heat transmission of a viscous fluid were investigated between contracting rotating disks ^[43]. Hussain et al. ^[44] investigated the radiation flow of a viscous nanofluid over a porous stretched rotating disc with extended slip. Turkyilmazoglu and Senel ^[45] investigate flow of viscous liquid and heat/mass transfer using a porous disc with rotating frame. Zhou et al. ^[46] study the numerical analysis of thermal radiative Maxwell nanofluid flow over-stretching porous rotating disk.

Stochastic numerical computing methodologies are produced for the solution of linear and non-linear differential equations describing various applications occurring in different fields by using the power of evolutionary/swarming computing-based optimization techniques associated to neural network models. The most recent implementation of stochastic numerical computing solutions comprises bio-mathematical model ^{[47,48,49,50,51,52]}, Mathematical model for fluid dynamic problems ^{[53,54,55,56,57,58,59]}, astrophysics ^{[60,61,62,63,64,65]} and fractional model ^[66]. The related articles ^[69,70] can be referred to for further details.

The importance of algorithm-based artificial intelligence (AI) solvers and above cited research work inspired the authors to develop the fluidic system MHD-MNRD to implement the soft computing paradigm for its heuristic solution and statistical analysis.

The innovation contributions of the present study for backpropagation networks for magnetohydrodynamics micro-polar nanofluid flow over a rotating disk model along with the partial slip condition are highlighted as follows.

● The numerical computation has been designed through the Levenberg-Marquardt backpropagation with neural network (LMB-NN) for the comparative study of magnetohydrodynamics micro-polar nanofluid flow over a rotating disk (MHD-MNRD) model along with the partial slip condition.

● The governing mathematical model of the magnetohydrodynamics micro-polar nanofluid flow over a rotating disk (MHD-MNRD) model represented with nonlinear PDEs is reduced to a nonlinear system of ODEs by the competency of similarity adjustments.

● A reference data of designed networks is constructed effectively for variants of MHD-MNRD demonstrating the scenarios for micro-polar parameters, Brownian motion, Lewis number, magnetic parameter, velocity slip parameter and thermophoresis parameter by applying the Adams numerical method.

● The Mathematica software is used to compute the dataset for designed LMB-NN for the variation of micro-polar parameters, Brownian motion, Lewis number, magnetic parameter, velocity slip parameter and thermophoresis parameter.

● MATLAB software is used to interpret the solution and the absolute error analysis plots of the MHD-MNRD model.

● The training, testing, and validation based process block structure of LMB-NN exploited to calculate the approximate solutions of MHD-MNRD and comparative study validate the consistent accuracy.

● The worthy performance of the designed network was additionally established by a learning curve on MSE based fitness, histograms and regression metrics.

Neural networks are also ideally adapted to helping people solve difficult problems in everyday life. They can investigate and simulate difficult and complicated, multidimensional interactions between inputs and outputs, simplify complex relationships and draw conclusions from them, as well as model high volatility data. Neural networks, therefore, have the potential to enhance decision-making in fields like: Transportation network logistics optimization, voice and character recognition, which are frequently referred to as natural language processing, detection of credit card and Medicare fraud, targeted marketing, robotic control systems, disease and medical diagnosis, energy demand and Electrical load forecasting, financial predictions for stock prices and chemical compounds classification, etc.

The objective of this work is to developed a new ANN technique to solve the problem "A predictive neuro-computing approach for micro-polar nanofluid flow due to a rotating disk in the presence of magnetic field and partial slip effect" through stochastic technique (LMB-NN). Furthermore, the motivation to set a platform for further studies to take help from this new technique. The advantages of this paper are to account for different parameters is the level of accuracy ranging from 10^-10 to 10^-13, the recommended approach is distinguishable from the proposed and reference outcomes. Validation, convergence, stability and verification of LMB-NN for solution predictive strength of the proposed model are certified in terms of achieved accuracy, regression index measurements, and analysis of error histogram illustrations. The numerical n graphical solution is shown in the results and discussion section. Besides of this work other advantages of this paper are to obtain some statistical data of the model that is Mean square error, gradient, performance, Mu.

The rest of the analysis is structured as follows: in Section 2, the formulation of the problem of the three-dimensional micro-polar Nano-fluid flow system is described, the solution technique is outlined in Section 3, along with the results of the suggested LMB-NN on various variants of MHD-MNRD, while in the last section, the final comments and possible future analysis are discussed.

2.   Problem formulation

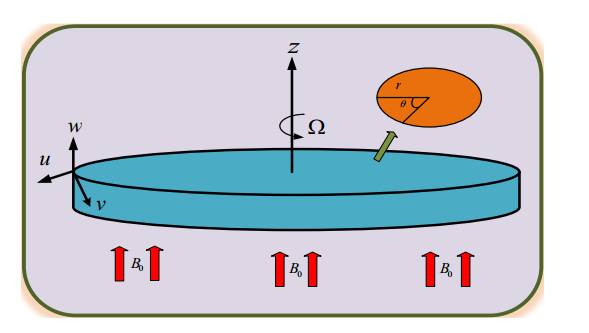
Consider the steady flow of an incompressible and electrically conducting micropolar nanofluid due to an infinite rotating disk as shown in Figure 1. The disk is rotating with a constant angular velocity $\Omega$. The consequences of the velocity slip condition are taken into consideration. ${N_1}, \, \, {N_2}, \, \, {N_3}$ are sued to micro-rotation components and $r, \, \, \theta, \, \, z$ cylindrical co-ordinates with $u, \, \, v, \, \, w$ velocity components are to be used. Here neglecting the body forces and body couples. Under the action applied normal to the fluid and magnetic field with strength ${B_0}$, the flow is examined. Under the given assumption, equations of the boundary layer problem can be written as follows ^[16,17,18]:

These equations can be written in the form of components

In the given flow system, boundary conditions as follow:

In the above expression the material constant (viscosity Coefficient) are denoted by $\alpha \, , \, \beta \, , \, \gamma \, , \, k$ and absolute viscosity is indicated by $\mu$. Fluid density, fluid heat capacity and Nanoparticles are represented by ${\rho _f}$, ${\left({\rho C} \right)_f}$ and ${\left({\rho C} \right)_p}$, respectively. The thermophoretic diffusion co-efficient and the Brownian diffusion co-efficient are indicated by ${D_T}$ and ${D_B}$, respectively and $C$ is the concentration distribution. Concentration and Temperature at the surface are indicated by ${C_w}$ and ${T_w}$, and away from surface, the ambient concentration and temperature values are showed by ${C_\infty }$ and ${T_\infty }$ respectively.$\eta$ is indicated dimensionless distance from disk and the velocity, and micro-rotation components in non-dimensional form are introduced to solve the system of Eqs (4−12) as follow:

By using the dimensionless and non- dimensionless quantities, transformed the Eqs (4−12) into the following forms ^[68]:

Using the boundary condition (13), which reduce into

From above expression, $f$ and $g$ are the components of velocity along $\, \, x\, - axis\, \, and\, \, y\, - axis$, respectively, while ${F_1}, \, \, {F_2}$ and ${F_3}$ are denoted components of micro-rotation in the directions of $x, \, \, y$ and $z$ respectively. In above transformed equations, the dimensionless parameters are, $({A_1} - {A_6})$ the micro-polar parameter, $(Nb)$ Brownian motion parameter, $(M\, )$ magnetic parameter, $(\delta)$ velocity slip parameter, $(Nt)$ thermophoresis parameter, $(Le)$ Lewis number and $(\Pr)$ Prandtl number are expressed as follow:

Skin-friction co-efficient and local Nusselt number are the physical dimensionless quantity, which is listed as:

where $k* = \frac{k}{\mu }$ and ${{\rm{Re}} _r}$ are indicated the material parameter and rotational Reynold number, respectively.

3.   Methodology

There are two parts of the methodology described here: the first part provides the appropriate description for the construction of the LMB-NN dataset, whereas, in Section 2, the implementation methodology approved for LMB-NN is described. In the Figure 2, the illustration of the workflow is shown in the process block structure.

The comparative solutions, i.e., the LMB-NN dataset, are de termined using the Mathematica programming package in which 'NDSolve' is exploited by using the Adams numerical solver. The 'ND Solve' procedure is operated with default parameter settings including the goal of accuracy, tolerances and step size for the differential equation to be solved.

The suggested LMB-NN consists of a combination of the structure of a multi-layer neural network and computation with backpropagation by Levenberg-Marquardt. For neural network methodology, Figure 3 presents a single neuron model. The proposed LMB-NNs are implemented in the Matlab software package via the 'nftool' neural network toolbox routine using appropriate hidden neuron settings, training data, validation data, testing data and learning methodology.

4.   Numerical analysis with description

Numerical computations through the designed LMB-NN are provided here for the presented fluidic systems based on steady 3-D micro-polar Nano-fluid system as given in the Eqs (15−23). For all the six scenarios of system (15–23) model by variation of $M, \, \delta, \, Nt, Nb, \, Le$ and all cases$({A_1}, {A_2}, {A_3}, {A_4}, {A_5}, {A_6})$, designed for 3 cases for different values of $Pr$ are presented in Table 1 for micro-polar material constants and all 6 different scenarios of model MHD-MNRD in Table 2.

For all 6 scenarios, the reference solutions $f(\eta), \, \, \, f'(\eta), \, \, \, g(\eta), \, \, \, {F_1}(\eta), \, \, \, {F_2}(\eta), \, \, \, \, {F_3}(\eta), \, \, \, \, \theta (\eta)\, \,$ and $\phi (\eta)$, i.e., the LMB-NN dataset, are deliberated with the Adams method for similar variable η lies in 1 and 4, with step size 0.02, for all 3 cases of the model MHD-MNRD in Eqs (15–23). The dataset generated by the Adams technique in terms of $f(\eta), \, \, \, f'(\eta), \, \, \, g(\eta), \, \, \, {F_1}(\eta), \, \, \, {F_2}(\eta), \, \, \, \, {F_3}(\eta), \, \, \, \, \theta (\eta)\, \,$ and $\phi (\eta)$ which will be incorporated for comparative study as well.

MHD-MNRD model has received the optimal outcomes through the designed stochastic solver LMB-NN which is provided in Eqs (15–23) using the 'nftool' procedure with 10 (neurons), 80% of training data values, 10% testing and 10% for validation and Levenberg-Marquardt backpropagation efficient optimization strength. The neural network structure is showed in Figure 4 and the suggested LMB-NN method is recurrent for variation $M, \, Nb, \delta, \, \, Le, \, Nt$ and all cases$({A_1}, {A_2}, {A_3}, {A_4}, {A_5}, {A_6})$ of all 6 different scenarios of model MHD-MNRD with numerical values are presented in Table 2.

The consequences of the LMB-NN of all 6 scenarios for case 3 of the MHD-MNRD model are presented in Figures 5−19. The results for case 3 of all six scenarios $(M, \delta, Nb, Nt, Le$ and all cases$({A_1}, {A_2}, {A_3}, {A_4}, {A_5}, {A_6})$) in terms of efficiency and transition states are described in Figures 5 and 6, respectively. For different scenarios, for the respective case 3, Figures 7−12 showed fitting designs for error analysis for the presented mathematical model. The regression analyses are shown in Figures 14−19, while the error histograms are illustrated in Figure 13 for 3 different variants of the MHD micro-polar nanofluid model. In addition, for validation, training, and testing, backpropagation measures, executed epochs, performance and time complexity, in terms of MSE, the convergence achieved is described in Tables 3−8 for all six scenarios respectively, for the micro-polar Nano-fluid MHD-MNRD model.

In Figures 5a−5f, subfigures are showed the Mean square error (MSE) convergence for best curve, test, validation and train are denoted for case 3 of micro-polar Nano-fluid model MHD-MNRD. One can see that the best performance of the network is attained at 104,114,104, 90,106 and 119 epochs with mean square error (MSE) in the range of ${10^{ - 10}}$, ${10^{ - 10}}$, ${10^{ - 10}}$, ${10^{ - 12}}\, to\, \, {10^{ - 11}}$, ${10^{ - 10}}$ and ${10^{ - 10}}$ respectively. Values of Mu and gradient of Levenberg-Marquardt backpropagation are [${10^{ - 09}},$${10^{ - 09}},$ ${10^{ - 09}},$${10^{ - 10}},$${10^{ - 09}},$${10^{ - 09}}$] and [$9.99 \times {10^{ - 08}},$ $9.88 \times {10^{ - 08}},$$9.92 \times {10^{ - 08}},$$9.97 \times {10^{ - 08}},$$9.98 \times {10^{ - 08}},$ $9.84 \times {10^{ - 08}}$] as shown in Figures 6a−6f, respectively. All these graphics illustrated that the LMB-NN scheme are convergent, reliable and accurate for every case of the MHD-MNRD model.

The Adams procedure reference numerical results, compare with LMB-NN performance, for case 3 of the MHD-MNRD model is shown in Figures 7−12 along with the step size 0.02, error plots with an input between 1 to 4. In the LMB-NN scheme, the maximum error for validation, test and train inputs are around $2 \times {10^{ - 10}}, \, \, \, \, 9 \times {10^{ - 10}}, \, \, \, \, 3 \times {10^{ - 10}}, \, \, \, \, \, 1 \times {10^{ - 10}}, \, \, \, \, 2 \times {10^{ - 10}}$ and $6 \times {10^{ - 10}}$ for all various cases of the MHD-MNRD model. Figures 13−18 of the outcomes of various six variations of the MHD-MNRD model also use co-relation studies to analysis regression studies. Further, histograms measures are used to analyze the error analysis for the input grid and corresponding outputs are indicated in Figures 19a−19f for all 6 scenarios 1−6, respectively, of case 3, of the MHD-MNRD model given in Eqs (15−23). The average value of the error bin with the zero line error reference are around $- 1.4 \times {10^{ - 06}},$$- 6.3 \times {10^{ - 06}},$$- 2.0 \times {10^{ - 06}},$$- 1.4 \times {10^{ - 06}},$$- 2.0 \times {10^{ - 06}}$ and $- 1.2 \times {10^{ - 06}}$, for respective 6 scenarios of the MHD-MNRD model. It is shown that correlation R values are around unity for testing, training and validation, i.e., scenario of perfect modeling, which certified the LMB-NN methodology correctness to solve the MHD-MNRD model.

In addition, for scenarios 1–6 of the MHD-MNRD model, the corresponding numerical values are listed in Tables 3−8, illustrating that performance on MSE for the suggested LMB-NN technique is around ${10^{ - 10}},$${10^{ - 10}},$${10^{ - 10}},$${10^{ - 13}}\, to\, \, {10^{ - 10}},$${10^{ - 10}}$ and ${10^{ - 10}}$ for the MHD-MNRD model. All numerical consequences are presented in Tables 3−8, indicated the robust efficiency of LMB-NN for solving the micro-polar nano-fluid MHD-MNRD model.

In addition, the analysis should be presented on the first elements of velocity component, i.e., $f(\eta)$, the investigation for variation of velocities profile $f'(\eta)$ and $g(\eta)$, Micro rotation profiles ${F_1}(\eta), {F_2}(\eta), {F_3}(\eta)$, temperature profile $\theta (\eta)$ and concentration profile $\phi (\eta)$ should be extended. Consequently, the LMB-NN consequences are determined for $g(\eta)$, $\theta (\eta)$ and $\phi (\eta)$ for scenarios 1 to 6 of the MHD-MNRD model and illustrated in Figures 20−25.

The outcomes of velocities, temperature and concentration profiles $f'(\eta), \, \, \, g(\eta), \, \, \, \theta (\eta)$ and $\phi (\eta)$ for all six scenarios are shown in Figures 20−25, respectively, of MHD-MNRD model. From the Figures 20a, 21a, 22a, 23a, 24a and 25a, it is noted that the velocity profiles impacted by magnetic field, both show declining performance. The reduction in velocity is due to Lorentz forces in the magnetic field, which act as a resistive force against fluid motion. It is also important to note that the velocity field decreases as the slip parameter's value increases. It is observed that the temperature increases for increasing values of $Nb$ while the temperature and Nanoparticle field efficiency increases for increasing $Nt$ thermophoresis parameter values. It is also noted that increasing the Le value reduces the Nanoparticle profile and its associated thickness of the boundary layer. It can be observed that the low velocity profile is achieved nearest to surface by intruding the material parameter ${A_1}, {A_2}, {A_3}, {A_4}, {A_5}\, \, and\, \, {A_6}$ values for the case(i) as compared to the rest of the cases for the different material parameter ${A_1}, {A_2}, {A_3}, {A_4}, {A_5}\, \, and\, \, {A_6}$ values (described in Table 1).

Absolute error obtained by the designed solver can be seen via Figures 20b, 21b, 22b, 23b, 24b and 25b, for all six scenarios, respectively, of the MHD-MNRD model. It is noted that, for all six scenarios, the AE are around ${10^{ - 08}}\, to\, {10^{ - 04}}, \, \, \, {10^{ - 07}}\, to\, {10^{ - 04}}, \, \, {10^{ - 07}}\, to\, {10^{ - 04}}, \, \, {10^{ - 08}}\, to\, {10^{ - 05}}, \, \, {10^{ - 07}}\, to\, {10^{ - 05}}$ and ${10^{ - 07}}\, to\, {10^{ - 04}}$, respectively, of MHD-MNRD model. The numerical and graphical diagrams demonstrate that the LMB-NN approach for the MHD-MNRD model solution is reliable, robust and convergent.

All of the characteristics stated above have a wide variety of applications in real-world physics, which are briefly covered below. In many fluid flow situations, micro-polar fluids are fluids with microstructure. They are classified as polar fluids because they have a non-symmetric stress tensor. Physically, micro-polar fluids are fluids composed of stiff, randomly oriented (spherical) particles suspended in a viscous medium, with no regard for fluid particle deformation. Magnetohydrodynamics is essential in many fields of physics, including solar physics (where we shall examine the magnetohydrodynamics of the sun), astrophysics, plasma physics, and so on. The effects of the magnetic field on the dynamic conducting fluid are the primary focus of MHD physics. Magnetic medication targeting, cancer tumour therapy, magnetic devices for cell separation, magnetic endoscopy, and regulating blood flow during surgery are some of the uses of MHD. A dimensionless number that is an intrinsic characteristic of a fluid is the Prandtl number. Fluids with low Prandtl numbers are free-flowing liquids with excellent thermal conductivity, making them ideal for heat transmitting liquids. Small Prandtl numbers, $Pr < < 1$, indicate that thermal diffusivity is dominant. With large levels of $Pr > > 1$, momentum diffusivity dominates the behaviour. For example, the reported value for liquid mercury implies that heat conduction is more important than convection, implying that thermal diffusivity is dominating. However, in engine oil, convection is more effective than pure conduction at transferring energy from a region, therefore momentum diffusivity is dominant. Brownian motion, also known as Brownian movement, any of several physical processes in which a quantity undergoes continual tiny, random changes. Brownian motion of nanoparticles at the molecular and nanoscale levels has been discovered to be a crucial factor influencing the thermal behaviour of nanoparticle-fluid suspensions ("nanofluids"). We developed a theoretical model that accounts for dynamic nanoparticles' basic involvement in nanofluids. Brownian motion causes particles in a fluid to be constantly in motion. This inhibits particles from resting, resulting in colloidal solution stability. With the assistance of this motion, a genuine solution may be recognised from a colloid. Thermophoresis is the transport force that happens when a temperature gradient exists. This force moves gas-borne particles with diameters smaller than 10 m towards the lower temperature area. Thermophoresis is important in high temperature zones, such as a boiler's radiant portion. The thermophoretic force is useful in a variety of situations. Because various particle types travel independently under the force of the temperature gradient, the particle types can be separated by that force after they've been mixed together, or prevented from combining if they're already separated, which is the foundation for applications. Because the greater temperature makes the transition structure necessary for atomic leaps more possible, impurity ions may travel from the cold side of a semiconductor wafer to the hot side. Depending on the materials used, the diffusive flow can occur in either direction (up or down the temperature gradient). Commercial precipitators have employed thermophoretic force for purposes comparable to electrostatic precipitators. It is used in vacuum deposition procedures to manufacture optical fibre. It has the potential to be useful as a transport mechanism in fouling. Thermophoresis has also been proven to offer potential in helping drug development by permitting the identification of aptamer binding by comparing the target molecule's bound vs unbound motion. This approach is referred to as microscale thermophoresis. Furthermore, thermophoresis has been shown to be a flexible approach for controlling single biological macromolecules such as genomic-length DNA and HIV virus in micro- and Nano-channels by light-induced local heating. In field flow fractionation, one of the ways used to separate distinct polymer particles is thermophoresis. The Lewis number is used to describe fluid flows with simultaneous heat and mass transfer. The Lewis number compares the thickness of the thermal boundary layer to the concentration boundary layer. It is used to describe fluid flows with simultaneous heat and mass transfer. As a result, the Lewis number is a measure of the relative thicknesses of the thermal and concentration boundary layers. The Prandtl and Schmidt numbers can also be used to express the Lewis number. Slip velocity is defined as the mean velocity of near-wall particles (often within a layer thickness of one mean free path), with a greater proportion of specular reflections resulting in a higher slip velocity. It has been observed that when the velocity slip parameter grows, the velocity profile decreases, as does skin friction and heat transfer, but mass transfer increases. Heat and mass transport rates decrease as the thermal slip parameter is increased. The velocity of cutting that falls down because to gravitation is known as slip velocity. The influence of mud flow upward direction and mud characteristics must be larger than cutting slip velocity in order to efficiently clean the hole.

5.   Conclusions

A stochastic numerical computation through designed solvers LMB-NN is implemented for the solution of the presented fluidic system based on magnetohydrodynamics micro-polar Nano-fluid by using. PDEs of the mathematical system are shifted to corresponding ODEs representing the dynamics of the problem under consideration by using the capability of suitable equivalence replacements of the suggested system model MHD-MNRD.

The formation of data set for the designed computational networks LMB-NN approach is carried out by using the Adams numerical method with the aid of Mathematica for variations of the MHD-MNRD system based on numerous parameters of interest in terms of micro-polar parameters, velocity slip parameter, magnetic parameter, Brownian motion, Lewis number, thermophoresis parameters and Prandtl number. To adapt the designed LMB-NN with 10 unseen neuron numbers, 80%, 10% and 10% of reference data are used as testing, validation and training. The LMB-NN scheme accuracy is certified by both suggested and reference results with ${10^{ - 13}}\, to\, \, {10^{ - 10}}$ level matching. Furthermore, the accuracy is also explained via numerical and graphical descriptions of convergence plots on the MSE index, regression analysis and error histograms.

Future work direction: The authors intend to implement the following local search algorithms ^[68,69,70] for the presented fluid flow system based on magnetohydrodynamics micro-polar nanofluid flow over a rotating disk model along with the partial slip condition.

Acknowledgments

This study is supported via funding from Prince Sattam bin Abdulaziz University project number (PSAU/2023/R/1444).

Conflict of interest

All authors declare no conflicts of interest in this paper.