Application of fuzzy Malliavin calculus in hedging fixed strike lookback option

1.   Introduction

In the financial market, volatility varies from time to time, so uncertain information is more common than certain information. The uncertainty of this information may come from the natural variability of the market or the lack of information such that people are unable to fully comprehend the trend of the market. The traditional option pricing model is derived by stochastic differential equations, but it is not suitable for conveying nonrandom uncertainties. For instance, statements such as "the stock price went up approximately 6$\%$" and "the interest rate of the bond is almost 10$\%$-20$\%$" are hardly accounted for by randomness alone. The concept of the fuzzy set was first introduced by Zadeh^[1] such that the value in the interval [0, 1] can be used to represent the degree of agreement between the discussed object and the fuzzy concept, which greatly improves the accuracy of the description of the problem. Fuzzy theory is applicable in the investigation of numerous engineering and economic problems. There are two main methods to study option pricing in a fuzzy environment. One is to regard the parameters of the financial market as fuzzy numbers and fuzzify the parameters in the stochastic model (see, e.g. ^[2,3]), and the results of this method do not involve any theory of fuzzy stochastic processes. The other method regards the pricing model as fuzzy stochastic differential equations and derives the $\alpha$-cut of the fuzzy option price by the definition of fuzzy random variable expectations (see, e.g. ^[4,5,6]). These two approaches lead to two different results. We will use the latter method to study option hedging in a fuzzy environment because it avoids fuzzing every parameter in the model, especially if there are too many parameters.

The theories of fuzzy stochastic differential equations can be found in ^[7,8,9]. As parts of fuzzy stochastic differential equations, fuzzy random variables and fuzzy stochastic processes play fundamental roles. The notion of a fuzzy random variable that combines randomness and fuzziness has been introduced by Kwakernaak ^[10] and Puri ^[11]. There are many different perspectives to consider fuzzy stochastic differential equations. The main problem leading to this phenomenon is the various concepts of the fuzzy stochastic Itô integral, whose crisp counterpart is a notion of the classical stochastic Itô integral. In ^[12] the fuzzy stochastic Itô integral is regarded as a fuzzy set of the space of square integrable random vectors, and in ^[13], we can find a proof of the existence of solutions with respect to fuzzy stochastic differential equations. On the other hand, in ^{[14,15,16,17,18,19]}, the diffusion term of the fuzzy stochastic differential equation is a fuzzy random variable, and the solutions are the fuzzy non anticipating stochastic processes driven by the Wiener process. However, given the fuzzy stochastic Itô integral driven by 1-dimension Brownian motion only with the single-valued in these works, there are not many crucial properties that are needed in our applications, so we give an explanation of the necessity that the integrand is not single-valued in Section 4.2. In order to construct the fuzzy stochastic differential equation in the Skorohod sense, the fuzzy stochastic integral with anticipating integrands is studied in this study. The Skorohod (anticipating) integral, which turns out to be an extension of the traditional Ito integral, allows integrands to not always be modified. In this paper, we treat the pricing model as a Skorohod fuzzy stochastic differential equation. We limit ourselves to adjusted linear coefficients for the sake of simplicity.

The financial market usually adopts the methods of $\Delta$-hedging to hedge a contingent claim. The method of $\Delta$-hedging is to apply the Itô formula to the payoff function and uses the definition of a self-financing portfolio and conclusions about partial differential equations to obtain the hedging portfolio. However, satisfying the differentiability conditions is difficult if these contingent claims have a complex payoff function. The other approach of Malliavin calculus requires that the payoff function $F$ is square integrable, and the Malliavin derivative of $F$ satisfies some specific conditions to remedy the deficiency of $\Delta$-hedging. Research on Malliavin calculus in fuzzy spaces is still in its infancy. In ^[20] shows the definitions of first order fuzzy Malliavin calculus and obtains the sensitive analysis of European options Greeks. To date, there are few studies on options hedging in the fuzzy environment. In ^[21] a methodology is proposed for hedging European options with fuzzy parameters. In ^[22] presents the optimal fuzzy hedging portfolio strategy with options, maximizing the expected value of the portfolio and minimizing its value-at-risk. From the perspective of complementing the field, our research is meaningful and contributory. In this paper, we will give the definition of the $n$th fuzzy Malliavin derivative $\widetilde{D}^n$ and its adjoint operator ${\tilde{\delta}}^n$ (also called divergence operator). In terms of Wiener chaos expansion, the fuzzy Clark-Ocone formula is proposed, which makes options hedging accessible in fuzzy space.

To obtain an expression for the hedging portfolio for fixed strike lookback options, we develop a probabilistic method. The expectations of fuzzy random variables mentioned in the current manuscript are proposed by Yoshida et al. ^[23]. The primary reason lookback options are more complicated to price and hedge than barrier options is that lookback options have extremes (maximum or minimum) in both the payout amount and the payoff condition, which leads to more complicated expectations calculations. For this problem, we adopt the Esscher transform and the reflection principle of Brownian motion in fuzzy space. The Esscher transform introduced by ^[24] is applied to determine an equivalent martingale measure in the financial market. The contributions in ^[25] make the Esscher transform an efficient technique for option pricing. The reflection principle is usually used in pricing barrier options, which plays a crucial role in eliminating extremes. We also practice this principle to lookback options pricing and hedging since the extreme exists in the payoff. By the properties of the reflection principle, the cumulative distribution function of the Brownian motion and its maximum (or minimum) can be explicitly computed.

This paper is organized as follows. Section 2 introduces some notions about fuzzy theories, including fuzzy numbers, fuzzy random variables, and fuzzy stochastic processes. We also study the fuzzy stochastic integral with anticipating integrands. In Section 3, we define the fuzzy Malliavin derivative and its adjoint operator, and the fuzzy Clark-Ocone formula is presented successively. In Section 4, we develop a pricing model based on the fuzzy stochastic differential equation in the sense of Skorohod. By the fuzzy Clark-Ocone formula, we hedge fixed strike lookback options in fuzzy space. The analytical solutions of the hedging portfolio are obtained by the Esscher transform and reflection principle. Section 5 performs some numerical simulation. We analyze the sensitivity of hedging portfolios to different parameters. We also consider the rational expected hedging portfolio of the lookback options and financial investors' permissible range of expected prices.

2.   Preliminaries of fuzzy theories

This section mainly introduces some theories of fuzzy sets and fuzzy stochastic processes. We also describe the construction of a fuzzy Itô integral. The reader can refer to ^[26,27,28] for more details.

2.1.   Fuzzy numbers and fuzzy random variable

Definition 2.1. (Metric of Hausdorff) Denote $\mathcal{K}\left(\mathbb{R}\right)$ the family of all nonempty, bounded, compact and convex subsets of $\mathbb{R}$. The Hausdorff metric $d_H$ is defined as follows

Let $L^{2}\left(\mathbb{R}\right)$ denote the set of $\mathbb{R}$-valued stochastic processes. If $f \in L^{2}\left(\mathbb{R}\right)$, then the norm of f as follows

Definition 2.2. (Fuzzy number) Let $\mathcal{F}(\mathbb{R})$ denote the family of all the fuzzy sets

such that $\left[u\right]_\alpha\in\mathcal{K}\left(\mathbb{R}\right)$ for every $\alpha\in[0, 1]$, in which $\left[u\right]_\alpha$ is a $\alpha$-level set can be expressed as $[u]_{\alpha} = \{x \in \mathbb{R}: u(x) \geq \alpha\} = \left[u_{\alpha}^{L}, u_{\alpha}^{U}\right]$ for $\alpha\in(0, 1]$ and $\left[u\right]_{0}:\sup u = cl\{x \in \mathbb{R}: \tilde{u}(x) > 0\}$. $u(x)$ is interpreted as the degree of membership of $x$ in the fuzzy set $u$. If $u$ is normal, convex and upper semicontinuous, we call $u$ a fuzzy number.

Definition 2.3. (Metric on $\mathcal{F}(\mathbb{R})$) Assume $C, D \in \mathcal{F}(\mathbb{R})$ are two fuzzy numbers, $\alpha \in[0, 1]$, then a metric between them is defined as follows

Then $d_{\infty}: \mathcal{F}(\mathbb{R}) \times \mathcal{F}(\mathbb{R}) \rightarrow [0, \infty)$, and $\left(\mathcal{F}(\mathbb{R}), d_{\infty}\right)$ is a complete metric space.

Definition 2.4. (Fuzzy arithmetic operations) Let $a$ and $b$ be two fuzzy numbers. Then $a \oplus b$, $a \circ b$ and $\frac{a}{b}$ are also fuzzy numbers, for all $\alpha \in[0, 1]$, their $\alpha$-level sets are:

$(a \oplus b)_{\alpha} = \left[a_{\alpha}^{L}+b_{\alpha}^{L}, a_{\alpha}^{U}+b_{\alpha}^{U}\right]$,

$(a \circ b)_{\alpha} = \left[\min \left\{a_{\alpha}^{L} b_{\alpha}^{L}, a_{\alpha}^{L} b_{\alpha}^{U}, a_{\alpha}^{U} b_{\alpha}^{L}, a_{\alpha}^{U} b_{\alpha}^{U}\right\}, \max \left\{a_{\alpha}^{L} b_{\alpha}^{L}, a_{\alpha}^{L} b_{\alpha}^{U}, a_{\alpha}^{U} b_{\alpha}^{L}, a_{\alpha}^{U} b_{\alpha}^{U}\right\}\right]$.

If $\alpha$-level set $b_{\alpha}$ does not contain 0, then we have$\left.\left(\frac{a}{b}\right)_{\alpha} = \left[\min \left\{\frac{a_{\alpha}^{L}}{b_{\alpha}^{L}}, \frac{a_{\alpha}^{L}}{b_{\alpha}^{U}}, \frac{a_{\alpha}^{U}}{b_{\alpha}^{L}}, \frac{a_{\alpha}^{U}}{b_{\alpha}^{U}}\right\}\right], \max \left\{\frac{a_{\alpha}^{L}}{b_{\alpha}^{L}}, \frac{a_{\alpha}^{L}}{b_{\alpha}^{U}}, \frac{a_{\alpha}^{U}}{b_{\alpha}^{L}}, \frac{a_{\alpha}^{U}}{b_{\alpha}^{U}}\right\}\right].\nonumber$

Due to the particularity of the difference between two fuzzy numbers, which is closely related to the differentiability, we will discuss it in the Section 3.

Definition 2.5. (Fuzzy random variable) Let $\left(\Omega, \mathcal{A}, P\right)$ be a probability space. For all $\alpha \in[0, 1]$, if $\left[X\right]_{\alpha}: \Omega \rightarrow \mathcal{K}\left(\mathbb{R}\right)$ is an $\mathcal{A}$-measurable function, then a map $X: \Omega \rightarrow \mathcal{F}\left(\mathbb{R}\right)$ is called a fuzzy random variable.

For any metric $d_s$ in $\mathcal{F}(\mathbb{R})$, let $\mathcal{B}_{d_{s}}$ be a $\sigma$-algebra generated by the topology induced by the metric $d_s$, then we can consider a fuzzy random variable if and only if the mapping $u: \left(\Omega, \mathcal{A}\right)\rightarrow \left(\mathcal{F}(\mathbb{R}), \mathcal{B}_{d_{s}}\right)$ is $\mathcal{A} |\mathcal{B}_{d_{s}}$ measurable, with the Skorohod metric $d_s$ (definition in ^[29]).

Let ${X}$ is an integrally bounded fuzzy random variable, the expectation of fuzzy random variable is proposed by Yoshida et al. ^[23]. In what follows we recall this definition. For every $\alpha\in\left[0, 1\right]$ and $x \in \mathbb{R}$, the expectation $E\left({X}\right)$ of the fuzzy random variable ${X}$ is defined by a fuzzy number

where

2.2.   Fuzzy stochastic integral

Definition 2.6. (Fuzzy stochastic process) Let us consider a fuzzy family $\{X(t), t \in [0, T]\}$ on probability space $\left(\Omega, \mathcal{A}, \left\{\mathcal{A}_{t}\right\}_{t \in [0, T]}, P\right)$, $\left\{\mathcal{A}_{t}\right\}_{t \in [0, T]}$ is an increasing and right continuous family of sub-$\sigma$-algebras of $\mathcal{A}$. For every $t \in [0, T]$, a fuzzy random variable $X(t, \cdot)$ can expressed as $X: \Omega \rightarrow \mathcal{F}\left(\mathbb{R}\right)$. Then we call $X = \{X(t)\}_{t \in [0, T]}: [0, T] \times \Omega \rightarrow \mathcal{F}\left(\mathbb{R}\right)$ a fuzzy stochastic process.

If almost all trajectories $X(\cdot, \omega): [0, T] \rightarrow \mathcal{F}\left(\mathbb{R}\right)$ are $d_{\infty}$-continuous functions, then we call that the fuzzy stochastic process $X$ is $d_{\infty}$-continuous. A fuzzy stochastic process $f$ is adapted if and only if for every $\alpha\in [0, 1]$, $[f]_\alpha$ is measurable with respect to the $\sigma$-algebra $\mathcal{N}$, which can be defined as follows

where $M_{t} = \{\omega:(t, \omega) \in M\}$, $\mathcal{B}([0, T])$ denotes the Borel $\sigma$-algebra of subsets of $[0, T]$. If there exists a real-valued stochastic process $h \in L^{p}\left([0, T] \times \Omega, \mathcal{N}; \mathbb{R}\right)$ such that $\left\|\left|[X(t, \omega)]^{0}\right|\right\| \leq h(t, \omega)$, a fuzzy stochastic process $X = \{X(t, \omega): t \in[0, T]\}$ is called $L^{p}$-integrably bounded.

Definition 2.7. (^[30] Fuzzy Aumann Type Lebesgue Integral) Denote the set of all adapted and $L^{p}$-integrably bounded fuzzy stochastic processes by $L^{p}\left([0, T] \times \Omega, \mathcal{N}; \mathcal{F}\left(\mathbb{R}\right)\right)$. Assume that $X \in L^{p}\left([0, T] \times \Omega, \mathcal{N}; \mathcal{F}\left(\mathbb{R}\right)\right)$, and for $\alpha\in[0, 1]$, there exists $\Omega_{X_{\alpha}} \in \mathcal{A}$ and $P\left(\Omega_{X_{\alpha}}\right) = 1$ such that for each $\omega \in \Omega_{X_{\alpha}}$

Considering a fuzzy stochastic process $X_{\alpha} \in L^{p}\left([0, T] \times \Omega, \mathcal{N}; \mathcal{F}\left(\mathbb{R}\right)\right)$, for any $\alpha \in[0, 1]$, we define the Aumann type Lebesgue integral $L_{\alpha, t}\left(X_{\alpha}\right)(\omega)$ by

To correlatethe the Skorohod integral with the fuzzy stochastic integral concerning the wiener process $W$, let us briefly review some definition of Malliavin calculus in crisp case. Let ${\mathcal{S}}$ denote the set of all smooth random variables of the form

Where $n\geq 1$, $X\left(h_{i}\right), i = 1, \cdots, n$ are Gaussian random variables, $h_{i}$ belongs to a real separable Hilbert space $\mathcal{H}$, then $f: \mathbb{R} \rightarrow \mathcal{F}(\mathbb{R})$ is an infinitely differentiable function and all the partial derivatives of $f$ have at most polynomial growth. For simplicity, we consider the $1$th Malliavin derivative

Let ${\mathbb{D}}^{1, 2}$ denote the closure of ${\mathcal{S}}$ with respect to the norm

We denote the adjoint of operator $D$ by $\delta$. The Dom $\delta$ is the subset of $L^{2}\left[[0, T] \times\Omega\right]$ composed of those square integrable random variables $h$ such that

For $h \in \text{Dom}\, \delta$, $\delta\left(h\right)$ is also called Skorohod integral with the form

Skorohod integral is the extension of the Itô integral for anticipating processes. Particularly, the operator $\delta$ restricted to $L^2\left(\left[0, T\right]\times\Omega\right)$ coincides with the Itô stochastic integral.

Let $\mathcal{U}$ be a real separable Hilbert space, then the space $\mathcal{S}_\mathcal{U}$ is the collection of all smooth $\mathcal{U}$-valued random elements of the type $h = \sum_{i = 1}^{n} F_{i} v_{i}$, where $F_{i} \in \mathcal{S}$, $v_i\in \mathcal{U}$. One can extend the domain of $D$ to the space ${\mathbb{D}}^{1, 2}(\mathcal{U})$, which is defined as the closure of $\mathcal{S}_\mathcal{U}$ with respect to the norm

If $\mathcal{U} = L^2\left([0, T]\right)$, then ${\mathbb{D}}^{1, 2}\left(L^2\left([0, T]\right)\right)$ coincides with the class of processes $h\in L^2\left([0, T]\times\Omega\right)$ such that $h(t)\in\mathbb{D}^{1, 2}$ for almost all $t$.

Next, let us recall some notations of fuzzy stochastic integral. Denote $L^{2}\left([0, T] \times \Omega, \mathcal{N}, \lambda \times P; \mathcal{F}\left(\mathbb{R}\right)\right)$ by $L_{\mathcal{N}}^{2}(\lambda \times P)$, $\lambda$ is the Lebesgue measure on $([0, T], \mathcal{B}([0, T]))$. Let $\{F(t)\}_{t \in [0, T]}$ be a set-valued stochastic process with values in $\mathcal{K}\left(\mathbb{R}\right)$. It means that there exists a mapping $F: [0, T] \times \Omega \rightarrow \mathcal{K}\left(\mathbb{R}\right)$, we call $F$ is adapted if it is $\mathcal{N}$-measurable. Considering a set

Let $F:[0, T]\times\Omega\rightarrow \mathcal{K}\left(\mathbb{R}\right)$ is $L_\mathcal{N}^2\left(\lambda\times P\right)$-integrably bound, then by Kuratowski and Ryll-Nardzewski Selection Theorem (see e.g.^[32]) it follows that $S_\mathcal{N}^2\left(F, \lambda\times P\right)\neq\emptyset$.

Considering a set-valued functional stochastic integral of $F$ with respect to the standard Brownian motion $W_t$, we mean the set

is called the set-valued stochastic integral of $F$ with respect to the wiener process $W$. Let a process $h$ in class ${\mathbb{D}}^{1, 2}(L^2\left[0, T\right])$, then we give an assumption:

$\rm(C1)$ For $f\in S_{\mathcal{N}}^{2}(F)$, $E \left [\int_{0}^{T}\left(\int_{0}^{T}\left(D_{s} f_{t}\right)^{2} d s\right)^{\frac{p}{2}} d t\right] < \infty$, $p > 2$.

Proposition 2.8. (Proposition 3.15 of ^[31]) Let $F: [0, T] \times \Omega \rightarrow \mathcal{K}(\mathbb{R})$ be $L^2$-integrally set-valued mapping, and $S_{\mathcal{N}}^{2}(F) \subset \mathbb{D}^{1, 2}$. We assume the (C1) is hold, then we have the following conclusions

$\rm(a)$ $S_{\mathcal{N}}^{2}(F)$ is a closed, convex, bounded, weakly compact and decomposable subset of $L^2\left([0, T]\times \Omega\right)$,

$\rm(b)$ $\int_{0}^{t} F(s) d W_{s}$ is a bounded closed, weakly compact and convex subset of $L^{2}\left(\Omega, \mathcal{A}_{t}, P, \mathbb{R}_{+}\right)$.

Theorem 2.9. (Theorem 3.1 of ^[33]) Let $\mathcal{C} \subset \mathbb{R}$ be a nonempty set and let $\left\{C_{\alpha}: \alpha \in[0, 1]\right\}$ be a family of subsets of $\mathcal{C}$ such that

$\rm(1)$ $C_{0} = \mathcal{C}$.

$\rm(2)$ $C_{0} \supset C_{\alpha} \supset C_{\beta}$ for $0 \leq \alpha \leq \beta$.

$\rm(3)$ If $\alpha_{n} \nearrow \alpha$ then $C_{\alpha} = \cap_{n = \mathbb{N}} C_{\alpha_{n}}$.

Then there exists $u \in\mathcal{F}\left(\mathbb{R}\right)$ such that $[u]_{\alpha} = C_{\alpha}$ for any $\alpha \in(0, 1]$, and $[u]_{0} \subset C_{0}$. Moreover

On the other hand, for $u \in \mathcal{F}\left(\mathbb{R}\right)$ the family of sets $C_{0} = [u]_{0}$, $C_{\alpha} = [u]_{\alpha}$, $\alpha \in (0, 1]$ satisfies conditions (1) and (2).

Theorem 2.10. Let $F_{n}: [0, T] \times \Omega \rightarrow \mathcal{K}\left(\mathbb{R}\right)$ is a sequence of decreasing and adapted set-valued stochastic processes such that $F_{1}$ is $L_{\mathcal{N}}^{2}(\lambda \times P)$- integrably bounded and $F_{1} \supset F_{2} \supset \cdots \supset \mathrm{F}$. Where $\bigcap_{n \geq 1} F_{n} = F$, then for every $t \in [0, T]$, it holds

As mentioned above, let us start discussing the fuzzy-valued stochastic integrals driven by 1-dimension Brownian motion.

Definition 2.11. (Fuzzy-valued stochastic integrals) According to Proposition 2.8, Theorems 2.9 and 2.10, we can conclude that for every $t \in [0, T]$ and $\alpha \in [0, 1]$, there exists a fuzzy set $\left(X\left(t, F\right)\right)$ such that $\left(X\left(t, F\right)\right)_\alpha = \int_{0}^{t}(F(s))_{\alpha}d W_{s}$. Then for an anticipating and $L^{P}$-integrably bounded fuzzy stochastic process $F$, a family of fuzzy sets $\{X(t, F)\} \in \mathcal{F}\left(L^{2}\left(\Omega, \mathcal{A}_{t}, P; \mathbb{R}\right)\right)$, which can be denoted by

In this way, the fuzzy Itô integral obtained under the assumption is bounded, which is the crucial property needed in applications.

3.   Malliavin calculus in fuzzy space

The fuzzy Malliavin derivative and divergence operator in the sense of the stochastic gradient are defined in this section. In the following part, we put forth a crucial theory known as the fuzzy Clark-Ocone formula that offers theoretical backing for lookback options hedging.

3.1.   Fuzzy Malliavin derivative

Definition 3.1. (Generalized Hukuhara difference) Let $x, y \in \mathcal{F}(\mathbb{R})$, we define the generalized Hukuhara difference of $x$ and $y$ if there exist a fuzzy number $z$ such that the following conditions are satisfied

Condition (i) corresponds to the conception of Hukuhara difference. The generalized Hukuhara difference of $x$ and $y$ is denoted by $z = x \ominus_{g h}y$. For any $\alpha \in [0, T]$, if $[x]_{\alpha}$ and $[y]_{\alpha}$ are two fuzzy closed intervals, the gH-difference is given by

However, the gH-difference for some pairs of fuzzy number are undefined. For instance, if $A = (1, 2, 3)$, $B = (4, 5)$, $A \ominus_{gH} B$ is undefined. Fortunately, the generalized difference proposed in ^[34] solves this problem. The generalized difference $x \ominus_{g}y$ is defined levelwise as

where $conv$ denotes the convex hull.

Definition 3.2. (^[35] Generalized differentiable) Assume a fuzzy-number-valued function $F: \left(a, b\right)\rightarrow \mathcal{F}\left(\mathbb{R}\right)$ is generalized differentiable, then for $x_{0} \in (a, b)$, the following limit

exists and equals to a fuzzy number. We denote this fuzzy number by $F_{g}^{\prime}(x)$ and call $F$ generalized differentiable at $x_{0}$.

Next, let us start with the definition of the fuzzy Malliavin derivative. Denote by $\widetilde{\mathcal{S}}$ the set of all fuzzy smooth random variables of the form

Where $X\left(h_{i}\right), i = 1, \cdots, n$, are fuzzy Gaussian random variables with the form of $X(h_i) = \int_{0}^{T} h_{i}(t) \circ dW(t)$, $h_{i}\in\mathcal{H}$, $\mathcal{H}$ is a real separable Hilbert space. Assume that $f: \mathbb{R} \rightarrow \mathcal{F}(\mathbb{R})$ is an infinitely differentiable function and all the partial derivatives of $f$ have the most polynomial growth.

Let $\mathcal{H}^{\odot n}$ is a separable Hilbert space generated by the $\mathcal{H}^{\odot n}$-valued fuzzy random variables $f$ that are square integrable and symmetric. Denote the symmetric tensor product by $\odot$, $f_s$ is called the symmetrization of $f$. In order to express the meaning of "symmetric", we introduce the following equation

where $\sigma = \left(\sigma_{1}, \cdots \sigma_{n}\right)$ is permutations of $(1, \cdots, n)$.

Definition 3.3. (Fuzzy Malliavin derivative) Let $F: \Omega \rightarrow \mathcal{F}(\mathbb{R})$ is given by (3.1), $n\geq 1$ is an integer. Assume $f$ is generalized differentiable, $\left\{X\left(h_{i}\right)\right\}$ is a centered Gaussian family, then the Malliavin derivative of $F$ in $L^{2}\left[\Omega \times \mathcal{H}^{\odot n}; \mathcal{F}(\mathbb{R})\right]$ is defined by

where "$\otimes$" denotes the tensor product. In particular, ${\widetilde{D}}^{1} F$ can be simply denoted as ${\widetilde{D}}F$. For $h\in\mathcal{H}$, it holds

it means that $\widetilde{D}F$ can be regarded as a direction derivative.

Assume that the fuzzy random variable $FG\in{\widetilde{S}}$ can be represented in the form of (3.1), denote by $N(x)$ the density of the standard normal distribution on $\mathbb{R}$, that is

Hence

It means that operator $\widetilde{D}^{n}$ is closable. Let $\widetilde{\mathbb{D}}^{n, 2}$ denote the closure of $\widetilde{\mathcal{S}}$ with respect to the norm

$\widetilde{\mathbb{D}}^{n, 2}$ is also called the domain of the operator $\widetilde{D}^{n}$ in $L^{2}\left(\Omega; \mathcal{F}\left(\mathbb{R}\right)\right)$.

We suppose that the separable Hilbert space $\mathcal{H}$ is an $L^{2}$ space of the form $\mathcal{H} = L^{2}([0, T], \mathcal{B}, \mu)$, where $\mu$ is a $\sigma$-finite atomless measure on a measurable space $([0, T], \mathcal{B})$. The derivative of a fuzzy random variable $F \in \widetilde{\mathbb{D}}^{n, 2}$ will be a fuzzy stochastic process due to the identification between $L^{2}\left[\Omega \times \mathcal{H}^{\odot n}; \mathcal{F}(\mathbb{R})\right]$ and $L^{2}\left[[0, T]^{\otimes n} \times \Omega, \mathcal{N}; \mathcal{F}\left(\mathbb{R}\right)\right]$. For $n\ge1$, the derivative $\widetilde{D}^{n} F = \left\{\widetilde{D}_{t_{1}, \cdots, t_{n}}^{n} F, t_{i} \in T\right\}$ is a $\mu^{n}\times P$ measurable function. Specially, $D_{t}F$ is defined almost everywhere with respect to the measure $\mu\times P$.

Lemma 3.4. (Chain rule) Let $F$ and $\Psi \in C^{1}(\mathcal{F}(\mathbb{R}))$ be a generalized differentiable fuzzy function. Assume that $F$ is a fuzzy random variable whose components are elements of $\widetilde{\mathbb{D}}^{1, 2}$, and $g^{\prime}(F) \widetilde{D}_{t} F \in L^{2}(P \times \lambda)$, then we have the chain rule

Proof. For any direction $\gamma \in \Omega$ we have

So the proof is completed.

Definition 3.5. (Duality formula) We denote the adjoint of operator $\widetilde{D}^{n}$ by $\tilde{\delta}^{n}$, and Dom $\tilde{\delta}^{n}$ is represented as the subset of $L^{2}\left[\Omega \times \mathcal{H}^{\odot n}; \mathcal{F}(\mathbb{R})\right]$ composed of those random variables $h$ such that

where $F \in \widetilde{\mathcal{S}}$, $c > 0$ is a constant. For $F \in \widetilde{\mathbb{D}}^{n, 2}$, if $h \in \text{Dom}\, \tilde{\delta}^{n}$, then ${\tilde{\delta}^{n}}(h)$ is the unique element of $L^{2}[\Omega; \mathcal{F}(\mathbb{R})]$ characterized by the following duality formula

The operator $\tilde{\delta}^{n}$ is called the divergence operator of order $n$.

Combining computations (3.3) and (3.5), {it is easy to} deduce that $\tilde{\delta}(h) = X(h)$ when $G = 1$, we call $\tilde\delta(h)$ is the fuzzy Skorohod stochastic integral of $h$.

Let $\mathcal{G}$ be another real separable Hilbert space, then the space $\widetilde{\mathcal{S}}_\mathcal{G}$ is the collection of all smooth $\mathcal{G}$-valued fuzzy random elements of the type $F = \sum_{i = 1}^{n} F_{i} v_{i}$, where $F_{i} \in \widetilde{\mathcal{S}}$, $v_i\in \mathcal{G}$. For $k\ge 1$, the $k$th Malliavin derivative of any $F \in \widetilde{\mathcal{S}}_\mathcal{G}$ can be expressed as $\widetilde{D}^{k} F = \sum_{i = 1}^{n} \widetilde{D}^{k} F_{i} \otimes v_{i}$.

Theorem 3.6. Let $\mathcal{G} = \mathcal{H}$, and denote the class of $\mathcal{H}$-valued smooth fuzzy random variables by $\widetilde{\mathcal{S}}_{\mathcal{H}}$, for all $h \in \widetilde{\mathcal{S}}_{\mathcal{H}}$ such that $h$ can be written as $\sum_{i = 1}^{n} F_{i} v_{i}$, where $F_{i} \in \widetilde{\mathcal{S}}$, $v_{i} \in \mathcal{H}$. Let $\tilde \delta(h) \in \widetilde{\mathbb{D}}^{1, 2}$, $h \in \mathcal{S}_{\mathcal{H}} \subset \mathit{\text{Dom}}\, \tilde{\delta}^{n}$, then we have

Proof. For all $g, f \in \widetilde{\mathbb{D}}^{1, 2}$, $u \in \mathcal{H}$, according to (3.5), we get

Let $g = 1$, it has $\tilde{\delta}(f u) = \tilde{\delta}(u) f-\langle \widetilde{D} f, u\rangle_{\mathcal{H}}$. Then we can deduce that

such that

and

Subtract $\widetilde{D} \tilde{\delta}(h)$ and $\tilde{\delta}(\widetilde{D} h)$, then we complete this proof.

Fix $k\ge 1$ is an integer, we can know $\mathcal{H}^{\otimes n} = \mathcal{H}^{\otimes n-k} \otimes \mathcal{H}^{\otimes k}$. For $h \in \mathcal{H}^{\otimes n}$ which can be written as $h = \sum_{i = 1}^{n} f_{i} u_{i}$, where $f_{i} \in \mathcal{H}^{\otimes n-k}$ and $u_{i} \in \mathcal{H}^{\otimes k}$, such that $\tilde{\delta}^{n}(f)$ be a $\mathcal{H}^{\otimes n-k}$-valued fuzzy random variable

It means that $\tilde{\delta}^{k}(h) \in L^{2}\left(\Omega, \mathcal{H}^{\otimes n-k}; \mathcal{F}(\mathbb{R})\right)$ and for $\tilde\delta^{n}(f) \in \widetilde{\mathbb{D}}^{1, 2}$, we can easily deduce the following equation by Theorem 3.6 and induction

3.2.   Fuzzy Clark-Ocone formula

In order to prove the Clark-Ocone formula in fuzzy space, we first recall some definitions and lemmas.

Definition 3.7. (Fuzzy iterated Itô integral) Let $f \in L^{2}\left([0, T]^{\odot n}; \mathcal{F}(\mathbb{R})\right)$ be symmetric, then the fuzzy iterated Itô integral is defined as follows

It can be seen that the $n$-fold iterated integral $I_{n}(f) = \tilde{\delta}^{n}(f)$.

Theorem 3.8. (Wiener chaos expansion) Suppose that $F \in L^{2}(\Omega; \mathcal{F}(\mathbb{R}))$ is a fuzzy random variable defined as (3.1), for some unique collection of kernels $f_{n} \in \mathcal{H}^{\odot n}$, $F$ can be expanded as

where $f_{0} = E[F]$, and $I_{0}$ is an identity mapping such that $I_{0}\left(f_{0}\right) = E[F]$.

Proof. Assume that $\mathcal{M}_n$ is the closed subset of $L^{2}(\Omega; \mathcal{F}(\mathbb{R}))$ composed by the fuzzy random variables of the type $H_n (X(f))$, $\left\{H_{n}\right\}_{n \geq 0}$ denotes the Hermite orthogonal polynomials. Thence by property of Hermite polynomials, $\mathcal{M}_n$ is orthogonal to $\mathcal{M}_m$ when $n \ne m$, $\mathcal{M}_0 = \mathcal{F}(\mathbb{R})$. With the help of Theorem 2.2.4 in ^[36], we know that the linear space $\mathcal{M}_n$ is dense in $L^{2}(\Omega; \mathcal{F}(\mathbb{R}))$. It means that

We can know that $H_n (X(f)) = I_n (f_n)$ by means of $I_n (f) = \tilde{\delta}^{n}(f)$, so we can regard $\mathcal{M}_n$ as a dense subspace of $L^{2}(\Omega; \mathcal{F}(\mathbb{R}))$ generated by class $I_n (f_n)$, then the proof is completed.

By (3.7), we can deduce $\widetilde{D}I_n (f_n) = nI_{n-1} (f_n)$, so that for $F \in \widetilde{\mathbb{D}}^{1, 2}$, it holds

where $f_{n} \in \mathcal{H}^{\odot n}$. From the perspective of Wiener chaos expansion in term of fuzzy iterated integrals, we also defined the fuzzy Malliavin derivative.

Theorem 3.9. (Fuzzy Clark-Ocone formula) Let $F \in \widetilde{\mathbb{D}}^{1, 2}$ be $\mathcal{A}_T$ measurable and $W_t$ is a 1-dimension Brownian motion. Then we have

Proof. Following the Proposition 3.11 in ^[37], for $f_{n} \in \mathcal{H}^{\odot n }$, we can know that $E\left[\left.I_{n}\left(f_{n}\right) \right | \mathcal{A}_{G}\right] = I_{n}\left(f_{n} 1_{G}\right)$, where $G$ is a Borel set in $[0, T]$. $\mathcal{A}_G$ is a completed $\sigma$-algebra generated by fuzzy random variables of the form (3.1). Then we can deduce that

where $\left.I_{n-1}\left(f_{n}(t, \cdot \right)\right)$ is means that only $n-1$ fuzzy variables in the kernel $f_n$ are integrated out, while the others act as free parameters.

4.   Lookback options hedging in the fuzzy framework

In this section, we will construct a portfolio to replicate a fixed strike lookback option in fuzzy space. Let us denote the fuzzy notation by "$\sim$", it means {for} a fuzzy random variable $\widetilde{X}$, its crisp counterpart is a random variable $X$. Then we will use the theories of fuzzy Malliavin calculus proved above, and explicitly calculated hedging portfolio $\tilde{\beta}$ in a probabilistic approach.

4.1.   Fuzzy stochastic differential equations

To build our pricing model, we need to introduce some theories of fuzzy stochastic differential equations in the Skorohod sense firstly. Considering a fuzzy stochastic differential equation, we restrict ourselves to adapted linear coefficients for simplicity of the exposition

where $X_0$ is a fuzzy random variable, $\sigma\in L^{2}[0, T]$. Let $S_\mathcal{N}^2\left(F\right)\subset{\widetilde{\mathbb{D}}}^{n, 2}\left(L^{2}[0, T]\right)\subset Dom\; \tilde{\delta}$, and assume that $b$ is a fuzzy random function satisfies the following assumption:

$(\rm C2)$ Let $\widetilde{b}:[0, T]\times\mathbb{R}\times\Omega\rightarrow \mathcal{F}\left(\mathbb{R}\right)$ is a measurable function such that there exists an integrable function $\gamma_t$ on $[0, T]$, $\gamma_t\geq0$, a constant $L > 0$, and a set $N_1\in\mathcal{A}$ of probability one, for every $x, y\in\mathcal{F}\left(\mathbb{R}\right)$, $t\in [0, T]$, it holds

Then consider two transformations

such that $\widetilde{A}_t\left(\omega\right)_s\widetilde{B}_t\left(\omega\right)_s = \widetilde{B}_t\left(\omega\right)_s\widetilde{A}_t\left(\omega\right)_s = Identity$. $\tilde{\lambda}_{t} = \exp \left(\int_{0}^{t} \sigma d W_{s}-\frac{1}{2} \int_{0}^{t} \sigma^{2} d s\right)$ can be defined as a Radon-Nikodym derivative, then $E\left[Y\left(B_t\right)\tilde{\lambda}_t\right] = E\left[Y\right]$ holds for any fuzzy random variable $Y\in L^1\left(\Omega; \mathcal{F}\left(\mathbb{R}\right)\right)$ by Girsanov's theorem. Then we can call (4.1) a fuzzy stochastic differential equation in the Skorohod sense, For $x\in\mathcal{F}\left(\mathbb{R}\right)$ and $\omega\in\Omega$, we have the following equation

Theorem 4.1. For a fixed initial condition $\widetilde{X}_0\in L^P\left(\Omega; \mathcal{F}\left(\mathbb{R}\right)\right)$, $p > 2$, and assumptions $\rm (C1), \rm (C2)$ are held, we define

Then the process $\widetilde{X} = \left\{\widetilde{X}_t, t\in [0, T]\right\}$ satisfies $1_{\left[0, t\right]}\sigma \widetilde{X}_t\in Dom\ \tilde{\delta}$. $X$ is the unique solution of (4.1), $\widetilde{X}\in L^2\left([0, T]\times\Omega; \mathcal{F}\left(\mathbb{R}\right)\right)$. The proof of the solution's existence and uniqueness can be found in ^[31,38].

4.2.   Hedging with the fuzzy Clark-Ocone formula

Considering a market consisting of two assets: a risk-less asset of price $B_t$ and a stock of price ${\widetilde{S}}_t$, and replicate a fixed strike lookback option $\widetilde{F}$ with the self-financing strategy in fuzzy space. The dynamic of the model takes the following form

and the dynamic of $B_t$ is

where risk-free rate $r$ and volatility $\sigma$ are regarded as positive constants, $W_t$ is a standard Brownian motion. Let pricing model (4.3) be consistent with the principle of fuzzy stochastic differential equation in the Skorohod sense, then the fuzzy Itô integral $\int_{0}^{t}\left.\sigma{\widetilde{S}}_t\circ d W_t\right.$is bounded. According to Theorem 4.1 we have

We denote $Z_t\left(\omega, \widetilde{S}_0\right)$ by $Z_t$ in order to simplify the notation. Then we can solve (4.3) as follows

By (4.2) we know that the fuzzy model has the unique solution

it can be solved as

Let ${\tilde{\eta}}_t$ be the number of non-risky assets and ${\tilde{\beta}}_t$ be the number of stocks owned by the investor at time t, we call the couple ${\tilde{\phi}}_t = \left({\tilde{\eta}}_t, {\tilde{\beta}}_t\right)$ is a fuzzy portfolio with the value process

We can express ${\tilde{\eta}}_t$ as $\tilde{\eta}_{t} = \frac{V\left(\tilde{\phi}_{t}\right) \ominus_{g} \tilde{\beta}_{t}\circ \widetilde{S}_{t}}{B_{t}},$ then (4.6) can be written as

By observing the above formula, the issue of hedging is equivalent to the question about finding a suitable ${\tilde{\beta}}_t$ such that these two opposite positions offset. Plainly, for a fixed strike lookback option $\widetilde{F}$ at maturity time $T$, exist the following equation

Considering the discounted prices of this portfolio

assume that $\widetilde{F}\in{\widetilde{\mathbb{D}}}^{1, 2}$, then apply the fuzzy Clark-Ocone formula of Theorem 3.9 to $\widetilde{H} = e^{-rT}\widetilde{F}$ with the following form

By (4.7) and the correspondence of (4.8) and (4.9), it holds $E\left[\widetilde{H}\right] = V\left({\tilde{\phi}}_0\right),$ and

Observing the above formulas, if the fuzzy stochastic Itô integrals involved in (2.2) having only single-valued integrands will lead to the result in (4.10) is identical to crisp case, so this embody the importance of making the integrand a fuzzy number.

Considering a call lookback option with fixed strike price $K$, the payoff at maturity time $T$ is $\widetilde{F} = \left({\widetilde{M}}_S^{T}-K\right)^+$, where ${\widetilde{M}}_S^{T} = \max\limits_{t\in\left[0, T\right]}{{\widetilde{S}}_t}$. Then the Eq (4.10) with the following form

Theorem 4.2. Assume that $\widetilde{S}_t\in{\widetilde{\mathbb{D}}}^{1, 2}$, for $0\le t\le T$, then the fuzzy Malliavin derivative of $\widetilde{M}_S^T$ can be calculated as

Proof. In order to obtain $\widetilde{D}_t{\widetilde{M}}_S^T$, we need to compute $\widetilde{D}_t{\widetilde{S}}_s$ firstly, $0\le t\le s$, By Taylor expansion, we can know $e^{\sigma W_s}\rightarrow \sum_{k = 0}^{\infty}\frac{\left(\sigma W_s\right)^k}{k!}$ in $L^2\left(\Omega; \mathcal{F}\left(\mathbb{R}\right)\right)$. Since $\sum_{k = 0}^{\infty}\frac{\left(\sigma W_s\right)^k}{k!}\in\widetilde{\mathcal{S}}$, we have

So we can solve $\widetilde{D}_t{\widetilde{S}}_s$ as follows

Then we can obtain $\widetilde{D}_t{\widetilde{M}}_S^T = \sigma{\widetilde{M}}_S^T$ from the crisp case in Corollary 1 of ^[39].

It is easy to see $\left({\widetilde{M}}_S^{T}-K\right)^+$ can be expressed equivalently as $\varphi\left({\widetilde{M}}_S^T\right) = \max{\left({\widetilde{M}}_S^T, K\right)-K}$. When $\varphi\left({\widetilde{M}}_S^T\right)$ is a Lipschitz function and $\varphi\left({\widetilde{M}}_S^T\right)\in{\widetilde{\mathbb{D}}}^{1, 2}$, according to the chain rule in Lemma 3.4 we can deduce that

So (4.11) can be written as

4.3.   Calculation of the hedging portfolio $\tilde{\beta}_t$

We will adopt a completely probabilistic approach to calculate hedging portfolio $\tilde{\beta}_t$. To begin with, we need to recall some useful lemmas.

Considering the crisp case of Eq (4.3) that can also be called the differential form of B-S model

Let $X_t = \ln{\frac{S_t}{S_0}}$, then we have $X_{t} = \left(r-\frac{1}{2} \sigma^{2}\right) d t+\sigma W_{t}$. Denote $\sup\limits_{t\in\left[0, T\right]}{X_t} = M_X^T$ and $k = \ln{\frac{K}{S_0}}$.

Lemma 4.3. (Reflection principle) We assume that $W_t$ is a standard Brownian motion, $P$ is the cumulative distribution function, and $N$ is the standard normal distribution. We denote $M_W^T = \sup\limits_{t\in\left[0, T\right]}{W_t}$, then we have the following reflection principle

where $x\le y$, $y > 0$. It implies that

By Lemma 4.3, the joint probability density function $X_T$ and $M_X^{T}$ can be written as follows

Lemma 4.4. (^[40] Esscher transform) For a risk-neutral measure Q, the process $\frac{e^{cX_T}}{E^Q\left[e^{cX_T}\right]}$ can be regarded a Radon-Nikodym derivative such that

where $Y$ is a random variable which is a real-valued function of $\left\{X_t, 0\le t\le T\right\}$, then a new probability measure $Q_1$ is called the Esscher measure concerning parameter $c$. In order to express conveniently, we denote $E^{Q_1}\left[Y\right] = E\left[Y; c\right]$. Under Esscher measure of parameter $c$, the diffusion coefficient is still $\sigma$, but the drift coefficient is changed from $u$ to $u+c\sigma^2$. For $\xi = \frac{2u}{\sigma^2}$, we have

the cumulative distribution function of $X_T$ is

thence for a constant $c$, it holds

Theorem 4.5. Assume the underlying asset price follows the fuzzy stochastic differential equation as shown in (4.3), for every $\alpha\in\left[0, 1\right]$, we obtain the analytical expression for hedging portfolio of lookback options as follows

and

where $\xi = 2\frac{u}{\sigma^2}, u = r-\frac{\sigma^2}{2}$. The other notations in the above equation are the same as previously mentioned.

Proof. We consider a crisp expectation $E\left[\left.\left.M_X^T\right.1_{\left\{M_S^T > K\right\}}\right|\mathcal{A}_t\right]$ which can be solved by (4.14) as follows

We will calculate it separately. The first term of (4.15) can be calculated as

The second term of (4.15) can be solved by integration by parts and Esscher transform as follows

The last identity of (4.15) can be solved by the same technique with the following form

Then the hedging portfolio in the crisp case $\beta_0 = e^{r(t-T)}\sigma^{-1}\left(S_t\right)^{-1}E^Q\left[\left(\sigma M_S^T\right.1_{\left\{M_S^T > K\right\}}\right]$ can be solved explicitly as follows

from the definition of fuzzy expectation of fuzzy random variables, the fuzzy hedging portfolio in (4.12) can be written as

Combine Eqs (4.15)–(4.19), the proof of Theorem 4.5 is completed.

5.   Numerical results

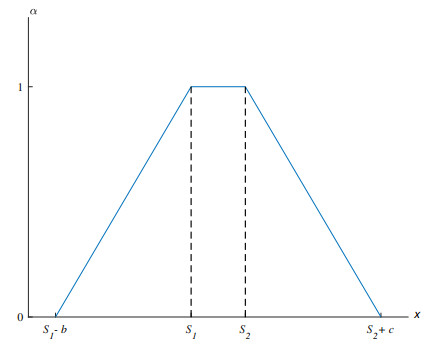
In this section, we will perform some numerical simulations to illustrate the theoretical results obtained in the previous sections. First of all, let us introduce the construction of a trapezoidal fuzzy number (see Figure 1).

For a fuzzy stochastic process $\left\{{\widetilde{S}}_t\right\}_{t\in\left[0, T\right]}$, then its membership function takes the following form

where $\left[S_1, S_2\right]$ is called tolerance interval, $b_t > 0$ is the left-width, $c_t > 0$ is the right-width. Assumed that the trapezoidal fuzzy numbers ${\widetilde{S}}_t$ are symmetrical, it means $b_t = c_t$. Following ^[41], we can get the $\alpha$-level set of ${\widetilde{S}}_t$ with the form of $\left({\widetilde{S}}_t\right)_\alpha = \left[\left({\widetilde{S}}_t^L\right)_\alpha, \left({\widetilde{S}}_t^U\right)_\alpha\right] = \left[S_1-\left(1-\alpha\right)b_t, S_2+\left(1-\alpha\right)c_t\right]$.

Let us consider a fixed strike lookback options with the payoff $\widetilde{F} = \left({\widetilde{M}}_S^{T}-K\right)^+$. We assume $S_1 = 32$, $S_2 = 3$4, $K = 28$, $T = 1$, $\sigma = 0.2$, $r = 0.05$, and left and right width $b = c = 5$. To simplify the notation, we will write $\beta_0 = \beta$, $b_0 = b$, $c_0 = c$. Table 1 shows the $\alpha$-level closed intervals of the fuzzy hedging portfolio $\tilde{\beta}$. For $\alpha = 0.95$, the hedging portfolio $\tilde{\beta}$ lies in the closed interval [1.4063, 1.6130], which means that financial investors can choose any value from this interval as their later portfolio to hedge target options if they are comfortable with this belief degree 0.95. From another aspect of view, a risk aversion investor may pick the value of $\tilde{\beta}$ with a higher belief degree. On the contrary, risk adventurer investors may be acceptable to a relatively low belief degree and select the corresponding interval if they think it is reasonable.

5.1.   Sensitivity analysis

In this subsection, we will analyze the sensitivity of the left and right points of the $\alpha$-cut of the fuzzy hedging portfolio of $F$ with respect to the parameters $r$, $\sigma$ and $T$. For this purpose, we take a control variable approach, changing one parameter at a time and keeping the other parameters constant. One thing to note is that the experiments were done at $\alpha = 0.95$ in this subsection.

Figure 2 shows the left and right points of the $\alpha$-cut of the hedging portfolio $\tilde{\beta}$ against some model parameters. (a) reflects the relation of risk-free interest rate $r$ and $\tilde{\beta}_\alpha$, we find that the function of ${\tilde{\beta}}_\alpha$ with respect to of risk -free interest rate $r$ is not monotonous. With the increases of $r$, the value of ${\tilde{\beta}}_\alpha$ firstly increases and then decreases but generally tends to be stable. (b) shows the relation of volatility $\sigma$ and ${\tilde{\beta}}_\alpha$, it is also not a monotonous function, but the overall trend is decreasing. (c) embodies the longer the maturity time, the smaller hedging portfolio ${\tilde{\beta}}_\alpha$. Through the sensitivity analysis of the above parameters, we know that volatility is the biggest factor in the choice of hedge portfolio, which can be suspected by the fact that the greater volatility, the greater the price of the underlying asset, so we only need a smaller number of the portfolio.

5.2.   The expected hedging portfolio of lookback options

In order to obtain the financial investors' subjective judgment about hedging portfolios, Yoshida in ^[4] proposes a kind of utility function method which can represent the investors' satisfaction with the portfolios that can be traded in the current market. Next, let us recall this definition. Considering a fuzzy goal by a fuzzy set $\psi:\mathbb{R}\rightarrow \left[0, 1\right]$, which is a continuous and increasing function with $\psi\left(0\right) = 0$ and $\lim\limits_{x\rightarrow \infty}{\psi\left(x\right) = 1}$. Then we can get the $\alpha$-cut $\psi_\alpha = \left[\psi_\alpha^-, \infty\right]$ for every $\alpha\in\left[0, 1\right]$. The fuzzy expectation of fuzzy values $\tilde{\beta}$ which is given in Section 2.1 can be defined as

where $\tilde{m}$ is the possibility measure generated by density $\psi$ and $\int d\tilde{m}$ denotes Sugeno integral. The fuzzy expectation (5.1) implies the degree of financial investors' satisfaction regarding fuzzy portfolio $\tilde{\beta}$. Then the fuzzy goal $\psi\left(x\right)$ means a kind of utility function for expected portfolio $x$ in (5.1), it represents a financial investors' subjective judgment. It means that for a real number $x^\ast\in\mathbb{R}_+$ which is called a rational expected portfolio if it attains the supremum of the fuzzy expectation (5.1), i.e.,

then we have the following definition

where $\alpha^+$, $\alpha^-$ are the grade of the fuzzy expectation of lookback options hedging portfolio, and we can deduce that

According to Theorem 4.1 in ^[4], we can know that the rational expected portfolio of the lookback option is given by

Combine (5.2) and (5.4) we can get the interval $\left[x^-, x^+\right]$, {which} can be written as

which is the range of hedging portfolio $x$ such that the reliability degree of the expected hedging portfolio, $\tilde{\beta}(x)$ is greater than the degree of financial investors' satisfaction, $\psi(x)$. Therefore, this interval means financial investors' permissible range of expected hedging portfolio under their fuzzy goal.

Next, let us consider a fuzzy goal

Then we have $\psi_\alpha^- = -\ln{\left(1-\alpha\right)}$ for $\alpha\in\left(0, 1\right)$. By (5.3) we can easily calculate the grade of the fuzzy expectation of the fuzzy hedging portfolio, respectively $\alpha^-\approx0.7275$, $a^+\approx0.8108$. The grades means the degrees of financial investors' satisfaction in hedging. From (5.4), the corresponding permissible range of rational expected hedging portfolio with respect to the lookback option under one's fuzzy goal $\psi$ is $\left[x^-, x^+\right]\approx\left[1.3002, 1.6647\right]$. In Figure 3, we can more intuitively comprehend this correspondence. When $b = c = 0$, $S_1 = S_2 = 32$, the crisp expected hedging portfolio is calculated as 1.4690, which is included in the interval (5.5). (5.5) shows the financial investor a confidence interval of expected hedging portfolio of lookback option under uncertainty.

6.   Conclusions

In this paper, we proposed a hedging technique using fuzzy space Malliavin calculus for fixed strike lookback options. Our pricing model is based on the fuzzy stochastic differential equation in the Skorohod sense. With the help of the properties of $n$th fuzzy Malliavin derivative and its adjoint (divergence operator), we obtained the fuzzy Clark-Ocone formula, which plays a significant role in hedging. Then, we derived the explicit expression for the fuzzy hedging portfolio of fixed strike lookback options by reflection principle and Esscher transform. Finally, some numerical experiments are carried out. On the one hand, we proceeded the sensitivity analysis of the hedging portfolio $\beta_t$. On the other hand, we considered the financial investors' subjective judgment, the permissible range of the expected hedging portfolio of fixed strike lookback options such that the reliability degree of the optimal expected hedging portfolio is greater than the degree of one's satisfaction is given.

However, two further extensions of the application of fuzzy malliavin calculus in hedging would be interesting. One possible extension is turning our model into multidimensional so that the hedging results are more consistent with the real market. Another extension would be to extend the research on the exotic options to make our conclusions more general.

Acknowledgments

This work is supported by the Education Department of Jilin Province (JJKH20200030KJ), the department of Science and Technology of Jilin Province (YDZJ202102ZYTS156), the project of natural science foundation joint fund of Jilin Province (YDZJ202101ZYTS167), and Beihua University Youth Research and Innovation Team. We also thank the referee and associate editors for their comments and suggestions, which led to numerous improvements.

Conflict of interest

The authors declare that they have no competing interests in this paper.