Stability results for fractional integral pantograph differential equations involving two Caputo operators

1.   Introduction

In the realms of economics and game theory, the term "duopoly game" is used to describe a scenario in which only two dominant companies or competitors are active within a particular market or industry ^[1]. These two companies, with their substantial market share, have a significant impact on market dynamics. In a duopoly game, each firm's conduct is highly dependent on the other, since its strategic choices like pricing, output levels, and marketing tactics directly affect each other's results and market positions ^[2].

With the worsening environmental pollution and the advancement of the circular economy concept, remanufacturing has emerged as a compelling subject in both business and academia. Remanufacturing used products can decrease the government's spending on environmental pollution treatment, enhance resource utilization by businesses and society, and simultaneously achieve mutually beneficial economic, environmental, and social outcomes ^[3,4]. In the electronics manufacturing sector, renowned international companies such as Apple, HP, and Fuji Xerox have integrated remanufacturing into their overall business strategy to achieve the development of both the economy and environment. Xerox, for instance, succeeded in conserving $＄200$ million in raw material costs through remanufacturing over five years ^[5]. The Global Refurbished and Used Mobile Phones Market reached an estimated value of about USD $＄57.45$ billion in 2022 ^[6], and the global Automotive Parts Remanufacturing Market reached an estimated value of about USD $＄66.30$ billion in the same year 2022 ^[7].

Manufacturers frequently face the decision of whether or not to remanufacture their end-of-life products, and they often avoid remanufacturing due to concerns that remanufactured products may adversely affect sales of higher-margin new products. For example, in 2005, third-party remanufacturer (TPR) represented $54\%$ of the aftermarket for automotive parts in Europe and $66\%$ worldwide ^[8]. Manufacturers face this dilemma when assessing the benefits of remanufacturing against the potential negative effects on new products. The decision-making process involves a range of considerations, encompassing economic, environmental, and social factors. However, this approach could have negative consequences for manufacturers in industries where their end-of-life products are attractive to third-party remanufacturers. These third-party remanufacturers may significantly undercut the sales of the original manufacturer. This dilemma highlights the complex dynamics of the remanufacturing industry and the potential impact on the sales and market position of the original manufacturer. The attractiveness of end-of-life products to third-party remanufacturers introduces a competitive challenge that manufacturers must carefully consider when deciding whether to pursue remanufacturing.

Recent research literature has shown considerable interest in exploring remanufacturing problems. Geyer ^[9] examined the remanufacturing strategies of various manufacturers, including BMW, Kodak, and Xerox, and showed that they achieved significant profitability by realizing cost savings through remanufacturing practices. Guide ^[10] investigated the competitive dynamics between remanufacturing and manufacturing by developing a novel optimal pricing model. Vorasayan ^[11] employed mathematical programs to establish the best recycling price and quantity. In ^[12], the authors developed a two-period model that involves competition between the original equipment manufacturer (OEM) and an independent operator capable of producing remanufactured products in the second period.

Financial dynamical systems have the potential to exhibit chaotic behavior, where even minor alterations can lead to significantly amplified and unpredictable consequences, contributing to fluctuations and instabilities within the game ^[2,14,15].

The complex interaction among investors, geopolitical factors, and economic policies can potentially thrust the market into chaos, resulting in unforeseen fluctuations in asset values, extreme volatility in prices, or sudden market collapses ^{[2,12,18,19,20,21]}. Consequently, accurately forecasting long-term trends becomes notably challenging. Hence, such chaotic behavior is deemed unsuitable for economic and financial systems, proving to be harmful. Thus, the manufacturer and the third-party both desire market stability, as it enables them to make decisions more easily and consistently pursue maximum profits. However, the closed-loop supply chain market is intricate; altering decision variables can shift the market from stability to chaos. Therefore, the manufacturer must collaborate with the third-party and implement measures to mitigate or prevent chaos, promoting market development and stability.

Numerous researchers and scholars have invested significant effort in devising effective methods to manage or eradicate such undesirable behavior ^{[18,23,24,25]}. While many of them are devoted to investigating chaos control in duopoly games ^{[26,27,28,29]}, there is a scarcity of literature specifically addressing chaos control in remanufacturing duopoly games. Furthermore, the Ott, Grebogi, and Yorke (OGY) control method has not been explored in such remanufacturing models to the best of our knowledge.

This study focuses on the dynamic exploration and chaos control in a remanufacturing duopoly game ^[12,30]. Within the market, we examine two firms: an OEM that exclusively produces new products, and a TPR that exclusively produces distinct products. The OEM and the TPR engage in repeated output competition, with access to only partial market information. It is understood that customers' willingness to pay for original and remanufactured products differs due to the need to distinguish between new products sold by the OEM and remanufactured products sold by the TPR. The OEM manufactures and sells new products in period "$t$" with a marginal cost of $c_n$, while the TPR remanufactures these products in period "$t+1$" with a marginal cost of $c_r$, satisfying the condition $c_n > c_r$. The symbol $\delta$ represents a consumer's willingness to pay for a remanufactured product, which is a fraction of their willingness to pay for the new products. Consumer willingness to pay is uniformly distributed in the range $[0, 1]$ and is heterogeneous. The variables $q_{n}$ and $q_{r}$ denote the demand for remanufactured and new products, respectively ^[12,30].

This paper is organized as follows: In the second section, we delve into an examination of the nature of the game under consideration, accompanied by a brief analysis of the stability of the Nash equilibrium. The third section is dedicated to exploring the presence of chaos using Lyapunov exponents (LEs), bifurcation diagrams, and spectral entropy (SE), incorporating a comparative analysis of the results obtained from these three analytical tools. Section 4 introduces and applies the OGY method to stabilize the unstable Nash equilibrium point. In Section 5, numerical simulations are conducted to validate the effectiveness of the OGY method in stabilizing the game, employing the marginal costs $c_n$ and $c_r$. The paper is then concluded in the final section.

2.   The model

We consider a recurrent remanufacturing duopoly game with diverse competition strategies and heterogeneous players, assuming that the original equipment manufacturer is boundedly rational and pursues profit maximization as its business objective, while the third-party remanufacturer is adaptive and aims for share maximization based on achieving a certain profit. The dynamics of the resulting remanufacturer duopoly game are described by the following two-dimensional discrete system ^[12]:

Here, $\alpha$, $\beta\in [0, 1]$ are the relative speed of output adjustment of OEM and TPR. The attitude between the profit and market share for the TPR is given by $v\in [0, 1]$.

The stability has been thoroughly examined in ^[12]. Let $\bar{\delta}$ denote the critical quantity

and we then distinguish two cases.

2.1.   Fixed points and stability if $0 < \delta\leq\bar{\delta}$

In this case, system (2.1) has only one fixed point $E(q_n^*, q_r^*)$, called the Nash equilibrium, provided that

Here,

and

Proposition 2.1. The Nash equilibrium $E^*$ is locally asymptotically stable, provided that

Or, equivalently,

2.2.   Fixed points and stability if $\bar{\delta} < \delta < 1$

In this case, the game has two equilibrium points: a boundary equilibrium $E_{0} = (0, 0)$ and a conditional equilibrium point $E = \left(\frac{1-c_n}{2+\delta}, \frac{1-c_n}{2+\delta}\right),$ for $c_n < 1.$

Proposition 2.2. The boundary equilibrium $E_{0}$ is unstable (saddle point), and the conditional equilibrium $E$ is locally asymptotically stable, provided that:

where $c_n^{NS} = 1-\dfrac{2+\delta}{\delta\alpha},$ and $c_n^F = 1-\dfrac{2(2+\delta)}{\alpha(2-\delta)}.$

Example 2.1. Considering the marginal cost $c_n\in]0, 1]$ as a control parameter:

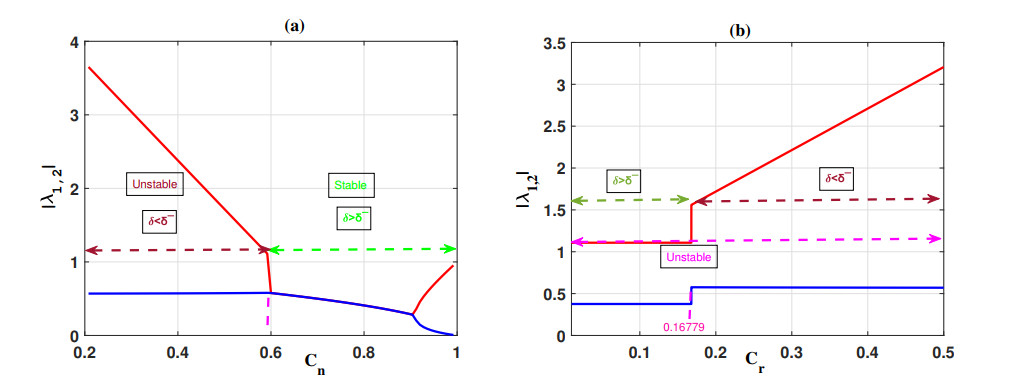
a) Taking the set of parameter values $\alpha = 5.8, \ b = v = 0.5, \ \delta = 0.3353,$ and $c_r = 0.2,$ we have $\delta = \bar{\delta} = 0.3353$ for $c_n = \bar{c}_n\approx 0.5962,$ and thus

● for $c_n < \bar{c}_n,$ we have $\bar{\delta} > \delta,$ (in this case $\tilde{c}_n\approx 0.9727,$ but $c_n < \bar{c}_n < \tilde{c}_n,$ thus $E^*$ is unstable. This aligns with the observation from Figure 1(a), where $\vert \lambda_{1}\vert > 1$ and $\vert \lambda_{2}\vert < 1$ signify the instability of the Nash equilibrium $E^*$, characterized as a saddle point).

● for $c_n > \bar{c}_n$ we have $\bar{\delta} < \delta,$ (in this case $\tilde{c}_n\approx 0.5163,$ so $c_n > \tilde{c}_n,$ thus $E^*$ is locally asymptotically stable. This aligns with the observation from Figure 1(a), where $\vert \lambda_{1, 2}\vert < 1$).

b) Taking the set of parameter values $\alpha = 5.8, \ \beta = v = c_n = 0.5,$ and $\delta = 0.3353,$ we have $\delta = \bar{\delta} = 0.3353$ for $c_r = \bar{c}_r\approx 0.16779,$ and thus

● for $c_r < \bar{c}_r,$ we have $\delta > \bar{\delta},$ (in this case $\tilde{c}_n\approx 0.5163,$ but $c_n = 0.5 < \tilde{c}_n,$ thus $E^*$ is unstable. This corresponds to the observation from Figure 1(b), where $\vert \lambda_{1}\vert > 1$ and $\vert \lambda_{2}\vert < 1$ indicate the instability of the Nash equilibrium $E^*$, identified as a saddle point).

● for $c_r > \bar{c}_r,$ we have $\delta < \bar{\delta},$ (in this case $\tilde{c}_r\approx 0.0544,$ but $c_r > \bar{c}_r > \tilde{c}_r,$ thus $E^*$ is unstable. This aligns with the observation from Figure 1(b), where $\vert \lambda_{1}\vert > 1$ and $\vert \lambda_{2}\vert < 1$ signify the instability of the Nash equilibrium $E^*$, characterized as a saddle point).

3.   Complexity and chaos

There are various tools for the investigation of the complexity and chaos in dynamical systems, such as Lyapunov exponent, bifurcation diagram, $0-1$ test, phase portrait SE, and others ^[19,20,21]. First, we highlight the complexity of the model by using the SE test.

3.1.   SE analysis

By employing the correlation algorithm, when we refer to the complexity of chaotic systems, we describe how much a chaotic sequence resembles a random one ^[1]. The more a model is close to the random sequence, the higher its complexity.

We employ the SE algorithm to quantify the complexity of the understudy duopoly game (2.1).

Here is an outline of the SE complexity algorithm, which can generate an energy distribution via the Fourier transform and determine the corresponding spectrum entropy using the Shannon entropy ^[19].

Step 1: Let ${Z^{N}(n), n = 0, 1, \ldots, N-1}$ be a chaotic pseudo-randomness sequence of length $N$. With the aim of the spectrum being able to reflect the signal's energy information more effectively, we should first remove the DC (direct current) part of $Z^{N}$ using the subsequent formula:

Step 2: We apply a discrete Fourier transform to the sequence $z(n)$.

Step 3: In this step, we calculate the relative power spectrum. The first half of the sequence for converted $Z(k)$ is taken and calculated using Parseval's theorem. At one of its frequency points, the power spectrum's value is

Then, the relative power spectrum of the sequence is given by

Step 4: The SE $se$ is then obtained by utilizing the Shannon entropy and the relative power spectral density $P_k$.

If $P_k = 0$, define $P_k \ln P_k = 0$. It is demonstrable that the value of the SE converges to $\ln (N / 2)$. For comparative analysis, the SE $\mathrm{SE}$ is normalized as

The presence of a non-uniform distribution in the sequence power spectrum leads to a simpler structure in the sequence spectrum and a distinct oscillation pattern in the signal. In such cases, the SE measure is smaller, indicating a lower complexity. Conversely, when the distribution is more uniform, the complexity is higher. Figure 2 depicts the relationship between SE and the parameters $c_n$ and $c_r$ for the understudy model (2.1).

Figure 2(a) illustrates the SE versus the marginal cost $c_n$ of the OEM for $c_n \in [0.49, 0.65]$. We can see that the SE increases when the marginal cost $c_n$ decreases, indicating a possible appearance of the chaotic behavior in the windows $c_n \in [0.4893, 0.547]$.

Figure 2(b) illustrates the evolution of the SE versus the marginal cost $c_r,$ of the TPR firm, within the range $c_r \in [0;0.25].$ The SE shows an increase as the marginal cost $c_r$ rises, with the possible appearance of the chaotic behavior in the windows $c_n \in [0.16, 0.25]$.

3.2.   Bifurcation diagram and Lyapunov exponents

The Lyapunov exponents tool aims to assess the divergence or convergence of two trajectories initiated from nearby points. These exponents provide a means to discern various dynamics within the underlying game, such as regular, periodic, chaotic, and hyperchaotic behavior. The presence of at least one positive Lyapunov exponent signifies the chaotic nature of the game.

Investigating now the dynamics of the duopoly game (2.1) by employing bifurcation diagrams and the Largest Lyapunov Exponent (LLE) calculated using the Wolf Swift algorithm ^[20].

Figure 3 illustrates the LLE and bifurcation diagram versus the marginal cost $c_n$ for the set of parameter values: $\alpha = 5.8,$ $\beta = \nu = 0.5,$ $\delta = 0.3353,$ and $c_r = 0.2.$ It is evident that LLE is positive for $c_n\in [0.4897, 0.5466]$ confirming the chaotic behavior previously predicted by the SE. Additionally, we can infer that the game exhibits periodic behavior (period-8 points, period-4 points, and period-2 points) within the interval $c_n\in[0.5466, 0.5961].$ We observe the stationary behavior for $c_n\in [0.5962, 0.65].$

Figure 4 depicts the LLE and the bifurcation of $q_r(t)$ with respect to the marginal cost $c_r\in [0, 0.25]$, for the parameter values $\alpha = 5.8,$ $\beta = c_n = \nu = 0.5,$ and $\delta = 0.3353.$ Obviously, LLE is positive for almost $c_r$ $\in [0.1533, 0.2366]$ confirming the chaotic behavior predicted by the SE. Furthermore, the game exhibits periodic behavior in the interval $[0, 0.1533].$ It is apparent that the largest Lyapunov exponents align well with the bifurcation diagram.

The duopoly game (2.1) exhibits strange attractors for various parameter values, some of them are illustrated in Figures 5 and 6, in blue, accompanied by the corresponding unstable Nash equilibrium depicted in red.

For instance, considering the parameter values $\alpha = 5.8$, $\beta = v = c_n = \frac{1}{2}$, $\delta = 0.3353$, and $c_r = \frac{1}{5}$, we obtain the following Lyapunov exponents: $\lambda_{1} = 0.4476, \lambda_{2} = -1.0816.$ As $\lambda_{1} > 0$, it indicates that the duopoly game (2.1) features a chaotic attractor. The Kaplan–Yorke dimension is calculated as $d = 1.5177$, revealing a fractal nature.

It is not advisable to select parameter values for $c_n$ and $c_r$ within the chaotic zone, as this would result in the duopoly game (2.1) exhibiting chaotic behavior in the market. Given that both firms lack knowledge of each other's strategies, we propose implementing control measures in the game to prevent the occurrence of chaotic market conditions. The objective is to assist the firms in the duopoly game (2.1) in making informed decisions by selecting appropriate values for their marginal costs $c_n$ and $c_r$.

3.3.   Market performance measures

To evaluate the system's performance, particularly when it displays chaos, we use aggregate market profits as a measure. Let $M_T(\alpha, c_r)$ denote the aggregate market profits during the time period $T$, then

where, $\Pi_n$ and $\Pi_r$ represent the profit functions of OEM and TPR respectively given by Eqs (4) and (5) in ^[12]. We consider the adjustment speed $\alpha$ and the TPR cost $c_r$ as a variable parameters and adopt the same parameter configurations as illustrated in Figure 2, and $T = 100$. The diagram in Figure 7 depicts the aggregate profits versus $\alpha$ and $c_r$ where we observe that, when the adjustment speed of the OEM or TPR cost $c_r$ falls within the chaotic range, the market's aggregate profits experience a significant decrease in comparison to the equilibrium state case, meaning that the chaotic output dynamics is harmful to the market.

4.   Chaos control of the duopoly game using OGY method

Chaotic behavior in economics is unwelcome, as it adversely affects investor confidence, economic growth, and operational challenges. It also heightens volatility and financial risks. The manifestation of chaos in duopoly games leads to unpredictability in the output decisions of both OEM and TPR players due to its sensitivity to infinitesimal errors. Consequently, there is a desire to discover methods to control chaos within economic systems. Various approaches have been suggested, including feedback control ^[23], adaptive control ^[24], and OGY method ^[18,25], among others. In this study we opt for the OGY method due to its non-invasive application (very small parameter adjustment during a very small time period), ensuring that the game's evolution between TPR and OEM will be stabilized without great effort.

The fundamental concept behind the OGY method involves making small time-dependent perturbations to an accessible control parameter of the system to guide the system state toward its unstable equilibrium, utilizing the stable manifold as a vehicle to achieve the desired outcome as illustrated in Figure 8.

Consider the map

where $x_{n}\in\mathbb{R}^{2},$ $F: \mathbb{R} ^{2}\times \mathbb{R}\rightarrow \mathbb{R}^{2},$ and $p\in\mathbb{R}$ is an externally accessible control parameter.

The map (4.1) can be linearized around the fixed point $x_{F}(\bar{p})$ as follows:

where $A = \left. \frac{\partial F}{\partial x}\right\vert _{x = x_{F}(\bar {p})}$ and $B = \left. \frac{\partial F}{\partial p}\right\vert _{p = \bar{p}}.$ Then,

ere, $K$ is a gain vector that will be determined later. The controlled system can be written as

The stability of the controlled system is determined by the eigenvalues of $(A-BK^T)$. The system is controllable if the controllability matrix

has full rank $2$.

Assume the matrix $A$ has two eigenvalues $\lambda_{s}$ and $\lambda_{u}$, with two left eigenvectors $v_{s}$ and $v_{u},$ and two right eigenvectors $w_{s}$ and $w_{u}$. We adjust the parameter $p$ such that $w_{u}^{T}(x_{n+1}-x_{F}(\bar{p})) = 0$. We get

Then, the control law can be written as

4.1.   Stabilization of the unstable Nash equilibrium $E=(q_{n}^*, q_{r}^*)$

● If $0 < \delta < \bar{\delta}$. Then,

The $c_r$ controllability matrix is

and its determinant is

Thus, we conclude that TPR can stabilize the Nash equilibrium $E$ by adjusting its marginal cost $c_r$.

● If $\bar{\delta} < \delta < 1$, then

The $c_n$ controllability matrix is

and its determinant is

Then, we conclude that the OEM firm can stabilize the game around the Nash equilibrium $E$ by adjusting its marginal cost $c_n$.

5.   Numerical simulation

We conduct numerical simulations to confirm the theoretical findings. First, we use the OEM marginal cost $c_n$ as the control parameter, and then we use the TPR marginal cost $c_r$ as the control parameter.

5.1.   Stabilizing the unstable Nash equilibrium using the OEM marginal cost $c_n$

Let us consider $c_n$ as a control parameter and set the other parameters as follows: $\alpha = 5.8, \ \beta = \delta = v = 0.5,$ and $c_r = 0.2$. For $c_n = c^*_n = 0.5$ we have $E^* = (0.2279, 0.1317),$ and the Jacobian matrix

and the control gain $K^T = (1.3, 0.26)$.

Figure 9 illustrates the response of the controlled duopoly game along with the applied control effort. The control is activated when the system state approaches the unstable equilibrium $E^*$ at $t = 54$ and the marginal cost $c_n$ is adjusted by a small perturbation of order $10^{-3}$ during the short time period $t\in [54, 56]$. Subsequently, the control is established at $t = 57$, stabilizing the duopoly game to its Nash equilibrium.

5.2.   Stabilizing the unstable Nash equilibrium using the TPR marginal cost $c_r$

Let us consider $c_r$ as a control parameter and set the other parameters as follows:

$\alpha = 5.8, \ \beta = v = c_n = 0.5,$ and $\delta = 0.3353$. For, $c_r = c^*_r = 0.2,$ we get the Nash equilibrium $E \approx (0.2279, 0.1317)$, the Jacobian matrix

and the control gain $K^T = (7.6930, 1.5368)$.

Figure 10 shows the response of the controlled duopoly game along with the control effort. The control was activated when the system state is sufficiently close to the unstable equilibrium $E^*$ at $t = 96$ and the TPR marginal cost $c_r$ is slightly adjusted by a perturbation of order $10^{-4}$ during the short time period $t\in [96, 102]$. Subsequently, the control is established at $t = 103$, stabilizing the duopoly game to its Nash equilibrium.

5.3.   Results and discussion

In contrast to other control methods, the application of the OGY method to stabilize markets offers the advantage of achieving control with minimal effort of a single firm within a brief time frame. This means that the method can lead the market towards stability in a smooth manner without compromising the firms in the game.

For example, in the present study, the control was realized through adjusting the OEM cost $c_n$ by $|\Delta c_n| < 6 \times 10^{-3}$ over only two units of time. Additionally, it was accomplished when adjusting the TPR cost $c_r$ by a perturbation $|\Delta c_r| < 1.1 \times 10^{-3}$ over only 6 units of time. In the counter party, Kopel's model was controlled in ^[26] using a state feedback method through adjusting state of the first firm with a perturbation $|u(t)| < 0.4$ over about 60 units of time. In ^[26], a Cournot model was stabilized using a delay feedback control (Pyragas method) by adjusting the state of the first firm during approximately 50 units of time. In ^[27], a Cournot model was stabilized using the state variable feedback and parameter variation method during approximately 40 units of time.

6.   Conclusions and discussion

We examined a duopoly game model involving distinct competition strategies and heterogeneous players. The findings reveal significant impacts of the marginal cost $c_n$ for the original equipment manufacturer (OEM) and the marginal cost $c_r$ for the third-party remanufacturer (TPR) on their competitive dynamics within the game. Under specific parameter configurations, a decrease in $c_n$ induces a transition in game behavior from chaos to regular, while an increase in $c_r$ results in a shift from regular to chaotic behavior. By applying a control law derived from the OGY method, with either the marginal cost $c_n$ of the OEM or the marginal cost $c_r$ of the TPR as a control parameter, the chaotic behavior is effectively eliminated, leading to the stabilization of the duopoly game at its Nash equilibrium point $E$.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research has been funded by Scientific Research Deanship at University of Ha'il–Saudi Arabia through project number (RG-23 045).

Conflict of interest

All authors declare no conflicts of interest in this paper.