Numerical approximations of stochastic Gray-Scott model with two novel schemes

1.   Introduction

In recent years, reaction-diffusion systems have gained central importance in different fields of chemistry and biochemistry such as the lattice Boltzmann model ^[1], Brusselator model ^[2], Lengyel-Epstein model ^[3], Schnakenberg model ^[4], glycolysis model ^[5] etc. A common and envoy chemical reaction model which explains the irreversible chemical reaction process is the Gray-Scott model. The Gray-Scott model was proposed by P. Gray and S. K. Scott at the University of Leeds in the $1980s$. Its mechanism is given as

where $\Psi, \Phi$ are reactants, $Q$ represents the product of the reaction, $\phi, \psi$ are the chemical concentrations of the reactants $\Phi, \Psi$ respectively, and $k_1, k_2$ are the reaction rates and positive constants. It is also used as a predator-prey model that describes the predominance of one species over the other. The key feature of the reaction-diffusion systems is pattern formation. The Gray-Scott model has been extensively studied for the different patterns such as self-replicating patterns, the annular pattern emerging from circular spots, self-replicating spots, stationary spots, growing stripes, labyrinthian patterns, spatialtemporal chaos, stripe filaments, travel spots, and many others ^{[6,7,8,9,10,11,12,13]}.

The dimensionless Gray-Scott ^[14] model is given below:

$D_u, D_v$ are the diffusion the coefficients of the $u$ and $v$ concentrations respectively, $F$ is the flow rate and $k$ is the decay constant.

Here, we consider the 1-D coupled Gray-Scott model under the influence of the multiplicative time noise as given below:

with the initial conditions

and the boundary conditions may be dirichlet or homogenous Neumann conditions.

where $\Psi, \Phi$ represent the chemical concentrations, $\alpha_1, \alpha_2$ are the diffusion rates, $A$ represents the reaction rate of Eq (1.2) and $B$ is the feed rate of Eq (1.3). The noise strengths are represented by $\nu_1$ and $\nu_2$ and these are the Borel functions. The time series of white noise are $\dot W_1(t)$ and $\dot W_2(t)$. The $W_1(t)$ and $W_2(t)$ are the standard Brownian motions. The state variables are independent of the state of the Brownian motion. The steady-state equilibrium point of the underlying model is $(\Psi^*, \Phi^*) = (1, 0)$.

One can use the three types of boundary conditions i.e., Dirichlet, Neumann and Robin. We have used the Dirichlet and homogenous Neumann boundary conditions and the problems are uniquely solvable under these conditions. When we see the majority of the physical systems at the micro-level, some kind of stochastic behavior is observed. So, it is better to consider the classical model perturbed with some kind of noise. If the noise in the differential equation's solution is constrained, then these systems are stochastic differential equations (SDEs). The numerical solutions of the stochastic differential are the need of the hour and are a tough job. It becomes more difficult when we have nonlinear stochastic partial differential equations (SPDEs). We have provided the solution to such nonlinear SPDEs with two different schemes. Both schemes are consistent with given SPDEs in the mean square sense. We have discussed the stability of the schemes by using the von-Neumann technique. Both schemes are time efficient. We have the random selection on each time step of the numerical scheme which leads to abrupt behavior of the solution and it has been controlled in the numerical scheme supported by stability and consistency.

In real-life problems, the physical phenomena are generally affected by stochastic factors and production fluctuations. The stochastic effect may be intrinsic or extrinsic. If one is considering the partial differential equations with noise as a source term then such equations are known as SPDEs. The source term may exist in the equations or the conditions. So, SPDEs are taken into account for a better representation of the physical systems. The analytical solutions of SPDEs are rarely exists or are impossible to obtain, so the numerical approximation is carried out for such issues. The classical numerical techniques fail to yield the approximation; due to this reason different new techniques have been proposed by various researchers. Shardlow worked on the numerical approximation of the Barkley model of excitable media perturbed with noise by using spectral approximation and the Barkley method. He concluded that the effectiveness depends upon the SPDEs under consideration ^[15]. BabuAika et al. considered the elliptic SDPEs and they proposed a stochastic collocation method and obtained the numerical results and performed convergence analysis ^[16]. Another group considered the heat equation under the influence of time series of noise, where the noise may be additive or multiplicative and discussed the convergence analysis of the given SPDE and concluded that the rate of the convergence can be improved if there is additive noise present in the equation and there is no improvement for multiplicative noise ^[17]. Yasin et al. worked on the numerical solution of the stochastic FitzHugh-Nagumo equation by using a stochastic forward Euler (SFE) finite difference scheme^[18]. In ^[19], the authors extracted the numerical approximation of the fractional elliptic SPDEs with spatial white noise, analyzed the approximation of mean- square error and derived an explicit rate of convergence. Namjoo and Mohebbian worked on the numerical solutions of SPDEs and showed the consistency, stability, and convergence of the proposed scheme ^[20]. Gyöngy and Martine studied the lattice approximation of the elliptic SPDEs perturbed by white noise on a bounded domain $R^d$ for $d = 1, 2, 3$; they obtained the convergence rates of the approximation ^[21]. Roth used the finite difference methods with Wong-Zakai methods for the numerical approximation of the hyperbolic SPDEs. He proved the consistency, stability, and convergence of the schemes ^[22]. Iqbal et al. considered the stochastic Newell-whitehead-Segel equation and extracts its numerical solutions by two schemes. The consistency and stability of the schemes were discussed. The smoothness of the solution was also derived ^[23]. Du and Zhang worked on the numerical solutions of the linear SPDEs with special additive noise. They discussed the error analysis and convergence results of the finite difference methods and finite elements methods ^[24]. Pettersson and Signahl developed a numerical scheme for SPDEs of the Itô type and discussed the uniform convergence ^[25]. Some more work on the solution of the differential equations under the influence of the noise can be found ^{[26,27,28,29,30,31,32,33]}. Baccouch and his co-authors ^[34,35] proposed a discontinuous Galerkin method for SDEs. They proved that the method is convergent in the mean-square sense.

The novelty and contributions of the article are as follows:

$(1)$ When physical systems are observed at the micro level, randomness is present. Naturally, it is quite better to use the classical models under the influence of some random process. So, we are considering the classical Gray-Scott system under the effect of some Brownian motion.

$(2)$ For the sake of the numerical investigation of the underlying model, two new schemes have been developed.

$(3)$ Both schemes are consistent with the given set equations of nonlinear SPDEs of the Itô type.

$(4)$ The stability of the schemes is shown with the help of the von-Neumann technique. The proposed scheme I is conditionally stable and its stability condition is derived. The proposed scheme II is unconditionally stable.

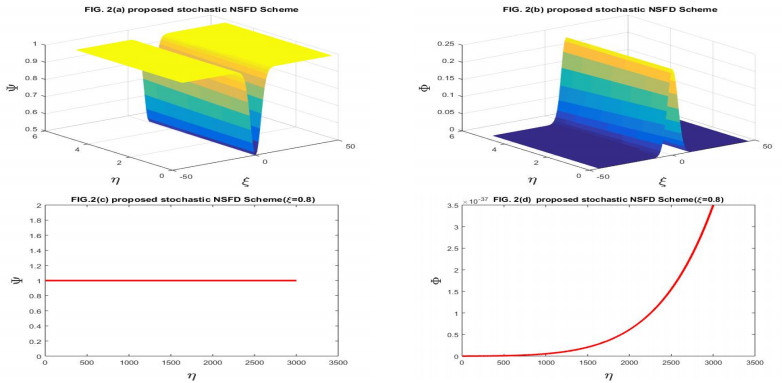
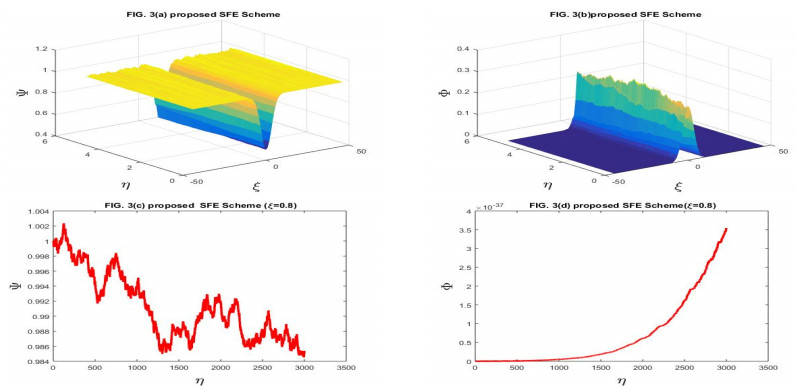
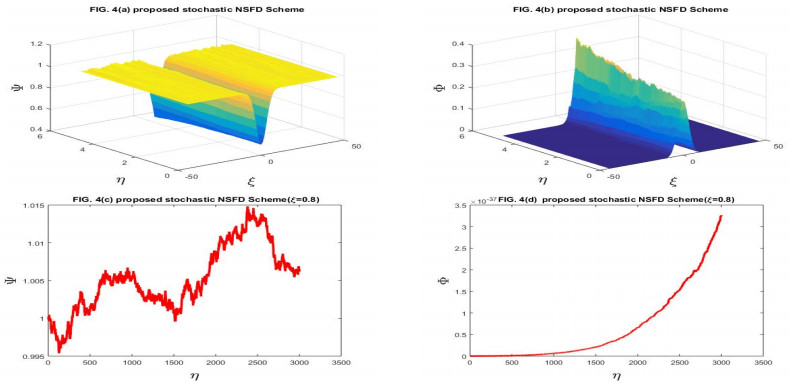
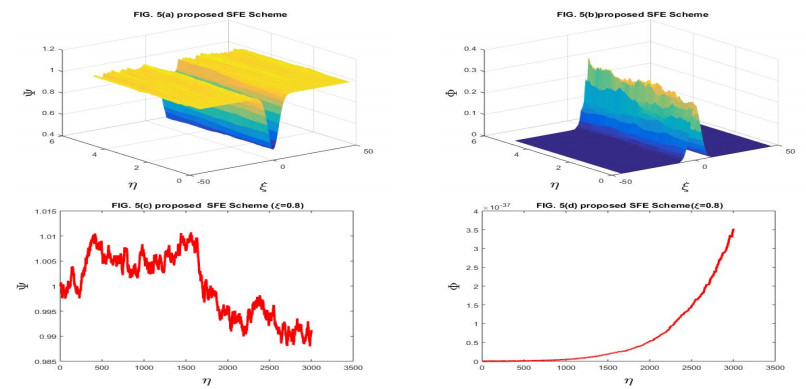
$(5)$ The graphical behavior of the test problem is observed for various values of the parameters. For the value of noise strength $\nu_1 = \nu_2 = 10^{-16}$, the stochastic Gray-Scott system resembles the classical Gray-Scott system. When the values of the noise strength increased, the pattern formed start to destroy.

$(6)$ MATLAB 2015a was used for the simulations of the test problem.

The following describes the consistency of the schema.

Definition 1.1. ^[36,37,38] A stochastic finite difference scheme $L|_{r, s}U|_{r, s} = G|_{r, s}$ is consistent with the SPDE $LU = G$ at a point $(\xi, \eta)$; if there is any continuously differentiable function $\Psi = \Psi(\xi, \eta)$ then

as $\Delta \xi\rightarrow 0, \; \Delta \eta \rightarrow 0$ and $(q \Delta \xi, (r+1)\Delta \eta)\rightarrow (\xi, \eta)$.

2.   Proposed stochastic forward Euler scheme

Equations (1.2), and (1.3) are nonlinear SPDEs. The variable $\Psi_\eta, \Phi_\eta, \Psi_{\xi\xi}$ and $\Phi_{\xi\xi}$ are approximated as given below:

where $\Delta \xi$ and $\Delta \eta$ are the space and time step sizes respectively. Also, let us assume that we divide the spatial and temporal coordinates:

Let $r_1 = \frac{\Delta \eta \alpha_1}{\Delta \xi^2}$ and $r_2 = \frac{\Delta \eta\alpha_2}{\Delta \xi^2}$ and by replacing all values in Eqs (1.2) and (1.3), they can be reduced to the following equations:

So, Eqs (2.1) and (2.2) constitute the required proposed SFE scheme (proposed scheme-I) for Eqs (1.2) and (1.3).

2.1.   Consistency of proposed scheme-I

The consistency of the scheme is proved in the mean square sense.

Theorem 2.1. The proposed SFE scheme for $\Psi$ and $\Phi$ in Eqs (2.1) and (2.2) is consistent with Eqs (1.2) and (1.3) in the mean square sense.

Proof. Suppose that $\Psi_1(\xi, \eta)$ and $\Phi_1(\xi, \eta)$ are smooth functions and applying $L(f) = \int^{(r+1)\Delta \eta}_{r\Delta \eta} {f} du$ to Eq (1.2), we get

By applying the proposed SFE scheme to Eq (1.2), we get

In the mean square sense, the above two equations can be written as

By using the Itô's integral square property, we get

$E|L(\Phi_1)|_{q, r}-L|_{q, r} \Phi_1|^2\rightarrow 0$ as $q\rightarrow \infty$ and $r \rightarrow \infty,$ so the proposed scheme for $\Psi$ is consistent with (1.2).

Similarly, we use the same step to show the consistency of Eq (2.2).

By applying the proposed SFE scheme to Eq (1.3), we get

In the mean square sense, the above two equations can be written as

By using Itô's integral square property, we get

$E|L(\Phi_1)|_{q, r}-L|_{q, r} \Phi_1|^2\rightarrow 0$ as $q\rightarrow \infty$ and $r \rightarrow \infty,$ so the proposed scheme for $\Phi$ is consistent with (1.3).

2.2.   Stability of the proposed scheme-I

The stability of the current scheme is shown with the help of von- Neumann criteria.

2.3.   Von-Neumann criteria

By this method, $\Psi_{q, r}$ is replaced in the differential equation as given below:

and by doing some basic calculations, one gets the amplification factor as follows ^[39]:

where $\chi$ is a constant.

It is a necessary and sufficient condition of stability.

Theorem 2.2. If $\left|1+ A \Delta \eta-4r_1\sin^2(\frac{\beta \Delta \xi}{2})\right|^2\leq 1$ and $\left|1- (A+B) \Delta \eta-4r_2\sin^2(\frac{\beta \Delta \xi}{2})\right|^2 \leq 1$, then the proposed SFE is stable with $(r+1)\Delta \eta = T$.

Proof. As it is a linear analysis, Eq (2.1) is linearized:

By using Eq (2.3), the above equation takes the following form:

Using the independence of the Brownian motion and amplification factor can be written as given below:

if $\left|1+ A \Delta \eta-4r_1\sin^2(\frac{\beta \Delta \xi}{2})\right|^2\leq 1$, then

where $|\nu_1|^2 = \chi$ is a constant, so the given scheme for $\Psi$ is stable. Repeating the same procedure for the stability of Eq (2.2), we get the following equation:

if $\left|1- (A+B) \Delta \eta-4r_2\sin^2(\frac{\beta \Delta \xi}{2})\right|^2 \leq 1,$ then the above equation reduces to

where $|\nu_2|^2 = \chi$ is a constant, so the given scheme for $\Phi$ is stable.

2.4.   Convergence of the proposed scheme-I

The convergence of the scheme is discussed in the mean square sense.

Theorem 2.3. The proposed scheme-I given by Eqs (2.1) and (2.2) is convergent in the mean square sense.

Proof.

as the proposed scheme-I is consistent in the mean square sense i.e., $L_{q, r}\Psi|_{q, r} \rightarrow L_{q, r}\Psi$ as $\Delta \xi \rightarrow0, \Delta \eta \rightarrow0$ and $(q\Delta \xi, r\Delta \eta)\rightarrow (\xi, \eta)$.

also, because the scheme is stable, this $(L_{q, r})^{-1}$ is bounded. So, $E\bigg|\Psi|_{q, r}-\Psi \bigg|^2 \rightarrow 0$. Hence the proposed scheme-I for $\Psi$ is convergent in the mean square sense.

as the proposed scheme-I is consistent in the mean square sense i.e., $L_{q, r}\Phi|_{q, r} \rightarrow L_{q, r}\Phi$ as $\Delta \xi \rightarrow 0, \Delta \eta \rightarrow 0$ and $(q\Delta \xi, r\Delta \eta)\rightarrow (\xi, \eta)$.

also, because the scheme is stable, this $(L_{q, r})^{-1}$ is bounded. So, $E\bigg|\Phi|_{q, r}-\Phi \bigg|^2 \rightarrow 0$. Hence, the proposed scheme-I for $\Phi$ is convergent in the mean square sense.

3.   Proposed stochastic non-standard finite difference scheme

Equations (1.2) and (1.3) are nonlinear SPDEs. The variable $\Psi_\eta, \Phi_\eta, \Psi_{\xi\xi}$ and $\Phi_{\xi\xi}$ are approximated as given below:

By replacing all values in Eqs (1.2) and (1.3), they can be reduced to following equations:

Equations (3.1) and (3.2) are the required proposed stochastic non-standard finite-difference (NSFD) scheme (proposed scheme-II) for Eqs (1.2) and (1.3).

3.1.   Consistency of proposed scheme-II

The consistency of the scheme is proved in the mean square sense.

Theorem 3.1. The proposed stochastic NSFD scheme for $\Psi$ and $\Phi$ in Eqs (3.1) and (3.2) is consistent with Eqs (1.2) and (1.3) in the mean square sense.

Proof. Suppose that $\Psi_1(\xi, \eta)$ and $\Phi_1(\xi, \eta)$ are smooth functions; applying the $L(f) = \int^{(r+1)\Delta \eta}_{r\Delta \eta} {f} du$ to Eq (1.2), we get

Applying the proposed stochastic NSFD scheme to Eq (1.2) gives

In the mean square sense, the above two equations can be written as

Applying Itô's integral square property gives

$E|L(\Phi_1)|_{q, r}-L|_{q, r} \Phi_1|^2\rightarrow 0$ as $q\rightarrow \infty$ and $r \rightarrow \infty,$ so this proposed scheme for $\Psi$ is consistent with (1.2).

Similarly, we use the same step to show the consistency of Eq (3.2).

Applying the proposed stochastic NSFD scheme to Eq (1.3) gives

In the mean square sense, the above two equations can be written as

Applying the Itô's integral square property gives

$E|L(\Phi_1)|_{q, r}-L|_{q, r} \Phi_1|^2\rightarrow 0$ as $q\rightarrow \infty$ and $r \rightarrow \infty,$ so this proposed scheme for $\Phi$ is consistent with (1.3).

3.2.   Stability of the scheme

Theorem 3.2. The proposed stochastic NSFD scheme is unconditionally stable with $(r+1)\Delta \eta = T$.

Proof. Equation (3.1) is linearized as given below:

By using Eq (2.3), the above equation takes the following form:

Using the independence of the Brownian motion and amplification factor yields

Given that $\left|\frac{1+ A \Delta \eta-4r_1\sin^2(\frac{\beta \Delta \xi}{2})}{(1-2r_1+ A \Delta \eta)}\right|^2 < 1,$ and $|\frac{\nu_1}{(1-2r_1+ A \Delta \eta)}|^2 = \chi$, the above equation takes the form:

so the given scheme for $\Psi$ is stable.

Similar to doing calculations on the same pattern, the amplification factor for $\Phi$ takes the form

where $\left|\frac{1+2r_2-4r_2\sin^2(\frac{\beta \Delta \xi}{2})}{(1+2r_2+ (A+B) \Delta \eta)}\right|^2 < 1$ and $|\frac{\nu_2}{((1+2r_2+ (A+B) \Delta \eta)}|^2 = \chi$. The above equation takes the form

So, the given scheme for $\Phi$ is stable.

3.3.   Convergence of the proposed scheme-II

The convergence of the proposed scheme-II can be proved in the same pattern as proved for the proposed scheme-I.

4.   Graph and discussion

In this section of the article, we are taking two test problems for the numerical results.

Problem 4.1.

which have the following initial and boundary conditions ^[40],

Problem 4.2.

which have the following initial and homogeneous Neumann boundary conditions ^[41],

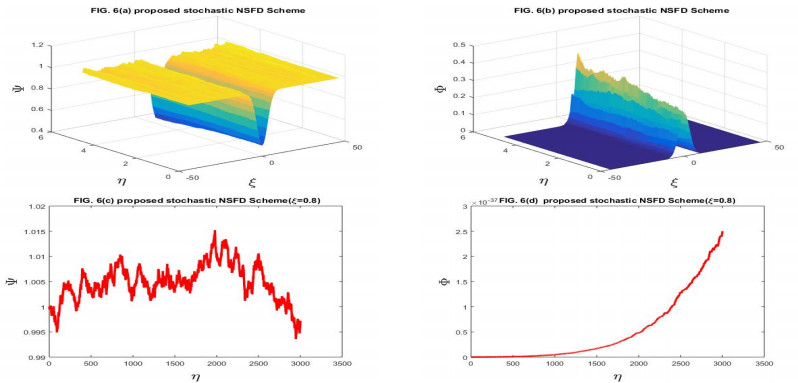
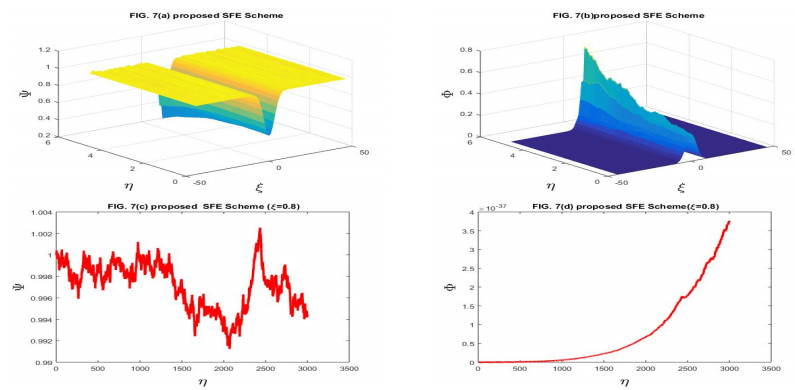
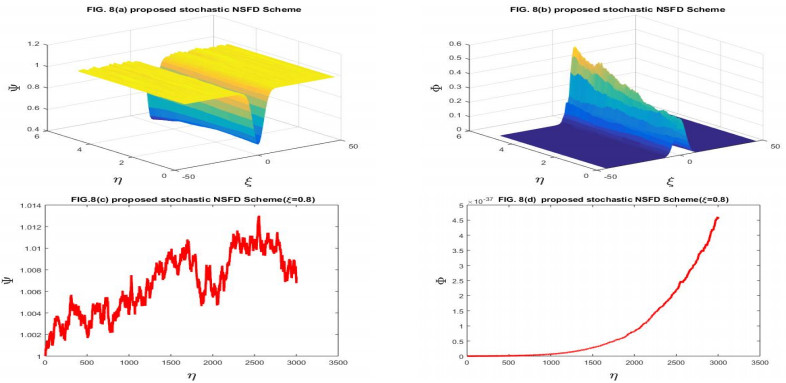
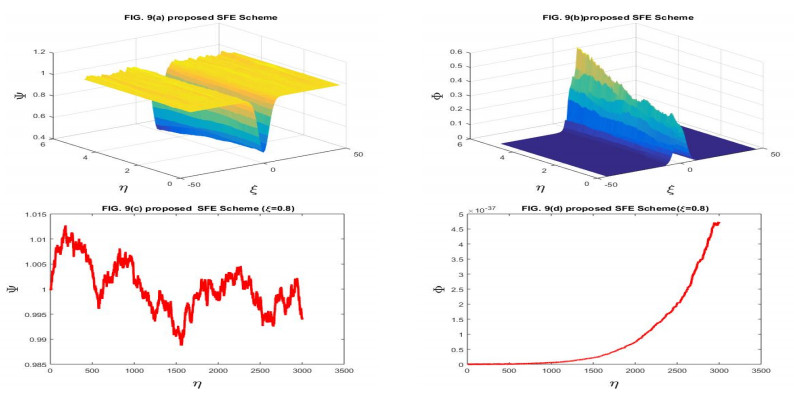
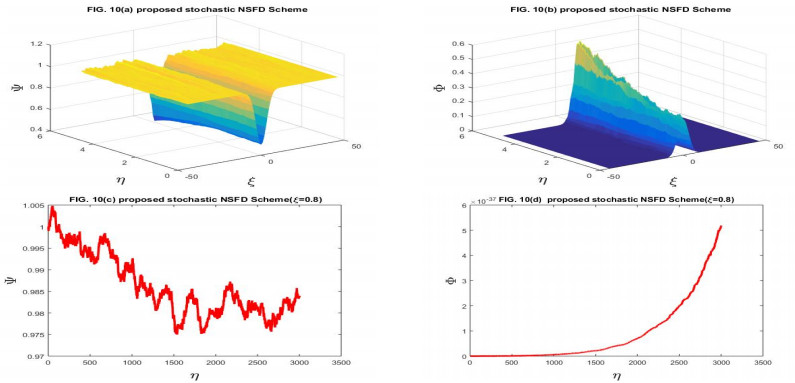
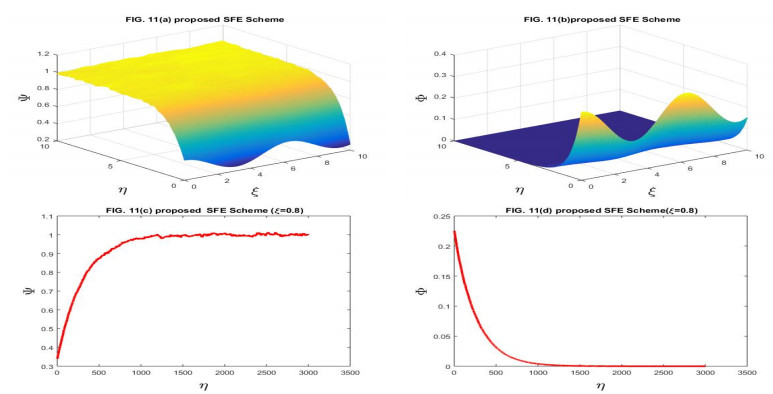
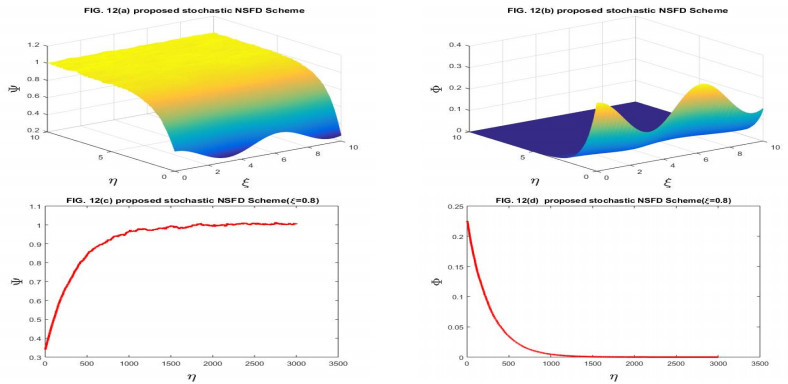
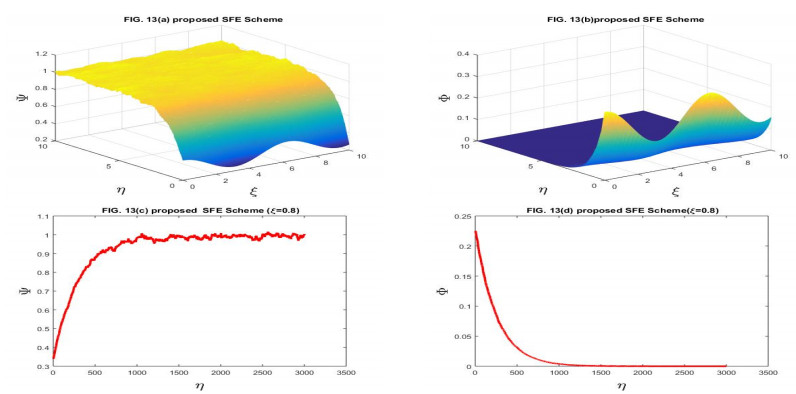
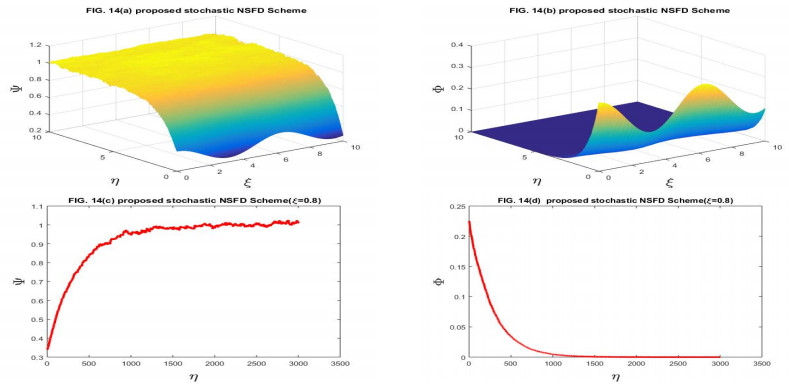
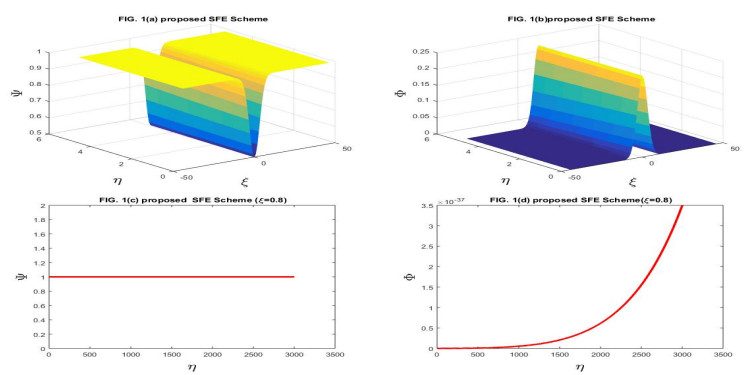
Here, we have taken the problems for the numerical solution of the stochastic Gray-Scott model perturbed by time series with white noise. The physical behavior of Problems 4.1 and 4.2 is depicted through Figures 1–14 respectively. We have compared the numerical results of the stochastic Gray-Scott model with the classical Gray-Scott model when the noise strength $\nu_1 = \nu_2\rightarrow 0$ and these results are the same. When the values of the noise strength increased, the fluctuation in the plots increased. The noisy strength disturbed the pattern formed in Gray-Scott models and it can be controlled with the parameter $\nu_1$ and $\nu_2$. The proposed SFE finite difference scheme is conditionally stable and conditions are given in the corresponding stability theorem of the scheme. The proposed stochastic NSFD scheme is unconditionally stable. The schemes are novel and time efficient. The proposed scheme-I does not converge toward the steady state point for the whole domain but the proposed scheme-II converges towards the steady state point $(\Psi^*, \Phi^*) = (1, 0)$. The graphical behavior depicts the efficacy of both schemes. When the noise strength $\nu_1 = \nu_2 = 10^{-16}\rightarrow 0$, then the stochastic Gray-Scott model converges to the classical Gray-Scott model and it is shown in this Figures 1 and 2. As the values of the noise strength increased, the destruction of the pattern was observed. Such fluctuations are controlled with the control parameters $\nu_1$ and $\nu_2$ which represent the Borel function. The reaction-diffusion models are used to describe various physical phenomena, such as reversible reaction processes and irreversible reaction processes and different types of spatial and temporal patterns are formed. The Gray-Scott system is a reaction-diffusion model and various patterns are formed according to the problem. For our test problem, replicating behavior was observed for different values of the parameters and these patterns were damaged due to the increase in the noise strength. The Gray-Scott system is a chemical concentration model and this system has specific properties such as positivity, and boundedness. So, there should be such a numerical scheme that preserves the true traits of the system and for such models, there is a proposed NSFD scheme that preserves such properties. The graphical behavior of the test problem is performed using MATLAB R2015a and the CPU had the following specifications Intel$^{(R)}$ Core$^{(TM)}$.

5.   Conclusions

In this manuscript, the stochastic Gray-Scott model has been numerically discussed. The underlying model is an autocatalytic chemical reaction-diffusion system that produces a variety of patterns. The 3D plots of chemical concentration represent the self-replication behavior was is observed in all 3D plots. The numerical solution has been obtained by using the proposed SFE scheme and the proposed stochastic NSFD scheme. The linear stability analysis of each scheme with the help of the von- Neumann criteria has been presented. The proposed SFE scheme is conditionally stable and the condition of stability is given in the corresponding stability theorem the stochastic NSFD scheme is unconditionally stable. Both schemes are consistent in the mean square sense with a given system of equations. The convergence of each scheme is also proved. When $\nu_1 = \nu_2 = 10^{-16}$, the stochastic Gray-Scott model truly resembles classical Gray-Scott models as shown in Figures 1 and 2 for two proposed schemes. When the value of the noise strength increased then the pattern deformed. The 3D and 2D graphical representations yielded the efficacy of the time-efficient schemes. Both schemes are novel and time efficient. The stochastic behavior of the underlying model is the novelty. This article will motivate and encourage the researchers, providing deep insight into the chemical reaction models under the influence of random processes.

Acknowledgements

This research was funded by the National Natural Science Foundation of China (Grant No.11861053). The authors are grateful to anonymous referees for their valuable suggestions, which significantly improved this manuscript.

Conflict of interest

The authors declare no conflicts of interest.