Event-triggered sliding mode control for a class of uncertain switching systems

Abbreviations:

$R$: the set of real numbers; ${\mathbb{N}^ + }$: the set of positive integers; ${R^n}$: the real n-dimensional space; ${R^{m \times n}}$: the real matrix space; $\left\| \cdot \right\|$: the Euclidean norm; ${X^T}$: the transpose of matrix $X$; $P > 0$: $P$ is positive definite symmetric matrix; $I$: an identity matrix of appropriate dimensions; $*$: an ellipsis for terms induced for symmetry; $rank\left(\cdot \right)$: the rank of a matrix; ${\lambda _{\max }}\left(\cdot \right)$: the maximum eigenvalue of a symmetric matrix; ${\lambda _{\min }}\left(\cdot \right)$: the minimum eigenvalue of a symmetric matrix

1.   Introduction

Switched systems belong to an essential class of hybrid dynamical systems, which can be composed of a series of continuous-time or discrete-time dynamic subsystems and switched rules that coordinate the switching between several subsystems. Due to its wide application in different fields such as flight control systems, underwater vehicle systems, multi-agent vehicle formation planning systems and mechanical systems, it has attracted great attention from researchers ^{[1,2,3,4,5,6,7]}. Switched signal has a significant influence on the stability analysis of the switched system. For many systems, such as unmanned vehicles and robots, as the operating environment changes, such as road conditions, applied loads and communication structures, the entire system will experience different dynamic characteristics, which can be called switched between different subsystems. With the development of the switched system theory, the stability analysis and control of the switched system have become a research hotspot. Based on the public Lyapunov functional method, zhang et al. propose a robust integral sliding mode control for uncertain switched systems ^[8]. Fei et al. adopted the average dwell time (ADT) method to study the stability of the switched systems ^[9].

It is well known that the sliding mode control (SMC) method has strong robustness to the disturbance of unknown boundary and it has the advantages of simple structure, fast response and good transient response. However, in the actual system, there are often external disturbances, modeling errors and other uncertainties, such as input channel interference and external environmental interference. Therefore, the SMC strategy has attracted a lot of attention and has been applied to different systems, including switched systems, fuzzy systems, Markov jump systems and stochastic systems ^{[10,11,12,13,14,15,16,17,18]}. Among them, the main idea of SMC is to utilize a discontinuous control to drive the system state enter into the bounded sliding mode region and keep in there in the subsequent time so that the expected performance such as stability, disturbance suppression and robustness can be achieved.

The design method of SMC is generally divided into two steps: (1) Designing the sliding mode surface function that meets the relevant performance requirements; (2) The approach law method is used to design the sliding mode controller to drive the system state to the sliding mode surface or quasi-sliding mode band. It is worth noting that unlike the design process of SMC for general linear systems, the SMC of switched systems is more complicated due to the presence of switching signals. In ^[19], a layered SMC scheme for all signals with arbitrary switching is studied. In ^[20], the SMC problem of a class of continuous-time switched systems with stochastic perturbation was studied.

From these studies, it can be found that the SMC of switched systems is mostly carried out in a time-triggered manner, which leads to resource depletion. Therefore, the event-triggered mechanism has been peoposed and developed rapidly. In the event-triggered mechanism, only when the sampling point meets the event-triggered conditions, is the transmission carried out. Different from traditional time-triggered control, event-triggered control is more convenient and effective in reducing unnecessary data sampling, which can reduce unnecessary resource waste ^[21,22]. Due to the superiority of the event-triggered control in saving resources, the event-triggered control strategy has been gradually applied in many practical systems, such as linear systems ^[23], nonlinear systems ^{[13,17,24,25]}, uncertain systems ^[26,27] and stochastic systems ^[28,29,30].

In addition, there are attempts to combine SMC with the event-triggered mechanism, ensuring the robustness of the system with a smaller event execution time. At present, the event-triggered SMC approach has made great progress. Wu and Gao et al. discussed the strategy of combining the event-triggered scheme with SMC to obtain the stability of the closed-loop system ^[17]. In ^[23], a class of event-triggered control schemes for switched systems based on data sampling was considered. Wen et al. studied the event-triggered SMC method for a class of fuzzy systems with induced delay ^[31]. However, it should be pointed out that the issue of event-triggered control of uncertain switched systems needed to be improved.

Motivated by the above discussions, we aim to solve the SMC problem of uncertain switching systems by an event-triggered mechanism. Unlike most existing results, we propose an event-triggered mechanism by combining the switched properties and reachability of switched sliding mode dynamics. The major contributions of this paper can be listed as follows:

(1) The sliding mode control problem of a class of discrete-time uncertain switching systems with matching disturbance is considered, and the purpose of saving resources is realized based on the event-triggered strategy.

(2) A linear sliding mode surface is designed. Based on Lyapunov function theory and ADT method, sufficient conditions for the exponential stability of the switching sliding mode dynamics equation are provided.

(3) Based on the characteristics of sliding mode control of switching system, a new sliding mode control law is proposed using event triggering mechanisms, and a triggering rule is established to realize the event-triggered sliding mode control of switching system. This reduces the conservative nature of the control strategy.

2.   System description and problem statement

Consider the following uncertain discrete switched systems with disturbances:

where $x(k) \in {R^n}$ represents the state, $u(k) \in {R^n}$ represents the control input. $\big\{ {{A_{\sigma (k)}}, {B_{\sigma (k)}}:\sigma} {\in {\cal N}} \big\}$ represents a family of known constant matrices that depends on the index set ${\cal N} = \left\{ {1, 2, \cdots, N} \right\}$. $\sigma (k)$: ${\mathbb{N}^ + } \to {\cal N}$ represents the switching signal, which is a piecewise constant function of time $k$.

In addition, $\sigma (k) = i$ means that the $i$th subsystem is activated. For simplicity, we denote

In this paper, it is assumed that the admissible uncertainty $\Delta {A_i}$, $\sigma \in {\cal N}$ satisfies $\Delta {A_i} = {E_i}{M_i}(k){H_i}$, where ${E_i}$ and ${H_i}$ represent known constant matrices, ${M_i}(k)$ represents an unknown time-varying function matrix satisfying ${M_i}^T(k){M_i}(k) \le I$. Furthermore, ${f_i}(k)$ represents the external disturbances function and satisfies $\left\| {{f_i}(k)} \right\| \le {d_i}$, where ${d_i} > 0$ is a known scalar. Thus, system (2.1) can be rewritten as

Assumption 1. The matrix ${B_i}$ is full column rank.

Lemma 1. Let $D, H$ be real constant matrix with appropriate dimensions and $G(t)$ satisfies that ${G^T}(t)G(t) \le I$. Then, for any $\varepsilon > 0$, we have the following inequality

Next, we will give the concepts of ADT and exponential stability of switched systems.

Definition 1. The sliding trajectory of switched system (2.2) is known as in quasi-sliding mode band (QSMB) if there exist positive constant $\delta > 0$ and $\tilde k > 0$ satisfy $\left\| {s(k)} \right\| \le \delta$ for any $k > \tilde k$. In this case, the constant $\delta$ is called a QSMB.

Definition 2. For any ${k_2} > {k_1} > 0$, let ${N_{\sigma (k)}}({k_1}, {k_2})$ denote the number of the switching signals of $\sigma (k)$ over $({k_1}, {k_2})$. If

holds for ${T_\sigma } > 0$ and ${N_0} \ge 0$, then, ${T_\sigma }$ is called an ADT. We choose ${N_0} = 0$, which is also commonly used in previous literature.

Definition 3. ^[2] The switched sliding mode dynamics (2.1) is said to be exponential stability under the switching signal $\sigma (k)$, if there are scalar $\rho > 0$, $0 < \beta < 1$ such that the state $x(k)$ of the system satisfies

In this paper, the stability of the sliding mode dynamics is analyzed first. Then, the SMC law is designed to ensure that the state trajectory of the system reaches the specified sliding mode surface in a finite time. For the discrete-time switched system in (2.2), we design the following sliding mode surface function:

where matrix ${G_i}$ is chosen so that ${G_i}{B_i}$ is nonsingular.

Obviously, when the system state arrive at the sliding surface (2.3), the ideal sliding surface function satisfies

From (2.3) and (2.4), it can be concluded that

From this, the equivalent control can be obtained as

Substituting (2.6) into (2.2) yields

3.   Exponential stability analysis

In this section, we use the ADT method to analyze the exponential stability of sliding mode dynamics (2.7).

Theorem 1. Consider the discrete-time switched system (2.1) with a sliding mode surface as shown in (2.3) and the system satisfies Assumption 1. For any scalar $0 < \gamma < 1$, if the parameters ${\varepsilon _{i1}} > 0$, ${\varepsilon _{i2}} > 0$, $i \in {\cal N}$ and matrix ${P_i} > 0$ exist, satisfing the following linear matrix inequalities (LMIs):

where

Then, with the parameter

and the average dwell time ${T_\sigma }$ satisfies

the system (2.7) is exponential stability. Furthermore, the state is estimated by

and the parameters satisfy

Proof. For system (2.7), construct the following Lyapunov function

where ${P_i}$ is the positive-definite matrix to be determined later. From Eq (2.7), we obtain

From (3.8) and Schur's complement lemma, we know that

We only have to do is

where

From (3.10), it can be concluded that

where

From Eqs (3.1) and (3.2) and Schur's complement, (3.11) can be obtained. It can be shown from (3.11) that

Therefore, for any $k \in \left[{{k_l}, {k_{l + 1}}} \right)$, it can be derived by (3.12)

According to (3.3) and (3.13), the following inequation

holds.

Considering (3.6), we have

and

By (11)

Combining (3.14)–(3.17), we yield

Then (2.7) is exponential stability. □

4.   Event-triggered SMC law analysis

Next, an event-triggered SMC law is designed to ensure the reachability of the state trajectories of the switching system in a finite time. To realize the control objectives, the following reaching law approach is considered for the system in Eq (2.2):

where

${r_i}$ is the given switching gain scalar. Based on the sliding mode surface (2.3) and the switched system (2.2), as well as the constant reaching law (4.1), the following SMC law can be obtained:

where

Since the controller (4.2) contains the uncertain $\tilde u(k)$, it is not suitable for practical. Therefore, the SMC law is recommended to be formulated as

where

and ${\eta _i}$ is a positive scalar.

Since ${G_i}{B_i}$ is invertible, the SMC law (4.2) can be easily obtained from the above equation.

On the result above, the event-triggered sliding mode controller design method will be developed. Assuming that $\left\{ {{s_l}, l \in \mathbb{N}, {s_0} = 0} \right\}$ is a triggering sequence generated by an event-triggered scheme. Therefore, the sliding mode controller will be updated at every ${s_l}$ instant and remain unchanged until the next triggered instant ${s_{l + 1}}$. Define the state error as

for all $k \in \left[{{s_l}, {s_{l + 1}}} \right)$ and the sliding surface function based on event-triggered scheme can be represented as

Moreover, the following event-triggered sliding mode controller can be obtained as

Then, the following theorem is given to ensure the effectiveness of the event-triggered sliding mode controller in (4.5).

Theorem 2. Considering the switched system (2.2), sliding surface function (2.3) and event-triggered SMC law (4.5), we assume that the event-triggered SMC law (4.2) is updated at the triggered instants ${\left\{ {{s_l}} \right\}_{l \in\mathbb{N} }}$. For a given parameter ${v_i} > 0$ and the switching gain ${r_i} > {v_i} + {\bar f_{id}} + {\eta _i}$, if the following equation

holds for all $k$. Then, the state trajectory of the switched system (2.2) under the event-triggered SMC law (4.5) converges to the sliding mode surface (2.3) in a finite time and maintaines it there all the time. Further, the practical QSMB is expressed as

where

Proof. From the switched system (2.2) and the sliding mode surface function(2.3), we have

From (4.5), we obtain

Choose the following Lyapunov function

Therefore, according to (4.8), it can be concluded

It can be obtained from the above formula

Therefore, it can be concluded from (4.10) that when $\left\| {s(k)} \right\| > {\psi _i}$, $\Delta {V_s}\left(k \right) < 0$ can be obtained by selecting ${r_i} > {v_i} + {\bar f_{id}} + {\eta _i}$, ensuring the reachability of sliding mode dynamics in a finite time.

However, if $\left\| {s(k)} \right\| \le {\psi _i}$, $\Delta {V_s}\left(k \right) < 0$ can not be guaranteed, but it can be determined that the trajectory of the sliding surface function $s(k)$ is bounded. Next, we calculate the value of the sliding surface function at the next time instant $s(k + 1)$, according to $\left\| {s(k)} \right\| \le {\psi _i}$ and (4.10), we have

Then, the maximum deviation of the $s(k)$ can be calculated as

In summary, we obtain the QSMB in (4.7), which completes the proof. □

Based on the above research, the stability of the switched system (2.2) with external disturbances can be guaranteed by designing the event-triggered SMC law (4.5). According to the condition (4.6), the next event trigger time ${s_{l + 1}}$ can be determined as follows:

Thus, we can obtain the sequence of triggering instants $\{s_l, l\in \mathbb{N}, s_0 = 0\}$ for the SMC law (4.5). In addition, it can be seen from (4.11) that for triggering conditions, there is always an interval between events, so Zeno phenomenon is excluded.

In particular, the triggering condition is established based on the reachability of the switched SMC system, which reduces conservative of the switched system.

5.   Simulation example

Consider the switched system (2.1), which has two modes and parameters as follows.

Subsystem 1:

Subsystem 2:

Select ${G_1} = {G_2} = \left[{\begin{array}{*{20}{c}}{ - 3.9002} & {0.6240} \end{array}} \right]$ and scalar $\gamma = 0.9$, solving LMIs (3.1) and (3.2) yields

Therefore, the event-triggered sliding surface function (4.4) can be expressed by

According to Theorem 1, the parameters $\mu$ and ${T_\sigma }$ are designed as follows:

Therefore, it can be concluded

Select the event-triggered parameters as ${v_1} \! = \!{v_2}\! = \! 0.05$. According to (4.11), the triggering instants ${s_l}$ is determined by

Select the parameter ${\eta _1} = {\eta _2} = 0.8$, we get

Therefore, the event-triggered SMC law can be calculated as

To reduce the chattering phenomenon, the sign function $\operatorname{sgn} (S(k))$ is replaced by $\frac{{S(k)}}{{\left\| {S(k)} \right\| + 0.1}}$. For the initial state

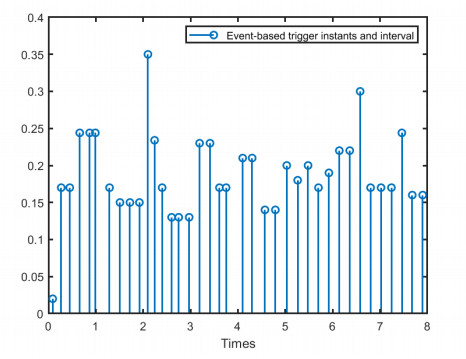
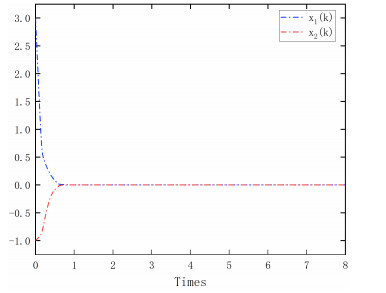
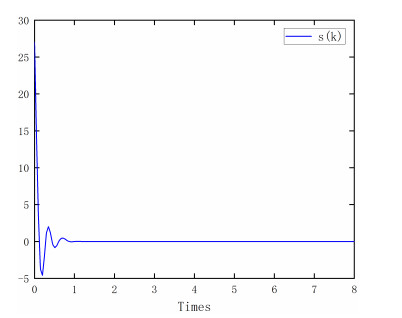
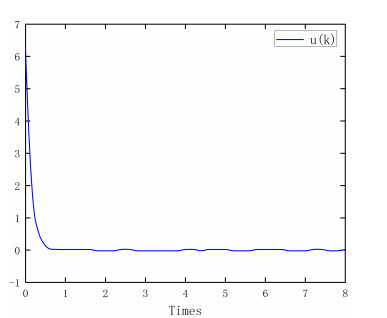
the switched signal is shown in Figure 1. Figure 2 shows the trigger instants and intervals of the event-triggered mechanism. It can be seen that the event-triggered scheme can reduce the number of control task execution. Figure 3 shows the state trajectory of the system, indicating that asymptotically converges to zero in a finite time. Figure 4 describes the event-triggered sliding surface and the event-triggered SMC law is shown in Figure 5.

6.   Conclusions

In this paper, we have investigated the problem of the event-triggered SMC for a class of discrete-time switched systems. Based on the Lyapunov function technique and the ADT strategy, the exponential stability of the correlated sliding mode dynamics is analyzed by linear matrix inequalities. In addition, the event-triggered SMC law is designed using the event-triggered mechanism, which can guarantee that the state trajectory of the system reaches the bounded sliding mode region in a finite time. Furthermore, a sequence of triggering instants are generated by establishing triggering conditions, which can effectively improve the execution efficiency of control tasks. However, chattering decrease is a challenge problem of sliding mode control, and the gain scheduling using fuzzy rules is an effective approach ^[32]. These may be further considered in the future research.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by the National Natural Science Foundation of China under Grant 62103289.

Conflict of interest

The authors declare that they have no conflicts of interest.