Existence results of certain nonlinear polynomial and integral equations via $\digamma$-contractive operators

1.   Introduction

The Banach contraction principle (BCP)^[1], as one of the most acclaimed tools in nonlinear analysis, took on a noteworthy role and opened up a gateway in metric fixed point theory. Over the years, researchers have worked tremendously to extend this principle towards different wide-ranging directions. One of such generalizations satisfying the contractive inequality of rational type was presented by Jaggi ^[2]. Refer to Cho ^[3] for some extensive advancements of fixed point results of contraction mappings.

Owing to the versatility of metric fixed point (FP) theory, a lot of attention has been given to generalizing the metric space (MS) and worthy of note are those given by Gähler ^[4] in 1963 (called 2-MS) and Dhage ^[5] in 1992 (called D-MS). The concept of generalized MS (or simply $G$-MS) was first proposed by Mustafa and Sims ^[6] in 2006 as an extension of MSs, where each triplet of elements of an abstract set is given a non-negative real number. This was aimed at addressing some flaws in the idea of generalized MS given by Dhage and to properly depict the geometry of three points along the perimeter of a triangle. Consequently, Mustafa et al. ^[7] established some FP results of Hardy-Rogers type for mappings satisfying certain constraints on a complete $G$-MS. However, according to Jleli et al. ^[8] as well as Samet et al. ^[9], several invariant point outcomes in the framework of $G$-MS can be inferred from some earlier findings in (quasi)-MS. In essence, an equivalent FP result in symmetric spaces if the contraction constraint of the invariant point theorems in $G$-MS can be reduced to two variables from three variables. Although, as observed by ^[10,11], this is pertinent only if the contractive conditions in the result can be reduced to two variables. Consult Jiddah et al. ^[12] for a comprehensive survey on the developments of FP results in $G$-MS.

In a bid to generalize and enrich the BCP, Suzuki ^[13] in 2008 refined the results of Edelstein and Banach; hence introducing a family of mappings known as the Suzuki-type generalized non-expansive mappings. The existence and uniqueness of FPs for this class of mappings were discussed in the set-up of a compact MS. Also, in 2012 Wardowski ^[14] pioneered a new class of contractions known as $\digamma$-contraction and proved an invariant point result. Piri and Kumam ^[15] in 2014 extended the result of Wardowski by enforcing less stringent additional constraints on a self map defined on a complete MS. In 2015, Alsulami et al. ^[16] presented the concept of generalized $\digamma$-Suzuki type contraction in the setting of $b$-MS and investigated the existence of FPs of such a family of mappings. Minak et al. ^[17] discussed some new FP results for a variant of $\digamma$-contraction including $\acute{C}$iri$\acute{c}$-type generalized $\digamma$-contraction on a complete MS. A new form of applying the Hardy-Roger type contraction in $G$-MSs was analysed by Singh et al. ^[18] and this enhanced the main work of ^[15]. Aydi et al. ^[19] pioneered a modification of $\digamma$-contraction via $\alpha$-admissible mappings and discussed the subsistence and uniqueness of such mappings. For some important trends in $\digamma$-contraction type FP results, refer to Joshi and Jain ^[20], Fabiano et al. ^[21].

Karapinar and Fulga ^[22] pioneered a new hybrid type contraction that combines interpolative-type contractions and Jaggi-type contractions in the framework of a complete symmetric space. The notion of Jaggi-Suzuki-type hybrid contraction mappings was initiated by Noorwali and Yeşilkaya ^[23] with the aim of putting together Suzuki-type contractions, Jaggi hybrid type contractions and hence investigating some theorems that guarantees the existence and uniqueness of FPs of such contractions. Jiddah et al. ^[24] unified the work of ^[23] in the setting of $G$-MS and proved some invariant point results via ($G$-$\alpha$-$\phi$)-contraction. Based on our surveyed literature, we noticed that a hybrid form of Jaggi and Suzuki invariant point results has not been adequately examined, notwithstanding the fact that hybrid FP theorems have enormous applications in various areas of nonlinear analysis. Motivated by this background orientation, we propose an innovative approach called Jaggi-Suzuki-type hybrid $\digamma$-($G$-$\alpha$-$\phi$)-contraction, and via the aid of some supplementary functions, certain FP results are discussed in the set-up of a complete $G$-MS. A comparative, non-trivial example is given to authenticate the applicability of our results and its enhancement over previous findings. It is important to highlight that the principal ideas presented herein cannot be shrunk to any known results. It has been determined, with the help of some obtained consequences, that the notion put forth here is an extension of several existing FP results in the area of $\digamma$-contraction in the setting of $G$-MS. Moreover, one of the corollaries acquired is applied to establish the existence and uniqueness of solutions of certain nonlinear polynomial and integral equations.

The paper is organized as follows: In Section 1, the overview and introduction of relevant literature are highlighted. The fundamental results and mathematical notations employed in this work are outlined in Section 2. In Section 3, the key findings and some special cases of the obtained FP results are discussed. The criteria for the existence of a solution to a polynomial equation is analyzed in Section 4. Using one of the acquired consequences herein, the existence and uniqueness of solutions of certain nonlinear integral equations are investigated in Section 5. An open problem on a discretized population model is highlighted in Section 6. In Section 7, deductions, recommendations and conclusions are given.

2.   Preliminaries

In this section, we will present some fundamental mathematical notations and results that will be adopted throughout this manuscript. Every set $\Theta$ is assumed to be non-empty. We represent by $\mathbb{N}$, $\mathbb{R_{+}}$ and $\mathbb{R}$ as the set of natural numbers, the set of non-negative real numbers and the set of real numbers, respectively.

Consistent with Mustafa and Sims^[6], the following definitions and results will be needed in the sequel.

Definition 2.1. ^[6] Let $\Theta$ be a non-empty set and let $G: \Theta \times \Theta \times \Theta \longrightarrow \mathbb{R_{+}}$ be a function satisfying:

$(G_{1}) \; G(x, y, z) = 0$ if $x = y = z$;

$(G_{2}) \; 0 < G(x, x, y)$ for all $x, y \in \Theta$ with $x\neq y$;

$(G_{3}) \; G(x, x, y)\leq G(x, y, z)$, for all $x, y, z\in \Theta$ with $z\neq y$;

$(G_{4}) \; G(x, y, z) = G(x, z, y) = G(y, x, z) = ...$ (symmetry in its three variables);

$(G_{5}) \; G(x, y, z)\leq G(x, k, k) + G(k, y, z)$, for all $x, y, z, k \in \Theta$ (rectangle inequality).

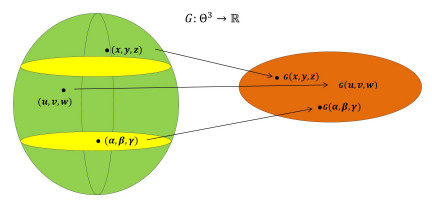
The function $G$ is called a generalized metric (or precisely a $G$-metric) and $\Theta$ endowed with the function $G$ is called a $G$-MS.

Figure 1 hereunder is a 3$D$ visualisation of $G$-metric spaces.

Definition 2.2. ^[7] A sequence $\{x_{i}\}$ of points of a $G$-MS $(\Theta, G)$ is said to be $G$-convergent to a point $x$ if $\lim_{i, j\rightarrow \infty}G(x, x_{i}, x_{j}) = 0$; in other words, given $\epsilon > 0$, we can find $i_{0} \in \mathbb{N}$ such that $G(x, x_{i}, x_{j}) < \epsilon$, $\forall i, j \geq i_{0}$. $x$ is referred to as the limit of the sequence $\{x_{i}\}$.

The following Figure 2 represents the topological notion of convergence in $G$-metric spaces. We can observe from the 3D representation that the limiting value of $G(x, x_{i}, x_{j})$ (as $i, j\longrightarrow \infty$) is zero.

Proposition 1. ^[7] Let $(\Theta, G)$ be a $G$-MS. Then the following are equivalent:

(i) $\{x_{i}\}$ is $G$-convergent to $x$.

(ii) $G(x, x_{i}, x_{j}) \longrightarrow 0$, as $i, j \rightarrow \infty$.

(iii) $G(x_{i}, x, x) \longrightarrow 0$, as $i \rightarrow \infty$.

(iv) $G(x_{i}, x_{i}, x) \longrightarrow 0$, as $i \rightarrow \infty$.

Definition 2.3. ^[7] Let $(\Theta, G)$ be a $G$-MS. A sequence $\{x_{i}\}$ is called $G$-Cauchy if given $\epsilon > 0$, then there exists $i_{0} \in \mathbb{N}$ such that $G(x_{i}, x_{j}, x_{k}) < \epsilon$, $\forall \; i, j, k \geq i_{0}$. That is, $G(x_{i}, x_{j}, x_{k}) \longrightarrow 0$, as $i, j, k \rightarrow \infty$.

Definition 2.4. ^[7] A $G$-Cauchy sequence in a $G$-MS $(\Theta, G)$ is said to be $G$-complete (or complete $G$-metric) if it converges to a point in $(\Theta, G)$.

The subsequent finding was demonstrated by Mustafa ^[25] in the set-up of $G$-MS.

Theorem 2.5. ^[25] Given a complete $G$-MS $(\Theta, G)$ and let $\gamma: \Theta\longrightarrow\Theta$ be a mapping satisfying the ensuing constraint

for all $x, y, z \in\Theta$ where $0 \leq\eta < 1$, then $\gamma$ has a unique FP (say $u$, i.e., $\gamma u = u$), and $\gamma$ is $G$-continuous at $u$.

Jaggi ^[2], in an attempt to enrich the BCP, initiated and proved the following theorem involving rational inequality:

Theorem 2.6. ^[2] Let $\gamma$ be a continuous self-map defined on a complete MS $(\Theta, \rho)$ and assume that $\gamma$ satisfies the following contractive condition:

for all $x, y\in \Theta$ with $x\neq y$ and for some $\alpha, \beta\in [0, 1)$ with $\alpha + \beta < 1$. Then, $\gamma$ has a unique FP in $\Theta$.

Another intriguing generalization of the BCP presented by Suzuki ^[26] is given hereunder:

Theorem 2.7. ^[26] Let $(\Theta, \rho)$ be a compact MS and $\gamma$ be a mapping defined on $\Theta$. Assume that

for $x, y\in \Theta$. Then, $\gamma$ has a unique FP.

Following in the direction of ^[14], the idea of $\digamma$-contraction is defined as follows:

Definition 2.8. ^[14] Let $\mathcal{F}$ denote the family of functions $\digamma: \mathbb{R_{+}} \longrightarrow \mathbb{R}$ satisfying the following auxiliary conditions:

$(F1) \; \digamma$ is strictly increasing; that is, for all $\alpha, \beta \in\mathbb{R_{+}}$, if $\alpha < \beta$ then $\digamma(\alpha) < \digamma(\beta)$;

($F2$) for every sequence $\{\upsilon_{i}\}_{i\in\mathbb{N}} \; \subseteq\mathbb{R_{+}}$, $\lim_{i\rightarrow \infty}\upsilon_{i} = 0$ if and only if $\lim_{i\rightarrow \infty}\digamma(\upsilon_{i}) = -\infty$;

($F3$) there exists $0 < \eta < 1$ such that $\lim_{\upsilon\rightarrow {0^{+}}}\upsilon^{\eta}\digamma(\upsilon) = 0$.

Definition 2.9. ^[14] Let $(\Theta, \rho)$ be an MS. A self-mapping $\gamma$ on $\Theta$ is called an $\digamma$-contraction if there exists $\vartheta > 0$ and $\digamma\in\mathcal{F}$ such that for all $x, y\in\Theta$,

Remark 1. From (F1) and (2.7), it is obvious that if $\gamma$ is an $\digamma$-contraction, then $\rho(\gamma x, \gamma y) < \rho(x, y)$, for all $x, y \in\Theta$ such that $\gamma x \neq \gamma y$. In other words, $\gamma$ is a contractive mapping and hence, every $\digamma$-contraction is a continuous mapping.

Wardowski ^[14] presented a variation of the Banach FP theorem as follows:

Theorem 2.10. Let $(\Theta, \rho)$ be a complete MS and $\gamma: \Theta\longrightarrow\Theta$ be an $\digamma$-contraction. Then, $\gamma$ has a unique FP $x\in\Theta$ and for every $x_{0}\in\Theta$ a sequence $\{\gamma^{i}x_{0}\}_{i\in\mathbb{N}}$ is convergent to $x$.

In line with ^[27], denote by $\Phi$ the family of all non-decreasing functions $\phi : \mathbb{R_{+}} \longrightarrow \mathbb{R_{+}}$ with $\lim_{i\rightarrow +\infty}\phi^{i}(\mu) = 0$ for all $\mu \in (0, +\infty)$.

Given $\phi \in \Phi$ be such that we can find $i_{0}\in \mathbb{N}$, $\eta\in (0, 1)$ and a series of positive terms which is convergent $\sum^{\infty}_{i = 1}t_{i}$

for $i\geq i_{0}$ and any $\mu > 0$. Then $\phi$ is termed a $(c)$-comparison function ^[28].

Lemma 2.11. ^[28] If $\phi\in\Phi$, then the following hold:

(i) $\{\phi^{i}(\mu)\}_{i\in\mathbb{N}} \; \rightarrow 0$ as $i\rightarrow \infty$ for $\mu\geq 0$;

(ii) $\phi(\mu) < \mu$ for $\mu\in \mathbb{R_{+}}$;

(iii) $\phi$ is continuous;

(iv) $\phi(\mu)$ = $0$ if and only if $\mu = 0$;

(v) For $\mu\geq 0$, the series $\sum_{i = 1}^{\infty}\phi^{i}(\mu)$ converges.

Popescu ^[29] presented the subsequent definitions in the framework of MSs.

Definition 2.12. ^[29] Given two mappings $\alpha: \Theta\times \Theta\longrightarrow\mathbb{R}_{+}$ and $\gamma: \Theta\longrightarrow\Theta$, then $\gamma$ is referred to as $\alpha$-orbital admissible if for all $x\in \Theta$, $\alpha(x, \gamma x)\geq 1$ implies $\alpha(\gamma x, \gamma^{2}x)\geq 1$.

Definition 2.13. ^[29] Given two mappings $\alpha: \Theta\times \Theta\longrightarrow\mathbb{R}_{+}$ and $\gamma: \Theta\longrightarrow\Theta$, then $\gamma$ is referred to as triangular $\alpha$-orbital admissible if for all $x\in\Theta$, $\gamma$ is $\alpha$-orbital admissible, $\alpha(x, y)\geq 1$ and $\alpha(y, \gamma y)\geq 1$ implies $\alpha(x, \gamma y)\geq 1$.

The above definitions were modified and presented in the setting of $G$-MS by Jiddah et al. ^[24] as follows:

Definition 2.14. ^[24] Let $\alpha: \Theta\times \Theta\times \Theta\longrightarrow\mathbb{R}_{+}$ be a function. A mapping $\gamma: \Theta\longrightarrow\Theta$ is said to be ($G$-$\alpha$)-orbital admissible if for all $x\in\Theta$, $\alpha(x, \gamma x, \gamma^{2}x)\geq 1$ implies $\alpha(\gamma x, \gamma^{2}x, \gamma^{3}x)\geq 1$.

Definition 2.15. ^[24] Let $\alpha: \Theta\times \Theta\times \Theta\longrightarrow\mathbb{R_{+}}$ be a function. A mapping $\gamma: \Theta\longrightarrow\Theta$ is said to be triangular ($G$-$\alpha$)-orbital admissible if for all $x\in \Theta$, $\gamma$ is ($G$-$\alpha$)-orbital admissible, $\alpha(x, y, \gamma y)\geq 1$ and $\alpha(y, \gamma y, \gamma^{2}y)\geq 1$ implies $\alpha(x, \gamma y, \gamma^{2}y)\geq 1$.

Jiddah, et al.^[24] presented the following definition of Jaggi-Suzuki-type hybrid contraction ($G$-$\alpha$-$\phi$)-contraction in $G$-MS.

Definition 2.16. ^[24] Let $(\Theta, G)$ be a $G$-MS. A mapping $\gamma:\Theta\longrightarrow\Theta$ is called a Jaggi-Suzuki-type hybrid ($G$-$\alpha$-$\phi$)-contraction, if we can find $\phi\in\Phi$ and $\alpha: \Theta\times \Theta\times \Theta\longrightarrow\mathbb{R_+}$ such that

for all $x, y\in\Theta\backslash Fix(\gamma)$, where

$\delta_{1}, \delta_{2}\geq 0$ with $\delta_{1}+ \delta_{2} = 1$ and $Fix(\gamma) = \{x\in\Theta: \gamma x = x\}$.

3.   Main results

In this section, the approach of Jaggi-Suzuki-type hybrid $\digamma$-($G$-$\alpha$-$\phi$)-contraction is introduced in the set-up of $G$-MS and conditions for the existence of invariant points for such class of operators are investigated.

Definition 3.1. Let $(\Theta, G)$ be a $G$-MS. A mapping $\gamma:\Theta\longrightarrow\Theta$ is called a Jaggi-Suzuki-type hybrid $\digamma$-($G$-$\alpha$-$\phi$)-contraction if we can find $\vartheta > 0$, $\phi\in\Phi$, $\digamma\in\mathcal{F}$ and $\alpha:\Theta\times \Theta\times \Theta\longrightarrow\mathbb{R_{+}}$ such that $G(\gamma x, \gamma y, \gamma^{2}y) > 0$ and $\frac{1}{2}G(x, \gamma x, \gamma^{2}x)\leq G(x, y, \gamma y)$ imply

for all $x, y\in\Theta\backslash Fix(\gamma)$, where

$\delta_{1}, \delta_{2}\geq 0$ with $\delta_{1}+\delta_{2} = 1$ and $Fix(\gamma) = \{x\in\Theta: \gamma x = x\}$.

Remark 2. (1) Clearly, by taking $\digamma(\mu) = \ln(\mu), \; \mu > 0$, inequality (3.1) reduces to

as given by Jiddah et al. (see ^[24], Definition 14). Notice that inequality (3.3) is valid for all $x, y\in \Theta$ such that $G(\gamma x, \gamma y, \gamma^{2}y) = 0$.

(2) If we let $\alpha(x, y, \gamma y) = 1$, $\gamma y = z$, $\delta_{1} = 0$, $\delta_{2} = 1$ and $\kappa > 0$ in inequality (3.3), then, we have

which coincides with the result of Shatanawi (see ^[27], Theorem 3.1).

(3) Also, taking $\phi(t) = \eta t, \; \mu > 0$ and $\eta\in (0, 1)$, we have

which reduces to the result of Mustafa ^[25]. Unfortunately, the inequality (3.5) was criticized for some drawbacks. For example, take $y = z$, then the FP results using (3.5) coincide with the metric version.

Next, we present our main results as follows.

Theorem 3.2. Let $(\Theta, G)$ be a complete $G$-MS and $\gamma:\Theta\rightarrow \Theta$ be a Jaggi-Suzuki-type hybrid $\digamma$-($G$-$\alpha$-$\phi$)-contraction. Suppose also that:

(i) $\gamma$ is triangular ($G$-$\alpha$)-orbital admissible;

(ii) we can find $x_{0}\in\Theta$ such that $\alpha(x_{0}, \gamma x_{0}, \gamma^{2}x_{0})\geq 1$;

(iii) either $\gamma$ is continuous or $\gamma^{3}$ is continuous and $\alpha(x, \gamma x, \gamma^{2}x)\geq 1$ for each $x\in$Fix($\gamma^{3}$).

Then, $\gamma$ possesses an FP in $\Theta$.

Proof. By assumption (ii), we have $\alpha(x, \gamma x, \gamma^{2}x)\geq 1$. Let $x_{0}\in \Theta$ be an arbitrary but fixed, and consider a sequence $\{x_{i}\}_{i\in\mathbb{N}}$ in $\Theta$ defined by $x_{i} = \gamma^{i}x_{0}$ for all $i\in\mathbb{N}$. If $x_{i_{0}+1} = x_{i_{0}}$ for some $i_{0}\in \mathbb{N}$, then $x_{i_{0}}$ is an FP of $\gamma$. Suppose on the contrary that $x_{i}\neq x_{i-1}$ for all $i\in \mathbb{N}$. Since $\gamma$ is triangular ($G$-$\alpha$)-orbital admissible, then $\alpha(x_{0}, \gamma x_{0}, \gamma^{2}x_{0}) = \alpha(x_{0}, x_{1}, x_{2})\geq 1$ implies $\alpha(\gamma x_{0}, \gamma x_{1}, \gamma x_{2}) = \alpha(x_{1}, x_{2}, x_{3})\geq 1$.

Proceeding in like manner, we obtain

Owing to the fact that $\gamma$ is a Jaggi-Suzuki-type hybrid $\digamma$-($G$-$\alpha$-$\phi$)-contraction, then from (3.1),

Together with (3.6) and on account of (F1), (3.7) becomes

Next, we analyse the following cases of (3.2).

Case $1$: For $\kappa > 0$, we have

Therefore, (3.8) becomes

Suppose that $G(x_{i-1}, x_i, x_{i+1}) \leq G(x_i, x_{i+1}, x_{i+2})$. Using the nondecreasing property of $\phi$, then (3.9) yields

which is a contradiction. Therefore,

for all $i\in\mathbb{N}$. Hence, (3.9) becomes

By letting $\Lambda_i = G(x_i, x_{i+1}, x_{i+2})$, we can deduce from (3.10) that

for all $i\in\mathbb{N}$ with $x_{i+1}\neq x_{i+2}$.

Letting $i\rightarrow \infty$ in (3.11),

Condition $(F2)$ yields

As a result of $(F3)$, we can find $0 < \eta < 1$ such that

By (3.11), the following holds for all $i\in \mathbb{N}$:

Letting $i\rightarrow \infty$ in (3.14) and using (3.12) and (3.13) gives

Observe that from $(3.15)$, we can find ${i_1}\in\mathbb{N}$ such that $i{\Lambda_i}^\eta \leq 1$ for all $i \geq i_1$. It follows that

Consider $i, j \in\mathbb{N}$ such that $j > i\geq i_1$ and by rectangle inequality, we have

Since the series $\sum\limits_{h = i}^{\infty} {\frac{1}{h^\frac{1}{\eta}}}$ converges, it follows that the sequence $\{{x_i}\}_{i\in\mathbb{N}}$ is Cauchy in $(\Theta, G)$. Hence, by the completeness of $(\Theta, G)$, we can find $x^{*}\in \Theta$ such that $\{x_i\}$ is $G$-convergent to $x^{*}$. In other words, $\lim_{i\rightarrow \infty} G(x_i, x_i, x^{*}) = 0$.

We demonstrate that $x^{*}$ is an FP of $\gamma$. By Hypothesis (iii) of Theorem 3.2, we obtain

and so we get $\gamma x^{*} = x^{*}$. Hence, we can conclude that $x^{*}$ is an FP of $\gamma$.

In a similar way, suppose that $\gamma^{3}$ is continuous, we have

To prove that $\gamma x^{*} = x^{*}$, suppose on the contrary that $\gamma x^{*}\neq x^{*}$. Then, by (3.1) we have

Hence,

where

Therefore, (3.16) becomes

which is a contradiction. It follows that $\gamma x^{*} = x^{*}$.

Case 2: For $\kappa = 0$, we attain

Assume that $G(x_{i-1}, x_{i}, x_{i+1}) \leq G(x_{i}, x_{i+1}, x_{i+2})$, then

Hence, (3.8) becomes

which is a contradiction. Therefore,

Furthermore, by (3.8) we have

By concurrent method as in the Case of $\kappa > 0$, we can show that $\{x_i\}$ in $(\Theta, G)$ is $G$-Cauchy and consequently, by the completeness of $(\Theta, G)$ we can find a point $x^{*} \in\Theta$ such that $\lim_{i\rightarrow \infty}x_i = x^{*}$. Similarly, under the hypothesis that $\gamma$ is continuous and by the uniqueness of the limit, we obtain $\gamma x^{*} = x^{*}$. That is, $x^{*}$ is an FP of $\gamma$. Also, if $\gamma^{3}$ is continuous as in Case 1, we have $\gamma^{3}x^{*} = x^{*}$. Suppose on the contrary that $\gamma x^{*}\neq x^{*}$. Then

where

Thus, (3.17) gives

which is a contradiction. It follows that $\gamma x^{*} = x^{*}$. □

Theorem 3.3. If in Theorem 3.2, we impose an additional condition that $\alpha(x^{*}, y^{*}, \gamma y^{*})\geq 1$ for any $x^{*}, y^{*}\in\;$Fix$(\gamma)$, then the FP of $\gamma$ is distinct.

Proof. Let $x^{*}, y^{*}\in\;$Fix$(\gamma)$ be such that $x^{*}\neq y^{*}$. Using this in (3.1) and applying the supplementary assumption, we have $\frac{1}{2}G(x^{*}, \gamma x^{*}, \gamma^{2}x^{*})\leq G(x^{*}, y^{*}, \gamma y^{*})$,

Case 1: For $\kappa > 0$, where

Therefore, (3.18) yields

which is a contradiction. Thus, we can conclude that $x^{*} = y^{*}$ and so, it follows that the FP of $\gamma$ is unique.

Case 2: For $\kappa = 0$,

Hence, by (3.18) we have

Alongside $(F1)$ and $(G2)$, we have that

It follows that

which is a contradiction. Therefore, we conclude that $\gamma$ possesses a distinct FP in $(\Theta, G)$. □

Definition 3.4. ^[28] Let $\alpha:\Theta\times \Theta\times \Theta\longrightarrow\mathbb{R_{+}}$ and $\gamma:\Theta\longrightarrow\Theta$ be two mappings. Then, $\gamma$ is said to be $\alpha$-admissible if for all $x, y, z\in \Theta$, $\alpha(x, y, z)\geq 1$ implies $\alpha(\gamma x, \gamma y, \gamma z)\geq 1$.

Definition 3.5. ^[28] Let $(\Theta, G)$ be a $G$-MS and let $\gamma:\Theta\longrightarrow\Theta$ be a given mapping. We say that $\gamma$ is a $G$-$\alpha$-$\phi$-contractive mapping of type I if there exist two functions $\alpha:\Theta\times \Theta\times \Theta\longrightarrow\mathbb{R_+}$ and $\phi\in\Phi$ such that for all $x, y, z\in \Theta$, we have

Consistent with Definition 3.5, we have the following concept:

Definition 3.6. Let $(\Theta, G)$ be a $G$-MS and let $\gamma:\Theta\longrightarrow\Theta$ be a given mapping. Then, $\gamma$ is said to be a Suzuki-type $\digamma$-($G$-$\alpha$-$\phi$)-contraction if we can find functions $\alpha:\Theta\times \Theta\times \Theta\longrightarrow\mathbb{R_{+}}$, $\phi\in\Phi$, $\digamma\in\mathcal{F}$ and a constant $\vartheta > 0$ such that for all $x, y, z\in \Theta$, we have $G(\gamma x, \gamma y, \gamma z) > 0$ and $\frac{1}{2}G(x, \gamma x, \gamma^{2}x)\leq G(x, y, z)$ imply

Theorem 3.7. Let $(\Theta, G)$ be a complete $G$-MS. Suppose that $\gamma:\Theta\longrightarrow\Theta$ is a Suzuki-type $\digamma$-($G$-$\alpha$-$\phi$)-contraction satisfying the following conditions:

(i) $\gamma$ is $\alpha$-admissible;

(ii) there exists $x_{0}\in\Theta$ such that $\alpha(x_{0}, \gamma x_{0}, \gamma^{2}x_{0})\geq 1$;

(iii) $\gamma$ is $G$-continuous.

Then, $\gamma$ has an FP in $\Theta$.

Proof. Let $x_{0}\in\Theta$ be arbitrary but fixed such that $\alpha(x_{0}, \gamma x_{0}, \gamma^{2}x_{0})\geq 1$. Define a sequence $\{x_i\}_{i\in\mathbb{N}}$ in $\Theta$ by $x_{i+1} = \gamma x_i$ for all $i\geq 0$. If $x_{i_0} = \gamma x_{{i_0}+1}$ for some $i_0\in\mathbb{N}$, then $x_{i_0}$ is an FP of $\gamma$. Assume that $x_{i}\neq x_{i+1}$ for all $i\in\mathbb{N}$. Since $\gamma$ is $\alpha$-admissible, we have

Inductively, we have

Since $\gamma$ is a Suzuki-type $\digamma$-($G$-$\alpha$-$\phi$)-contraction and using (3.19), it follows that for all $i\geq 1$, we have

By letting $\Lambda_i = G(x_i, x_{i+1}, x_{i+2})$ in (3.20) and since $\phi$ is nondecreasing, we can infer inductively that

for all $i\geq 1$. Letting $i\rightarrow \infty$ in (3.21),

Hence, Condition (F2) yields

From (F3), we can find $\eta\in(0, 1)$ such that

By (3.21), the following holds for all $i\in\mathbb{N}$:

Letting $i\rightarrow \infty$ in (3.22), we have

Note that from (3.23), we can find $i_{1}\in\mathbb{N}$ such that $i{\Lambda_{i}}^{\eta}\leq 1$, for all $i\geq i_1$. We have

For $i, j\in\mathbb{N}$ such that $j > i\geq i_1$ and by rectangle inequality, we have

Since the series $\sum\limits_{h = i}^{\infty}\frac{1}{h^{\frac{1}{\eta}}}$ converges, it follows that $\{x_i\}_{i\in\mathbb{N}}$ is a $G$-Cauchy sequence in the $G$-MS $(\Theta, G)$. Due to the completeness of $(\Theta, G)$, there exists $x^{*}\in\Theta$ such that $\{x_i\}_{i\in\mathbb{N}}$ is $G$-convergent to $x^{*}$. From the continuity of $\gamma$, we see that $\{\gamma x_i\}$ is $G$-convergent to $\gamma x^{*}$. By the uniqueness of the limit, we have $x^{*} = \gamma x^{*}$. □

In what follows, we construct an illustration in the form of an example to substantiate the assumptions of Theorems 3.2 and 3.3.

Example 3.8. Let $\Theta = [0, 2]$ and define a mapping $\gamma:\Theta\longrightarrow\Theta$ by

Take $G(x, y, \gamma y) = \left|x-y\right| + \left|x-\gamma y\right| + \left|y-\gamma y\right|$, $\quad\forall \; x, y\in\Theta$. Then $(\Theta, G)$ is a complete $G$-MS. Define the mappings $\phi:\mathbb{R_+}\longrightarrow\mathbb{R_+}$ by $\phi(\mu) = \frac{\mu}{2}, \; \mu\geq0$ and $\alpha:\Theta\times \Theta\times \Theta\longrightarrow\mathbb{R_+}$ by

It is obvious that $\gamma$ is triangular ($G$-$\alpha$)-orbital admissible and we can find $x_{0} = 1 \in\Theta$ such that $\alpha(x_{0}, \gamma x_{0}, \gamma^{2}x_{0}) = \alpha(1, \gamma 1, \gamma^{2}1) = \alpha(1, \frac{6}{7}, \frac{6}{7}) = 4 > 1$. We can see that $\gamma$ is not continuous but $\gamma^{3}$ is continuous for any $x\in\mathrm{Fix}(\gamma^{3})$. To verify inequality (3.1), first let $\vartheta = \ln(\frac{5}{4}), \digamma(\mu) = \ln(\mu^{2} + \mu), \; \mu > 0$ and $\delta_{1} = \delta_{2} = \frac{1}{2}$. Then, we analyse the subsequent cases:

Case 1: For $x, y\in [0, 1]$, we have $G(\gamma x, \gamma y, \gamma^{2}y) = 0$. Hence, the inequality (3.1) holds.

Case 2: For $x = 0$ and $y = 2$, take $\kappa = 2$,

For $\kappa = 0$,

Since $\alpha(x, y, \gamma y) = 0$ for other cases, we can conclude that all the hypothesis of Theorems 3.2 and 3.3 are satisfied. Hence, $x = \frac{6}{7}$ is the unique FP of $\gamma$.

Figure 3 shows that FP results of $\digamma$-($G$-$\alpha$-$\phi$)-contraction subsume the corresponding results in ($G$-$\alpha$-$\phi$)-contraction, $\digamma$-contraction and Banach contraction. In other words, if the usual implication is denoted by $\Rightarrow$, then Figure 3 represents the following implications:

However, the converse of the above implications is not always true.

To deduce some consequences of our principal findings given hereunder, we suppose that for all $x, y\in\Theta$,

Corollary 1. Let $(\Theta, G)$ be a complete $G$-MS and $\gamma:\Theta\rightarrow \Theta$ be a continuous mapping. If there exist $\vartheta > 0, \phi\in\Phi$ and $\digamma\in\mathcal{F}$ such that

for each $x, y\in\Theta$ where $\kappa\geq 0; \delta_{i}\geq 0, i = 1, 2$ and $\delta_{1}+\delta_{2} = 1$. Then, $\gamma$ possesses only one FP in $\Theta$.

Proof. For $\kappa\geq 0$, letting $\alpha(x, y, \gamma y) = 1$ for $x, y\in\Theta$, the result follows from Theorem 3.3. □

Corollary 2. Given a complete $G$-MS $(\Theta, G)$ and let $\gamma:\Theta\rightarrow \Theta$ be a continuous mapping, if there exists $\eta\in (0, 1)$ such that

for each $x, y\in\Theta$; $\vartheta > 0, \digamma\in\mathcal{F}$ and $\phi\in\Phi$, where $\kappa\geq 0;\delta_{i}\geq 0, i = 1, 2$ and $\delta_{1}+\delta_{2} = 1$. Then, $\gamma$ has a unique FP in $\Theta$.

Proof. For $\kappa > 0$; it suffices to take $\delta_{1} = 0, \delta_{2} = 1$ and $\phi(\mu) = \eta\mu$ for $\mu\geq 0$ in Corollary 1. □

Corollary 3. Let $(\Theta, G)$ be a complete $G$-MS and $\gamma:\Theta\rightarrow \Theta$ be a continuous mapping. If there exists $\eta\in (0, 1)$ such that

for each $x, y\in\Theta\backslash\mathrm{Fix}(\gamma); \vartheta > 0, \digamma\in\mathcal{F}$ and $\phi\in\Phi$, then $\gamma$ possesses a unique FP in $\Theta$.

Proof. For $\kappa = 0$, letting $\delta_{1} = \delta_{2} = \frac{1}{2}$, the proof follows from Corollary 2. □

Corollary 4. Let $(\Theta, G)$ be a complete $G$-MS and let $\gamma:\Theta\rightarrow \Theta$ be a continuous mapping. If we can find a constant $\eta\in (0, 1)$ such that

for all $x, y, z\in \Theta$. Then, $\gamma$ possesses a unique FP in $\Theta$.

Proof. It suffices to take $\gamma y = z$ in Corollary 2. □

Corollary 5. Given a complete $G$-MS $(\Theta, G)$ and let $\gamma:\Theta\rightarrow \Theta$ be a continuous mapping. If we can find $\vartheta > 0$ and $\digamma\in\mathcal{F}$ such that

for all $x, y, z\in \Theta$. Then, $\gamma$ has an FP in $\Theta$.

Proof. From (3.24) of Corollary 1, using the property of $(c)$-comparison and the fact that $\digamma$ is non-decreasing, we have

Putting $\gamma y = z$, (3.25) becomes

Hence, letting $\delta_{1} = 0$ and $\delta_{2} = 1$ in $M(x, y, z)$, (3.26) reduces to

Therefore, the existence of FP follows from Theorem 3.2. □

More consequences of our principal findings are pointed as follows:

Corollary 6. ([24, Theorem 2]) Let $(\Theta, G)$ be a complete $G$-MS and $\gamma:\Theta\longrightarrow\Theta$ be a Jaggi-Suzuki-type hybrid ($G$-$\alpha$-$\phi$)-contraction. Then, $\gamma$ has an FP in $\Theta$.

Proof. It is sufficient to take $\digamma(\mu) = \ln\mu, \mu > 0$ in Theorem 3.2. □

Corollary 7. (see [28, Thorem 29]) Let $(\Theta, G)$ be a complete $G$-MS. Suppose that $\gamma:\Theta\longrightarrow\Theta$ is a $G$-$\alpha$-$\phi$-contractive mapping of type A, then $\gamma$ has an FP in $\Theta$.

Proof. Taking $\digamma(\mu) = \ln\mu, \mu > 0$ and $z = \gamma x$ in Theorem 3.7, the result follows. □

4.   Application to j$^{th}$ degree polynomial

One of the fundamental roles of fixed point theory is in the solutions of polynomial equations. In this context, many useful results have been developed (e.g., see ^[30] and the citations in there). Going in this frame, we present the following application:

Theorem 4.1. Given any natural number $j\geq3$, the equation

has a unique real solution in the interval $[-1, 1]$.

Proof. If $\left|x\right| > 1$, then the solution of Eq (4.1) does not exist. Therefore, $\left|x\right|\leq 1$. Let $\Theta = [-1, 1]$, then for any $x, y, z\in \Theta$, define the metric $G:\Theta\times \Theta\times \Theta\longrightarrow\mathbb{R_+}$ by

It is easy to show that $(\Theta, G)$ is a complete $G$-MS. To reformulate (4.1) as an FP problem, consider a mapping $\gamma:\Theta\longrightarrow\Theta$ defined by

and let $\digamma:\mathbb{R_+}\longrightarrow\mathbb{R_+}$ be defined by $\digamma(\mu) = \ln\mu, \mu > 0$, then $\digamma\in\mathcal{F}$. We will now show that $\gamma$ is a Jaggi-Suzuki-type hybrid $\digamma$-($G$-$\alpha$-$\phi$)-contraction.

Since $j\geq 3$, then we can say that $j^{5}\geq 243$. Therefore,

Taking the natural logarithm of both sides, gives

Hence, using the definition of $\digamma$, we obtain

with

Thus, all the assumptions of Corollary 5 are satisfied and therefore, $\gamma$ possesses only one FP in $\Theta$, which is a distinct real solution of Eq (4.1). □

5.   Applications to solution of nonlinear integral equation

Younis et al. ^[31] applied their proposed techniques to analyse and examine the existence of solutions for some class of integral equations. Motivated by this, we study new criteria for the existence of a solution to the following integral equation:

where

are continuous functions and $x(\mu)$ is an unknown function. Let $\Theta = C([q_{1}, q_{2}], \mathbb{R})$ be the set of all real-valued continuous functions defined on $[q_{1}, q_{2}]$ and let $G:\Theta\times \Theta\times \Theta\longrightarrow\mathbb{R_+}$ be endowed with the metric defined by

It can be easily verified that $(\Theta, G)$ is a complete $G$-MS. Define a mapping $\gamma: \Theta\rightarrow \Theta$ by

then $x(\mu)$ is an FP of $\gamma$ if and only if it is a solution to (5.1).

Under the assumptions of the following theorem, we study the existence of solution of the integral equation (5.1).

Theorem 5.1. Assume that the following conditions hold:

(i) there exists a constant $\eta\in (0, 1)$ such that

(ii)

for some constant $\vartheta > 0$.

Then, the integral equation (5.1) has a solution in $\Theta$.

Proof. Using the assumptions (i) and (ii) alongside the inequality (5.1), we have

That is,

Taking the logarithm of both sides in (5.4) yields

Hence, we obtain

Defining $\digamma:\mathbb{R_+}\longrightarrow\mathbb{R_+}$ by $\digamma(\mu) = \ln(\mu)$ for all $\mu > 0$, inequality (5.5) becomes

Therefore,

Thus, all the hypotheses of Corollary 2 are satisfied and so, we can conclude that $\gamma$ has a unique FP $x$ in $\Theta$, which is the unique solution of the integral equation (5.1) in $\Theta$. □

Example 5.2. Take $\Theta = C([0, 1], \mathbb{R})$ and consider the following integral equation:

In a bid to find the solution of (5.6), it is important to show that $x(\mu)$ is indeed an FP of $\gamma$. That is, $\gamma x(\mu) = x(\mu)$, where

It is obvious that the integral equation (5.6) is a special case of (5.1), where

We can see that $\Omega(\hat{s}, x(\hat{s})), \sigma(\mu)$ and $\mathcal{W}(\mu, \hat{s})$ are continuous. For $x, y\in\mathbb{R}$,

Also,

Consequently, all the assumptions of Theorems 3.2 and 3.3 are satisfied and hence, the integral equation (5.6) has a solution in $\Theta = C([0, 1], \mathbb{R})$.

6.   Open problem

The following open problem is proposed as a direction for further consideration.

A model representing a discretized population balance for continuous systems at a steady state can be given by the integral equation:

Using any of the results proposed herein, we are yet to ascertain whether or not it is possible to obtain the existence conditions for the solution of (6.1).

Remark 3. (i) Several consequences of our principal results can be obtained by particularizing some of the parameters in Definition 3.1.

(ii) None of the results proposed in this work can be written in the form of $G(x, y, y)$ or $G(x, x, y)$. Therefore, they cannot be inferred from their analogues in MS.

7.   Conclusions

An interesting extension of the BCP was presented by Wardowski ^[14], called $\digamma$-contraction and this has attracted the interest of researchers over the years. In this manuscript, a new family of contractions called Jaggi-Suzuki-type hybrid $\digamma$-($G$-$\alpha$-$\phi$)-contraction was introduced in the setting of $G$-MS and some FP results that cannot be derived from their corresponding results in MS were discussed. To demonstrate the applicability of the proposed results and to show that they are in fact generalizations of some existing concepts in the literature, a comparative, non-trivial example was provided. We noted that via variants of $\digamma$-contractive operators, more than a handful of existing results can be deduced from our proposed hybrid $\digamma$-($G$-$\alpha$-$\phi$)-contraction. A few of these special cases have been pointed out as corollaries. From an application viewpoint, one of the corollaries gotten was applied to analyse the sufficient criteria for the existence of solutions to a class of nonlinear integral equations. The totally abstract nature of the mathematical framework, analysis and results presented in this work places restriction on its applicability. The proposed family of contractions can be extended in other well-known spaces and new invariant point results can be obtained.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgements

This work was supported and funded by the Deanship of Scientific Research at Imam Mohammad Ibn Saud Islamic University (IMSIU) (grant number IMSIU-RP23070).

Conflict of interest

The authors declare that there is no competing interest.