Solution of fractional differential equation by fixed point results in orthogonal $\mathcal{F}$-metric spaces

1.   Introduction

Failure and many causes of failure usually emerge in various application disciplines such as reliability, engineering, and lifetime study due to the complexity of internal structure and external environment, which is referred to as competing risks model in literature. In most literature, inference for competing risk models is studied under the assumption of independent causes of failure. Sarhan and Balakrishnan ^[28], Sarhan, El-Gohary, El-Bassiouny, and Balakrishnan ^[29], El-Gohary and Sarhan ^[10], Sarhan, Hamilton, Smith, and Kundu ^[30], Kundu, Sarhan, and Gupta ^[16], Sarhan, Apaloo, and Kundu ^[27] and Sarhan ^[26] proposed bivariate/multivariate lifetime distributions using independent shock or competing risks models. This research mostly used bivariate distributions to fit bivariate data sets. However, the assumption of independence among the causes of failure may be inaccurate. For example, the classic two-unit series system failed due to shocks from three shock sources. The first and second shock sources affect the first and second units, respectively, and the third shock source hits both units at the same time. It is clear that the causes of failure in this system are dependent. In practice, the associated failure reasons may be independent or dependent. In a clinical medicine study, the causes of failure of colon cancer are cancer recurrence or death, and it is observed that such failure causes are also dependent in this situation. As a result, inference for dependent competing risks models will be more practical in reliability, engineering, and other related fields, and in the study of competing risks models involving dependent causes of failure, it is natural to consider a bivariate or multivariate distribution for the lifetimes.

Bivariate lifetime distributions are useful in modeling competing risks when there are two dependent reasons of failure. Wada, Sen, and Shimakura ^[33] and Wang and Ghosh ^[34] used bivariate exponential lifetime models to analyze data with two associated risk components. In situations where there is a positive probability of two failure modes occurring simultaneously, the Marshall-Olkin bivariate exponential (MOBE) distribution introduced by Marshall and Olkin ^[19] is probably the most extensively used model. Pena and Gupta ^[25], Kotz, Balakrishnan, and Johnson ^[13], Kundu and Dey ^[14], Li, Sun, and Song ^[18], Kundu and Gupta ^[15], Sarhan, Apaloo and Kundu ^[27], Alqallaf and Kundu ^[5], Sarhan and Kundu ^[31], and references therein are all worth reading.

The inverse exponential (IE) distribution is a life time model that can simulate real-world events, such as bathtub failure rates. Attempts to extend the flexibility of the IE distribution gave rise to the generalized inverted exponential (GIE) distribution by Abouammoh and Alshingiti ^[2]. Oguntunde et al. ^[24] presented a new lifetime distribution known as the exponentiated generalized inverted exponential (EGIE) distribution. The cumulative distribution function (cdf), probability density function (pdf), and hazard rate function (hrf) of EGIE are given, respectively, by

and

The EGIE distribution generalizes some well known lifetime distributions, and among them we list two special cases.

$1)$ When $\gamma = 1$, EGIE $(\lambda, \gamma, \alpha)$ reduces to the inverted exponential distribution, IE$(\lambda, \alpha)$, see Sanku ^[9].

$2)$ When $\lambda = 1$, EGIE $(\lambda, \gamma, \alpha)$ reduces to the exponentiated inverted exponential distribution, GIE$(\gamma, \alpha)$, see Kawsar and Ahmad ^[12].

The primary objective of this paper is to utilize the EGIE in proposing a novel bivariate distribution by employing a shock model with three independent shocks, each following a non-identical EGIE distribution. One advantage of the proposed distribution is its flexibility, as it generalizes several well-known bivariate distributions, such as the bivariate exponentiated inverse exponential, bivariate inverse exponential, and bivariate inverse Weibull distributions. This versatility allows it to fit a wide range of real data sets. However, a key disadvantage is its singularity, which complicates the theoretical calculations of certain statistical properties, such as expectations, variances, correlation coefficient, and entropy of its variables.

In some applications, we may encounter bivariate data where one variable is discrete and the other is continuous. In such cases, semiparametric approaches for bivariate modeling are highly recommended. Examples include Copula-Based semiparametric models (see Genest et al. ^[11]) and semiparametric transformation models (see Chen et al. ^[7]).

An alternative approach for proposing bivariate distributions involves the use of copulas. Several studies have employed this method, including a recent work by Al-Shomrani ^[4], which introduces a new bivariate family of distributions based on a copula function. As a special case of this family, Al-Shomrani proposed the bivariate Topp-Leone-Exponential-Exponential (BFGMTLEE) distribution. However, they did not apply the BFGMTLEE to fit any real data. In this manuscript, we will compare the performance of our newly proposed model with the BFGMTLEE distribution in fitting real data.

The rest of the paper is organized as follows. Section 2 introduces the BEGIE distribution and discusses some of its fundamental properties. Dependence measures, including correlation, joint entropy, and positively likelihood ratio dependent, are discussed in Section 3. Random samples generation from the proposed model is discussed in Section 4. Section 5 discusses the maximum likelihood method using bivariate data and dependent competing risks data. Section 6 discusses the Bayesian estimation of the model parameters. A simulation study is presented in Section 7. In Section 8, we analyze three real-world data sets using the new suggested distribution and compare it to the IE distribution and GIE distribution as sub-models and some other non-nested models. Section 9 concludes the paper.

2.   BEGIE distribution

Now, we introduce the new bivariate exponentiated generalized inverted exponential (BEGIE) distribution as a mathematical model. Consider three independent random variables, denoted as $U_j$, $j = 1, 2, 3$. Each $U_j$ follows an EGIE distribution with parameters $(\lambda, \gamma, \alpha_j)$ for $j = 1, 2, 3$. Define $X_i = \max(U_i, U_3)$ for $i = 1, 2$. In this scenario, the pair of random variables $(X_1, X_2)$ follows the BEGIE distribution with parameters $(\lambda, \gamma, \alpha_1, \alpha_2, \alpha_3)$.

In a reliability context, this distribution can be understood as follows: Imagine a reliability system consisting of two units. These system units are exposed to three independent sources of shocks. In this scenario, a shock originating from the first source targets unit 1, a shock from the second source targets unit 2, and a shock from the third source affects both units. Unit 1 is considered destroyed when it receives shocks from both sources 1 and 3, while unit 2 is considered destroyed upon experiencing shocks from both sources 2 and 3. Let $X_1$ and $X_2$ represent the lifetimes of system units 1 and 2, respectively. In this context, we have $X_1 = \max(U_1, U_3)$ and $X_2 = \max(U_2, U_3)$, where $U_1, U_2,$ and $U_3$ represent the times at which the shocks occur and are assumed to follow EGIE distributions, as previously described. As a consequence of this assumption, the joint distribution of $(X_1, X_2)$ will follow the BEGIE distribution.

The main characteristics of the BEGIE distribution are outlined in the following theorem. The proofs, which are straightforward, are omitted for brevity.

Theorem 1. Suppose $(X_1, X_2) \sim$ BEGIE$(\lambda, \gamma, \alpha_1, \alpha_2, \alpha_3)$. Then,

1) The bivariate cumulative distribution function (cdf) of $(X_1, X_2)$ is

2) The bivariate probability density function (pdf) of $(X_1, X_2)$ is

3) The marginal distribution of $X_j$ follows EGIE$(\lambda, \gamma, \alpha_j + \alpha_3)$, $j = 1, 2$.

It is important to note that due to the relationship $P\left(X_1 = X_2\right) = \frac{\alpha_3}{\alpha_1+\alpha_2+\alpha_3}$ and the set $A = \{\left(x_1, x_2\right) \mid x_1 = x_2 > 0\}$ having Lebesgue measure zero, the BEGIE distribution contains both absolutely continuous and singular components. As a result, the BEGIE distribution is continuous, but not absolutely continuous with respect to the standard Lebesgue measure on $(0, \infty) \times(0, \infty)$.

Substituting from (1.2) into (2.2), we can derive $f_1(x_1, x_2)$, $f_2(x_1, x_2)$, and $f_3(x)$ in the following forms:

and

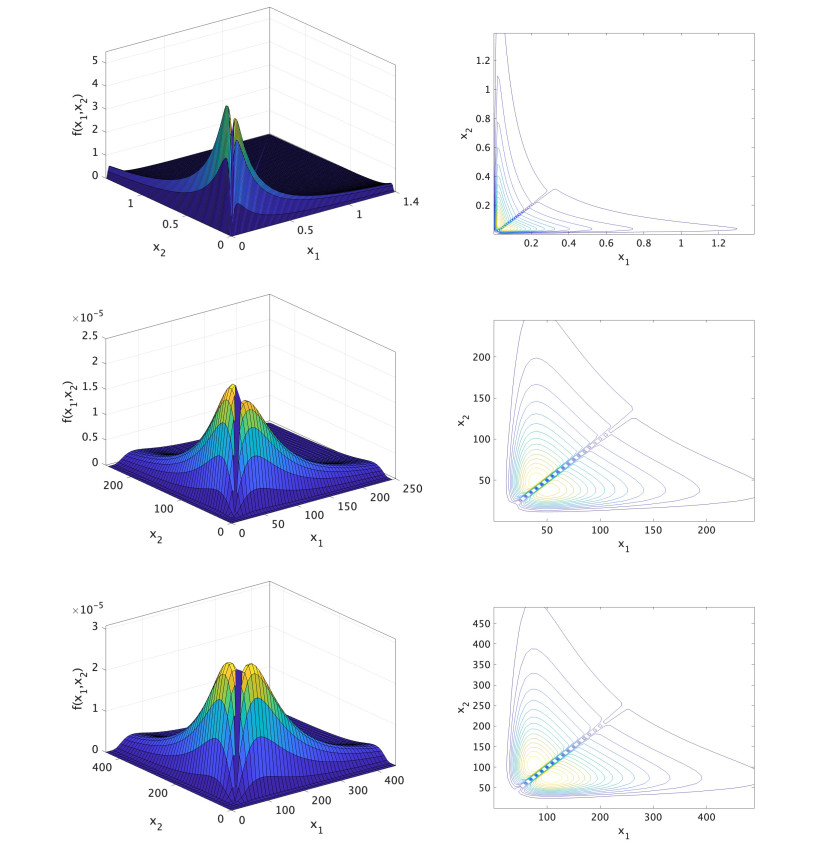
Figure 1 portrays the continuous components of the joint pdf (jpdf) for $(X_1, X_2)$, accompanied by corresponding contour plots illustrating various parameter values of the model. Simultaneously, Figure 2 displays the pdf and hrf of the marginal distribution for $X_1$, while Figure 3 showcases the singular segments of the jpdf, utilizing three distinct sets of parameter values to emphasize diverse hazard function shapes. These figures were generated using MATLAB. It becomes evident from these figures that the distribution's support varies in response to the model parameters' values and the profiles of the pdf and hrf.

The BEGIE$(\lambda, \gamma, \alpha_1, \alpha_2, \alpha_3)$ distribution generalizes the following distributions:

$1)$ Bivariate inverted exponential distribution, denoted by BIE$(\lambda, \alpha_1, \alpha_2, \alpha_3)$, by setting $\gamma = 1$;

$2)$ Bivariate exponentiated inverted exponential distribution, denoted by BEIE$(\gamma,$ $\alpha_1,$ $\alpha_2,$ $\alpha_3)$, by setting $\lambda = 1$.

Alqallaf and Kundu ^[5] applied a similar concept to propose a bivariate inverse generalized exponential (BIGE) distribution by combining three independent inverse generalized exponential (IGE) distributions. While the IGE distribution is a submodel of the EGIE distribution when $\alpha = 1$, the BIGE is not a submodel of the BEGIE.

Now, we discuss the Marshall–Olkin (MO) copula associated with the BEGIE distribution. The BEGIE distribution can be derived by applying the MO copula to EGIE distributions as the marginals. For any bivariate distribution function $F_{1, 2}(x_1, x_2)$ with marginals $F_{X_1}(x_1)$ and $F_{X_2}(x_2)$, there exists a unique copula $C: [0, 1]^2 \rightarrow [0, 1]$ that has uniform margins, satisfying $F_{1, 2}(x_1, x_2) = C(F_{X_1}(x_1), F_{X_2}(x_2))$ for all $(x_1, x_2) \in \textbf{R}^2$, see Nelson ^[22]. The MO copula is given by

for $0 < \theta_1, \theta_2 < 1$. By setting $u_j = F_{X_j}(x_j), \, j = 1, 2$, where $X_j \sim\mbox{EGIE}(\lambda, \gamma, \alpha_j+\alpha_3)$ and $\theta_j = \frac{\alpha_3}{\alpha_j+\alpha_3}$, we obtain the same joint cumulative distribution function $F_{1, 2}(x_1, x_2)$ as in (2.1).

3.   Dependence and information

This section discusses three mathematical properties of the BEGIE distribution. Correlation measures the linear relationship between two random variables, while joint entropy captures their combined uncertainty. Positively likelihood ratio dependent variables show a form of positive dependence.

Correlation coefficient: The correlation coefficient of $X_1$ and $X_2$, which has a joint pdf $f_{1, 2}(x_1, x_2)$, is

where Cov$(X_1, X_2) = E(X_1\, X_2) - E(X_1)\, E(X_2)$ and

Substituting from (2.2) into the above equations, we can get $E(X_i)$, $E(X_1 X_2)$, and $\sigma_{X_i}$, and then we use (3.1) to get $\rho$. Unfortunately, those integrals cannot be computed analytically. Therefore, we should use numerical methods to get $\rho$.

Joint entropy: Joint entropy for bivariate distributions is a measure of the uncertainty or randomness associated with the joint distribution of two random variables. In information theory, entropy provides a quantitative way to capture the amount of information in a distribution. For bivariate distributions, this concept extends to joint entropy. The joint entropy $H(X_1, X_2)$ of two random variables $X_1$ and $X_2$ is a measure of the uncertainty associated with their joint distribution. It is defined as (see Cover and Thomas ^[6]):

For the underlying model, $H$ does not have an analytical solution. Therefore, as for $\rho$, numerical methods must be used to compute $H$ for specific parameter values.

We performed numerical calculations for the marginal means, standard deviations, covariance of $(X_1, X_2)$, correlation, and joint entropy for two parameter sets: Set I ($\lambda = 69, \gamma = 2, \alpha_1 = .4, \alpha_2 = .3$) and Set II ($\lambda = 69, \gamma = 2, \alpha_1 = 2.4, \alpha_2 = 2.3$), with varying values of $\alpha_3 = 0.1, 0.2, \cdots, 3.5$. The results are presented in Tables 1 and 2. Additionally, Figure 4 illustrates the behavior of $\rho$ and $H$ as functions of $\alpha_3$. From these results, we observe a positive correlation between the two variables that decreases with $\alpha_3$. A decreasing correlation does not necessarily imply that there is no relationship between the variables, it simply means the linear relationship is weakening. We also observe that $H$ increases and then decreases as $\alpha_3$ increases. The "up then down" pattern in $H$ indicates that the variables initially move towards independence (increasing uncertainty) but later exhibit stronger dependence, reducing uncertainty. This pattern often reflects dynamic interactions between variables as their relationship evolves under changing conditions.

Positively likelihood ratio dependent (PLRD): PLRD is a concept in probability and statistics that refers to a specific type of dependence between two random variables; for more details, see Lehmann ^[17]. It is a form of positive dependence that is stronger than simple positive correlation. Two random variables $X_1$ and $X_2$ are said to be PLRD if for any values $x_{11} < x_{12}$ and any value $x_2$, the likelihood ratio $\mbox{LR} = \frac{f_{2|1}(x_2|x_{12})}{f_{2|1}(x_2|x_{11})}$ is non-decreasing in $x_2$. Here, $f_{2|1}(x_2|x_{1})$ is the conditional pdf of $X_2$, given $X_1 = x_1$. The following theorem summarizes PLRD in the BEGIE case. The proof is straightforward, so it is omitted for brevity.

Theorem 2. Let $(X_1, X_2)$ follow BEGIE$(\lambda, \gamma, \alpha_1, \alpha_2, \alpha_3)$. Then, $X_1$ and $X_2$ are PLRD if $\alpha_2\leq \alpha_1+\alpha_3$.

It is important to note that PLRD is a stronger condition than positive correlation. While positive correlation implies that higher values of one variable are associated with higher values of another, PLRD imposes a stricter requirement on how their joint distribution behaves.

4.   Random samples generation

When generating random numbers from the EGIE$(\lambda, \gamma, \alpha)$ distribution, if $X$ follows EGIE$(\lambda, \gamma, \alpha)$, the subsequent equation provides the $q^{\text{th}}$ quantile of $X$:

The following algorithm can be followed to generate bivariate data from the BEGIE$(\lambda, \gamma, \alpha_1, \alpha_2, \alpha_3)$ distribution.

$1)$ Specify the sample size $n$;

$2)$ Specify the values of the model parameters $\lambda, \gamma, \alpha_1, \alpha_2, \alpha_3$;

$3)$ Generate the samples, each with size $n$, from EGIE$(\lambda, \gamma, \alpha_j)$, $j = 1, 2, 3$, according to Eq (4.1). Use $U_j$, $j = 1, 2, 3$, to denote these three generated samples respectively. That is, for $j = 1, 2, 3$, the $j^{\mbox{th}}$ element in vector $U_j$, is

where $q_{ji}$ is randomly generated from a uniform distribution on the $(0, 1)$ interval.

$4)$ Generate a sample with size $n$ of $(X_1, X_2)$ by applying the following relationships:

The random sample $(X_{1i}, X_{2i})$ obtained from this algorithm follow a BEGIE$(\lambda, \gamma, \alpha_1, \alpha_2, \alpha_3)$ distribution. This bivaraite sample of $(X_1, X_2)$ can be used to generate a dependent competing risks sample, say $(T_i, \delta_i)$, $i = 1, 2, \cdots, n$, from the underlying distribution by setting $T_i = \min(X_{1i}, X_{2i})$ and

5.   Maximum likelihood estimation

In this section, we estimate the model parameters $\Theta = (\alpha_{1}, \alpha_{2}, \alpha_{3}, \lambda, \gamma)$ using two different types of data. Type I data consists of simple random samples of the bivariate vector $(X_{1}, X_{2})$ that follows the new bivariate distribution. Type II data consists of dependent competing risks data $(T, \delta)$, with $T = \min(X_{1}, X_{2}),$ where $(X_{1}, X_{2})$ follows a bivariate lifetime distribution and $\delta \, \in \{1, 2, 3\}$ represents the cause of failure. Theorem 1 will be helpful to estimate the model parameters using data of Type I. The following theorem is needed for Type II data.

Theorem 3. The pdf of $T = \min(X_{1}, X_{2})$, for a given cause of failure $\delta\in \{1, 2, 3\}$, is

where

and

Proof. Based on (2.1), one can show that the pdf of $T = \min (X_1, X_2)$ is

where $\overline{G}(t; \lambda, \gamma, \alpha_j) = 1- G(t; \lambda, \gamma, \alpha_j)$ is the survival function of $U_j$, $j = 1, 2, 3$. Substituting from (1.2) and (1.1) into (5.4), we complete the proof.

The maximum likelihood method is utilized for estimating model parameters, employing both types of data. Additionally, we also apply the Bayesian method, specifically for bivariate data. Although the Bayesian method could similarly be applied to dependent competing risks data, it was omitted from the paper due to length constraints. For more details on estimation methods, we refer to Wang et al. ^[8] and Albert (2009) ^[3].

5.1.   Bivariate data

Let us assume that $(X_{11}, X_{21}), (X_{12}, X_{22}), \cdots, (X_{1n}, X_{2n})$ is an independent and identically distributed random sample of $(X_{1}, \; X_{2})$ that follows $\mbox{BEGIE}(\alpha_{1}, \; \alpha_{2}, \; \alpha_{3}, \; \lambda, \; \gamma)$. For simplicity, let us introduce the indicator variables $\delta_{i},$ $i = 1, 2, ..., n,$ where

Using the above bivariate sample, the likelihood function can be expressed as

Substituting from (2.3)–(2.5) into (5.5), we get the log-likelihood function as

where $n_{j} = \sum_{i = 1}^{n} I[\delta_{i} = j], \; j = 1, 2, 3$ with $I[A] = 1$ if $A$ is true and $0$ otherwise.

Consequently, the maximum likelihood estimates (MLEs) of the unknown parameters can be determined by maximizing the log-likelihood function pertaining to the given data in relation to these parameters. Similarly, we can formulate the likelihood equations, which result from equating the first partial derivatives of the log-likelihood function concerning the unknown parameters to zero. The MLEs correspond to the solutions of these derived likelihood equations, at which point the Fisher information matrix should exhibit positive definiteness. This Fisher information matrix encompasses the second partial derivatives of the log-likelihood function with respect to the parameters.

In the case of the distribution under consideration, the likelihood equations are not amenable to an analytical solution. Consequently, we have resorted to employing numerical techniques within the R software framework to solve the system of five non-linear equations involving five unknown parameters.

5.2.   Dependent competing risks data

In this type of data, we observe a pair of quantities: $T,$ the system time to failure, and $\delta$, an indicator of the cause of failure. This means that the observations in this case are $(T_{i}, \, \delta_{i}), i = 1, 2, ..., n.$ The lifetime experiment that produces this type of data can be illustrated as follows: (1) we put $n$ independent and identical devices (system/objects) on the life test; (2) each system is under attack from two dependent competing risks which occur at times $X_{1}$ and $X_{2}$, and the system will fail once it receives one of the two attacks; (3) $(X_{1}, X_{2})$ follows the BEGIE distribution; (4) we observe $(T_{i}, \delta_{i}), i = 1, 2, ..., n,$ where $T_{i} = \min(X_{1i}, X_{2i}),$ and $\delta_{i}$ is defined as $\delta_{i} = 1$ if risk 1 causes the failure $(X_{1i} < X_{2i}), \; \delta_{i} = 2$ if risk 2 causes the failure $(X_{2i} < X_{1i})$, and $\delta_{i} = 3$ if both risks cause the failure $(X_{1i} = X_{2i})$. The likelihood function using such dependent competing risks data is

where $f_j^{*}(t)$ are given in Theorem 3. Substituting (5.2) and (5.3) into (5.7), we can get the log-likelihood function as

where $n_{j} = \sum_{i = 1}^{n} I[\delta_{i} = j], \; j = 1, 2, 3$.

To get the MLE of the model parameters, using dependent competing risks data, we set the first partial derivatives of ${\cal{L}}_{2}$ with respect to the five parameters $\alpha_{1}, \alpha_{2}, \alpha_{3}, \lambda, \gamma$ equal to zero, and we get a system of five non-linear equations in five unknowns. Solving the first three equations in $\alpha_{j},$ $j = 1, 2, 3$, we get $\alpha_{j}$ as a function of $(\lambda, \gamma)$:

and

Substituting (5.9) and (5.10) into (5.8), we can express the log-likelihood function as a function of two parameters $(\lambda, \gamma)$, say ${\cal{L}}_{2}^{*}(\lambda, \gamma)$. This will make the optimization of the log-likelihood function much easier since we will deal only with two parameters instead of five. Once we get the MLE of $\lambda$ and $\gamma$, we can use (5.9) and (5.10) to get the MLE of $\alpha_{j}$, $j = 1, 2, 3$.

Since the MLE of the parameters using either type of data are not obtained in closed form, we cannot get the explicit sampling distributions of the MLEs of these parameters. Therefore, we cannot obtain exact confidence intervals for the model parameters. Alternatively, we can use the large sample distribution of the MLE and the corresponding observed Fisher information matrix to derive approximate confidence intervals for the model parameters.

6.   Bayesian estimation

In this section, we implement a Bayesian approach to estimate the model parameters. We will demonstrate this method using the two types of data previously discussed. To derive Bayesian estimations, we assume independence among the five model parameters: $\lambda$, $\gamma$, $\alpha_{1}$, $\alpha_{2}$, and $\alpha_{3}$, considering them as independent random variables following gamma prior distributions. These gamma prior distributions have the hyperparameters $(a_i, b_i)$, where $i = 1, 2, \cdots, 5$, respectively. This implies that the logarithm of the joint prior density of these five parameters, referred to as $g(\theta)$, is up to a normalized constant, given by

where, $\theta_j$ is the j$^{\mbox{th}}$ component in the vector of unknown parameter $\theta$. Combining the logarithm of the joint prior density function with the logarithm of likelihood function allows us to formulate the logarithm of the joint posterior density function of $\theta$, given data, up to a normalized constant as

Substituting (6.1) and (5.6) into (6.2), we can obtain the $\log g(\theta|\mbox{data})$ for the bivariate data, as

While substituting (6.1) and (5.8) into (6.2), we can obtain the $\log g(\theta|\mbox{data})$ for the dependent competing risks data, as

The logarithm of the posterior density functions, $\log g_{I}(\theta|\mbox{data})$ and $\log g_{II}(\theta|\mbox{data})$ does not take the form of well-known multivariate distributions, making it challenging to derive analytic solutions for the Bayesian analysis of the model parameters. Consequently, we will need to resort to numerical computational methods. Specifically, in this paper, we will utilize the Markov chain Monte Carlo (MCMC) and sampling importance resampling (SIR) methods to approximate Bayesian estimations for the model parameters. Within MCMC, our primary task involves simulating samples from a proposal distribution that closely resembles the posterior distribution. For more comprehensive insights, readers are directed to Albert ^[3]. Typically, multivariate normal and $t$ distributions serve as common proposal distributions. However, as the underlying parameters are all positive, whereas these distributions have real-valued support, we need to re-parameterize $\theta$ into $\phi = \log(\theta) \in \mathbf{R}_5$. Through this logarithmic transformation of $\theta$, we can derive the logarithm of the posterior density functions, of $\phi$, as

and

We will also consider the normal prior distribution of $\phi_j = \log \theta_j\sim N(\mu_j, \sigma_j)$. In this case, $\log g(\theta)$, given in (6.1), will be replaced with

7.   Simulation study

To demonstrate the robustness of the model and its practical implications under various theoretical conditions, we conduct a simulation study of the bivariate model using two different sets of model parameters. The study follows the steps outlined below:

$1)$ Specify the parameter values:Define the sample size $n$ and the model parameters $\lambda, \gamma, \alpha_1, \alpha_2$, and $\alpha_3$.

$2)$ Generate random samples: Using the random sample generation method outlined in Section 3, generate $M$ random samples of $(X_1, X_2)$.

$3)$ Estimate parameters:For each sample generated in Step 2, compute the MLE, Bayes estimate (BE) of each parameter, and the corresponding asymptotic 95% confidence interval and 95% credible interval.

$4)$ Compute performance metrics: Using the $M$ results from Step 3, calculate the following:

(a) The average of the point estimation (APE), using the MLE and BE.

(b) The mean squared error (MSE), using the MLE and BE.

(c) The average length of the confidence/credible interval (ALCI).

(d) The coverage probability (CP) for both maximum likelihood and Bayes methods.

The mean squared error (MSE) and average of the point estimations (APE) are calculated as

where $\hat \theta^{(i)}$ is the either the MLE or BE of the parameter $\theta$, $\theta = \lambda, \gamma, \alpha_1, \alpha_2, \alpha_3$, for the i-th sample, $i = 1, 2, \cdots, M$.

Table 3 presents the results of the simulation study for sample sizes $n = 50, 75, 100,$ and $150$, with $M = 5000$, using two sets of model parameter values. Based on the results in Table 3, we observe the following trends for each parameter:

1. APE approaches actual value: As the sample size increases, both the average MLE and Bayesian estimate (APE) converge toward the true parameter value.

2. MSE decreases: The mean squared error (MSE) associated with the point estimates, using both MLE and Bayesian estimates, decreases with increasing sample size, indicating improved estimation accuracy.

3. ALCI decreases: The average length of the confidence/credible interval (ALCI) decreases as the sample size increases, reflecting greater precision in the intervals.

4. CP aligns with nominal confidence level: The coverage probability (CP), using either method, remains very close to the nominal confidence level, confirming the reliability of the intervals.

5. No significant difference between methods: There is no significant difference between the results obtained from the maximum likelihood and Bayesian methods.

8.   Applications

To demonstrate the applicability of the proposed model, this section focuses on the analysis of three distinct real data sets: two bivariate data and one dependent competing risks data. The primary objective is to illustrate the practical application and effectiveness of the proposed model in a real-world context. By examining these data sets, we aim to demonstrate how the proposed model can be applied to address complex scenarios and provide valuable insights in practical settings.

8.1.   Bivariate data

First bivariate data set (UEFA Champions League): The UEFA Champions League data, sourced from Meintanis ^[21] and displayed in Table 4, pertains to soccer matches. This data set captures instances where the home team scores at least one goal, as well as instances where a goal is scored directly from a penalty kick, foul kick, or any other direct kick (referred to as kick goals) by any team under consideration. In this data set, the variable $X_1$ represents the time in minutes when the first kick goal is scored by any team, while $X_2$ represents the time in minutes when the first goal of any type is scored by the home team.

The initial step in analyzing this dataset involved constructing a non-parametric and parametric scaled TTT-transform plot, using the EGIE distribution, for the marginal variables $X_1$ and $X_2$, as illustrated in Figure 5.

The visual analysis of the plot in Figure 5 leads to the inference that (for illustration see Aarset ^[1]) the hazard rate initially exhibits an upward trend and subsequently experiences a decline as time progresses or aging occurs. Consequently, considering the discerned pattern in the hazard rate, it is reasonable to anticipate that the EGIE distribution would be well-suited for modeling the marginal distribution of the data.

To facilitate a thorough comparison between the EGIE distribution and its sub-model distributions, to fit the marginal data, we conducted the following two hypotheses:

$1)$ $X_1$ and/or $X_2$ follows IE vs they follow EGIE, by testing $H_0: \gamma = 1$ vs $H_1: \gamma \neq 1$.

$2)$ $X_1$ and/or $X_2$ follows GIE vs they follow EGIE, by testing $H_0: \lambda = 1$ vs $H_1: \lambda \neq 1$.

To accomplish this objective, the likelihood ratio test statistic, $\Lambda = -2({\cal{L}}_0 - {\cal{L}}_1)$, is used. Table 5 displays the model, null hypothesis, MLE, negative log-likelihood value, the likelihood ratio statistic value, degrees of freedom (df), and p-value using marginal data.

From Table 5, it can be concluded that for both $X_1$ and $X_2$, at any significance level greater than or equal to $0.00224 (0.0573)$, the IE and GIE distributions are rejected in favor of the EGIE distribution as a better fit for the marginal data. This suggests that the BEGIE distribution may be more appropriate for fitting the current bivariate data set. To further investigate, the BGIE, BIE, and BEGIE distributions were applied, with the results summarized in Table 6. Based on these findings, there is significant evidence to reject both the BIE and BGIE distributions in favor of the BEGIE distribution for fitting the current dataset. Moreover, we compare the goodness of fit of the BEGIE model with the BFGMTLEE and BIGE distributions, whose joint PDFs are provided in Appendix A. This comparison is conducted using the Akaike information criterion (AIC). Table 7 displays the MLE, $-{\cal{L}}$, and AIC values for BFGMTLEE and BIGE. The AIC for the BEGIE is $640.282$. Based on the AIC values, we can conclude that the BEGIE model provides a better fit for the current data set than both the BFGMTLEE and BIGE models.

We also used the Bayesian approach to estimate the five parameters of the BEGIE distribution by adopting two sets of the hyperparameters for both the two types of prior distributions (gamma on the original parameters and normal on the log-transformed ones), as shown in Table 8.

Under the above two sets of hyperparameters and the two types of prior distributions, we conducted 50, 000 random draws from the joint posterior distribution using the MCMC and SIR algorithms. For the MCMC, we used the multivariate normal distribution with mean vector equal to the MLE of the logarithm of the vector of the five unknown parameters and variance-covariance matrix equal to 2 times the Fisher information matrix associated with the MLE. Subsequently, we approximated the posterior mean, median, and 95% credible interval "the 2.5th and 97.5th percentiles" for each parameter. The results are shown in Table 9.

As diagnostic tests for the random draws using the MCMC and SIR methods from the posterior distribution, we present trace plots for 2, 000 draws out of the 50, 000 generated draws using two sets of hyperparameters, as shown in Figures 6 and 7. These figures demonstrate well-mixed draws, indicating that the samples are randomly generated from the posterior distribution. Additionally, the trace plots suggest that the acceptance rate is higher for Set II of hyperparameters compared to Set I.

Utilizing the draws generated through the MCMC and SIR algorithms, we present histograms that illustrate the marginal posterior distributions of the model parameters as shown in Figures 8–11. The figures suggest that the normal prior distribution, particularly in scenarios with limited prior information about the parameters, does not perform as effectively as when more substantial prior information is available. However, this discrepancy is not observed when using the gamma prior distribution.

Second bivariate data set (cholesterol data set): This dataset includes cholesterol levels measured at 5 and 25 weeks after treatment in 30 patients. Shoaee ^[32] applied three bivariate distributions of the Marshall-Olkin type to model this data: the bivariate Weibull (BWG), bivariate Chen (BCHG), and bivariate Gompertz (BGG) distributions. For computational reasons, Shoaee ^[32] transformed the marginal data values using the formula $\frac{(X - 150)}{100}$ before conducting the analysis. The transformed data are presented in Table 10.

Based on AIC statistics, Shoaee ^[32] reported that the BCHG model is the best fit for this dataset. In the current work, we use the BEGIE model to reanalyze this data and compare its performance with the aforementioned three models, as well as the BFGMTLEE model by Al-Shomrani ^[4]. Table 11 presents the MLE, negative log-likelihood values, and AIC for the five models used to analyze this dataset. It is important to note that the results for the BWG, BCHG, and BGG models are sourced from Shoaee ^[32]. Based on the AIC criterion, the BEGIE model provides a better fit for this data than the other four models.

A Bayesian analysis can be conducted similarly to how we approached the first dataset. However, we have not included the Bayesian component for the second dataset due to the appropriate length considerations.

8.2.   Diabetic retinopathy application

Diabetic retinopathy is a significant ocular condition capable of inducing vision loss and blindness in individuals with diabetes. It affects the blood vessels within the retina, which is the light-sensitive tissue layer at the back of the eye. The National Eye Institute in Bethesda, Maryland, conducted an experiment involving 71 patients to investigate the impact of laser treatment on reducing the risk of blindness associated with diabetic retinopathy. In this study, laser treatment was administered to a randomly selected eye for each patient. The study recorded the time to blindness and whether one or both eyes became blind. The recorded data are presented in Table 12. This data was analyzed by Sarhan, Apaloo, and Kundu ^[27] and Manshi, Sarhan, and Smith ^[20]. For more information about diabetic retinopathy, we refer the readers to ^[23].

The primary objective of this experiment was to assess whether the laser treatment could effectively delay the onset of blindness in individuals with diabetic retinopathy. The dataset derived from this study can be treated as one involving dependent competing risks data, with two potential causes of failure (blindness).

We utilize the BEGIE distribution along with its sub-models (BIE and BGIE) to perform fitting on this dataset, followed by a subsequent comparison. To facilitate this comparative analysis, Table 13 provides the MLEs, corresponding log-likelihood functions, and Akaike information criterion (AIC) for all the aforementioned models. Additionally, the likelihood ratio test (LRT) statistic and corresponding p-values for the sub-models are also included in the table. The outcomes presented in Table 13 lead us to the conclusion that the sub-models BIE and BGIE distributions exhibit statistical significance in their rejection, favoring the BEGIE distribution instead, as evidenced by their considerably small p-values.

To ascertain whether the laser treatment significantly contributes to delaying blindness among individuals with Diabetic Retinopathy, a straightforward hypothesis testing approach can be employed. Previous studies conducted by Sarhan, Apaloo, and Kundu ^[27] and Manshi, Sarhan, and Smith ^[20] concluded that the laser treatment does not yield a substantial impact in delaying blindness in these patients. In this study, we address the same question by utilizing the BEGIE distribution. To this end, we consider the following hypotheses for testing:

Null Hypothesis ($H_0$): The laser surgery does not exhibit a significant effect in delaying blindness ($\alpha_1 = \alpha_2$).

Alternative Hypothesis ($H_1$): The laser surgery has a meaningful impact in delaying blindness ($\alpha_1 \neq \alpha_2$).

We can employ the likelihood ratio test to assess the aforementioned hypotheses, defined as $\Lambda = - 2(\hat{\cal{L}}_{02} - \hat{\cal{L}}_{2})$, which conforms to a chi-square distribution with one degree of freedom. In this context, $\hat{\cal{L}}_{02}$ and $\hat{\cal{L}}_{2}$ signify the maximum values of the log-likelihood functions under $H_0$ and $H_1$, respectively.

Deriving the log-likelihood function under $H_0$ involves a special case of Eq (5.8), where we assume $\alpha_1 = \alpha_2 = \alpha$, thus yielding:

Under the null hypothesis, the MLEs of the unknown parameters are as follows: $\hat{\lambda} = 1308.073$, $\hat\gamma = 1.382$, $\hat{\alpha}_1 = \hat{\alpha}_2 = 0.301$, and $\hat{\alpha}_3 = 0.982$. The corresponding log-likelihood value is calculated as $- 588.06$. Consequently, the test statistic value is determined as $\Lambda = -2 (-588.06 + 587.83) = 0.46$, and the resulting p-value is remarkably small at $0.498$. This leads us to the conclusion that the null hypothesis ($H_0$) cannot be significantly rejected in favor of the alternative hypothesis ($H_1$). Consequently, we can confidently affirm that the laser treatment does not exhibit a significant effectiveness in delaying the onset of blindness.

9.   Conclusions

In this study, we harnessed the fatal shock model concept to introduce a fresh bivariate distribution in the realm of the Marshall-Olkin type. This distribution incorporates three independent univariate random variables following the exponentiated generalized inverted exponential distribution. Termed the "bivariate exponentiated generalized inverted exponential distribution" (BEGIE), this novel proposal extends the scope of both the bivariate inverted exponential (BIE) and bivariate exponentiated inverted exponential (BGIE) distributions. We explore several statistical properties inherent to this newly introduced distribution.

The versatility of the BEGIE distribution is demonstrated through its application in modeling dependent competing risks data and bivariate data scenarios. Estimation of the unknown parameters within the BEGIE distribution was achieved via the maximum likelihood method, effectively applied to both bivariate and dependent competing risks datasets.

A Bayesian technique is applied on the dependent competing risks data. Additionally, the performance of the BEGIE distribution was evaluated using real datasets, comparing its effectiveness against the BIE and BGIE distributions. The results prominently indicated the BEGIE distribution's superior fit for these datasets.

Looking ahead, we are considering the utilization of step-stress acceleration life test plans or progressively type-II censored data as part of our future research trajectory. These approaches will aid in estimating BEGIE distribution parameters, particularly in scenarios involving bivariate data or dependent competing risks data.

Author contributions

A.M.S.: Conceptualization, Methodology, Software, Validation, Formal analysis, Investigation, Writing-original draft preparation, Writing-review and editing, Visualization; R.S.G.: Methodology, Validation, Resources, Writing-original draft preparation, Writing-review and editing; N.A.: Formal analysis, Investigation; A.M.M.: Methodology, Writing-original draft preparation, Writing-review and editing. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

The authors would like to thank the five external experts and the editor for their valuable comments, which have significantly enhanced the overall quality and presentation of the manuscript. This research is supported by researchers supporting project number (RSPD2024R548), King Saud University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare no conflict of interest.

Appendix

A.   The joint pdf of non-nested models

The joint probability density function (pdf) of the BFGMTLEE, as introduced by Al-Shomrani ^[4]:

where $\alpha_1, \alpha_2, \lambda_1, \lambda_2 > 0,$ and $-1\leq \delta\leq 1$.

The joint pdf of the BIGE, as given by Alqallaf and Kundu ^[5], is

where

Note: $f_{\mbox{IGE}}(x; \alpha, \lambda)$ can be obtained from (1.2) by setting $\gamma = \alpha$ and $\alpha = 1$.