Research on VIKOR group decision making using WOWA operator based on interval Pythagorean triangular fuzzy numbers

1.   Introduction

Fractional differential equations (FDEs) have a profound physical background and rich theoretical connotations and have been particularly eye-catching in recent years. Fractional order differential equations refer to equations that contain fractional derivatives or integrals. Currently, fractional derivatives and integrals have a wide range of applications in many disciplines such as physics, biology, and chemistry, etc. For more information see ^[1,2,3,45].

Langevin equation is an important tool of many areas such as mathematical physics, protein dynamics ^[6], deuteron-cluster dynamics, and described anomalous diffusion ^[7]. In 1908, Langevin established first the Langevin equation with a view to describe the advancement of physical phenomena in fluctuating conditions ^[8]. Some evolution processes are characterized by the fact that they change of state abruptly at certain moments of time. These perturbations are short-term in comparison with the duration of the processes. So, the Langevin equations are a suitable tool to describe such problems. Besides the intensive improvement of fractional derivatives, the Langevin (FDEs) have been presented in 1990 by Mainardi and Pironi ^[9], which was trailed by numerous works interested in some properties of solutions like existence and uniqueness for Langevin FDEs ^{[10,11,12,13,14,15,16,17,18,19]}. We also refer here to some recent works that deal with a qualitative analysis of such problems, including the generalized Hilfer operator, see ^{[20,21,22,23,24]}. Recent works related to our work were done by ^{[25,26,27,28,29,30]}. The monotone iterative technique is one of the important techniques used to obtain explicit solutions for some differential equations. For more details about the monotone iterative technique, we refer the reader to the classical monographs ^[31,32].

Lakshmikantham and Vatsala ^[25] studied the general existence and uniqueness results for the following FDE

by the monotone iterative technique and comparison principle. Fazli et al. ^[26] investigated the existence of extremal solutions of a nonlinear Langevin FDE described as follows

via a constructive technique that produces monotone sequences that converge to the extremal solutions. Wang et al. ^[27], used the monotone iterative method to prove the existence of extremal solutions for the following nonlinear Langevin FDE

Motivated by the novel advancements of the Langevin equation and its applications, also by the above argumentations, in this work, we apply the monotone iterative method to investigate the lower and upper explicit monotone iterative sequences that converge to the extremal solution of a fractional Langevin equation (FLE) with multi-point sub-strip boundary conditions described by

where $^{H}D_{0^{+}}^{\mu _{1}, \beta _{1};\phi }\ $ and $^{H}D_{0^{+}}^{\mu _{2}, \beta _{2};\phi }$ are the $\phi$-Hilfer fractional derivatives of order $\ \mu _{1}\in \left(0, 1\right] \ $ and $\mu _{2}\in \left(1, 2\right]$ respectively, and type $\beta _{1}, \beta _{2}\in \left[0, 1\right], \sigma _{i} > 0, \lambda _{1}, \lambda _{2}\in\mathbb{R}^{+},$ $\delta _{i} > 0,$ $m\geq 1,$ $0 < \zeta _{1} < \zeta _{2} < ...... < 1$, $f:(0, b]\times \mathfrak{\mathbb{R}}\rightarrow \mathfrak{\mathbb{R}}$ is a given continuous function and $\phi$ is an increasing function, having a continuous derivative $\phi ^{\prime }$ on $(0, b)$ such that $\phi ^{\prime }(\varkappa)\neq 0,$ for all $\varkappa \in (0, b]$. Our main contributions to this work are as follows:

$\bullet$ By adopting the same techniques used in ^[26,27], we derive the formula of explicit solutions for $\phi$-Hilfer-FLEs (1.1) involving two parameters Mittag-Leffler functions.

$\bullet$ We use the monotone iterative method to study the extremal of solutions of $\phi$-Hilfer-FLE (1.1).

$\bullet$ We investigate the lower and upper explicit monotone iterative sequences that converge to the extremal solution.

$\bullet$ The proposed problem (1.1) covers some problems involving many classical fractional derivative operators, for different values of function $\phi$ and parameter $\mu _{i}, i = 1, 2$. For instance:

$\bullet$ If $\phi (\varkappa) = \varkappa$ and $\mu _{i} = 1$, then the FLE (1.1) reduces to Caputo-type FLE.

$\bullet$ If $\phi (\varkappa) = \varkappa$ and $\mu _{i} = 0$, then the FLE (1.1) reduces to Riemann-Liouville-type FLE.

$\bullet$ If $\mu _{i} = 0$, then the FLE (1.1) reduces to FLE with the $\phi$-Riemann-Liouville fractional derivative.

$\bullet$ If $\phi (\varkappa) = \varkappa$, then the FLE (1.1) reduces to classical Hilfer-type FLE.

$\bullet$ If $\phi (\varkappa) = \log \varkappa$, then the FLE (1.1) reduces to Hilfer-Hadamard-type FLE.

$\bullet$ If $\phi (\varkappa) = \varkappa ^{\rho }$, then the FLE (1.1) reduces to Katugampola-type FLE.

$\bullet$ The results obtained in this work includes the results of Fazli et al. ^[26], Wang et al. ^[27] and cover many problems which do not study yet.

The structure of our paper is as follows: In the second section, we present some notations, auxiliary lemmas and some basic definitions which are used throughout the paper. Moreover, we derive the formula of the explicit solution for FLE (1.1) in the term of Mittag-Leffler with two parameters. In the third section, we discuss the existence of extremal solutions to our FLE (1.1) and prove lower and upper explicit monotone iterative sequences which converge to the extremal solution. In the fourth section, we provide a numerical example to illustrate the validity of our results. The concluding remarks will be given in the last section.

2.   Auxiliary notions

To achieve our main purpose, we present here some definitions and basic auxiliary results that are required throughout our paper. Let $\mathcal{J}: = \left[0, b\right],$ and $\mathcal{C}\left(\mathcal{J}\right)$ be the Banach space of continuous functions $\ \upsilon :\mathcal{J}\rightarrow\mathbb{R}$ equipped with the norm $\left\Vert \upsilon \right\Vert = \sup \{\left\vert \upsilon (\varkappa)\right\vert :\varkappa \in \mathcal{J}\}.$

Definition 2.1. ^[2] Let $f\ $ be an integrable function and $\mu > 0$. Also, let $\phi$ be an increasing and positive monotone function on $(0, b)$, having a continuous derivative $\phi ^{\prime }$ on $(0, b)$ such that $\phi ^{\prime }(\varkappa)\neq 0,$ for all $\varkappa \in \mathcal{J}.$ Then the $\phi$-Riemann-Liouville fractional integral of $f$ of order $\mu$ is defined by

Definition 2.2. ^[33] Let $n-1 < \mu < n,$ $(n\in \mathbb{N}),$ and $f, \phi \in \mathcal{C}^{n}\left(\mathcal{J}\right)$ such that $\phi ^{\prime }(\varkappa)$ is continuous and satisfying $\phi ^{\prime }(\varkappa)\neq 0$ for all $\varkappa \in \mathcal{J}.$ Then the left-sided $\phi$-Hilfer fractional derivative of a function $f$ of order $\mu$ and type $\beta \in \left[0, 1\right]$ is defined by

where

Lemma 2.3. ^[2,33] Let $n-1 < \mu < n,$ $0\leq \beta \leq 1,$ and $n < \delta \in \mathbb{R}.$ For a given function $f:\mathcal{J}\rightarrow \mathbb{R}$, we have

and

Lemma 2.4. ^[33] Let $f:\mathcal{J}\rightarrow \mathbb{R},$ $n-1 < \mu < n$, and $0\leq \beta \leq 1$. Then

(1) If $f\in \mathcal{C}^{n-1}\left(\mathcal{J}\right),$ then

(2) If $f\in \mathcal{C}\left(\mathcal{J}\right)$, then

Lemma 2.5. For $\mu \mathfrak{, }\beta, \mathfrak{\gamma } > 0$ and $\lambda \in \mathbb{R} ,$ we have

where $E_{\gamma, \beta }$ is Mittag-Leffler function with two-parameterdefined by

Proof. See ^[34].

Lemma 2.6. ^[27] Let $\mu \in \left(1, 2\right]$ and $\beta > 0$ be arbitrary. Then the functions $E_{\mu }(\cdot),$ $E_{\mu, \mu }(\cdot)$ and $E_{\mu, \beta }(\cdot)$ are nonnegative. Furthermore,

for $\chi < 0.$

Lemma 2.7. Let $\mu \mathfrak{, }k, \beta > 0$, $\lambda \in \mathbb{R}$ and $f\in C\left(\mathcal{J}\right).$ Then

Proof. See ^[34].

For some analysis techniques, we will suffice with indication to the classical Banach contraction principle (see ^[35]).

To transform the $\phi$-Hilfer type FLE (1.1) into a fixed point problem, we will present the following Lemma.

Lemma 2.8. Let $\mathfrak{\gamma }_{j} = \mu _{j}+j\beta _{j}-\mu_{j}\beta _{j}$, $\left(j = 1, 2\right)$ such that $\mu _{1}\in \left(0, 1\right], \mu _{2}\in \left(1, 2\right],$ $\beta _{j}\in \left[0, 1\right], \lambda _{1}, \lambda _{2}\geq 0$ and $\ \mathfrak{\hslash }$ is a functionin the space $\mathcal{C}\left(J\right)$. Then, $\upsilon$ is a solutionof the $\phi$-Hilfer linear FLE of the form

if and only if $\upsilon$ satisfies the following equation

where

Proof. Let $\left(^{H}D_{0^{+}}^{\mu _{2}, \beta _{2};\phi }+\lambda _{2}\right) \upsilon (\varkappa) = P(\varkappa)$. Then, the problem (2.1) is equivalent to the following problem

Applying the operator $I_{0^{+}}^{\mu _{1}, \phi }$ to both sides of the first equation of (2.4) and using Lemma 2.4, we obtain

where $c_{0}$ is an arbitrary constant. For explicit solutions of Eq (2.4), we use the method of successive approximations, that is

and

By Definition 2.1 and Lemma 2.3 along with Eq (2.6), we obtain

Similarly, by using Eqs (2.6)–(2.8), we get

Repeating this process, we get $P_{k}(\varkappa)$ as

Taking the limit $k\rightarrow \infty$, we obtain the expression for $P_{k}(\varkappa)$, that is

Changing the summation index in the last expression, $i\rightarrow i+1$, we have

From the definition of Mittag-Leffler function, we get

By the condition $P(0) = 0,$ we get $c_{0} = 0$ and hence

Equation (2.9) reduces to

Similarly, the following equation

is equivalent to

By the condition $\upsilon (0) = 0,$ we obtain $c_{2} = 0$ and hence Eq (2.11) reduces to

By the condition $\upsilon (b) = \sum_{i = 1}^{m}\delta _{i}$ $I_{0^{+}}^{\sigma _{i}, \phi }\upsilon (\zeta _{i})$, we get

Put $c_{0}$ in Eq (2.12), we obtain

Substituting Eq (2.10a) into Eq (2.14), we can get Eq (2.2).

On the other hand, we assume that the solution $\upsilon$ satisfies Eq (2.2). Then, one can get $\upsilon (0) = 0.$ Applying $^{H}D_{0^{+}}^{\mu _{2}, \beta _{2};\phi }$ on both sides of Eq (2.2), we get

Since $\gamma _{2} = \mu _{2}+\beta _{2}-\mu _{2}\beta _{2},$ then, by Lemma 2.3, we have $^{H}D_{0^{+}}^{\mu _{2}, \beta _{2};\phi }\left[\phi (\varkappa)-\phi (0)\right] ^{\gamma _{2}-1} = 0$ and hence Eq (2.15) reduces to the following equation

By using some properties of Mittag-Leffler function and taking $\varkappa = 0,$ we obtain

Thus, the derivative condition is satisfied. The proof of Lemma 2.8 is completed.

Lemma 2.9. (Comparison Theorem). For $j = 1, 2,$ let $\mathfrak{\gamma }_{j} = \mu _{j}+j\beta _{j}-\mu _{j}\beta _{j}$, $\mu _{1}\in \left(0, 1\right], \mu _{2}\in \left(1, 2\right],$ $\beta _{j}\in \left[0, 1\right], \lambda_{1}\geq 0$ and $\ \upsilon \in \mathcal{C}\left(\mathcal{J}\right)$ be acontinuous function satisfies

then $\upsilon (\varkappa)\geq 0,$ $\varkappa \in (0, b].$

Proof. If $z\geq 0$, then from Lemma 2.6, we have $E_{\mu, \beta }(z)\geq 0$. If $z < 0,$ then $E_{\mu, \beta }(z)$ is completely monotonic function ^[35], that means $E_{\mu, \beta }(z)$ possesses derivatives for all arbitrary integer order and $\left(-1\right) ^{n}\frac{d^{n}}{dz^{n}}E_{\mu, \beta }(z)\geq 0.$ Hence, $E_{\mu, \beta }(z)\geq 0$ for all $z\in\mathbb{R}.$ In view of Eq (2.2), Eq (2.9), and from fact that $E_{\mu _{1}, \gamma _{1}}(\cdot)\geq 0$ and $E_{\mu, \mu }(\cdot)\geq 0$ with help the definition of $\phi$, we obtain $\upsilon (\varkappa)\geq 0$, for $\varkappa \in (0, b]$. (Alternative proof). Let $\left(^{H}D_{0^{+}}^{\mu _{2}, \beta _{2};\phi }+\lambda _{2}\right) \upsilon (\varkappa) = P(\varkappa).$ Then, we have

Assume that $P(\varkappa)\geq 0$ (for all $\varkappa \in (0, b]$) is not true. Then, there exist $\varkappa _{1}, \varkappa _{2}$, $\left(0 < \varkappa _{1} < \varkappa _{2}\leq b\right)$ such that $P(\varkappa _{2}) < 0, P(\varkappa _{1}) = 0$ and

Since $\lambda _{1}\geq 0,$ we have $\left(^{H}D_{0^{+}}^{\mu _{1}, \beta _{1};\phi }+\lambda _{1}\right) P(\varkappa)\geq 0$ for all $\varkappa \in \left(\varkappa _{1}, \varkappa _{2}\right).$ In view of

the operator $I_{0^{+}}^{1-\gamma _{1};\phi }P(\varkappa)$ is nondecreasing on $\left(\varkappa _{1}, \varkappa _{2}\right)$. Hence

On the other hand, for all $\varkappa \in \left(\varkappa _{1}, \varkappa _{2}\right),$ we have

which is a contradiction. Therefore, $P(\varkappa)\geq 0$ $\left(\varkappa \in (0, b]\right).$ By the same technique, one can prove that $\upsilon (\varkappa)\geq 0$, for all $\varkappa \in (0, b].$

As a result of Lemma 2.8, we have the following Lemma.

Lemma 2.10. For $j = 1, 2,$ let $\mathfrak{\gamma }_{j} = \mu _{j}+j\beta_{j}-\mu _{j}\beta _{j}$, $\mu _{1}\in \left(0, 1\right], \mu _{2}\in \left(1, 2\right],$ $\beta _{j}\in \left[0, 1\right] \ $ and $f:\mathcal{J}\times \mathbb{R} \rightarrow \mathbb{R}$ is continuous function $.$ If $\upsilon \in \mathcal{C}\left(\mathcal{J}\right)$ satisfies the problem (1.1), then, $\upsilon$ satisfies thefollowing integral equation

3.   Existence of extremal solutions

In this part, we focus on the existence of lower and upper explicit monotone iterative sequences that converge to the extremal solution for the nonlinear $\phi$-Hilfer FLE (1.1). The existence of unique solution for the problem (1.1) is based on Banach fixed point theorem. Now, let us give the following definitions:

Definition 3.1. For $\mathcal{J} =$ $\left[0, b\right] \subset\mathbb{R}_{+}$. Let $\upsilon \in \mathcal{C(J)}$. Then, the upper and lower-control functions are defined by

and

respectively. Clearly, $\overline{f}\left(\varkappa, \upsilon (\varkappa)\right)$ and $\underline{f}\left(\varkappa, \upsilon (\varkappa)\right)$ are monotonous non-decreasing on $\left[a, b\right]$ and

Definition 3.2. Let $\overline{\upsilon }$, $\underline{\upsilon }$ $\in \mathcal{C}\left(\mathcal{J}\right)$ be upper and lower solutions of the problem (1.1) respectively. Then

and

According to Lemma 2.8, we have

and

Theorem 3.3. Let $\overline{\upsilon }(\varkappa)$ and $\underline{\upsilon }(\varkappa)$ be upper and lower solutions of the problem (1.1), respectively such that $\underline{ \upsilon }$ $\left(\varkappa \right)\leq \overline{\upsilon }\left(\varkappa \right)$ on $\mathcal{J}.$ Moreover, the function $f\left(\varkappa, \upsilon \right)$ is continuouson $\mathcal{J}$ and there exists a constant number $\kappa > 0$ such that $\left\vert f\left(\varkappa, \upsilon \right) -f\left(\varkappa, v\right)\right\vert \leq \kappa \left\vert \upsilon -v\right\vert,$ for $\upsilon, v\in \mathbb{R} ^{+},$ $\varkappa \in \mathcal{J}$. If

then the problem (1.1) has a unique solution $\upsilon \in C\left(\mathcal{J}\right).$

Proof. Let $\Xi = P- \underline{ P }$, where $P(\varkappa) = \left(^{H}D_{0^{+}}^{\mu _{2}, \beta _{2};\phi }+\lambda _{2}\right) \upsilon (\varkappa)\ $ and $\underline{P}(\varkappa) = \left(^{H}D_{0^{+}}^{\mu _{2}, \beta _{2};\phi }+\lambda _{2}\right) \underline{\upsilon }(\varkappa).$ Then, we get

In view of Lemma 2.9, we have $\Xi \left(\varkappa \right) \geq 0$ on $\mathcal{J}\ $ and hence $\underline{ P }$ $\left(\varkappa \right) \leq P\left(\varkappa \right)$. Since $P(\varkappa) = \left(^{H}D_{0^{+}}^{\mu _{2}, \beta _{2};\phi }+\lambda _{2}\right) \upsilon (\varkappa)\ $ and $\underline{P}(\varkappa) = \left(^{H}D_{0^{+}}^{\mu _{2}, \beta _{2};\phi }+\lambda _{2}\right) \underline{\upsilon }(\varkappa),$ by the same technique, we get $\underline{ \upsilon }$ $\left(\varkappa \right) \leq \upsilon \left(\varkappa \right)$. Similarly, we can show that $\upsilon \left(\varkappa \right) \leq \overline{\upsilon }\left(\varkappa \right).$ Consider the continuous operator $\mathcal{G}:\mathcal{C}\left(\mathcal{J} \right) \rightarrow \mathcal{C}\left(\mathcal{J}\right)$ defined by

Clearly, the fixed point of $\mathcal{G}$ is a solution to problem (1.1). Define a closed ball $\mathbb{B}_{R}$ as

with

where

and $\mathcal{P} = \sup_{s\in \mathcal{J}}\left\vert f(s, 0)\right\vert.$ Let $\upsilon \in \mathbb{B}_{R}$ and $\varkappa \in \mathcal{J}$. Then by Lemma 2.6, we have

Now, we will present the proof in two steps:

$\textsf{First step:}$ We will show that $\mathcal{G}(\mathbb{B}_{R})\subset \mathbb{B}_{R}.$ First, by Lemma 2.6 and Definition 2.1, we have

Next, for $\upsilon \in \mathbb{B}_{R}$, we obtain

Thus $\mathcal{G}(\mathbb{B}_{R})\subset \mathbb{B}_{R}.$

$\textsf{Second step:}$ We shall prove that $\mathcal{G}$ is contraction. Let $\upsilon, \widehat{\upsilon }\in \mathbb{B}_{R}$ and $\varkappa \in \mathcal{ J}$. Then by Lemma 2.6 and Definition 2.1, we obtain

Thus, $\mathcal{G}$ is a contraction. Hence, the Banach contraction principle theorem ^[35] shows that the problem (1.1) has a unique solution.

Theorem 3.4. Assume that $\overline{\upsilon }, \underline{\upsilon }\in C\left(\mathcal{J}\right)$ be upper and lower solutions of the problem (1.1), respectively, and $\underline{ \upsilon }$ $\left(\varkappa \right)\leq \overline{\upsilon }\left(\varkappa \right)$ on $\mathcal{\ J}$. Inaddition, If the continuous function $f:\mathcal{\ J}\times \mathbb{R} \rightarrow \mathbb{R}$ satisfies $f\left(\varkappa, \upsilon \left(\varkappa \right) \right)\leq f\left(\varkappa, y\left(\varkappa \right) \right)$ for all$\underline{ \upsilon }$ $\left(\varkappa \right) \leq \upsilon \left(\varkappa \right) \leq y(\varkappa)\leq \overline{\upsilon }\left(\varkappa \right), \varkappa \in \mathcal{\ J}$ then there exist monotoneiterative sequences $\left\{ \underline{\upsilon }_{j}\right\}_{j = 0}^{\infty }$ and $\left\{ \overline{\upsilon }_{j}\right\}_{j = 0}^{\infty }$ which uniformly converges on $\mathcal{J}$ to the extremal solutions of problem (1.1) in $\Phi = \left\{ \upsilon \in \mathcal{C}\left(\mathcal{J}\right) :\underline{\upsilon }\left(\varkappa \right)\leq \upsilon \left(\varkappa \right) \leq \overline{\upsilon }\left(\varkappa \right), \varkappa \in \mathcal{J}\right\}.$

Proof. $\textsf{Step (1):}$ Setting $\underline{\upsilon }_{0} = \underline{\upsilon }$ and $\overline{\upsilon }_{0} = \overline{\upsilon }$, then given $\left\{ \underline{\upsilon }_{j}\right\} _{j = 0}^{\infty }$ and $\left\{ \overline{ \upsilon }_{j}\right\} _{j = 0}^{\infty }$ inductively define $\underline{ \upsilon }_{j+1}$ and $\overline{\upsilon }_{j+1}$ to be the unique solutions of the following problem

and

By Theorem 3.3, we know that the above problems have a unique solutions in $\mathcal{C}\left(\mathcal{J}\right)$.

$\textsf{Step (2):}$ Now, for $\varkappa \in \mathcal{J},$ we claim that

To confirm this claim, from (3.1) for $j = 0,$ we have

With reference to the definitions of the lower solution $\underline{\upsilon }(\varkappa) = \underline{\upsilon }_{0}(\varkappa)$ and putting $\Xi (\varkappa) = P_{1}(\varkappa)-$ $\underline{ P }$ $_{0}(\varkappa)$, where $P_{1}(\varkappa) = \left(^{H}D_{0^{+}}^{\mu _{2}, \beta _{2};\phi }+\lambda _{2}\right) \upsilon _{1}(\varkappa)\ $ and $\underline{P}_{0}(\varkappa) = \left(^{H}D_{0^{+}}^{\mu _{2}, \beta _{2};\phi }+\lambda _{2}\right) \underline{\upsilon }_{0}(\varkappa).$ Then, we get

Consequently, Lemma 2.9 implies $\Xi (\varkappa)\geq 0,$ that means $\underline{ P }$ $_{0}(\varkappa)\leq P_{1}(\varkappa), \varkappa \in \mathcal{J}$ and by the same technique, where $P(\varkappa) = \left(^{H}D_{0^{+}}^{\mu _{2}, \beta _{2};\phi }+\lambda _{2}\right) \upsilon (\varkappa)$ we get $\upsilon (\varkappa)\geq 0.$ Hence, $\underline{ \upsilon }_{0}(\varkappa)\leq \underline{\upsilon }_{1}(\varkappa), \varkappa \in \mathcal{J}.$ Now, from Eq (3.4) and our assumptions, we infer that

Therefore, $\underline{\upsilon }_{1}$ is a lower solution of problem (1.1). In the same way of the above argument, we conclude that $\underline{ \upsilon }_{1}(\varkappa)\leq \underline{\upsilon }_{2}(\varkappa), \varkappa \in \mathcal{J}.$ By mathematical induction, we get $\underline{ \upsilon }_{j}(\varkappa)\leq \underline{\upsilon }_{j+1}(\varkappa), \varkappa \in \mathcal{J}, j\geq 2.$

Similarly, we put $\Xi (\varkappa) = \overline{P}_{1}(\varkappa)-\underline{P }_{1}(\varkappa)$, where $\overline{P}_{1}(\varkappa) = \left(^{H}D_{0^{+}}^{\mu _{2}, \beta _{2};\phi }+\lambda _{2}\right) \overline{ \upsilon }_{1}(\varkappa)\ $ and $\underline{P}_{1}(\varkappa) = \left(^{H}D_{0^{+}}^{\mu _{2}, \beta _{2};\phi }+\lambda _{2}\right) \underline{ \upsilon }_{1}(\varkappa).$ Then, we get

Consequently, Lemma 2.9 implies $\Xi (\varkappa)\geq 0,$ that means $\overline{P}_{1}(\varkappa)\leq \underline{P}_{1}(\varkappa), \varkappa \in \mathcal{J}$ and by the same technique, we get $\overline{\upsilon } _{1}(\varkappa)\geq \underline{\upsilon }_{1}(\varkappa), \varkappa \in \mathcal{J}.$ By mathematical induction, we get $\overline{\upsilon } _{j}(\varkappa)\geq \underline{\upsilon }_{j}(\varkappa),$ $\varkappa \in \mathcal{J},$ $j\geq 0.$

$\textsf{Step (3):}$ In view of Eq (3.3), one can show that the sequences $\left\{ \underline{\upsilon }_{j}\right\} _{j = 0}^{\infty }$ and $\left\{ \overline{\upsilon }_{j}\right\} _{j = 0}^{\infty }$ are equicontinuous and uniformly bounded. In view of Arzela-Ascoli Theorem, we have $\lim_{j\rightarrow \infty }\underline{\upsilon }_{j} = \upsilon _{\ast }$ and $\lim_{j\rightarrow \infty }\overline{\upsilon }_{j} = \upsilon ^{\ast }$ uniformly on $J$ and the limit of the solutions $\upsilon _{\ast }$ and $\upsilon ^{\ast }$ satisfy the problem (1.1). Moreover, $\upsilon _{\ast }$, $\upsilon ^{\ast }\in \Phi$.

$\textsf{Step (4):}$ We will prove that $\upsilon _{\ast }$ and $\upsilon ^{\ast }$ are the extremal solutions of the problem (1.1) in $\Phi$. For this end, let $\upsilon \in \Phi$ be a solution of the problem (1.1) such that $\overline{\upsilon }_{j}(\varkappa)\geq \upsilon (\varkappa)\geq \underline{\upsilon }_{j}(\varkappa), \varkappa \in \mathcal{J},$ for some $j\in \mathbb{N}.$ Therefore, by our assumption, we find that

Hence

and

Consequently, $\overline{\upsilon }_{j+1}(\varkappa)\geq \upsilon (\varkappa)\geq \underline{\upsilon }_{j+1}(\varkappa), \varkappa \in \mathcal{J}$. It follows that

Taking the limit of Eq (3.5) as $j\rightarrow \infty$, we get $\upsilon ^{\ast }(\varkappa)\geq \upsilon (\varkappa)\geq \upsilon _{\ast }(\varkappa)$, $\varkappa \in \mathcal{J}$. That is, $\upsilon ^{\ast }$ and $\upsilon _{\ast }$ are the extremal solutions of the problem (1.1) in $\Phi$.

Corollary 3.5. Assume that $f:\mathcal{J}\times \mathbb{R} ^{+}\rightarrow \mathbb{R} ^{+}$ is continuous, and there exist ${\bm{\aleph}} _{1}, {\bm{\aleph}} _{2} > 0$ such that

Then the problem (1.1) has at least one solution $\upsilon (\varkappa)\in \mathcal{C}\left(\mathcal{J}\right).$ Moreover

and

Proof. From Eq (3.6) and definition of control functions, we get

Now, we consider the following problem

In view of Lemma 2.8, the problem (3.10) has a solution

Taking into account Eq (3.9), we obtain

It is obvious that $\overline{\upsilon }(\varkappa)$ is the upper solution of problem (1.1). Also, we consider the following problem

In view of Lemma 2.8, the problem (3.11) has a solution

Taking into account Eq (3.9), we obtain

Thus, $\underline{\upsilon }(\varkappa)$ is the lower solution of problem (1.1).

The application of Theorem 3.4 results that problem (1.1) has at least one solution $\upsilon (\varkappa)\in \mathcal{C}\left(\mathcal{J} \right)$ that satisfies the inequalities (3.7) and (3.8).

4.   An example

Example 4.1. Let us consider the following problem

Here $\mu _{1} = \frac{1}{2}, \mu _{2} = \frac{3}{2}, \beta _{1} = \beta _{2} = \frac{1 }{3}, \gamma _{1} = \frac{2}{3}, \gamma _{2} = \frac{4}{3}, \lambda _{1}\mathcal{ = } \lambda _{2} = 10, m = 1, \delta _{1} = \frac{1}{4}, \sigma _{1} = \frac{2}{3}, \zeta _{1} = \frac{3}{4}, b = 1$, $\phi = e^{\varkappa }, \lambda _{1}\mathcal{ = }\lambda _{2} = 10$ and we set $f\left(\varkappa, \upsilon (\varkappa)\right) = 2+\varkappa ^{2}+\frac{\varkappa ^{3}}{5\left(1+\upsilon (\varkappa)\right) }\upsilon (\varkappa).$ For $\upsilon, w\in\mathbb{R}^{+},$ $\varkappa \in \mathcal{J}$, we have

By the given data, we get $Q_{1}\approx 0.9 < 1$ and hence all conditions in Theorem 3.3 are satisfied with $\kappa = \frac{1}{5} > 0.$ Thus, the problem (4.1) has a unique solution $\upsilon \in C\left(\mathcal{J }\right).$ On the other hand, from Theorem 3.4 and Theorem 3.3, the sequences $\left\{ \underline{ \upsilon }_{n}\right\} _{n = 0}^{\infty }$ and $\left\{ \overline{\upsilon } _{n}\right\} _{n = 0}^{\infty }$ can be obtained as

and

Moreover, for any $\upsilon \in\mathbb{R}^{+}$ and $\varkappa \in \left[0, 1\right]$, we have

It follows that

Thus, by Corollary 3.5, we get ${\bm{\aleph}}_{1} = 2$ and ${\bm{\aleph}}_{2} = \frac{16}{5}.$ Then by Definitions 3.1 and 3.2, the problem (4.1) has a solution which verifies $\underline{ \upsilon }$ $\left(\varkappa \right) \leq \upsilon \left(\varkappa \right) \leq \overline{ \upsilon }\left(\varkappa \right)$ where

and

are respectively the upper and lower solutions of the problem (4.1) and

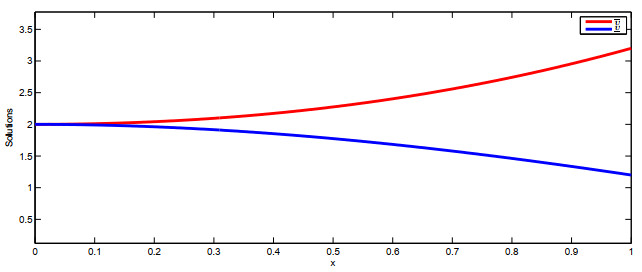
Let us see graphically, we plot in Figure 1 the behavior of the upper solution $\overline{\upsilon}$ and lower solution $\underline{\upsilon}$ of the problem (4.1) with given data above.

5.   Conclusions

In this work, we have proved successfully the monotone iterative method is an effective method to study FLEs in the frame of $\phi$-Hilfer fractional derivative with multi-point boundary conditions. Firstly, the formula of explicit solution of $\phi$-Hilfer type FLE (1.1) in the term of Mittag-Leffler function has been derived. Next, we have investigated the lower and upper explicit monotone iterative sequences and proved that converge to the extremal solution of boundary value problems with multi-point boundary conditions. Finally, a numerical example has been given in order to illustrate the validity of our results.

Furthermore, it will be very important to study the present problem in this article regarding the Mittag-Leffler power low ^[36], the generalized Mittag-Leffler power low with another function ^[37,38], and the fractal-fractional operators ^[39].

Acknowledgments

Researchers would like to thank the Deanship of Scientific Research, Qassim University for funding the publication of this project. The authors are also grateful to the anonymous referees for suggestions that have improved manuscript.

Conflict of interest

The authors declare that they have no competing interests.