In this paper, we consider a predator–prey model given by a reaction–diffusion system. This model encompasses the classic Holling Ⅰ, Holling Ⅱ, Holling Ⅲ, and Holling Ⅳ functional responses. We investigate the stabilization problem of the considered system using multiplicative controls. By linearizing the system and using the maximum principle, we construct a multiplicative control that exponentially stabilizes the system towards its steady-state solutions. The proposed feedback control allows us to reach a large class of steady-state solutions. The global well-posedness is obtained via Banach fixed point. Applications and numerical simulations to Holling responses Ⅰ, Ⅱ, Ⅲ, and Ⅳ are presented.
Citation: Ilyasse Lamrani, Imad El Harraki, M. A. Aziz-Alaoui, Fatima-Zahrae El Alaoui. Feedback stabilization for prey predator general model with diffusion via multiplicative controls[J]. AIMS Mathematics, 2023, 8(1): 2360-2385. doi: 10.3934/math.2023122
| [1] | Teekam Singh, Ramu Dubey, Vishnu Narayan Mishra . Spatial dynamics of predator-prey system with hunting cooperation in predators and type I functional response. AIMS Mathematics, 2020, 5(1): 673-684. doi: 10.3934/math.2020045 |
| [2] | Shanshan Yu, Jiang Liu, Xiaojie Lin . Multiple positive periodic solutions of a Gause-type predator-prey model with Allee effect and functional responses. AIMS Mathematics, 2020, 5(6): 6135-6148. doi: 10.3934/math.2020394 |
| [3] | Jinting Lin, Changjin Xu, Yiya Xu, Yingyan Zhao, Yicheng Pang, Zixin Liu, Jianwei Shen . Bifurcation and controller design in a 3D delayed predator-prey model. AIMS Mathematics, 2024, 9(12): 33891-33929. doi: 10.3934/math.20241617 |
| [4] | Heping Jiang . Complex dynamics induced by harvesting rate and delay in a diffusive Leslie-Gower predator-prey model. AIMS Mathematics, 2023, 8(9): 20718-20730. doi: 10.3934/math.20231056 |
| [5] | Wei Ou, Changjin Xu, Qingyi Cui, Yicheng Pang, Zixin Liu, Jianwei Shen, Muhammad Zafarullah Baber, Muhammad Farman, Shabir Ahmad . Hopf bifurcation exploration and control technique in a predator-prey system incorporating delay. AIMS Mathematics, 2024, 9(1): 1622-1651. doi: 10.3934/math.2024080 |
| [6] | Chuanfu Chai, Yuanfu Shao, Yaping Wang . Analysis of a Holling-type IV stochastic prey-predator system with anti-predatory behavior and Lévy noise. AIMS Mathematics, 2023, 8(9): 21033-21054. doi: 10.3934/math.20231071 |
| [7] | Yingyan Zhao, Changjin Xu, Yiya Xu, Jinting Lin, Yicheng Pang, Zixin Liu, Jianwei Shen . Mathematical exploration on control of bifurcation for a 3D predator-prey model with delay. AIMS Mathematics, 2024, 9(11): 29883-29915. doi: 10.3934/math.20241445 |
| [8] | Xiaoming Su, Jiahui Wang, Adiya Bao . Stability analysis and chaos control in a discrete predator-prey system with Allee effect, fear effect, and refuge. AIMS Mathematics, 2024, 9(5): 13462-13491. doi: 10.3934/math.2024656 |
| [9] | Binfeng Xie, Na Zhang . Influence of fear effect on a Holling type III prey-predator system with the prey refuge. AIMS Mathematics, 2022, 7(2): 1811-1830. doi: 10.3934/math.2022104 |
| [10] | Chuangliang Qin, Jinji Du, Yuanxian Hui . Dynamical behavior of a stochastic predator-prey model with Holling-type III functional response and infectious predator. AIMS Mathematics, 2022, 7(5): 7403-7418. doi: 10.3934/math.2022413 |
In this paper, we consider a predator–prey model given by a reaction–diffusion system. This model encompasses the classic Holling Ⅰ, Holling Ⅱ, Holling Ⅲ, and Holling Ⅳ functional responses. We investigate the stabilization problem of the considered system using multiplicative controls. By linearizing the system and using the maximum principle, we construct a multiplicative control that exponentially stabilizes the system towards its steady-state solutions. The proposed feedback control allows us to reach a large class of steady-state solutions. The global well-posedness is obtained via Banach fixed point. Applications and numerical simulations to Holling responses Ⅰ, Ⅱ, Ⅲ, and Ⅳ are presented.
The dynamics between prey and predator species in natural systems can be represented by a coupled system of nonlinear reaction-diffusion equations. This type of system is usually represented by a system of partial differential equations, rather than a system of ordinary differential equations, which are often used to represent interactions between prey and predator populations without diffusion (see for instance, [13] and [30] and references therein). We are concerned with the following mathematical model, which expresses the conservation of predator and prey densities:
| {∂y1(t,x)∂t=Δy1+y1h(y1)−y1y2k(y1),x∈Ω,t>0∂y2(t,x)∂t=δΔy2−ay2+by1y2k(y1),x∈Ω,t>0∂y1∂v=∂y2∂v=0,(t,x)∈Σ=(0,∞)×∂Ωy1(0,x)=y01(x),y2(0,x)=y02(x),x∈ˉΩ | (1.1) |
where y1 and y2 represent the prey and predator population densities at time t respectively. The function y1h(y1) is the intrinsic growth rate of the prey y1 and signifies its growth rate in the absence of the predator. It can be linear if h(y1)=r1, logistic if h(y1)=r1(1−y1/κ1), Gompertz if h(y1)=h0ln(κ1/y1)(h0,r1,κ1>0) etc. See [1,2] and the references therein. The predator's functional response to prey is y1k(y1), which represents the number of prey individuals consumed per unit area and unit time per predator. It includes as particular cases of various classical functional responses: y1k(y1)=βy1 (Holling type Ⅰ), y1k(y1)=βy1/(1+μy1) (Holling type Ⅱ), y1k(y1)=βy21/(1+μy21) (Holling type Ⅲ; see [3]), y1k(y1)=βy1/(γ+μy1+y21) (Holling type Ⅳ; see [4]) etc. Here β,γ>0,μ≥0.
There is a large amount of literature related to the mathematical study of prey-predator systems of the diffusion type. In [24], Morita and Tachibana showed the existence of an entire solution (i.e., a solution that exists for all (t,x)∈R2) of the predator-prey reaction-diffusion systems with Holling type Ⅰ. The proof is carried out by applying the comparison principle and an appropriate pair of a subsolution and a supersolution. For Holling Ⅱ functional response, Garvie and Trenchea proved the existence of a solution by using semigroup theory and application of the invariant region method of Smoller (see [15]). In [1], Apreutesei and Dimitriu studied the well-posedness of a predator-prey reaction-diffusion system with Holling type Ⅲ. They show the existence of the solutions provided that the initial data are positive and satisfy a specific regularity. For more results on the well-posedness of these systems, we refer, for instance, to [8,9,10] and the reference therein. Recently, Mi et al. [23] considered a nonlocal predator–prey model with double mutation; they defined pair of upper and lower solutions, and they designed a new comparison principle that ensures the existence of the solutions.
In our case, the situation is quite complicated due to the generalized nonlinearity considered, which encompasses all Holling functional responses nonlinearities. Consequently, we use the Banach fixed point and the stabilization of an associated system to obtain the global well-posedness. The existence and stability results concerning the steady states of these systems have been extensively studied see, for example, [2,5,7,21] and the references therein. The results show that the system exhibits very unusual behavior for some parameter values, while some steady states are stable under system parameter constraints. It would be interesting to investigate a method that allows driving the systems to these equilibrium states without adding additional constraints on the system parameters that might contradict the measures taken during the modelling. To this end we use multiplicative controls to stabilize the system, this choice is determined by the real application. In fact, for the prey predator model, these controls can be interpreted as harvesting efforts. A huge amount of literature has been devoted to stabilizing uncoupled linear systems via multiplicative controls. For example, we mention the works of [4,17,26] and the references therein. However, the choice of such control in the nonlinear cases generates new difficulties. Indeed, the first difficulty is that the stabilization of nonlinear parabolic coupled systems by using multiplicative controls remains an open problem. Another difficulty of the problem lies in the fact that these controls are nonlinear, which doubles the nonlinearity of the system. Note also that the controllability of bilinear systems is an open problem see [3]. For hyperbolic coupled systems we refer to [19], where the authors characterize the stabilization of a class of coupled hyperbolic systems by using multiplicative controls. They showed the equivalence between stabilization and the observability of the uncontrolled system. In this work, we hope to achieve the stabilization result. More precisely, let
| f(y1,y2)=y1h(y1)−y1y2k(y1)andg(y1,y2)=−ay2+by1y2k(y1). | (1.2) |
We obtain from (1.1) the following system
| {∂y1(t,x)∂t=Δy1+f(y1,y2),x∈Ω,t>0∂y2(t,x)∂t=δΔy2+g(y1,y2),x∈Ω,t>0∂y1∂v=∂y2∂v=0,(t,x)∈Σ=(0,∞)×∂Ωy1(0,x)=y01(x),y2(0,x)=y02(x),x∈ˉΩ | (1.3) |
We say that (ye1,ye2) is an equilibrium state of (1.3) if and only if:
1- (ye1,ye2)∈H2(Ω)∩H10(Ω).
2- (ye1,ye2) solves the following elliptic system
| {Δye1+f(ye1,ye2)=0,x∈ΩδΔye2+g(ye1,ye2)=0,x∈Ω∂ye1∂v=∂ye2∂v=0,x∈∂Ω |
Translate (ye1,ye2) into zero via the following change of variable z1=y1−ye1 et z2=y2−ye2. Obviously (z1,z2) solves the following system
| {∂z1(t,x)∂t=Δz1+f(z1+ye1,z2+ye2)−f(ye1,ye2),x∈Ω,t>0∂z2(t,x)∂t=δΔz2+g(z1+ye1,z2+ye2)−g(ye1,ye2),x∈Ω,t>0∂z1∂v=∂z2∂v=0,(t,x)∈Σ=(0,∞)×∂Ωz1(0,x)=z01(x):=y01(x)−ye1,z2(0,x)=z02(x):=y02(x)−ye2,x∈ˉΩ | (1.4) |
then stabilizing (1.3) towards (ye1,ye1) is reduced to the stability of the null solution to system (1.4). By injecting a multiplicative control into the prey and predator equations, we obtain from (1.4) the following system
| {∂z1(t,x)∂t=Δz1+f(z1+ye1,z2+ye2)−f(ye1,ye2)+v(t)Bz1,x∈Ω,t>0∂z2(t,x)∂t=δΔz2+g(z1+ye1,z2+ye2)−g(ye1,ye2)+v(t)Bz2,x∈Ω,t>0∂z1∂v=∂z2∂v=0,(t,x)∈Σ=(0,∞)×∂Ωz1(0,x)=z01(x):=y01(x)−ye1,z2(0,x)=z02(x):=y02(x)−ye2,x∈ˉΩ | (1.5) |
where v(t) is a feedback control to be determined. The control operator B is assumed to be bounded from L2(Ω) to L2(Ω). The terms v(t)Bz1 and v(t)Bz2(t) can be regarded as the effort applied to harvest the prey and predator, respectively. System (1.5) represents the evolution of predator-prey densities under the action of harvesting. In the following, we construct the the control feedback v(t), ensuring the exponential stabilization of (1.5).
The rest of the paper is organized as follows. In section 2, we present the assumptions and main results. We start with the stabilization of the linearized system and extend the result to the nonlinear system, where we show the well-posedness and exponential stabilization using Banach fixed points. In section 3, we illustrate the obtained results for different Holling responses.
For a bounded open set Ω⊂RN, we denote by H the Lebesgue space L2(Ω) endowed with the inner product ⟨.,.⟩ and its corresponding norm ‖.‖, H the Cartesian product L2(Ω)×L2(Ω) with the norm ‖.‖H and H=H1(Ω)×H1(Ω) with the norm ‖.‖H.
The following assumptions will be in effect everywhere in the following:
(H1) (ye1,ye2)∈C(¯Ω)
(H2) f,g∈C1(R×R) satisfy the growth condition
| |f(y,z)|+|g(y,z)|⩽ | (2.1) |
where m_0 is a positive integer and r_i, 1 \leqslant i \leqslant m_0 , are such that
| \begin{equation} 1 \leq r_1 < r_2... < r_{m_0}\leq m_0\nonumber \end{equation} |
(H_3) y_1(t, x)\geq 0 and y_2(t, x)\geq 0 provided that y^{0}_{1}(x)\geq 0 and y^{0}_{2}(x)\geq 0 .
Assumptions (H_1) and (H_2) for Holling types Ⅰ, Ⅱ, Ⅲ and Ⅳ, imply, in particular that: f_y(y^{e}_{1}, y^{e}_{2}), f_z(y^{e}_{1}, y^{e}_{2}), g_y(y^{e}_{1}, y^{e}_{2}), g_z(y^{e}_{1}, y^{e}_{2})\in L^{\infty}(\Omega) . Assumption (H_3) is proved for Holling type Ⅰ, Ⅱ, Ⅲ and Ⅳ; see, for instance, [1,8].
Consider System (1.5),
| \begin{equation} \left\{\begin{array}{l} \frac{\partial z_1(t, x)}{\partial t} = \Delta z_1+f\left(z_1+y^{e}_{1}, z_2+y^{e}_{2}\right)-f(y^{e}_{1}, y^{e}_{2})+v(t)Bz_1, \quad x \in \Omega, t > 0 \\ \frac{\partial z_2(t, x)}{\partial t} = \delta \Delta z_2+g\left(z_1+y^{e}_{1}, z_2+y^{e}_{2}\right)-g(y^{e}_{1}, y^{e}_{2})+v(t)Bz_2, \quad x \in \Omega, t > 0 \\ \frac{\partial z_{1}}{\partial v} = \frac{\partial z_{2}}{\partial v} = 0, \quad(t, x) \in \Sigma = (0, \infty) \times \partial \Omega \\ z_1(0, x) = z_{1}^{0}(x): = y_{1}^{0}(x)-y^{e}_{1}, \quad z_2(0, x) = z_{2}^{0}(x): = y_{2}^{0}(x)-y^{e}_{2}, \quad x \in \bar{\Omega} \end{array}\right. \end{equation} | (2.2) |
The linearized system associated with (2.2) is given by
| \begin{equation} \left\{\begin{array}{l} \frac{\partial z_1(t, x)}{\partial t} = \Delta z_1+f_y\left(y^{e}_{1}, y^{e}_{2}\right)z_1+f_z\left(y^{e}_{1}, y^{e}_{2}\right)z_2+v(t)Bz_1, \quad x \in \Omega, t > 0 \\ \frac{\partial z_2(t, x)}{\partial t} = \delta \Delta z_2+g_y\left(y^{e}_{1}, y^{e}_{2}\right)z_1+g_z\left(y^{e}_{1}, y^{e}_{2}\right)z_2+v(t)Bz_2, \quad x \in \Omega, t > 0 \\ \frac{\partial y_{1}}{\partial v} = \frac{\partial y_{2}}{\partial v} = 0, \quad(t, x) \in \Sigma = (0, \infty) \times \partial \Omega \\ z_1(0, x) = z_{1}^{0}(x): = y_{1}^{0}(x)-y^{e}_{1}, \quad z_2(0, x) = z_{2}^{0}(x): = y_{2}^{0}(x)-y^{e}_{2}, \quad x \in \bar{\Omega} \end{array}\right. \end{equation} | (2.3) |
In this section, we establish the exponential stabilization of the linearized system (2.3).
Spectral proprieties
Let a = \sup_{x\in \Omega}|f_y(y_1^{e}(x), y_2^{e}(x))| , b = \sup_{x\in \Omega}|f_z(y_1^{e}(x), y_2^{e}(x))| , c = \sup_{x\in \Omega}|g_y(y_1^{e}(x), y_2^{e}(x))| and d = \sup_{x\in \Omega}|g_z(y_1^{e}(x), y_2^{e}(x))| .
Let A: = \Delta+aI where D(A) = D(\Delta) = H^{2}(\Omega)\cap H^{1}_{0}(\Omega) . It is clear that A is a self-adjoint operator with a compact resolvent; hence, the spectrum of A reduces to its point spectrum. More precisely, the eignvalues (\lambda_{i})_{i\in \mathbb{N^*}} of A are reals. We suppose that there exists a finite positive integer N such that \{\lambda_{i}\geq 0, \quad\forall i\in \{1, ..., N\}\} which is guaranteed thanks to the assumption f_y(y_1^{e}, y_2^{e})\in L^{\infty}(\Omega) .
Let us consider the following auxiliary linear system:
| \begin{equation} \left\{\begin{array}{l} \frac{\partial Z_1(t, x)}{\partial t} = A Z_1 +bZ_2+v(t) BZ_1, \quad x \in \Omega, t > 0 \\ \frac{\partial Z_2(t, x)}{\partial t} = \delta A Z_2+cZ_1+c_0Z_2+v(t)BZ_2, \quad x \in \Omega, t > 0 \\ \frac{\partial Z_{1}}{\partial v} = \frac{\partial Z_{2}}{\partial v} = 0, \quad(t, x) \in \Sigma = (0, \infty) \times \partial \Omega \\ Z_1(0, x) = Z_{1}^{0}: = \max\limits_{x\in \Omega}z^{0}_{1}(x), \quad Z_2(0, x) = Z_{2}^{0}: = \max\limits_{x\in \Omega}z^{0}_{2}(x), \quad x \in \bar{\Omega} \end{array}\right. \end{equation} | (2.4) |
where c_0 = \sup_{x\in \Omega}\left|d-\delta a\right| . We mention that a simple application of the maximum principle (see [29]) gives that 0\leq z_1(t)\leq Z_1(t) and 0\leq z_2(t)\leq Z_2(t) for
| 0\leq z^{0}_{1}(x)\leq Z^{0}_{1}: = \max\limits_{x\in \Omega}z^{0}_{1}(x)\quad\text{and}\quad 0\leq z^{0}_{2}(x)\leq Z^{0}_{2}: = \max\limits_{x\in \Omega}z^{0}_{2}(x) |
Theorem 2.1. Let B be a bounded operator on H ; suppose that assumptions (H_1) , (H_2) and (H_3) hold; then, the feedback
| \begin{equation} v(t) = \begin{cases} (-D-\eta)\frac{\left(\|Z_1(t)\|^2+\|Z_2(t)\|^2\right)}{\langle BZ_1(t), Z_1(t)\rangle+\langle BZ_2(t), Z_2(t)\rangle }\qquad{{if}}\: (Z_1, Z_2)\neq (0, 0)\\ 0\qquad\qquad {{else}} \end{cases} \end{equation} | (2.5) |
where D = (2\lambda+b+c+2\delta\lambda+2c_0) , \lambda = \max_{1\leq i \leq N}(\lambda_{i}) and \eta > 0 , ensures the exponential stabilization of system (2.3).
Remark 2.1. In the case where B = I_d , the feedback control v(t) will be a constant, that is, v(t) = -D-\eta
Proof. On the one hand, from the first equation of (2.4), we have
| \begin{align} \frac{1}{2}\dfrac{\partial}{\partial t}\|Z_1(t)\|^{2}& = \langle AZ_1(t), Z_1(t)\rangle+b \langle Z_2(t), Z_1(t)\rangle+v(t)\langle BZ_1(t), Z_1(t)\rangle\\ &\leq \lambda \|Z_1(t)\|^2+b \langle Z_2(t), Z_1(t)\rangle+v(t)\langle BZ_1(t), Z_1(t)\rangle\qquad \lambda = \max\limits_{1\leq i \leq N}(\lambda_{i})\\ &\leq \lambda \|Z_1(t)\|^2+b \| Z_2(t)\|\|Z_1(t)\|+v(t)\langle BZ_1(t), Z_1(t)\rangle\\ &\leq\lambda \|Z_1(t)\|^2+\frac{b}{2}\|Z_1(t)\|^2+\frac{b}{2}\|Z_2(t)\|^2+v(t)\langle BZ_1(t), Z_1(t)\rangle \end{align} |
then
| \begin{equation} \dfrac{\partial}{\partial t}\|Z_1(t)\|^{2}\leq \left(2\lambda+b\right)\|Z_1(t)\|^2+b\|Z_2(t)\|^2+2 v(t)\langle BZ_1(t), Z_1(t)\rangle. \end{equation} | (2.6) |
On the other hand, from the second equation of (2.4), we have
| \begin{align*} \frac{1}{2}\dfrac{\partial}{\partial t}\|Z_2(t)\|^{2}&\leq \delta\lambda\|Z_2(t)\|^{2}+c\langle Z_1(t), Z_2(t)\rangle+c_0\|Z_2(t)\|^{2}+v(t)\langle B Z_2(t), Z_2(t)\rangle\\ &\leq\left(\delta\lambda+c_0+\frac{c}{2}\right)\|Z_2(t)\|^{2}+\frac{c}{2}\|Z_1(t)\|^{2}+v(t)\langle BZ_2(t), Z_2(t)\rangle \end{align*} |
then
| \begin{equation} \dfrac{\partial}{\partial t}\|Z_2(t)\|^{2}\leq\left(2\delta\lambda+2c_0+c\right)\|Z_2(t)\|^{2}+c\|Z_1(t)\|^{2}+2v(t)\langle BZ_2(t), Z_2(t)\rangle. \end{equation} | (2.7) |
Combining (2.6) and (2.7), we obtain
| \begin{equation} \dfrac{\partial}{\partial t}\left\|\left(Z_1(t), Z_2(t)\right)\right\|_{\mathcal{H}}^{2}\leq D \left\|\left(Z_1(t), Z_2(t)\right)\right\|_{\mathcal{H}}^{2}+2v(t)\Big(\langle BZ_1(t), Z_1(t)\rangle+\langle BZ_2(t), Z_2(t)\rangle \Big)\nonumber \end{equation} |
where D = (2\lambda+b+c+2\delta\lambda+2c_0) .
Using the expression of v(t) , we obtain
| \begin{equation} \dfrac{\partial}{\partial t}\left\|\left(Z_1(t), Z_2(t)\right)\right\|_{\mathcal{H}}^{2}\leq-2\eta\left\|\left(Z_1(t), Z_2(t)\right)\right\|_{\mathcal{H}}^{2}. \end{equation} | (2.8) |
Integrating over [k, k+1] for k\in\mathbb{N^*} , we obtain
| \begin{equation} \left\|(Z_1(k+1), Z_2(k+1))\right\|_{\mathcal{H}}^{2}-\left\|(Z_1(k), Z_2(k))\right\|_{\mathcal{H}}^{2}\leq -2\eta \left\|(Z_1(k+1), Z_2(k+1))\right\|_{\mathcal{H}}^{2}, \end{equation} | (2.9) |
then
| \begin{equation} \left\|(Z_1(k+1), Z_2(k+1))\right\|_{\mathcal{H}}^{2}\leq \frac{1}{2\eta+1}\left\|(Z_1(k), Z_2(k))\right\|_{\mathcal{H}}^{2}.\nonumber \end{equation} |
By the recurrence argument, one can obtain
| \begin{equation} \left\|(Z_1(k), Z_2(k))\right\|_{\mathcal{H}}\leq \frac{1}{(2\eta+1)^{\frac{k}{2}}}\left\|(Z^0_1, Z^0_2)\right\|_{\mathcal{H}}. \end{equation} | (2.10) |
Since \left\|(Z_1(k+1), Z_2(k+1))\right\| decreases then for t\geq k , we have
| \begin{equation} \left\|(Z_1(t), Z_2(t))\right\|_{\mathcal{H}}\leq {\rm{e}}^{-mt}\left\|(Z^0_1, Z^0_2)\right\|_{\mathcal{H}}, \end{equation} | (2.11) |
where m = \ln(1+2\eta) > 0 . Recalling that 0\leq z_1(t)\leq Z_1(t) and 0\leq z_2(t)\leq Z_2(t) for
| 0\leq z^{0}_{1}(x)\leq Z^{0}_{1}: = \max\limits_{x\in \Omega}z^{0}_{1}(x)\quad\text{and}\quad 0\leq z^{0}_{2}(x)\leq Z^{0}_{2}: = \max\limits_{x\in \Omega}z^{0}_{2}(x) |
hence,
| \begin{equation} \left\|(z_1(t), z_2(t))\right\|_{\mathcal{H}}\leq {\rm{e}}^{-mt}\left\|(Z^0_1, Z^0_2)\right\|_{\mathcal{H}}, \end{equation} | (2.12) |
and therefore, there exists a positive constant M_3 such that
| \begin{equation} \left\|(z_1(t), z_2(t))\right\|_{\mathcal{H}}\leq M_3 \;{\rm{e}}^{-mt}\left\|(z^0_1, z^0_2)\right\|_{\mathcal{H}}. \end{equation} | (2.13) |
This completes the proof of Theorem 2.1.
In this section, we shall prove that if \|(z^{0}_{1}, z^{0}_{2})\|_{\mathcal{H}}\leq\epsilon for \epsilon small enough, then the local solution of (2.2) is global by using a Banach fixed point. Moreover, we show that this solution is exponentially stabilizable.
Theorem 2.2. Well-posedness
Let B be a bounded operator on H , suppose that assumptions (H_1) , (H_2) and (H_3) ; then, for (z^{0}_{1}, z^{0}_{2})\in \mathcal{H} such that \|(z^{0}_{1}, z^{0}_{2})\|_{\mathcal{H}}\leq \epsilon , where \epsilon is sufficiently small, system (2.2) admits a global solution (z_1, z_2)\in L^{r}(0, \infty; \mathbb{H}) for some r\geq 1 .
Proof. System (2.2) can be written as
| \begin{equation} \begin{cases} \dfrac{\partial}{\partial t}\left(z_{1}(t), z_{2}(t)\right) = \mathcal{A}(z_1, z_2)+\mathcal{A}_{0}(z_1, z_2)+\Phi(z_1, z_2) +v(t)\mathcal{B}(z_1, z_2), \quad t > 0, \\ \frac{\partial z_{1}}{\partial v} = \frac{\partial z_{2}}{\partial v} = 0, \quad(t, x) \in \Sigma = (0, \infty) \times \partial \Omega \\ (z_1(0), z_2(0)) = \left(z_1^{0}, z_2^{0}\right) \equiv\left(y^{0}_1-y^e_{1}, y^{0}_2-y^{e}_2\right), \end{cases} \end{equation} | (2.14) |
where
| \mathcal{A} = \left(\begin{array}{cc} \Delta & 0 \\ 0 & \alpha \Delta \end{array}\right), \quad \mathcal{A}_{0} = \left(\begin{array}{cc} f_y(y^{e}_1(x), y^{e}_2(x)) I_{d} & f_z(y^{e}_1(x), y^{e}_2(x)) I_{d} \\ g_y(y^{e}_1(x), y^{e}_2(x)) I_{d} & g_z(y^{e}_1(x), y^{e}_2(x))I_{d} \end{array}\right), \quad \mathcal{B} = \left(\begin{array}{c} B \\ B \end{array}\right) |
and
| \begin{equation} \begin{aligned} \Phi(z_1, z_2) \equiv &\left(\Phi^{1}(z_1, z_2), \Phi^{2}(z_1, z_2)\right) \\ = &\left(f\left(z_1+y^{e}_{1}, z_2+y^{e}_{2}\right)-f\left(y^{e}_{1}, y^{e}_{2}\right), g\left(z_1+y^{e}_{1}, z_2+y^{e}_{2}\right)-g\left(y^{e}_{1}, y^{e}_{2}\right)\right) \nonumber\\ & \quad -\mathcal{A}_{0}(z_1, z_2). \end{aligned} \end{equation} |
According to assumptions (H_1) and (H_2) , we deduce that
| \begin{align*} \|\Phi(z_1, z_2)\|_{\mathcal{H}}&\leq C \sum\limits_{i = 1}^{m}\big(\|z_1\|^{r_i}+\|z_2\|^{r_i}\big), \\ &\leq 2C\sum\limits_{i = 1}^{m}\|(z_1, z_2)\|^{r_i}_{\mathcal{H}}, \end{align*} |
for some positive integer m , where r_i are such that 1\leq r_1 < \cdots < r_{m}\leq m .
Let us consider
| \begin{equation} \Big\{X\in L^{r}(0, \infty; \mathcal{H});\quad \|X\|_{L^{r}(0, \infty;\mathbb{H})}\leq \rho\Big\} = S(0, \rho), \nonumber \end{equation} |
where 1\leq r\leq m . We note by (\Gamma(t, s))_{0 \leq s \leq t} the evolution system generated by (z_1, z_2):\longrightarrow \mathcal{A}(z_1, z_2)+\mathcal{A}_0(z_1, z_2)+v(t)\mathcal{B}(z_1, z_2) (see Definition 5.3 p 126 [25]). Let the map
| \begin{equation} (\Lambda (z_1, z_2))(t)\equiv \Gamma(t, 0)(z^0_{1}, z_{2}^0)+\int_{0}^{t}\Gamma(t, s)\Phi(z_1(s), z_2(s))ds. \end{equation} | (2.15) |
From (2.13), we conclude that \Gamma(t, .)(z_1, z_2)\in L^{r}(0, \infty; \mathcal{H}) , that is
| \begin{equation} \int_{0}^{\infty}\|\Gamma(t, s)(z_1, z_2)\|_{\mathcal{H}}^{r}ds < \infty, \qquad \forall (z_1, z_2)\in \mathcal{H}, \end{equation} | (2.16) |
(see p 299 [12]). Moreover, using the superposition property of the evolution system (\Gamma(t, s))_{0 \leq s \leq t} , we deduce from (2.13) and (2.16) that there exists a positive constant M_4 such that
| \begin{equation} \int_{0}^{\infty}\|\Gamma(t, s) (z_1, z_2)\|_\mathbb{H}^{r} d s \leq M_{4}\|(z_1, z_2)\|_\mathcal{H}^{r}. \end{equation} | (2.17) |
● We start by showing the invariance of \Lambda . We define
| \begin{equation} (\mathcal{N}(z_1, z_2) )(t): = \int_0^t \Gamma(t, s)\Phi(z_1(s), z_2(s)) ds \end{equation} | (2.18) |
By duality arguments as in [31] page 197, we obtain
| \begin{equation} \|(\mathcal{N}(z_1, z_2)(t)\|_{L^r(0, \infty ; \mathbb{H})} \leq M_4 \sum\limits_{r = 1}^{m}\rho^r, \end{equation} | (2.19) |
for all (z_1, z_2)\in S(0, \rho) .
Then
| \begin{equation} \|(\mathcal{N}(z_1, z_2)(t)\|_{L^r(0, \infty ; \mathbb{H})} \leq M_4 \sum\limits_{r = 1}^{m}\rho^r = M_4\frac{1-\rho^m}{1-\rho}. \end{equation} | (2.20) |
Substituting in (2.15), we obtain
| \begin{align} \|(\Lambda (z_1, z_2))\|^{r}_{L^{r}(0, \infty; \mathbb{H})}&\leq 2^{r-1}\|\Gamma(t, 0)(z^{0}_{1}, z^{0}_{2})\|^{r}_{L^{r}(0, \infty; \mathbb{H})}+2^{r-1}\big\|\int_{0}^{t}\Gamma(t, s)\Phi(z_1(s), z_2(s))ds\big\|^{r}_{L^{r}(0, \infty; \mathbb{H})}\\ &\leq 2^{r-1} M^{r}_3\|(z^{0}_{1}, z^{0}_{2})\|^{r}_{\mathcal{H}}+2^{r-1}\left(M_4\frac{1-\rho^{m}}{1-\rho}\right)^{r}, \qquad (\text{using} \quad (2.20)) \end{align} |
and hence
| \begin{equation} \|\Lambda(z_1, z_2)\|^{r}_{L^{r}(0, \infty;\mathbb{H})}\leq 2^{r-1} M^{r}_3\|(z^{0}_{1}, z^{0}_{2})\|^{r}_{\mathcal{H}}+2^{r-1}\left(M_4\frac{1-\rho^{m}}{1-\rho}\right)^{r}.\nonumber \end{equation} |
Let us consider \rho > 0 , which is chosen to satisfy the following constraints
| \begin{equation} 2^{r-1} M^{r}_3\|(z^{0}_{1}, z^{0}_{2})\|^{r}_{\mathcal{H}}\leq \frac{1}{2}\rho^{r}, \quad 2^{r-1}\left(M_4\frac{1-\rho^{m+1}}{1-\rho}\right)^{r}\leq \frac{1}{2}\rho^{r}, \quad \rho\neq 1 \end{equation} | (2.21) |
and hence
| \|\Lambda(z_1, z_2)\|^{r}_{L^{r}(0, \infty;\mathbb{H})}\leq \rho^{r}. |
Therefore
| \Lambda(z_1, z_2)\in S(0, \rho). |
● Now we show that \Lambda is a contraction map on S(0, \rho) .
Let us consider (y_1, z_1), (y_2, z_2)\in S(0, r) , then there exists a constant C such that:
| \begin{align} \big\|\Phi(y_1, z_1)-\Phi(y_2, z_2)\big\|_{\mathcal{H}}&\leq C\Big(\sum\limits_{i = 1}^{m}\|y_1-y_2\|^{r_i}+\|z_1-z_2\|^{r_i}\Big), \\ &\leq C\|y_1-y_2\|\sum\limits_{i = 1}^{m}\|y_1-y_2\|^{r_i-1}+C\|z_1-z_2\|\sum\limits_{i = 1}^{m}\|z_1-z_2\|^{r_i-1}, \\ &\leq C \big\|(y_1-y_2), (z_1-z_2)\big\|_{\mathcal{H}}\sum\limits_{i = 1}^{m}\|y_1-y_2\|^{r_i-1}\\ & \quad + C \big\|(y_1-y_2), (z_1-z_2)\big\|_{\mathcal{H}}\sum\limits_{i = 1}^{m}\|z_1-z_2\|^{r_i-1}, \\ &\leq C\big\|(y_1, z_1)-(y_2, z_2)\big\|_{\mathcal{H}}\Big(\sum\limits_{i = 1}^{m}\|y_1-y_2\|^{r_i-1}+\sum\limits_{i = 0}^{m}\|z_1-z_2\|^{r_i-1}\Big). \end{align} | (2.22) |
| \begin{align} &\leq 2C\big\|(y_1, z_1)-(y_2, z_2)\big\|_{\mathcal{H}}\Big(\sum\limits_{i = 1}^{m}\left(\|(y_1, z_1)\|+\|(y_1, z_1)\|\right)^{r_i-1}\Big), \end{align} | (2.23) |
where the following argument is used
| \begin{equation} \|y_1-y_2\|\leq \|y_1\|+\|y_2\|\leq \|(y_1, z_1)\|_{\mathcal{H}}+\|(y_2, z_2)\|_{\mathcal{H}}, \nonumber \end{equation} |
| \begin{equation} \|z_1-z_2\|\leq \|z_1\|+\|z_2\|\leq \|(y_1, z_1)\|_{\mathcal{H}}+\|(y_2, z_2)\|_{\mathcal{H}}, \nonumber \end{equation} |
In the other hand, similar to (2.19), one can show as well that
| \begin{align} \big\|\Lambda(y_1, z_1)-\Lambda(y_2, z_2)\big\|_{L^{r}(0, \infty; \mathbb{H})}&\leq 2 C \big\|(y_1, z_1)-(y_2, z_2)\|_{L^{r}(0, \infty;\mathbb{H})}\sum\limits_{r = 1}^{m}(2\rho)^{r-1}, \\ &\leq 2C \frac{1-(2\rho)^{m}}{1-2\rho}\big\|(y_1, z_1)-(y_2, z_2)\|_{L^{r}(0, \infty;\mathbb{H})}. \label{cnp49} \end{align} |
Then \Lambda is a contraction on S(0, \rho) for \rho chosen such that
| \begin{equation} 2C \frac{1-(2\rho)^{m}}{1-2\rho} < 1, \qquad\rho\neq\frac{1}{2} \end{equation} | (2.24) |
then according to the Banach fixed point, system (2.2) has for (z^{0}_{1}, z^{0}_{2}) sufficiently small, a unique solution
| \begin{equation} (z_1, z_2)\in L^{r}(0, \infty; \mathbb{H}).\nonumber \end{equation} |
Now we characterize the exponential stabilization of (2.2). Theorem 2.3 below is the main result of this paper.
Theorem 2.3. Let B be a bounded operator on H , suppose that assumptions (H_1) , (H_2) and (H_3) hold, then the following feedback
| \begin{equation} v(t) = \begin{cases} \frac{(-D-\eta)\left(\|Z_1(t)\|^2+\|Z_2(t)\|^2\right)}{\langle BZ_1(t), Z_1(t)\rangle+\langle BZ_2(t), Z_2(t)\rangle }\qquad{{if}}\: (Z_1, Z_2)\neq (0, 0)\\ 0\qquad\qquad {{else}} \end{cases} \end{equation} | (2.25) |
where D = 2\lambda+b+c+2\delta\lambda+2c_0 , \lambda = \max_{1\leq i \leq N}(\lambda_{i}) , exponentially stabilizes (2.2).
Proof. We start by showing that the solution (z_1, z_2) of (2.2) obeys the following estimate:
| \begin{equation} \|(z_1, z_2)\|^{r}_{L^{r}(0, \infty; \mathbb{H} )}\leq\frac{2^{r-1}M^{r}_{3}}{1-C_{\rho, 1}}\|(z^{0}_{1}, z^{0}_{2})\|^{r}_{\mathcal{H}}: = C_\rho\|(z^{0}_{1}, z^{0}_{2})\|^{r}_{\mathcal{H}}, \end{equation} | (2.26) |
where
| C_{\rho, 1} = 2^{r}C_3\Big(\frac{1-\rho^{m}}{1-\rho}\Big)^{r}. |
In fact, according to the variation of constants formula, we have
| \begin{equation} (\Lambda (z_1, z_2))(t)\equiv \Gamma(t, 0)(z^{0}_{1}, z^{0}_{2})+\int_{0}^{t}\Gamma(t, s)\Phi(z_1(s), z_2(s))ds, \end{equation} | (2.27) |
then
| \begin{align} \big\|\Lambda(z_1, z_2)\big\|^{r}_{L^{r}(0, \infty;\mathbb{H})}& = \int_{0}^{\infty}\|\Lambda(z_1(t), z_2(t))\|^{r}_{\mathbb{H}}dt\\ &\leq 2^{r-1} M^{r}_3 \|(z^{0}_{1}, z^{0}_{2})\|^{r}_{\mathcal{H}}+2^{r-1}\int_{0}^{\infty}\big\|\int_{0}^{t}\Gamma(t, s)\Phi(z_1(s), z_2(s))ds\big\|_{\mathbb{H}}^{r}dt. \end{align} | (2.28) |
Using (2.19) in (2.28), we deduce that there exists a positive constant C_3: = CM_4 such that
| \begin{align} &\|(z_1, z_2)\|^{r}_{L^{r}(0, \infty; \mathbb{H} )}: = \big\|\Lambda(z_1, z_2)\big\|^{r}_{L^{r}(0, \infty;\mathbb{H})}, \\ &\leq 2^{r-1}M^{r}_{3}\|(z^{0}_{1}, z^{0}_{2})\|^{r}_{\mathcal{H}}+2^{r}C_3\Big(\sum\limits_{r = 0}^{m}\|(z_1, z_2)\|^{r}_{L^{r}(0, \infty; \mathbb{H})}\Big)^{r}, \\ &\leq 2^{r-1}M^{r}_{3}\|(z^{0}_{1}, z^{0}_{2})\|^{r}_{\mathcal{H}}\\ &\quad+2^{r}C_3\|(z_1, z_2)\|^{r}_{L^{r}(0, \infty;\mathbb{H})}\Big(\sum\limits_{r = 1}^{m}\|(z_1, z_2)\|^{r-1}_{L^{r}(0, \infty; \mathbb{H})}\Big)^{r}, \\ &\leq 2^{r-1}M^{r}_{3}\|(z^{0}_{1}, z^{0}_{2})\|^{r}_{\mathcal{H}}\\ &\quad+2^{r}C_3\|(z_1, z_2)\|^{r}_{L^{r}(0, \infty;\mathbb{H})}\Big(\sum\limits_{r = 1}^{m}\rho^{r-1}\Big)^{r}, \\ &\leq 2^{r-1}M^{r}_{3}\|(z^{0}_{1}, z^{0}_{2})\|^{r}_{\mathcal{H}}\\ &\quad+2^{r}C_3\Big(\frac{1-\rho^{m}}{1-\rho}\Big)^{m+1}\|(z_1, z_2)\|^{r}_{L^{r}(0, \infty;\mathbb{H})}, \end{align} |
then
| \begin{equation} \|(z_1, z_2)\|^{r}_{L^{r}(0, \infty; \mathbb{H} )}\leq\frac{2^{r-1}M^{r}_{3}}{1-C_{\rho, 1}}\|(z^{0}_{1}, z^{0}_{2})\|^{r}_{\mathcal{H}}: = C_\rho\|(z^{0}_{1}, z^{0}_{2})\|^{r}_{\mathcal{H}}, \end{equation} | (2.29) |
where
| C_{\rho, 1} = 2^{r}C_3\Big(\frac{1-\rho^{m}}{1-\rho}\Big)^{r}. |
Now, we prove the following lemma to achieve the proof of Theorem 2.3.
Lemma 2.1. There exist a time T > 0 and a constant 0 < \gamma < 1 such that
| \begin{equation} \|(z_1(T), z_2(T))\|_{\mathcal{H}}\leq \gamma\|(z^{0}_{1}, z^{0}_{2})\|_{\mathcal{H}}. \end{equation} | (2.30) |
Proof. According to the variation of constants formula (2.15), there exists a positive constant K: = \sup_{s\in[0, T]}\|\Gamma(t, s)\|_{\mathcal{L}(\mathcal{H})} such that we have
| \begin{align*} \|(z_1(T), z_2(T))\|_{\mathcal{H}}&\leq M_3\;{\rm{e}}^{-\lambda T}\|(z^{0}_{1}, z^{0}_{2})\|_{\mathcal{H}}+K\int_{0}^{T}\|\Phi(z_1(s), z_2(s))\|_{\mathcal{H}}ds, \\ &\leq M_3\;{\rm{e}}^{-\lambda T}\|(z^{0}_{1}, z^{0}_{2})\|_{\mathcal{H}}+K\int_{0}^{\infty}\|\Phi(z_1(s), z_2(s))\|_{\mathcal{H}}ds, \\ &\leq M_3\;{\rm{e}}^{-\lambda T}\|(z^{0}_{1}, z^{0}_{2})\|_{\mathcal{H}}+2KC\sum\limits_{r = 1}^{m}\|(z_1(s), z_2(s))\|^{r}_{L^{r}(0, \infty;\mathbb{H})}, \\ &\leq M_3\;{\rm{e}}^{-\lambda T}\|(z^{0}_{1}, z^{0}_{2})\|_{\mathcal{H}}+M_5\sum\limits_{r = 1}^{m}\|(z^{0}_{1}, z^{0}_{2})\|^{r}_{\mathcal{H}}, \qquad\qquad \text{(using (2.29))}\\ &\leq M_3\;{\rm{e}}^{-\lambda T}\|(z^{0}_{1}, z^{0}_{2})\|_{\mathcal{H}}+M_5\|(z^{0}_{1}, z^{0}_{2})\|_{\mathcal{H}}\sum\limits_{r = 1}^{m}\|(z^{0}_{1}, z^{0}_{2})\|^{r-1}_{\mathcal{H}}, \\ &\leq M_3\;{\rm{e}}^{-\lambda T}\|(z^{0}_{1}, z^{0}_{2})\|_{\mathcal{H}}+M_5\|(z^{0}_{1}, z^{0}_{2})\|_{\mathcal{H}}\sum\limits_{r = 1}^{m}\left(\frac{\rho}{2M_3}\right)^{r-1}, \qquad \text{(using (2.21))}\\ &\leq M_3\;{\rm{e}}^{-\lambda T}\|(z^{0}_{1}, z^{0}_{2})\|_{\mathcal{H}}+M_5 \frac{1-(\frac{\rho}{2M_3})^{m}}{1-\frac{\rho}{2M_3}}\|(z^{0}_{1}, z^{0}_{2})\|_{\mathcal{H}}, \\ &\leq \big( M_3\;{\rm{e}}^{-\lambda T}+M_5 \frac{1-(\frac{\rho}{2M_3})^{m}}{1-\frac{\rho}{2M_3}}\|\big)(z^{0}_{1}, z^{0}_{2})\|_{\mathcal{H}} \end{align*} |
then
| \begin{align*} \|z_1(T), z_2(T)\|_{\mathcal{H}} &\leq \big( M_3\;{\rm{e}}^{-\lambda T}+M_5 \frac{1-(\frac{\rho}{2M_3})^{m}}{1-\frac{\rho}{2M_3}}\|\big)(z^{0}_{1}, z^{0}_{2})\|_{\mathcal{H}} , \\ &\leq \Big( M_3\;{\rm{e}}^{-\lambda T}+\alpha \rho^{r}\Big)\|(z^{0}_{1}, z^{0}_{2})\|_{\mathcal{H}}, \qquad\qquad\qquad\qquad(\text{for some } \alpha > 0)\\ &\leq \Big( M_3\;{\rm{e}}^{-\lambda T}+h(\rho)\Big)\|(z^{0}_{1}, z^{0}_{2})\|_{\mathcal{H}}, \end{align*} |
where h(\rho) = \alpha \rho^{m} ; we have
| h(0) = 0, \quad h^{\prime}(\rho) > 0. |
We can take \rho = R > 0 sufficiently small and T sufficiently large so that
| \gamma: = C M_3\;{\rm{e}}^{-\lambda T}+h(R) < 1; |
then, (2.30) yields.
We reiterate the argument obtaining
| \begin{equation} \|(z_1(n T), z_2(nT)\|_{\mathcal{H}} \leq \gamma\|\big(z_1((n-1) T), z_2((n-1)T)\big)\|_{\mathcal{H}} \leq \gamma^{n}\|(z^{0}_{1}, z^{0}_{2})\|_{\mathcal{H}}, \quad n = 1, 2, \ldots \nonumber \end{equation} |
Let us consider t_1 = nT , then for all t\geq t_1 we conclude that
| \begin{equation} \|(z_1(t), z_2(t))\|_{\mathcal{H}}\leq \gamma^{n}\|(z^{0}_{1}, z^{0}_{2})\|_{\mathcal{H}};\nonumber \end{equation} |
hence, there exist two positives constants N and \alpha_1 such that
| \begin{equation} \|(z_1(t), z_2(t))\|_{\mathcal{H}}\leq N\;{\rm{e}}^{-\alpha_1 t}\|(z^{0}_{1}, z^{0}_{2})\|_{\mathcal{H}}.\nonumber \end{equation} |
In this section, we apply the exponential stabilization result for the different Holling response functions Ⅰ, Ⅱ, Ⅲ and Ⅳ. We present numerical simulations for each example in two-dimensional space.
In the following, we consider the two-dimensional closed rectangular habitat \Omega: = \{(x, y)/\:0\leq x \leq a, \: 0\leq y\leq b\} . The eigenvalues and eigenfunctions respectively of the Laplacian operator \Delta with the Neumann boundary in \Omega are given by (see [16])
| \begin{equation} \lambda_{M, N} = -\pi^{2}\left[\left(M^{2} / a^{2}\right)+\left(N^{2} / b^{2}\right)\right] ; \quad M, N = 0, 1, 2, \ldots \end{equation} | (3.1) |
and
| \begin{equation} \psi_{M, N}(x, y) = \cos (M \pi x / a) \cos (N \pi y / b). \end{equation} | (3.2) |
Let consider the following prey-predator-diffusion with a Holling type Ⅰ functional response.
| \begin{equation} \left\{\begin{array}{l} \frac{\partial y_1(t, x, y)}{\partial t} = \Delta y_1+f(y_1, y_2), \quad (x, y) \in \Omega, t > 0 \\ \frac{\partial y_2(t, x, y)}{\partial t} = \delta \Delta y_2+g(y_1, y_2), \quad (x, y) \in \Omega, t > 0 \\ \frac{\partial y_{1}}{\partial v} = \frac{\partial y_{2}}{\partial v} = 0, \quad(t, x, y) \in \Sigma = (0, \infty) \times \partial \Omega \\ y_1(0, x, y) = y_{1}^{0}(x, y), \quad y_2(0, x) = y_{2}^{0}(x, y), \quad (x, y) \in \Omega \end{array}\right. \end{equation} | (3.3) |
where f(y_1, y_2) = r_1y_1(1-y_1/\kappa_{1})-\beta y_1y_2\: and g(y_1, y_2) = -r_2y_2+b\beta y_1y_2 .
Steady state solutions analysis:
System (3.3) has the following constant steady states
| \begin{equation} (0, 0), \: (\kappa_{1}, 0), \: (y^*, z^*) \end{equation} | (3.4) |
where (y^*, z^*) is the solution of the following system
| \begin{equation} \begin{cases} r_1y^*(1-y^*/\kappa_{1})-\beta y^*z^* = 0, \\ -r_2z^*+by^*z^* = 0. \end{cases} \end{equation} | (3.5) |
and (y(x), z(x)) , where (y(x), z(x)) is a non-constant positive function when it exists. The asymptotic behavior of these steady states has been studied extensively; see, e.g., [6,11]. Furthermore, Kishimoto and Weinberger [18] showed that (3.3) has no stable positive steady-state solution when the domain \Omega is convex, while, according to Theorem 2.3, these equilibrium states can be reached; more precisely, let z_1 = y_1-y^{e}_1 and z_2 = y_2-y^{e}_2 ; then, we have the following system:
| \begin{equation} \left\{\begin{array}{l} \frac{\partial z_1(t, x, y)}{\partial t} = \Delta z_1+f(z_1+y^{e}_1, z_2+y^{e}_2)-f(y^{e}_1, y^{e}_2)+v(t)Bz_1, \quad (x, y) \in \Omega, t > 0 \\ \frac{\partial z_2(t, x, y)}{\partial t} = \delta \Delta z_2+g(z_1+y^{e}_1, z_2+y^{e}_2)-g(y^{e}_1, y^{e}_2)+v(t)Bz_2, \quad (x, y) \in \Omega, t > 0 \\ \frac{\partial z_{1}}{\partial v} = \frac{\partial z_{2}}{\partial v} = 0, \quad(t, x, y) \in \Sigma = (0, \infty) \times \partial \Omega \\ z_1(0, x, y) = z_{1}^{0}(x, y): = z_{1}^{0}(x, y)-y_1^{e}, \quad z_2(0, x) = z_{2}^{0}(x, y): = z_{2}^{0}(x, y)-y_2^{e}, \quad (x, y) \in \Omega \end{array}\right. \end{equation} | (3.6) |
where BY = \frac{2}{1+\mu(x, y)}Y, \quad \forall Y\in L^2(\Omega) and \mu\in L^{\infty}(\Omega) such that \mu(x, y)\geq 1, \: \forall (x, y)\in \Omega , is exponentially stabilizable for all equilibrium states (y_1^{e}, y_2^{e}) .
Let us verify the conditions of Theorem 2.3
-Following [20], system (3.3) has a unique smooth non-negative solution for y_{1}^{0}(x)\geq 0 and y_{2}^{0}(x)\geq 0 .
- By simple calculus, there exist positive constants C_1, C_2, C_3, C_4, C_5 and C_6 such that
| \begin{equation} \left|f(y_1(t, x), y_2(t, x))\right|\leq C_1|y_1(t, x)|+C_2|y_1(t, x)|^2+C_3|y_2(t, x)|^2\nonumber \end{equation} |
and
| \begin{equation} \left|g(y_1(t, x), y_2(t, x))\right|\leq C_4|y_2(t, x)|+C_5|y_1(t, x)|^2+C_6|y_2(t, x)|^2;\nonumber \end{equation} |
then (H_2) holds for r_1 = 1 , r_2 = 2 , m_0 = 2 and C = \max\{C_1, C_2, C_3, C_4, C_5, C_6\}.
Numerical simulations:
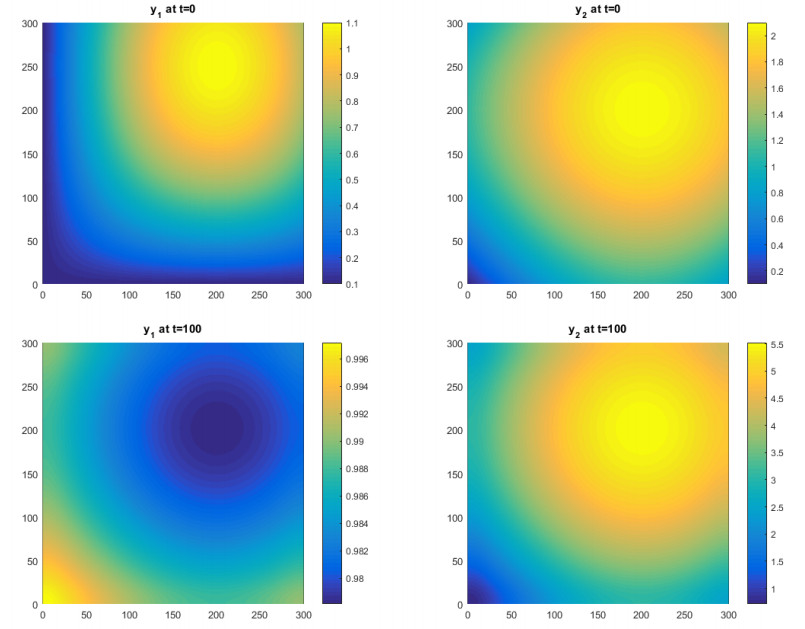
Let \Omega = [0,300]\times[0,300] , B = I_d , r_1 = 1 , \kappa_{1} = 1 , e = 2.5 , \beta = 0.4 , \delta = 1 , r_2 = 0.6 and b = 5 . The choice of parameters for numerical simulation was inspired from [22]. We illustrate numerically the exponential stabilization of (3.6) towards (y^{e}_1, y^{e}_2) = (0, 0) . To this end we start by the explicitation of the feedback control v(t) . On the one hand, by simple calculus we have:
| \begin{equation} a = 1, b = 0, c = 0, d = 0.6 \;\text{and}\; c_0 = 0.4. \end{equation} | (3.7) |
On the other hand, the eigenvalues of A: = \Delta+aI are:
| \lambda_{M, N} = 1-\pi^2\big[M^2/300^2+N^2/300^2\big];\qquad M, N = 0, 1, 2... |
It is clear that A has a finite number of positive eigenvalues, the largest one being \lambda_{0, 0}: = 1 . Then following Theorem 2.3, we obtain v(t) = -5 . Let
| \begin{equation} y_{1}^{0}(x, y) = 0.1+\sin(\frac{\pi }{400}x)\sin(\frac{\pi }{500}y), \quad\forall (x, y)\in , \Omega\nonumber \end{equation} |
and
| \begin{equation} y_{2}^{0}(x, y) = 0.1+\sin(\frac{\pi }{400}x)+\sin(\frac{\pi }{400}y), \quad\forall (x, y)\in \Omega.\nonumber \end{equation} |
Using the 2D finite difference (see [14]), we obtain Figure 1, which shows the densities of the uncontrolled system, and Figure 2, which shows the densities of the controlled system.
Let us consider the following prey-predator- diffusion with a Holling type Ⅱ functional response.
| \begin{equation} \left\{\begin{array}{l} \frac{\partial y_1(t, x, y)}{\partial t} = \Delta y_1+f(y_1, y_2), \quad (x, y) \in \Omega, t > 0 \\ \frac{\partial y_2(t, x, y)}{\partial t} = \delta \Delta y_2+g(y_1, y_2), \quad (x, y) \in \Omega, t > 0 \\ \frac{\partial y_{1}}{\partial v} = \frac{\partial y_{2}}{\partial v} = 0, \quad(t, x, y) \in \Sigma = (0, \infty) \times \partial \Omega \\ y_1(0, x, y) = y_{1}^{0}(x, y), \quad y_2(0, x, y) = y_{2}^{0}(x, y), \quad (x, y) \in \Omega \end{array}\right. \end{equation} | (3.8) |
where f(y_1, y_2) = r_1y_1(1-y_{1}/\kappa_{1})-\frac{\beta y_1y_{2}}{1+ey_1}\: and g(y_1, y_2) = -r_2y_2+\frac{b\beta y_1y_{2}}{1+ey_1} .
Steady state solutions analysis:
System (3.8) has the following constant steady states
| \begin{equation} (0, 0), \quad (\kappa_{1}, 0), \quad (y^*, z^*) \end{equation} | (3.9) |
where (y^*, z^*) is the positive solution of the system
| \begin{equation} \left\{\begin{array}{l} y^*+r_1y^*(1-y^*/\kappa_{1})-\frac{\beta y^*z^*}{1+ey^*} = 0, \\ -r_2z^*+\frac{b\beta y^*z^*}{1+ey^*} = 0; \end{array}\right. \end{equation} | (3.10) |
and (y(x), z(x)) where (y(x), z(x)) is a non-constant positive function when it exists. Camara and Aziz-Alaoui (see [8] and [7]) show that for suitable conditions on r_1, \beta and e , system (3.8) has at least one positive solution. They have shown that (0, 0) and (\kappa_{1}, 0) are unstable, while, according to Theorem 2.3, these equilibrium states can be reached; more precisely, let z_1 = y_1-y^{e}_1 , z_2 = y_2-y^{e}_2 ; then, we have the following system
| \begin{equation} \left\{\begin{array}{l} \frac{\partial z_1(t, x, y)}{\partial t} = \Delta z_1+f(z_1+y^{e}_1, z_2+y^{e}_2)-f(y^{e}_1, y^{e}_2)+v(t)Bz_1, \quad (x, y) \in \Omega, t > 0 \\ \frac{\partial z_2(t, x, y)}{\partial t} = \delta \Delta z_2+g(z_1+y^{e}_1, z_2+y^{e}_2)-g(y^{e}_1, y^{e}_2)+v(t)Bz_2, \quad (x, y) \in \Omega, t > 0 \\ \frac{\partial z_{1}}{\partial v} = \frac{\partial z_{2}}{\partial v} = 0, \quad(t, x, y) \in \Sigma = (0, \infty) \times \partial \Omega \\ z_1(0, x, y) = z_{1}^{0}(x, y): = z_{1}^{0}(x, y)-y_1^{e}, \quad z_2(0, x) = z_{2}^{0}(x, y): = z_{2}^{0}(x, y)-y_2^{e}, \quad (x, y) \in \Omega \end{array}\right. \end{equation} | (3.11) |
where BY = \mu(x, y)Y, \quad \forall Y\in L^2(\Omega) and \mu\in L^{\infty}(\Omega) such that \mu(x, y)\geq 1, \: \forall (x, y)\in \Omega , is exponentially stabilizable for all equilibrium states (y_1^{e}, y_2^{e}) . Let us verify the conditions of Theorem 2.3:
-Following Lemma 14.20 [27], system (3.8) has a non-negative solution for y^{0}_{1}(x)\geq 0 and y^{0}_{2}(x)\geq 0 .
-By simple calculus, there exist positive constants C_1, C_2, C_3 and C_4 such that
| \begin{equation} |f(y_1(t, x), y_2(t, x))|\leq C_1|y_1(t, x)|+C_2|y_1(t, x)|^{2}+C_3|y_2(t, x)|\nonumber \end{equation} |
and
| \begin{equation} |g(y_1(t, x), y_2(t, x))|\leq C_4|y_2(t, x)|, \nonumber \end{equation} |
then (H_2) holds for r_1 = 1 , r_2 = 2 , m_0 = 2 and C = \max\{C_1, C_2, C_3, C_4\}.
Numerical simulations:
Let \Omega = [0,500]\times[0,500] , B = I_d , r_1 = 1 , \kappa_{1} = 1 , e = 2.5 , \beta = 0.4 , \delta = 1 , r_2 = 0.6 , b = 5 . Let explicit the feedback control that stabilizes the solution of (3.11) towards (y^{e}_1, y^{e}_2) = (0, 0) . The eigenvalues of A: = \Delta+aI are:
| \lambda_{M, N} = 1-\pi^2\big[M^2/500^2+N^2/500^2\big];\qquad M, N = 0, 1, 2... |
It is clear that A has a finite number of positive eigenvalues, the largest one being \lambda_{0, 0}: = 1 . By simple calculations we obtain
| \begin{equation} v(t) = -5. \end{equation} | (3.12) |
Let
| \begin{equation} y_{1}^{0}(x, y) = 6/35-2 \times 10^{-7}\left(x-0.1 y-225\right)\left(x-0.1 y-675\right), \quad\forall (x, y)\in \Omega, \nonumber \end{equation} |
and
| \begin{equation} y_{2}^{0}(x, y) = 116/245-3 \times 10^{-5}\left(x-450\right)-1.2 \times 10^{-4}\left(y-150\right), \quad\forall (x, y)\in \Omega.\nonumber \end{equation} |
Using the 2D finite difference (see [14]), we obtain Figure 3, which shows the densities of the uncontrolled system, and Figure 4, which shows the densities of the controlled system.
Let us consider the following prey-predator- diffusion with a Holling type Ⅲ functional response:
| \begin{equation} \left\{\begin{array}{l} \frac{\partial y_1(t, x, y)}{\partial t} = \Delta y_1+f(y_1, z_1), \quad (x, y) \in \Omega, t > 0 \\ \frac{\partial y_2(t, x, y)}{\partial t} = \delta \Delta y_2+g(y_1, z_1), \quad (x, y) \in \Omega, t > 0 \\ \frac{\partial y_{1}}{\partial v} = \frac{\partial y_{2}}{\partial v} = 0, \quad(t, x, y) \in \Sigma = (0, \infty) \times \partial \Omega \\ y_1(0, x, y) = y_{1}^{0}(x, y), \quad y_2(0, x, y) = y_{2}^{0}(x, y), \quad (x, y) \in \Omega \end{array}\right. \end{equation} | (3.13) |
where f(y_1, y_2) = r_1y_1(1-y_{1}/\kappa_{1})-\frac{\beta y_1^{2}y_{2}}{1+ey^{2}_1} and g(y_1, y_2) = -r_2y_2+\frac{b\beta y_1^{2}y_{2}}{1+ey^{2}_1}.
Steady state solutions analysis:
System (3.13) has the following constant steady states
| \begin{equation} (0, 0), \quad (\kappa_{1}, 0), \quad (y^*, z^*) \end{equation} | (3.14) |
where (y^*, z^*) is the solution of the following system
| \begin{equation} \left\{\begin{array}{l} ry^*(1-y^*/\kappa_{1})-\frac{\beta(y^*)^2z^*}{1+e(y^*)^2} = 0, \\ -r_2z^*+\frac{b\beta (y^*)^2z^*}{1+e(y^*)^2} = 0. \end{array}\right. \end{equation} | (3.15) |
Tian and Weng in [28] showed that (y^*, z^*) exists and is positive for appropriate assumptions on \beta, e, b and r_2 , and they discussed the stability of this stationary solution. However, we have seen that, by using Theorem 2.3, these equilibrium states can be reached; more precisely, let z_1 = y_1-y^{e}_1 , z_2 = y_2-y^{e}_2 ; then, we have then the following system
| \begin{equation} \left\{\begin{array}{l} \frac{\partial z_1(t, x, y)}{\partial t} = \Delta z_1+f(z_1+y^{e}_1, z_2+y^{e}_2)-f(y^{e}_1, y^{e}_2)+v(t)Bz_1, \quad (x, y) \in \Omega, t > 0 \\ \frac{\partial z_2(t, x, y)}{\partial t} = \delta \Delta z_2+g(z_1+y^{e}_1, z_2+y^{e}_2)-g(y^{e}_1, y^{e}_2)+v(t)Bz_2, \quad (x, y) \in \Omega, t > 0 \\ \frac{\partial z_{1}}{\partial v} = \frac{\partial z_{2}}{\partial v} = 0, \quad(t, x, y) \in \Sigma = (0, \infty) \times \partial \Omega \\ z_1(0, x, y) = z_{1}^{0}(x, y): = z_{1}^{0}(x, y)-y_1^{e}, \quad z_2(0, x) = z_{2}^{0}(x, y): = z_{2}^{0}(x, y)-y_2^{e}, \quad (x, y) \in \Omega \end{array}\right. \end{equation} | (3.16) |
where BY = (\mu(x, y)-1)(\mu(x, y)+1)Y, \quad \forall Y\in L^2(\Omega) and \mu\in L^{\infty}(\Omega) such that \mu(x, y)\geq 1, \: \forall (x, y)\in \Omega , is exponentially stabilizable for all equilibrium states (y^{1}_e, y^{2}_e) . Now, let us verify the conditions of Theorem 2.3:
-Following Lemma 14.20 [27], system (3.13) has a non-negative solution for y^{0}_{1}(x)\geq 0 and y^{0}_{2}(x)\geq 0 .
-By simple calculus, there exist positive constants C_1, C_2, C_3 and C_4 such that
| \begin{equation} |f(y_1(t, x), y_2(t, x))|\leq C_1|y_1(t, x)|+C_2y^{2}_1(t, x)+C_3|y_2(t, x)|\nonumber \end{equation} |
and
| \begin{equation} |g(y_1(t, x), y_2(t, x))|\leq C_4|y_2(t, x)|, \nonumber \end{equation} |
then (H_2) holds for r_1 = 1 , r_2 = 2 , m_0 = 2 and C = \max\{C_1, C_2, C_3, C_4, C_5, C_6\}.
Numerical simulations:
Let \Omega = [0,350]\times[0,350] , B = I_d , r_1 = 1 , \kappa_{1} = 1 , e = 2.5 , \beta = 0.4 , \delta = 1 , r_2 = 0.6 , b = 5 . Let explicit the feedback control that stabilizes the solution of (3.16) towards (y^{e}_1, y^{e}_2) = (0, 0) . The eigenvalues of A: = \Delta+aI are:
| \lambda_{M, N} = 1-\pi^2\big[M^2/350^2+N^2/350^2\big];\qquad M, N = 0, 1, 2... |
It is clear that A has a finite number of positive eigenvalues, the largest one being \lambda_{0, 0}: = 1 . By simple calculations we obtain
| \begin{equation} v(t) = -3. \end{equation} | (3.17) |
Let
| \begin{equation} y_{1}^{0}(x, y) = 1-0.1 \sin(\frac{\pi}{400}x)\cos(\frac{\pi}{350}y), \quad\forall (x, y)\in \Omega\nonumber \end{equation} |
and
| \begin{equation} y_{2}^{0}(x, y) = 0.5+0.1sin(\frac{\pi}{200}x)+0.01\cos(\frac{\pi}{300}y), \quad\forall (x, y)\in \Omega.\nonumber \end{equation} |
Using the 2D finite difference (see [14]), we obtain Figure 5, which shows the densities of the uncontrolled system, and Figure 6, which shows the densities of the controlled system.
Let us consider the following prey-predator- diffusion with a Holling type Ⅳ functional response:
| \begin{equation} \left\{\begin{array}{l} \frac{\partial y_1(t, x, y)}{\partial t} = \Delta y_1+f(y_1, z_1), \quad (x, y) \in \Omega, t > 0 \\ \frac{\partial y_2(t, x, y)}{\partial t} = \delta \Delta y_2+g(y_1, z_1), \quad (x, y) \in \Omega, t > 0 \\ \frac{\partial y_{1}}{\partial v} = \frac{\partial y_{2}}{\partial v} = 0, \quad(t, x, y) \in \Sigma = (0, \infty) \times \partial \Omega \\ y_1(0, x, y) = y_{1}^{0}(x, y), \quad y_2(0, x, y) = y_{2}^{0}(x, y), \quad (x, y) \in \Omega \end{array}\right. \end{equation} | (3.18) |
where f(y_1, y_2) = r_1y_1(1-y_{1}/\kappa_{1})-\frac{\beta y_1^{2}y_{2}}{e_1+ey_1+e_2y^{2}_{1}}, \: g(y_1, y_2) = -r_2y_2+\frac{b\beta y_1^{2}y_{2}}{e_1+ey_1+e_2y^{2}_{1}} .
Steady state solutions analysis:
System (3.18) has the following constant steady states
| \begin{equation} (0, 0), \quad (\kappa_{1}, 0), \quad (y^*, z^*), \end{equation} | (3.19) |
where (y^*, z^*) is the solution of the following system
| \begin{equation} \left\{\begin{array}{l} ry^*(1-y^*/\kappa_{1})-\frac{\beta(y^*)^2z^*}{e_1+ey^*+e_2(y^*)^2} = 0, \\ -r_2z^*+\frac{b\beta (y^*)^2z^*}{e_1+ey^*+e_2(y^*)^2} = 0. \end{array}\right. \end{equation} | (3.20) |
We refer to [9] for discussions on the existence and stability of these equilibrium states. However, we have seen that, by using Theorem 2.3, these equilibrium states can be reached; more precisely, let z_1 = y_1-y^{e}_1 , z_2 = y_2-y^{e}_2 , then the following system
| \begin{equation} \left\{\begin{array}{l} \frac{\partial z_1(t, x, y)}{\partial t} = \Delta z_1+f(z_1+y^{e}_1, z_2+y^{e}_2)-f(y^{e}_1, y^{e}_2)+v(t)Bz_1, \quad (x, y) \in \Omega, t > 0 \\ \frac{\partial z_2(t, x, y)}{\partial t} = \delta \Delta z_2+g(z_1+y^{e}_1, z_2+y^{e}_2)-g(y^{e}_1, y^{e}_2)+v(t)Bz_2, \quad (x, y) \in \Omega, t > 0 \\ \frac{\partial z_{1}}{\partial v} = \frac{\partial z_{2}}{\partial v} = 0, \quad(t, x, y) \in \Sigma = (0, \infty) \times \partial \Omega \\ z_1(0, x, y) = z_{1}^{0}(x, y): = z_{1}^{0}(x, y)-y_1^{e}, \quad z_2(0, x) = z_{2}^{0}(x, y): = z_{2}^{0}(x, y)-y_2^{e}, \quad (x, y) \in \Omega \end{array}\right. \end{equation} | (3.21) |
where BY = (1-\mu(x))Y, \quad \forall Y\in L^{2}(\Omega) and \mu\in L^{\infty}(\Omega) , is exponentially stabilizable for all equilibrium states (y^{1}_e, y^{2}_e) .
Now, let us verify the conditions of Theorem 2.3:
-Following Lemma 14.20 [27], system (3.18) has a non-negative solution for y^{0}_{1}(x)\geq 0 and y^{0}_{2}(x)\geq 0 .
-By simple calculus, there exist positive constants C_1, C_2, C_3 and C_4 such that
| \begin{equation} |f(y_1(t, x), y_1(t, x))|\leq C_1|y_1(t, x)|+C_2y^{2}_1(t, x)+C_3|y_2(t, x)|\nonumber \end{equation} |
and
| \begin{equation} |g(y_1(t, x), y_1(t, x))|\leq C_4|y_2(t, x)|;\nonumber \end{equation} |
then (H_2) holds for r_1 = 1 , r_2 = 2 , m_0 = 2 and C = \max\{C_1, C_2, C_3, C_4\}.
Numerical simulation:
Let \Omega = [0,400]\times[0,400] , B = I_d , r_1 = 1 , \kappa_{1} = 1 , e = 0.7 ; e_1 = 0.5 , e_2 = 2.5 , \beta = 0.4 , \delta = 1 , r_2 = 0.6 and b = 5 . Let explicit the feedback control that stabilizes the solution of (3.21) towards (y^{e}_1, y^{e}_2) = (0, 0) . The eigenvalues of A: = \Delta+aI are
| \lambda_{M, N} = 1-\pi^2\big[M^2/400^2+N^2/400^2\big];\qquad M, N = 0, 1, 2... |
It is clear that A has a finite number of positive eigenvalues, the largest one being \lambda_{0, 0}: = 1 . By simple calculations we obtain
| \begin{equation} v(t) = -2.85. \end{equation} | (3.22) |
Let
| \begin{equation} y_{1}^{0}(x, y) = 1-\sin(\frac{\pi}{400}x)\sin(\frac{\pi}{500}y), \quad\forall (x, y)\in \Omega, \nonumber \end{equation} |
and
| \begin{equation} y_{2}^{0}(x, y) = 1+{\rm{e}}^{-0.4x}+{\rm{e}}^{-0.009y}, \quad\forall (x, y)\in \Omega.\nonumber \end{equation} |
Using the 2D finite difference (see [14]), we obtain Figure 7, which shows the densities of the uncontrolled system, and Figure 8, which shows the densities of the controlled system.
The problem of exponential stabilization of reaction-diffusion systems simulating predatory prey systems has been investigated. We constructed a multiplicative control that exponentially stabilizes the solution of the system to its equilibrium state. The designed controller has the advantage of reaching all equilibrium states. Numerical simulations show the efficiency of the used control.
This work was supported by the Ministry of Higher Education, Scientific Research and Innovation, the Digital Development Agency (DDA) and the National Center for Scientific and Technical Research (CNRST) under Project ALKHAWARIZMI/2020/19.
The authors declare that there is no conflict of interests regarding this paper.
| [1] |
N. Apreutesei, G. Dimitriu, On a prey–predator reaction–diffusion system with holling type iii functional response, J. Comput. Appl. Math., 235 (2010), 366–379. https://doi.org/10.1016/j.cam.2010.05.040 doi: 10.1016/j.cam.2010.05.040

|
| [2] |
M. A. Aziz-Alaoui, M. D. Okiye, Boundedness and global stability for a predator-prey model with modified leslie-gower and holling-type ii schemes, Appl. Math. Lett., 16 (2003), 1069–1075. https://doi.org/10.1016/S0893-9659(03)90096-6 doi: 10.1016/S0893-9659(03)90096-6

|
| [3] |
J. M. Ball, J. E. Marsden, M. Slemrod, Controllability for distributed bilinear systems, SIAM J. Control Optim., 20 (1982), 575–597. https://doi.org/10.1137/0320042 doi: 10.1137/0320042

|
| [4] |
L. Berrahmoune, Stabilization and decay estimate for distributed bilinear systems, Syst. Control Lett., 36 (1999), 167–171. https://doi.org/10.1016/S0167-6911(98)00065-6 doi: 10.1016/S0167-6911(98)00065-6

|
| [5] |
R. Bhattacharyya, B. Mukhopadhyay, M. Bandyopadhyay, Diffusion-driven stability analysis of a prey-predator system with holling type-iv functional response, Systems Analysis Modelling Simulation, 43 (2003), 1085–1093. https://doi.org/10.1080/0232929031000150409 doi: 10.1080/0232929031000150409

|
| [6] |
P. N. Brown, Decay to uniform states in ecological interactions, SIAM J. Appl. Math., 38 (1980), 22–37. https://doi.org/10.1137/0138002 doi: 10.1137/0138002

|
| [7] | B. I. Camara, M. A. Aziz-Alaoui, Dynamics of a predator-prey model with diffusion, Dynamics of Continuous, Discrete and Impulsive System, series A, 15 (2008), 897–906. |
| [8] | B. I. Camara, M. A. Aziz-Alaoui, Turing and hopf patterns formation in a predator-prey model with leslie-gowertype functional response, Dynamics of Continuous, Discrete & Impulsive Systems B, 16 (2009), 479–488. |
| [9] |
X. Chen, Y. Qi, M. Wang, A strongly coupled predator–prey system with non-monotonic functional response, Nonlinear Anal.-Theor., 67 (2007), 1966–1979. https://doi.org/10.1016/j.na.2006.08.022 doi: 10.1016/j.na.2006.08.022

|
| [10] |
C. Cosner, A. C. Lazer, Stable coexistence states in the volterra–lotka competition model with diffusion, SIAM J. Appl. Math., 44 (1984), 1112–1132. https://doi.org/10.1137/0144080 doi: 10.1137/0144080

|
| [11] | P. De Mottoni, Qualitative analysis for some quasi-linear parabolic systems, Inst. Math. Pol. Acad. Sci. Zam, 1979. |
| [12] | K.-J. Engel, R. Nagel, S. Brendle, One-parameter semigroups for linear evolution equations, volume 194, Springer, 2000. |
| [13] |
H. I. Freedman, A model of predator-prey dynamics as modified by the action of a parasite, Math. Biosci., 99 (1990), 143–155. https://doi.org/10.1016/0025-5564(90)90001-F doi: 10.1016/0025-5564(90)90001-F

|
| [14] |
M. R. Garvie, Finite-difference schemes for reaction–diffusion equations modeling predator–prey interactions in matlab, B. Math. Biol., 69 (2007), 931–956. https://doi.org/10.1007/s11538-006-9062-3 doi: 10.1007/s11538-006-9062-3

|
| [15] |
M. R. Garvie, C. Trenchea, Spatiotemporal dynamics of two generic predator–prey models, J. Biol. Dynam., 4 (2010), 559–570. https://doi.org/10.1080/17513750903484321 doi: 10.1080/17513750903484321

|
| [16] |
H. P. W. Gottlieb, Eigenvalues of the laplacian with neumann boundary conditions, The ANZIAM Journal, 26 (1985), 293–309. https://doi.org/10.1017/S0334270000004525 doi: 10.1017/S0334270000004525

|
| [17] | A. Y. Khapalov, Controllability of partial differential equations governed by multiplicative controls, Springer, 2010. https://doi.org/10.1007/978-3-642-12413-6 |
| [18] | K. Kishimoto, H. F. Weinberger, The spatial homogeneity of stable equilibria of some reaction-diffusion systems on convex domains, 1988. |
| [19] |
I. Lamrani, I. El Harraki, A. Boutoulout, F.-Z. El Alaoui, Feedback stabilization of bilinear coupled hyperbolic systems, Discrete & Continuous Dynamical Systems-S, 14 (2021), 3641. https://doi.org/10.3934/dcdss.2020434 doi: 10.3934/dcdss.2020434

|
| [20] |
Y. Lou, W.-M. Ni, Diffusion, self-diffusion and cross-diffusion, J. Differ. Equations, 131 (1996), 79–131. https://doi.org/10.1006/jdeq.1996.0157 doi: 10.1006/jdeq.1996.0157

|
| [21] |
T. Ma, X. Meng, T. Hayat, A. Hobiny, Stability analysis and optimal harvesting control of a cross-diffusion prey-predator system, Chaos, Solitons & Fractals, 152 (2021), 111418. https://doi.org/10.1016/j.chaos.2021.111418 doi: 10.1016/j.chaos.2021.111418

|
| [22] |
A. B. Medvinsky, S. V. Petrovskii, I. A. Tikhonova, H. Malchow, B.-L. Li, Spatiotemporal complexity of plankton and fish dynamics, SIAM review, 44 (2002), 311–370. https://doi.org/10.1137/S0036144502404442 doi: 10.1137/S0036144502404442

|
| [23] | S.-Y. Mi, B.-S. Han, Y. Yang, Spatial dynamics of a nonlocal predator–prey model with double mutation, Int. J. Biomath., (2022), 2250035. |
| [24] |
Y. Morita, K. Tachibana, An entire solution to the lotka–volterra competition-diffusion equations, SIAM J. Math. Anal., 40 (2009), 2217–2240. https://doi.org/10.1137/080723715 doi: 10.1137/080723715

|
| [25] | A. Pazy, Semigroups of linear operators and applications to partial differential equations, volume 44, Springer Science & Business Media, 2012. |
| [26] |
J. P. Quinn, Stabilization of bilinear systems by quadratic feedback controls, J. Math. Anal. Appl., 75 (1980), 66–80. https://doi.org/10.1016/0022-247X(80)90306-6 doi: 10.1016/0022-247X(80)90306-6

|
| [27] | J. Smoller, Shock waves and reaction—diffusion equations, volume 258, Springer Science & Business Media, 2012. |
| [28] |
Y. Tian, P. Weng, Stability analysis of diffusive predator–prey model with modified leslie–gower and holling-type iii schemes, Appl. Math. Comput., 218 (2011), 3733–3745. https://doi.org/10.1016/j.amc.2011.09.018 doi: 10.1016/j.amc.2011.09.018

|
| [29] |
W. Walter, Differential inequalities and maximum principles: theory, new methods and applications, Nonlinear Anal.-Theor., 30 (1997), 4695–4711. https://doi.org/10.1016/S0362-546X(96)00259-3 doi: 10.1016/S0362-546X(96)00259-3

|
| [30] |
H. Zhang, Y. Cai, S. Fu, W. Wang, Impact of the fear effect in a prey-predator model incorporating a prey refuge, Appl. Math. Comput., 356 (2019), 328–337. https://doi.org/10.1016/j.amc.2019.03.034 doi: 10.1016/j.amc.2019.03.034

|
| [31] | I. Munteanu, Boundary stabilization of parabolic equations, volume 44, Springer International Publishing, 2019. |
| 1. | Imad El Harraki, Ilyasse Lamrani, Exponential stabilization of semilinear parabolic systems, 2023, 360, 00160032, 7294, 10.1016/j.jfranklin.2023.05.017 | |
| 2. | Ilyasse Lamrani, Imad El Harraki, Fatima-Zahrae El Alaoui, Rapid stabilization of parabolic coupled system, 2025, 197, 01676911, 106027, 10.1016/j.sysconle.2025.106027 |