Ergodic stationary distribution of stochastic virus mutation model with time delay

1.   Introduction

Different mathematical models have been used to study the dynamical behavior of infectious diseases by many researchers. Stone et al. ^[1] analyzed classical models of seasonal forced SIR epidemics and to further understand the nonlinear dynamics of recurrent disease. A cutaneous leishmaniasis disease model was proposed by Sinan et al. ^[2], who investigated the basic properties of the model. Sheergojri et al. ^[3] built a mathematical model of tumor development using a fuzzy logic method. Sabbar ^[4] studied the conditions for asymptotic extinction and sustained survival in a stochastic infectious disease model with different intervention measures. The dynamical behavior of the fractional-order models for infectious disease was studied in ^[5,6,7]. Ahmadet et al. ^[8] built a fractional-order model about COVID-19 to predict the second wave of COVID-19 transmission in Pakistan in the next 50 days.

In recent years, during the environmental change, the virus will mutate due to the influence of various factors in the transmission process, which is expected to lead to a large-scale outbreak of diseases ^[9,10,11]. With the normalization of COVID-19 prevention and control, the researchers paid more attention to the virus mutation models ^[12,13,14]. Cacciapaglia et al. ^[15] used a modified SIR model to simulate the interplay and competition of COVID-19 virus variants within a given population. Dobie ^[16] discussed the stability of a model based on horizontal and vertical transmissions, size variation and virus mutation. Avila-Ponce de León et al. ^[17] applied mathematical models to simulate the potential effects of the Omicron variant on the USA population. A study with multiple vaccinations and virus mutations found that early vaccination is the key to reducing disease mutations ^[18]. Meanwhile, utilizing the principle of epidemic dynamics, Liu et al. ^[19] established an SEIR model with a mutated virus in wireless sensor networks, which had guiding significance to control the spread of a mutated virus. Xu et al. ^[20] proposed a complex network model with virus variation and considered the influence of virus variation factors on network transmission.

Due to the pathogenesis and epidemic law of infectious diseases, some scholars considered stochastic and time delays for an infectious disease model. Liu et al. ^[21] studied the dynamics of a stochastic delayed SIR epidemic model with dual diseases and vaccination driven by L$\mathrm{\acute{e}}$vy jumps. Zhang and Liu ^[22] analyzed the sufficient conditions for extinction and persistence of a stochastic delayed model with vertical transmission and vaccination. The stochastic delayed SIRS model was investigated by Xu and Li ^[23] found that the immunity period of vaccination would affect the threshold of extinction or persistence. In ^[24,25], stochastic delayed models with Markov switching was discussed. A delayed differential model of the tumor and immune system with noise was investigated by Alsakaji et al. ^[26]. Ali and Khan ^[27] proposed a stochastic delayed SIRS model with exponential birth and saturated incidence rates, and they found that a large amount of noise would lead to the extinction of the disease. In order to further study the persistent effects of stochastic disturbance on models with time delays, many scholars considered the ergodic stationary distribution of stochastic delayed models ^[28]. Khan et al. ^[29] proposed an epidemic model of SEIQ with stochastic disturbance and time delay, they used the Lyapunov function to analyze the ergodic stability. In ^[30], the ergodic stationary distribution of a hepatitis B virus system with a higher-order stochastic delayed differential model is investigated. Ikram et al. ^[31] built a stochastic delayed COVID-19 model with cross-immune class and transmission terms to study the effects of white noise on disease extinction. Liu et al. ^[32] used Markov semigroup theory to obtain the existence and uniqueness of ergodic stationary distribution. Sun et al. ^[33] studied the ergodic stationary distribution of a stochastic viral model with cytotoxic T lymphocyte responsiveness and time delay. By analyzing the threshold conditions for the persistence of ergodic stationary distribution, the effects of time delay and noise on disease were obtained ^[34]. Although the scholars have studied a lot on ergodic stability analysis for infectious disease models with noise and time delay, there are few studies on ergodic stability analysis of mutation models. In this paper, by considering the time delay from pre-mutation to post-mutation in the stochastic mutation model, we study the influence of different factors on the persistence and extinction for a model based on analyzing the ergodic stationary distribution.

This paper is presented as follows. In Section 2, we set up a stochastic virus mutation model with time delay. The existence and uniqueness of global positive solutions for the model are given in Section 3. In Section 4, we obtain the ergodic stationary distribution of the stochastic model with time delay. In the last section, the theoretical results are verified by numerical simulations.

2.   Model building

After the virus infects the susceptible individuals and goes through an incubation period, some of the latent individuals will transform into infected individuals. During this period, the virus will mutate due to environmental factors and the infected individuals are either pre-mutation individuals or post-mutation individuals. Both groups of infected individuals are infectious during this period of treatment. Considering that the virus will mutate within a certain period of time $\tau$, the SEIR model with virus variation and time delay is established. Besides, the following assumptions were taken into consideration while formulating the model:

1) All initial population sizes are non-negative.

2) Variables and parameters are non-negative.

3) All groups of individuals experienced natural death.

4) $\tau$ is the time delay before and after virus mutation.

Considering the above assumptions, the deterministic virus mutation model with time delay can be expressed by the following differential equations in Eq (2.1):

where $S(t)$, $E(t)$, ${I_1}(t)$, ${I_2}(t)$, $R(t)$ denote the sizes of susceptible ($S$), latent ($E$), pre-mutation patient (${I_1}$), post-mutation patient (${I_2}$) and recovered individuals ($R$), respectively, which satisfy $N(t) = S(t) + E(t) + {I_1}(t) + {I_2}(t) + R(t)$. The parameters in Eq (2.1) have the following meanings: $A$ is the birth rate, ${\beta _1}$ and ${\beta _2}$ represent the coefficients of patient infection rate before and after virus mutation respectively, $u$ is the rate at which the pre-mutation patient becomes the post-mutation patient, $\varepsilon$ represents the rate at which the latent person becomes the pre-mutation patient, ${r_1}$ and ${r_2}$ are the patient recovery rate before and after virus mutation respectively, $\tau$ is the time delay before and after virus mutation and $d$ is the death rate. All parameters are positive. The recovered population $R(t)$ has no effect on the dynamics of $S(t)$, $E(t)$, ${I_1}(t)$ ${I_2}(t)$, so the following simplified model can be obtained:

set $\Omega = \left\{ {\left. {S(t), E(t), {I_1}(t), {I_2}(t)|S(t) \ge 0, E(t) \ge 0, {I_1}(t) \ge 0, {I_2}(t) \ge 0} \right\}} \right.$, and the basic reproductive number of Eq (2.2) is

The dynamical behavior of Eq (2.2) is obtained as follows:

(ⅰ) If ${R_0} \le 1$, Eq (2.2) has the unique disease-free equilibrium

which is globally asymptotically stable.

(ⅱ) If ${R_0} > 1$, disease-free equilibrium ${E_0}$ is unstable and Eq (2.2) has a unique positive endemic equilibrium ${E_1} = ({S^*}, {E^*}, I_1^*, I_2^*)$, which is globally asymptotically stable, where

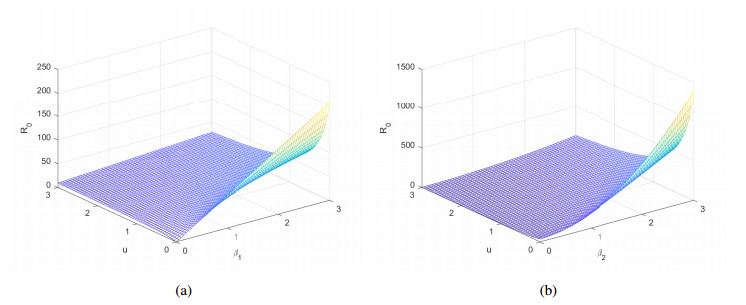
The sensitivity analysis of ${R_0}$ in Figure 1 shows that the related parameters ${\beta _1}$ and ${\beta _2}$ each have a great effect on disease transmission. Considering that biological systems are inevitably disturbed by uncertain environmental factors, we use white noise to represent stochastic interference, which can be represented by external interventions, policy interventions, drug therapy, media reports, vaccination and so on. In this paper, Gaussian white noise represents stochastic disturbance and the stochastic model with time delay is proposed as follows:

where ${B_i}(t)\; (i = 1, 2, 3, 4)$ denotes independent standard Brownian motions and ${\sigma _i} > 0\; (i = 1, 2, 3, 4)$ represents the intensities of ${B_i}(t)$. The variables in Eq (2.3) are constrained by the following initial conditions:

where ${\psi _i}(\theta) \in C\; (i = 1, 2, 3, 4)$ such that $C$ is a family of Lebesgue integrable functions from $[-\tau, 0]$ to $R_ + ^4$.

3.   Existence and uniqueness of global positive solutions

To study the dynamical behavior of a stochastic infectious model with time delay, it is necessary to verify that the solution of Eq (2.3) is non-negative and has a unique global positive solution (that is no explosion in finite time), so we have the following theorem.

Theorem 1. For the any given initial value (2.4), the system (2.3) has a unique positive solution $(S(t), E(t), {I_1}(t), {I_2}(t))$ on $t \ge - \tau$, and the solution remains in $R_ + ^4$ with a probability of 1.

Proof: For the given initial approximation $\left\{ {S(0), \; E(0), \; {I_1}(0), \; {I_2}(0)} \right\}$, the coefficients of Eq (2.3) are locally Lipschitz continuous, so there is a unique local solution $\left\{ {S(t), \; E(t), \; {I_1}(t), \; {I_2}(t)} \right\}$ on $t \in [ - \tau, {\tau _e}]$, where ${\tau _e}$ refers the explosion time. In order to show that this solution is global, we need to show that ${\tau _e} = \infty$ is true. Assume that ${\xi _0} \ge 1$ is so large that $S(\theta) \in [\frac{1}{{{\xi _0}}}, {\xi _0}]$, $E(\theta) \in [\frac{1}{{{\xi _0}}}, {\xi _0}]$, ${I_1}(\theta) \in [\frac{1}{{{\xi _0}}}, {\xi _0}]$, ${I_2}(\theta) \in [\frac{1}{{{\xi _0}}}, {\xi _0}]$ and $\theta \in [ - \tau, 0]$ are all satisfied. For each integer $\xi > {\xi _0}\; (\xi > 0)$, define the stopping time as follows:

Consider $\inf\phi = \infty\; (\phi\; is\; void\; set)$. ${\tau _\xi }$ is increasing as $\xi \to \infty$. Assume that ${\tau _\infty } = \mathop {\lim }\limits_{n \to \infty } {\tau _n}$ and let ${\tau _\infty } \le {\tau _e}$ a.s. Hence, we need to prove that ${\tau _\infty } = \infty$ a.s., then ${\tau _e} = \infty$ a.s. and $\left\{ {S(0), E(0), {I_1}(0), {I_2}(0)} \right\} \in R_ + ^4$ a.s. Otherwise, there exist the constants $T > 0$ and $\delta \in (0, 1)$ which yield that $P({\tau _\infty } \le T) > \delta$. Then there exist the integers ${\xi _1} > {\xi _0}$ which take

Define a $C^{2}$-function $V: R_{+}^{4}\rightarrow R_{+}$ as follows:

where $a > 0$ is a constant. According to $\mathrm{It\hat o's}$ formula

where

let $a = \frac{{d + {r_1}}}{{u + {\beta _1}}}$, then we can obtain

where ${K_1} > 0$, we can get

integrate both sides of Eq (3.3) from 0 to ${\tau _\xi } \wedge T$, and then obtain

take the expectation of both sides of Eq (3.4)

Let ${\Omega _\xi } = \left\{ {{\tau _\xi } \le T} \right\}$, for $\xi > {\xi _1}$ and in view of Eq (3.1), we obtain $P({\Omega _\xi }) \ge \delta$ such that for each $w \in {\Omega _\xi }$ there is at least one among $S({\tau _\xi }, w), E({\tau _\xi }, w), {I_1}({\tau _\xi }, w)\; and\; {I_2}({\tau _\xi }, w)$ that is equal either $\xi$ or $\frac{1}{\xi }$. Then

it follows that

where ${1_{{\Omega _\xi }}}$ is the indicative function of ${\Omega _\xi }$. Taking $\xi \to \infty$ gives

This contradicts the initial condition, so ${\tau _\infty } = \infty$ holds almost everywhere. Therefore, Theorem 1 is proved.

4.   The existence of ergodic stationary distribution

In this section, we construct an appropriate random $\mathrm{Lyapunov}$ function to study the existence and uniqueness of the ergodic stationary distribution of Eq (2.3). Taking $X(t)$ as a regular time-homogeneous Markov process defined in $d$ dimensional $\mathrm{Euclidean}$ space ${E^d}$, which can be expressed by the stochastic differential equation

the corresponding diffusion matrix is

Lemma 1. (^[35]) The $\mathrm{Markov}$ process of $X(t)$ has one ergodic stationary distribution $\pi (\cdot)$ and a bounded domain $U \subset {R^d}$ with the regular boundary $\Gamma$, then the following is true:

(ⅰ) There is a positive number $K$ such that $\sum\limits_{i, j = 1}^d {{a_{ij}}(x)} {\xi _i}{\xi _j} \ge K{\left| \xi \right|^2}$, $x \in U$, $\xi \in {R^d}$.

(ⅱ) There is a non negative ${C^2}$ operator ${\rm{V}}$ such that $LV$ is negative for any ${R^d}\backslash U$.

Then $\mathrm{Markov}$ process $X(t)$ has a unique ergodic stationary distribution $\pi (\cdot)$.

In order to get the conditions of the existence of ergodic stationary distribution, we set Theorem 2.

Theorem 2. Define

assuming ${R^*} > 1$ and $d - \frac{{\sigma _1^2 \vee \sigma _2^2 \vee \sigma _3^2 \vee \sigma _4^2}}{2} > 0$, then, for any given initial value $(S(0), E(0), {I_1}(0), {I_2}(0)) \in R_ + ^4$, the solution $(S(t), E(t), {I_1}(t), {I_2}(t))$ of Eq (2.3) is normal and has a unique ergodic stationary distribution $\pi (\cdot)$.

Proof: To prove Theorem 2, we need to verify that conditions (ⅰ) and (ⅱ) in Lemma 1 are satisfied. First, we verify (ⅱ).

Define a $C^{2}$-function $V: R_{+}^{4}\rightarrow R_{+}$ as follows:

where ${a_i}\; (i = 1, 2, 3)$ is a positive constant. Notice that $V(S, E, {I_{1}}, {I_2})$ is not only continuous, but also tends to $\infty$ as $(S, E, {I_{1}}, {I_2})$ approaches the boundary of $R_ + ^4$. So it must be lower bounded and achieve this lower bound at a point $(S(0), E(0), {I_1}(0), {I_2}(0))$ in the interior of $R_ + ^4$. Thus the ${C^2}$-function $\tilde V$ can be defined as follows:

where $(S, E, {I_1}, {I_2}) \in (\frac{1}{n}, n) \times (\frac{1}{n}, n) \times (\frac{1}{n}, n) \times (\frac{1}{n}, n)$, $n > 1$ is a sufficiently large integer. According to Eq (4.2), ${{\rm{V}}_{\rm{1}}}$, ${{\rm{V}}_{\rm{2}}}$, ${{\rm{V}} _{\rm{3}}}$, ${{\rm{V}}_{\rm{4}}}$, ${{\rm{V}}_{\rm{5}}}$ are respectively defined as follows:

$\mathrm{It\hat o's}$ formula is applied to ${V_1}$ as follows:

where

Applying $\mathrm{It\hat o's}$ formula to ${V_2}, {V_3}, {V_4}, {V_5}$, we can get

where

So, applying $\mathrm{It\hat o's}$ formula to $\tilde V$, we can get

$m > 1$ is a constant that satisfies

$M$ is a sufficiently large value satisfying the following condition

where

Now we construct compact subsets $U$ such that condition (ⅱ) in Lemma 1 is satisfied. We define bounded closed sets as follows:

For $\delta > 0$, in the set $R_ + ^4\backslash U$, we choose $\delta$ to satisfy the following conditions:

where

Then, we prove that $L\tilde V \le - 1$ holds for any $(S, E, {I_1}, {I_2}) \in R_ + ^4\backslash U$ by dividing $R_ + ^4\backslash U$ into eight regions $R_ + ^4\backslash U = U_{i = 1}^8{U_i}$ as follows:

We prove that $L\tilde V(S, E, {I_1}, {I_2}) \le - 1$ holds for any $(S, E, {I_1}, {I_2}) \in R_ + ^4\backslash U$. This is equivalent to proving that it holds in each of the above right regions.

Case 4.1. If $(S, E, {I_1}, {I_2}) \in {U_1}$, we get

Case 4.2. If $(S, E, {I_1}, {I_2}) \in {U_2}$, we get

Case 4.3. If $(S, E, {I_1}, {I_2}) \in {U_3}$, we get

Case 4.4. If $(S, E, {I_1}, {I_2}) \in {U_4}$, we get

Case 4.5. If $(S, E, {I_1}, {I_2}) \in {U_5}$, we get

Case 4.6. If $(S, E, {I_1}, {I_2}) \in {U_6}$, we get

Case 4.7. If $(S, E, {I_1}, {I_2}) \in {U_7}$, we get

Case 4.8. If $(S, E, {I_1}, {I_2}) \in {U_8}$, we get

Obviously, from Eq (4.3) to Eq (4.11), we can obtain that $L\tilde V(S, E, {I_1}, {I_2}) \le - 1$ is true for any $(S, E, {I_1}, {I_2}) \in R_ + ^4\backslash U$. Therefore, condition (ⅱ) in Lemma 1 is satisfied.

On the other hand, to verify condition (ⅰ) in Lemma 1, the diffusion matrix of Eq (2.3) can be given as follows:

Obviously, the matrix $A$ is positive definite for any compact subset of $R_ + ^4$, so condition (ⅰ) in Theorem 2 is satisfied. From Theorem 2, we can know that Eq (2.3) has a unique ergodic stationary distribution $\pi (\cdot)$.

5.   Numerical simulation

In this section, we present numerical simulations to illustrate the influence of stochastic disturbance on disease persistence and extinction. We used the Euler-Maruyama method ^[36,37] to solve Eq (2.3) numerically. In order to apply the numerical method to Eq (2.3), we discretized the interval. Then, we computed the discrete Brownian path and used it to generate the desired increment in Eq (2.3). The discretization transformation takes the form as follows:

where $h$ is an integer and the time delay can be expressed by the step size as $\tau = h\Delta t$. ${\varepsilon _{i, n}}\; (i = 1, 2, 3, 4)$ denotes independent random variables and subject to Gaussian distribution $N(0, 1)$. ${\sigma _i} > 0\; (i = 1, 2, 3, 4)$ represents the intensity of white noise.

The parameter values in Table 1 were derived.

5.1.   Theoretical verification

We analyzed the ergodic stationary distribution of Eq (2.3) and selected the parameter values in Figure 2 as follows:

By direct calculation we have

as well as

The conditions in Theorem 2 are satisfied. According to the conclusion of Theorem 2, we can get the trend of the Eq (2.3) with unique ergodic stationary distribution which is shown in Figure 2. From the curves of the $S, E, {I_1}, {I_2}$, it can be found that susceptible, latent, pre-mutation and post-mutation individuals are asymptotically stable and the disease is persistent. In a biological sense, it means that the disease will not disappear under current conditions. If there is no intervention, the disease will spread in local areas.

We selected the parameters in Figure 3 as follows:

By direct calculation we have

as well as

The conditions in Theorem 2 are not satisfied. That is, the condition for ergodic stationary distribution is not satisfied. From Figure 3 we can see that the pre-mutation patient and post-mutation patient gradually tended to zero with the increase of time and that the stochastic model Eq (2.3) is extinct with a probability of 1. That is, the external conditions required for disease occurrence have changed and there is a high possibility that the disease will disappear in local areas.

5.2.   Influence of time delay on disease

We applied $\tau = 2.6$, $\tau = 3.6$ and $\tau = 4.6$ while the other parameters in Figure 3 remained unchanged. By direct calculation we have

as well as

It can be seen that the conditions for ergodic stationary distribution are not satisfied. When the time delay $\tau$ is increased in Figure 4, the curves of ${I_1}$ and ${I_2}$ fluctuate and no longer tend to zero whereas the curves of $S$ and $E$ continue to fluctuate. The disease will manifest as periodic outbreaks as shown in Figure 4 and lead to the reinfection of susceptible, latent and infected individuals. Through the analysis of Figure 4, it can be seen that with the increase of time delay, the disease will break out periodically at higher frequencies.

In a biological sense, after a fairly regular interval, the disease will outbreak again locally and have the necessary conditions for exogenous pathogens to cause disease. Therefore, during the spread of an infectious disease, we can realize the periodic law of virus mutation through systematic scientific research and take relevant protective measures. We can develop drugs and improve the effectiveness of vaccines, so that they can adapt to different mutations of the virus antibodies.

5.3.   Influence of noise on disease

As shown in Figure 5, we increased the intensities of the noise and applied ${\sigma _1} = 0.09, {\sigma _2} = 0.08, {\sigma _3} = 0.1, {\sigma _4} = 0.09$. As shown in Figure 6, we continued to increase the intensities of the noise and applied ${\sigma _1} = 0.2, {\sigma _2} = 0.1, {\sigma _3} = 0.2, {\sigma _4} = 0.1$. For the results shown in Figures 5 and 6, the other parameters were consistent with those in Figure 4, where the ergodic stationary distribution of Theorem 2 is also not satisfied. We respectively studied the effect of increasing noise on disease extinction when $\tau = 2.6$, $\tau = 3.6$ and $\tau = 4.6$. It can be seen from Figures 5 and 6 that the curves of ${I_1}$ and ${I_2}$ gradually approach zero as time goes on, and that the periodic outbreak of disease caused by time delay $\tau$ can be reduced by increasing the intensity of the noise. It means that diseases with periodic outbreaks will become extinction again. Through the analysis of Figures 5 and 6, it can be found that noise has a great influence on the persistence and extinction of a virus mutation model with time delay.

On the basis of the above research, we can enhance noise interference in different measures to promote the extinction of the disease, such as the government strengthening the early warning of the disease to avoid wide spread, strengthening personal protection through the media for the public and hospitals strengthening prevention and control measures against large-scale diseases.

6.   Conclusions

In infectious disease models, the combination of white noise and time delay has great influence on the spread and disappearance of an infectious disease, which makes the dynamic behavior of an the system complicated. We considered the effects of stochastic disturbance on the persistence of virus mutations in a model with time delay. First, the existence and uniqueness of the positive solution of the proposed model was proved using stochastic inequalities. Second, by constructing an appropriate stochastic Lyapunov function, if ${R^*} > 1$ and $d - \frac{{\sigma _1^2 \vee \sigma _2^2 \vee \sigma _3^2 \vee \sigma _4^2}}{2} > 0$ are satisfied, the proposed model has an ergodic stationary distribution which means that the disease is persistent; otherwise, the disease will die out. Finally, numerical simulations were carried out to verify the theoretical results. The results show that stochastic disturbance has great influence on the spread and persistence of infectious diseases with time delay.

Through the above theoretical and numerical analyses, we found that with the increase of the time delay from pre-mutation to post-mutation, the virus will undergo periodic outbreaks and susceptible, latent and infected people will be reinfected. When the noise intensity is large enough under certain constraints, the periodic diseases caused by the time delay can become extinct again. Therefore, the following measures can be taken to prevent and control the spread of mutated infectious diseases. On the one hand, we can reduce the periodic outbreaks of disease by reducing the time delay before and after the virus mutates. It is necessary to realize the periodicity of virus mutations and carry out drug research according to the conditions of periodic outbreaks so as to strengthen the resistance of vaccines to the mutated environment. On the other hand, we can promote disease extinction by increasing stochastic perturbations. The government should strengthen early warnings of the disease, increase personal protection and strengthen prevention and control measures against large-scale diseases.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This work was supported by grants from the Natural Science Foundation (No. 11772002 and No. 12202005), Ningxia Higher Education First-Class Discipline Construction Funding Project (NXYLXK2017B09), Major Special Project of North Minzu University (No. ZDZX201902) and Postgraduate Innovation Project of North Minzu University (YCX23069).

Conflict of interest

The authors declare that there is no conflict of interest.