Reliability analysis of constant partially accelerated life tests under progressive first failure type-II censored data from Lomax model: EM and MCMC algorithms

1.   Introduction

Constrained optimization is particularly challenging because certain constraints must be satisfied while optimizing the objective function. This type of problem has a wide range of applications in many fields, such as economics, engineering, and natural sciences. The mathematical model of the constrained optimization problem is expressed as follows ^[1]:

where $f(x)$ is the objective function, $g(x)$ is an inequality constraint, $h(x)$ is an equality constraint, $x$ is a decision variable, $D$ is the dimension of decision variable, $q$ is the number of inequality constraints, $m$ is the number of constraints, and $L_{i}$ and $U_{i}$ are the lower and upper bounds of the $i$th component, respectively.

For the above problem, the violation degree of any decision vector $x$ regaiding the $j$th constraint can be defined as follows:

Here, $\delta$ is the positive slack of the equality constraint. Therefore, the violation degree of decision variable $x$ with respect to all constraints can be defined as follows:

If $G(x) = 0$, then the decision variable $x$ is a feasible solution to the constrained optimization problem. The goal of solving the constrained optimization problem is to find the feasible solution with the minimum function value.

Due to the limitations of the constraints, solving a constrained optimization problem is more difficult than solving an unconstrained optimization problem. Therefore, effectively addressing constraints becomes the top priority. At present, the commonly used constraint processing methods include the penalty function method ^[2], feasibility rule method ^[3], $\varepsilon$-constraint method ^[4], multiobjective method ^[5], and stochastic ranking method ^[6]. With the development of computer technology and optimization algorithms, intelligent optimization algorithms with a global optimization capability and objective function gradient independence are widely used to solve constrained optimization problems. Karaboga ^[7] described a modified artificial bee colony algorithm (mcABC) for constrained optimization problems, and for constraint handling, this algorithm uses feasibility rule, consisting of three simple heuristic rules and a probabilistic selection scheme for feasible solutions based on their fitness values and for infeasible solutions based on their violation values. Shi ^[8] proposed an improved fruit fly optimization algorithm (IFOA) with multi-strategy hybrid co-evolution, and the convergence accuracy of the algorithm was improved through real-time dynamic updating of the optimal information of the swarm and a local in-depth search strategy. Jia ^[9] proposed an improved coati optimization algorithm (ICOA) to solve constrained engineering optimization problems. Wang ^[10] proposed a compound differential evolution algorithm that balances the diversity and convergence, improving algorithm convergence for solving constrained optimization problems. Wang ^[11] proposed an improved genetic algorithm based on two-direction crossover and grouped mutation (GA-TDX) to efficiently solve constrained optimization problems, enhancing search efficiency by leveraging directional information and maximizing the benefits of distinct mutation operators. Peng ^[12] designed a hybrid constraint-handling technique (HCT) based on population evolution information to balance the objective function and constraints, and proposed an evolutionary constrained optimization algorithm with HCT (ECO-HCT) to solve solve constrained optimization problems.

Among the many intelligent optimization algorithms, the PSO algorithm ^[13] was proposed by Drs. Eberhart and Kennedy in 1995 and is used by many researchers to solve constrained optimization problems and real-world problems ^[14] because of its computational simplicity and flexibility. Lu ^[15] proposed a double-track schema within PSO called double-track PSO (DTPSO) to address the nonlinear constrained optimization problem. When an infeasible region blocks a particle, the DTPSO algorithm creates a copy of the particle. Different search strategies are used for the original and copied particles so that the algorithm can move to feasible and infeasible regions. Liu ^[16] proposed a new hybrid PSO differential evolution (PSODE) algorithm to solve constrained optimization problems. When the particles in the PSODE algorithm stagnate, the DE algorithm is used to activate the particles to continue the optimization search. Wang ^[17] designed a hybrid multi-swarm PSO algorithm (HMPSO) to address the constrained optimization problem. This algorithm uses the parallel search operator to search for each subswarm simultaneously and the DE algorithm to improve the state of the personal best position to better expand the search range. Guo ^[18] used a feasibility-based rule to process constraints and used DE to optimize the personal best position with the PSO algorithm (PSO-DE) to improve the convergence efficiency of the algorithm. Venter ^[19] transformed all the constraints into an objective; therefore, the constrained optimization problem was transformed into an unconstrained dual-objective optimization problem, and the model was solved using a multi-objective PSO algorithm. Ang ^[20] proposed a constrained multi-swarm particle swarm optimization without velocity (CMPSOWV), incorporating constraint handling, dual evolution phases for robustness, and diversity maintenance schemes to overcome limitations and prevent premature convergence in solving COPs.

Although many studies have been performed to solve constrained optimization problems with the PSO algorithm, quickly optimizing the objective function value and controlling the constraint violation degree are difficult at this stage, and balancing the two has always been the main research direction. The optimization principles of the PSO algorithm depend mainly on the selection of the best position. Therefore, generating a personal best position population while considering objective functions and constraints is our focus. Hence, we propose a personal best position update method that integrates the $\varepsilon$-constraint, DE strategy, and feasibility rule. First, this method utilizes the $\varepsilon$-constraint method to give infeasible solutions located at the boundary of the feasible region the opportunity to enter the intermediate personal best position population. Second, the DE strategy is used to further guide the intermediate personal best position population towards the feasible region, forming an intermediate evolutionary population. Finally, using feasibility criteria, a stricter selection is made between the intermediate personal best position population and the intermediate evolutionary population to promote the rapid convergence of the algorithm. Compared with previous single constraint processing methods, this composite evolutionary updating method not only considers the objective function and constraints simultaneously, but also utilizes the powerful optimization capabilities of the DE strategy to select the personal best position population that can better guide the population close to the global best position, thereby ensuring the convergence speed and accuracy of the ICPSO algorithm.

2.   The classical PSO algorithm

The PSO algorithm is a swarm intelligence algorithm proposed by simulating the foraging behavior of a flock of birds. In the PSO algorithm, a solution to the problem is represented as a particle in a decision space. The entire swarm is guided by the personal and global best positions and flies within the solution space to find the optimal solution. To better balance local exploitation and global exploration, this section introduces a PSO algorithm ^[21] with a linearly decreasing inertia weight. The specific flow is as follows:

Algorithm 1. PSO algorithm

Step 1: Assume a population size $N$, self-cognitive coefficient $c_{1}$ and social cognitive coefficient $c_{2}$. Let each particle be an individual in the $D$ dimensional space, let the position vector of the $i$th particle be $x_{i} = (x_{i1}, x_{i2}, \cdots, x_{iD})$, let the velocity vector be $v_{i} = (v_{i1}, v_{i2}, \cdots, v_{iD})$, where $i = (i, 2, \cdots, N)$, and let the maximum number of iterations be $T$. Randomly generate $N$ individuals to create the initial population $X(0)$, and set $t = 0$.

Step 2: Calculate or estimate the fitness of each particle in $X(t)$.

Step 3: Update the speed and position of each particle as follows:

where $\omega_{max}$ and $\omega_{min}$ are the maximum and minimum inertia weights, respectively.

Step 4: Update the personal best position of each particle $p_{ibest}$ and the global best position $g_{best}$.

Step 5: If the termination criterion is met, then output $g_{best}$ as the optimal solution, and terminate the calculation. Otherwise, set $t = t+1$, and go to Step 2.

3.   An improved composite particle swarm optimization algorithm for constrained optimization problems (ICPSO)

The classical PSO algorithm is good at searching for the best solution in unconstrained continuous space, but has no advantageous strategy for dealing with constraints. Therefore, in this paper, an improved composite particle swarm optimization algorithm is proposed for constrained optimization problems. The algorithm effectively combines strategies such as the $\varepsilon$-constraint, DE strategy, and feasibility rule to construct a novel method for updating the personal best position. This method enhances the algorithm's ability to find feasible solutions and quickly converge to the global optimal solution.

3.1.   Feasibility rule

The feasibility rule is a constraint processing mechanism proposed by Deb ^[22] in 2000, and the specific rules are as follows: For two individuals $x_{i}$ and $x_{j}$, if $x_{i}$ is superior to $x_{j}$, one of the following conditions should be satisfied:

(1) When $G(x_{i}) = G(x_{j}) = 0$, $f(x_{i}) < f(x_{j})$;

(2) When $G(x_{i})\neq 0$ and $G(x_{j})\neq0$, $G(x_{i}) < G(x_{j})$;

(3) $G(x_{i}) = 0$ and $G(x_{j})\neq0$.

3.2.   $\varepsilon$-constraint

The $\varepsilon$-constraint method is a constraint processing mechanism proposed by Takahama and Sakai ^[23] in 2010. The specific rules are as follows: For two individuals $x_{i}$ and $x_{j}$, if $x_{i}$ is superior to $x_{j}$, one of the following conditions should be satisfied:

(1) When $G(x_{i})\leq \varepsilon \bigwedge G(x_{j})\leq \varepsilon$, $f(x_{i}) < f(x_{j})$;

(2) When $G(x_{i}) = G(x_{j})$, $f(x_{i}) < f(x_{j})$;

(3) In other cases, $G(x_{i}) = 0 < G(x_{j})$.

Here, $\varepsilon = \left\{\begin{array}{ll} \varepsilon_{0}(1-\frac{t}{T}), & if\; \frac{t}{T}\leq p; \\ 0, & otherwise\\ \end{array}\right.$ is a numerical value that decreases as the number of iterations increases, $\varepsilon_{0}$ is the initial threshold, usually the maximum constraint violation degree of the initial population, and $cp = -\frac{\log \varepsilon_{0}+\lambda}{\log(1-p)}$, where $\lambda$ is 6, and $p$ is the degree to which the information that controls the objective function is used.

3.3.   DE strategy

Although the PSO algorithm is simple and easy to implement, it is prone to becoming trapped in a local extremum during the search process. To address this shortcoming, researchers are constantly attempting to incorporate new strategies to enhance the global exploration ability. The DE strategy is one of the recognized effective strategies. PSODE algorithm ^[16] applied the DE strategy to the current population to help it break out of the stagnation state. However, this method uses only the DE strategy when the threshold is reached. Thus, this method has limited effectiveness. HMPSO algorithm ^[17] and PSO-DE algorithm ^[18] both used the DE strategy to find the personal best position population. However, when performing the DE operation on any personal best position, three other personal best positions are selected for mutation, and the personal best position information is not used. However, for the PSO algorithm, the personal best position stores the historical information of the individual flight and should not be completely discarded. Therefore, in this paper, the DE/rand/1 strategy is used when performing the mutation operation, and the personal best position is retained as $x_{r_{1}}$. Then, two personal best positions are randomly selected as $x_{r_{2}}$ and $x_{r_{3}}$. The other operations are the same as those in the standard DE strategy. Finally, an intermediate evolutionary population with the personal best position is generated.

3.4.   Best position update strategy

The optimization of the PSO algorithm mostly depends on learning the global best position and personal best positions. Therefore, the selection and update of the best position are particularly important. Moreover, an effective solution to the constrained optimization problem requires a balance between the degree of constraint violation and the objective function value. If these two indicators can be considered simultaneously when updating the best position, this could help the algorithm converge.

3.4.1.   Personal best position population update with composite concepts

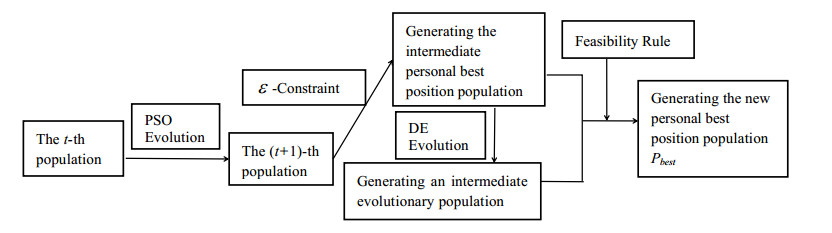
To update the personal best position population $P_{best}$, there are two constraint selections steps and one evolution step in the ICPSO algorithm. The first constraint selection step targets the new population produced after PSO evolution. To expand the search space of the algorithm and fully utilize valuable information from partially infeasible solutions, a relatively relaxed constraint violation method, the $\varepsilon$-constraint method, is adopted to guide the update of the population, thus forming the intermediate personal best position population; to increase the search speed of the algorithm, the DE strategy is employed to optimize and evolve the intermediate personal best position population, generating the intermediate evolutionary population. Finally, to ensure the superiority of the personal best population $P_{best}$, a more stringent feasibility rule with higher constraint requirements is applied to conduct a rigorous comparison and selection between the intermediate personal best position population and the intermediate evolutionary population. Clearly, the adoption of this composite updating strategy to guide the update process effectively balances the two metrics of constraint violation and objective function value, facilitating algorithm convergence. The detailed operation is shown in Figure 1.

3.4.2.   Global best position update

The goal of constrained optimization is to find the feasible solution with the minimum function value. To ensure that the population effectively moves to the feasible region, when updating the global best position $g_{best}$, the feasibility rule with stronger constraints is used to guide the generation of a new $g_{best}$.

3.5.   ICPSO algorithm

The specific process of the ICPSO algorithm is as follows, and the flowchart of ICPSO algorithm is given in Figure 2:

Algorithm 2. ICPSO algorithm

Step 1: Randomly initialize the position vector and speed vector and set the parameters $c_{1}$, $c_{2}$, $\omega_{max}$, and $\omega_{min}$, the crossover factor $F$ and $CR$, the maximum number of iterations $T$, the population size $N$, and $t = 0$.

Step 2: Calculate the fitness of each particle in the initial population, set the initial best personal position as $P_{best} = X(0)$, and use the feasibility rule to select the global best position $g_{best}$ from the population $P_{best}$.

Step 3: Use speed update (Eq (2.1)) and position update (Eq (2.2)) to update the current population and form a new population, use Eq (3.1) to address the cross-boundary particles ^[24]:

Step 4: Calculate the fitness of each particle in the current population.

Step 5: Use the $\varepsilon$-constraint method and the current population to generate the intermediate personal best position population.

Step 6: Apply the DE strategy to the personal best position population to form an intermediate evolutionary population.

Step 7: Use the feasibility-based rule to compare the best personal position population and the intermediate evolutionary population to form the final $P_{best}$.

Step 8: Use the feasibility-based rule to select the global best position $g_{best}$ from the population $P_{best}$.

Step 9: If the termination criterion is satisfied, output $g_{best}$ as the optimal solution and terminate the calculation. Otherwise, set $t = t+1$ and go to Step 3.

3.6.   Complexity analysis

We present the computational time complexity of the ICPSO algorithm below, the main steps during one iteration for a population of size $N$, the dimension is $D$.

(1) Updating a particle: $O(N\times D)$;

(2) Generate the intermediate personal best position population: $O(N)$;

(3) Generate the intermediate evolutionary population by DE strategy: $O(N\times D)$;

(4) Renew the personal best position population: $O(N)$;

(5) Renew the global best position: $O(N)$.

Thus, the computational time complexity of the ICPSO algorithm is $O(N\times D)$, which demonstrates that this algorithm is computationally efficient.

4.   Numerical experiment and result analysis

4.1.   Test questions and parameter settings

To further test the performance of the ICPSO, 13 constrained optimization benchmark functions from the IEEE CEC2006 dataset and 28 constrained optimization benchmark functions from the IEEE CEC2017 dataset were selected for testing. Table 1 shows the specific characteristics of 13 functions from the IEEE CEC2006 dataset. $D$ represents the number of decision variables, $\rho$ represents the ratio between the feasible region and the search space estimated by stochastic simulation, $LI$ and $NI$ represent the numbers of linear and nonlinear inequality constraints, respectively, $LE$ and $NE$ represent the numbers of linear and nonlinear equality constraints, respectively, $a$ represents the number of active constraint functions near the optimal solution, and $f(x^{*})$ represents the global optimal function value, that is, the known optimal solution of these functions. The detailed mathematical formulation are presented in the technical report of Liang ^[25].

Table 2 shows the specific characteristics of 28 functions from the IEEE CEC2017 dataset. $E$ and $I$ represent the numbers of inequality constraints and equality constraints, respectively. The detailed mathematical formulation of all CEC2017 functions are presented in the technical report of Wu ^[26].

The parameters of the ICPSO algorithm are set as follows: $c_{1} = c_{2} = 2.05$, $\omega_{max} = 1$, $\omega_{min} = 0.4$, $F = 0.7$, $CR = 1.0$, $N = 60$ and number of evaluations of the fitness function$= 5\times 10^5$ for CEC2006, $N = 100$ and number of evaluations of the fitness function$= 2\times 10^5$ for CEC2017, the slack of the equality constraint is $\delta = 0.0001$. The algorithm was coded using MATLAB R2016a and run on a computer with an Intel(R) Core(TM) i7-6567U central processing unit (CPU) @ 3.30 GHz or 3.20 GHz and 8.00 GB of installed memory.

4.2.   Results analysis

4.2.1.   Comparison between ICPSO and its variant

To better illustrate the effectiveness of the various combinations of strategies proposed in this paper, two improved PSO algorithms without the DE strategy were constructed: The PSO+Eps algorithm and the PSO+Deb algorithm. The selected strategy for the constraint-guided update of the personal best position differs between the two methods, with the former using the $\varepsilon$-constraint method and the latter using the feasibility-based rule. Moreover, an improved algorithm containing the DE strategy PSO+DE+Deb+Deb was constructed. The difference between this algorithm and the ICPSO algorithm is that this algorithm uses the feasibility-based rule to guide the two update methods for the personal best position. To ensure the comparability of the numerical results, the parameter settings of the four algorithms are exactly the same. In this section, the Wilcoxon rank-sum test was used to compare the performances of the algorithms. The null hypothesis is that there is no significant difference in performance between the ICPSO algorithm and the other algorithms. Three symbols are used to indicate whether there is a significant difference in performance between the ICPSO algorithm and the other algorithms: (+) indicates that at the significance level of $\alpha = 0.05$, the performance of the ICPSO algorithm is significantly improved compared to that of the other algorithms (-) indicates that the performance of the ICPSO algorithm is inferior to that of the other algorithms; and ( = ) indicates that there is no significant difference in performance between the algorithms.

(1) Performance evaluation using CEC2006 benchmark functions

Figure 3 shows the proportion of optimal solutions that are feasible for the 13 benchmark functions after 25 independent runs of each algorithm. As long as the constraint processing mechanism is used, the PSO algorithm is more effective at solving the constrained optimization problem. Of course, for functions F04 and F10, the PSO+Deb and PSO+Eps algorithms converge to an infeasible solution; however, as long as the DE strategy is added to the algorithm, it can be guaranteed that the algorithms can converge to the feasible domain for all 13 test problems, reflecting the effectiveness of the DE strategy.

The data in Table 3 are the numerical results of the 4 algorithms after 25 independent runs of the 13 test problems. In the table, Best is the best solution, Worst is the worst solution, Median is the median value, Mean is the mean value, and Std is the standard deviation. Wil test is the Wilcoxon test result. Except for F06, F11, and F12 (on which the four algorithms obtain the same result), ICPSO outperforms the other algorithms, in particular, it has a smaller variance, indicating that ICPSO has better stability. For F01, F02, and F13, ICPSO achieves the optimal results in terms of both the mean and variance. For F03, F05, and F09, ICPSO and PSO+DE+Deb+Deb can obtain the same optimal mean value, but ICPSO appears to be more stable with a smaller variance. For F10, PSO+DE+Deb+Deb performs better than ICPSO, and PSO+Deb outperforms PSO+Eps, indicating that for a linear problem, the constraint processing mechanism guided by the feasibility-based rule is better than that of the $\varepsilon$-constraint method. The Wilcoxon rank-sum test shows that, except for F13, the ICPSO and PSO+DE+Deb+Deb algorithms had no significant differences in performance. However, these two algorithms are far better than the PSO+Esp and PSO+Deb algorithms, demonstrating that the introduction of the DE strategy greatly improves the performance of the algorithm.

Figure 4 shows the mean convergence of the 13 functions for the 4 algorithms. The x-axis is the number of evaluations of the fitness function, and the y-axis is the mean of the function values for 25 runs. As shown in Figure 4, since the algorithm that uses the $\varepsilon$-constraint method as the constraint-guided strategy has a moderate slack effect on the infeasible solutions in the early stage, the convergence range is expanded and the convergence speed is reduced in the early stage. The results for F06, F07, F10 and F11 are shown in Figure 4. The convergence is accelerated after a short period of adjustment and is more stable for the same number of evaluations. The result for F05 in Figure 4 further shows that the $\varepsilon$-constraint method guides the algorithm update process. To enhance the global search ability in the early stage, some infeasible solutions with smaller objective function values are allowed to appear. However, as the number of evolutionary generations increases, the algorithm can instead converge to the optimal solution more quickly and stably.

(2) Performance evaluation using CEC2017 benchmark functions

In this section, the scalability of the proposed ICPSO algorithm in addressing constrained optimization problems is further evaluated using another 28 benchmark functions that were introduced in CEC2017. These CEC2017 benchmark problems pose a greater challenge compared to those of CEC2006, as they encompass a broader array of constraints. Note that the experimental results of those benchmark functions, in which both the ICPSO and the other three algorithms cannot find feasible solutions consistently, have been excluded from the comparative analysis (C17–C19 and C26–C28).

Figure 5 shows the proportion of optimal solutions that are feasible for the 22 benchmark functions after 25 independent runs of each algorithm. For C11, except for the ICPSO algorithm with a success rate of 4%, all other algorithms did not obtain feasible solutions in 25 runs; for C06, the success rate of ICPSO is 100%, PSO+DE+DEB+DEB is 96%, and the other two variants of PSO algorithms obtained only 80% and 60%, respectively; and the PSO+Deb algorithm did not achieve a success rate of 100% for C22. It is not difficult to find that the IPSO algorithm with a composite optimization strategy can improve the success rate of PSO algorithm in solving these 22 constrained optimization problems.

The Best, Worst, Median, Mean, and Std values obtained by the compared algorithms in solving CEC2017 benchmark functions after 25 runs are presented in Table 4. Figure 6 shows the mean convergence of the 22 functions for the 4 algorithms. For C04, C07, C13–C16, C20, C21, and C23, the ICPSO algorithm achieved the best results. As shown in Figure 6, ICPSO algorithm can stably converge on these functions. For C1–C3, C5, C8–C10, C12, and C24, both ICPSO and PSO+DE+Deb+Deb performed well, especially for C01–C03 and C05. The two algorithms stably converged to 0 in 25 calculations. For C06, combined with the success rate and Figure 6(f), it can be found that only ICPSO is much better than the other three algorithms in solving this problem. C11 is difficult to solve. Except for ICPSO, other 3 algorithms cannot obtain its feasible solution. The success rate of ICPSO is also very low. Therefore, effective solving strategies need to be set according to the characteristics of this function. The results presented in Tables 4 show that ICPSO is superior to the other 3 algorithms for solving the 22 functions; that is, the composite strategy for updating personal best position can improve the ability of the PSO algorithm to solve the constrained optimization problems. The results of the Wilcoxon test show that the performance of ICPSO is significantly better than PSO+Eps and PSO+Deb, which is equivalent to PSO+DE+Deb+Deb. However, combined with the success rates, the composite strategy can be used to solve these 22 problems.

4.2.2.   Comparison and analysis regarding algorithms in other studies

To further validate the performance of the ICPSO algorithm in solving constrained problems, the ICPSO algorithm was compared with two intelligent algorithms proposed in recent years and three improved PSO algorithms with the DE strategy for CEC2006 benchmark functions; and compared with three new intelligent algorithms for CEC2017 benchmark functions. The data of all comparison algorithms are derived from cited references, the main parameters of each algorithm were set as follows:

mcABC algorithm: The number of evaluations of the fitness function was $2.5\times10^5$, and the correction rate was $0.8$;

IFOA algorithm: $N = 100$, $T = 5000$, Selection probability $P = 0.8$;

PSO-DE algorithm: $c_{1} = c_{2} = 1.5$, $\omega_{max} = 0.8$, $\omega_{min} = 0.4$, $F = 0.95$, $CR = 0.95$;

HMPSO algorithm: The number of evaluations of the fitness function was $3\times10^5$, $N = 60$, the size of each sub-swarm $N_{s} = 8$, $F = 0.7$, $CR = 1.0$, $T = 2500$;

PSODE algorithm: The number of evaluations of the fitness function was $\in[1.06\times10^4, 1.401\times10^5]$, $F\in[0.9, 1.0]$, and $CR\in[0.95, 1]$;

CMPSOWV algorithm: $N = 100$, subpopulation $N^k = 10$ with $k = 1, \cdots, 10$, acceleration coefficients $c_{1} = c_{2} = c_{3} = 4.1/3$;

GA-TDX algorithm: $N = 100$, $T = 1000$, Penalty parameter $m = 10^10$, the proportion of the best group in the population $\beta = 0.2$, the shape parameter $\gamma = 6$;

ECO-HCT algorithm: The number of evaluations of the fitness function was $2\times10^5$, $N = 50$, $F = 0.8$, $CR = 0.9$, Elite replacement strategy control parameters $\omega_{min} = 0.2, \omega_{max} = 0.8$, Archive $A_{2}$ size $\alpha_{1} = 40$.

Table 5 shows that the ICPSO algorithm achieves the optimal mean function values for F03–F09 and F11–F13. The standard deviations for F08 and F11 obtained by the ICPSO algorithm are inferior to those obtained by the HMPSO and PSO-DE algorithms, respectively; however, the accuracy of ICPSO is greater than $10^{-30}$, which reflects the stability of this algorithm. For F01, F02, and F10, the performance of the ICPSO algorithm needs to be improved.

In Table 6, $\nabla$ represents a method cannot achieve at least a feasible solution on a benchmark function at the end of 25 runs. From Table 6, we observe that ICPSO is able to solve these CEC2017 benchmark functions, achieving 8 best mean values and 6 second-best mean values. This indicates promising search accuracies in solving these challenging problems. Moreover, other algorithms such as CMPSOWV, GA-TDX, and ECO-HCT are reported to be able to produce 6, 6, and 10 best mean values, respectively, in solving all CEC2017 benchmark functions. Specifically, for C11, ECO-HCT fails to produce a feasible solution.

4.3.   Engineering applications

To further verify the performance of ICPSO, four real-world application examples are used ^[27]. The ICPSO algorithm is tested against three of latest evolutionary algorithms: the self-adaptive spherical search algorithm (SASS) ^[28], L-SHADE for constrained optimization with Lévy flight (COLSHADE) ^[29], and modified covariance matrix adaptation evolution strategy (sCMAgES) ^[30].

4.3.1.   Pressure vessel design

The goal of this problem is to optimize the cost of vessel welding, material, and formation. This problem has four constraints that need to be satisfied, and four variables are used to calculate the objective function: Shell thickness, head thickness, inner radius, and vessel length (excluding the head). The current theoretical optimal solution is 5885.3327736. The mathematical model of this problem is as follows:

Table 7 lists the calculation results of the four algorithms for the pressure vessel design problem. The overall results have certain deviations from the optimal solution. However, the ICPSO and SASS algorithms perform slightly better than the other two algorithms, and the ICPSO algorithm outperforms the SASS algorithm in terms of standard deviation by 5 orders of magnitude, indicating that the ICPSO algorithm is more stable.

4.3.2.   Weight minimization of a reducer

This problem involves the design of a small aircraft engine reducer. The current theoretical optimal solution is 2994.4244658. The mathematical model of this problem is as follows:

Table 8 lists the calculation results of the weight minimization problem for the reducer. For this problem, all the algorithms obtain similar results. The stability of ICPSO, SASS, and COLSHADE is similar, and all reach $10^{-13}$, indicating that the ICPSO algorithm is stable and effective at solving this type of problem.

4.3.3.   Design of tension/compression springs (Case 1)

The goal of this problem is to optimize the weight of a tension or compression spring. This problem contains four constraints and uses three variables to calculate the weight: The wire diameter, average coil diameter, and number of active coils. The current theoretical optimal solution is 0.012665232788. The mathematical model of this problem is as follows:

Table 9 lists the calculation results for the tension/compression spring design problem (Case 1). For this problem, all the algorithms obtain similar results. Among them, SASS is the most stable, followed by ICPSO, with a standard deviation of $10^{-24}$, which is far lower than those of sCMAgES and COLSHADE, demonstrating the stability of the ICPSO algorithm in solving this problem.

4.3.4.   Design of tension/compression springs (Case 2)

The goal of this problem is to optimize the volume of steel wire needed to construct a helical compression spring. There are three design variables in this problem, namely, the outer diameter (continuous variable), the number of spring coils (integer variable), and the spring wire diameter (discrete variable). This problem contains eight nonlinear inequality constraints, and the current theoretical optimal solution is 2.6138840583. The mathematical model of this problem is as follows:

Table 10 lists the calculation results for the tension/compression spring design problem (Case 2). For this problem, except for the sCMAgES algorithm, the algorithms all obtain similar results. Among them, the ICPSO algorithm is the most stable, with a standard deviation of $10^{-31}$, which is far lower than those of the other algorithms, demonstrating the high stability of the ICPSO algorithm in solving this problem.

5.   Conclusions

Our results present the improved composite particle swarm optimization algorithm algorithm (ICPSO) for solving constrained optimization problems. We develop a new method for updating the personal best position population, which is a composite strategy consisting of two constrained selections steps and one evolution step. The method utilizes the relaxation mechanism of the $\varepsilon$-constraint to absorb some "excellent" infeasible solutions into the intermediate personal best position population. To accelerate convergence, the DE strategy is used to optimize this population and generate the intermediate evolutionary population. Finally, using a feasibility rule method with strict constraint control, we select individuals with better constraint violation degrees from the two intermediate populations to enter the personal best position population, thereby guiding the population to efficiently converge towards the global optimal position. To verify the effectiveness of the composite strategy in the ICPSO algorithm, we construct three comparative algorithms that use partial strategies: PSO+EPS, PSO+Deb, and PSO+DE+Deb+Deb. The numerical results indicate that the composite strategy in the ICPSO algorithm is effective. When one or more components are missing, the convergence performance of the algorithm is significantly reduced. Finally, comparing the performance of the ICPSO algorithm to that of other algorithms demonstrated the effectiveness and stability of the proposed algorithm for solving the 13 functions from CEC2006, 22 functions from CEC2017, and 4 real-world constraint optimization problems.

In the future, we will mostly focus on two areas. First, more effective mechanisms based on ICPSO will be considered to handle more complex constrained optimization problems, such as large-scale constrained optimization problems ^[31] and multi-objective constrained optimization problems ^[32]. Second, more effective and targeted operators will be designed to form an operator pool, enabling the ICPSO algorithm to solve more real-world problems.

Use of AI tools declaration

The authors declare that they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

This research was supported by the Natural Science Foundation of NingXia Hui Autonomous Region (No. 2021AAC03185), the Research Startup Foundation of North Minzu University (No. 2020KYQD23), the First-Class Disciplines Foundation of NingXia (No. NXYLXK2017B09) and the Major Project of North Minzu University (No. 2019MS003).

Conflict of interest

The authors declare no conflicts of interest.