An inertial iterative method for solving split equality problem in Banach spaces

1.   Introduction

Let $H_1$, $H_2$ and $H_3$ be three real Hilbert spaces. Let $C$ and $Q$ be nonempty closed convex sets of $H_1$ and $H_2$, respectively. The split equality problem (SEP) for mapping $A:H_1\to H_3$ and $B:H_2\to H_3$ was proposed by Moudafi ^[17] as finding

When $B = I$, the SEP reduces to the split feasibility problem (SFP) presented by Censor and Elfving ^[5] as follows:

which appears in many practical applications, such as signal processing ^[3] and medical image reconstruction ^[2]. The SFP can also be applied to simulate intensity-modulated radiation therapy ^[6]. In order to approximate the solution of SFP, many algorithms have been proposed (see ^{[11,15,16,20,24,25,29,31]}).

The application of SEP can cover many aspects, such as decomposition methods for PDEs, and applications in game theory ^[1]. Many important issues, for instance, null point problem of maximal monotone operators, equilibrium problems and optimization problems, can be converted into SEP ^[17].

The algorithm to solve SEP in Hilbert spaces was first proposed by Moudafi ^[17] in 2013, also known as the alternating $CQ$-algorithm ($ACQA$):

where $\{\gamma_n\}$ is a nondecreasing sequence. They proved that $\{(s_n, t_n)\}$ generated by (1.3) converges weakly to a solution of SEP.

To get strong convergence results, Shi et al. ^[23] introduced a modification of Moudafi's $ACQA$ algorithm:

where $\{\mu_n\}$ is a positive sequence in $(0, 1)$. It was proved that $\{(s_n, t_n)\}$ generated by (1.4) converges strongly to a solution of the SEP.

To accelerate the convergence, Polyak ^[19] firstly proposed the inertial extrapolation method for solving the smooth convex minimization problem. The inertial algorithm is a two-step iterative method, using the first two iterations to define the next iteration. Nesterov ^[18] introduced a modified method to improve the convergence rate as follows:

where $\beta_n\in[0, 1)$ is an extrapolation factor, and $\{\lambda_n\}$ is a positive sequence. The inertia is denoted by the term $\beta_n(s_n-s_{n-1})$. It is worth noting that the inertial term greatly improves the performance of the algorithm and has a good convergence property ^[18]. Encouraged by the inertial term, many authors have proposed different algorithms with inertial techniques to solve a number of different problems(see ^{[9,10,11,20,33,34]}).

Very recently, Sahu ^[20] proposed a relaxed $CQ$ algorithm with the inertial term for solving the SFP in Hilbert spaces:

where $\{\nu_n\}$ is a positive sequence. The sequence $\{s_n\}$ generated by (1.6) converges weakly to a solution of the SFP was proved by the author.

Since the setting of Banach spaces sometimes allows for more realistic modeling of problems arising in industrial and natural science applications, solving SFP and SEP in Banach space is interesting not only from a theoretical point of view, but also for solving related application problems in the real world.

In ^[21], Schöpfer et al. proposed the following algorithm for solving the SFP in Banach spaces:

where $\lambda_n$ is a positive parameter, $\Pi_C$ denotes the Bregman projection, $J_p$, $J_q^*$, $J$ are duality mappings, and $P_Q$ denotes the metric projection. They showed the weak convergence of the algorithm (1.7).

In some applied disciplines, norm convergence is preferable to weak convergence. Wang ^[30] proposed an algorithm for solving the following multiple-sets split feasibility problem (MSSFP): find a point $s^{\ell}\in E_1$, such that

where $E_1$, $E_2$ are Banach spaces, $\{C_k\}_{k = 1}^{m}$, $\{Q_t\}_{t = 1}^{r}$ are nonempty, closed and convex subsets of $E_1$ and $E_2$, respectively. When $m = r = 1$ in (1.8), the MSSFP reduces to SFP. The author proposed the following iterative algorithm and proved the strong convergence: for any $n\in\mathbb{N}$,

where $i(n) = n\mod(r+d)+1$, and $0\leq \delta\leq \delta_n\leq (\frac{q}{c_q||A||^q})^{\frac{1}{q}}$, $c_q$ is a constant. For any $s_0$, $\{s_n\}$ is generated by the following iteration:

The author proved that the sequence $\{s_n\}$ generated by (1.9) converges strongly to a point in the solution set $\Omega$.

Recently, Zhou et al.^[33] proposed an improved shrinking projection algorithm with inertial technique to solve the split common fixed point problem (SCFPP) in Banach space. The SCFPP was proposed by Censor and Segal ^[7] in 2009, as finding a point $s^\ell$ satisfies the following:

where $K: E_1\rightarrow E_1$ and $L: E_2\rightarrow E_2$ are two mappings, $F(K)$ and $F(L)$ represent the sets of fixed point of $K$ and $L$, respectively. The iterative algorithm was proposed by Zhou et al.^[33] as follows:

where $0 < \rho_n < (\frac{q}{C_q\|A\|^q})^{\frac{1}{q-1}}$, $\{\tau_n\}\subset(0, \ 1)$ and $\{\beta_n\}\subset(-\infty, \ +\infty)$ denoted the sequences of real numbers. The strong convergence of the algorithm was proved by the authors.

It can be observed that the step size $\delta_n$ in the algorithm (1.9) and $\rho_n$ in the algorithm (1.11) depend on the norm of operator $A$, which is not an easy task in general practice.

Inspired by previous works, we propose a new self-adaptive algorithm with the inertial technique for solving the SEP in Banach spaces. The step size selection of our algorithm does not require a prior estimate of operator norm, and the inertial term improves the performance of the algorithm. Furthermore, we prove the strong convergence theorem under some mild conditions. Our algorithm includes the inertial technique, which is novel for solving the SEP in Banach spaces.

The rest of this paper is organized as follows: In Section 2, some basic facts and helpful lemmas are given for use in subsequent proofs. In Section 3, the result of strong convergence of the proposed algorithm is demonstrated. In Section 4, in terms of applications, the results are applied to the split equality fixed point problem and the split equality variational inclusion problem. In Section 5, we give numerical examples to verify the effectiveness of the proposed algorithm.

2.   Preliminaries

In this section, we first recall some notations and results that will be needed in the sequel. We suppose that $E$ is a real Banach space and $C$ is a nonempty closed convex subset of $E$. The dual space of $E$ is denoted by $E^*$. $s_n \rightharpoonup s$ and $s_n\rightarrow s$ indicate that $\{s_n\}\subset E$ weak and strong convergence to $s$, respectively, and $\omega_w(s_n)$ represents the weak $w$-limit set of $\{s_n\}$.

Let $1\le q\leq 2\leq p < \infty$ with $\frac{1}{p}+\frac{1}{q} = 1$. The modulus of convexity $\delta_E(\varepsilon): [0, 2]\to [0, 1]$ is defined as

$E$ is called uniformly convex if $\delta_E(\varepsilon) > 0$ for any $\varepsilon\in (0, 2]$, strictly convex if $\delta_E(2) = 1$. If there is a $c_p > 0$ such that $\delta_E(\varepsilon)\geq c_p\varepsilon^p$ for any $\varepsilon\in (0, 2]$, then $E$ is called $p$-uniformly convex. The modulus of smoothness $\rho_E(\tau): [0, \infty)\to [0, \infty)$ is defined by

$E$ is called uniformly smooth if $\lim\limits_{\tau\rightarrow \infty}\frac{\rho_E(\tau)}{\tau} = 0$, $q$-uniformly smooth if there is a $c_q > 0$ so that $\rho_E(\tau)\leq c_q\tau^q$ for any $\tau > 0$. It is known that $E$ is $p$-uniformly convex if and only if its dual $E^*$ is $q$-uniformly smooth ^[14].

For $p > 1$, the duality mapping $J_p^E: E\to 2^{E^*}$ is defined by

If $E$ is reflexive, strictly convex and smooth, then $J_p^E$ is one-to-one single-valued and $J_p^E = J_q^{E^*}$, where $J_q^{E^*}$ is the duality mapping of $E^*$ (see^[4,14,22]).

Given a $G\hat{a}teaux$ differentiable function $f: E \rightarrow \mathbb{R},$ the Bregman distance with respect to $f$ is defined as:

Let $f_p(x) = \frac{1}{p} ||x||^p$. In this case, the duality mapping $J_p^E$ is the derivative of $f_p$.

Definition 2.1. The Bregman distance with respect to $f_p$ is defined as

In general, the Bregman distance is not symmetric and does not satisfy the triangle inequality. However, it possesses some distance-like properties, and it has the following important properties ^[13,26]:

For $p$-uniformly convex space, the metric and Bregman distance have the following relation (see ^[21,26]):

where $\tau > 0$ is some fixed number.

The metric projection

is the unique minimizer of the norm distance, which can be characterized by a variational inequality ^[12]:

Similar to the metric projections, the Bregman projection is defined as

is the unique minimizer of the Bregman distance. It can be characterized by a variational inequality ^[21]:

from which one has

In Hilbert spaces, the metric projection and the Bregman projection are consistent with respect to $f(x) = \frac{1}{2}||x||^2$, but in general they are different.

The following inequality in $q$-uniformly smooth spaces was proved by Xu ^[32]:

Lemma 2.2. ^[32] If $E$ is a $q$-uniformly smooth Banach space, then there exists a $c_q > 0$ such that for every $x, \ y\in E$, the following inequality exists

3.   Main results

In this section, we propose the self-adaptive algorithm with the inertial technique to solve the split equality problem in Banach spaces. Subsequently, the strong convergence of the proposed algorithm is analyzed and established. The following assumptions are made throughout this section:

$\bullet$ $E_1$, $E_2$ and $E_3$ are $p$-uniformly convex and uniformly smooth real Banach spaces,

$\bullet$ $C$ and $Q$ are nonempty closed convex subsets of $E_1$ and $E_2$,

$\bullet$ $A: E_1\to E_3$ and $B: E_2\to E_3$ are two bounded linear operators,

$\bullet$ The solution set $\Gamma$ of SEP is nonempty:

Let $S = C\times Q$ in $E = E_1\times E_2$, $w = (x, y)\in S$, define $G:E\to E_3$ by $G = [A, -B]$. Then, the original SEP becomes finding $w = (x, y)\in S$ with $Gw = 0$.

We now introduce our inertial algorithm for solving SEP as follows.

Algorithm 3.1. Let $\{\alpha_n\}\subset \mathbb{R}$ be a bounded set. Set $w_0, \ w_1\in S$. The sequence $\{w_n\}$ is defined by the following iteration:

for all $n\geq0$ where $\rho_n^{q-1}\in(\epsilon, \frac{q||Gu_n||^p}{c_q||G^*J_p^{E_3}Gu_n||^q}-\epsilon).$

Lemma 3.2. The sequence $\{w_n\}$ generated by Algorithm 3.1 is well-defined.

Proof. In order to prove that $\{w_n\}$ is well-defined, first of all, we need to prove that $D_n\cap E_n$ is nonempty closed and convex for all $n\geq1$. Obviously, $D_n$ is closed and $E_n$ is closed and convex. To prove the convexity of $D_n$, note that

then, using (2.1) we have

that is,

so $D_n$ is a half-space, which means $D_n$ is convex. Hence, $D_n\cap E_n$ is closed and convex. Secondly, we show that $D_n\cap E_n\neq \emptyset$. To do this, it suffices to prove that

If (3.1) holds, we notice that $\Gamma\neq\emptyset$, so $D_n\cap E_n\neq\emptyset$. Next we show $\Gamma\subset D_n$. Let $z\in \Gamma$, $m_n = J_p^E(u_n)-\rho_n G^*J_p^{E_3}G(u_n), \ \ \forall n\geq1$. From Lemma 2.2, we get

From (2.7) and (3.2), we have

By using the value of $\{\rho_n^{q-1}\}$, we have

This implies that $\Gamma\subset D_n.$

Finally, we show that $\Gamma\subset E_n$. For $n = 0$, we have $E_0 = E$, so $\Gamma\subseteq E_0$. Given $w_k$ and suppose $\Gamma\subseteq D_k\cap E_k$ for some $k\in\mathbb{N}$. Then, there exists $w_{k+1}$ such that

Using (2.6), we have

Therefore, $\Gamma\subset E_{k+1}$. By induction, we can get that $\Gamma\subset E_n\ \ \forall n\in\mathbb{N}$. In conclusion, this completes the proof.

Lemma 3.3. Let $\{w_n\}$ be generated by Algorithm 3.1. Then

(i) $\lim\limits_{n\rightarrow \infty}||u_n-w_n|| = 0$;

(ii) $\lim\limits_{n\rightarrow \infty}||w_n-z_n|| = 0$.

Proof. The definition of $E_n$ actually implies that $w_n = \Pi_{E_n}(w_0)$. Combined with the fact that $\Gamma\subset E_n$ and the definition of Bregman projection, we get

And since $v: = \Pi_\Gamma(w_0)\in \Gamma$, we obtain

which means that $\{\Delta_p(w_n, w_0)\}$ is bounded. Hence, we know from (2.4) that $\{w_n\}$ is bounded. On the other hand, according to $w_{n+1}\in E_n$ and (2.6), we have $\langle J_p^E(w_0)-J_p^E(w_n), w_{n+1}-w_n \rangle\leq0$ and by (2.7)

Which means that

Thus, $\{\Delta_p(w_n, w_0)\}$ is nondecreasing and since $\{\Delta_p(w_n, w_0)\}$ is bounded, we get $\lim\limits_{n\rightarrow \infty}\Delta_p(w_n, w_0)$ exists. And then from (3.5) we have

Hence, we obtain from (2.4) that

Since $J_p^E$ is norm-to-norm uniformly continuous, we get

According to the definition of $\{u_n\}$ in the Algorithm 3.1 that

Therefore,

Since $J_q^{E^*}$ is also norm-to-norm uniformly continuous, we have

This completes (i).

In addition,

This shows that,

From (2.4), we have

Since $w_{n+1}\in D_n$, we have that

This implies that

From (3.6) and (3.7) we get

This completes (ii).

Lemma 3.4. Let $\{w_n\}$ be generated by Algorithm 3.1. Then the sequence $\{w_n\}$ has a weak cluster point and $\omega_w(w_n)\subseteq \Gamma.$

Proof. We know from Lemma 3.3 that $\{w_n\}$ is bounded. Since $E$ is a reflexive Banach space, $\omega_w(w_n)$ is nonempty. Therefore, we take a subsequence $\{w_{n_j}\}$ of $\{w_n\}$ such that $w_{n_j}\rightharpoonup z\in \omega_w(w_n)$. Since $||w_n-z_n||\rightarrow0, \ \ n\rightarrow \infty$, we can get $z_{n_j}\rightharpoonup z$. Obviously we have $z\in S$. And since $||w_n-u_n|| = 0$, there exists a subsequence $\{u_{n_j}\}$ of $\{u_n\}$ such that $u_{n_j}\rightharpoonup z$. From (3.3), we have

By (2.2), we get

combine this with (2.4) we get

Therefore, we have

Since $\rho_n^{q-1} < \frac{q||Gu_n||^p}{c_q||G^*J_p^{E_3}Gu_n||^q}-\epsilon$, we get

Thus,

From (3.9) and (3.10), we get $\lim\limits_{n\rightarrow \infty}||Gu_n|| = 0$, so $\lim\limits_{n\rightarrow \infty}||Gu_{n_j}|| = 0$. By the continuity of $G$, we obtain $Gw_{n_j}\rightharpoonup Gz$ and

Hence, we have that $||Gw_{n_j}|| = 0.$

Therefore,

Thus $Gz = 0$ and hence $z\in\Gamma.$

Now let us give the convergence analysis of the proposed algorithm.

Theorem 3.5. The sequence $\{w_n\}$ generated by Algorithm 3.1 converges strongly to a point $\Pi_{\Gamma}(w_0).$

Proof. We know that $w_{n_j}\rightharpoonup z$. From Lemma 3.4 it follows that $z\in\Gamma$. Since $w_{n+1}\in E_n$ and $\Pi_{E_n}(w_0) = \arg\min_{w\in E}\Delta_p(w_0, w)$, then we get

By Lemma 3.2, $\Pi_{\Gamma}(w_0)\in \Gamma\subseteq E_{n+1}$. So

Therefore,

From (2.2) and (2.3), we can obtain

Taking $\limsup$, we get

Therefore, $\lim\limits_{j\rightarrow \infty}\Delta_p(w_{n_j}, \Pi_{\Gamma}(w_0)) = 0$ and $w_{n_j}\rightarrow \Pi_{\Gamma}(w_0)$. From the arbitrariness of $\{w_{n_j}\}$ and the uniqueness of $\Pi_\Gamma(w_0)$, we have $w_n\rightharpoonup\Pi_{\Gamma}(w_0)$. Using (2.4), it follows from (3.11) that

Taking limit of the above inequality, we obtain that $w_n\rightarrow \Pi_{\Gamma}(w_0).$

Remark 3.6. It is worth mentioning that there are some advantages of our main result as follows:

(1) The methods in this paper can be applied to solve SEP in $p$-uniformly convex and uniformly smooth Banach spaces, which are more general than Hilbert spaces (^{[10,17,27,29]}).

(2) The choice of step size of our algorithm is self-adaptive, which means that $\rho_n$ does not depend on a prior estimate of the operator norm $G$. This allows our algorithm to be computed more simply than the computation of the step size in algorithm (1.9) and (1.11).

(3) The strong convergence result obtained in this paper is more desirable than the weak convergence counterparts for solving many problems in applied disciplines.

(4) Our algorithm with inertial effects is new for solving SEP in Banach spaces, even in Hilbert spaces. If $A = B$ in our problem, then Algorithm 3.1 can be reduced to solve SFP.

Our algorithm reduces to the following form in Hilbert space (the function $\Delta_p$ changes to $\Delta_p(x, y) = \frac{1}{2}\|x-y\|^2$ and $\Pi_S$ is the equivalent of $P_S$).

Corollary 3.7. Let $H$ be a Hilbert space, $\{\alpha_n\}\subset \mathbb{R}$ be a bounded set. Set $w_0, \ w_1\in H$. The sequence $\{w_n\}$ is defined by the following iteration:

4.   Applications

4.1.   Split equality fixed point problem

Let $H_1$, $H_2$ and $H_3$ be three Hilbert spaces. Let $K: H_1\rightarrow H_1$ and $L: H_2\rightarrow H_2$ be two nonlinear operators whose sets of fixed points are denoted by $F(K)$ and $F(L)$, respectively. The split equality fixed point problem for mappings $A: H_1\rightarrow H_3$ and $B: H_2\rightarrow H_3$ was introduced by Moudafi ^[17] as

When $B = I$, the split equality fixed point problem (4.1) is degraded to the split common fixed point problem (1.10). Let $H = H_1\times H_2$, $U = K\times L$, define $G: H\rightarrow H_3$ by $G = [A, -B]$. In this case, the split equality fixed point problem can be redescribed as

Regarding this problem, we formulate the following theorem based on the result of Theorem 3.5.

Theorem 4.1. Let $H$ be a Hilbert space, $\{\alpha_n\}\subset \mathbb{R}$ be a bounded set. Set $w_0, \ w_1\in H$. The sequence $\{w_n\}$ is defined by the following iteration:

where $U$ is a quasi-nonexpansive operator and $\rho_n\in(\epsilon, \frac{2||Gu_n||^2}{||G^*Gu_n||^2}-\epsilon)$. If the solution set $\Gamma = \{w\in F(S): Gw = 0\}\neq\emptyset$, then the sequence generated by (4.2) converges strongly to a point $\check{w} = P_\Gamma w_0\in \Gamma$.

Proof. Set $C = F(K)$ and $Q = F(L)$, that is, $S = F(U)$. Without difficulty, it can be seen that $P_{F(U)}$ is a nonexpansive mapping, such that the conclusion clearly holds according to Theorem 3.5.

4.2.   Split equality variational inclusion problem

Let $H$ be a Hilbert space, $N: H\rightarrow 2^{H}$ be a set-valued mapping with $dom (N) = \{x\in H:\ N(x)\neq\emptyset\}$. In the following, we first introduce the definition of monotone operator and maximal monotone operator.

Definition 4.2. An operator $N: H\rightarrow 2^{H}$ is said to be:

(i) monotone operator, if $\langle s-t, x-y\rangle\geq0$, $\forall s\in Nx, \ t\in Ny$.

(ii) maximal monotone operator, if its graph: $gra(N) = \{(x, y):\ x\in dom(N), \ y\in dom(N)\}$ is not properly contained in the graph of any other monotone operator.

Lemma 4.3. ^[28] Let $N: H\rightarrow 2^{H}$ be a maximal monotone operator on a real Hilbert space $H$. The resolvent is defined by $J_{\nu}^N = (I+\nu N)^{-1}$ for $\nu > 0$. Then the following properties hold:

(i) For each $\nu > 0$, $J_{\nu}^N$ is a single-valued and firmly nonexpansive mapping.

(ii) $dom(J_{\nu}^N)$ = $H$ and $F(J_{\nu}^N) = N^{-1}(0) = \{x\in dom(N), \ 0\in Nx\}$.

Definition 4.4. ^[8] Let $H_1$, $H_2$ and $H_3$ be three Hilbert spaces. Let $M: H_1\rightarrow 2^{H_1}$ and $P: H_2\rightarrow 2^{H_2}$ be maximal monotone operators. Then split equality variational inclusion problem for mappings $A: H_1\rightarrow H_3$ and $B: H_2\rightarrow H_3$ can be formulated as

Let $H = H_1\times H_2$, define $G: H\rightarrow H_3$ by $G = [A, -B]$. We assume that $J_{\nu}^{T} = [J_{\nu}^M, J_{\nu}^P]$, then the split equality variational inclusion problem is equivalent to

Theorem 4.5. Let $H$ be a Hilbert space, $\{\alpha_n\}\subset \mathbb{R}$ be a bounded set. Set $w_0, \ w_1\in H$. The sequence $\{w_n\}$ is defined by the following iteration:

where $\rho_n\in(\epsilon, \frac{2||Gu_n||^2}{||G^*Gu_n||^2}-\epsilon)$. If the solution set $\Gamma\neq\emptyset$, then the sequence generated by (4.4) converges strongly to a point $\check{w} = P_\Gamma w_0\in \Gamma$.

Proof. Set $C = F(J_{\nu}^M)$ and $Q = F(J_{\nu}^P)$, that is, $S = F(J_{\nu}^T)$. It is easy to see that $P_{F(J_{\nu}^T)}$ is a nonexpansive mapping. Therefore, the strong convergence theorem is obviously proved.

5.   Numerical example

In this section, we give some numerical examples and compare Algorithm 3.1 with Algorithm (1.4) in Hilbert spaces to demonstrate the effectiveness of our newly proposed method. All codes were written in MATLAB2015B. The numerical results were carried out on Intel(R) Core(TM) i5-7200 CPU @ 3.1 GHz.

Example 5.1. We give the numerical example in $(\mathbb{R}^3, ||\cdot||_2)$ of the problem considered in this paper. Let $S: = \{w = (w_1, w_2, w_3)\in \mathbb{R}^3:||w||\leq 1\}$. For Algorithm 3.1, we take $\alpha_n = \frac{1}{n+1}$ and $\rho_n = \rho = 0.01$, for Algorithm (1.4), we take $\mu_n = \frac{1}{n+1}$ and $\gamma = 0.01$. And let

The iteration was stopped with ${\rm{error}} = \frac{||w_{n+1}-w_n||}{||w_2-w_1||}\leq \epsilon$, where $\epsilon = 10^{-5}$ and $10^{-10}$. We assume $w_0 = (0, 0, 0)$ and take different $w_1$:

(i) Case Ⅰ: $w_1 = (1, 1, -1)$.

(ii) Case Ⅱ: $w_1 = (-6, -3, -1)$.

Then, we summarize the comparison of Algorithm 3.1 and Algorithm 1.4 in Table 1.

Example 5.2. Finally, we consider our problem in $E = E_3 = L_2[0, 1]$ with the inner product $\langle u, v\rangle: = \int_{0}^{1}u(t)v(t)\, dt$. Let

where $a = t/4$ and $b = 1$, we have

We assume $Gw(t) = w(t)/2$ and $G = G^*$. We compare Algorithm 3.1 and Algorithm (1.4) with initial points $w_0(t) = w_1(t) = e^{2t}$ and $w_0(t) = w_1(t) = \sin 2t$. For Algorithm 3.1, we take $\alpha_n = \alpha = 0.1$ and $\rho_n = \rho = 1$, for Algorithm (1.4), we take $\gamma = 1$. The iteration was stopped with ${\rm{error}} = ||w_n-\Pi_Sw_n||\leq \epsilon$, where $\epsilon = 10^{-5}$ and $10^{-8}$.

(i) Case Ⅰ: $w_0(t) = w_1(t) = e^{2t}$.

(ii) Case Ⅱ: $w_0(t) = w_1(t) = \sin 2t$.

Then, we summarize the comparison of Algorithm 3.1 and Algorithm 1.4 in Table 2.

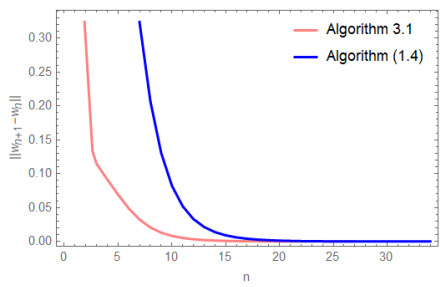
From the above Figures 1 - 8, we can see that the error value decreases as the number of iterative steps increases, which means that all the algorithms for solving SEP are valid. In addition, Algorithm 3.1 shows a faster decrease in error values, fewer iteration steps and shorter CPU time than Algorithm (1.4), which reflects the better effect of Algorithm 3.1.

6.   Conclusions

In this paper, we propose a new self-adaptive algorithm with the inertial technique for solving the SEP in Banach spaces. The inertial term greatly improves the performance of the algorithm and has a good convergence property. Furthermore, the choice of step size is self-adaptive, which means that $\rho_n$ does not depend on a prior estimate of the operator norm $G$. This allows our algorithm to be computed more simply. Under some mild conditions, the strong convergence theorem of the algorithm for solving SEP is obtained. In the meantime, the proposed algorithm is extended by us to solve the split equality fixed point problem and the split equality variational inclusion problem. Through numerical experiments, the effectiveness of the algorithm was verified by comparing it with existing results.

Acknowledgments

The authors would like to express their sincere thanks to the editors and reviewers for reading our manuscript very carefully and for their valuable comments and suggestions.

Conflict of interest

All authors declare no conflicts of interest in this paper.