1.
Introduction
Magnetic resonance imaging (MRI), a kind of non-invasive medical imaging, can reconstruct the internal structure of the human body. MRI has been widely used in medical diagnosis [1,2,3]. The MRI images with abundant details and high clarity are effective in helping doctors to make observations and get a diagnosis for the interior tissue of the human body.
There exists noise and the contrast of light and shade is high in MRI images, that impede the doctor's diagnosis. Recently we can obtain the MRI images nearly undisturbed by noise with the development of imaging technology and the improvement of the hardware devices. MRI images are used as a diagnostic evidence, so the interior tissue of the human body in the MRI images are expected not only to be visible but also be seen clearly. However the weak details of the MRI images are easily covered up. Highlighting the details to benefit diagnosis is essential in MRI images enhancement.
The enhancement methods [4,5,6] available include spatial domain based methods, transform domain based methods and deep learning based methods. The spatial domain based methods contain histogram equalization (HE) [7,8], contrast limited adaptive histogram equalization (CLAHE) [9,10], unsharp-mask filtering (UM) [11,12] and et al. [13,14]. Spatial domain based methods have some deficiencies confronting with the MRI images enhancement. The HE concerns with the distribution of the whole gray-level in images. When the contrast of light and shade is high in an image, the HE will introduce obvious whitewashed effect to the enhanced result. That affects the image interpretation [15]. The CLAHE considers the distribution of the local gray-level in images and can enhance the contrast of the local region. But this method can also enhance the noise appearing in the scene. The UM enhances the details in the MRI images effectively, while it is susceptible to noise. The noise existing in the images, even a tiny amounts of noise, will be enhanced by the UM [16]. The enhancement methods based on transform have advantages in MRI images enhancement [17,18,19,20,21]. The transform based enhancement methods distinguish the coefficients corresponding to noise, weak edges, and strong edges by appropriate thresholds. The enhancement procedure is accomplished by setting the coefficients corresponding to noise as 0, enhancing the coefficients corresponding to weak edges, and retaining the coefficients corresponding to strong edges. However, the appropriate thresholds are difficult to choose if there is lack of prior knowledge of MRI images. Deep learning based methods are a new kind of methods for image enhancement, which have achieved favorable results. It can't be ignored that the set of parameters in the deep network is complicated, and the design of parameters will directly affect the efficiency of the algorithm.
Wavelet transform possesses favorable properties in time-frequency analysis, which has been used widely in MRI images enhancement. It has been found that wavelet transform can't capture the intrinsic geometrical information in images with further research [22]. The NSCT, a multiscale geometrical analysis method, makes up for the deficiency of the wavelet transform [23]. The NSCT can capture the edges, contours and texture information in images effectively [24,25]. The NSCT is suitable for expressing the MRI images bearing abundant detail information.
To overcome the drawbacks of the image enhancement methods available and take advantage of the good descriptive ability of the NSCT, we propose an MRI image enhancement method based on feature clustering. According to the different exhibitions of the noise, weak edge and strong edge in the high-frequency directional subbands, the three-dimensional feature is extracted. Without adjusting complicated threshold parameters, the Fuzzy C-means (FCM) clustering method is introduced in this paper to classify the noise component, weak edge component and strong edge component of the high-frequency directional subbands coefficients. The gain rule is designed to modify the high-frequency coefficients. Experiments show its effectiveness.
2.
The NSCT decomposition of MRI images
The NSCT transform is a shift-invariant version of the contourlet transform. The NSCT inherits the favorable characteristics of the contourlet transform, as multi-scale, locality, multi-directionality and anisotropy. The NSCT allows redundancy, therefore, it can possess abundant basis functions. That is very favourable to express the MRI images with plenty of detail information. High-frequency directional subbands in different scales and different directions will be obtained after the NSCT decomposition of an image. The High-frequency directional subbands and the original image have the same size. The wavelet transform has high-frequency subbands with limited directions. Unlike the wavelet transform, the number of the high-frequency subbands of the NSCT is the arbitrary powers of two, which can be set up artificially. The detail information of images in fine scales is more plentiful than that in coarse scales. So the number of the NSCT high-frequency subbands in fine scales is set up with a large value in order to capture more detail information.
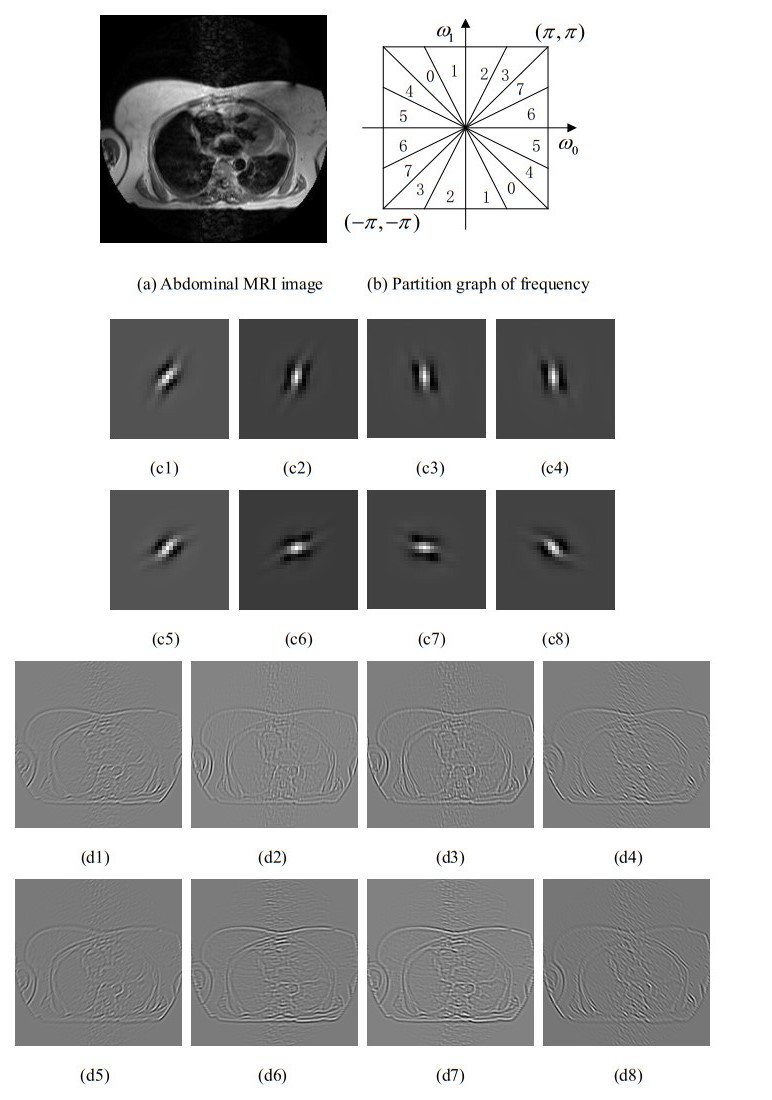
Figure 1 is the NSCT decomposition of a real MRI image on the abdomen. We decompose the MRI image into 4 scales. The numbers of high-frequency directional subbands from fine scale to coarse scale are 8, 8, 4 and 4 respectively. The equivalent filter for the k-layer scale decomposition of the signal is:
A directional decomposition can be obtained by iterating the non-downsampling direction filter bank U(Z) :
Q is a matrix.
Figure 1(a) is the original MRI image. Figure 1(b) is the partition graph of frequency in 8 directions. It can be seen that the frequency domain is divided into 8 wedge-shaped subbands. Figure 1(c1)-(c8) are the basis functions carrying out the NSCT decomposition in 8 directions. Figure 1(d1)-(d8) are the high-frequency directional subbands obtained corresponding to the basic functions in Figure 1(c1)-(c8). The basic functions of the NSCT have abundant directions and shapes, so the NSCT is able to capture the geometrical structure effectively.
Take an observation about the high-frequency directional subbands in the same scale, as shown in Figure 1(d1)-(d8). As in Ref. [20], it can be found that:
1) Strong edges have significant directional characteristic. At the same scale, the coefficients corresponding to strong edges exhibit large amplitude in each high-frequency directional subband.
2) Weak edges also have geometrical structure. At the same scale, the coefficients corresponding to weak edges exhibit large amplitude in some high-frequency directional subbands while exhibit small amplitude in others.
3) Noise does not have geometrical structure. At the same scale, the coefficients corresponding to noise exhibit rather small amplitude in each high-frequency directional subband.
These characteristics present the advantages of the NSCT in multi-directional expression of images. We also acquire the basis to divide coefficients as strong edges component, weak edges component and noise component.
3.
Feature clustering in the NSCT domain
3.1. Feature selection
The image enhancement methods based on transform distinguish the coefficients into strong edges component, weak edges component and noise component by appropriate thresholds. The threshold can be seem as the 1-dimensional feature. According to the observation of NSCT coefficients in Section 2, we don't cling to 1-dimensional feature and provide the strategy of feature selection. We expect the features selected are able to classify the NSCT coefficients as strong edges component, weak edges component and noise component effectively.
I(m,n) is the input image with the size M×N. After employing a L-level decomposition of the NSCT, we will get high-frequency directional subbands {Dl,i(m,n)} in different scales. 0⩽l<L−1, 1⩽i⩽kl, 1⩽m⩽M, 1⩽n⩽N. kl denotes the number of high-frequency directional subbands at the scale 2−l. The high-frequency directional subbands at the same scale are represented as a matrix Dl with the size M×N×kl. The elements of Dl at the location (m,n) constitute a kl -dimensional vector. That is Dl(m,n)=[Dl,1(m,n),Dl,2(m,n),...,Dl,kl(m,n)]T. We extract 3-dimensional feature from Dl, viz. mean value, variance and maximum value. The strategy of feature selection is detailed as follows:
1) The mean value feature
The coefficients corresponding to noise have small modulus in each high-frequency directional subband at the same scale. So, if Dl(m,n) corresponds to noise, the mean value of the elements modulus in Dl(m,n) is small. The coefficients corresponding to weak edges have large modulus in some high-frequency directional subbands at the same scale. So, if Dl(m,n) corresponds to weak edges, the mean value of the elements modulus in Dl(m,n) is at medium level. The coefficients corresponding to strong edges have large modulus in each high-frequency directional subband at the same scale. So, if Dl(m,n) corresponds to strong edges, the mean value of the elements modulus in Dl(m,n) is large. We adopt the mean value of the elements modulus in Dl(m,n) as a feature to distinguish the three different components. The feature is represented as Zlmean(m,n). We have
2) The standard deviation feature
The standard deviation is generally used to measure the dispersion of data apart from the mean value. At the same scale, the coefficients corresponding to weak edges in some high-frequency directional subbands have large modulus, but the coefficients corresponding to weak edges have small modulus in other high-frequency directional subbands. So, if Dl(m,n) corresponds to weak edges, the dispersion of elements modulus in Dl(m,n) is large. That means the standard deviation of elements modulus in Dl(m,n) is large. The modulus of the coefficients corresponding to noise or strong edges have small dispersion in high-frequency directional subbands at the same scale. If Dl(m,n) corresponds to noise or strong edges, the standard deviation of elements modulus in Dl(m,n) is small. We adopt the standard deviation of the elements modulus in Dl(m,n) as another feature to distinguish the three different components. The feature is represented as Zlstd(m,n). We have
3) The maximal modulus feature
At the same scale, the coefficients corresponding to noise in each high-frequency directional subbands have small modulus. If Dl(m,n) corresponds to noise, the maximal modulus of elements in Dl(m,n) is still small. The coefficients corresponding to weak edges in some high-frequency directional subbands have large modulus at the same scale. If Dl(m,n) corresponds to weak edges, the maximal modulus of elements in Dl(m,n) is large. The coefficients corresponding to strong edges in each high-frequency directional subbands have large modulus. If Dl(m,n) corresponds to strong edges, the maximal modulus of elements in Dl(m,n) is larger than that corresponding to weak edges or noise. We adopt the maximal modulus of elements in Dl(m,n) as the third feature to distinguish the three different components. The feature is represented as Zmax. We have
In conclusion, we extract 3-D dimensional feature vector from high-frequency directional subbands at the same scale. That is
3.2. FCM feature clustering based on NSCT
Without estimating the threshold, we introduce the FCM [26,27] to distinguish the three components in NSCT coefficients by using the 3-D dimensional feature vector constructed. The FCM is an unsupervised classification methods, which acquires labels of the data by minimizing the global cost function. The features of coefficients at different scale are clustered respectively. The data to be clustered is {\boldsymbol{Z}^l}(m, n) , 0 \leqslant l < L - 1 , 1 \leqslant m \leqslant M , 1 \leqslant n \leqslant N . At the scale {2^{ - l}} , if {\boldsymbol{Z}^l}(m, n) is divided into a certain class (noise, weak edges or strong edges), the coefficients at the scale {2^{ - l}} in each high-frequency directional subband at the location (m, n) are deem to belong to this class.
The feature clustering method based on FCM needs to minimize the objective function. That is
where the objective function J(\boldsymbol{U}, \boldsymbol{V};{\boldsymbol{Z}^l}) is the weighted square of error between data \boldsymbol{Z}_q^l and cluster center {\boldsymbol{V}_p} . {\left\{ {\boldsymbol{Z}_q^l} \right\}_{1 \leqslant q \leqslant MN}} = {\left\{ {{Z^l}(m, n)} \right\}_{1 \leqslant m \leqslant M, 1 \leqslant n \leqslant N}} . That means the 2-dimensional indexes of the data \left\{ {{\boldsymbol{Z}^l}(m, n)} \right\} are changed to the 1-dimensional form. r is the weighted index in the FCM based clustering. The r is set as 2 in our algorithm. {\boldsymbol{V}_p} is computed by
{d_{p, q}} is the distance between data \boldsymbol{Z}_q^l and cluster center {\boldsymbol{V}_p} , which is defined as
{U_{p, q}} is the degree of membership from data \boldsymbol{Z}_q^l to cluster center {\boldsymbol{V}_p} .
The objective function J(\boldsymbol{U}, \boldsymbol{V};{\boldsymbol{Z}^l}) is minimized by iterating formulas (6)-(8) until the optimal membership matrix \boldsymbol{U}_q^ * = {[U_{1, q}^ *, U_{2, q}^ *, U_{3, q}^ *]^T} of data {\left\{ {\boldsymbol{Z}_q^l} \right\}_{1 \leqslant q \leqslant MN}} is obtained. For the reason of timeliness, the iteration is stopped in the case that the number of iterative time is more than 50 or the change is smaller than 0.001 in {\boldsymbol{V}_p} and {U_{p, q}} . U_{{p^{'}}, q}^ * = \max \left\{ {U_{1, q}^ *, U_{2, q}^ *, U_{3, q}^ * } \right\} , {p^{'}} \in \left\{ {1, 2, 3} \right\} . If the degree of membership between \boldsymbol{Z}_q^l and class {p^{'}} has the largest value, \boldsymbol{Z}_q^l is classified into class {p^{'}} . The feature clustering method based on FCM in NSCT domain for dividing the noise component, weak edges component and strong edges component is summarized in Table 1.
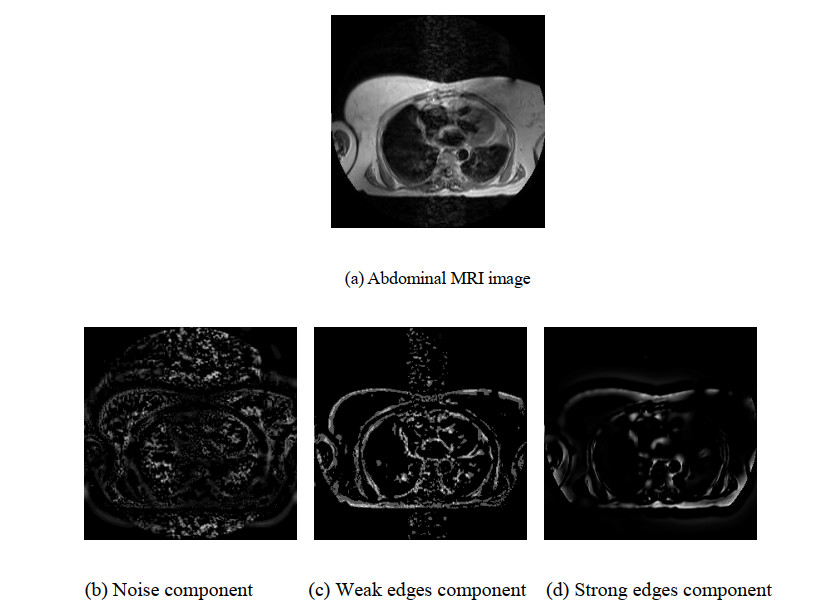
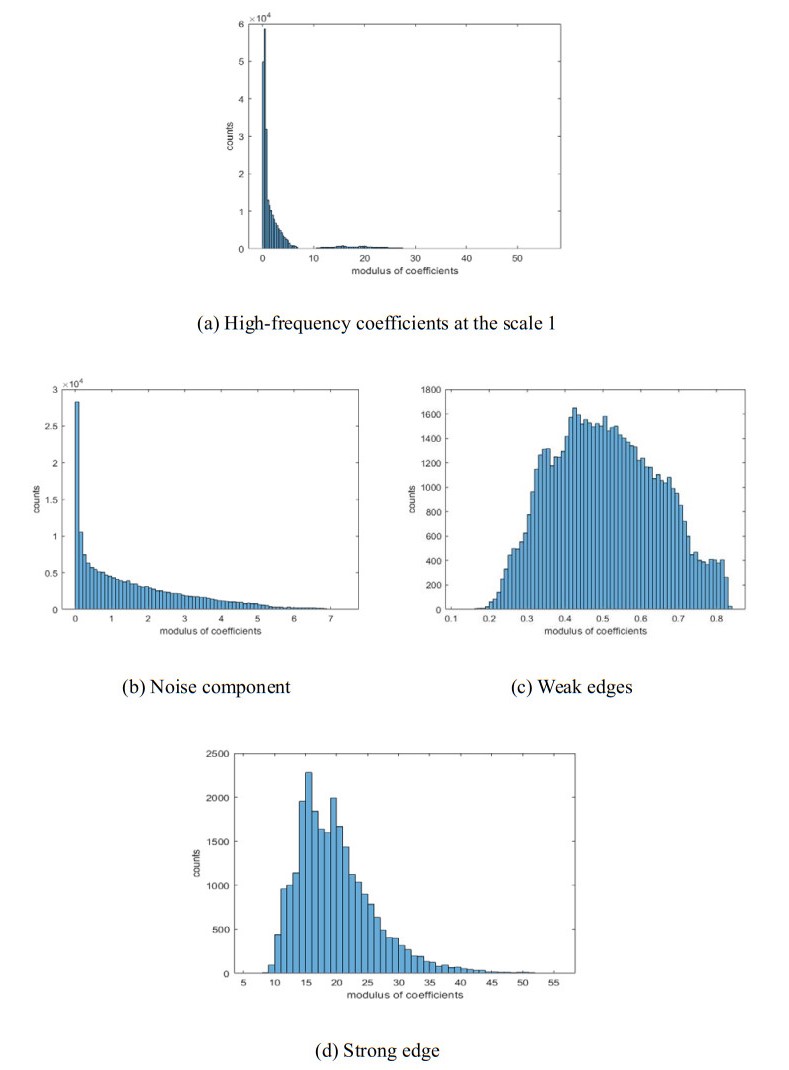
We apply NSCT to the abdominal MRI image (Figure 2(a)) and cluster the coefficients of the high-frequency directional subbands by the method described in Table 1. After acquiring the category attributes of the high-frequency coefficients, we set low-frequency coefficients to zero and make NSCT inverse transform only to the coefficients corresponding to noise, weak edges or strong edges respectively. The clustering results of the three high-frequency components will be obtained. Figure 2(b)-(d) are the noise, weak edges or strong edges respectively. Comparing the figures of the three high-frequency components with the original abdominal MRI image, it can be seen that the proposed method classifies the three components in images effectively. Figure 3 gives the modular value distribution of the coefficients after clustering on scale 1. It is observed that high-frequency coefficients at the scale 1 is divided into three different interval segments after FCM feature clustering.
4.
Design of gain rules and nonlinear gain function
The high-frequency coefficients {D_{l, i}}(m, n) are classified as noise component, weak edges component and strong edges component by feature clustering in NSCT domain. 0 \leqslant l < L - 1 , 1 \leqslant i \leqslant {k_l} , 1 \leqslant m \leqslant M , We adopt different gain factors to coefficients of different classifications. D_{l, i}^I(m, n) and D_{l, i}^{I'}(m, n) are denote the high-frequency coefficients of the input image I and enhanced image I' respectively. The gain rules are defined as:
where {A_l} is the maximum modulus of high-frequency coefficients at the scale {2^{ - l}} . Set {a_0} = 0 and the coefficients corresponding to noise are set to 0. The coefficients corresponding to strong edges will be enhanced moderately by adjusting parameter {a_2} . Set {a_2} > 1 . {a_1}(\bullet) is the nonlinear gain function.
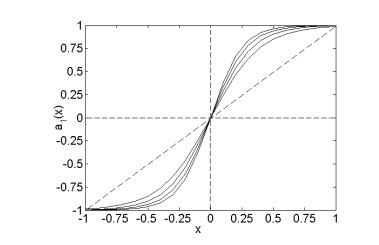
The nonlinear gain function should satisfy monotonicity and antisymmetry. Meanwhile the component with low contrast should be highly enhanced, the sharp edges should be kept and avoid over enhancement. Due to the selection of thresholds included, the classical nonlinear gain function proposed by A. F. Laine needs adjusting several parameters (the generalized adaptive gain method) [28,29]. We simplify the gain function and adopt only one parameter t to control the degree of enhancement. Set t > 1 . The lager the t is set, the higher the degree of enhancement will be. The value of t needs to be chosen properly in order to avoid over enhancement. Figure 4 shows the curves of nonlinear gain function {a_1}(\bullet) . The four curves from the bottom to the top correspond to the setting of t is 5, 6, 7 and 8 respectively. The expression of {a_1}(x) is
where x is the input data and - 1 \leqslant x \leqslant 1 .
And in our algorithm
5.
MRI image enhancement based on feature clustering in NSCT domain
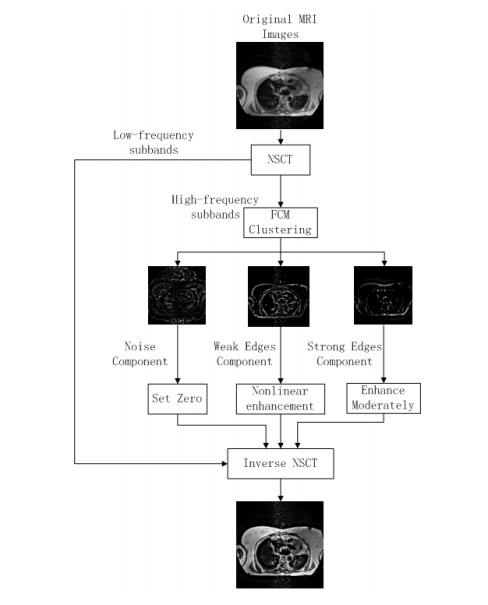
The low-frequency subband and high-frequency directional subbands are obtained by applying NSCT decomposition to the MRI image. In our enhancement algorithm, we keep the coefficients of low-frequency subband which describe the profile information of images. The coefficients of high-frequency subbands describe the detail information, such as edges, contours and textures, etc. Taking advantages of the different expression of noise, weak edges and strong edges in high-frequency subbands, we classify the coefficients of high-frequency subband by feature clustering. The new high-frequency subbands with modified coefficients will be obtained after setting the noise component as zero, enhancing the weak edges component and adjusting the strong component moderately. Applying NSCT inverse transform to the low-frequency subband of the original image and the newly acquired high-frequency subbands, the final enhanced MRI images will be obtained. The procedure of MRI images enhancement based on feature clustering in NSCT domain is shown in Figure 5. The enhancement algorithm is summarized in Table 2.
6.
Experiments and results
The test images used in experiments are real MRI images with little noise. The abdominal MRI images are from the CHAOS datasets downloaded at https://chaos.grand-challenge.org/Download/. The brain MRI images are from the Whole Brain Atlas datasets downloaded from http://www.med.harvard.edu/AANLIB/home.html. The size of the test images is 256×256. The methods based on spatial domain, as HE, CLAHE and UM, the GAG parameter adjusting methods [28,29] in wavelet (WT), contourlet (CT), stationary wavelet (SWT) and NSCT domain (NSCT) respectively, and the SMIPC [30] are compared with the proposed enhancement method. The algorithm performs contrast experiments at the PC end of the MATLAB R2018b. The HE, CLAHE UM, SWT adopt the MATLAB built-in function. The HE and UM use the default parameters. The CLAHE uses the common parameters, as 'ClipLimit' = 0.02 and 'Distribution' = 'rayleigh'. The parameters [28] adopted in wavelet (WT), contourlet (CT), stationary wavelet (SWT) and NSCT (NSCT) based enhancement methods are {T_1} = 0.0025 , {T_2} = 0.05 , {T_3} = 0.9 , c = 10 and b = 0.2.
We apply 4-level decomposition to test images. The wavelet transform and stationary wavelet transform adopt '9-7' wavelet basis function. Contourlet transform and NSCT adopt the '9-7' pyramid decomposition and the McClellan transformed directional filters [30]. From fine scale to coarse scale, the number of high-frequency directional subbands is 8, 8, 4, and 4 respectively. We set {a_2} = {\text{1}}.2{\text{5}} in the gain rule, viz. formula (12). We choose parameter t = 7 in the nonlinear gain function {a_1}(\bullet) , viz. formula (14).
The number of highfrequency directional subbands subband was chosen based on the following considerations: 1) The number of directional subbands on the fine scale should be higher than that on the coarse scale in order to capture the more details. 2) The number of directional subbands on one scale should not be too much to prevent data redundancy and time loss in data mining. The parameters we choosed in the gain rule according to experiment experience. The two parameters, {a_2} = {\text{1}}.2{\text{5}} , t = 7 , were not adjusted for different MRI images after setting.
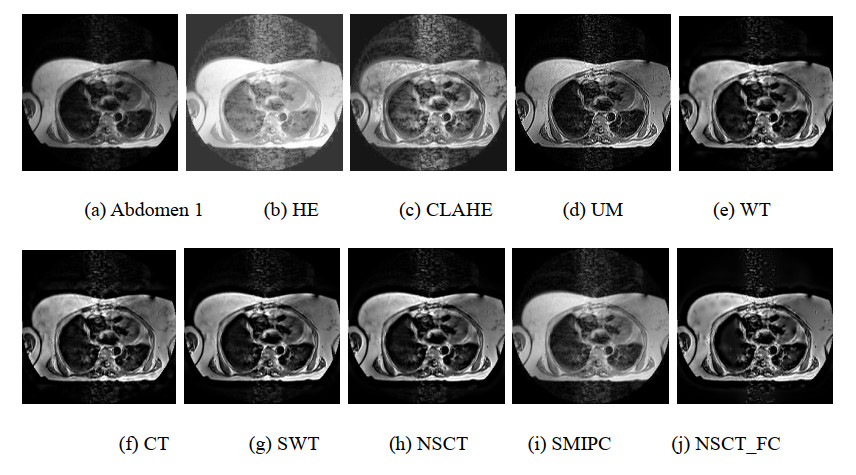
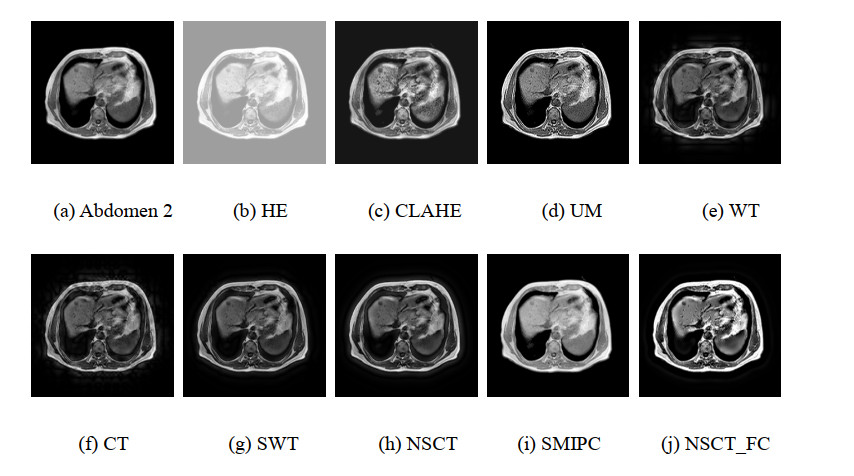
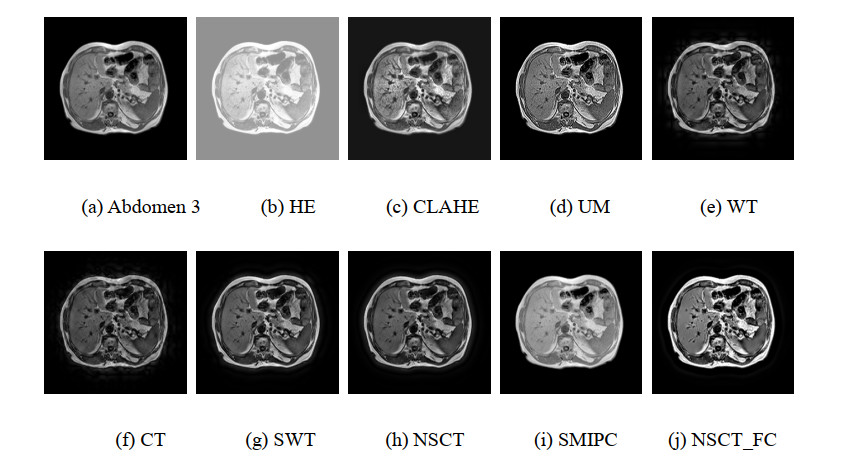
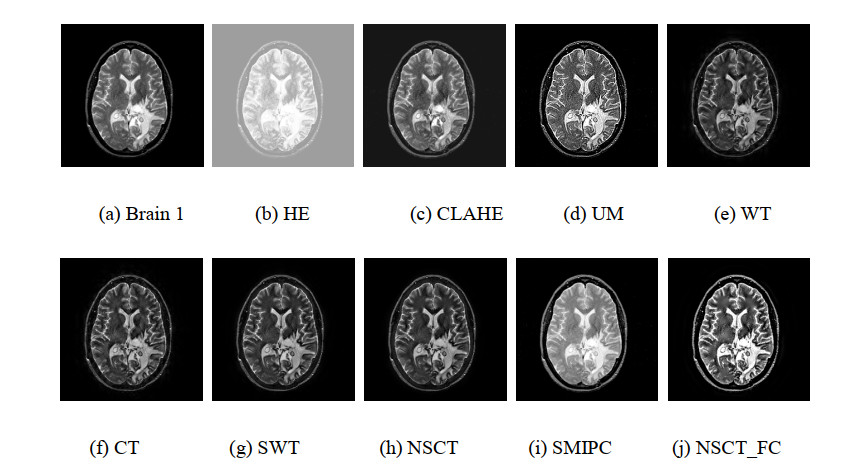
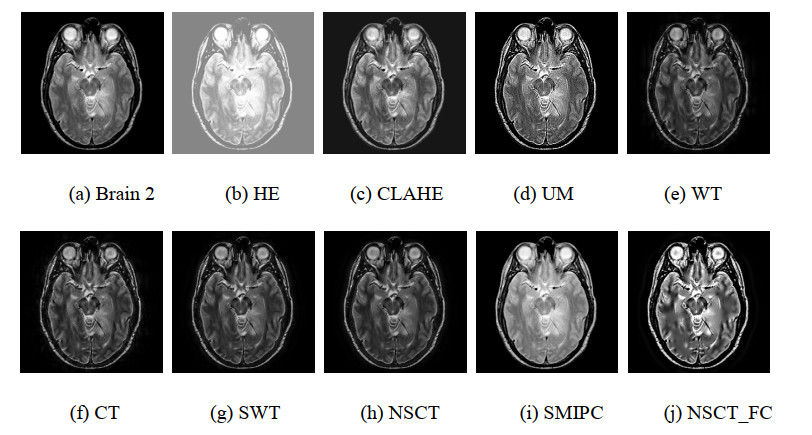
Figures 6, 8, 10, 12 and 14 are the enhancement results of MRI images. HE based method produces obvious whitewashed effect, that reduces the readability of the image. CLAHE based and UM based methods enhance the details of the images, meanwhile enhance the noise in the images. The methods based on WT, CT, SWT and NSCT acquire enhancement results with clear details and smooth uniform regions. The enhancement capacity of the SMIPC for detail is limited. Compared to other methods, our method obtains the most abundant details and highlights the weak edges which hard to observe in the original images (as the middle and lower part of the abdominal cavity and the the right part of the abdominal cavity in Figures 6, 8 and 10, as the middle part of the brain in Figures 12 and 14). The enhancement results we acquired have smooth uniform regions and high clarity.
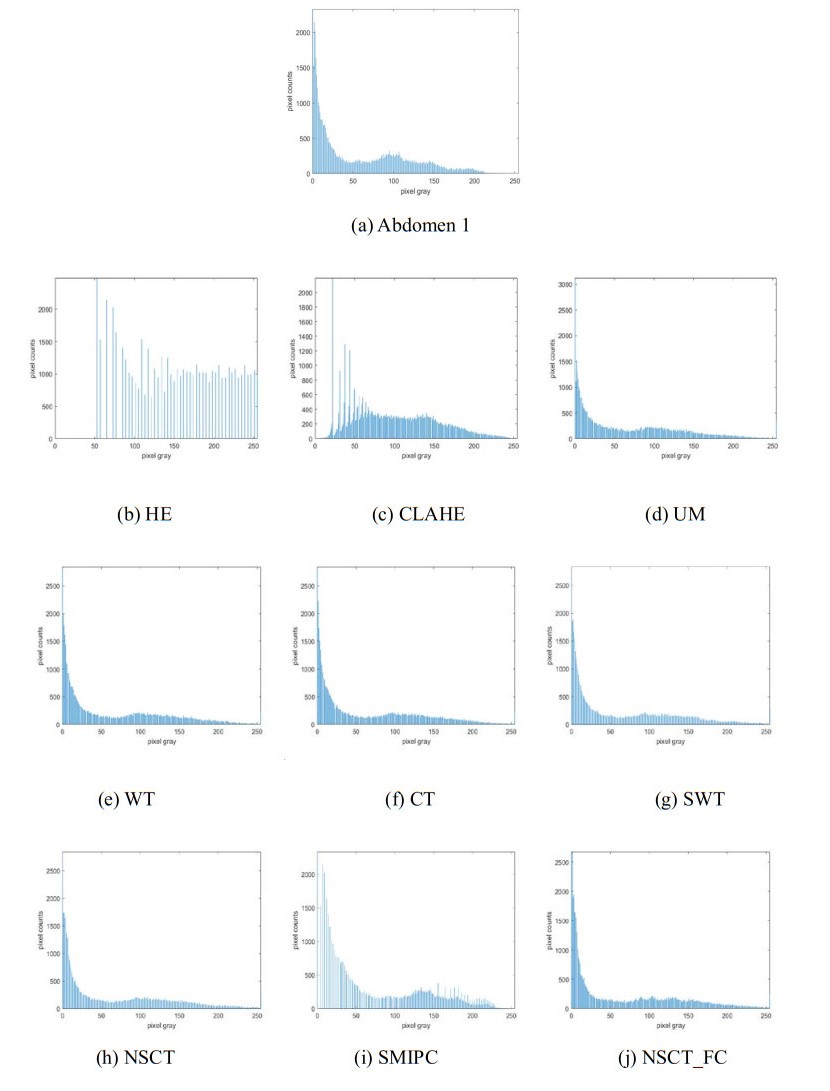
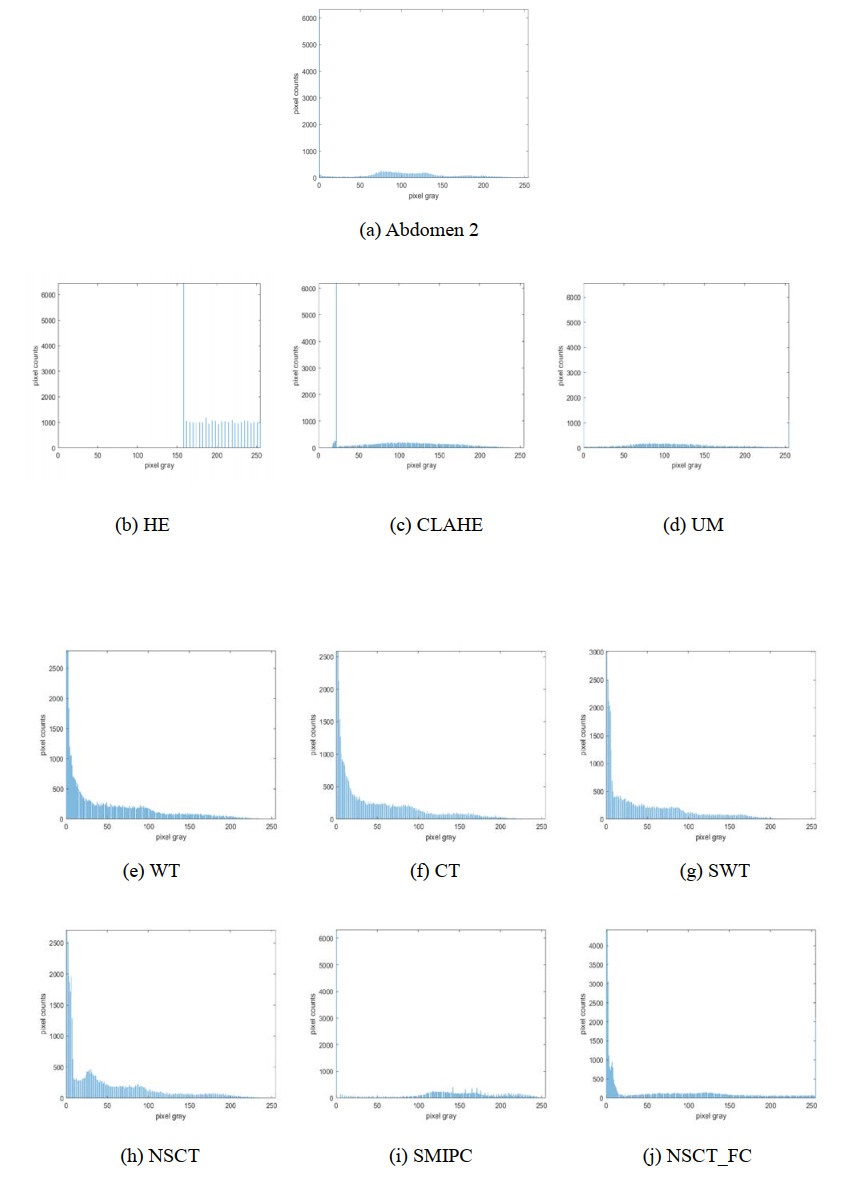
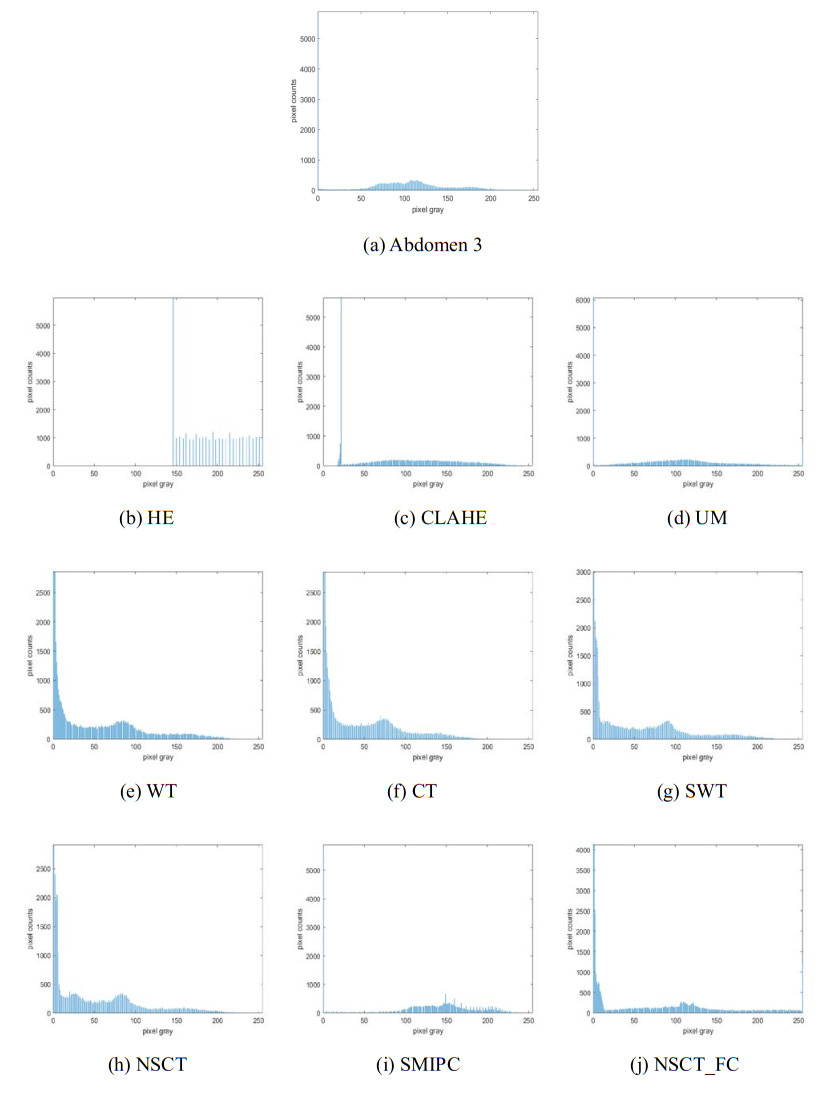
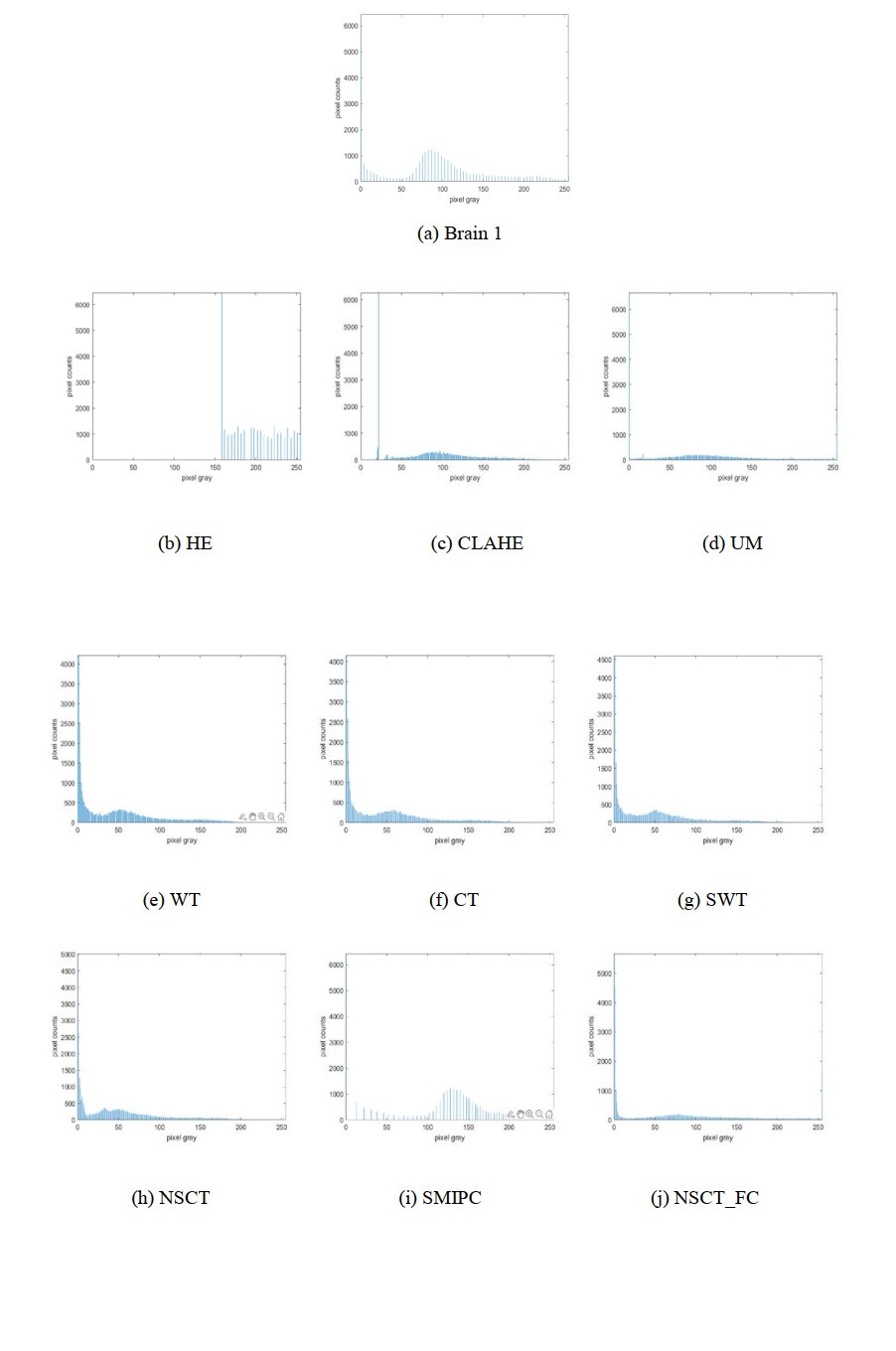
Figures 7, 9, 11, 13 and 15 are the histogram distribution of the enhancement results. The MRI images with large difference in intensity distribution. The number of the pixels is zero at the left part of the gray value internal in the histogram distribution of HE results, which makes the enhancement image demonstrating whitewashed effect. CLAHE method extends the grayscale range of the original images. But the outline of histogram distribution of the CLAHE results have large difference compared to that of original image. The outlines of histogram distributions of UM, WT, CT, SWT, NSCT, SMIPC and our results are similar, which indicates that the enhancement results maintain the whole structure of the original images.
Tables 3-7 give the values of objective evaluation indexes on information entropy (IE), gray mean of the pixels (MV), standard variance (STD), average gradient (AG), grayscale contrast (GC), structural similarity index (SSIM). Information entropy reflects the amount of information contained in the enhanced images. The higher value of the information entropy is, the more information entropy of the enhanced images is. The gray mean of the pixels reflects the average brightness of the images. The gray mean of the pixels will increase after image enhancement. The standard variance reflects the degree of the dispersion that the gray value of pixels deviate from the gray mean. The detail information in the images is more abundant, the standard variance of the image is larger. The average gradient reflects the richness of the texture details and the clarity of the image. The AG is defined as:
where \Delta {I_x} = f(x, y) - f(x - 1, y) f and \Delta {I_y} = f(x, y) - f(x, y - 1) . The larger AG value indicates that the image possesses more abundant detail information and higher definition. The GC reflects the hierarchical change of the image from black to white. The higher the GC value, the stronger the gray expression ability. The GC is defined as:
where \delta (i, j) = \left| {i - j} \right| is a gray value difference of adjacent pixels, {P_\delta }(i, j) is the distribution probability of the pixels with the gray difference of the neighboring pixels at \delta . The SSIM is an index to measure the similarity of two images. When the two images are identical, the value of the SSIM is equal to 1.
The whitewashed effect and the enhanced noise in the results cause an obviously increase in the values of evaluation indexes of HE, CLAHE and UM results. Compared to the WT, CT, SWT, NSCT and SMIPC methods, our method has a superiority in the indexes of average gradient, grayscale contrast, and is at a middle level on the other indexes. The proposed method bears an advantage is that it can effectively enhance the weak edge components in the image. The prominences of the components make the details of the enhancement results increase and the changes in gray scale increase. So the values obtained by our algorithm can be observed in the AG and GC indicators are relatively high. The UM method does not take into account the noise in the image. In the enhancement process, the noise is also enhanced as a detail component (especially the smoothing region of body in Figure 6), which makes the value of the evaluation indexes high. Our resulting images with the detail components highlighted are different from the original image. While the more similar the experimental results are to the original image, the larger the SSIM value. So our results do not have advantages on SSIM.
7.
Conclusions
MRI images contain abundant edges, contours and texture information. The MRI images with clear object region and high contrast usually can't be obtained due to the limitation of imaging condition, that affects the diagnosis. The visual quality of MRI images should be improved. An MRI images enhancement method based on feature clustering in NSCT domain is proposed. Benefiting from the favorable description ability of the NSCT, according to the different expression forms of noise, weak edges and strong edges in high-frequency subbands, we extract the 3-dimensional feature of high-frequency coefficients in the same scale. The FCM clustering algorithm is introduced to classify the high-frequency coefficients into noise component, weak edges component and strong edges component. The high-frequency coefficients are modified by the gain rules and gain functions designed without adjusting tedious threshold parameters. Compared with the state of art methods based on spatial domain and transform domain, our method has a certain superiority. The enhanced results we obtained possess high clarity, distinct details and smooth uniform area, that will help doctors make diagnosis. The method proposed is an effective and feasible method for MRI image enhancement.
Acknowledgments
This work was supported in part by the Ningxia Natural Science Foundation (No. 2022AAC03236), by the National Natural Science Foundation of China (No. 11961001 and No. 61907012), by the First Class Disciplines Foundation of Ningxia (No. NXYLXK2017B09), by the Major Project of North Minzu University (No. ZDZX201801), by the Special Project of North Minzu University (No. FWNX01), by the Master Degree Candidate Innovation Program (No. YCX22106) and by the Hongyang soft project.
Conflict of interest
The authors declare that there is no conflict of interests.









 DownLoad:
DownLoad: