Multiplicity result to a system of over-determined Fredholm fractional integro-differential equations on time scales

1.   Introduction

With China's digital economy continuing to grow at a rapid pace, e-commerce (EC) has entered an era of inventive growth in 2020. According to the Global Payments Report 2021, China has been the world's largest EC market ^[1]. It is expected to reach a total value of ＄3.17 trillion by 2024. The rapid development of EC has aided in the flourishing growth of the logistics (LOG) industry ^[2]. In 2022, the national express delivery business generated revenue of 10566.7 billion yuan, a 2.3% increase from the previous year. The total volume of express deliveries exceeded 110.58 billion pieces, a 2.1% year-on-year increase, according to the State Post Bureau of the People's Republic of China. LOG plays a crucial role in EC, improving customers' purchasing experience through the prompt delivery of goods ^[3]. The rapid progress of EC relies on the backing of LOG, while the innovation and enhancement of efficiency in the LOG business influences the evolution of EC in turn. However, this close connection also makes it possible for any impact of the LOG industry to be quickly transmitted to the EC industry, causing volatility and vice versa.

Spillover effects are a frequent topic of interest in economics research ^[4]. The interaction between EC and LOG has produced significant spillover effects. Specifically, the widespread use of EC platforms promotes the surge in LOG demand and drives the continuous innovation and upgrading of LOG technology ^[5]. Once technologies such as intelligent warehousing systems, automated sorting equipment, and big data analytics are implemented in the LOG industry, these technological innovations generate spillover effects that spread to other industries and promote broader efficiency improvements and accuracy ^[6]. Efficient and frictionless transportation of goods is essential for both domestic and cross-border EC. The inefficiency of the LOG system, which includes freight transportation, warehousing, border clearance and domestic postal delivery, exacerbates the cost of trade for enterprises involved in EC. Therefore, maximizing the positive impact of transport and LOG on EC can also improve the efficiency of the LOG chain ^[7]. In addition, the synergistic development of EC and LOG also has a positive spatial spillover effect on the regional economy by optimizing resource allocation and improving the overall efficiency of the supply chain. This effect helps to narrow the development gap between urban and rural areas, promote the process of regional economic integration, and achieve more balanced and sustainable development ^[8]. However, the current international economic situation is complex and volatile. When various extreme risk events occur internationally or domestically, China's stock market tends to experience varying degrees of volatility, which further exacerbates the risks in the financial market ^[9]. For example, the Sino-U.S. trade friction has affected the foreign trade operations of Chinese EC companies, making many Chinese companies face higher export costs and trade restrictions, making it necessary to adjust their supply chain and market strategies ^[10]. The global energy crisis has pushed up LOG, transportation and warehousing costs, making the company's operating costs higher ^[11]. This is particularly severe for small EC firms and LOG service providers. COVID-19 has contributed to the surge in online shopping by consumers, leading to increasing pressure on LOG, with LOG firms having to deal with a large number of orders and delivery demand issues. At this point, the development of EC in China is hampered by a variety of issues, including LOG development ^[1].

Based on Tang and Wang ^[12] and Guo ^[13], we acknowledge the close interdependence between the EC and LOG sectors, which constitute a significant portion of the national economy. However there's also the potential that this close relationship will increase and transmit risk between the two markets; especially when faced with extreme events, this risk spillover effect will be amplified ^[14]. Thus, this paper's goal is to explore the dynamics of asymmetric spillovers between the LOG and EC industries and to reveal how they interact in extreme situations. We combine the findings of Tian et al. ^[15] and Tian et al. ^[16] to further explore the underlying mechanisms of such extreme risk spillovers and the potential threats they may pose to the stable development of the EC and LOG industries, as well as to provide policymakers, firms, and investors with useful suggestions on how to better manage and mitigate extreme risk spillovers.

Previous research, such as that of Giuffrida et al. ^[17], Zennaro et al. ^[18] and Yu et al. ^[5], only carried out theoretical and some descriptive analyses. While they demonstrated that the growth of e-commerce has aided in the logistics industry's prosperity ^[19], these studies lacked an engaging discussion of the relationship between EC and LOG. As a result, we contribute in three dimensions to the corpus of current literature. First, the Bayes positive diagonal BEKK generalized autoregressive conditional heteroskedasticity (Bayes-pdBEKK-GARCH) model is employed to illustrate the asymmetric spillover and evolving connection between the two markets. Our work differs from Zeng et al. ^[19] in that the latter uses a two-way fixed-effects model to investigate the relationship between logistics density and EC transaction size. Then the adaptive Fourier decomposition (AFD) methodology is employed to reconstruct transient time-frequency distributions (TTFD) of EC and LOG volatilities, overcoming restrictions of common statistical models and frequency analyses, such as overlooking frequency information, requiring basis functions, and encountering modal aliasing, while also highlighting structural changes in the frequency domain ^[20]. Third, the studies by Kawa and Światowiec-Szczepańska ^[21] and Zeng et al. ^[19] only examine the linear relationship between EC development and e-commerce. This paper also examines the study from a nonlinear perspective and assesses extreme risk spillovers in both markets using a GARCH-copula quantile regression model to measure volatility clustering, tail dependency, and possibly asymmetric effects of two markets under extreme shocks, and to evaluate the extreme risk spillovers between them.

This study analyzes data from January 2, 2014, to November 30, 2023, comprising 2,413 observations. It includes significant events like China's stock market crisis in 2015, the Sino-U.S. trade friction, the COVID-19 epidemic, the EC "either-or choice" monopoly policy, and the Russo-Ukrainian war. It is found that: (1) there is a unique dynamic relationship between the EC and LOG markets, which is characterized by volatility spillovers and positive correlation. This implies that when one market is volatile, the other markets are also affected, and the mutual impact is asymmetrical. (2) Both markets have structural changes that result in fluctuations in volatility. (3) The relationship between EC and LOG markets alters based on risk levels, and the dynamic risk spillover impact also shows variability, evolving over time. The smallest downside risk spillover occurs in the LOG market, whereas the upside risk spillover is observed in the EC market. Extreme events such as China's stock market crash, the Sino-U.S. trade friction, the COVID-19 epidemic, and the EC "either-or choice" monopoly can significantly impact EC and LOG markets, leading to heightened market uncertainty and risky volatility spillovers.

The article is structured as follows: Section 2 summarizes the relevant literature. Section 3 describes the approaches used in this paper. Section 4 describes the relevant data used. Section 5 conducts an empirical analysis. Section 6 concludes the full paper and makes recommendations accordingly.

2.   Literature review

2.1.   EC and LOG interactions

The information industry's growth has led to significant expansion in LOG and EC, with LOG being recognized as a crucial element in facilitating EC transactions. An effective, logical, and smooth LOG system allows EC to take full advantage of its strengths ^[22]. Teng et al. ^[1] discovered that the progress of LOG positively impacts EC, and this connection is affected by the growth rate of LOG. Also, Barenji et al. ^[22] stated that LOG plays such an important role in the EC process that shipping costs can account for up to 40% of the price of a product. Currently, competition in the EC industry has transitioned from business models to LOG services ^[19]. Guo ^[13] suggests that this change is increasing the demand for faster delivery of the LOG network. How to improve the timeliness of LOG distribution is a problem that all EC enterprises must face and urgently need to solve. To address this problem, Guo ^[13] suggested a dual-layer planning approach for the location of LOG urban distribution service systems to enhance distribution efficiency, decrease transportation distance, and lower fuel costs. Feng ^[23] adopted the third-party delivery paradigm as a LOG strategy and applied the colony of ants optimization method to calculate the most efficient routes and expenses. This approach enhances LOG and distribution efficiency while also lowering LOG costs. Teng ^[24] used a recurrent neural network to plan the LOG route of cross-border EC of agricultural products and selected the optimal distribution path, so as to improve the timeliness of LOG distribution. Researchers have studied methods to enhance the punctuality of LOG and transportation. They discovered that enhancing the timeliness of LOG distribution has resulted in numerous advantages. In my opinion, improving the timeliness of LOG and distribution can not only improve customer experience, but also increase the repeat purchase rate, reduce the customer churn rate, and thus improve the competitiveness of the EC platform.

The development of EC also promotes the growth of the LOG sector ^[19]. This is because the development of EC can decrease the social transaction costs of businesses, such as credit charges, time costs, and transportation costs ^[12]. The rise of EC can result in a notable rise in the volume of packages and deliveries to urban areas, leading to an increase in urban freight transportation demands, particularly in last-mile LOG ^[25]. Furthermore, online shopping has heightened customers' expectations for convenience, leading them to desire the ability to autonomously select the time and location for receiving their online purchases. Therefore, at this time, consumers not only expect fast and free delivery but also flexibility in choosing when and where to pick up their goods ^[26]. Viu-Roig and Alvarez-Palau ^[25] stated that the recent growth of EC has strengthened the importance of the "last mile" in LOG, which offers clients the option to select delivery sites outside house delivery, including lockers or collection points. Zhang et al. ^[27] believes that when the LOG industry is affected by abnormal fluctuations or extreme events (such as weather disasters, traffic jams, strikes, etc.), it may lead to problems such as delay, loss, damage, or nondelivery of LOG transportation. These issues can impact the distribution and delivery services of EC, resulting in a compromised consumer experience, increased order return rates, and inventory overstock. From the above, we can see that each of these shocks creates volatility in another market. Therefore, we need to investigate the dynamic link between LOG and EC and quantify the extreme risk transmission between them.

2.2.   Methodology of the volatility spillover

Ross ^[28] was the first to introduce the notion of volatility spillovers. He contended that information flow between markets influences volatility in prices, which is connected to the rate of information dissemination in the market. The direction of volatility spillovers reflects the direction of information flow. Specifically, when A market undergoes fluctuations such as shocks or price changes, these variations impact B market through an information transmission process, leading B market to exhibit similar volatile behavior. On the other hand, from a modern financial perspective, volatility embodies asset risk. Thus, the core concept underlying the phenomenon of volatility spillover is the intricate propagation of risk across diverse markets ^[29].

Numerous scholars commonly use a variety of methods to explore the volatility spillover effects between markets, including GARCH models, vector autoregression (VAR) models, Diebold and Yilmaz (DY) methods, and so on. Several forms of GARCH models can be used to analyze volatility spillovers between markets, including the BEKK-GARCH model and dynamic conditional correlation (DCC-) GARCH model ^[30]. However, the GARCH model lacks the capacity for simultaneous consideration of both the directional aspects and dynamic properties of volatility spillovers ^[31]. Though the BEKK-GARCH model excels at capturing the directional movement of volatility, it falls short in accounting for time-varying characteristics ^[32]. Conversely, although the DCC-GARCH model proficiently depicts temporal variations, it is inadequate in discerning the directional flow of volatility ^[33]. To address the limitations of the GARCH model, Diebold and Yilmaz ^[34] developed the DY spillover index, an innovative measure of volatility spillovers derived from the variance decomposition of VAR prediction errors. However, DY has certain methodological and substantive constraints. Methodologically, DY only addresses aggregate spillovers and overlooks the direction of spillovers. Therefore, Diebold and Yilmaz ^[35,36], enhanced this method by employing a generalized VAR framework, effectively addressing its shortcomings and improving its analytical capabilities. Besides, the estimation using the BEKK-GARCH model falls short in capturing temporally dynamic characteristics. More significantly, it may generate negative diagonal coefficients. While these negative diagonal coefficients do not pose inherent challenges during the estimation process, they introduce potential interpretational complexities ^[37]. Therefore, Rast et al. ^[38] set positive restrictions on the diagonal elements of the ARCH(A) and GARCH(B) parameters, requiring $diag({\mathbf{A}}) \geqslant 0$ and $diag({\mathbf{B}}) \geqslant 0$, thus enabling a pdBEKK parameterization. This method was initially applied mainly in psychological research, but now it has also been applied to volatility predictions and financial decision-making. Cheng et al. ^[37] investigated the correlation between crude oil and gold by employing the Bayes-pdBEKK-GARCH model.

Considering that financial time series are also characterized by frequency dimension, some scholars have also investigated the spillover effects of financial markets under different time frequencies ^[39]. Common methods for frequency domain analysis include wavelet transform and empirical modal decomposition (EMD). Wavelet transform's limitation lies in selecting the wavelet basis function and decomposition level, which can significantly influence the graphical manifestation of time-frequency domain representations ^[40]. While the EMD method overcomes this issue, it faces modal aliasing problems which reduces the analysis of data details and confidence. Wu and Huang ^[41] presented an ensemble empirical mode decomposition technique, building upon the foundations of EMD methodology. Although it does not entirely resolve the modal aliasing issue in EMD, the reconstructed signal does help reduce the remaining noise. The constraints noted above can be bypassed by the AFD approach. The AFD decomposition was an algorithm introduced by Tao et al. ^[42], which applied variants and implementations of the greedy algorithm (matching pursuit) in Hardy $H^2$ and $L^2$ spaces. This method is utilized to examine the instantaneous frequency of a specific signal and has been proven to be robust. AFD has demonstrated strong performance in signal compression and denoision ^[43,44]. The AFD approach has also been used in financial time series in recent years. Li et al. ^[45] employed the AFD method to analyze carbon price fluctuations in China. They reconstructed the model's single component, identified components with various time-frequency scales, compared the decomposition results with EMD and variational mode decomposition (VMD), and found that the AFD effectively captures valuable price information derived by all these methods the best. In addition to this, Li et al. ^[46] demonstrated that the detailed elements of AFD more accurately indicate the structural changes in the original time series.

2.3.   Methodology of the return spillover

The volatility spillover approach mentioned above can be used to capture linear dependence in the financial domain, but it is not possible to measure nonlinear relationships between financial time series ^[47]. Therefore the copula function theory of Embrechts ^[48] can be used to study nonlinearities in finance and also to capture return spillovers. In recent years, copula specification has been used by more and more scholars to study risk spillover effects in finance ^[49,50]. Although value-at-risk (VaR) constitutes an efficacious methodology for assessing the extremity of risks associated with individual assets or standalone financial markets, it demonstrates a notable deficiency in accounting for the interconnected risks that propagate between dissimilar financial assets or market sectors. Therefore, Adrian and Brunnermeier ^[51] presented conditional VaR (CoVaR) as a new risk measure. Unlike Adrian and Brunnermeier ^[51], we use a GARCH-copula quantile regression model rather than a quantile regression model or a GARCH-copula model to estimate CoVaR. GARCH-copula models are effective in capturing nonlinear tail dependence between markets, accurately representing sharp peaks, thick tails of marginal distributions, biases, serial correlations, and phenomena of volatility clustering ^[15,52,53]. Nevertheless, a limitation of such copula-based models lies in their assumption of a static nature for the nonlinear tail dependence structure, which might fail to adequately capture the dynamic nature of financial interactions over time ^[15]. Time-varying coefficient (TVC) models were subsequently presented by Patton ^[54], where the structural composition of the copula remains invariant, and the allowance for temporal fluctuations in tail dependence endows these models with a crucial degree of dynamism. Implementing a TVC model could result in an unreliable VaR for asset portfolios and assets. Bouyé and Salmon ^[55] introduced a copula quantile regression model. This model fails to account for serial correlation and the clustering of volatilities within the marginal distributions, potentially resulting in inaccurate estimations of the outcomes. Tian and Ji ^[56] advocated for the implementation of a GARCH-copula quantile regression framework to quantify the downside-CoVaR (DCoVaR), emanating from four distinct financial markets toward the developed market financial system. This model is considered more rational than the traditional GARCH-copula model and simpler to manage than the TVC model. On this basis, Tian et al. ^[15] applied this model to evaluate the upward and downward tail dependence between oil prices and stock market returns for different risk levels. We employ the aforementioned model to investigate the spillover effects of extreme risks, both in terms of upward and downward movements, between EC and LOG markets. Subsequently, we assess the significance and asymmetry of the model's results using the two-sample bootstrap Kolmogorov-Smirnov (KS) test.

3.   Methodology

To assess the asymmetric transmission of risk between LOG and EC markets, we employ a Bayes-pdBEKK-GARCH model to investigate the asymmetric spillover effects and dynamic interactions in them. The model not only portrays the time-varying characteristics of market volatility, but also reveals the transmission mechanism of volatility across different markets, thus laying a solid foundation for the subsequent risk spillover analysis. Subsequently, in order to specifically quantify the extent of spillovers revealed by the Bayes-pdBEKK-GARCH model and to detect whether structural mutations are embedded in it, we use the AFD method. Its powerful signal processing capability helps to identify potential structural mutation points, providing important clues to extreme risk. Finally, to quantify and assess extreme risk, we use the GARCH- copula quantile regression (CQR) model. This model combines the GARCH model with the copula function, which not only captures the tail risk characteristics of market returns, but also calculates the conditional CoVaR, which provides us with a powerful tool to measure extreme risk. To ensure the significance and asymmetry of the GARCH-CQR model results, a two-sample KS test is also used to ensure that our analytical conclusions are both robust and reliable.

3.1.   Bayes-pdBEKK-GARCH model

Given the observation sample $y = {y_1}, ..., {y_D}$, the conditional likelihood function $\theta = ({\phi _0}, \phi, \psi, C, A, B, \beta, \upsilon)$ of the Bayes-pdBEKK-GARCH(1, 1) model is:

where the joint density function $\eta_{t}$ of ${p_\eta }$ of is assumed to be a standard multivariate normal distribution. To better accommodate the thick-tailed characteristics of the data, we use the multivariate Student-t distribution $St(\nu, 0, I)$ with the degree of freedom $\nu$, proposed by Geweke ^[57], instead of the Gaussian distribution. Assume that $\mu_{t}$ is a multivariate autoregressive moving average model (ARMA)(1, 1) model, i.e., $\mu_{t} = \phi_{0}+\phi y_{_{t-1}}+\psi(y_{_{t-1}}-\mu_{_{t-1}})$; $\phi_{0}$ is a $d \times d$ vector of intercepts; $\phi$ is a $d \times d$ matrix denoting the AR(1) components; and $\psi$ is a $d \times d$ matrix denoting the MA(1) components. Let $\boldsymbol{H}_{t} = \begin{pmatrix}h_{11, t}&h_{12, t}\\h_{21, t}&h_{22, t}\end{pmatrix}$ be the covariance matrix, $\boldsymbol{C} = \begin{pmatrix}c_{11} & 0\\c_{21}&c_{22}\end{pmatrix}$ be the constant term matrix, $\boldsymbol{A} = \begin{pmatrix}a_{11}&a_{12}\\a_{21}&c_{22}\end{pmatrix}$ be the ARCH coefficient matrix, and $\boldsymbol{B} = \begin{pmatrix}b_{11}&b_{12}\\b_{21}&b_{22}\end{pmatrix}$ be the GARCH coefficient matrix. The constant variance $\boldsymbol{C} = sR_{c}s$, where $R_{c}$ is the correlation, $\mathit{s}$ is the standard deviation, and the matrix $\mathit{diag(s) = exp(X\beta)}$ comprises solely elements derived from the linear model, while on the logarithmic scale, the standard deviation is denoted as $\beta\sim N(0, 3I)$. Lewandowski et al. ^[58] proposed the correlation matrix prior $R_c\sim LKJ(\nu = 1)$, which is employed to specify the prior distribution of the correlation matrix, where $\nu$ controls the shape of the distribution.

Both ARCH and GARCH have invariant elements that are constrained to ensure smoothness during the process. This allows us to specify the prior distribution directly since the prior is defined as a uniform prior with lower and upper bounds. For the Bayes-pdBEKK-GARCH model, it is a prerequisite that the absolute eigenvalues of the Kronecker product between the ARCH(A) and GARCH(B) processes are required to be both less than 1, and thus the prior distribution is assumed to be $\boldsymbol{A}\sim U(a_l, a_u)$, $\boldsymbol{B}\sim U(b_l, b_u)$ ^[38].

3.2.   AFD test

3.2.1.   AFD method

The Takenaka-Malmquist (TM) system, also known as the modified Blaschke product, is defined as:

$a_n\in\mathbb{D}(n = 1, 2, ...)$, $\mathbb{D} = \begin{Bmatrix}z\in\mathbb{C}:|z| < 1\end{Bmatrix}$, where $\mathbb{C}$ is a complex plane ^[59]. For any $a_{n}$ in $\mathbb{D}$, the system ${B_n}(z)$ is orthogonal. Within this system, a condition for hyperbolic indivisibility exists if and only if

In the case of infinite sequences, the above conditions are sufficient and necessary ${B_n}(z)$ to form a basis ${H^2}\left(D \right)$ space. For $\forall F \in {H^2}$, utilizing the Cauchy formula, we derive for the case the following expression:

where ${e_{\left\{ a \right\}}}$ is called the evaluator or normalized reproduction kernel at the point $a$, which is

A relationship exists for a real-valued signal $\tilde{G}$:

where $c_0$ represents the power expansion coefficient of $F$, ${G^ + } \in {H^2}$. $\tilde{G}$ can be reconstructed by $G^{+}$. The precise steps are as follows:

Step 1: Use the maximized projection to select ${\left| {{G_1}, {e_{\left\{ a \right\}}}} \right|^2}$. In the first decomposition layer, for any $a \in D$:

we can get ${a_1} = \arg \max {\left| {{G_1}, {e_{\left\{ a \right\}}}} \right|^2}$.

Step 2: Set ${G_1}(z) = \langle {{G_1}, {e_{\left\{ {{a_1}} \right\}}}} \rangle {e_{\left\{ {{a_1}} \right\}}} + {R_1}(z)$, where ${R_1}(z) = {G_2}(z)\dfrac{{z - {a_1}}}{{1 - {{\overline a }_1}z}}$.

Step 3: Use maximum screening ${G_1}$ to obtain ${G_2}$.

AFD amplification ${G^ + }$ was obtained by the above process.

For a real-valued signal $\tilde{G}$, the signal G can be reconstructed by the decomposition method described above, and this process is called AFD decomposition.

3.2.2.   AFD-based transient time-frequency distribution

The analytic signal obtained after AFD decomposition can be denoted as $x(t) = \rho (t){e^{j\mu (t)}}$, and its TTFD is defined as ^[20] :

where

$M$ is a huge positive integer. If $M$ is 1, then $\delta_M(\xi-\varphi^{\prime}(t))$ is a unit pulse function.

There are 3 key features of TTFD. First, the transient frequency is the same for all channels in a decomposition layer. Second, the shown transient frequencies are always positive ^[59,60]. Third, because of the traits of the TM system, ${\omega _n}(t) < {\omega _{n + 1}}(t)$. At each time instance, there is no overlapping spectral content among the various decomposition scales ^[20].

Assuming that orthogonal decomposition applies to the analytic representation of a monocomponent signal $x(t)$, the corresponding TTFD is defined as:

where ${P_k}(t, \xi)$ is the TTFD of a single component ${x_k}$.

3.3.   GARCH-CQR models based on CoVaR

3.3.1.   Marginal distribution model

In this section, we introduce the ARMA-GARCH model, which captures the correlation, volatility, and conditional heteroscedasticity properties of the return series. The ARMA(p, q)-EGARCH(m, n) model is

where $p$ and $q$ are nonnegative integers; ${\varphi _0}$ is the constant term, ${\varphi _i}$ and ${\psi _t}$ are the autoregressive and moving average parameters, respectively; $\sigma _t^2$ is the conditional variance; sequence $\{ {\varepsilon _t}\}$ comprises independent and identically distributed (i.i.d) random variables, which adhere to a standardized skewed Student-t probability distribution ^[61]; $\xi$ is the skewness, $\nu$ is the degree of freedom, $\omega > 0$, ${a_i} \geqslant 0$, ${\beta _j} \geqslant 0$ and $\sum\nolimits_{j = 1}^{\max (m, n)} {({a_i} + {\beta _j})} < 1$; ${g_i}({\varepsilon _{t - i}}) = ({\alpha _i}\varepsilon + {\gamma _i}(\left| {{\varepsilon _i}} \right| - E\left| {{\varepsilon _i}} \right|))$; the parameter ${\alpha _i}$ represents the sign effect; and the parameter ${\gamma _i}$ represents the magnitude effect, which indicates the asymmetric effect of positive and negative return fluctuations.

3.3.2.   CQR model

Using the Sklar theorem proposed by Sklar ^[62], the marginal distribution $u = {F_X}(x)$ of the random variable $X$ and the marginal distribution $v = {F_Y}(y)$ of $Y$ are connected into a multivariate distribution function, which is ${F_{XY}}(x, y) = C({F_X}(x), {F_Y}(y); \delta)$. Based on the conditional probability that $Y$ is in the quartile $\tau$ given $X = x$, we get

which is the ${\tau ^{th}}$ copula quartile curve for $(u, v)$. Thus we can obtain the CQR function of $(x, y)$ at the $\tau$ quantile :

The $(1 - \tau)^{th}$ copula quantile curve of $(u, v)$ can be generated based on the definition of the upside-CoVaR (UCoVaR):

This is the ${(1 - \tau)^{th}}$ copula quantile curve of $(u, v)$. Thus the CQR function of $(x, y)$ at the $(1 - \tau)$ quantile is:

3.3.3.   CoVaR model

According to the measures of VaR and CoVaR given by Adrian and Brunnermeier ^[51], conditional on the downside $VaR_{\beta, t}^{log }$ and upside $VaR_{1 - \beta, t}^{log }$ of the LOG market returns for a given confidence level $1 - \beta$, the $DCoVaR_{\tau |\beta, t}^{ec|log }$ and $UCoVaR_{1 - \tau |1 - \beta, t}^{ec|log }$ of the EC market are satisfied as follows for a given confidence level $1 - \tau$:

where ${r_{ec, t}}$ and ${r_{ec, t}}$ represent the returns of the EC and LOG markets, respectively. Therefore, at a confidence level $1 - \tau$, the risk spillover $\Delta CoVaR_{\tau |\beta, t}^{ec|log }$ from the LOG market to the EC market is:

where $CoVaR_{\tau |\beta, t}^{ec|log }$ and $CoVaR_{\tau |0.5, t}^{ec|log }$ represent the VaR ratios of the EC market during troubled and benchmark states of the LOG market, respectively.

Similarly, the upside risk spillovers are

In the later work, we use the single-parameter copula family including Clayton copula, Joe Copula, Gumbel copula, Galambos copula, Hüsler-Reiss copulas, as well as their corresponding rotated forms ^[63,64], which are shown in Appendix A. Here the Clayton copula better describes the downward tail dependence between EC and LOG, and the Joe copula, the Gumbel copula, the Galambos copula, and the Hüsler-Reiss copula better describes the upward tail dependence between EC and LOG, and their rotated forms can describe the opposite dependency structure. We use the parameter $C(u, v; \delta)$ to represent the copula and the parameter ${C_1}(v|u; \delta) = \dfrac{{\partial C(u, v; \delta)}}{{\partial u}}$ to represent the conditional copula, which are shown in Appendix B.

3.3.4.   GARCH-CQR model based on CoVaR

Let ${F_{log, t}}$ and ${F_{ec, t}}$ denote the marginal distribution functions of returns ${r_{log, t}}$ and ${r_{ec, t}}$ in the LOG and EC markets, respectively, which are available according to the definition of CoVaR, Eqs (14) and (15):

where ${D_{log }}$ and ${D_{ec}}$ denote the marginal distribution functions of ${\varepsilon _{log, t}}$ and ${\varepsilon _{ec, t}}$, respectively, and the standardized residuals of ${r_{log, t}}$ and ${r_{ec, t}}$; ${\mu _{log, t}}$, ${\mu _{ec, t}}$, and ${\sigma _{log, t}}$, ${\sigma _{ec, t}}$ are the conditional means and standard deviations of the returns in the LOG and EC markets, respectively. Therefore, the DCoVaR can be obtained by the following estimation:

where $D_{ec}^{ - 1}$ is a quantile function of ${\varepsilon _{ec, t}}$. Eq (23) represents the inlying algorithm for the non-linear quantile regression model ^[65] at the $\tau ^{th}$ quantile:

where ${Q_\tau }(\left. {{\varepsilon _{ec, t}}} \right|{\varepsilon _{log, t}})$ is the $\tau ^{th}$ conditional quantile of ${\varepsilon _{ec, t}}$ given ${\varepsilon _{log, t}}$, ${\eta _\tau }$ is the scaling parameter, and ${\theta _\tau }$ is the translation parameter. Thus, given confidence levels $\tau$ and $\beta$, conditional on the downside $VaR_{\beta, t}^{log }$ of the LOG market, the $DCoVaR_{\tau |\beta, t}^{ec|log }$ of the EC market can be obtained:

Equation (24) is the DCoVaR-based GARCH-CQR model ^[56]. Meanwhile, the UCoVaR-based GARCH-CQR model ^[15] is:

Correspondingly, under the condition that the LOG market is in the benchmark state ($\beta = 0.5$), the DCoVaR and UCoVaR for the EC market can be computed utilizing Eqs (24) and (25), thereby yielding expressions for the respective downside and upside risk spillover effects as follows:

and

3.3.5.   Two-sample bootstrap KS test

To discern if the risk spillovers from the LOG market to the EC market are statistically significant, we use the two-sample bootstrap KS test ^[15] to compare the cumulative distribution function of the baseline CoVaR with those of the dynamic DCoVaR and UCoVaR. The pertinent statistical quantities for the significance test were defined as follows:

where ${F_m}(x)$ represents the cumulative distribution function (CDF) of the baseline CoVaR, while ${G_n}(x)$ denotes the CDF corresponding to the DCoVaR(UCoVaR). Here, and $m$ and $n$ denote the sizes of the two samples being compared. The null hypotheses underlying the significance tests for both DCoVaR and UCoVaR are formulated as follows:

and

Finally, the asymmetry test is conducted to investigate whether the contribution of upside risk spillovers from the LOG market to the EC market is greater than or equal to that of downside risk spillovers. This asymmetry assessment can also be facilitated through a two-sample bootstrap KS test. The original hypothesis for this asymmetry test is stated as follows:

4.   Data

This paper selects daily data from January 2, 2014, to November 30, 2023, which contained a total of 2413 observations. The year 2014 is an extremely important year for the development of China's EC and LOG. China's two major EC companies JD.com and Alibaba listed in the United States, and the State Council of China had a new plan for China's LOG, issuing the "Medium and Long-term Plan for the Development of the Logistics Industry (2014-2020)". These three events have greatly promoted the development of EC in China. Extreme events such as the 2015 Chinese stock market crisis, the 2018 Sino-U.S. trade friction, the 2020 COVID-19 pandemic, the 2021 Chinese EC monopoly incident, and the 2022 Russia-Ukraine war are all included in the sample range.

For the variable EC, we adopt the China Securities Index (CSI) E-Commerce Thematic Index which selects the securities of listed companies involved in EC platforms, trading services and commodity sales as the index sample to reflect the overall performance of the securities of EC-related listed companies in the Shanghai Stock Exchange and Shenzhen Stock Exchange in China. For the variable LOG, we choose the CSI Logistics Industry Index which selects the securities of listed companies involved in Shanghai Stock Exchange and Shenzhen Stock Exchange in China. The data is obtained from the official website of CSI (https://www.csindex.com.cn/about/overview). Note that China Securities Index Co., Ltd. (CSI), a financial market index provider, was jointly funded in August 2005 by China's two major stock exchanges, the Shanghai Stock Exchange and the Shenzhen Stock Exchange, which means it has a certain authority (https://www.csindex.com.cn/about/overview).

We compute returns by taking logarithmic differences of prices:

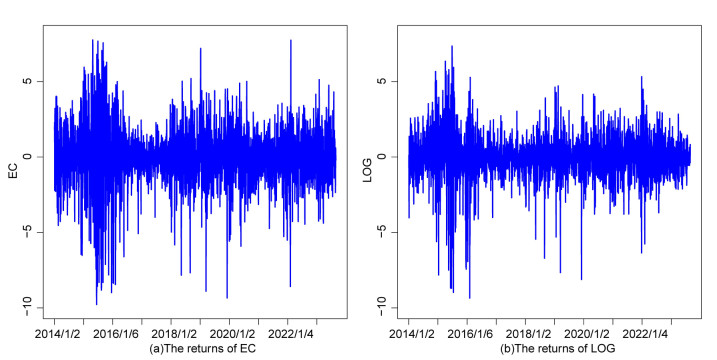
where ${R_{i, t}}$ is the original price series of the EC(LOG) index at the time t. Figure 1 reveals the plots of EC and LOG.

4.1.   Descriptive analysis

Figure 1 shows the logarithmic returns for the EC and LOG markets. The return series shows significant volatility and clustering patterns. The EC and LOG markets experienced large fluctuations in 2015–2016, which corresponded to the Chinese stock market crisis of 2015 ^[66]. In 2018, both EC and LOG were affected by the Sino-U.S. trade friction, and their development was hindered ^[67], showing a downside trend. During the outbreak of COVID-19 in 2020, the restriction of people's travel made it possible for EC transactions to increase dramatically ^[68], which also drove the development of LOG. In 2021, the "either-or choice" of China's EC monopoly policy limited competition in the EC market which hindered the development of other EC firms and inhibited the growth and innovation of the industry as a whole. In 2022, the continued impact of COVID-19 and the imposition of high tariffs on Chinese goods has hampered the development of China's EC into overseas markets ^[69].

Table 1 presents descriptive statistics for the return series of the EC and LOG markets. The average of all returns is close to zero. The large difference between the maximum and minimum values of EC and LOG proves that they have significant fluctuations of their own. The skewness of EC and LOG is less than 0, which is left-skewed. Their peaks are greater than 3, which is in line with the peak characteristics EC and LOG are characterized by "sharp peaks and thick tails", which suggests that there is a high probability that EC and LOG exhibit extreme tail events. At the 1% significant level, the ADF results show that the return series of EC and LOG are smooth, and the results of the Jarque-Bera (JB) test indicate that EC and LOG do not adhere to a normal distribution. Furthermore, the results of the Ljung-Box (LB) test also refute the original hypothesis of autocorrelation with a lag of 9 periods. The results of Engle's Lagrange multiplier (LM) test reveal that there is a significant ARCH effect in both markets.

4.2.   Bayesian pdBEKK-GARCH model

The Bayes-pdBEKK-GARCH model is employed on stationary time series data to investigate the dynamics of conditional covariance and conditional correlation structures. This model with a lag order of (1, 1) has been shown to better characterize the volatility spillovers between markets ^[37]. We utilize the Bayes-pdBEKK-GARCH(1, 1) model in this study to evaluate the volatility spillovers between EC and LOG markets.

Table 2 describes in detail the volatility spillover results between EC and LOG. The estimation results indicate that the diagonal elements ${\alpha _{11}}\left({0.17} \right)$, ${\alpha _{22}}\left({0.27} \right)$, ${\beta _{11}}\left({0.98} \right)$, and ${\beta _{22}}\left({0.94} \right)$ of matrix $\mathbf{A}$ and matrix $\mathbf{B}$ are significant. This indicates the presence of significant ARCH and GARCH effects in both markets, implying that EC and LOG are susceptible to idiosyncratic shocks and persistent volatility. We also examine the non-diagonal elements of the matrices, ${\alpha _{ij}}$ and ${\beta _{ij}}$, $i \ne j$, which capture the cross-market effects of the two markets, i.e., the volatility and persistence spillovers between the EC and LOG markets. Specifically, the ${\alpha _{21}}$ parameter in the ARCH and GARCH results indicates that LOG generates a short-run negative shock to EC, ${\beta _{21}}$ indicates that LOG generates a long-run positive volatility spillover to EC, respectively, and the ${\beta _{12}}$ parameter indicates that EC generates a long-run negative volatility spillover to LOG. Thus, in both EC and LOG markets, the present conditional volatility on either side is found to be influenced not solely by its prior volatility, but also by the preceding volatility of the opposing market. The results confirm the interdependence between EC and LOG markets. In addition, there is a conditional correlation between the volatility of EC and LOG over time (as shown in Figure 2). In most cases, a substantial positive correlation was found between the two markets.

4.3.   AFD test

First, we apply the AFD method, rooted in the TM system, to break down the volatility estimates obtained from the Bayes-pdBEKK-GARCH(1, 1) estimation. Then, TTFD of volatility is created to identify structural changes in the two markets. After identifying the breakpoints, the volatility characteristics of the two markets in the vicinity of the breakpoints are analyzed to study the effect of a shock in one market that leads to structural breaks in the other market.

EC market and LOG market volatility are decomposed and reconstructed based on the TM system. Figure 3(a) shows the decomposition and reconstruction results for EC. "Decomposition no" denotes the maximum step size of the decomposition, and "MSE" denotes the discrepancy between the initial volatility signal of EC and the rebuilt volatility signal. The smaller the error, the smaller the signal loss obtained from the reconstruction, which means the more original information is retained. The blue line depicts the actual fluctuation pattern, whereas the red line displays the rebuilt fluctuation sequence. From Figure 3(a), it can be seen that the reconstructed fluctuation signal and the original fluctuation signal are the same, and the error is 0.0061. Figure 3(b) shows the decomposition and reconstruction results of LOG, which has an error of 0.0146. We will use the results to support the decomposition and reconstruction, and then proceed to create their TTFD maps.

Figure 4(a) shows the TTFD of EC, which consists of many colored dots. The x-axis is the time point under study and the y-axis is the frequency of EC. Higher frequencies indicate stronger changes in volatility. With 70 decompositions and reconfigurations, the peaks will overlap or increase with each other, and the volatility jitter will also be more violent, indicating the presence of structural breaks. According to Figure 4(a), the peaks of the TTFD of EC volatility occur in 2015, 2018, 2020, 2021, and 2022. Figure 4(b) shows the TTFD of LOG, similar to Figure 4(a). According to Figure 4(b), the peaks of the TTFD of EC volatility occur in 2015, 2018, 2020, and 2023. These events, such as China's stock market turmoil in 2015 ^[70], the United States imposing large-scale tariffs on goods imported from China, the COVID-19 outbreak in 2020 ^[71], and the Russia-Ukraine conflict in 2022, bring serious risk spillovers to China's EC and LOG industries. The economic downturn, exchange rate depreciation, and major stock market turmoil directly affected consumers' purchasing power and confidence, which may lead to a decline in EC transactions and a decrease in LOG demand. The large-scale tariffs imposed by the U.S. on China's goods, the COVID-19 epidemic, and disruptions in the global supply chain have left EC companies to deal with unreliable raw material availability, increased costs, and disruptions in LOG transportation. The Russia-Ukraine conflict and the global food and energy crisis have caused serious damage to the global industrial and supply chains, which may lead to multiple risks such as a tight import and export trade environment, rising LOG costs, and unstable supply chains. These challenges require EC and LOG enterprises to respond more cautiously, strengthen risk management, and innovate coping strategies.

4.4.   GARCH-CQR models

4.4.1.   Estimation of the marginal distribution

To capture the distributional properties of the posterior tail, skewness, autocorrelation, and volatility aggregation, marginal return distributions of EC and LOG markets are formulated using ARMA-EGARCH frameworks, adopting standard normal, Student-t, and skewed Student-t distributions. Model selection is guided by the log-likelihood function (LLF) and Akaike information criterion (AIC), tabulated in Table 3. The superior fit is discerned as the ARMA(1)-EGARCH(1) model with a skewed Student-t distribution, as indicated by the lowest AIC and highest LLF values.

The selected models in Table 3 were used for estimation, and the estimated parameters in Table 4 were obtained by the LB test and ARCH test. Applying the LB test on standardized residuals and their squared values derived from the ARMA(1)-EGARCH(1) model with Skewed Student-t distributed errors, we fail to reject the null hypothesis of no serial correlation up to lag 9 at a 5% significance level. Consistently, the LM test fails to detect any ARCH influence in the EC and LOG returns. Parameter and standard deviation estimates validate the adequacy of the ARMA(1)-EGARCH(1) specification. Moreover, the Skewed Student-t distribution's parameter estimates confirm the non-normality of standardized residuals, corroborating the detected left-skewness and kurtosis in Table 1.

4.4.2.   Copula model estimation and selection

The marginal inference function (IMF) method ^[64] is used on the standardized residuals $({\varepsilon _{ec, t}}, {\varepsilon _{log, t}})$ to select the optimal copula function for pairing EC and LOG markets. Based on the LLF and AIC values given in Table 5, the rotating Gumbel copula and Gumbel copula models are more effective in capturing the DCoVaR and UCoVaR between EC and LOG markets, respectively. Therefore, we choose these two copula models in the rest.

4.4.3.   Estimation of the CQR model

The rotating Gumbel CQR model and the Gumbel CQR model were fitted using residuals $({\varepsilon _{ec, t}}, {\varepsilon _{log, t}}), t = 1, 2, ...$, at the 5% and 95% quantiles to estimate coefficients $\delta$, $\theta$, and $\eta$. The results are presented in Table 6, and the corresponding fitted curves can be seen in Figure 5. To illustrate this desirable property and the robustness of the method, we generate 2000 random values of $(u, v)$ for Gumbel copula and Rotated Gumbel copula with different parameters $\delta$. The marginal distributions of x and y follow the Skewed Student-t distribution with different parameters. We show the robustness of the results by plotting the CQR curves for the Gumbel copula and Rotated Gumbel copula series in Appendix C.

The parameters $\delta$ for the EC and LOG markets show that the EC market has both stronger downside and upside tail dependence, while the LOG market shows stronger dependence only in the upside tail and the strongest dependence of all the upside tail dependence. The panning parameter $\theta$ is greater than 0 at the 95% quantile. The scaling factor $\eta$ is greater than 1 at the 5% quantile and less than 1 at the 95% quantile. The analysis of the $\delta$ estimation in Table 6 indicates that the GARCH-CQR model is more likely than the GARCH copula model with a constant tail structure dependence, as it accounts for the varying nonlinear relationship between the two markets based on the risk level.

4.4.4.   Dynamic risk spillover between the two markets

We conduct an estimation of dynamic CoVaR and assess risk spillover with the 95% level of statistical significance. $DCoVaR_{\tau |\beta, t}^{ec|log }$ and $UCoVaR_{1 - \tau |1 - \beta, t}^{ec|log }$ for the EC and LOG markets can be calculated by Eqs (24) and (25). To determine whether mutual spillovers between the two markets hold, we apply significance to their dynamic CoVaR. The significance test presented in Table 7 reveals a rejection of the original hypothesis at a 1% significance level. Therefore, it can be said that EC and LOG markets influence each other.

However, the average absolute value of the downside risk spillover exceeds the upside risk spillover in both markets, meaning that pronounced asymmetry exists in risk spillovers. This finding aligns with the last column of Table 4 and corroborates the outcomes derived from the prior Bayes-pdBEKK-GARCH model estimation.

Figure 6 shows the dynamic CoVaR and $\Delta CoVaR$ of the two markets at the 95% confidence level. The gray points are the standard deviation of log returns, and the red and blue lines indicate the CoVaR at the 0.5 and 0.05 quartiles, respectively. The trends of CoVaR and $\Delta CoVaR$ are the same over time, and the risk spillovers reflect the impacts of some major events, such as the 2015 China stock market crash, Sino-U.S. trade friction, COVID-19, and the Fed's contractionary monetary policy. In 2015, China's A-share market crashed and the Chinese yuan (CNY) plummeted ^[66]. This led to an increase in the cost of imported goods, which greatly impacted EC companies that rely on imported goods, and at the same time the cost of export goods also rose, putting pressure on export LOG companies. In 2018, the U.S. government announced tariffs on some imports from China, which led to a decline in export sales on Chinese EC platforms, as consumers may reduce their purchases of these goods as a result of rising costs ^[72]. In 2020, COVID-19 spread and many countries or regions implemented measures such as embargoes and export restrictions, leading to supply chain disruptions and unstable supply of goods ^[71]. At this time, EC companies faced more LOG and customs clearance challenges to keep their cross-border EC business running normally. The LOG industry is also affected by transportation restrictions, rising costs, etc. In 2022, the Fed's contractionary monetary policy caused the exchange rates of many currencies to fall to record lows, imported inflationary pressures increased sharply, the risk of debt defaults rose, and financial markets fluctuated violently. These affected international trade in China's EC and LOG sectors.

5.   Conclusions

This paper investigates asymmetric spillovers between EC and LOG markets. First, the Bayes-pdBEKK-GARCH model is used as the starting point of the analysis, which is an extension of the BEKK-GARCH model that integrates Bayesian inference with the positive diagonal BEKK parameterization methodology, aiming to more accurately capture and analyze the asymmetric volatility spillovers and dynamic relationships between the two markets. It is found that significant asymmetric volatility spillovers and positive correlations do exist between the EC and LOG markets, which lays the theoretical foundation and provides key findings for the subsequent risk spillover analysis. In order to deeply quantify the extent of volatility spillovers and explore structural changes among markets, the AFD methodology of observing frequency shifting to detect potential structural mutations not only helps to reconstruct the transient time-frequency distributions of EC and LOG volatility, but also identifies important clues that the market may have suffered or is experiencing shocks from extreme events, which provides important clues for the subsequent analysis of extreme risk spillovers. After identifying the presence of asymmetric volatility spillovers and potential structural mutations between markets, we employ a GARCH-CQR model to capture volatility clustering, tail dependence, and potential asymmetric effects in the data. The GARCH model partially and efficiently fits the volatility of market returns, while the copula function is used to characterize the tail dependence between the variables, in particular the upper and lower tails of the asymmetric dependence structure of the tails. Through quantile regression, the model is able to portray the market behavior under different risk levels in a more detailed way, and CoVaR is calculated accordingly to accurately measure the extreme risk spillover between the two markets. The experimental results show that both downside and upside tail dependence are strong in the EC market, while the LOG market shows strong dependence only in the upside tail, which is the strongest dependence among all the upside tail dependence. It is also confirmed that the nonlinear dependence structure between the two markets varies with the level of risk.

In summary, it can be obtained that: First, there exists a distinctive dynamic connection between the EC and LOG markets, which is characterized by volatility spillovers and positive correlation. This means that when one market experiences volatility, the other market is also impacted, and their relationship is marked by asymmetry. In addition, both markets are found to experience structural changes, potentially resulting in varying behavioral patterns and volatility shifts throughout specific time frames. Second, the EC and LOG markets exhibit a nonlinear interdependence, where their relationship dynamically adjusts according to the prevailing risk levels. These changes require market participants to consistently evaluate their risk management techniques and business models. At the same time, the dynamic risk spillovers exhibit heterogeneity and change over time. This indicates that the transfer of risk between two markets is neither uniform nor steady, but instead an intricate process affected by several circumstances. In particular, the LOG market has the least downside risk spillover, possibly attributed to the LOG industry's inherent high threshold and stability, rendering it resilient to specific risk factors. EC market is strongest on upside risk spillover, indicating that the growth of the EC sector is more likely to significantly benefit the LOG market during prosperous times. This is likely because the EC industry's expansion directly drives the increased need for LOG services. Third, extreme events such as China's stock market turmoil, the Sino-U.S. trade friction, COVID-19, and EC's "either-or choice" monopoly can significantly impact both the EC and LOG markets, which heightened market uncertainty and increased extreme risk spillovers between the two markets. Our research fills a gap in the literature and thus more accurately expresses the spillover relationship between EC and LOG markets.

Based on the above findings, our study suggests the following policy and regulatory implications: first, market authorities should enhance the control of EC and LOG industries, particularly in light of the "either-or choice" monopoly incident in EC, rigorously combatting monopolistic practices to foster fair market competition. Second, the government has to enhance the management and oversight of the supply chain to mitigate the effects of unexpected occurrences on the LOG industry. It should also bolster international collaboration to enhance the stability of the supply chain. Third, increased investment and resources should be allocated to the LOG sector, particularly for the advancement of technology and digitalization within the business, to enhance efficiency and competitiveness in the market. Fourth, investors and fund managers should consider including assets from both the EC and LOG sectors in their portfolios, capitalizing on the positive correlation and spillover effects between the two to implement a diversification strategy. It is also important to keep an eye on market volatility and asymmetric spillover and adjust investment weightings to diversify risk when appropriate. Given the significant upside risk spillover from the EC market, focus on its positive momentum and increase exposure to the LOG market when it performs well.

Author contributions

Liushuang Meng: Conceptualization, methodology, software, validation, formal analysis, investigation, resources, data curation, writing- original draft, writing – review and editing; Bin Wang: Conceptualization, methodology, investigation, writing – review and editing, supervision, funding acquisition. All authors have read and approved the final version of the manuscript for publication.

Acknowledgments

This article was supported partially by the National Natural Science Foundation of China (No.11961015) and Natural Science Foundation of Guangxi (No.2018GXNSFAA050031).

Conflict of interest

The authors declare no conflict of interest.

A.   Appendix A

B.   Appendix B

C.   Appendix C