1.
Introduction
There is growing interest in studying generalized supergeometry, that is, geometry of graded manifolds where the grading group is not Z2, but Zn2=Z2×…×Z2. The foundational aspects of the theory of Zn2−manifolds were recently studied in [1,2,3,4]. This generalization is used in physics, see [5]. Also in Mathematics, there exist many examples of Zn2−graded Zn2−commutative algebras: quaternions and Clifford algebras, the algebra of Deligne differential superforms, etc. Moreover, there exist interesting examples of Zn2−manifolds. In this paper, we study the Zn2−grassmannians as Zn2−manifolds and their constructions.
In the context of manifolds, homogeneous superspaces have been defined and investigated extensively using the functor of points approach in [6,7,8]. In this paper, we show that Zn2−grassmannians G→k(→m) are homogeneous, c.f. section 3. To this end, we show that the Zn2−Lie group GL(→m), c.f. section 2, acts transitively on Zn2−grassmannian G→k(→m), c.f. section 3.
In the first section, we recall briefly all necessary basic concepts such as Zn2− grading spaces, Zn2−manifolds, Zn2−Lie groups and an action of a Zn2−Lie group on a Zn2−manifold. We use these concepts in the case of Z2−geometry in [6] and [8].
In section 2, we study the Zn2−grassmannians extensively. The supergrassmannians are introduced by Manin in [9], but here by developing an efficient formalism, we fill in the details of the proof of this statement.
In section 3, by a functor of points approach, an action of the Zn2−Lie group GL(→m) on the Zn2−grassmannian G→k(→m) is defined by gluing local actions. Finally it is shown that this action is transitive.
2.
Preliminaries
Let Zn2=Z2×…×Z2 be the n−fold Cartesian product of Z2. From now on, we set q:=2n−1 and by →k, we mean (k0,k1,…,kq) such that ki∈N. Consider the bi-additive map
The even subgroup (Zn2)0 consists of elements γ∈Zn2 such that ⟨γ,γ⟩=0, and the set (Zn2)1 consists of odd elements γ∈Zn2 such that ⟨γ,γ⟩=1.
One can fix an ordering on Zn2; based on this ordering, each even element is smaller than each odd element. Given two even (odd) elements (a1,a2,…,an) and (b1,b2,…,bn), the first one is smaller than the second one for the lexicographical order, if ai<bi, for the first i where ai and bi differ. For example, the lexicographical ordering on Z32 is
Obviously, Zn2 with lexicographical ordering is totally ordered set. Thus it may be diagrammed as an ascending chain as follows
In the supergeometry, the sign rules between generators of the algebra are completely determined by their parity. One can define a grading by (2.1) such that ϵ(a,b)=(−1)⟨a,b⟩ will be a sign rule what will lead to Zn2−geometry. Also, it has been shown that any other sign rule for finite number of coordinates is obtained from the above sign rule for sufficiently big n. See [1] for more details.
2.1. Zn2−geometry
The Zn2−graded objects like Zn2−algebras, Zn2−ringed spaces, Zn2−domains and Zn2−manifolds have been studied in [1,3,4]. In the following, we recall the necessary definitions from these references.
By definition, a Zn2−vector space is a direct sum V=⨁γ∈Zn2Vγ of vector spaces Vγ over a field K (with characteristic 0). For each γ∈Zn2, the elements of Vγ is called homogeneous with degree γ. If x∈Vγ be a homogeneous element of V, then the degree of x is represented by ˜x=γ.
A Zn2−ring R=⨁γ∈Zn2Rγ is a ring such that its multiplication satisfies
A Zn2−ring R is called Zn2−commutative, if for any homogeneous elements a,b∈R
For any Zn2−algebra R, let J be an ideal of R generated by all homogeneous elements of R having nonzero degree. If f:R→S is a morphism of Zn2−algebras, then f(JR)⊆JS. Let M be an R-module. The collection of sets {x+JkM}∞k=0 can be considered as a basis for a topology on M. This topology is called J−adic topology. Note that x runs over all elements of M. The J−adic topology plays a fundamental role in Zn2−geometry.
A Zn2−ring R with respect to J−adic topology is Hausdorff complete if the natural ring morphism R→lim←k∈NR/Jk is an isomorphism.
Example 2.1. Let R be a ring and ξ1,…,ξq be indeterminates with degree γ1,…,γq∈Zn2 respectively such that
Then R[[ξ1,…,ξq]] is the Zn2−commutative associative unital R−algebra of formal power series in the ξa with coefficients in R. If J be an ideal generated by all formal power series ∑→ka→kξk01…ξkqq whose first term a→k is equal to zero, then One can see R[[ξ1,…,ξq]] is J−adically Hausdorff complete.
By a Zn2−ringed space, we mean a pair (X,OX) where X is a topological space and OX is a sheaf of Zn2−commutative Zn2−graded rings on X. A morphism between two Zn2−ringed spaces (X,OX) and (Y,OY) is a pair ψ:=(¯ψ,ψ∗) such that ¯ψ:X→Y is a continuous map and ψ∗:OY→¯ψ∗OX is a homomorphism of weight zero between the sheaves of Zn2−commutative Zn2−graded rings. Let q=2n−1, the Zn2-ringed space
is called Zn2-domain such that C∞Rm0 is the sheaf of smooth functions on Rm0. By evaluation of f=∑fIξI at x∈U, denoted by evx(f), we mean f∅(x). Also for each open U⊂Rm0,
is the Zn2−commutative associative unital Zn2−algebra of formal power series in formal variables ξji's of degrees γi which commuting as follows:
Let J(U) be the ideal generated by all homogeneous formal power series of nonzero degree. Then it is easily seen that OR→m(U) is Hausdorff complete with respect to J(U)-adic topology. Equivalently there is a canonical ring isomorphism between O(U) and lim←kO(U)/Jk(U). Let V⊂U. Then the following diagram is commutative
where rUV:O(U)→O(V) is the restriction map and RUV is induced morphism. This shows that the notion of adic topology may be extended for sheaf O such that each stalk Op, p∈Rm0, is Hausdorff complete with respect to Jp−adic topology.
A Zn2-manifold of dimension →m is a Zn2-ringed space (¯M,OM) that is locally isomorphic to R→m. In addition ¯M is a second countable and Hausdorff topological space. A morphism between two Zn2-manifolds M=(¯M,OM) and N=(¯N,ON) is a local morphism between two local Zn2-ringed spaces.
Let (M,OM) be a Zn2−manifold, and let J be the ideal sheaf J, defined by
The structure sheaf OM is J−adically Hausdorff complete as a sheaf of Zn2− commutative Zn2−rings. See Proposition 6.9 in [3] for more details.
Analogous with supergeometry, one can obtain a Zn2−manifold by gluing Zn2− domains. We will use this method to construct the Zn2−grassmannian as a Zn2− manifold in section 3.
In order to introduce the concept of Jacobian, we need a few definitions and a proposition from [10].
Definition 2.2. Let M be a Zn2-manifold and m∈¯M. The tangent space of M at m, denoted by TmM, is the real Zn2-vector space of R−derivations Om→R.
Definition 2.3. Let ψ:M→N be a morphism of Zn2-manifolds. Assume ¯ψ(m)=n∈¯N for a point m∈¯M. The tangent map of ψ at m is a morphism of Zn2-vector spaces denoted by (dψ)m:TmM→TnN and defined by
Let ψ:M→N and φ:N→Q be two morphisms of Zn2-manifolds, one can use the above definition to show that for any point m∈¯M,
Here we state the chain rule for Zn2-manifolds and use it to relate the tangent map to the Zn2-graded Jacobian matrix. See Proposition 2.10 in [10].
Proposition 2.4. Let U→p, U→r be Zn2-domains, with coordinates uα, vβ respectively. Let ψ:U→p→U→r be a morphism of Zn2-manifolds. Then,
Let us study the matrix representation of the equation (2.2). Assume ψ=(vγ(u)) and φ=(wα(v)) are local representations of Zn2-morphisms ψ:M→N and φ:N→S around m and ¯ψ(m) respectively, one has
Definition 2.5. Let ψ be a Zn2-morphism between Zn2-domains U and V. If u↦(vi(u)) is a representation of ψ, then the Jacobian of ψ is a Zn2-matrix of degree zero as follow
At the end of this section, it is worth mentioning that some of the required concepts of category theory are given in the Appendix. At there, among other things, we talked about Yoneda lemma (Lemma A.1). According to this lemma two objects X,Y∈Obj(C) are isomorphic if and only if the functor of points associated to them are isomorphic. Indeed, the Yoneda embedding is an equivalence between C and a subcategory of representable functors in [C,SET] since not all functors are representable. See (Appendix A.1) for more details.
2.2. Zn2−Lie groups
Let ZSM be the category of Zn2−manifolds. This is a category whose objects are Zn2−manifolds whose morphisms are morphisms between two Zn2−manifolds. ZSM is a locally small category and has finite product property, see [11] for more details. In addition it has a terminal object R→0, that is the constant sheaf R on a singleton {0}.
Let M=(¯M,OM) be a Zn2−manifold and p∈¯M. There is a map jp=(¯jp,jp∗) where:
So, for each Zn2−manifold T, one can define the morphism
as a composition of jp and the unique morphism T→R→0.
By Zn2−Lie group, we mean a group-object in the category ZSM. This group is a Zn2−graded group. Graded Lie groups are extensively studied in [12]. The category ZSM has group-object because of existence categorical products and terminal object. Also, one can show that any Zn2−Lie group G induced a group structure over its T-points for any arbitrary Zn2−manifold T. This means that the functor T→G(T) takes values in category of groups. Moreover, for any other Zn2−manifold S and morphism T→S, the corresponding map G(S)→G(T) is a homomorphism of groups. See Appendix for more details. As another form, one can also define a Zn2−Lie group as a representable functor T→G(T) from category ZSM to category of groups.
Example 2.6. Consider the Zn2−domain R→m and an arbitrary Zn2−manifold T. Let fji∈O(T)γi, 0≤i≤q, 1≤j≤mj, be γi−degree elements. By Theorem 6.8 in [1] (Fundamental theorem of Zn2-morphisms), One may define a unique morphism ψ:T→R→m, by setting ξji↦fji where (ξji) is a global coordinates system on R→m. Thus ψ may be represented by (fji).
One can see a degree zero square matrix with entries in the standard block format
is invertible if and only if Bii is an invertible matrix for all 0≤i≤q, see Proposition 1.5 and Proposition 6.1 in [10].
Let V be a finite dimensional Zn2-vector space of dimension →m=m0|m1|…|mq. One can define the Zn2−Lie group GL(V) which is denoted by GL(→m) if V=R→m. For more details, see (Appendix A.2). It can be shown that T−points of GL(→m) are the →m×→m invertible Zn2−matrices of weight zero where the elements of the mk×mu block Bku have degree γk+γu and the multiplication is the matrix product.
Let x∈¯G, one can define the left and right translation by x as
where ΔG is the diagonal map on G and ˆxG is as above. One can show that pullbacks of above morphisms are as following
One may also use the language of functor of points to describe two morphisms (2.4) and (2.5).
One can see the definition of vector fields on a graded Lie group G in [12]. According to the standard superspace, we have the following definition:
Definition 2.7. Let G be a Zn2−Lie group. A Vector field X on G is called right invariant vector field, if we have
Similarly, one can use (1⊗X)∘μ∗=μ∗∘X, for a left invariant vector field X.
The bracket of two right invariant vector fields is right invariant. So we have
Definition 2.8. Let G be a Zn2− Lie group. The set of all right invariant vector fields is denoted by g and is called the Zn2−Lie algebra associated with the Zn2−Lie group G, and we write g=Lie(G)
Similar to standard supergeometry, one can show that g=Lie(G) is a finite dimensional Zn2−vector space canonically identified with the tangent space at the identity of the Zn2−Lie group G.
Definition 2.9. Let M be a Zn2−manifold and let G be a Zn2−Lie group with μ,i and e as its multiplication, inverse and unit morphisms respectively. A morphism a:M×G→M is called a (right) action of G on M, if the following diagrams commute
where ˆeM,ΔM are as above. In this case, we say G acts from right on M. One can define left action analogously.
According to the above diagrams, one has:
By Yoneda lemma (Lemma A.1), one may consider, equivalently, the action of G as a natural transformation:
As in [13], for each p∈M and g∈G, one can define the morphisms ap and ag and use the functor point language to show that the maps ap and ag satisfy the relations
where rg is the right translation on Lie Zn2-group G.
For proof of the following proposition, see (Appendix A.3).
Proposition 2.10. Let a:M×G→M be an action of a Lie Zn2-group G on a Zn2-manifold M. Then
(1) ag is a Zn2-diffeomorphism for all g∈¯G.
(2) ap has constant rank for all p∈¯M.
Before next definition, we recall that a morphism between Zn2−manifolds, say ψ:M→N is a submersion at x∈¯M, if (dψ)x is surjective and ψ is called submersion, if it is surjective at each point. (For more details, refer to [10]). Also ψ is a surjective submersion, if in addition ψ0 is surjective.
Definition 2.11. Let G acts on M with action a:M×G→M. The action a is called transitive, if there exist p∈¯M such that ap is a surjective submersion.
It is shown that, if ap is a submersion for one p∈¯M, then it is a submersion for all point in ¯M. Also one can show that a is transitive if and only if ¯a is a transitive action in classical geometry and (dap)e is a surjective because of Proposition 2.10. The following proposition will be required in the last section.
Proposition 2.12. Let a:M×G→M be an action of a Lie Zn2-group G on a Zn2-manifold M. Let p∈¯M and dimG=→r=(r0,r1,…,rq) and →r′:=(0,r1,…,rq). If the map
is surjective, then a is a transitive action.
Proof. According to above argument, it is enough to show that ¯a is a transitive action in classical geometry and (dap)e is surjective.
Let (ap)R→r′ be surjective. Looking at the reduced part of each morphism in
we have that
is surjective. So ¯a is a classical transitive action. Let now {t,ξ1,…,ξq} be coordinates in a neighbourhood U of m∈¯M. Consider the element Φ∈M(R→r′) defined by
By surjectivity of (ap)R→r′, there exists ψ∈G(R→r′) such that (ap)R→r′(ψ)=Φ and we have
This implies that (TmM)γ≠0 is in the image of (dap)¯ψ. Since, by our previous considerations, ¯ap is a submersion, (TmM)0 is in the image ¯ap. Hence, due to Proposition 8.1.5 we are done.
In the following, after introducing the concept of stabilizer, we state some related results without any proofs, since the proofs are the same as the proofs of the similar results in supergeometry with appropriate modifications without any extra difficulties regarding Zn2−geometry. For more details see [6] and [8].
Definition 2.13. Let G be a Zn2−Lie group and let a be an action of G on Zn2−manifold M. By stabilizer of p∈¯M, we mean a Zn2−manifold Gp equalizing the diagram
Proposition 2.14. Let a:M×G→M be an action, then
1. The following diagram admits an equalizer Gp
2. Gp is a Zn2−sub Lie group of G.
3. The functor T→(G(T))ˆpT is represented by Gp, where (G(T))ˆpT is the stabilizer in ˆpT of the action of G(T) on M(T).
Proposition 2.15. Suppose G acts transitively on M. There exists a G-equivariant isomorphism
3.
Zn2-grassmannian
Supergrassmannians Gk|l(m|n) are introduced and studied by Manin in [9] and [14]. Also the authors have studied them in more details in [13] and [15]. In this section, we introduce the Zn2-grassmannian which is denoted by G→k(→m) shortly, or Gk0|k1|…|kq(m0|m1|…|mq). For convenience from now, we set
and also decompose any Zn2−matrix into 2n×2n blocks
such that the elements of block Bku have degree γk+γu. By a Zn2-grassmannian, G→k(→m), we mean a Zn2-manifold which is constructed by gluing the following Zn2- domains
For i=0,1,…,q, let Ii⊂{1,…,mi} be a sorted subset in ascending order with ki elements. The elements of Ii are called γi-degree indices. The multi-index →I=(I1,...,Iq) is called →k-index. Set U→I:=(¯U→I,O→I), where
Let each Zn2-domain U→I be labeled by a Zn2−matrix →k×→m of weight zero, say A→I, with 2n×2n blocks Bij each of which is a ki×mj matrix. In addition, except for columns with indices in I0∪I1∪…∪Iq, which together form a Zn2−submatrix denoted by M→IA→I, the matrix is filled from up to down and left to right by x→Ia,ξ→Ib, the free generators of O→I(Rβ0) each of them sits in a block with same degree. This process impose an ordering on the set of generators. In addition M→IA→I is supposed to be the identity matrix.
For example, consider G1|2|1|1|2|2|2|2. Then let I0={1},I1={1,2},I2={1},I3={2}, so →I is a 1|2|1|1-index. In this case the set of generators of O→I(Rβ0) is
and A→I is:
Note that, in this example,
is corresponding total ordered set of generators.
By ˜U→I,→J, we mean the set of all points of ¯U→I, on which M→JA→I is invertible. Obviously ˜U→I,→J is an open set. The transition map between the two Zn2-domains U→I and U→J is denoted by
Note that g→I,→J=(¯g→I,→J,g∗→I,→J), where g∗→I,→J is an isomorphism between sheaves determined by defining on each entry of D→I(A→I) as a rational expression which appears as the corresponding entry provided by the pasting equation
where D→I(A→I) is a matrix which is remained after omitting M→IA→I. Clearly, the left hand side of (3.2) is defined whenever M→IA→J is invertible. The morphism g∗→I,→J induces the continuous map ¯g→I,→J (in the case n=1, see [16], lemma 3.1).
For example in G1|2|1|1(2|2|2|2) suppose
so →I,→J are 1|2|1|1-indices. We have:
The maps g→I,→J are gluing morphisms. In fact, a straightforward computation shows the following proposition holds.
Proposition 3.1. Let g→I,→J=(¯g→I,→J,g∗→I,→J) be as above, then
1. g∗→I,→I=id.
2. g∗→J,→I∘g∗→I,→J=id.
3. g∗→S,→I∘g∗→J,→S∘g∗→I,→J=id.
Proof. For first equality, note that the map g∗→I,→I is obtained from the following equality:
where the matrix M→IA→I is identity. So g∗→I,→I is defined by the following equality:
This shows the first equality. For second equality, let →J be an another →k-index, so g∗→J,→I is obtained by the following equality:
One may see that g∗→J,→I∘g∗→I,→J is obtained by following equality:
For left side, we have
Accordingly the map g∗→J,→I∘g∗→I,→J is obtained by D→IA→I=D→IA→I and it shows that this map is identity. For third equality, it is sufficient to show that the map g∗→S,→I∘g∗→J,→S∘g∗→I,→J is obtained from
This case obtains from case 2 analogously.
So the sheaves (¯U→I,O→I) may be glued through the g→I,→J to construct the Zn2−grassmannian G→k(→m). Indeed, according to Lemma 3.1 in [10], the conditions of the above proposition are necessary and sufficient for gluing.
4.
Zn2−grassmannian as homogeneous Zn2−space
In this section, we study construction of the quotients of Zn2−Lie groups. Although this study is parallel its analogue in supergeometry, see [18] for Z2 graded case, but generalizing related results in Zn2 setting necessitates working with J−adic topology.
Let G=(¯G,OG) be a Zn2−Lie group and H=(¯H,OH) be a closed Zn2−Lie supgroup of G. One can define a Zn2−manifold structure on the topological space ¯X=¯G/¯H as follows:
Let g=Lie(G) and h=Lie(H) be the Zn2−Lie algebras corresponding with G and H. For each Z∈g, let DZ be the left invariant vector field on G associated with Z. For h, a Zn2−subalgebra of g, set:
On the other hand, for any open subset U⊂¯G set:
where rx0 is the right translation by x0 in (2.5). If ¯H is connected, then Oinv(U)=Oh(U). Let ¯π:¯G→¯X be the natural projection. For each open subset ¯W⊂¯X=¯G/¯H, the structure sheaf OX is defined as following
where W=¯π−1(¯W). One can show that OX is a sheaf on ¯X and the ringed space X=(¯X,OX) is a Zn2−domain locally. Indeed, according to the definition of distribution in [19], we have a distribution spanned by the vector fields in h which is denoted by Dh. This distribution is involutive, because h is a Zn2−Lie algebra. By using the local Frobenius theorem, Dh is integrable. For more details about Frobenius theorem in the Zn2−graded category, see [19]. So there is an open neighborhood U of identity element 1 and coordinates (x,ξ1,…,ξq) such that Dh is spanned on U by
Let D′h be spanned by
on U. One can use the local Frobenius theorem again, so D′h is involutive distribution. One can show that Zn2−manifold X is obtained by gluing the integral Zn2−manifolds of the local distributions D′h. So X is a Zn2−manifold and is called homogeneous Zn2−space. The details of proof are similar to standard supergeometry in [6].
In this section, we want to show that the Zn2−grassmannian G→k(→m) is a homogeneous Zn2−space. According to the section 1, it is enough to find a Zn2−Lie group which acts on G→k(→m) transitively. For this, we need the following remark and the next lemma
Remark 4.1. Let X be an element of U→I(T) where →I is an arbitrary index. One can correspond to X a Zn2−matrix →k×→m called [X]→I as follows: Except for columns with indices in I0∪I1∪…∪Iq, the blocks are filled from up to down and left to right by fi,gj's where
according to the ordering (3.1), where (xi;ξj) is the global coordinates of the Zn2−domain U→I. The columns with indices in I0∪I1∪…∪Iq form an identity matrix.
Lemma 4.2. Let ψ:T→R→r be a T-point of R→r and (ztu) be a global coordinates of R→r with ordering as the one introduced in (3.1). If B=(ψ∗(ztu)) is the Zn2−matrix corresponding to ψ, then the Zn2−matrix corresponding to (g→I,→J)T(ψ) is as follows:
where [B]→J is introduced in Remark 4.1.
Proof. Note that g∗→I,→J may be represented by a Zn2−matrix as follows:
where A→J is the label of U→J. Let M→IA→J=(mtu) and (M→IA→J)−1=(mtu). If z=(zij) be a coordinates system on U→I, then one has
Then
For second equality one may note that ψ∗ is a homomorphism of Zn2−algebras and mtk(z) is a rational function of z. Obviously, the last expression is the (t,u)-entry of the matrix D→I((M→I[B]→J)−1[B]→J). This completes the proof.
Theorem 4.3. The Zn2−Lie group GL(→m) acts on Zn2−grassmannian G→k(→m).
Proof. First, we have to define a morphism a:G→k(→m)×GL(→m)→G→k(→m). For this, by Yoneda lemma, it is sufficient to define aT:
for each Zn2−manifold T or equivalently define
where P is a fixed arbitrary element in GL(→m)(T). For brevity, we denote (aT)P by A. One may consider GL(→m)(T), as the set of →m×→m invertible Zn2−matrices with entries in O(T), but there is not such a description for G→k(→m)(T), because it is not a Zn2−domain. We know each Zn2−grassmanian is constructed by gluing Zn2−domains (c.f. section 2), so one may define the actions of GL(→m) on Zn2−domains (¯U→I,O→I) and then shows that these actions glued to construct aT.
For defining A, it is needed to refine the covering {U→I(T)}→I. Set
where [P] is the matrix form of the fixed arbitrary element P in GL(→m)(T), see [8] and [21]. One can show that {U→J→I(T)}→I,→J is a covering for G→k(→m)(T) and A(U→J→I(T))⊆U→J(T). Now consider all maps
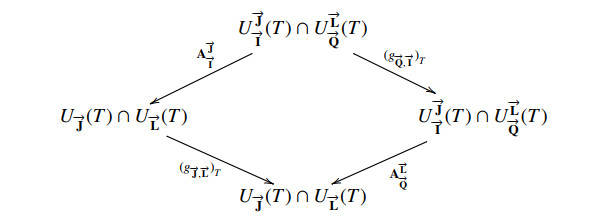
where, [ψ]→I is as above. We have to show that these maps may be glued to construct a global map on G→k(→m)(T). For this, it is sufficient to show that the following diagram commutes:
where (g→I,→J)T is the induced map from g→I,→J on T-points. The following proposition is used to show commutativity of the above diagram.
Proposition 4.4. The last diagram commutes.
Proof. We have to show that
for arbitrary →k-indices →I,→J,→Q,→L. Let ψ∈U→J→I(T)∩U→L→Q(T) be an arbitrary element. One has ψ∈U→J→I(T), so
From left side of (4.1), we have:
For right side of equation (4.1), we have
This shows that the above diagram commutes.
Therefore GL(→m) acts on G→k(→m) with action a. Now it is needed to show that this action is transitive.
Theorem 4.5. GL(→m) acts on G→k(→m) transitively.
Proof. By proposition 2.12, it is sufficient to show that the map
is surjective, where →r=(r0,r1,…,rq) is dimension of GL(→m) and one can consider →r′=(0,r1,…,rq). Let
be an element and ˉp0,ˉp1,…,ˉpq be the matrices corresponding to p0,p1,…,pq respectively as subspaces. As an element of G→k(→m)(T), one may represent ˆpT, as follows
where T is an arbitrary Zn2−manifold. For surjectivity, let
be an arbitrary element. We have to show that there exists an element V∈GL(→m)(R→r′) such that ˆpTV=W. Since the Lie group GL(mi) acts on manifold Gki(mi) transitively, then there exists an invertible matrix Hii∈GL(mi) such that ˉpiHii=Wii. In addition, the equations ˉpiZ=Wij have solutions since rank(ˉpi)=ki. Let Hij be solutions of these equations respectively. Clearly, One can see
satisfy in the equation ˆpTV=W. So (ap)R→r′ is surjective. By Proposition 2.12, GL(→m) acts on G→k(→m) transitively. Thus according to Proposition 2.15, G→k(→m) is a homogeneous Zn2−space.
A.
Basic Concepts
A.1. Category theory
By a locally small category, we mean a category such that the collection of all morphisms between any two of its objects is a set. Let X, Y are objects in a category and α,β:X→Y are morphisms between these objects. An universal pair (E,ϵ) is called equalizer if the following diagram commutes:
i.e., α∘ϵ=β∘ϵ and also for each object T and any morphism τ:T→X which satisfy α∘τ=β∘τ, there exists unique morphism σ:T→E such that ϵ∘σ=τ. If equalizer existed then it is unique up to isomorphism. For example, in the category of sets, which is denoted by SET, the equalizer of two morphisms α,β:X→Y is the set E={x∈X|α(x)=β(x)} together with the inclusion map ϵ:E↪X.
Let C be a locally small category, and X be an object in C. By T-points of X, we mean X(T):=HomC(T,X) for any T∈Obj(C). The functor of points of X is a functor which is denoted by X(.) and is defined as follows:
where X(φ):f↦f∘φ. A functor F:C→SET is called representable if there exists an object X in C such that F and X(.) are isomorphic. Then one may say that F is represented by X. The category of functors from C to SET is denoted by [C,SET]. It is shown that the category of all representable functors from C to SET is a subcategory of [C,SET].
Corresponding to each morphism ψ:X→Y, there exists a natural transformation ψ(.) from X(.) to Y(.). This transformation corresponds the mapping ψ(T):X(T)→Y(T) with ξ↦ψ∘ξ for each T∈Obj(C). Now set:
Obviously, Y is a covariant functor and it is called Yoneda embedding. The following lemma, is brought from [8] or the section III.2 in [20].
Lemma A.1. The Yoneda embedding is full and faithful functor, i.e. the map
is a bijection for each X,Y∈Obj(C).
Thus according to this lemma, X,Y∈Obj(C) are isomorphic if and only if their functor of points are isomorphic. The Yoneda embedding is an equivalence between C and a subcategory of representable functors in [C,SET] since not all functors are representable.
A.2. The Zn2−Lie group GL(V)
Let V be a finite dimensional Zn2-vector space of dimension →m=m0|m1|…|mq and let
be a basis of V for which the elements Rm0+...+mi−1+k, 1≤k≤mi, are of weight γi for 0≤i≤q.
Consider the functor F from the category ZSM to GRP the category of groups which maps each Zn2−manifold T to AutO(T)(O(T)⊗V) the group of zero weight automorphisms of O(T)⊗V. Consider the Zn2−manifold End(V)=(∏iEnd(Vi),A) where A is the following sheaf
where tk=∑γi+γj=γkmimj. Let Fij be a linear transformation on V defined by Rk↦δikRj, then {Fij} is a basis for End(V). If {fij} is the corresponding dual basis, then it may be considered as a global coordinates on End(V). Let X be the open submanifold of End(V) corresponding to the open set:
Thus, we have
It can be shown that the functor F may be represented by X. For this, one may show that Hom(T,X)≅AutO(T)(O(T)⊗V). To this end, first, one can notice Theorem 9 in [17] to see
It is known that each ψ∈Hom(A(X),O(T)) may be uniquely determined by {gij} where gij=ψ(fij), see Theorem 6.8 in [1]. Now set Ψ(Rj):=ΣgijRi. One may consider Ψ as an element of AutO(T)(O(T)⊗V). Obviously ψ↦Ψ is a bijection from Hom(T,X) to AutO(T)(O(T)⊗V). Thus the Zn2−manifold X is a Zn2−Lie group and denoted it by GL(V) or GL(→m) if V=R→m. Therefore T- points of GL(→m) are the →m×→m invertible Zn2−matrices of weight zero
where the elements of the mk×mu block Bku have degree γk+γu and the multiplication is the matrix product.
A.3. Proof of (Proposition 2.10)
Proof. The proof of (1) is easy because of (2.10). For (2), let M be a Zn2-manifold of dimension →m and G be a Lie Zn2-group of dimension →k. Let g be the Lie Zn2-algebra of G and let Jap be the Jacobian Zn2-matrix of ap in a neighborhood of a point g∈¯G. Since
and ag and rg−1 are diffeomorphisms, ¯Jap(g) has rank equal to dimg−dimker(dap)e for each g∈¯G. Recall that if X∈g we denote by DRX:=(X⊗1OG(U))μ∗ the right-invariant vector field associated with X. Using equation (2.8) we have, for each X∈ker(dap)e,
Because
If (ξ0=x,ξ1,…,ξq) and (η0=y,η1,…,ηq) are coordinates in a neighborhood U of e∈¯G, and in a neighborhood V⊇¯ap(U) of p∈¯M, respectively, then Jap may be represented as the following block matrix:
where by ∂a∗p(ηt)∂ξl, we mean a matrix as follows
and its sign in (5.3) is equal to
Now, we find a matrix A∈GL→k(OG(U)) such that JapA has a certain set of columns equal to zero. We are going to use equation (5.2). Let
and {Xu0}, … and {Xuq} be the bases of g0, … and gq such that for all nr if ur≤nr then Xur∈ker(dap)e. Consider a block matrix as follows:
where, for each uj, 0≤j≤q, αuj.is's are the coefficients appear in the following equality:
where γj+γs is the degree of αsuj,is and the sign of (t,l)-th block is
Since Xui and Xuj are linearly independent at each point, the reduced matrix ¯A is invertible and A∈GL→k(OG(U)). Now by equation (5.2), one may see that the matrix
has |→n|=n0+…+nq zero columns. Thus ¯Jap has rank equal to →k−→n with entries in OG(U). In addition the first |→k|−|→n| columns are non-zero. Thus one may describe Jap by (z0w0). Then it is not restrictive to assume that z invertible. Thus one has
where
For more explanation, assume Jap is a matrix of the form as below
Since ¯Jap has rank →k−→n, we can suppose that αii and βjj are invertible. By section 4 in [10], we can rearrange the matrix so that it takes the form (z0w0), with z invertible and the matrix G=(z−10−wz−1I) such that GJ=(I000). We can then conclude that Jap has constant rank in U and, by translation, in all of ¯G.
Conflict of interest
The author declares there is no conflict of interest.









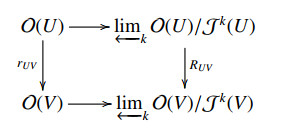





 DownLoad:
DownLoad: