Splitting type viscosity methods for inclusion and fixed point problems on Hadamard manifolds

1.   Introduction

Let $M : \mathbb{H} \rightrightarrows \mathbb{H}$ be a set-valued maximal monotone mapping and $K$ be a nonempty closed convex subset of Hilbert space $\mathbb{H}$. The inclusion problem:

was introduced by Rockafellar ^[19]. The iconic method for solving inclusion problem (1.1) is the proximal point method which was first introduced and studied by Martinet ^[15] for optimization problem and later generalized by Rockafellar ^[19] to solve the inclusion problem (1.1).

Many problems arising in nonlinear analysis, such as optimization, variational inequality problems, equilibrium problems and partial differential equations are convertible to the inclusion problem (1.1). Therefore, in the recent past, many authors have been extended and generalized the inclusion problem (1.1) in different directions using novel and innovative techniques, see for example ^{[1,4,7,9,11,12,13,20,24]} and references cited therein.

The fixed point problem of a nonexpansive self mapping $S:K\to K$ is defined as:

Most of the iterative methods to find the fixed point of nonexpansive mappings are due to Mann ^[14]. Moudafi ^[16] proposed the viscosity method by combining the nonexpansive mapping $S$ with a given contraction mapping $\varphi$ over $K$. For an arbitrary $x_0\in{K}$, compute the sequence $\{x_n\}$ generated by

where $\beta_n\in (0, 1)$ goes slowly to zero. The sequence $\{x_{n+1}\}$ achieved from this iterative method converge strongly to a fixed point of $S$. Common solution of fixed point problem (1.2) of a nonexpansive self mapping $S$ and variational inclusion problem studied by Takahashi et al. ^[22] in Hilbert spaces, which is defined as:

where $F$ is single valued monotone mapping and $M, S$ are same as defined above. Recently, Ansari et al. ^[1] extended the problem (1.3) to Hadamard manifolds and studied the Halpern and Mann type algorithms to solve problem (1.3) and discussed several applications on Hadamard manifold. Very recently, Al-Homidan et al. ^[2] extended the viscosity method for hierarchical variational inequality problems and discussed its several special cases on Hadamard manifolds. Konrawut et al. ^[10] studied the splitting algorithms for common solutions of equilibrium and inclusion problems on Hadamard manifolds.

In this article, encouraged and inspired by the work of ^[1,10,16], our motive is to introduce and study a splitting type viscosity method to find the common solution of inclusion problem (1.1) and fixed point problem (1.2) on Hadamard manifolds, that is,

where $K$ is a nonempty closed convex subset of Hadamard manifold $\mathbb{D}$. Our suggested method is like a double back-ward method for inclusion and fixed point problems and can be seen as the refinement of the work studied in ^[1]. The article is organized as follows:

The next section consists of preliminaries and some useful results of Riemannian manifolds. Section 3 deals with the main results explaining the splitting type viscosity method and convergence of the sequences obtained from it. In the last section, some applications of the proposed method and its convergence theorem to solve variational inequality, optimization and fixed point problems are given.

2.   Preliminaries and auxiliary results

Let $\mathbb{D}$ be a finite dimensional differentiable manifold and for a vector field $p\in \mathbb{D}$, the tangent space of $\mathbb{D}$ at $p$ is denoted by $T_p\mathbb{D}$ and the tangent bundle by $T\mathbb{D} = \cup_{p\in \mathbb{D}}T_p\mathbb{D}$. The tangent space $T_p\mathbb{D}$ at $p$ is a vector space and has the same dimension as $\mathbb{D}$. An inner product $\Re_p(\cdot, \cdot)$ on $T_p\mathbb{D}$ is the Riemannian metric on $T_p\mathbb{D}$. A tensor $\Re_p(\cdot, \cdot)$ is called a Riemannian metric on $T_p \mathbb{D}$, if for each $p\in \mathbb{D}$, the tensor $\Re(\cdot, \cdot)$ is a Riemannian metric on $\mathbb{D}$. We assume that $\mathbb{D}$ is endowed with the Riemannian metric $\Re_p(\cdot, \cdot)$ with the corresponding norm $\|.\|_p$. The angle between $0\neq x, y\in T_q\mathbb{D}$, denoted by $\angle_{p}(x, y)$ is defined as $\cos \angle_{p}(x, y) = \frac{\Re_p(\cdot, \cdot)}{\|x\|\|y\|}$. For the sake of simplicity, we donote $\|.\|_p = \|.\|, \Re_p(\cdot, \cdot) = \Re(\cdot, \cdot)$ and $\angle_{p}(x, y) = \angle(x, y)$.

For a given piecewise smooth curve $\gamma:[a, b]\to \mathbb{D}$ joining $p$ to $q$ $(i.e. \gamma(a) = p {\; \rm and\; } \gamma(b) = q)$, the length of $\gamma$ is defined as

The Riemannian distance $d(p, q)$ induces the original topology on $\mathbb{D}$, minimize the length over the set of all such curves joining $p$ to $q$.

Let $\triangledown$ be the Levi-Civita connection corresponding to Riemannian manifold $\mathbb{D}$. A vector field $U$ is said to be parallel along a smooth curve $\gamma$ if $\triangledown_{\gamma^{'}(s)}U = 0$. If $\gamma^{'}$ is parallel along $\gamma$, i.e., $\triangledown_{\gamma^{'}(s)}\gamma^{'}(s) = 0$, then $\gamma$ is called geodesic and in this case $\|\gamma^{'}\|$ is constant and if $\|\gamma^{'}\| = 1$, then $\gamma$ is said to be normalized geodesic. A geodesic joining $p$ to $q$ in $\mathbb{D}$ is called minimal geodesic if its length is equal to $d(p, q)$. A Riemannian manifold is called (geodesically) complete if for any $p\in \mathbb{D}$, all geodesics emanating from $p$ are defined for all $s\in (-\infty, \infty)$. We know by Hopf-Rinow Theorem ^[21] that if $\mathbb{D}$ is Riemannian manifold then following are equivalent:

${\rm (I)}$ $\mathbb{D}$ is complete.

${\rm (II)}$ Any pair of points in $\mathbb{D}$ can be joined by a minimal geodesic.

${\rm (III)}$ $(\mathbb{D}, d)$ is a complete metric space.

${\rm (IV)}$ Bounded closed subsets of $\mathbb{D}$ are compact.

Let $\gamma:[0, 1]\to \mathbb{D}$ be a geodesic joining $p$ to $q$. Then

Assuming $\mathbb{D}$ is a complete Riemannian manifold, the exponential mapping ${\rm exp}_p:T_p\mathbb{D}\to \mathbb{D}$ at $p$ is defined by ${\rm exp}_p(\vartheta) = \gamma_\vartheta(1, p)$ for each $\vartheta\in T_p\mathbb{D}$, where $\gamma(\cdot) = \gamma_\vartheta(\cdot, p)$ is the geodesic starting at $p$ with velocity $\vartheta$ (i.e., $\gamma(0) = 0\; {\rm and} \; \gamma^{'}(0) = \vartheta).$ We know that ${\rm exp}_q(s\vartheta) = \gamma_\vartheta(s, p)$ for each real number $s$. One can easily see that ${\rm exp}_{p}0 = \gamma_{\vartheta}(0;p) = p$, where $0$ is the zero tangent vector. The exponential mapping ${\rm exp}_{p}$ is differentiable on $T_p\mathbb{D}$ for any $p\in \mathbb{D}$. It is known to us that the derivative of ${\rm exp}_{p}({\bf 0})$ is equal to the identity vector of $T_p\mathbb{D}$. Therefore by inverse mapping theorem there exists an inverse exponential mapping ${\rm exp}^{-1}:\mathbb{D}\to T_p\mathbb{D}$. Moreover, for any $p, q \in \mathbb{D}$, we have $d(p, q) = \|{\rm exp}_{p}^{-1}q\|$.

A complete, simply connected Riemannian manifold of non-positive sectional curvature is called a Hadamard manifold.

Proposition 2.1. ^[21] Let $\mathbb{D}$ be a Hadamard manifold. Then ${\rm exp}_p:T_p \mathbb{D}\to \mathbb{D}$ is a diffeomorphism for all $p\in \mathbb{D}$ and for any two points $p, q\in \mathbb{D}$, there exists a unique normalized geodesic $\gamma:[0, 1]\to \mathbb{D}$ joining $p = \gamma(0)$ to $q = \gamma(1)$ which is in fact a minimal geodesic denoted by

A subset $K\subset\mathbb{D}$ is said to be convex if for any two points $p, q\in K$, the geodesic joining $p$ to $q$ is contained in $K$, that is, if $\gamma:[a, b]\to \mathbb{D}$ is a geodesic such that $p = \gamma(a)$ and $q = \gamma(b)$, then $\gamma((1-s)a+sb)\in K$ for all $s\in [0, 1]$. From now on, $K\subset\mathbb{D}$ will denote a nonempty, closed and convex subset of a Hadamard manifold $\mathbb{D}$. The projection onto $K$ is defined by

A function $g : K \to \mathbb{R}$ is said to be convex if for any geodesic $\gamma : [a, b]\to\mathbb{D}$, the composition function $g\circ\gamma : [a, b]\to \mathbb{R}$ is convex, that is,

Proposition 2.2. ^[21] The Riemannian distance $d: \mathbb{D} \times \mathbb{D}\to \mathbb{R}$ is a convex function with respect to the product Riemannian metric, i.e., given any pair of geodesics $\gamma_{1} : [0, 1] \rightarrow \mathbb{D}$ and $\gamma_{2}: [0, 1] \rightarrow \mathbb{D}$, the following inequality holds for all $s \in [0, 1]:$

In particular, for each $p \in \mathbb{D}$, the function $d(\cdot, p): \mathbb{D} \to \mathbb{R}$ is a convex function.

If $\mathbb{D}$ is a finite dimensional manifold with dimension n, then Proposition 2.1 shows that $\mathbb{D}$ is diffeomorphic to the Euclidean space $\mathbb{R}^n$. Thus, we see that $\mathbb{D}$ has the same topology and differential structure as $\mathbb{R}^n$. Moreover, Hadamard manifolds and Euclidean spaces have several similar geometrical properties. We describe some of them in the following results.

Recall that a geodesic triangle $\Delta(q_1, q_2, q_3)$ of Riemannian manifold is a set consisting of three points $q_1, q_2$ and $q_3$ and the three minimal geodesics $\gamma_j$ joining $q_j$ to $q_{j+1}$, where $j = {\rm 1, 2, 3\; mod\; (3)}.$

Lemma 2.1. ^[13] Let $\Delta(q_1, q_2, q_3)$ be a geodesic triangle in Hadamard manifold $\mathbb{D}$. Then there exist $q_1^{'}, q_2^{'}, q_3^{'}\in \mathbb{R}^2$ such that

The points $q_1^{'}, q_2{'}, q_3^{'}$ are called the comparison points to $q_1, q_2, q_3$, respectively. The triangle $\Delta(q_1^{'}, q_2^{'}, q_3^{'})$ is called the comparison triangle of the geodesic triangle $\Delta(q_1, q_2, q_3)$, which is unique upto isometry of $\mathbb{D}$.

Lemma 2.2. ^[13] Let $\Delta(q_1, q_2, q_3)$ be a geodesic triangle in Hadamard manifold $\mathbb{D}$ and $\Delta(q_1^{'}, q_2^{'}, q_3^{'})\in \mathbb{R}^2$ be its comparison triangle.

${\rm(i)}$ Let $\theta_1, \theta_2, \theta_3$ (respectively, $\theta_1^{'}, \theta_2^{'}, \theta_3^{'}$) be the angles of $\Delta(q_1, q_2, q_3)$ (respectively, $\Delta(q_1^{'}, q_2^{'}, q_3^{'})$) at the vertices $(q_1, q_2, q_3)$ (respectively, $q_1^{'}, q_2^{'}, q_3^{'}$). Then the following inequality holds:

${\rm(ii)}$ Let $p$ be a point on the geodesic joining $q_1$ to $q_2$ and $p^{'}$ be its comparison point in the interval $[q_1^{'}, q_2^{'}]$. Suppose that $d(p, q_1) = \|p^{'}-q_1^{'}\|$ and $d(p, q_2) = \|p^{'}-q_2^{'}\|$. Then

Proposition 2.3. ^[21] (Comparison Theorem for Triangle) Let $\Delta(q_1, q_2, q_3)$ be a geodesic triangle. Denote, for each $j = {\rm 1, 2, 3\; mod\; (3)}$, by ${\gamma }_j:[0, l_i]\to \mathbb{D}$ geodesic joining $q_j$ to $q_{j+1}$ and set $l_j = L(\gamma_j), \theta_j = \angle(\gamma_j^{'}(0), -\gamma_{j-1}^{'}(l_{j-1}))$. Then

In terms of distance and exponential mapping, (2.6) can be rewritten as

since

Following proposition characterizes the projection mapping.

Proposition 2.4. ^[23] Let $K$ be a nonempty closed convex subset of a Hadamard manifold $\mathbb{D}$. Then for any $p\in \mathbb{D}$, $P_{K}(p)$ is a singleton set and the following inequality holds:

The set of all single-valued vector fields $M :\mathbb{D} \to T\mathbb{D}$ is denoted by $\Omega(\mathbb{D})$ such that $M(p)\in T_p(\mathbb{D})$ for all $p\in \mathbb{D}$. We denote by $\chi(\mathbb{D})$ the set of all set-valued vector fields, $M :\mathbb{D} \rightrightarrows T\mathbb{D}$ such that $M(p)\subseteq T_p(\mathbb{D})$ for all $p\in D(M)$, where $D(M)$ is the domain of $M$ defined as $D(M) = \{p\in \mathbb{D}:M(p)\neq\emptyset\}.$

Definition 2.1. ^[17] A single-valued vector field $M\in \Omega(\mathbb{D})$ is said to be monotone if for all $p, q\in \mathbb{D}$,

Definition 2.2. ^[12] A single-valued vector field $M\in \Omega(\mathbb{D})$ is said to be firmly nonexpansive if for all $p, q\in K \subseteq \mathbb{D}$, the mapping $\psi:[0, 1]\to [0, \infty]$ defined by

is nonincreasing.

Definition 2.3. ^[8] A set-valued vector field $M\in \chi(\mathbb{D})$ is said to be monotone if for all $p, q\in D(\mathbb{D})$,

Definition 2.4. ^[12] Let $M\in \chi(\mathbb{D})$, the resolvent of $M$ of order $\lambda > 0$ is set-valued mapping $J_{\lambda}^{M}:\mathbb{D}\rightrightarrows D(M)$ defined by

Theorem 2.1. ^[12] Let $\lambda > 0$ and $M\in \chi(\mathbb{D})$. Then vector field $M$ is monotone if and only if $J_{\lambda}^{M}$ is single-valued and firmly nonexpansive.

Lemma 2.3. ^[13] Let $\{a_{n}\}$ and $\{b_{n}\}$ be two sequences of positive real numbers such that $\lim\limits_{n\to\infty}\frac{b_{n}}{a_{n}} = 0$ and $\sum\limits_{n = 1}^{\infty}a_{n} = +\infty$. Let $\{x_{n}\}$ be a sequence of positive real numbers satisfying the recursive inequality:

then $\lim\limits_{n\to\infty}x_{n} = 0$.

3.   Main results

We propose the following splitting type viscosity method for problem (1.4) on Hadamard manifold.

Algorithm 3.1. Suppose that $K$ be nonempty closed and convex subset of Hadamard manifold $\mathbb{D}$. Let $M:K \rightrightarrows{\mathbb{D}}$ be a set-valued vector field, $\varphi: K \to K$ be a contraction and $S : K \to K$ be a nonexpansive mapping such that ${\rm Fix}(S)\cap(M)^{-1}(0) \neq \emptyset$. For an arbitrary $x_0\in K,$ ${\alpha_n}, \beta_n \in (0, 1)$ and $\lambda > 0$, compute the sequences $\{y_n\}$ and $\{x_n\}$ as follows:

or, equivalently

where $\gamma_n:[0, 1]\to {\mathbb{D}}$ is sequence of geodesics joining $\varphi(x_n)$ to $S(y_n)$, that is, $\gamma_n(0) = \varphi(x_n)$ and $\gamma_n(1) = S(y_n)$ for all $n\geq 0$.

For the convergence of Algorithm 3.1, we require the following conditions on the sequences $\{{\alpha_n}\}$ and $\{{\beta_n}\}$ :

(${A_1}$) $\lim\limits_{n\to \infty}\alpha_n = 0, \; {\rm \; } \; \; \; \; \; \; \; \; \; \; \; \; \lim\limits_{n\to \infty}\beta_n = 0;$

(${A_2}$) $\sum\limits_{n = 0}^{\infty}\alpha_n = \infty, \; \; \; \; \; \; \; \; \; \; \; \; \; \; \sum\limits_{n = 0}^{\infty}\beta_n = \infty;$

(${A_3}$) $\sum\limits_{n = 0}^{\infty}|\alpha_{n+1}-\alpha_n| < \infty, \; \; \; \sum\limits_{n = 0}^{\infty}|\beta_{n+1}-\beta_n| < \infty$

If $S = I$, the identity mapping on $K$, then Algorithm 3.1 reduces to the following algorithm to find the solution of problem (1.1).

Algorithm 3.2. Suppose that $K$ be nonempty closed and convex subset of Hadamard manifold $\mathbb{D}$. Let $M:K \rightrightarrows{\mathbb{D}}$ be a set-valued vector field and $\varphi :K\to K$ be self mapping. For an arbitrary $x_0\in K,$ compute the sequences $\{y_n\}$ and $\{x_n\}$ as follows

where ${\alpha_n}, \beta_n \in (0, 1)$ and $\lambda > 0$ are same as given in Algorithm 3.1.

We can obtain the the following proposition by substituting $A = {\bf 0}$, zero vector field in Proposition 3.2 of ^[3].

Proposition 3.1. For any $x\in K$, the following assertions are equivalent:

${\rm(i)}$$x\in (M)^{-1}(0);$

${\rm(ii)}$$x = J^{M}_{\lambda}\big[{\rm exp}_{x}(-\lambda x) \big]$, for all $\lambda > 0$.

Remark 3.1. It can be easily seen that for a nonexpansive mapping $S$, the set ${\rm Fix}(S)$ is geodesic convex, for more details, (see ^[1,12]). Since $J_{\lambda}^{M}$ is nonexpansive, by Proposition 3.1, it follows that ${\rm Fix}\big(J_{\lambda}^{M}\big) = \big(M\big)^{-1}(0).$ Therefore $\big(M\big)^{-1}(0)$ is closed and geodesic convex in $\mathbb{D}$. Hence, ${\rm Fix}(S)\cap\big(M\big)^{-1}(0)$ is closed and geodesic convex in $\mathbb{D}$.

Theorem 3.1. Let $\mathbb{D}$ be a Hadamard manifold and $K$ be a nonempty, closed and convex subset of $\mathbb{D}$. Let $S:K\to K$ be a nonexpansive mapping and $\varphi:K\to K$ be a contraction with constant $\kappa$. Let $M:K\to T\mathbb{D}$ be a set-valued monotone vector field. Suppose $\{\alpha_n\},$ and $\{\beta_n\}$ are sequences in $(0, 1)$, satisfying the conditions ${A_1-A_3}$. If ${\rm Fix}(S)\cap (M)^{-1}(0)\neq \emptyset$, then the sequences achieved by Algorithm 3.1 converges to $w\in {\rm Fix}(S)\cap (M)^{-1}(0)$, where $w = P_{{\rm Fix}(S)\cap (M)^{-1}(0)}\varphi(w)$.

Proof. We divide the proof into following five steps.

Step I. We show that $\{y_n\}, \{x_n\}, \{\varphi(x_n)\}$ and $\{T(y_n)\}$ are bounded.

Let $x^{\star}\in {{\rm Fix}(S)\cap (M)^{-1}(0)}$, then $x^{\star}\in {\rm Fix}(S)$ and $x^{\star}\in (M)^{-1}(0)$. Since $y_{n} = \gamma_n(1-\alpha_n)$, by Proposition 3.1 and nonexpansive property of $J^{M}_{\lambda}$, we have

Since $x_{n+1} = \gamma_n(1-\beta_n)$, then by convexity of Riemannian distance, we have

which implies that the sequence $\{x_n\}$ is bounded and using (3.1), $\{y_n\}$ is also bounded. Since $S$ is nonexpansive, $\varphi$ is a contraction, we conclude that the sequences $\{S(y_n)\}$ and $\{\varphi(x_n)\}$ are also bounded.

Step II. We show that $\lim\limits_{n\to \infty}d(x_{n+1}, x_{n}) = 0$.

Since $S$ is nonexpansive and $\varphi$ is a contraction, then using (2.1), (2.4) and Proposition 2.2, we have

Again, by Algorithm 3.1 and nonexpansive property of $J^{M}_{\lambda}$, we have

Since $\{x_n\}$, $\{\varphi(x_n)\}$ and $\{J^{M}_{\lambda}(x_n)\}$ are bounded, then there exist constants $C_1, C_2$ and $C_3$, such that $d(x_n, J^{M}_{\lambda}(x_{n-1}))\leq C_1$, $d(\varphi(x_n), x^{\star})\leq C_2$, $d(x_n, x^{\star})\leq C_3$. Thus, we have

and

Combining (3.4), (3.5), (3.6) and (3.7), (3.3) becomes

where $\bar{\beta_n} = \beta_n(1-\kappa).$ Let $m\leq n$, then

Taking limit $n\to \infty$, we have

From condition $A_2$, we have $\prod\limits_{i = m}^{\infty}(1-\bar{\beta}_{i}) = 0$, from $A_3$, we get $\sum\limits_{i = m}^{\infty}|\alpha_i-\alpha_{i-1}| = 0$ and $\sum\limits_{i = m}^{\infty}|\beta_i-\beta_{i-1}| = 0$, as $m\to \infty$. Thus by taking $m\to \infty$, we get

Step III. Next, we show that $\lim\limits_{n\to \infty}d(x_{n}, y_n) = 0$. Since $\varphi$ is a contraction, then by using Algorithm 3.1 and (3.1), we obtain

Let $m\leq n$, then we have

By taking limit $n\to \infty$, we have

From $A_2$, it follows that $\lim\limits_{m\to\infty}\prod\limits_{j = m}^{\infty}(1-\bar{\beta}_{j}) = 0$ and from $A_1-A_2$, $\lim\limits_{m\to\infty}\sum\limits_{j = m}^{\infty}\bigg\{ \beta_j\prod\limits_{i = j+1}^{\infty}(1-\bar{\beta_{i}})\bigg\} = 0$. Hence by letting limit $m\to \infty$, we get

Step IV. Since $\{x_n\}$ is bounded, so there exists a subsequence $\{x_{n_k}\}$ of $\{x_n\}$ such that $x_{n_k}\to w$ as $k\to \infty$. Let $u_n = J^{M}_{\lambda}(x_n)$, by Algorithm 3.1, $y_n = {\rm exp}_{x_n}(1-\alpha_n) {\rm exp}_{x_n}^{-1}J^{M}_{\lambda}(x_n).$ Then we have $d(y_n, u_n) = \alpha_n d(x_n, u_n)$ and $d(y_n, u_n)\to 0$ as $n\to \infty$. Thus

By the contuinuity of $J^{M}_{\lambda}$, as $k\to \infty$, we have

This implies that $J^{M}_{\lambda}(w) = w$, by Proposition 2.1, we get $w\in (M)^{-1}(0)$.

Again, by using the convexity of Riemannian manifold, we have

Since $\{x_n\}$ is bounded and $\varphi$ is a $\kappa$-contraction, we get

This together with the condition $A_1$, implies that

Also, from (3.9) and with a subsequence $\{y_{n_k}\}$ of $\{y_n\}$, we have

that is, $\{y_{n_k}\}$ converges to $w$ as $k \to\infty$. Then, we obtain

and so, $w\in {\rm Fix}(S)$. Thus, we have $w\in{\rm Fix}(S)\cap(M)^{-1}(0)$.

Step V. Finally, we show that$\lim\limits_{n\to\infty} d(x_n, z) = 0.$

To prove the last step, we need to show that $\limsup\limits_{n\to \infty}\Re\big({\rm exp}_{z}^{-1} \varphi(z), \; {\rm exp}_{z}^{-1} S(y_n) \big)\leq 0,$ where $z$ is a fixed point of the mapping $P_{{\rm Fix(S)}\cap(M)^{-1}(0)}\varphi.$

Since $w\in {\rm Fix(S)}\cap(M)^{-1}(0)$ and $w = P_{{\rm Fix(S)}\cap(M)^{-1}(0)}\varphi(w)$, then by Proposition 4, we have $\Re\big({\rm exp}_{z}^{-1} \varphi(z), \; {\rm exp}_{z}^{-1} w \big)$ $\leq 0.$ Boundedness of $\{y_n\}$ implies that $\{\Re({\rm exp}_{z}^{-1} \varphi(z), {\rm exp}_{z}^{-1}S(y_n)) \}$ is bounded. Then, we have

Since $y_{n_k}\to w$ as $k\to \infty$ and by using continuity of $S$, we obtain

therefore,

For $n\geq 0$, set $v = \varphi(x_n)$, $q = S(y_n)$ and consider geodesic triangles $\Delta(v, q, z)$, $\Delta(\varphi(z), q, v)$ and $\Delta(\varphi(z), q, z)$, with their comparison triangles $\Delta(v^{'}, q^{'}, z^{'})$, $\Delta(\varphi(z)', q', v')$ and $\Delta(\varphi(z)^{'}, q^{'}, z^{'})$. From Lemma 2.1, we have

Recall that $x_{n+1} = {\rm exp}_{\varphi(x_n)}(1-\beta_n){\rm exp}_{\varphi(x_n)}^{-1}S(y_n) = {\rm exp}_{v}(1-\beta_n){\rm exp}_{v}^{-1}q.$ The comparison point of $x_{n+1}$ in $\mathbb{R}^2$ is $x^{'}_{n+1} = \beta_{n} v^{'}+(1-\beta_{n})q^{'}$. Let $\theta$ and $\theta^{'}$ denote the angles at $q$ and $q^{'}$ in the triangles $\Delta(\varphi(z), q, z)$ and $\Delta(\varphi(z)^{'}, q^{'}, z^{'})$, respectively. Therefore, $\theta\leq \theta^{'}$, and then, $\cos\theta'\leq \cos\theta$. By Lemma 2.2 (ii), using nonexpansive property of $S$ and contraction property of $\varphi$, we have

where $b_n = [1-2\beta_n+\beta_n^{2}+2\beta_n(1-\beta_n)\kappa]$ and $c_n = \frac{1}{b_n}[\beta_n^{2}d^2(\varphi(x_n), z)+ 2\beta_n(1-\beta_n) \Re({\rm exp}_{z}^{-1} \varphi(z), {\rm exp}_{z}^{-1} x_n)]$. By (3.19), $\lim\limits_{n\to\infty}c_n\leq 0$ and by conditions $A_1$ and $A_2$, we have $\lim\limits_{n\to \infty}b_{n} = 0$ and $\sum\limits_{n = 1}^{\infty}b_{n} = \infty$, respectively. Hence by Lemma 2.3, $\lim\limits_{n\to\infty}d(x_n, z) = 0$. This completes the proof.

We obtain the following convergence result for Algorithm 3.2, by replacing $S = I$, the identity mapping in Theorem 3.1.

Theorem 3.2. Let $K$ be a nonempty, closed and convex subset of Hadamard manifold $\mathbb{D}$. Let $\varphi:K\to K$ be a contraction mapping with constant $\kappa$ and $M:K\rightrightarrows T\mathbb{D}$ be a set-valued monotone vector field. If $(M)^{-1}(0)\neq \emptyset$, then the sequence achieved by Algorithm 3.2 converges to $w\in(M)^{-1}(0)$, where $w = P_{ (M)^{-1}(0)}\varphi(w)$.

Remark 3.2. We can obtain splitting type Mann's iterative methods for the said problems by putting $\varphi = I$, the identity mapping on $K$ in Algorithm 3.1 and Algorithm 3.2 and by putting $\kappa = 1$ in Theorem 3.1 and Theorem 3.2, we can obtain the convergence theorems.

To illustrate the convergence of our algorithms, we extend the example which was also considered in ^[4].

Example 3.1. Let $\mathbb{D} = \mathbb{R}_{++} = \{x \in \mathbb{R} : x > 0\}$. Then $\mathbb{M}$ is a Riemannian manifold with Riemannian metric $\langle \cdot, \cdot\rangle$ defined by $\langle u, v\rangle : = g(x)uv$ for all $u, v \in T_{x}\mathbb{D}$, where $g: \mathbb{R}_{++} \to (0, +\infty)$ is given by $g(x) = x^{-2}$. It directly follows that the tangent plane $T_{x}\mathbb{D}$ at $x\in \mathbb{D}$ is equal to $\mathbb{R}$ for all $x\in \mathbb{D}$. The Riemannian distance $d : \mathbb{D} \times \mathbb{D} \to \mathbb{R}_{+}$ is given by

Therefore, $(\mathbb{R}_{++}, \langle \cdot, \cdot\rangle)$ is a Hadamard manifold and the unique geodesic $\gamma : \mathbb{R} \to \mathbb{D}$ starting from $x = \gamma(0)$ with $v = \dot{\gamma}(0) \in T_{x}\mathbb{D}$ is defined by $\gamma(t) : = x e^{(v/x)t}$. In other words, $\gamma(t)$, in terms of initial point $\gamma(0) = x$ and terminal point $\gamma(1) = y$, is defined as $\gamma(t) : = x^{1-t}y^{t}$. The inverse of exponential mapping is given by

Consider a vector field $M : \mathbb{D} \rightrightarrows \mathbb{R}$ defined by

Note that $M$ is a monotone vector field and the resolvent of $M$ is given by

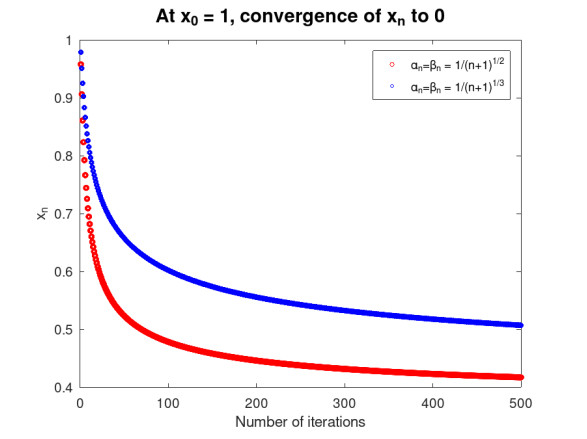
Let $\varphi$ be a contraction and $S$ be a nonexpansive mapping, defined by $\varphi(x) = \frac{1}{2}x$ and $S(x) = x$ for all $x \in \mathbb{D}$, respectively. Clearly, the solution set of the problem $(1.4)$ is $\{0\}$. Choose any initial guess $x_{0} = 1$, $\lambda = \frac{1}{2}$, $\alpha_{n} = \beta_n = \frac{1}{\sqrt{n+1}}$, and $\alpha_{n} = \beta_n = \frac{1}{({n+1})^\frac{1}{3}}$. Then all the conditions of Theorem 3.2 are satisfied, and hence, we conclude that the sequence $\{x_{n}\}_{n = 0}^{\infty}$ generated by Algorithm 3.1 converges to a solution of the problem $(1.4)$. The convergence of the sequence is shown in Figure 1.

4.   Applications

By adopting the techniques and methodologies of ^{[1,2,3,4,5,6]}, we drive the algorithm and convergence results for variational inequality and optimization problems using the proposed iterative methods.

4.1.   Variational inequality

Let $K$ be a nonempty, closed and convex subset of Hadamard manifold $\mathbb{M}$ and $A:K\to T\mathbb{M}$ be a single-valued vector field. N$\acute{e}$meth ^[18], introduced the variational inequality problem $VI(A, K)$ to find $x^{\star}\in K$ such that

It is known to us that $x\in K$ is a solution of $VI(A, K)$ if and only if $x$ satisfies (for more details, see ^[11])

where $N_{K}(x)$ denotes the normal cone to $K$ at $x\in K$, defined as

Let $I_{K}$ be the indicator function of $K$, i.e.,

Since $I_{K}$ is proper, lower semicontinuous, the differential $\partial I_{K}(x)$ of $I_{K}$ is maximal monotone, defined by

Thus, we have

Let $J^{\partial I_K}_{\lambda}$ be the resolvent of $\partial I_{K}$, defined as

Thus, for $A:K\to \mathbb{M}$ and for all for $x\in K$, we have

Now, we can state some results for the common solution of VI(A, K) and ${\rm Fix}(S)$.

Theorem 4.1. Let $\mathbb{D}$ be Hadamard manifold and $K$ be a nonempty, closed and convex subset of $\mathbb{D}$. Let $S:K\to K$ be a nonexpansive mapping, $\varphi:K\to K$ be a contraction mapping and $A:K\to T\mathbb{D}$ be a continuous vector field. Suppose $\{\alpha_n\}$ and $\{\beta_n\}$ are sequences in $(0, 1)$ satisfying the conditions $A_1-A_3$. If ${\rm Fix}(S)\cap VI(A, K)\neq \emptyset$, then the sequences $\{y_n\}$ and $\{x_n\}$ achieved by

converge to the solution of $VI(A, K)\cap {\rm Fix}(S)$, which is a fixed point of the mapping $P_{{\rm Fix}(S)\cap (M)^{-1}(0)}\varphi$.

Corollary 4.1. Let $\mathbb{D}$ be Hadamard manifold and $K$ be a nonempty, closed and convex subset of $\mathbb{D}$. Let $\varphi:K\to K$ be a contraction mapping and $A:K\to T\mathbb{D}$ be a continuous vector field. Suppose $\{\alpha_n\}$ and $\{\beta_n\}$ are sequences in $(0, 1)$ satisfying the conditions $A_1-A_3$. If $(M)^{-1}(0)\neq \emptyset$, then the sequences $\{y_n\}$ and $\{x_n\}$ achieved by

converge to the solution of $VI(A, K)$, which is a fixed point of the mapping $P_{ (M)^{-1}(0)}\varphi$.

4.2.   Optimization

For a proper lower semicontinuous and geodesic convex function $h: \mathbb{D}\to (-\infty, +\infty]$, the minimization problem is

We know that, the subdifferential $\partial h(p)$ at $p$ is closed and geodesic convex ^[1] and is defined as

Lemma 4.1. Let $h: \mathbb{D}\to (-\infty, +\infty]$ be a proper lower semicontinuous and geodesic convex function on Hadamard manifold $\mathbb{D}$. Then the subdifferential $\partial h(p)$ of $h$ is maximal monotone vector field.

If the solution set of minimization problem (4.5) is $\Omega$, then it can be easily seen that

Now, we can state some results for minimization problem (4.5), using Algorithm 3.1 and Algorithm 3.2.

Theorem 4.2. Let $\mathbb{D}$ be a Hadamard manifold. Let $h:\mathbb{D}\to \mathbb{D}$ be a proper lower semicontinuous and geodesic convex function, $S:K\to K$ be a nonexpansive mapping and $\varphi:K\to K$ be a $\kappa$-contraction. Suppose $\{\alpha_n\}$ and $\{\beta_n\}$ are sequences in $(0, 1)$ satisfying the conditions $A_1-A_3$. If ${\rm Fix}(S)\cap \Omega\neq \emptyset$, then the sequences $\{y_n\}$ and $\{x_n\}$ achieved by

converge to the solution of $\Omega\cap {\rm Fix}(S)$, which is a fixed point of the mapping $P_{{\rm Fix}(S)\cap \Omega}\varphi$.

Corollary 4.2. Let $\mathbb{D}$ be a Hadamard manifold. Let $h:\mathbb{D}\to \mathbb{D}$ be a proper lower semicontinuous and geodesic convex function and $\varphi:K\to K$ be a $\kappa$-contraction. Suppose $\{\alpha_n\}$ and $\{\beta_n\}$ are sequences in $(0, 1)$ satisfying the conditions $A_1-A_3$. If ${\rm Fix}(S)\cap \Omega\neq \emptyset$, then the sequences $\{y_n\}$ and $\{x_n\}$ achieved by

converge to the solution of $\Omega\cap {\rm Fix}(S)$, which is a fixed point of the mapping $P_{\Omega}\varphi$.

5.   Conclusions

In this paper, we studied the splitting type viscosity methods for inclusion and fixed point problem of nonexpansive mapping in Hadamard manifolds. We prove the convergence of iterative sequences obtained from the proposed method. Our method is new and can be seen as the refinement of methods studied in ^[1]. Some applications of the proposed method are given for variational inequalities, optimization and fixed point problems. We suppose that the method presented in this paper can be used to study some generalized inclusion and fixed point problems in geodesic spaces.

Acknowledgements

The second author would like to thank the Deanship of Scientific Research, Prince Sattam bin Abdulaziz University for supporting this work.

Conflict of interest

The authors declare no conflict of interest in this paper.