Numerical solution of full fractional Duffing equations with Cubic-Quintic-Heptic nonlinearities

1.   Introduction

A differential equation is the relation between a function and its derivatives, and surely, as a tool of mathematical science for modelling the natural phenomena, is very powerful ^[1,2]. As we know, the description and analysis of the behaviour of natural phenomena are possible through the study of related mathematical models.

A mathematical model is an interpretation of a real-world system using mathematical language, mentality, and ideas ^[3,4,5]. Undoubtedly, the differential equations are one of the fundamental tools in the engineering and basic sciences such as physics, chemistry, geology, and even biology (e.g., in the study of the organism growth, biochemical reactions, population dynamics, and prevalence of diseases ^[6]).

With a little attention, it can be seen that most of the phenomena in the real world have a non-linear nature. Therefore, in describing and analyzing the behavior of these phenomena, using non-linear differential equations seems unavoidable. Hence, the study of non-linear differential equations is crucial in all fields of sciences and technology. Examples are interactions between bridges and foundations (related to civil and structural engineering), between shafts and bearings (linked to the mechanical engineering), between ships and waves (in connection with the marine engineering), between wings/blades and air (in connection with the aerospace engineering) ^[6,7] and so on ^[8,9].

As we know, the exact solutions of some of these non-linear differential equations do not exist. Therefore, the probing of approximate solutions of these types of equations can play a vital role in the study of non-linear physical phenomena. Serious studies on the literature of forced non-linear oscillators had been done in the early 20thcentury by George Duffing, a German engineer of mechanical systems ^[6]. The general form of such equations is called Duffing equations and is given as follows

This equation presents a tremendous domain of well-known behavior in non-linear dynamical systems and is applied by many preceptors and researchers to illustrate such behavior. The equation seems simple at the first look but has a lot of awesome features.

In (1.1), can be a polynomial in terms of in the following cases:

● Case (1), $f(x) = bx+cx^3$,

● Case (2), $f(x) = bx+ cx^3+ dx^5$,

● Case (3), $f(x) = bx+ cx^3+ dx^5+ ex^7$.

The above three cases are called cubic, cubic-quintic and cubic-quintic-heptic, respectively. The domain of applications of the Duffing equation is very extensive. Some of these applications include: describing the chaotic behavior of a system ^[6], regulating the motion of a chaotic system around less complex attractors by injection of small damping signals ^[10], passive islanding detection of inverter-based distributed generation units ^[11], investigation of non-linear equation governing the motion of a rolling ship subjected to synchronous beam waves ^[12], modeling of free vibrations of a restrained uniform beam carrying intermediate lumped mass ^[13], studying homo-clinic and hetero-clinic bifurcations in the non-linear dynamics of a beam resting on an elastic substrate ^[14], propagation of an ultimately short electromagnetic pulse in a non-linear Medium ^[15], control of chaos by periodic stimulations in various systems such as, electronic systems ^[16], development of resonant mass sensors, inertial sensors, electromechanical signal processing systems ^[17], designing a model for the dynamics of the neuronal groups comprising the transient evoked potential ^[18], considering slow rolling regime ^[19], modeling of classical non-linear spring system with odd non-linear restoring characteristics ^[20], studying digital processing of certain systems such as digital communication and radar systems ^[21], exploring the control of a flexible beam in a simple mode approach ^[22], studying non-linear electrical circuit ^[23], and contrast enhancement in image processing ^[24].

Most papers written about Duffing equation have used approaches such as the differential transform method ^[25], the modified differential transform method ^[26], the harmonic balance method ^[7,27], the modified harmonic balance method ^[28], the homotopy analysis method ^[29,30], the homotopy perturbation method ^[31], the Jacobi elliptic functions ^[23,32], the variational iteration method ^[33], the Adomian decomposition method ^[34], the energy balance method ^[35,36], the multiple scales and homotopy perturbation method ^[22], the Laplace decomposition method ^[37], the power series method ^[38], and so on. Since the introduction of the Duffing equation as a widely used equation appearing in the study of many physical phenomena, particularly non-linear oscillators, several studies accomplished on the numerical solution display that this equation and its derivatives are very important in non-linear dynamics of real physical systems ^[6,39,40].

It can definitely be said that the appearance time of the theory of fractional calculus in the 18th century is the same as the differential calculus, but because of its inherent complexity, its application in various fields of science, engineering, and other modern sciences came into attention with a 200-year delay. The fractional calculus, in fact, is a natural extension of classical mathematics. The fractional differential equations are one of the relatively new branches of applied mathematics, which are based on arbitrary order of derivatives and integral. In other words, fractional derivatives and integrals have non-integer orders ^[40]. Due to the significance of this issue, scholars from other sciences have gradually used it in describing and analysis of different phenomena. The fractional differential models have more ability and better performance ^[41], which is widely used in the fields of physics, chemistry, medical engineering systems, biotechnology, dynamic systems, and so on ^{[3,5,7,21,42,43,44,45,46,47]}.

By choosing as the Case (3) and replace it in (1.1), we will have

The Eq (1.2) is named the cubic-quintic-heptic Duffing equation. In this equation, a is the damping controller. The full fractional form of equation (1.2) is as follow:

where and $0 < \alpha \leq 1$ and $1 < \beta \leq 2$. Most papers written about the fractional Duffing equation have used methods such as the Homotopy analysis method ^[48], the Jacobi elliptic function ^[49], the Lindstedt–Poincaré and the multiple-scale approach ^[50], the homotopy perturbation and variational iteration method ^[51], the multi-step differential transform method ^[52], the harmonic balance method ^[53], and mainly discussed about its stability have arisen. Considering the above mentioned the aim of this paper to calculate the numerical solution of the equation (1.3). For this purpose, we implement the orthogonal wavelet to study this equation and simulate its solution. The results of the performed comparison between the numerical solutions obtained from MATLAB software and what we have calculated indicate the effectiveness of our method.

The organization of this paper is as follows. In Section 2, we give some definitions and implications of the fractional calculus and orthogonal functions such as block-pulse wavelets, which have a basic role in the construction of our numerical method. In Section 3, we present the operational matrix for fractional integration. In Section 4, we will present our numerical method for solving full fractional Duffing equations with cubic-quintic-heptic nonlinearities. The bounded error of the method will be presented in Section 5. In Section 6, we illustrate our numerical method in some examples. Finally, in Section 7, the conclusions are presented.

2.   Preliminaries

In this section, we give some of the necessary definitions and theorems for the fractional calculations and pulse block wavelets.

Definition 2.1. The fractional derivative of $g(t) \in L_1[0, b]$ in sense of Caputo is defined as ^[54]

For a constant value as $C$, the derivative by means of Caputo is $0$, and we have

where $\lceil \alpha\rceil$ is the smallest integer number larger from $\alpha$.

Definition 2.2. The Riemann-Liouville fractional derivative of order $\alpha$ with respect to the variable t and with the starting point $t = a$ is ^[54]

Definition 2.3. By means of the Riemann-Liouville sense, the fractional integral of order $\alpha$ is defined as ^[54]

The relation between the Caputo operator and Riemann-Liouville is as follows ^[54]

Lemma 2.4. Let $\alpha, \beta \geq 0, d_{1}, d_{2} \in \mathbb{R}$ and $k(t), g(t) \in L_{1}[0, p],$ and then ^[54]

The two functions play a significant role in the fractional calculus, which we define them below.

Definition 2.5. The Gamma function which for $x > 0$ is defined as follows ^[45]

Some properties of this function are as follow:

Definition 2.6. The Mittag-Leffler function which for $\alpha > 0$ is as follows:

where they are called one and two-parameter, respectively. Some properties of this function are as follow

Definition 2.7. An $m$ -set of the block-pulse functions (BPFs) on $[0, T)$ is defined as follows ^[54] $b_{i}(t) = \left\{\begin{array}{ll}{1;} & {(i-1) h \leq t < i h} \\ {0;} & {\text { otherwise }}\end{array}, i = 1, 2, \ldots, m ~ and ~the ~step~ is ~ h = \frac{T}{m}\right.$ The properties of an $m$ -set of block-pulse functions are ^[55]:

● I) Disjoint, which is as follows,

● II) Orthogonal, which is as follows,

where $t \in[0, T), t_{r}, j = 1, 2, \ldots, m,$ and it is obtained from property $I$

● III) Complete, which it means that for every $g(t) \in L^{2}(0, T), \left\{a_{i}\right\}_{i = 1}^{\infty}$ is complete if $\int a g = 0$ then $g = 0$ almost everywhere. Because of completeness of (a), we have

for every real bounded function $g$ is square integrable in interval $t \in[0, t)$ and $g_{i} = \frac{T}{h} \int_{(i-1) T / m}^{i T / m} g(t) d t, i = 1, 2, \ldots, m$

Theorem 2.8. Suppose that $g$ is a function in $\operatorname{L}^{2}\left([0, T)\right),$ then it may be expanded by the block-pulse wavelet as follow

where the block-pulse coefficients $k_i$ are obtained as follows:

Proof. See ^[54].

In the next section, a new operational matrix of fractional order integration will be introduced.

3.   Operational matrix of the fractional integration

In this section, we introduce the operational matrix of fractional integration based on the block-pulse functions. According to (2.13), we know that for every $g$ in $L^2(0, T)$, we have

Where $K = (k_1, k_2, \cdots, k_m)$ and $B_m(t) = \left(b_1(t), b_2(t), \cdots, b_m(t) \right)$; therefore, the fractional integration of the block-pulse vector is defined as follows ^[28]

Where $F^{(\alpha)}$ is the block-pulse operational matrix of fractional order integration and ^[28]

and $c_{j} = (j+1)^{\alpha+1}-2 j^{\alpha+1}+(j-1)^{\alpha+1}, j = 0, 1, \ldots, (m-1)$ Note that in (3.1), if $g = v$ and $v$ be a constant value we hove

where $V = (v, v, \cdots, v)^{T}$. In the next section, we describe our method for solving fractional Duffing equation numerically.

4.   Numerical method

In this section by using the block-pulse wavelets, we solve the fractional Duffing fractional Duffing equation numerically. From (1.3), we have

To continue, initially, we present one lemma that is needed.

Lemma 4.1. According to Theorem 2.8, if $g$ be a function in $\mathrm{L}^{2}\left([0, \mathrm{T})\right)$, then it may be expanded by the block-pulse wavelet as (2.13). Because of the orthogonal property of block-puls functions we will have

Proof. At first we write $g^n (t) = (g(t))^{n}$. According to the assumptions of lemma we can write the above relation as follows

We know that $\sum_{i = 0}^{m-1} k_{i} b_{i}(t) = k_{1} b_{1}(t)+ k_{2} b_{2}(t)+\cdots+ k_{m-1} b_{m-1}(t),$ so with replacing it into above relation we have

Therefore, because of (2.10), we have

So

Now, by taking the fractional integral of order of $\beta$ on both sides of (4.1). we have

It is worth noting that if we can, from the right of equation (4.2) gets directly the integral of the fractional order of beta; otherwise, we first approximate it with the pulse block functions, and then we obtain the fractional integral of the result. Now, we call the sentences on the sides of the (4.2) $A, B, C, D, E, F$ and $G$ respectively, and each of these terms is described separately, so we have

We must note that the notation of $\lceil \beta\rceil$ presents the smallest integer number larger from $\beta$.

Because of (3.1) and (3.4) we have

For second term in (4.2) we have

From (4.4) and with regard to (3.1), (3.2) and (3.4) we have

For the third term in (4.2), because of (3.1) we have

According to the lemma 4.1, for the fourth, fifth, and the sixth term in (4.2) respectively, we have

Finally, because of (3.1) and (3.2) for the right hand side of (4.2) we have

By replacing the relations (4.4)-(4.9) into (4.2) and then simplifying them we have

where $f(t) = x_{0}+x_{1} \boldsymbol{t}+\frac{x_{0}}{\Gamma(\beta-\alpha+1)} t^{\beta-\alpha}+\boldsymbol{g}^{T} \boldsymbol{F}^{\beta}$. Now, by choosing $t_{i} = (i-1) \frac{T}{m}, i = 1, 2, \ldots, m$ as collocation points in (4.10) we have

where $M_{j}^{i}$, $i = 1, 2, \ldots, m, j = 1, 2, 3, 4$ is the $i^{t h}$ column of $\left(I+a F^{\beta-\alpha}+b F^{\beta}\right), c F^{\beta}, d F^{\beta}, e F^{\beta},$ respectively. Now, we can rewrite (4.11) as follows

where $\boldsymbol{f} = \left(f\left(t_{1}\right), f\left(t_{2}\right), \ldots, f\left(t_{m}\right)\right)$.

It is easy to understand that (4.12) is a nonlinear algebraic system, which can be solved to find the unknown vector $K$ ^[56].

5.   Error analysis

In this section, we want to investigate the convergence of the method described in the previous section. Let $(C[0, 1], \|\cdot\|)$ be the Banach space of all continuous functions with norm $\|g(t)\| = \max _{0 \leq t \leq1}|g(t)|$

Theorem 5.1. Let $g$ be an arbitrary real bounded function, which is square integrable in the interval $[0, T)$ and

where $h = \frac{T}{m}$.

Proof. See ^[57].

Since the numerical method presented in the previous section converts (1.3) to a nonlinear algebraic equation, and to solve this equation, using numerical methods, an error is created, it is logical that we analyse the effect of this error in the solution of (1.3) first. In the next theorems, we study this issue in more details.

Theorem 5.2. Assume that $\hat{K}$ is the approximate solution of the equation (4.12) with the help of some numerical methods such as $g(t) \simeq g_m(t) \simeq \hat{g}_{m}(t)$ where $g_{m}(t) = \boldsymbol{K}^{T} \boldsymbol{B}_{m}(t) \simeq \hat{\boldsymbol{K}}^{T} \boldsymbol{B}_{m}(t).$ Then we have

Proof.

where $||\cdot ||_{F}$ denotes the Frobenius norm ^[58].

Theorem 5.3. Suppose $\hat{g}_{m}$ is an approximation $ofg$ with some suitable numerical methods. When $m$ tends to infinity, so we have $err = \left\|\hat{g}_{m}-g\right\| \rightarrow 0$

Proof. We have

By replacing (5.1) and (5.2) in (5.3), we have

The last inequality shows when $m \rightarrow \infty$ then $err \rightarrow 0$

6.   Illustrative examples

In this section, we test our method by presenting some examples. The obtained results for our introduced method in different values of $\alpha$, $\beta$, $a$, $b$, $c$, $d$, $e$ and $g$ are mapped, then their graphs are compared with each other. It should be kept in mind that by changing $0 < \alpha < 0$ and $0 < \beta < 2$, the equation will be of the fractional order of derivative, and then, obtained solutions are compared in integer and the fractional order with each other.

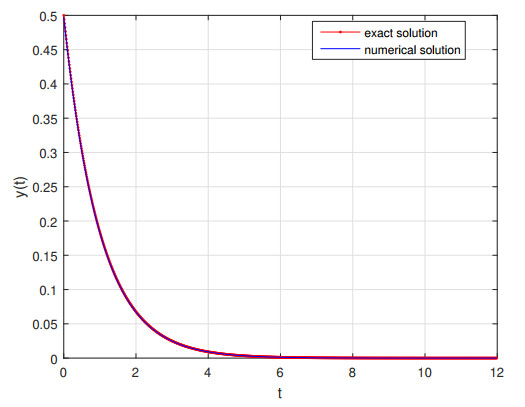
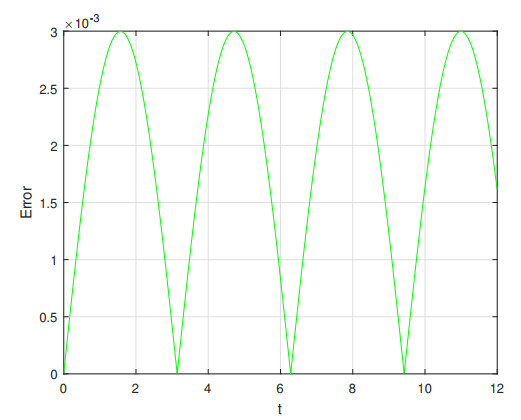
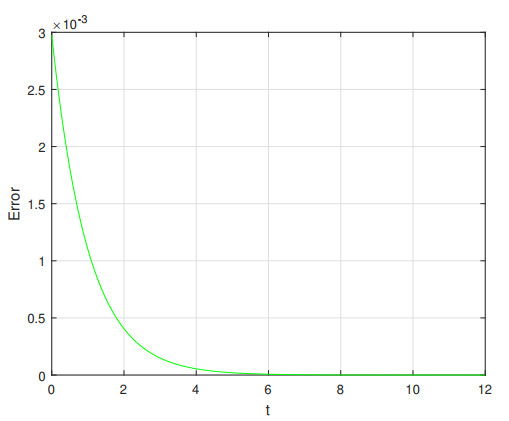
Example 1. In (4.1), suppose $g(t) = e^{-3t}$ with initial values $x_0 = 0.5$ and $x_1 = -0.5$. By setting $a = 2$, $b = 1$, $c = 8$, $d = 0$ and $e = 0$, the graphs of numerical solution with $\alpha = 1$ and $\beta = 2$ and the exact solution $x(t) = 0.5e^{-t}$are compared with each other as follows Figure 2 Also Figure 1 shows the difference between numerical and analytic solutions.

From Figure 2, the convergence of the method is obvious, and also it is very effective and precise. Table 1 presents the absolute error between exact and numerical solutions.

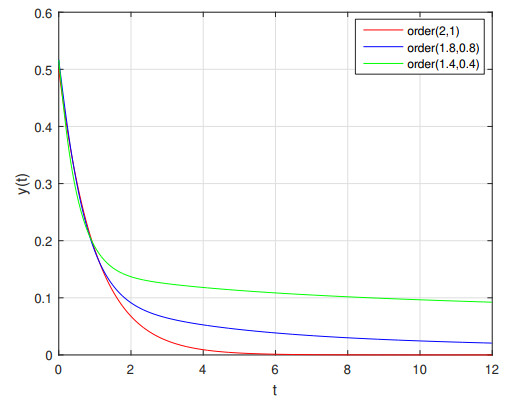
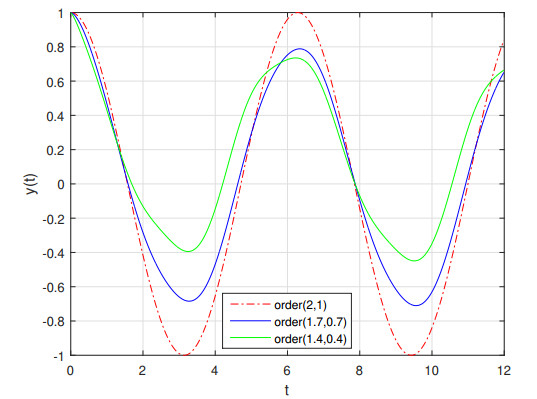
According to Table 1, we can see that the method is accurate. Now, we change ($\beta = 2$, $\alpha = 1$) to ($\beta = 1.8$, $\alpha = 0.8$) and ($\beta = 1.4$, $\alpha = 0.4$) keeping constant the rest of coefficients to investigate the possible variations of the solution. Results have been shown in Figure 3.

Considering Figure 3, we find that with applying the changes to the values of the $\alpha$ and $\beta$ from integer to fractional and with the increasing number of operating intervals (with the step increment $t = T/h$), an acceptable convergence was obtained. Besides, all three graphs show the same trend. However, with dropping of derivation order after $t = 1s$, the displacement of the oscillator increases.

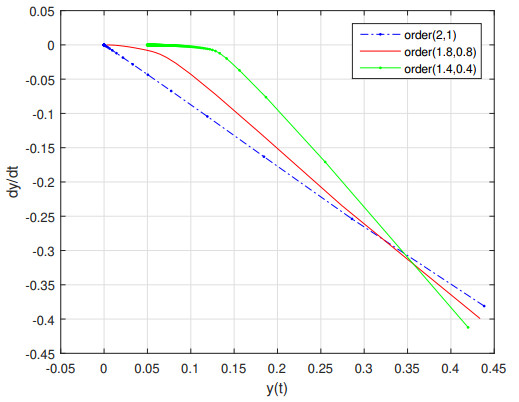
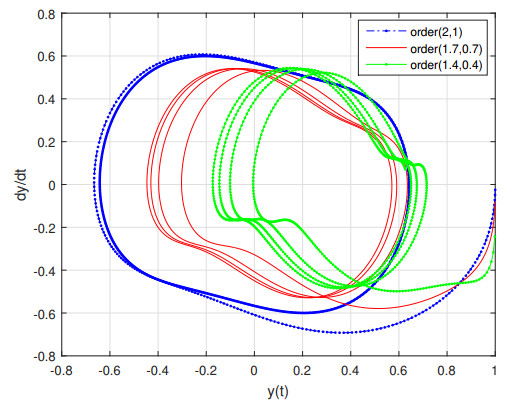
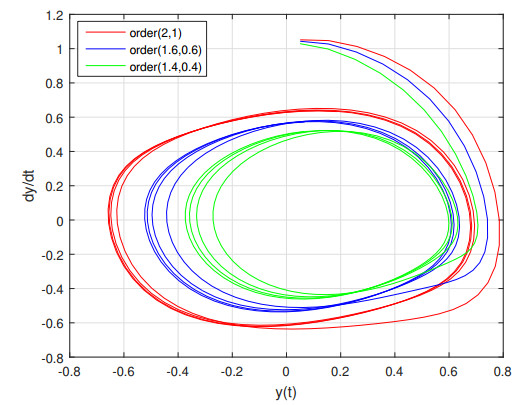
In the following, Figure 4 shows the changes made in the phase portrait due to the changes in derivatives of the equation from the integer values to the fractional values. Again, an identical behaviour is seen for all three cases. Physically, this behaviour explains a damping oscillation. Going away from the origin, the velocity oscillator decreases. Furthermore, the slope of dropping is higher for the lowest order of fractional derivation (i.e. for ($\beta = 1.4$, $\alpha = 0.4$)).

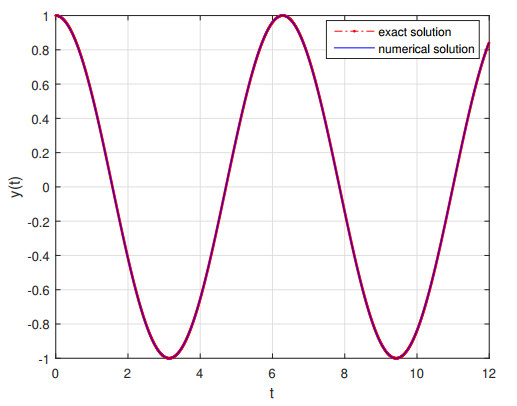
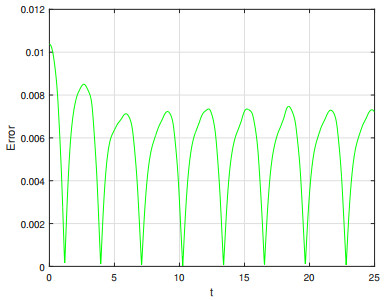
Example 2. In (4.1), suppose $g(t) = \cos^3 (t)-\sin(t)$. By setting $a = 1$, $b = 1$, $c = 1$, $d = 0$ and $e = 0$, the graphs of numerical solution with $\alpha = 1$ and $\beta = 2$ with initial values $x_0 = 1$ and $x_1 = 0$ and the exact solution $x(t) = \cos(t)$ are compared with each other as follows Figure 5.

According to Figure 5, the described method is efficient and accurate. Also, the convergence of the method is quite clear. Now, by keeping the previous coefficients constant, we change $\beta$ and $\alpha$ from $2$ and $1$ to $1.7$ and $0.7$ first and then $1.4$ and $0.4$, respectively. On the other Figure 6 shows the difference between numerical and analytic solutions.

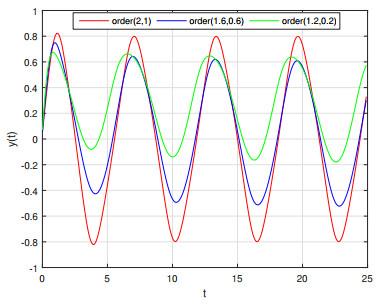
As shown in Figure 7, with applying the changes to the values of the $\alpha$ and $\beta$ from integer to fractional, it is obvious, that an acceptable convergence is achieved with the increasing number of operating intervals for the block-pulse functions (with the step increment as $m = T/h$).Physically, all graphs show the same period and frequency. However, with decreasing the fractional order from $(2, 1)$ to $(1.4, 0.4)$, the amplitude of the oscillator decrease, simplifying the decrease of the area of the phase diagrams. This is approved by plotting the phase diagram as is shown in Figure 8. Another feature of the phase diagram is that by decreasing of derivation order, the symmetry of the graph related to the equilibrium point ($y = 0$) goes away.

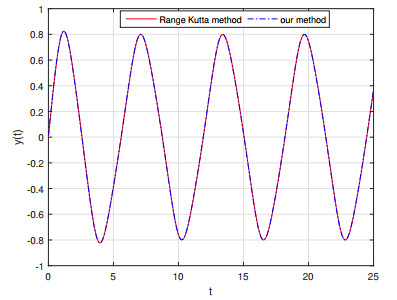
Example 3. In (4.1), suppose $g(t) = f\cos(\omega t)$ with initial values $x_0 = 0$ and $x_1 = 1$. By setting $a = 1$, $b = 1$, $c = 1$, $f = 1$, $d = 1$ and $e = 1$, the graphs of numerical solution with $\alpha = 1$ and $\beta = 2$. Since, with the assumed coefficients and initial values of the equation, there is no precise analytical solution, therefore, Figure 11 shows a comparison of the suggested numerical solution with the solution obtained by the Range-Kutta method of order 4.

Figure 9 shows the difference between numerical and analytic solutions. In Figure 10, the variation of the equation response is shown for derivation orders of $(2, 1)$, $(1.6, 0.6)$ and $(1.4, 0.4)$. As it comes from the figure, with decreasing of derivation order, the phase of the graphs is shifted left while the period and frequency does not change. Also Figure 11 shows that the method used has a reasonable accuracy compared to the Runge Kutta method. Besides, very good convergence was achieved.

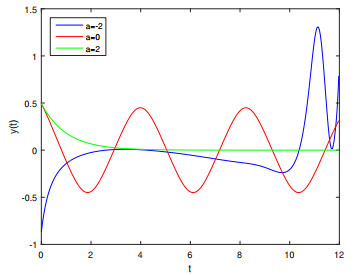
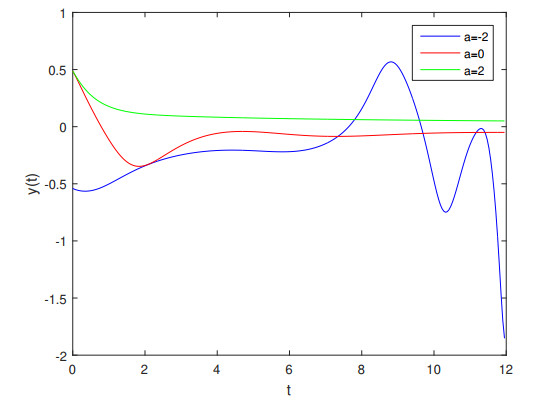
Now consider Example 1 again. In Figure 12, we examine the solutions of this equation with damping coefficients of $-2$, $0$ and $2$. We recall that, the derivations of the equation are integer. We know that the exact solution of this equation is $x(t) = 0.5e^{-t}$.

Figure 13 shows the variations of phase portrait of the solutions when we changed the orders of equation from integer to fraction. It is seen again that the symmetry of the graphs fades with decrement of derivation order. This is a characteristic behavior of a chaotic system and the fractional analysis can help us to analysis the evolution of the system accurately.

As we see from Figure 14, with changing the damping coefficient of the equation, the status of solutions changes to divergence (with $a = -2$), oscillating (with $a = 0$), and convergence (with $a = 2$).Changes in responses due to changes in damping coefficients are very obvious. In the next figure, we present the status of the above equation when the order of derivatives $\beta$ and $\alpha$ change from $2$ and $1$ to $1.6$ and $0.6$, respectively, but the other coefficients are constant. By changing the derivation order from an integer to fractional, the harmonic oscillation($a = 0$) changes to a critical damping oscillation.

7.   Conclusions

In this article, we investigated the fractional strongly nonlinear Duffing oscillators with cubic-quintic- heptic nonlinear restoring force numerically by using block-pulse wavelets. First, the method used in this paper, was described. This method translates the fractional Duffing equation to an algebraic nonlinear equation. Moreover, the convergence of this method was demonstrated. Different forms of the fractional Duffing equation have been analysed for different parameters of equation and its fractional derivative orders. The numerical results have been compared with each. In addition, as we can see in several examples, this method has a very good accuracy. The major conclusion is that this approach provides excellent approximation to the solution of these nonlinear systems with high accuracy. Therefore, it is an easy method to be used in solving nonlinear equations such as the Bratu's equation and other similar equations.

Conflict of interest

The authors declare no conflict of interest in this paper.