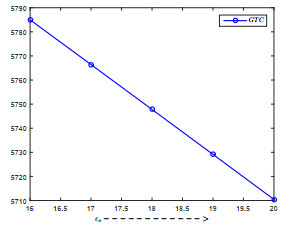
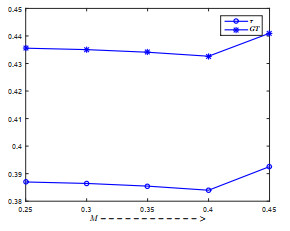
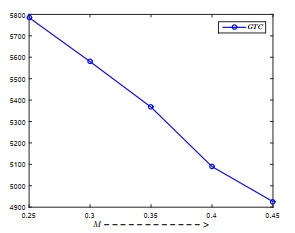
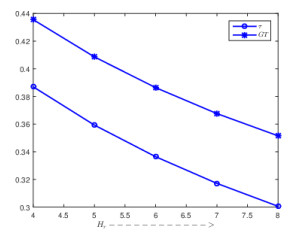
Most of the researchers developed their inventory models to forecast the optimal replenishment quantity and time in view of minimizing the total inventory cost by considering deterministic demand and the deterioration of the items. But, in real business these demands and deterioration are mostly fuzzy in nature due to many practical factors, such as increase or decrease in goodwill of the product, competition from the substitute products, scientific advancement in preserving facilities, change in environmental conditions and so on. So by following researcher's classical inventory model, retailer may order less or excess amount of items than the actual requirement. As a result, retailer may face loss in business or increase in cost. Moreover, in many cases, suppliers offer trade credit to increase their sales, and by availing the trade credit facility the retailer purchases a number of items more than the existing storage capacity (in own warehouse) in order to minimize the ordering cost and investment capital. To accommodate these excess amounts of items retailer may hire a warehouse on rent basis. In the light of these facts, we develop a cost optimization model for the inventory items having fuzzy demand and deterioration with two-warehouse facility under trade credit financing by considering triangular fuzzy numbers for the associated parameters. The Graded Mean Integration Representation defuzzification technique is used and numerical examples are provided to justify the validity of the proposed model. Finally, sensitivity analysis of major parameters has been incorporated to draw the managerial insight on optimal solution.
1.
Introduction
Due to the rapid growth of science and technology, ultra-high-dimensional data are more prevalent in various scientific study fields, including genomics, bio-imaging, and tumor classification. In ultra-high-dimensional data, the dimensionality of the variables is substantially larger than the sample size, and there are frequently very few variables among these variables that significantly influence the response variable. Therefore, it is crucial to screen a set of real covariates for this type of ultra-high-dimensional data problem. Fan and Lv [1] first proposed the method of ultra-high-dimensional feature screening and put forward the theory of sure screening, which lays the theoretical foundation for the ultra-high-dimensional feature screening method. Subsequently, a great deal of research has been developed for ultra-high-dimensional feature screening.
From the perspective of the model, current ultra-high-dimensional feature screening techniques are divided into three main categories: Based on parametric modeling assumptions, based on nonparametric and semiparametric modeling assumptions, and based on model-free assumptions. Ultra-high-dimensional feature screening based on parametric modeling assumptions: Fan and Lv [1] first proposed a marginal screening method (SIS) based on Pearson's correlation coefficient under linear modeling assumptions, where the magnitude of the absolute value of Pearson's correlation coefficient is used to measure the importance of the covariates. Given that the Pearson correlation coefficient is used to describe the degree of linear correlation between random variables, specific transformations can be applied to the covariates to account for nonlinear correlations. Therefore, Hall and Miller [2] proposed the generalized correlation coefficient to describe nonlinear relationships. Li et al. [3] proposed a robust rank correlation coefficient screening method by applying certain transformations to the response variables. Relaxing the linear model assumption to generalized linear models, Fan and Song [4] proposed a screening method based on maximum marginal likelihood estimation (MMLE-SIS). When there is less a priori knowledge about the model, nonparametric models are more adaptable than parametric models. Ultra-high-dimensional feature screening based on nonparametric and semiparametric modeling assumptions: Fan et al. [5] initially developed a marginal nonparametric screening (NIS) method for variables under the presumption of additive modeling. Liu et al. [6] proposed a conditional correlation coefficient screening method in the framework of variable coefficient modeling. In addition to the additive and variable coefficient models, Liang et al. [7] proposed a profile forward regression (PFR) screening method based on a partially linear model. It is vital to create model-free hypothetical screening methods with broad applicability when information about the model is absent. Ultra-high-dimensional feature screening based on model-free assumptions: Zhu et al. [8] first proposed a ranking screening approach (SIRS) based on covariance. The distance correlation coefficient (DC)-based screening approach was subsequently proposed by Li et al. [9]. He et al. [10] proposed the quartile adaptive screening method (QaSIS) by fitting marginal quantile regression. The correlation between two random vectors can be effectively measured by the Ball correlation, and based on this property, it can be used to rank predictor vectors. Then, Pan et al.[11] proposed a generic model-free sure independence screening procedure based on ball correlation, called BCor-SIS. Since many problems in practice cannot be accurately described by a single model, model-free screening methods can be applied more widely. Hence, studying a model-free feature screening procedure for ultra-high-dimensional data is the first focus of this work.
From a data type standpoint, the majority of existing ultra-high-dimensional feature screening methods implicitly assume that the response variable is a continuous variable. Yet, ultra-high-dimensional data with discrete response variables is also frequently found in many areas of scientific research. For example, in medicine, identifying which genes are correlated with certain types of tumors is of interest. When the response variable is discrete, Fan and Fan [12] proposed a marginal t-test screening statistic based on a normal distribution, but its performance is poor for heavy-tailed distributions or outlier data. For this reason, Mai and Zou [13] proposed the screening method with a response variable that is a binary based on the Kolmogorov-Smirnov test statistic, which they later extended to situations where the response variable is multi-categorical. Cui et al. [14] proposed a new test based on the mean-variance index for testing the independence between a categorical random variable Y and a continuous random variable X. When all covariates are categorical variables, Huang et al. [15] developed a screening approach based on Pearson's cardinality statistic (PC-SIS). It can be seen that most of the ultra-high-dimensional variable screening methods construct the corresponding statistical indexes based on the correlation between the covariates and the response variable. In recent years, some scholars have further searched for new indexes to measure the relationship between random variables or random vectors. Ni and Fang [16], from the perspective of the amount of information, proposed a model-less feature screening method for ultra-high-dimensional variable selection based on information gain (IG-SIS). In information theory, in addition to information gain, divergence has been widely developed as a useful tool for measuring differences between information in many fields, such as in the Dempster-Shafer evidence theory: Xiao [17] proposed a new Belief Jensen-Shannon divergence to measure the discrepancy and conflict degree between the evidence. A novel reinforced belief divergence measure, known as RB, was created by Xiao [18] to measure the discrepancy between basic belief assignments in the context of the Dempster-Shafer evidence theory. Xiao [19] developed a novel generalized evidential Jensen-Shannon divergence that measures the conflict and discrepancy across several sources of evidence. To measure the disparity and discrepancy between basic belief assignments in Dempster-Shafer theory, Xiao et al. [20] suggested and examined a number of generalized evidential divergences. And, as the convergence of information theory and statistics develops, it is attractive to generalize the divergence to ultra-high-dimensional feature screening.
This paper primarily examines the feature screening procedure for the binary categorical response variable according to the state of the current feature screening for ultra-high-dimensional data. Since most current methods directly measure the specific degree of correlation between the covariates and the response variable, there may be a potential problem with the existence of a class of unimportant covariates that are also highly correlated with the response variable due to their high correlation with the other covariates. And furthermore, in real classification problems, screening out important features is not the ultimate goal but rather using the features to make classification predictions. Therefore, we do not directly measure the correlation between the response variable and the covariates, but we start from the perspective of the contribution of the features to the classification, which is the second focus of this paper's work, by introducing the Jensen-Shannon divergence to measure the difference between the conditional probability distributions of the covariates when the response variables take on different values, thus reflecting the contribution of the covariates to the classification of the response variables. The larger the value of the Jensen-Shannon divergence, the stronger the covariate's contribution to the classification of the response variable, i.e., the more important the covariate is considered.
In this study, Jensen-Shannon divergence is referred to as JS divergence for readability. The main contributions of this paper are as follows:
(1) From the point of view of the contribution of the features to the classification, we examine a model-free feature screening procedure for binary categorical response variables, which implies less restrictive assumptions about the data and highlights the importance of features for classification prediction.
(2) The JS divergence is widely used, which is different from the I, J, and K divergences. JS divergence does not need the condition of absolute continuity of the probability distributions involved, and it has the advantages of symmetry, non-negativity, and boundedness [21], so it is very effective to use JS divergence to measure the differences between probability distributions.
(3) We propose two kinds of feature screening methods for binary response variables in different cases. When the number of covariate categories is the same, the screening method based on traditional JS divergence is used. Additionally, when the number of covariate categories is different, we propose a method to use the logarithmic factor of the number of categories to adjust the JS divergence and use it for screening variables, defined as AJS-SIS.
The suggested methods's sure screening and ranking consistency properties are further shown theoretically and through simulated studies. Furthermore, simulation experiments and real data analysis show the effectiveness, availability, and practicality of the methods proposed in this paper in terms of feature screening.
The rest of the paper is organized as follows: Section 2 describes the proposed method; Section 3 demonstrates the screening properties of the proposed method under certain conditions; Section 4 carries out simulation experiments to study the proposed method in comparison with an existing method; Section 5 is real data analysis; and Section 6 gives the conclusion.
2.
Feature screening method
2.1. Basic assumption
Suppose X=(xi1,xi2,…,xij) is an n×p-dimensional covariate matrix, where X obeys the assumption of independent identical distribution, and Y=(y1,y2,…,yi) is an n×1-dimensional binary categorical response variable, where j=1,2,…,p,i=1,2,…,n. Let xj={x1j,x2j,…,xij},i=1,2,…,n. The probability function of X is denoted by pj,l, the probability function of Y is denoted by pr, the conditional probability function of Y given xj is denoted by pj,lr, and the conditional probability function of xj given Y is denoted by plr,j.
The expression for pr is as follows:
When the covariate xj is a categorical variable, let xj have L categories, L={1,2,…,L}:
When the covariate xj is a continuous variable, reference is made to Ni and Fang [16] to cut xj into categorical data using standard normal distribution quantiles:
Where q(J) is the J/Jk quantile, and J=1,2,...,Jk, q(0)=−∞, q(JK)=+∞.
Define two index sets: D is the set of significant covariates, Dc is the set of non-significant covariates, and |D|=d0 is the number of variables in the set of significant covariates, which is expressed in set form as
2.2. Information entropy
Information entropy is the information theory Shannon borrowed from the concept of thermodynamics, where, in 1948, he proposed a measure of the size of the information index and also gave the mathematical formula [22]. Taking the covariate as a categorical discrete variable xj∈{1,2,…,L} as an example, the information entropy of the covariates xj and Y are given by
Where 0×log0=0, and the logarithmic base is 2.
Having understood the definition of information entropy, the conditional information entropy of the covariate xj given the response variable Y is defined as
2.3. IG-SIS
The information gain is derived from information entropy, which can represent the strength of the correlation between the covariates and the response variable, and the expression for the information gain between Y and xj is
IG(Y,xj) represents the difference of the response variable Y between the information entropy and the conditional information entropy of the given covariate xj. If xj is a significant variable, Y will be significantly impacted by xj, and thus the value of IG(Y,xj) is larger. Based on this, Ni and Fang [16] proposed the IG-SIS feature screening method.
The estimate of the information gain about Y and xj is
After obtaining the IG values of each covariate and response variable, sort and filter all the variables by importance and select the top d0 variables to be selected into the set of important variables.
The set of important variables is
2.4. JS-SIS
JS divergence (Jensen-Shannon divergence, abbreviated JSD) is a statistical measure based on the KL divergence (relative entropy). Assuming that there are two probability distributions G=Pr(xj=l∣Y=1) and Q=Pr(xj=l∣Y=2) for the same random variable xj in space, JS divergence can measure the degree of difference between these two distributions, and larger JS divergence implies that the covariates are more important. According to Lin [21], the value of JS divergence is non-negative, equal to 0 when G=Q, and it is upper bound by 1.
JS divergence is actually a variant form of KL divergence (relative entropy), and KL divergence can be computed in the following way:
Since KL divergence is asymmetric, it cannot accurately measure the real difference between G and Q. JS divergence solves this problem by constructing the average probability distribution of G and Q.
Assume that M=12(G+Q) is the average probability distribution of G and Q. The JS divergence of G and Q is defined as
The estimate of the JS divergence between G and Q is
The probability distributions G and Q based on continuous covariates are defined as G=Pr(xj∈(q(J−1),q(J)]∣Y=1), Q=Pr(xj∈(q(J−1),q(J)]∣Y=2).
2.5. AJS-SIS
The definition of Eq (2.2) may lead to the incorrect selection of non-significant covariates with a large number of categories because covariates with more categories may have larger calculated JS divergence values, especially when the number of categories involved in each covariate varies. To address this issue, this paper refers to Ni and Fang [16] applying (logJk)−1 to construct an adjusted JS divergence to measure the importance of xj:
The estimate of the adjusted JS divergence between G and Q is
When xj is a categorical variable, Jk equals the number of categories L of xj, and when xj is a continuous variable, Jk represents the number of categories into which xj is cut by the standard normal distribution quantile.
3.
Theoretical properties
Fan and Lv [1] mentioned that a method is meaningful if a feature screening method has a sure screening property. It is the basis of feature screening, which means that the probability of all significant covariates being selected tends to be 1. Therefore, subsequent feature screening methods that extend the SIS method demonstrate this property, such as those in the articles by Li et al. [9], Cui and Zhong [14], and Ni and Fang [16].
In addition to the sure screening property, a feature screening method should also have a ranking consistency property. It means that the feature screening approach is consistent and can guarantee that the values of all important covariate indexes are ranked before all other unimportant covariates.
These two properties eventually guarantee the usefulness and effectiveness of feature screening methods.
This subsection will illustrate the theoretical properties of the methods proposed in this paper under certain conditions, which are as follows:
(C1) p=o(exp(nδ)),δ∈(0,1), which means the variable dimension p is an exponential multiple of the sample capacity n.
(C2) There exist positive numbers c1, c2, such that 0<c1≤pj,lr≤c2<1, ∀l∈{1,Jk}, ∀r∈{1,2}, and ∀j=1,2,…,p.
(C3) There exist positive c>0 and 0≤τ<1/2, such that minj∈Dej≥2cn−τ.
(C4) There exists a constant c3 for ∀1≤r≤R such that 0<fk(x∣Y=r)<c3, and x is in the domain of definition of Xk, where fk(x∣Y=r) is the Lebesgue density function of Xk under the condition Y=r.
(C5) There exists a constant c4 and ∀1≤ρ≤1/2 such that fk(x)≥c4n−ρ, and x is in the domain of definition of Xk for ∀1≤k≤ρ, where fk(x) is the Lebesgue density function of Xk, and fk(x) is continuous in the domain of definition of Xk.
(C6) J=max1≤j≤pJk=O(nκ), κ>0, ∀1≤τ≤1/2 and ∀1≤ρ≤1/2 with 2τ+2ρ<1.
The above six conditions are frequently found in the literature on ultra-high-dimensional feature screening methods, such as Fan and Lv [1], Li et al. [9], Cui et al. [14], and Ni and Fang [16]. Condition (C1) indicates that it is a feature screening method used in ultra-high-dimensional problems; Condition (C2) indicates that the marginal probabilities of the response variable and the covariate are bounded by an upper and a lower limit to avoid the extreme case of the failure of the screening method; and Condition (C3) indicates that the values of the indexes belonging to the really important variables are bounded by a lower value. Condition (C4) ensures that the sample percentile is near to the true percentile by excluding an extreme case in which some Xk places a huge mass in a tiny range. Condition (C5) requires the density to have a lower bound of order n−ρ. Condition (C6) ensures that the number of categories of covariates diverges at a certain rate.
Under these six conditions, we give the theoretical properties of the feature screening method JS-SIS when the response is a binary categorical variable.
Since wj=ej/logJk, ˆwj=ˆej/logJk, and logJk≥log2≥1/2, it follows that Pr(|wj−ˆwj|>ϵ)=Pr(|ej−ˆej|>ϵ/2). Therefore, this paper gives the properties of sure screening and ranking consistency for feature screening using the index ej of the JS divergence and a detailed theoretical proof.
3.1. Sure screening property
To distinguish between types of covariates, discrete covariates are subscripted with j and continuous covariates are subscripted with k. If the covariate is categorical, L is the number of categories of the covariate, and if the covariate is continuous, Jk is the number of categories of the covariate.
Theorem 3.1. When the covariates are categorical, in conditions (C1) and (C2), 0≤τ<1/2, and there exists a positive number c such that
and when 0<δ<1−2τ, Pr(max1≤j≤p|ej−ˆej|>cn−τ)→0,n→∞. Under conditions (C1)–(C3), when n→∞, there exists a positive number c such that
Theorem 3.1 states that the probability that the set of true covariates D is contained in the set of simplified covariates ˆD as n→∞ converges to 1, which means that as the sample size n increases, eventually all the true covariates can theoretically be filtered out.
Theorem 3.2. When the covariates are continuous variables, there exist positive constants c5, c6, c7 under the conditions (C1), (C4)–(C6), and we have
and when n→∞
Theorem 3.3. When the covariates are continuous and categorical covariates coexist, there exists a positive constant c9 under the conditions (C1), (C2), (C4)–(C6), and we have
and when n→∞,
where p1+p2=p, d1+d2=d0.
3.2. Ranking consistency property
Theorem 3.4. When the covariates are categorical, under conditions (C1)–(C3), assume that minj⊆Dˆej−maxj⊆Dcˆej>0, then we have
Theorem 3.5. When the covariates are continuous variables, under conditions (C1), (C3)–(C6), assume that mink⊆Dˆek−maxk⊆Dcˆek>0, then we have
Theorem 3.6. When the covariates are continuous and categorical covariates coexist, under conditions (C1)–(C6), assume that minj⊆Dˆej−maxj⊆Dcˆej>0 and mink⊆Dˆek−maxk⊆Dcˆek>0, then we have
A detailed proof of the theoretical part is in the Appendix.
4.
Numerical simulation
In this section, we conduct simulation experiments to investigate the variable screening performance of our proposed methods, in which we analyze the simulation in terms of two main aspects: The type of distribution of the response variable and the type of the covariate. The methods proposed in this study are limited to binary response variables and make no assumptions regarding the data types of the covariates. In practice, four types of covariates are generally encountered: All the covariates are categorical with the same categories; all the covariates are categorical with different categories; all the covariates are continuous; both continuous and categorical covariates appear in the data, where the categories of the categorical variables differ. To examine the validity and viability of the proposed methods, we created four simulation experiments that tested them using the four kinds of data types of the covariates mentioned above. Of these, the similarities are that the response variable is binary and the type of distribution of the response variable is the same, while the differences are in the type of covariates and the generation method of the covariates. Besides, to determine whether varying the number of slices will affect the effectiveness of the suggested methods, we attempt to slice the continuous variables in the simulation experiments using varying numbers of slices. This can also provide some references for choosing the optimal categories of the continuous variables in practical applications.
4.1. Evaluation indexes
Three evaluation indexes were used to compare the effectiveness of the variable screening method. The first evaluation index is CP, coverage 1, which indicates the proportion of true significant covariates screened for inclusion in the set of significant covariates. And, with CP ∈[0,1], when the value is closer to 1, the more true significant covariates are selected to be included in the set of significant covariates. The second evaluation index is CPa, coverage 2, which indicates whether the selected set of significant covariates contains all the true significant covariates, where CPa=0,1, so the average value of CPa takes the range of [0,1]. The average value being closer to 1 indicates that the selection of significant covariates has a higher probability of including all of the actual significant variables. CP1 and CPa1 are used to denote the index values when the first [n/logn] variables are screened as the set of significant covariates, and CP2 and CPa2 are used to denote the index values when the first 2[n/logn] variables are selected as the set of significant covariates. The third evaluation index is the MMS, which represents the minimum model size at which all important variables will be screened and expresses the performance of the method by calculating the 5%, 25%, 50%, 75%, and 95% quantile points of the MMS. The value of the quartile of the MMS is in the range of [0,1], and the lower the value means that the screening method can select the truly essential variables while reducing dimensionality. In this paper, the final evaluation index is expressed as the average of the indexes of 100 simulation experiments. Hence, we calculated the standard deviation, where lower values indicate higher method stability as well as the feasibility of using the average value for evaluation.
4.2. Simulation experiments and results
4.2.1. Simulation 1
The response variable is binary categorical, all covariates are categorical, and each covariate has the same number of categories. We refer to the simulation experiment in Ni and Fang [16] and consider both balanced and unbalanced distributions for the response variable: (1) balanced, pr=Pr(Y=r)=1/R, with r=1,…,R, and R=2; (2) unbalanced, pr=2[1+(R−r)/(R−1)]/3R with max1≤r≤Rpr=2min1≤r≤Rpr. Define the set of true imporant variables as D, where D={1,2,…,10} with d0=|D|=10. Conditional on Y, the relevant categorical covariates are generated as Pr(xij=(1,2,3,4)∣yi=r)=(θrj/2,(1−θrj)/2,θrj/2,(1−θrj)/2) for 1≤r≤R and 1≤j≤d0, where θrj is given in Table 1. And, θrj=0.5 when 1≤r≤R, d0<j≤p. We take the dimensions of the covariates p=1000 and p=2000 with sample sizes of n=200 and n=400.
Tables 2 and 3 show that CP and CPa for all methods are higher when Y is a balanced distribution than when Y is an unbalanced distribution, and the MMS for all methods is closer to the number of significant variables d0=10. When the dimensionality of the covariates is p=1000, variable screening performs better than when p=2000, indicating that, for a given sample size, variable screening may become more challenging as the dimensionality of the covariates rises. Because all covariates are 4-categorical data in this simulation, the effects of JS-SIS and AJ-SIS are the same. The coverage CP and CPa of variable screening in JS-SIS and AJ-SIS are almost the same as in IG-SIS, except that the MMS in IG-SIS is a little closer to d0=10 than in JS-SIS and AJ-SIS. Besides, through Simulation 1, it can be seen that JS-SIS and AJS-SIS can effectively screen out important variables, indicating that JS-SIS and AJS-SIS apply to data where the covariates are all categorical variables with the same category.
4.2.2. Simulation 2
The response variables are set the same as in Simulation 1. The covariates were categorical, and each covariate had a different number of categories, set at 2, 4, 6, 8, and 10. Define the set of important variables as D={j=[j′p/10],j′=1,2,…,10}. Referring to the simulation experiment setup in [23], the latent variables zi=(zi,1,…,zi,p) are generated under the condition yi. Generate covariate xi,j by fj(εi,j+μi,j), where 1≤j≤p and fj(⋅) is the quantile function of the standard normal distribution. And εi,j∼N(0,1), μi,j=1.5×(−0.9)r when j∈D, and μi,j=0 when j∉D.
The specific steps for generating covariate data are as follows:
If 1≤j≤400, then L=2; if 401≤j≤800, then L=4; if 801≤j≤1200, then L=6; if 1201≤j≤1600, then L=8; if 1601≤j≤2000, then L=10.
This makes the number of covariates the same for two categorical, four categorical, six categorical, eight categorical, and ten categorical. We take p=2000, n=160,240,320.
Table 4 displays the outcomes of the simulation. The performance metrics of all methods for all conditions are exactly the same; the coverage CP and CPa are 1, and the MMS values are close to d0=10. Furthermore, Simulation 2 indicates that JS-SIS and AJS-SIS apply to data where the covariates are all categorical variables with different categories since it clearly shows that these two methods are effective at selecting significant variables.
4.2.3. Simulation 3
The response variables are set the same as in Simulation 1. The covariates are continuous variables, which we use the quantile function of the standard normal distribution to cut into categorical data with different numbers of slices Jk=4,8,10, respectively, and define the methods corresponding to the number of slices as JS-SIS-4, AJS-SIS-4, IG-SIS-4; JS-SIS-8, AJS-SIS-8, IG-SIS-8; JS-SIS-10, AJS-SIS-10, IG-SIS-10. The set of important variables is set up as in Simulation 1. We use the normal distribution to generate covariates, where xi={xi1,xi2,…,xip}∈Rp and xij(j=1,2,…,p) are distributed as N(μij,1) with μi={μi1,μi2,…,μip}. When Y=r and j∈D, μij=(−1)rθrj, otherwise j∉D, μij=0. We take p=5000 and n=400,600,800.
As can be seen from Tables 5 and 6, there are significant differences in the performance of the methods only when the sample size is relatively small. Therefore, the simulation results for the specific analyzed sample size of n=400 are as follows: By comparing the performance of different methods applying different numbers of slices, it is found that the CP and CPa values are the same for all three methods, and only the MMS values are slightly different. Specifically, JS-SIS and AJ-SIS have smaller MMS values than IG-SIS when Y is a balanced distribution, while IG-SIS has smaller MMS values than JS-SIS and AJS-SIS when Y is an unbalanced distribution. The performance indexes of JS-SIS and AJS-SIS are the same because the same number of slices is used for dividing all covariates. By comparing the two different distributions of Y, it is discovered that when Y is unbalanced, all methods' CP and CPa values are higher than when Y is balanced, and all methods' MMS values are lower. All approaches perform better when smaller slices are applied to continuous variables, according to comparisons between applications of various slice counts. In addition, it is evident from Simulation 3 that JS-SIS and AJS-SIS are capable of efficiently selecting significant variables, suggesting that they apply to data in which the covariates are all continuous.
4.2.4. Simulation 4
The response variables are set the same as in Simulation 1. There are two kinds of covariates: Continuous and categorical, and the treatment of continuous covariates is the same as in Simulation 3. The set of important variables is D={j=[j′p/20],j′=1,2,…,20}. To generate the covariates, the latent variables zi=(zi,1,…,zi,p) are first generated through the normal distribution by the same process as that used to generate the covariates in Simulation 3. We then refer to [23] and generate categorical and continuous covariates, where the first 1/4 of the covariates are four categorical, the middle 1/4 to 1/2 of the covariates are ten categorical, and the remaining 1/2 of the covariates are continuous. We take p=5000 and n=400,600,800.
As can be seen from Tables 7 and 8, the results of Simulations 4 and 3 are similar. Therefore, the simulation results for the specific analyzed sample size of n=400 are as follows: By comparing the performance of various methods used with various slice numbers, it is discovered that when Y is a balanced distribution, the CP and CPa values of the JS-SIS are smaller than those of the AJ-SIS and IG-SIS and fluctuate more, whereas those of the AJ-SIS and IG-SIS are the same and fluctuate much less. Regarding the MMS values, the MMS values of JS-SIS, although smaller than those of AJ-SIS and IG-SIS when the number of slices is large, fluctuate more, while the MMS values of AJ-SIS and IG-SIS are roughly the same size. By comparing two different distributions of Y, all methods perform better when Y is unbalanced than when Y is balanced, and all methods show better performance when the number of slices is small. And, as shown in Simulation 4, JS-SIS and AJS-SIS can effectively screen for significant variables, which means they are appropriate for data with both continuous and categorical covariates where the categories of the categorical variables differ.
4.3. Computational time cost
As the dimensionality of the data increases, the computational time also increases, so more efficient algorithms help to improve computational efficiency. We evaluated the computational time costs of the three methods. The median running time of each algorithm is obtained as a comparison index through simulation experiments, where the covariate X is set similarly to simulation experiment 2, and Y is set to a balanced distribution. The set of significant variables is D={j=[j′p/10],j′=1,2,…,10} such that 1/5 of the significant covariates are two categorical, 1/5 are four categorical, 1/5 are six categorical, 1/5 are eight categorical, and 1/5 are ten categorical. In this simulation experiment, the control sample size was constant at 400, the dimensionality of the covariates was increased from 1,000 to 10,000 at a rate of 1,000 per increase, and the experiment was repeated 100 times. Then, the median running time of the three methods in 100 experiments was calculated. All calculations were done on a Windows 10 computer with an Intel Core i7-8700 3.20 GHz CPU.
Table 9 shows the median values of the running time for the three methods, and it can be seen that, due to the linear variation of p, the running time also shows a linear trend of variation, increasing as p increases. The running times of the three methods do not differ much at low dimensions, and as p increases, the running times of JS-SIS and AJS-SIS are significantly shorter than those of IG-SIS. And, in every case, JS-SIS has the shortest run time, AJS-SIS has the second shortest run time, and IG-SIS has the longest run time.
4.4. Comprehensive analysis of simulation results
Overall, the suggested approaches' CP and CPa values are nearly equal to 1, the quartiles of MMS are nearly at the model size of the real essential variables, and the standard deviations of CP, CPa, and computation time are close to 0. This indicates that: (1) our suggested methods are efficient at screening significant variables; (2) they are very stable; (3) it is feasible to represent the methods' performance using the average of the indexes; (4) they perform well with a broad range of data types and can be applied to situations where the data contain categorical covariates with the same categories, categorical covariates with different categories, continuous covariates, and both continuous and categorical covariates appearing in the data, where the categories of the categorical covariates differ.
The specific analysis is as follows: The JS-SIS and AJS-SIS methods proposed in this paper are very similar to IG-SIS in terms of performance. When the sample size is small, there is a difference in performance between the methods, and the performance of JS-SIS is affected more by the number of slices compared to AJ-SIS and IG-SIS, which are more adaptive to the number of slices and are more robust. However, the performance of all techniques converges to the same as the number of screening variables or sample size grows. Both CP and CPa increase and converge to 1, the MMS value gets closer to d0=10, and all method performances are independent of the distribution of the response variable Y and the number of slices.
5.
Real data analysis
5.1. Experimental study with real data
5.1.1. Data description
To assess our proposed method, two popular public datasets [24,25] for cancer classification were utilized. The two datasets are high-dimensional, the variables are of continuous type, and the response variables are binary with values of 0 (normal) and 1 (cancer). The first is the prostate cancer dataset, where the distribution of response variables is roughly balanced, and the second is the B-cell lymphoma dataset, where the distribution of response variables is roughly unbalanced. Details about the two datasets are listed in Table 10.
5.1.2. Performance evaluation criteria
The dataset is divided into two parts using a 7:3 random ratio, with 70% of the data used as the training dataset and the other 30% as the test dataset. Then, the number of slices Jk=4,8,10 is taken to slice the continuous covariates in the training set, respectively. This process can also be thought of as cross-validation, whereby we choose the number of slices at which the methods perform optimally as the optimal categories for the continuous variable. On the training set, variables were screened using the JS-SIS, AJS-SIS, and IG-SIS screening approaches; on the test set, support vector machines were used to assess how well the variables were classified using these techniques. We utilized ten-fold cross-validation to reduce the impact of randomly divided data in the dataset on the model accuracy and repeated it 100 times while testing the classification effect to reduce the random error.
We used two evaluation indexes to assess classification effectiveness: Classification accuracy (CA) and the geometric mean (G-mean) of specificity (SPE) and sensitivity (SEN).
5.1.3. Results and discussion
Tables 11 and 12 show the categorization effects of the variables screened by applying the JS-SIS, AJS-SIS, and IG-SIS methods to the two datasets, respectively. CA1 (G-mean1) and CA2 (G-mean2) denote the index values when the number of screening variables is the first [n/logn] and the first 2[n/logn], respectively.
Table 11 shows the experimental results for the Prostate dataset. Comparison of the categorical prediction performance of the three methods when screening different numbers of variables for each method is as follows: When the number of screening variables is [n/logn], all three methods have similar CA and G-mean values for the same number of slices, while when the number of screening variables is 2[n/logn], JS-SIS has significantly higher CA and G-mean values than AJS-SIS and IG-SIS for the same number of slices, and the CA and G-mean values of AJS-SIS and IG-SIS are the same. Then, comparing the categorical prediction performance of the three methods for variables screened in different numbers of slices, it is found that the fluctuation of CA and G-mean values with the number of slices is higher in JS-SIS than in AJS-SIS and IG-SIS, while the fluctuation of CA and G-mean values is about the same in AJS-SIS and IG-SIS. Overall, JS-SIS is more impacted by the number of screens and slices than IG-SIS is, and AJS-SIS and IG-SIS are both impacted in a similar way. Moreover, regarding the performance of the categorical prediction accuracy of the screened variables, JS-SIS outperforms AJS-SIS and IG-SIS as the number of variables screened increases, while AJS-SIS and IG-SIS perform almost as well.
The experimental findings for the DLBCL dataset are displayed in Table 12. Comparing the categorical prediction performance of the three methods with different numbers of variables screened separately, the CA and G-mean values of the three methods are significantly different when the number of screened variables is [n/logn], respectively. However, when the number of screened variables is 2[n/logn], AJS-SIS's CA and G-mean values are significantly higher than those of JS-SIS and IG-SIS, while JS-SIS and IG-SIS were also significantly different. Comparing the categorical prediction performance of the three methods for variables screened in different numbers of slices, the fluctuations of CA and G-mean values are the largest for JS-SIS, while the fluctuations of CA and G-mean values for AJS-SIS are smaller than for IG-SIS. JS-SIS and AJS-SIS are both more and less affected by the number of screenings and slices, respectively, as compared to IG-SIS. AJS-SIS outperforms JS-SIS and IG-SIS in terms of the categorical prediction accuracy of the screened variables.
5.1.4. Comprehensive analysis of real experimental results
Combining the experimental results of the two real datasets, it can be seen that the methods JS-SIS and AJS-SIS proposed in this paper are very similar to IG-SIS in terms of performance, but AJS-SIS is more robust in terms of performance than JS-SIS and IG-SIS, where JS-SIS is a little bit weaker in terms of robustness compared to IG-SIS. Further, all methods perform better in the Prostate dataset than in the DLBCL dataset. This may be because the DLBCL dataset variables have larger dimensions than the Prostate dataset variables, but smaller sample sizes than the Prostate dataset variables, which may make it more challenging to screen the DLBCL dataset variables. Finally, the predictive effectiveness of the variables screened by all methods improved with the number of variables screened. Overall, experiments with real data illustrate that our methods can be applied to real datasets.
5.2. Applying methods to real data
Based on both numerical simulations and experiments with real data, it is shown that the methods proposed in this paper are well able to screen out important variables. Thus, in this section, we use a biological dataset with detailed information to further explore the specifics of the suggested approaches for screening variables in practical applications. This dataset is available from the R package "colonCA" (https://bioconductor.org/packages/release/data/experiment/html/colonCA.html). Table 13 displays detailed information about the dataset. The sample categories in this dataset are binary variables, and the gene variables are continuous.
The results of earlier experiments indicate that good results can be obtained when the number of variables screened is [n/logn]. For this reason, we select the essential variables as [n/logn] when applying the real dataset. Then, the training set and test set were divided in the same manner as the real-data experiments in Section 5. The significant gene variables were screened on the training set using the IG-SIS method and our suggested approaches, with the results displayed in Tables 14 and 15, respectively. Lastly, the test set is utilized to examine the classification effect of the selected gene variables, as shown in Table 16.
As can be observed from Tables 14 and 15, "Hsa.549" and "Hsa.6814" are the same gene variables among the [n/logn] gene variables selected by each technique at Jk=4,8,10, indicating that they might be the most significant gene variables. Then, according to Table 16, from the perspective of data analysis, it is evident that the Colon dataset exhibits optimal performance for the JS-SIS and AJS-SIS methods at Jk=4, and optimal performance for IG-SIS at Jk=8. Generally, the important gene variables selected by the proposed methods have good classification prediction performance, indicating the utility of the proposed methods.
6.
Conclusions
In this research, we established a model-free feature screening procedure based on JS divergence for binary categorical response variables, implying less restrictive data assumptions. We also suggested two different feature screening techniques for binary response variables in various scenarios. When the number of categories for each covariate is the same, the method based on JS divergence is used. Additionally, when the number of categories in each covariate is different, we investigated the AJ-SIS method for screening variables, which uses the logarithmic factor of the number of categories to adjust the JS divergence, which is used for feature screening. Afterward, theoretical proof showed that JS-SIS and AJS-SIS have sure screening and ranking consistency properties. Then, the screening performance of the proposed methods was evaluated through simulation experiments and real data analysis, which showed their effectiveness, availability, and practicality. It is also evident that a variety of data may be widely applicable to our suggested approaches and that they have good screening performance when the data contains categorical covariates, continuous covariates, and both continuous and categorical covariates appearing in the data. We suggested experimenting with several different numbers of slices and applying cross-validation to determine the optimal categories for continuous variables when dealing with continuous covariates. We can see that, in feature screening, the performance of the proposed methods JS-SIS and AJS-SIS in this paper is similar to IG-SIS. But, AJS-SIS performs better than IG-SIS when the covariates have a varying number of categories, particularly when the sample size is small. Moreover, in terms of computational time, JS-SIS and AJS-SIS are both shorter than IG-SIS. In addition to this, our method's perspective is appealing, and since JS divergence does not require the probability distributions to be absolutely continuous and has the advantages of symmetry, non-negativity, and boundedness, it can measure the differences between probability distributions very effectively. Finally, the methods proposed in this work only take into account situations when the response variable is binary, although, in reality, multicategorical responses are very frequent. Therefore, we will extend JS-SIS and AJS-SIS to situations in which the response variable is multicategorical in our future research.
Use of AI tools declaration
The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.
Acknowledgments
The National Natural Science Foundation of China [grant number 71963008] funded this research.
The authors would like to thank the editor and anonymous referees for their constructive comments and suggestions.
Conflict of interest
The author certifies that the publication of this paper does not involve any conflicts of interest.
Appendix
To prove Theorem 3.1, the following four lemmas are first introduced.
Lemma 1. Suppose that x1,x2,…,xn are mutually independent random variables with sample size n and Pr(xi∈[ai,bi])=1,1≤i≤n, where ai, bi are constants. Let ˉx=1/n∑ni=1xi. Then there exists a constant t for which the following inequality holds:
The proof of Lemma 1 is given in [26].
Lemma 2. Suppose a and b are two bounded random variables, and there exist constants M1>0,M2>0 such that |a|≤M1,|b|≤M2. Given a sample size n, the estimates corresponding to a,b can be obtained as ˆA,ˆB. Suppose that, ∀ε∈(0,1), there exist positive constants c1,c2 and s such that
Then, we have
where, C1=max{2c1+c2,c1+2c2+2c2M1,2c2M2}, C2=max{3c1+2c1M1,2c2M2}, C3=max{2c1,2c2,c1+c2}.
Furthermore, assuming that b is bounded and non-zero, and that there exists M3>0 such that |b|≥M3, then we have
where C4=max{c1+c2+c5,c2/M4,2c2M1/(M2M4)}, c5>0 and M4>0.
The proof of Lemma 2 is given in [15].
Lemma 3. When the covariates are categorical, we know that ej≥0. Only if Pr(xj=l∣Y=1)=Pr(xj=l∣Y=2), we have ej=0, that is, Y and xj are independent.
Proof of Lemma 3: Let G=Pr(xj=l∣Y=1), Q=Pr(xj=l∣Y=2), M=12(G+Q). Define f(x)=xlog(x). Since f(x) is a hypoconvex function, and through Jensen's inequality, we can get
Thus,
So, ej is larger than or equal to 0. The equation holds if and only if G=Q. And, when G=Q,
By the condition of independence, it can be inferred that Y and xj are independent. Thus, when there is a nonlinear relationship between Y and xj, the conditional probability distribution between them will not satisfy independence, and thus the JS divergence will be larger than zero.
Lemma 4. When the covariates are continuous, it follows from the proof of Proposition 2.2 in [16] that for a continuous variable X, there exists a sequence {xm,m=1,2,…} such that xm is a quantile of X and limn→∞xm=X, and there exist Jk and J such that x=q(J). Then, Pr(X≤x∣Y=r)=J/Jk does not depend on r. There is ej≥0, and when Y and xj are independent, ej=0.
The proof of Lemma 4 is similar to the proof of Proposition 2.2 in [16], so it is omitted here.
Proof of Theorem 3.1:
According to the definitions of ej and ˆej we have
and
Next, we prove that Ej1≤2Lexp{−nε2/2L2}.
Using the sample frequency to estimate the probability, we have
So, we have
and because Sn, Tn is an estimate of sn, tn, it follows from Lemmas 1 and 2 that
Thus, there is a convergence of ˆp(xj=l∣Y=1) by probability to its probability function p(xj=l∣Y=1), that is
Similarly, ˆp(xj=l∣Y=2) also converges to p(xj=l∣Y=2).
It can also be shown that log(ˆp(xj=l∣Y=1)) converges probabilistically to log(p(xj=l∣Y=1)). Let ˆp∗=ˆp(xj=l∣Y=1), p∗=p(xj=l∣Y=1):
Thus, we can get that log(ˆp(xj=l∣Y=1)) converges to log(p(xj=l∣Y=1)) with probability.
In a similar proof, we can get that log(ˆp(xj=l∣Y=2)) converges to log(p(xj=l∣Y=2)) with probability and log(ˆp(xj=l∣Y=1)+ˆp(xj=l∣Y=2)2) converges to log(p(xj=l∣Y=1)+p(xj=l∣Y=2)2) with probability.
Thus, we can obtain Ej1≤2Lexp{−nε2/2L2}. Similarly, the other three parts can be proved: Ej2≤2Lexp{−nε2/2L2}, Ej3≤2Lexp{−nε2/2L2}, Ej4≤2Lexp{−nε2/2L2}.
Thus, for 0<ϵ4<1, there is
For 0≤τ<1/2, there exists a positive number c with
and then
By (3), for 0<δ<1−2τ, we have
with n→∞. Thus, by (4), we have
Therefore, Pr(D⊆ˆD)→1, with n→∞.
Thus, by Theorem 3.1 the sure screening property holds under conditions (C1)–(C3).
Proof of Theorem 3.4:
Since minj∈Dej−maxj∈Dcej>0, there exists δ>0 such that minj∈Dej−maxj∈Dcej=δ, and then we have
From Fatou's Lemma, we have
So,
Thus, Theorem 3.4 holds.
Proof of Theorem 3.2: Let Fk(x∣y) be the cumulative distribution function of (Xk,Y) and ˆFk(x∣y) be the empirical cumulative distribution function of (Xk,Y). Then, by the proof of Lemma A.2 in [16], we can similarly show that, under conditions (C4) and (C5), ∀ϵ5>0,1≤r≤R,1≤J≤Jk, we have
where c6=3c8 and c7=min{1/2,c24/2c23} are positive constants.
Thus, ˆFk(ˆqk,(J)∣r) converges to Fk(qk,(J)∣r) with probability. The proof of the other parts is the same as in Theorem 3.1. Then, for 0<ϵ6<1, we have
Equation (7) is similar to the proof process of Eq (1) and will not be proved here.
Under condition (C6), there exists a constant c5 such that
With n→∞, we have
Therefore, Pr(D⊆ˆD)→1, n→∞.
Thus, the proof of Theorem 3.5 is similar to that of Eq (6), and we have
Theorems 3.3 and 3.6 combine Theorems 3.1, 3.2, 3.4 and 3.5, and the proof process is similar to them, so they will not be proven in detail.









 DownLoad:
DownLoad: