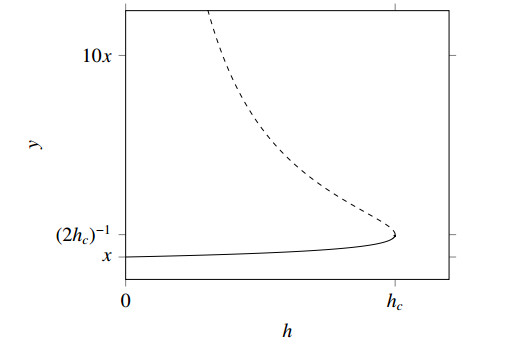
Implicit methods for the numerical solution of initial-value problems may admit multiple solutions at any given time step. Accordingly, their nonlinear solvers may converge to any of these solutions. Below a critical timestep, exactly one of the solutions (the consistent solution) occurs on a solution branch (the principal branch) that can be continuously and monotonically continued back to zero timestep.
Standard step-size control can promote convergence to consistent solutions by adjusting the timestep to maintain an error estimate below a given tolerance. However, simulations for symplectic systems or large physical systems are often run with constant timesteps and are thus more susceptible to convergence to inconsistent solutions. Because simulations cannot be reliably continued from inconsistent solutions, the critical timestep is a theoretical upper bound for valid timesteps.
1.
Introduction
In the general framework, Caputo and Fabrizio [1] proposed a new fractional derivative now called Caputo-Fabrizio (CF) fractional derivative in 2015. Compared with previous Riemann-Liouville (RL) and Riemann-Caputo (RC) fractional derivatives, this derivative has exponential kernel and non-singularity. The following comparison will reflect their differences. As we all know, when 0<γ<1, (t−τ)−γ and e−γ1−γ(t−τ) are the kernels of RC- and CF-fractional derivative with γ-order, respectively. Decidedly, (t−τ)−γ→∞ (singular) and e−γ1−γ(t−τ)→1 (non-singular), as τ→t. In other words, CF-fractional derivative has unique advantages in eliminating singularity. Therefore, many scholars have carried out detailed and in-depth research on the CF-fractional differential equation. For example, some of them have applied CF-fractional differential equations to describe closed groundwater flows [2], population dynamics [3,4], electrical circuit [5,6], epidemics [7,8,9] and others [10,11,12]. There have been some papers dealing with some theoretical problems of CF-fractional calculus. Tarasov [13] explored whether CF-fractional derivative operators represent memory or distributed-delay from the definition of CF-fractional derivative. Pan [14] studied the chaotic behavior of a four dimensional CF-fractional differential system. Zhang [15] investigated the exponential Euler schemes for numerical solutions of CF-fractional differential equation. Tariq et al. [16] obtained the new fractional integral inequalities for CF-fractional integral operators. Abbas et al. [17] studied a fractional differential equations with non instantaneous impulses. They applied measures of noncompactness and two fixed point theorems to obtain the existence of solutions. In addition, the study of Hilfer fractional differential equations as a generalization of fractional derivatives is one of the recent focuses. Alsaedi et al. [18] considered a ψ-Hilfer fractional integral boundary value problem with the p-Laplacian operator. The authors studied the existence and uniqueness of solutions by using Banach's contraction mapping principle. Zhou and He [19,20] studied the mild solutions to two fractional evolution equations by analytic semigroup theory.
In 1940s, Hyers and Ulam [21,22] put forward a new stability named Ulam and Hyers (UH) stability. After in-depth analysis of the UH-stability structure, some researchers have extended the concept of UH-stability, such as generalized UH-stability, Ulam-Hyers-Rassias stability, generalized Ulam-Hyers-Rassias, etc. The study on the UH-type stability of various dynamic systems has received great attention. Of course, the UH-type stability of fractional differential systems is also favored. There have been many papers dealing with UH-type stability of fractional differential system (see some of them [23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38,39]). However, there are rare works on the UH-type stability of CF-fractional differential system. It is worth to inquire into the stability of system with CF-fractional derivatives. In addition, when describing complex systems affected by many factors, fractional differential equations are more detailed and accurate than a single fractional differential equation. However, the study of the former is much more difficult than the latter. As far as I am concerned, there are no papers combining CF-fractional derivative with coupling Laplacian system, which is an interesting and challenging problem. Therefore, we emphasize on the below nonlinear CF-fractional coupled Laplacian equations
where a1,a2,b1,b2∈R, l>0, 0<μ1,μ2,ν1,ν2≤1 and p1,p2>1 are some constants, CFD∗0+ stands for the ∗–order Caputo-Fabrizio (CF) fractional derivative. Φpj(z)=|z|pj−2z(j=1,2) is pj–Laplacian. It is well known that the inverse of Φpj is Φqj, and 1pj+1qj=1, j=1,2. The nonlinear function Fj∈C([0,l]×R2,R), j=1,2.
This manuscript focuses on the solvability and stability of (1.1). In Section 2, we need to review some necessary knowledge of CF-fractional calculus. In Section 3, we apply the contraction mapping principle to prove that system (1.1) has a unique solution. We further established the GUH-stability of the system (1.1) in Section 4. Section 5 provides an example to illustrate the correctness of our major outcomes. We make a brief conclusion in Section 6.
2.
Preliminaries
In this section, we first need to introduce the definitions of CF-fractional derivative and integral and some basic properties of p-Laplacian operator.
Definition 2.1. [40] For 0≤α≤1, l>0 and U∈H1(0,l), the left–sided α–order Caputo–Fabrizio fractional integral of function U is defined by
where N(α) is a normalisation constant with N(0)=N(1)=1.
Definition 2.2. [1] For 0≤α≤1, l>0 and U∈H1(0,l), the left–sided α–order Caputo–Fabrizio fractional derivative of U is defined by
Lemma 2.1. [40] Let 0≤α≤1 and H∈C[0,∞). Then the unique solution of the following IVP
is expressed as
Lemma 2.2. Let p>1. The p–Laplacian operator Φp(z)=|z|p−2z admits the properties as follows:
(i) If z≥0, then Φp(z)=zp−1, and Φp(z) is increasing with respect to z;
(ii) For all z,w∈R, Φp(zw)=Φp(z)Φp(w);
(iii) If 1p+1q=1, then Φq[Φp(z)]=Φp[Φq(z)]=z, for all z∈R;
(iv) For all z,w≥0, z≤w⇔Φq(z)≤Φq(w);
(v)0≤z≤Φ−1q(w)⇔0≤Φq(z)≤w;
(vi)|Φq(z)−Φq(w)|≤{(q−1)¯Mq−2|z−w|, q≥2,0≤z,w≤¯M; (q−1)M_q−2|z−w|, 1<q<2,z,w≥M_≥0.
The following lemma is crucial to establishing our main results later.
Lemma 2.3. Let a1,a2,b1,b2∈R, l>0, 0<μ1,μ2,ν1,ν2≤1 and p1,p2>1 are some constants, Fj∈C([0,l]×R2,R), j=1,2. Then the nonlinear CF–fractional coupled Laplacian Eq (1.1) is equivalent to the following integral equations
where 1pj+1qj=1(j=1,2), and
Proof. Assume that (U1(t),U2(t))∈C([0,l],R)×C([0,l],R) satisfies the Eq (1.1). Then, from Lemma 2.1 and the first equation of (1.1), we have
It follows from (2.2) and (iii) in Lemma 2.2 that
where 1p1+1q1=1, p1>1. Denote G1(t,U1(t),U2(t)) by
Combined (2.3), (2.4) and Lemma 2.1, we obtain
Similar to (2.2)–(2.5), one derives from the second equation of (1.1) that
where 1p2+1q2=1,p2>1, and
Substituting the initial value conditions U1(0)=a1, U2(0)=a2, CFDμ10+U1(0)=b1 and CFDμ20+U2(0)=b2 into (2.4)–(2.7), one easily gets (2.1), that is, (U1(t),U2(t))∈C([0,l],R)×C([0,l],R) is a solution of the integral equations (2.1). Noticing that z→Φp(z) is reversible, one knows that the above derivation is completely reversible. Vice versa, if (U1(t),U2(t))∈C([0,l],R)×C([0,l],R) is the solution of the integral Eq (2.1), then it is also a solution of (1.1). The proof is completed.
3.
Existence and uniqueness of solution
This section mainly applies the contraction mapping principle to discuss the existence and uniqueness of solution to (1.1).
Lemma 3.1. (contraction mapping principle [41]) Let X be a Banach space and ϕ≠E⊂X be closed. If T:E→E is contract, then T admits a unique fixed point u∗∈E.
According to Lemma 2.3, we take X=C([0,l],R)×C([0,l],R). For all w=(u,v)∈X, define the norm ‖w‖=‖(u,v)‖=max{sup0≤t≤l|u(t)|,sup0≤t≤l|v(t)|}, then (X,‖⋅‖) is a Banach space. Subsequently, we will inquire into the solvability and stability of (1.1) on (X,‖⋅‖). For convenience, we introduce the following conditions and symbols.
(H1)a1≠0 or a2≠0, l,b1,b2>0, 0<μ1,μ2,ν1,ν2≤1 and p1,p2>1 are some constants, Fj∈C([0,l]×R2,R), j=1,2.
(H2) For all t∈[0,l], u,v∈R, there exist some constants mj,Mj>0 such that
(H3) For all t∈[0,l], u,¯u,v,¯v∈R, there exist some continuous functions Lj1(t), Lj2(t)≥0 such that
Denote
In this position, we present one of our main results as follows.
Theorem 3.1. Assume that (H1)–(H3) and Mj_>0(j=1,2) are true. Further assume that one of the conditions holds as follows: when q1,q2≥2, ¯κ1,¯κ2<1; or q1≥2,1<q2<2, ¯κ1,κ2_<1; or 1<q1<2,q2≥2, κ1_,¯κ2<1; or 1<q1,q2<2, κ1_,κ2_<1. Then system (1.1) has a unique nonzero solution (U∗1(t),U∗2(t))∈X.
Proof. (U1(0),U2(0))=(a1,a2)≠(0,0) indicates (\mathcal{U}_1(t), \mathcal{U}_2(t))\not\equiv(0, 0), \, \forall t\in[0, l] , that is, the solution of (1.1) is nonzero. For all (\mathcal{U}_1, \mathcal{U}_2)\in\mathbb{X} , based on Lemma 2.3, we define the vector operator \mathscr{T}:\mathbb{X}\to\mathbb{X} as
where
G_1(t, \mathcal{U}_1(t), \mathcal{U}_2(t)) and G_2(t, \mathcal{U}_1(t), \mathcal{U}_2(t)) are the same as (2.1).
For all \mathcal{U} = (\mathcal{U}_1, \mathcal{U}_2) and t\in[0, l] , we derive from (2.1), (\mathrm{H}_1) and (\mathrm{H}_2) that
and
Obviously, \underline{\mathcal{M}_1}\leq\overline{\mathcal{M}_1} , \underline{\mathcal{M}_2}\leq\overline{\mathcal{M}_2} . Thus, for all \mathcal{U} = (\mathcal{U}_1, \mathcal{U}_2) , \overline{\mathcal{U}} = (\overline{\mathcal{U}}_1, \overline{\mathcal{U}}_2)\in\mathbb{X} , and t\in[0, l] , it follows from (3.2), (3.4), (3.5), (\mathrm{H}_3) and (\mathrm{vi}) of Lemma 2.2 that
When q_1\geq2 , (3.8) gives
When 1 < q_1 < 2 , similar to (3.9), (3.8) leads
It is similar to (3.8)–(3.10) that
and
From (3.9)–(3.12), we obtain
Let \kappa_j\in\{\overline{\kappa_j}, \underline{\kappa_j}\}, j = 1, 2 , then 0 < \max\{\kappa_1, \kappa_2\} < 1 . So (3.13) means that \mathscr{T}:\mathbb{X}\to\mathbb{X} is contractive. Hence, we conclude from Lemma 3.1 and Lemma 2.2 that \mathscr{T} has a unique fixed point \mathcal{U}^*(t) = (\mathcal{U}_1^*(t), \mathcal{U}_2^*(t))\in\mathbb{X} , which is the solution of (1.1). The proof is completed.
4.
GUH-stability
In the portion, we mainly discuss the GUH-stability of (1.1) by direct analysis methods. We first give the definitions of UH- and GUH-stability corresponding to problem (1.1) as follows.
Let \mathcal{U} = (\mathcal{U}_1, \mathcal{U}_2)\in \mathbb{X} and \epsilon > 0 . Consider the following inequality
Definition 4.1. Assume that, \forall\, \epsilon > 0 and \forall\, \mathcal{U} = (\mathcal{U}_1, \mathcal{U}_2)\in \mathbb{X} satisfying (4.1), there exist a unique \mathcal{U}^* = (\mathcal{U}_1^*, \mathcal{U}_2^*)\in \mathbb{X} satisfying (1.1) and a constant \omega_1 > 0 such that
then problem (1.1) is called Ulam-Hyers (UH) stable.
Definition 4.2. Assume that, \forall\, \epsilon > 0 and \forall\, \mathcal{U} = (\mathcal{U}_1, \mathcal{U}_2)\in \mathbb{X} satisfying (4.1), there exist a unique \mathcal{U}^* = (\mathcal{U}_1^*, \mathcal{U}_2^*)\in \mathbb{X} satifying (1.1) and \vartheta\in C(\mathbb{R}, \mathbb{R}^+) with \vartheta(0) = 0 such that
then problem (1.1) is called generalized Ulam-Hyers (GUH) stable.
Remark 4.1. \mathcal{U} = (\mathcal{U}_1, \mathcal{U}_2)\in \mathbb{X} is a solution of inequality (4.1) iff there exists \phi = (\phi_1, \phi_2)\in \mathbb{X} such that
(1) \; |\phi_1(t)|\leq\epsilon , and |\phi_2(t)|\leq\epsilon , 0 < t\leq l;
(2) \; ^{\mathrm{CF}}\mathcal{D}_{0^+}^{\nu_1}\big[\Phi_{p_1}(\, ^{\mathrm{CF}}\mathcal{D}_{0^+}^{\mu_1}\mathcal{U}_1(t))\big] = F_1(t, \mathcal{U}_1(t), \mathcal{U}_2(t)) +\phi_1(t), \, \, 0 < t\leq l;
(3) \; ^{\mathrm{CF}}\mathcal{D}_{0^+}^{\nu_2}\big[\Phi_{p_2}(\, ^{\mathrm{CF}}\mathcal{D}_{0^+}^{\mu_2}\mathcal{U}_2(t))\big] = F_2(t, \mathcal{U}_1(t), \mathcal{U}_2(t)) +\phi_2(t), \, \, 0 < t\leq l;
(4) \; \mathcal{U}_1(0) = a_1, \, \mathcal{U}_2(0) = a_2, \, ^{\mathrm{CF}}\mathcal{D}_{0^+}^{\mu_1}\mathcal{U}_1(0) = b_1, \, ^{\mathrm{CF}}\mathcal{D}_{0^+}^{\mu_2}\mathcal{U}_2(0) = b_2.
Theorem 4.1. If all conditions of Theorem 3.1 hold, then problem (1.1) is GUH-stable.
Proof. Based on Lemma 2.3 and Remark 4.1, the inequality (4.1) is solved by
According to Theorem 3.1 and Lemma 2.3, the unique solution \mathcal{U}^*(t) = (\mathcal{U}_1^*(t), \mathcal{U}_2^*(t))\in\mathbb{X} of (1.1) satisfies (2.1). For all \epsilon > 0 ( \epsilon small enough), from (\mathrm{H}_1) , (\mathrm{H}_2) and (1) of Remark 4.1, it similar to (3.4)–(3.7) that
and
Clearly, 0 < \underline{\mathcal{M}_1}(\epsilon) < \underline{\mathcal{M}_1} < \overline{\mathcal{M}_1} < \overline{\mathcal{M}_1}(\epsilon) , 0 < \underline{\mathcal{M}_2}(\epsilon) < \underline{\mathcal{M}_2} < \overline{\mathcal{M}_2} < \overline{\mathcal{M}_2}(\epsilon) .
Similar to (3.8) and (3.9), when q_1\geq2 , we derive from (2.1), (4.2), (4.3) and (4.5) that
where \overline{\Upsilon_1}(\epsilon) = \Theta_1(q_1-1)\overline{\mathcal{M}_1}(\epsilon)^{q_1-2}(\|\mathcal{L}_{11}\|_l+\|\mathcal{L}_{12}\|_l) , \overline{\Delta_1}(\epsilon) = \Theta_1(q_1-1)\overline{\mathcal{M}_1}(\epsilon)^{q_1-2} .
Analogy to (4.9), we apply (4.6)–(4.8) to obtain
and
where \overline{\Upsilon_2}(\epsilon) = \Theta_2(q_2-1)\overline{\mathcal{M}_2}(\epsilon)^{q_2-2}(\|\mathcal{L}_{21}\|_l+\|\mathcal{L}_{22}\|_l) , \underline{\Upsilon_1}(\epsilon) = \Theta_1(q_1-1)\underline{\mathcal{M}_1}(\epsilon)^{q_1-2}(\|\mathcal{L}_{11}\|_l+\|\mathcal{L}_{12}\|_l) , \underline{\Upsilon_2}(\epsilon) = \Theta_2(q_2-1)\underline{\mathcal{M}_2}(\epsilon)^{q_2-2}(\|\mathcal{L}_{21}\|_l+\|\mathcal{L}_{22}\|_l) . \overline{\Delta_2}(\epsilon) = \Theta_2(q_2-1)\overline{\mathcal{M}_2}(\epsilon)^{q_2-2} , \underline{\Delta_1}(\epsilon) = \Theta_1(q_1-1)\underline{\mathcal{M}_1}(\epsilon)^{q_1-2} , and \underline{\Delta_2}(\epsilon) = \Theta_2(q_2-1)\underline{\mathcal{M}_2}(\epsilon)^{q_2-2} .
For all \epsilon > 0 ( \epsilon small enough), we have 0 < \overline{\Upsilon_1}(\epsilon), \underline{\Upsilon_1}(\epsilon), \overline{\Upsilon_2}(\epsilon), \underline{\Upsilon_2}(\epsilon) < 1 . Take \Upsilon_j(\epsilon)\in\{\overline{\Upsilon_j}(\epsilon), \underline{\Upsilon_j}(\epsilon)\} , and \Delta_j(\epsilon)\in\{\overline{\Delta_j}(\epsilon), \underline{\Delta_j}(\epsilon)\} , j = 1, 2 , then it follows from (4.9)–(4.12) that
Therefore, we know from (4.13) and Definition 4.2 that problem (1.1) is GUH-stable. The proof is completed.
5.
An illustrative example
The purpose of this section is to verify the correctness and applicability of our main results through an illustrative example.
To do so, consider the following specific nonlinear CF-fractional coupled Laplacian system
Obviously, l = 1 , \mu_1 = 0.7 , \nu_1 = 0.4 , \mu_2 = 0.3 , \nu_2 = 0.8 , a_1 = -1 , a_2 = b_1 = b_2 = 1 , F_1(t, u, v) = \frac{2+\cos(u)}{100}+\frac{1}{50}|\sin(t)|\frac{v}{1+v^2} , F_2(t, u, v) = \frac{2+\sin(3t)}{100}[\frac{3\pi}{4}+\arctan(u+v)] . Take \mathfrak{N}(x) = 1-x+\frac{x}{\Gamma(x)}, 0 < x\leq1 , then \mathfrak{N}(0) = \mathfrak{N}(1) = 1 . By a simple calculation, we have
Thus, the conditions (\mathrm{H}_1) – (\mathrm{H}_3) are true. Consequently, m_1 = \frac{1}{100} , M_1 = \frac{4}{100} , m_2 = \frac{\pi}{400} , M_2 = \frac{15\pi}{400} , \mathcal{L}_{11}(t) = \frac{1}{100} , \mathcal{L}_{12}(t) = \frac{|\sin(t)|}{100} , \mathcal{L}_{21}(t) = \mathcal{L}_{22}(t) = \frac{2+\sin(3t)}{100} , \|\mathcal{L}_{11}\|_l = \frac{1}{100} , \|\mathcal{L}_{12}\|_l = \frac{\sin(1)}{100} , \|\mathcal{L}_{21}\|_l = \|\mathcal{L}_{22}\|_l = \frac{3}{100} , and
Case 1: When p_1 = \frac{3}{2} , p_2 = \frac{5}{4} , then q_1 = 3 > 2 , q_2 = 5 > 2 , and
Thus, all conditions of Theorem 3.1 are fulfilled. From Theorem 3.1 and Theorem 4.1, we claim that system (5.1) has a unique solution and is GUH-stable.
Case 2: When p_1 = \frac{3}{2} , p_2 = 5 , then q_1 = 3 > 2 , 1 < q_2 = \frac{5}{4} < 2 , and the values of \underline{\mathcal{M}_1} , \underline{\mathcal{M}_2} , \overline{\mathcal{M}_1} , \overline{\mathcal{M}_2} and \overline{\kappa_1} are same as Case 1, as well as
Thus, all conditions of Theorem 3.1 are fulfilled. From Theorem 3.1 and Theorem 4.1, we claim that system (5.1) has a unique solution and is GUH-stable.
Case 3: When p_1 = 3 , p_2 = \frac{5}{4} , then 1 < q_1 = \frac{3}{2} < 2 , q_2 = 5 > 2 , and the values of \underline{\mathcal{M}_1} , \underline{\mathcal{M}_2} , \overline{\mathcal{M}_1} , \overline{\mathcal{M}_2} and \overline{\kappa_2} are same as Case 1, as well as
Thus, all conditions of Theorem 3.1 are fulfilled. From Theorem 3.1 and Theorem 4.1, we claim that system (5.1) has a unique solution and is GUH-stable.
Case 4: When p_1 = 3 , p_2 = 5 , then 1 < q_1 = \frac{3}{2} < 2 , 1 < q_2 = \frac{5}{4} < 2 , and the values of \underline{\mathcal{M}_1} , \underline{\mathcal{M}_2} , \overline{\mathcal{M}_1} , \overline{\mathcal{M}_2} , \underline{\kappa_1} and \underline{\kappa_2} are same as Cases 1–3. Thus, all conditions of Theorem 3.1 are fulfilled. From Theorem 3.1 and Theorem 4.1, we claim that system (5.1) has a unique solution and is GUH-stable.
6.
Conclusions
The integer order differential equation with p -Laplacian is a class of special second-order ordinary differential equations that have been extensively and deeply studied. Some scholars have also conducted some research on Riemann-Liouville or Caputo fractional differential equations with p -Laplacian. However, the study on CF-fractional differential equations p -Laplacian has not been seen so far. Therefore, it is novel and interesting for us to choose the system (1.1) as the research object. We establish the existence, uniqueness, and GUH-stability of the solution for problem (1.1) by using the Banach's contraction mapping principle and the direct analysis method. From the proof of Lemma 2.3 and Theorem 3.1, it can be seen that our difficulty lies in establishing the integral equation corresponding to system (1.1) and verifying the contractility of vector operator \mathscr{T} defined by (3.1)–(3.3). The methods and steps used in this manuscript can be summarized as follows: (i) Convert differential system (1.1) to integral system (2.1); (ii) Define an operator \mathscr{T} according to integral system (2.1); (iii) Prove that the operator \mathscr{T} is contractive. The above methods and steps can be used for reference in the study of other types of fractional differential equations. In addition, illuminated by some of the latest achievements [42,43,44,45,46,47,48], we intend to apply fractional calculus theory and diffusion partial differential equation theory to the study of some ecosystems in the future.
Acknowledgments
The author would like to express his heartfelt gratitude to the editors and reviewers for their constructive comments. The APC was funded by research start-up funds for high-level talents of Taizhou University.
Conflict of interest
All authors declare that they have no competing interests.













 DownLoad:
DownLoad: