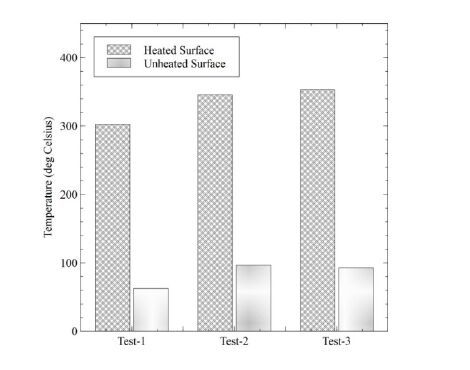
This study details a fabrication methodology envisaged to manufacture Glass/BMI honeycomb core aerogel-filled sandwich panels. Silica aerogel granules are used as core fillers to provide thermal insulation properties with little weight increase. Experimental heat transfer studies are conducted on these panels to study the temperature distribution between their two surfaces. Numerical studies are also carried out to validate the results. Despite exhibiting good thermal shielding capabilities, the Glass/BMI sandwich panels are found to oxidise at 180 ºC if exposed directly to heat. In order to increase the temperature bearing capacity and the operating temperature range for these panels, a way of coating them from outside with high temperature spray paint was tried. With a silicone-based coating, the temperature sustainability of these sandwich panels is found to increase to 350 ºC. This proved the effectiveness of the formed manufacturing process, selected high temperature coating, the coating method as well as the envisaged sandwich panel concept.
1.
Introduction
In this research, we mainly focused on wave equation to study and examine the coupled system. In this system, we assumed a bounded domain Ω∈RN where ∂Ω indicates sufficiently smooth boundary of Ω∈RN and take the positive constants ξ0,ξ1,σ,β1,β3 where m≥1 for N=1,2, and 1<m≤N+2N−2 for N≥3. The coupled system with these terms is given by
in which G=Ω×(τ1,τ2)×(0,∞) and τ1<τ2 are taken to be non-negative constants in a manner that β2, β4:[τ1,τ2]→R indicates distributive time delay while gi, i=1,2 are positive.
The viscoelastic damping term, whose kernel is the function g, is a physical term used to describe the link between the strain and stress histories in a beam that was inspired by the Boltzmann theory. There are several publications that discuss this subject and produce a lot of fresh and original findings [1,2,3,4,5], particularly the hypotheses regarding the initial condition [6,7,8,9,10,11,12] and the kernel. See [13,14,15,16,17]. As it concerns to the plate equation and the span problem, Balakrishnan and Taylor introduced a novel damping model in [18] that they dubbed the Balakrishnan-Taylor damping. Here are a few studies that specifically addressed the research of this dampening for further information [18,19,20,21,22,23].
Several applications and real-world issues are frequently affected by the delay, which transforms numerous systems into interesting research topics. Numerous writers have recently studied the stability of the evolution systems with time delays, particularly the effect of distributed delay. See [24,25,26].
In [1], the authors presented the stability result of the system over a considerably broader class of kernels in the absence of delay and Balakrishnan-Taylor damping ξ0=1,ξ1=δ=βi=0,i=1,…,4.
Based on everything said above, one specific problem may be solved by combining these damping terms (distributed delay terms, Balakrishnan-Taylor damping and infinite memory), especially when the past history and the distributed delay
are added. We shall attempt to throw light on it since we think it represents a fresh topic that merits investigation and analysis in contrast to the ones mentioned before. Our study is structured into multiple sections: in the second section, we establish the assumptions, notions, and lemmas we require; in the final section, we substantiate our major finding.
2.
Fundamental knowledge
In this section of the paper, we will introduce some basic results related to the theory for the analysis of our problem. Let us take the below:
(G1) hi:R+→R+ are a non-increasing C1 functions fulfills the following
and
(G2) One can find a function C1 functions Gi:R+→R+ holds true Gi(0)=G′i(0)=0.
The functions Gi(t) are strictly increasing and convex of class C2(R+) on (0,ϱ],r≤gi(0) or linear in a manner that
in which ζi(t) are a C1 functions fulfilling the below
(G3) β2, β4:[τ1,τ2]→R are a bounded function fulfilling the below
(G4) fi:R2→R are C1 functions with fi(0,0)=0, and one can find a function F in a way that
and
Take the below
and
Lemma 2.1. (Sobolev-Poincare inequality [27]). Assume that 2≤q<∞ for n=1,2 and 2≤q<2nn−2 for n≥3. Then, one can find c∗=c(Ω,q)>0 in a manner that
Moreover, choose the below as in [26]:
with
Take the auxiliary variable (see [28])
Then
Rewrite the problem (1.1) as follows
where
with
In the upcoming Lemma, the energy functional will be introduced.
Lemma 2.2. Let the energy functional is symbolized by E, then it is given by
The above fulfills the below
in which γ0=min{β1−∫τ2τ1|β2(r)|dr,β3−∫τ2τ1|β4(r)|dr}.
Proof. To prove the result, we take the inner product of (2.9) with vt,wt and after that integrating over Ω, the following is obtained
in which
Using mathematical skills, the following is obtained
further simplification leads us to the following
The following is obtained after calculation
In the same way, we have
Now, multiplying the equation (2.9) by −x|β2(r)|,−y|β4(r)|, and integrating over Ω×(0,1)×(τ1,τ2) and utilizing (2.7), the below is obtained
Similarly, we have
Here, we utilize the inequalities of Young as
and
Finally, we have
Thus, after replacement of (2.14)–(2.22) into (2.13), we determined (2.11) and (2.12). As a result, we obtained that E is a non-increasing function by (2.2)–(2.5), which is required.
Theorem 2.3. Take the function U=(v,vt,w,wt,x,y,ηt,ϑt)T and assume that (2.1)–(2.5) holds true. Then, for any U0∈H, then one can find a unique solution U of problems (2.9) and (2.10) in a manner that
If U0∈G1, then U fulfills the following
in which
3.
Analysis of stability
Here, the stability of the systems (2.9) and (2.10) will be established and investigated. For which the following lemma is needed
Lemma 3.1. Let us suppose that (2.1) and (2.2) fulfills.
where
Proof.
which is obtained through Young's inequality (Eq 3.1).
Lemma 3.2. (Jensens inequality). Let f:Ω→[c,e] and h:Ω→R are integrable functions in a manner that for any z∈Ω, h(z)>0 and ∫Ωh(z)dz=k>0. Furthermore, assume a convex function G such that G:[c,e]→R. Then
Lemma 3.3. It is mentioned in [12] that one can find a positive constant β, ˆβ in a manner that
in which
Proof. As the function E(t) is decreasing and utilizing (2.11), we have the following
for any t,s≥0. Further, we have
in which β=max{4E(0)l1,2} and μ(t)=∫∞0g1(t+s)(1+∫Ω∇u20(z,s)dz)ds.
In the same way, we can deduce that
in which ˆβ=max{4E(0)l2,2} and ˆμ(t)=∫∞0g2(t+s)(1+∫Ω∇w20(z,s)dz)ds. In the upcoming part, we set the following
and
and
Lemma 3.4. In (3.8), the functional Ψ(t) fulfills the following
for any ε,σ1>0 with l=min{l1,l2}.
Proof. To prove the result, differentiate (3.8) first and then apply (2.9), we have the following
We estimate the last 6 terms of the RHS of (3.12). The following is obtained by applying Young's, Sobolev-Poincare and Hölder's inequalities on (2.1) and (2.11), we have
In addition to this, for any σ1>0, by Lemma 3.1, we have the below
Taking same steps to I12, the below is obtained
Same steps for I11,I21 and I31, we have
Combining (3.13)–(3.21), (3.12) and (2.5), the required (3.11) is obtained.
Lemma 3.5. For any σ,σ2,σ3>0, the functional Φ(t) introduced in (3.9) holds true
where ˆl=max{l1,l2}, l0=min{g0,ˆg0} and ^l0=max{g0,ˆg0}.
Proof. To prove the result, simplification of (3.9) and (2.9) through mathematical skills leads us to the following
Here, we will find our the approximation of the terms of the RHS of (3.18). Using the well-known Young's, Sobolev-Poincare and Hölder's inequalities on (2.1), (2.11) and Lemma 3.1, we proceed as follows
and
In the same, we obtained the following
and to find the approximation of J61, we have
the (2.2) implies that
In the same steps, the estimation of Ji2, i=1,..,6 are obtained and
Here, put (3.19)–(3.25) into (3.18), the required result is obtained.
Lemma 3.6. The functional Θ(t) introduced in (3.10) fulfills the below
in which β5=max{β1,β3}.
Proof. To prove the result, using Θ(t), and (2.9), we obtained the following
Utilizing x(z,0,r,t)=vt(z,t),y(z,0,r,t)=wt(z,t), and e−r≤e−rρ≤1, for any 0<ρ<1, moreover, select γ1=e−τ2, we have
applying (2.4), the required proof is obtained. In the next step, we below functional are introduced
in which φ1(t)=∫∞tg1(s)ds,φ2(t)=∫∞tg2(s)ds.
Lemma 3.7. Let us suppose that (2.1) and (2.2) satisfied. Then, the functional F1=A1+A2 and fulfills the following
Proof. We can easily prove this lemma with the help of Lemma 3.7 in [13] and Lemma 3.4 in [15].
Now, we have sufficient mathematical tools to prove the below mentioned Theorem.
Theorem 3.8. Take (2.1)–(2.5), then one can find positive constants ςi,i=1,2,3 and positive function ς4(t) in a way that the energy functionalmentioned in (2.11) fulfills
in which
and
which are increasing and convex in (0, ϱ].
Proof. For the proof, we define the below functional
we determined the positive constants N,Ni,i=1,2,3. Simplifying (3.36) and utilizing 2.12, the Lemmas 3.4–3.6, we have
We select the various constants at this point such that the values included in parenthesis are positive in this stage. Here, putting
Thus, we arrive at
In the upcoming, we select σ in a manner that
After that, we take N2 in a way that
and take N3 large enough in a way that
As a result, for positive constants di,i=1,2,3,4,5, (3.33) can be written as
in which Cκ=max{Cκ,1,Cκ,2}.
We know that κg2i(s)κgi(s)−gi(s)≤gi(s), then from from Lebesgue Dominated Convergence, we have the below
which leads to
As a result of this, one can find 0<κ0<1 in a manner that if κ<κ0, then
From (3.8)–(3.10) through mathematical skills, we have the following
By the fact e−ρr<1 and (2.2), we have the below
that is
Here, set κ=12N and take N large enough in a manner that
we find
for some k2>0, and
for some c5,c6>0, we have
After that, the below cases are considered:
Case 3.9. Gi,i=1,2 are linear. Multiplying (3.40) by ζ0(t)=min{ζ1(t),ζ2(t)}, we find
The last two terms in (3.42), we have
To estimate I1, using (2.11),
and by (3.4), we get
In the same way, we obtained
As a result of this, we get
where β0=max{β4,ˆβ4} and w(t)=ˆζ(t)μ0(t).
Applying ζ′i(t)≤0, we get
with
we have
then, the following is obtained from (3.48)
Further analysis implies that
From the linearity of D, the linearity of the functions D2,D′2 and D4 can easily be determined. This implies that
which gives (3.29) with ς1=λ1, ς2=H1(0)k2, ς3=2β0λ2k2, and ς4(t)=Id(t)=t. Hence, the required proof is completed.
Case 3.10. Let Hi,i=1,2 are nonlinear. Then, with the help of (3.28) and (3.40). Assume the positive functional
then for all t≥0 and for some k3>0, the following holds true
with the help of (3.4), we have
Therefore
where k6=max{H2(0)k3,β0k3} and μ1(t)=1+∫t0μ0(ς)dς.
Corollary 3.11. The following is obtained from (2.11) and (3.53):
Now, we define ϕi(t),i=1,2 by
where B(t)=B0μ1(t) and 0<B0<min{1,l8k6}.
Then, by (3.53), we have
Further, we suppose that ϕi(t)>0,∀t>0,i=1,2. In addition to this, we define another functional Γ1,Γ2 by
Here, obviously Γi(t)≤−cE′(t),i=1,2. As Gi(0)=0,i=1,2 and Gi(t) are convex strictly on (0, ϱ], then
Applying (2.3) and (3.56), we get
Taking the same steps, ¯Gi,i=1,2 are C2-extension of Gi that are convex strictly and increasing strictlyon R+. From (3.59), we have the following
Putting (3.61) and (3.4) into (3.40), we have
Here, introduce K1(t) for ε0<r by
in which D′=min{G1,G2} and is equivalent to E(t). Because of this E′(t)≤0,¯Gi′>0, and ¯Gi′′>0,i=1,2. Also applying (3.62), we obtained that
According to [29], we introduce the conjugate function of ¯Gi by ¯Gi∗, which fulfills
For A=D′(ε0(E(t)B(t))/(E(0)))) and Bi=¯Gi−1((B(t)Γi(t))/(ζi(t))),i=1,2 and applying (3.64), we have
Here, we multiply (3.66) by ζ0(t) and get
where we utilized the following ε0(B(t)E(t)/E(0))<r, D′=min{G1,G2} and Γi<−cE′(t),i=1,2, and define the functional K2(t) as
Effortlessly, one can prove that K2(t)∼E(t), i.e., one can find two positive constants m1 and m2 in a manner that
then, we have
where β6=(k2E(0)−2cε0) and D2(t)=tD′(ε0t).
Choosing ε0 so small such that β6>0, since D′2(t)=D′(ε0t)+ε0tD′′(ε0t). As D′2(t),D2(t)>0 on (0, 1] and Gi on (0, ϱ] are strictly increasing. Applying Young's inequality (3.65) on the last term in (3.70)
with A=D′(ε0E(t)B(t)E(0)) and B=k6δμ(t), we find
Here, choose \sigma small enough in a manner that \beta_{6}-\sigma\varepsilon_{0} > 0 andcombining (3.70) and (3.71), we have
where \beta_{7} = \beta_{6}-\sigma \varepsilon_{0} > 0 , D_{3}(t) = t D'^{-1}\left(t\right) and D_{4}(t) = \overline{D}_{3}^{*}\left(t\right) .
In light of fact E' < 0 and \mathcal{B}' < 0 , then D_{2}(\frac{E(t) \mathcal{B}(t)}{E(0)}) is decreasing. As a consequences of this, for 0\leq t\leq T , we have
In the next step, combine (3.72) with (3.73) and multiply by \mathcal{B}(t) , the following is obtained
Since \mathcal{B}' < 0 , then for any 0 < t < T
Simplify (3.75) over [0, T] and apply \mathcal{B}(0) = 1 , the following is obtained
Consequently, we have
As a results of this, we obtain
As a result of this, we get
where, we have (3.29) with \varsigma_{1} = \frac{ E(0)}{\mathcal{B}(T)} , \varsigma_{2} = \frac{\mathcal{K}_{2}(0)}{\beta_{7}} , \varsigma_{3} = \frac{\sigma}{\beta_{7}} , and \varsigma_{4}(t) = \frac{k_{6}}{\sigma}\mathcal{B}(t) .
Hence, the required result is obtained 3.8.
4.
Conclusions
The purpose of this work was to study when the coupled system of nonlinear viscoelastic wave equations with distributed delay components, infinite memory and Balakrishnan-Taylor damping. Assume the kernels g_{i} :{\bf R}_{+}\rightarrow {\bf R}_{+} holds true the below
in which \zeta_{i} and G_{i} are functions. We prove the stability of the system under this highly generic assumptions on the behaviour of g_i at infinity and by dropping the boundedness assumptions in the historical data. This type of problem is frequently found in some mathematical models in applied sciences. Especially in the theory of viscoelasticity. What interests us in this current work is the combination of these terms of damping, which dictates the emergence of these terms in the problem. In the next work, we will try to using the same method with same problem. But in added of other dampings.
Acknowledgments
The researchers would like to thank the Deanship of Scientific Research, Qassim University for funding the publication of this project.
Conflict of interest
The authors declare there is no conflicts of interest.


















 DownLoad:
DownLoad: