In this article, we develop the existence and uniqueness of positive solutions to a class of fractional boundary value problems involving fractional order derivative with respect to another function for any given parameter. The analysis is based upon the fixed point theorems of concave operators in partial ordering Banach spaces. For the sake of discussing the existence of solutions for the problem, we first construct Green function and study its properties. Furthermore, some properties of positive solutions to the boundary value problem are proved under the different parameters. Examples illustrating the results are also presented.
1.
Introduction
Tropical stingless bees underwent long speciation processes perceived in their pantropical distribution in the Indo-Australia, Neotropics and Africa-Madagascar regions [1] with more than 600 species to date [2] and the oldest fossil record from the Cenozoic ca. 65-96 million years old [3,4]. Their biodiversity in the planet reached a maximum of 100 species in the Ecuadorian Amazon, in a 64 km2 parcel of the Yasuní National Park [5]. Polylectic foraging habits using available food resources by various stingless bee species may cause foraging competition by dietary niche overlap, and originate forage partitioning [6]. Stingless bee ecology was disseminated in a book in 1989 [7].
In food science, instead of looking at bee diets, pollen spectra of honey are valued to describe the botanical origin of a sample with diverse analytical scopes such as chemical, nutritional, bioactive or sensory descriptors. There are two terms used in the literature to refer to honey produced by bees foraging a major nectar source: monofloral and unifloral honey. The first one uses the Greek prefix mono- and the latter the Latin prefix uni- followed by a second Latin word floral (M.L. Piana, personal communication). The authors prefer unifloral honey instead of monofloral having a Greek prefix for the Latin word floral, as understood from Piana's explanation.
A tri-national team composed by the French Jean Louveaux, the Swiss Anna Maurizio and the German Günter Vorwohl produced a document with 2235 citations, including the unifloral honey concept for honey with more than 45% pollen counts from one plant taxa at species, genus, family or unidentified level [8] in a slide prepared with melissopalynological procedures [8,9]. In Brazil, four unifloral honeys of Tetragonisca angustula were identified for resources of Alchornea triplinervia Euphorbiaceae, Eucalyptus robusta Myrtaceae, Petroselinum hortense Apiaceae and Schinus terebinthifolius Anacardiaceae [10]. In Venezuela, three unifloral honeys of T. angustula collected in 1993 were observed for Combretum sp. Combretaceae, Moraceae sp. and Cordia alliodora Boraginaceae [11]. In Colombia, eleven unifloral honeys of T. angustula were identified in a study of 76 honey samples collected in the Andean (Antioquia, Cauca, Cundinamarca, Santander and Tolima) and the Caribbean (Cesar, Magdalena and Sucre) regions between years 2008 and 2010 [12]. These authors reported dominant pollen types for Euphorbia cotinifolia and Euphorbia hirta Euphorbiaceae, Fabaceae sp., Oryctanthus sp. Loranthaceae, Adenaria floribunda Lythraceae, Heliocarpus americanus Malvaceae-Grewioideae, Muntingia calabura Muntingiaceae, Gouania polygama Rhamnaceae, Coffea arabica Rubiaceae and Citrus sp. Rutaceae. From six T. angustula honey samples collected in diverse Brazilian biomes, four were unifloral for Carica papaya Caricaceae, Crotalaria sp. Fabaceae-Faboideae, Eupatorium sp. Asteraceae and Piptadenia sp. Fabaceae-Caesalpinioideae [13].
An overview of sustainable meliponiculture and conservation of plant resources in Costa Rica was summarized in a chapter [14]. Feral colonies of the gentle bee T. angustula are generally undetected and undisturbed by people. Indeed, stingless bee keepers rear this bee called Mariola in Costa Rica for its relished honey. Bee scientists also study T. angustula honey which was more active than MediHoney® against Pseudomonas aeruginosa and Staphylococcus aureus [15]. Its antibiofilm properties were proposed for wound dressings to treat Staphylococcus aureus biofilm infections [16].
In this study, the pollen spectrum of one honey sample produced by the stingless bee Tetragonisca angustula (Latreille, 1811) from Costa Rica was assessed using acetolyzed melissopalynology. This honey participated in the intercontinental post-harvest experiment following novel integrative methodology [9]. From a total of 79 pollen taxa, only four pollen grains presented dominant and secondary relative frequencies were palynologically described and their ecological and nutritional implications were discussed.
2.
Materials and methods
2.1. Collection of Tetragonisca angustula honey and stingless bee specimen
Tetragonisca angustula is a small stingless bee (4–5 mm) called Mariola in Costa Rica. In Figure 1, the stingless bee, entrance tube to the nest, honey pots and the collection site in Alajuela 9°58'18''N 84°25'32''W 906 m.a.s.l. were shown. A sample of pot-honey was collected by suction from sealed honey pots with a 10 mL syringe. A stingless bee specimen was collected in isopropyl alcohol, dehydrated and submitted for identification to the CINAT (Centro de Investigación de Apicultura Tropical) entomological collection.
2.2. Acetolyzed pollen analysis and microphotography
The recently reviewed acetolyzed pollen method for pot-honey [9] was used to prepare the honey sample on slides for microscopic analysis and microphotography. Pollen slides were observed at 400X magnification with a Nikon Eclipse Ni binocular scope and 300 pollen grains were counted. Microphotographs were captured at 1000X magnification with a Nikon DS-Ri1 camera system coupled to the Nikon scope under brightfield conditions. However, although there are other important but expensive methods (e.g., differential interference contrast -DIC-, confocal, transmission and/or scanning electron microscopy -TEM/SEM- etc.) our goal is to show the characteristics of pollen grains seen under normal light method that is available to any palynologist.
Standard terminology for palynology was used for morphological descriptions of pollen grains [17] and the major pollen grains in the pollen spectrum [18]. Pollen identifications were for plant family, genus and a number of species, when possible, were assigned after comparisons with pollen atlases and collections [19,20] and the taxonomic status of botanical taxa was updated by consulting Tropicos Missouri Botanical Garden database available online [21].
3.
Results
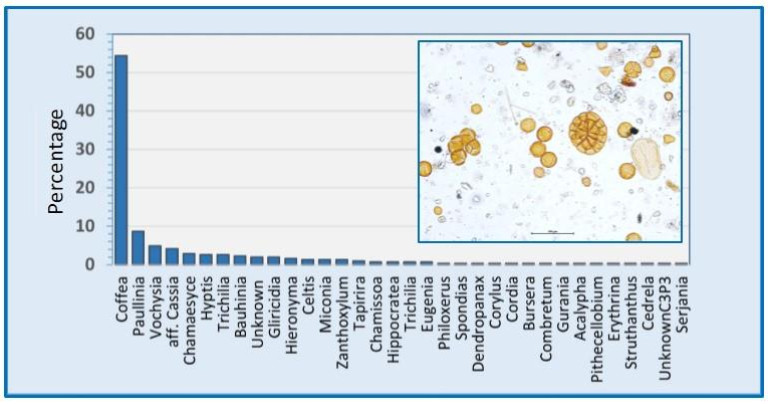
The identified taxa and percentages of the pollen spectrum investigated in the Tetragonisca angustula honey from Costa Rica were classified in alphabetical order for Eudicotyledonae, Monocotyledonae, Gymnospermae and related organisms (spores and microorganisms) in Table 1. The relative frequency of all 79 taxa was given in the column of their percentages (%) of the total pollen count in the slide. For this honey sample, 300 pollen grains were counted. In the following column the frequency classes for each type of pollen grain were given: D dominant (>45%), A accessory (>16–44%), S secondary (>3–15%), M minor (1–3%) and L low (<1%) pollen types. This modified classification from [8] was suggested for a better valorization of the lower frequencies so abundant in this honey. For example, the Ammandra decasperma Arecaceae closely related with Phytelephas spp. Arecaceae has been originally reported in Colombia, but probably occurs in Costa Rica. This would be the first report. The classic frequency class R rare (<3%) [8] was included in the last column.
Seventy-nine pollen types were recognized in the pollen spectrum, 95% of them < 3% frequency, representing 37 families and 67 genera of flowering plants. 15 of them (19%) were herbs, four (5%) herb/tree, nine (11%) lianas/vines, four (5%) shrubs, 40 (51%) trees, one (1%) shrub/tree and six of them (8%) had not assigned habit. According to the offered resource, 27 were nectariferous species (34%), 17 nectar-polleniferous (22%), 25 polleniferous (32%) and 10 of them not assigned resource (13%).
The main frequencies (dominant and accessory), intermediate (secondary) and some lowest frequencies (rare) for taxa in the pollen spectrum of T. angustula honey were presented in the histogram of Figure 2 measured as percentages. In this image, pollen grains from Figures 6, 8, 11, 12, 14 of diverse size and shape are visible. The largest ochre polyad of Inga sp. (34) Fabaceae-Mimosoideae, the gray monocolpate Scheelea zonensis (74) Arecaceae, smaller tetrads of Hippocratea volubilis (24) Celastraceae, monads of Coffea Arabica (59) Rubiaceae and the triangular Paullinia sp. (63) Sapindaceae.
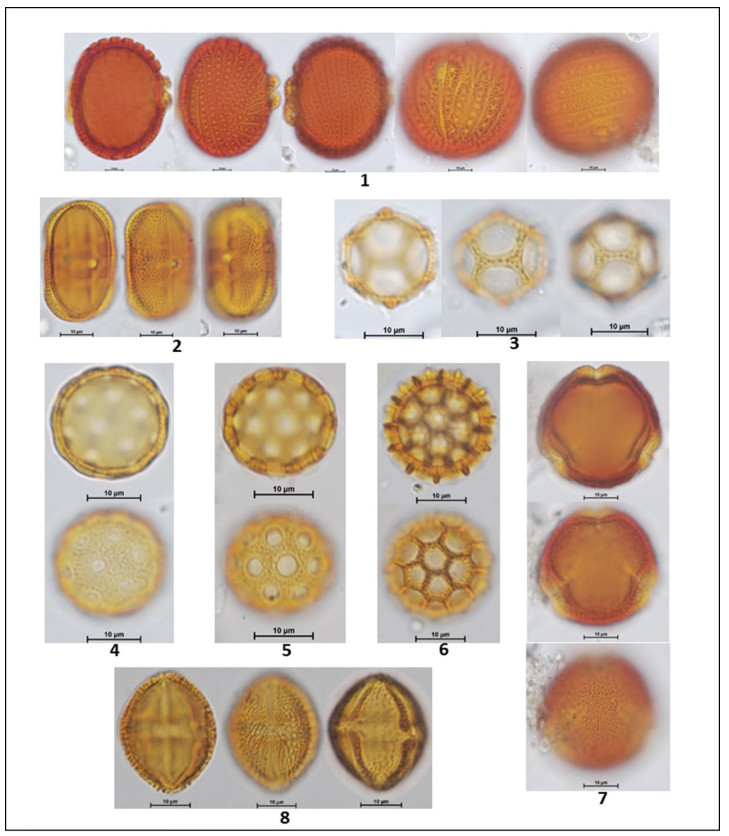
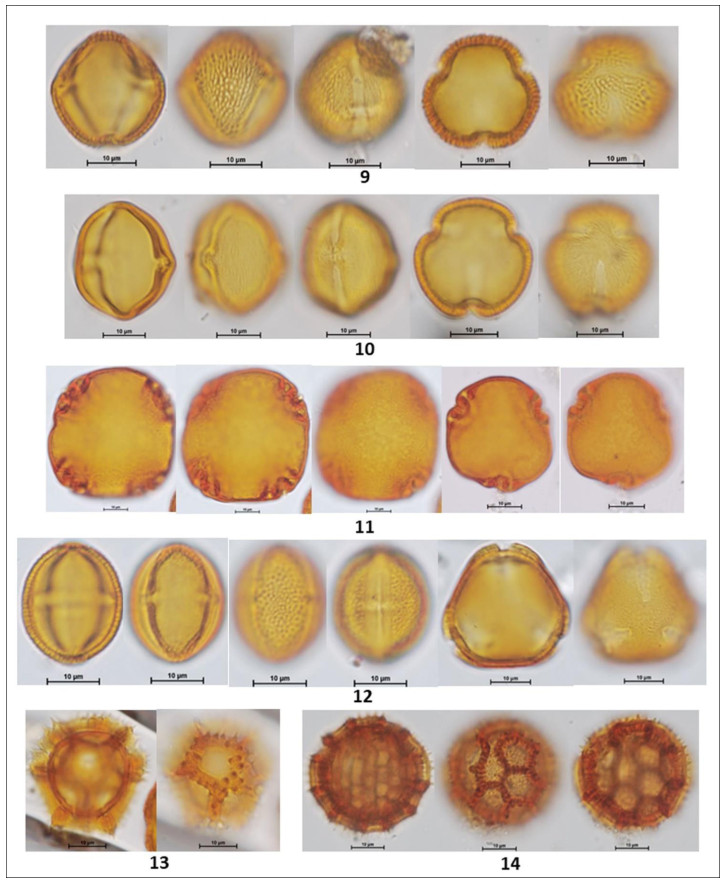
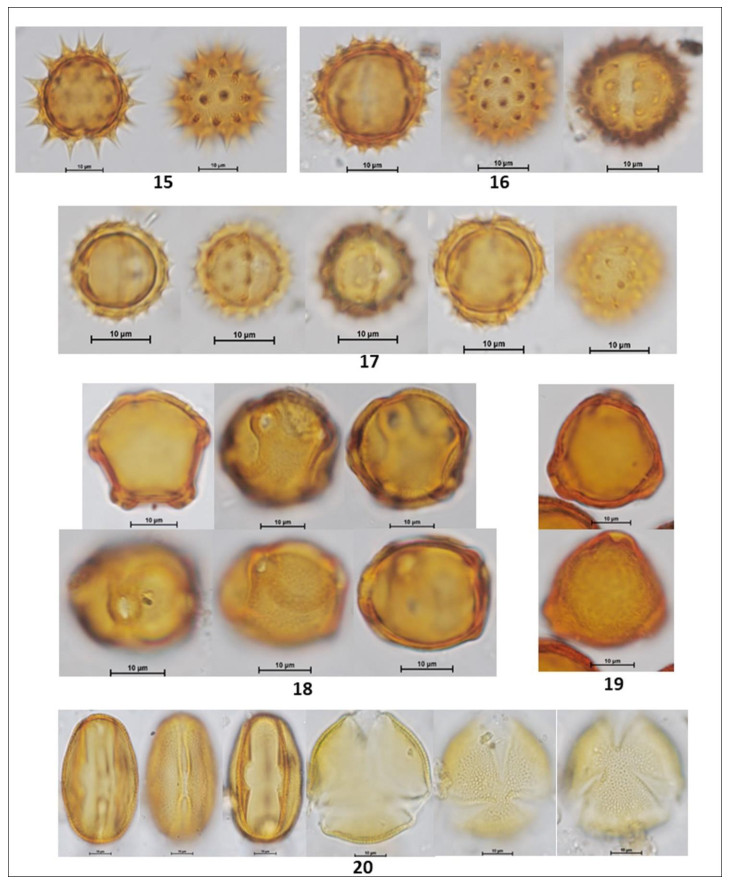
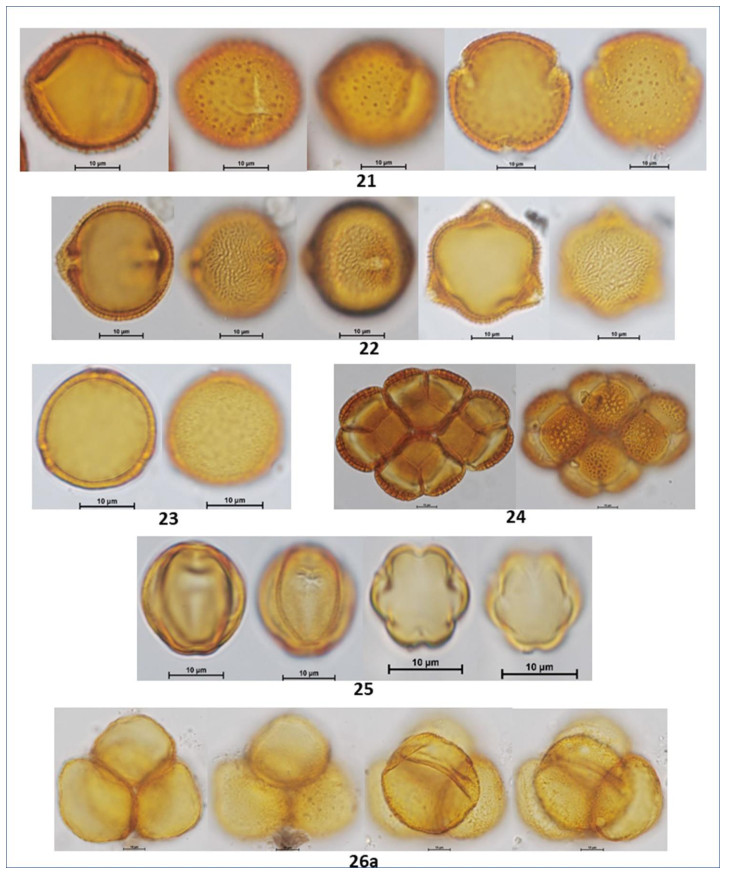
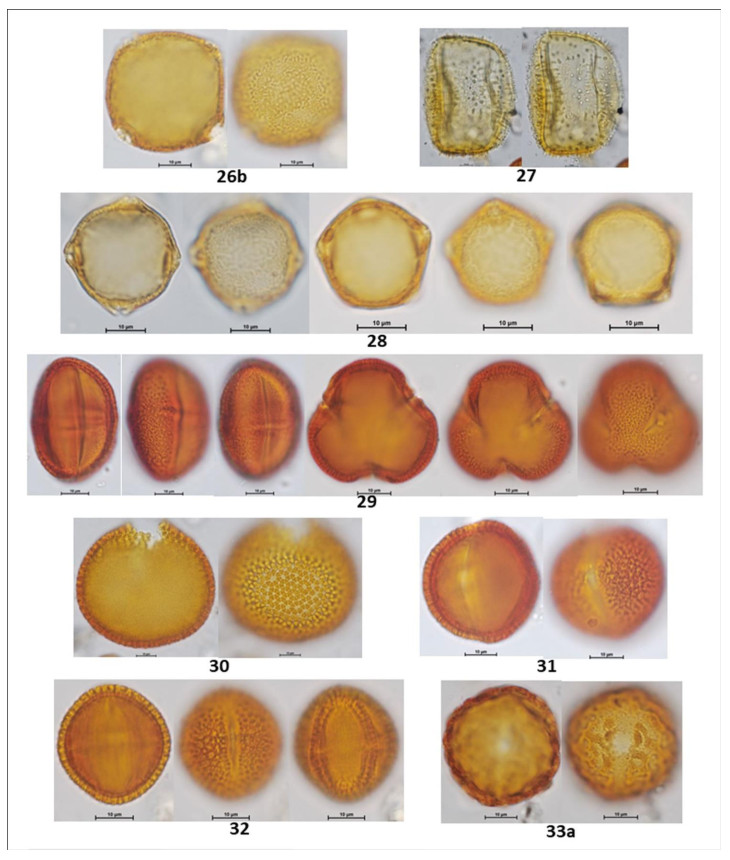
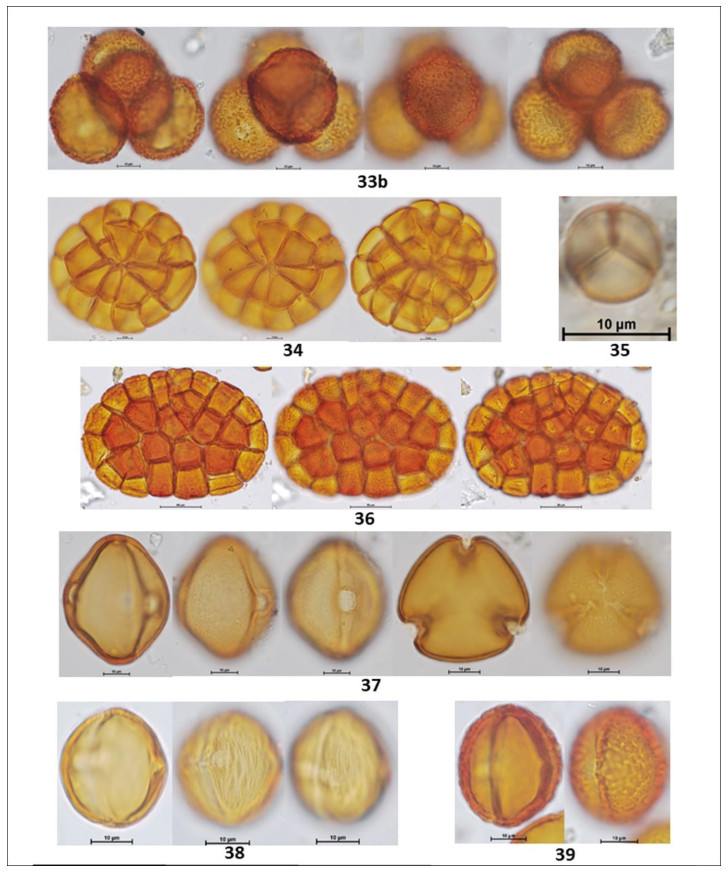
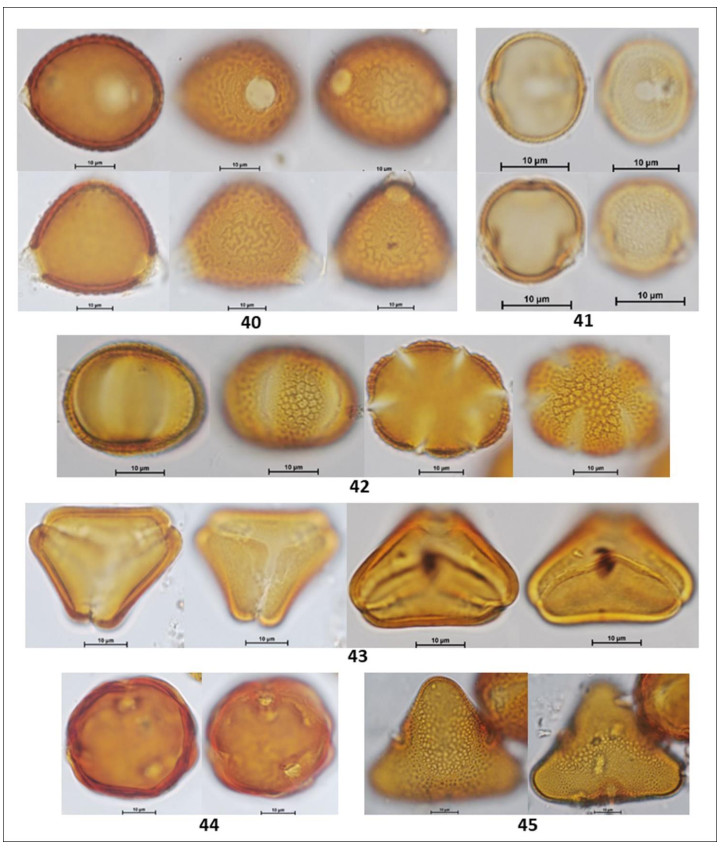
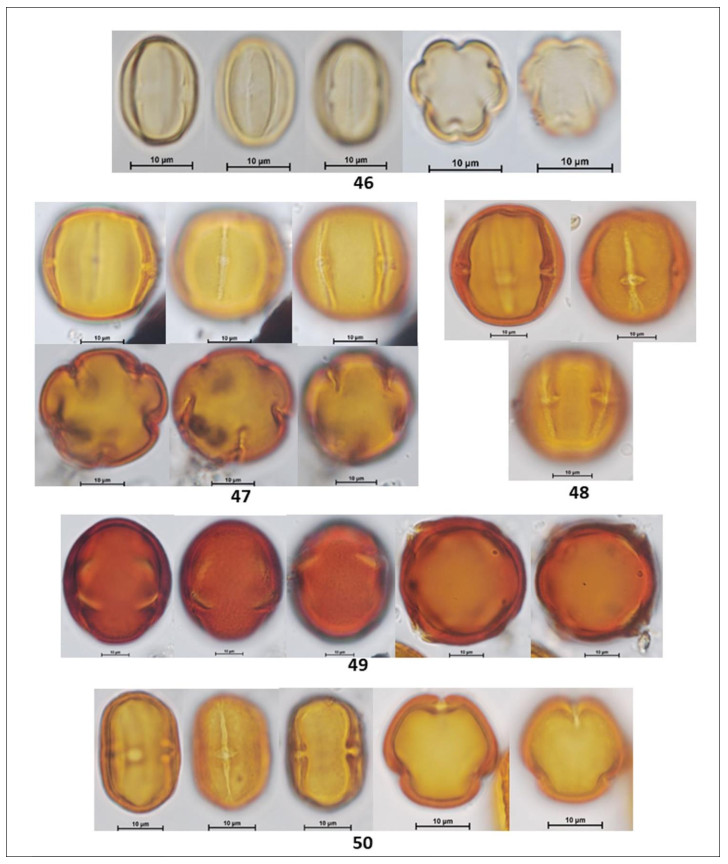
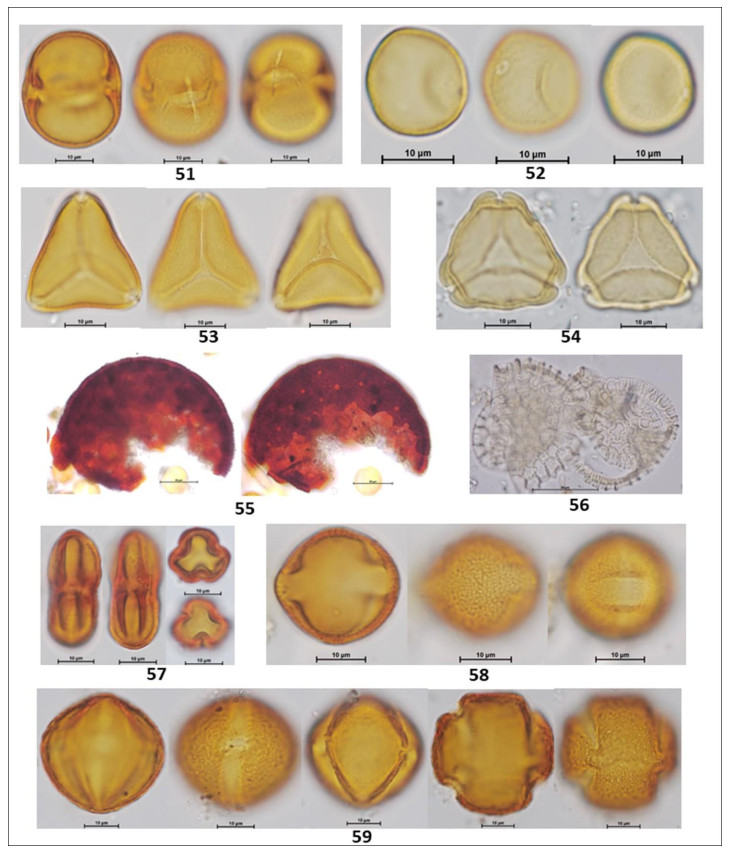
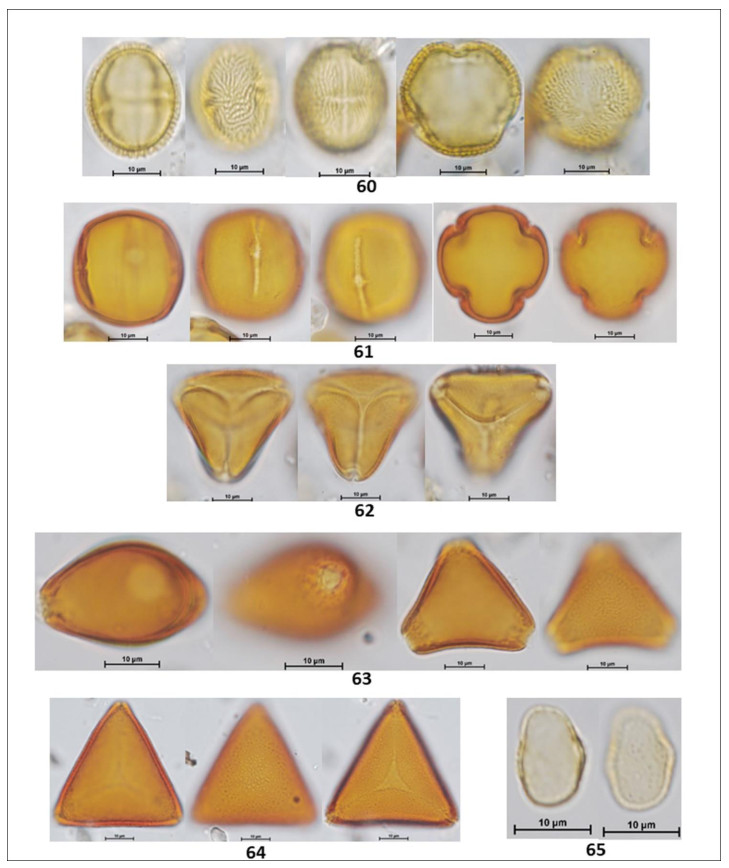
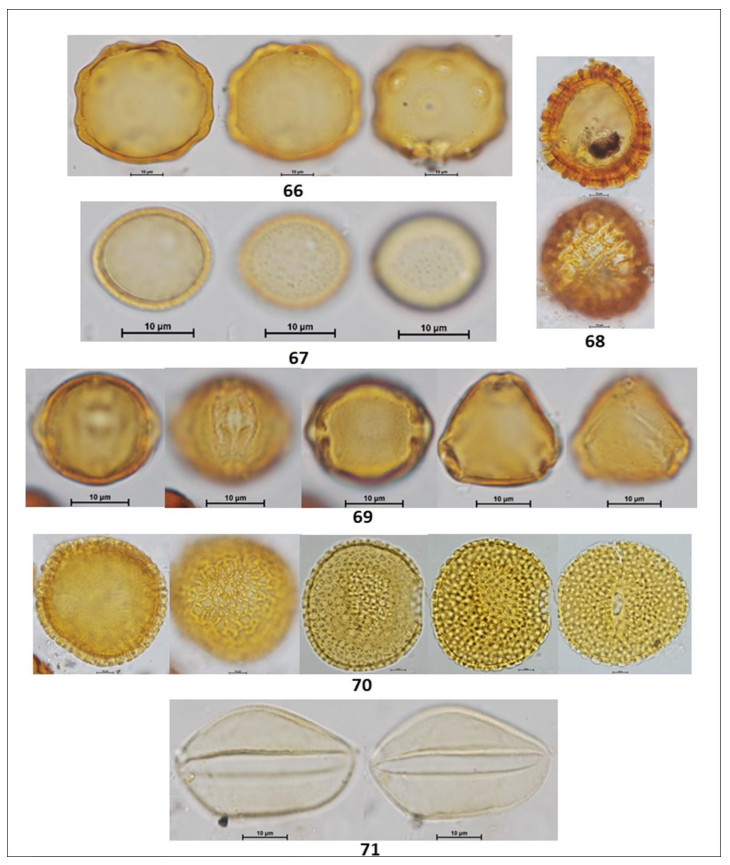
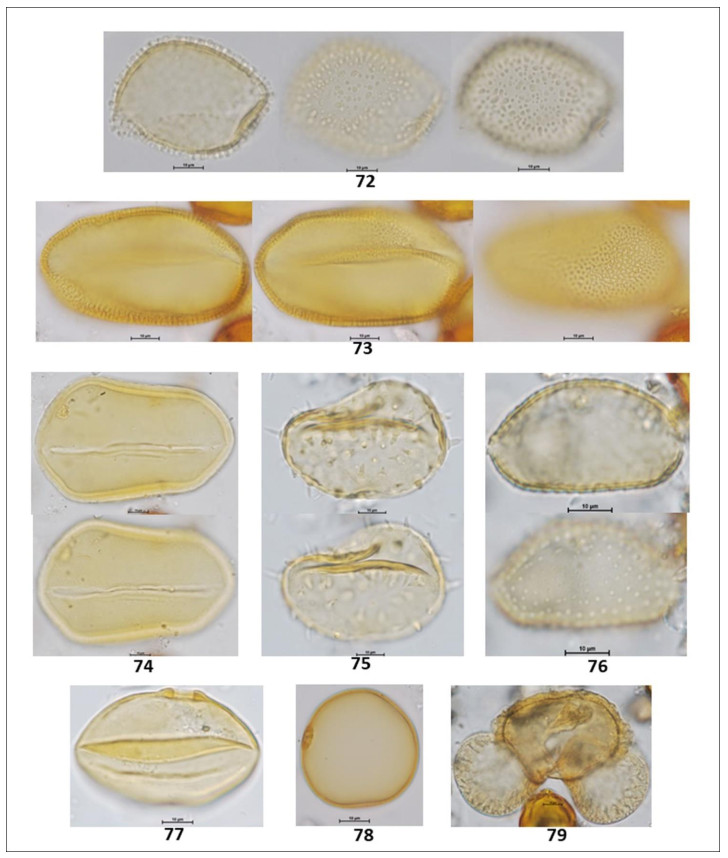
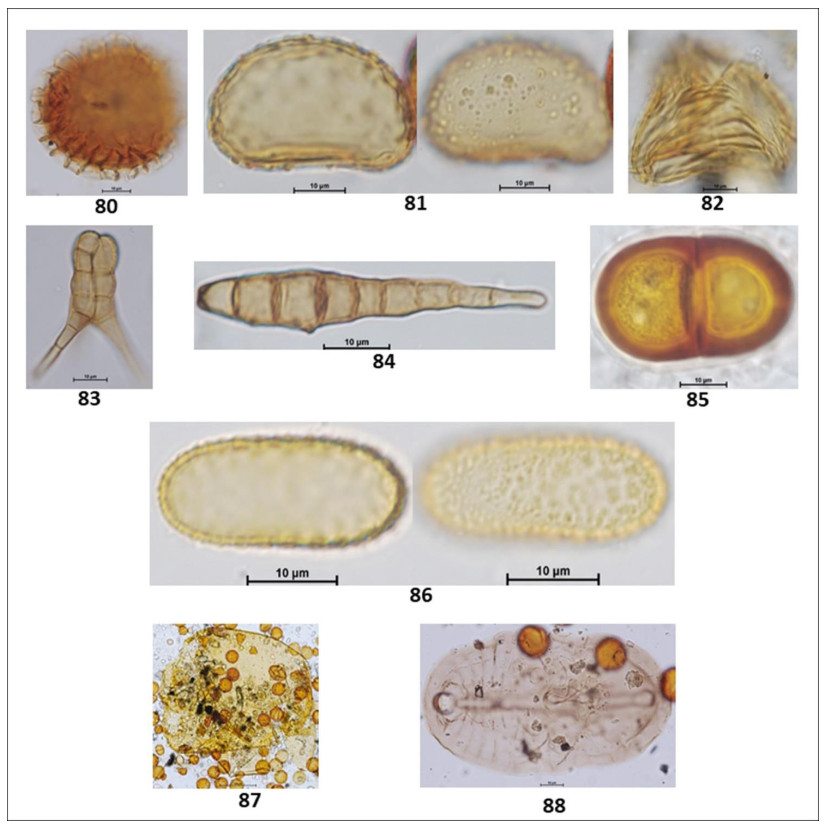
In the following Figures 3 to 15 microphotographs of the 88 taxa from Table 1 were visualized. The 69 pollen grains of Eudocotyledoneae (1–69), the nine pollen grains of Monocotyledonae (70–78), one Gymnospermae Pinus sp. (79) and the nine related organisms (80–88) including the Lycopodium marker, some fungi, acari and unknown morphologies.
The biodiversity of pollen morphologies was visualized with the majority (92.5%) of single grains (monads) and 7.5% of composed grains (tetrads and polyads). The Cucurbitaceae Gurania sp. (26) and the Fabaceae-Caesalpinioideae: Cassia sp. (33) had both monads and tetrads. Other composed grains were very conspicuous in the pollen assemblage. For example, see the inserted picture in Figure 2: Hippocratea volubilis (24) (Celastraceae); Inga sp. (34), Mimosa sp. (35) and Pithecellobium sp. (36) (Fabaceae-Caesalpinioideae). Pollen characteristics (v.gr. shapes, outlines, apertures, sculptural elements, etc.) and definitions were used and adapted [17,18,20]. Variations in aperture types of pollen grains showed 47% colporate taxa (3, 4, 5-colporate and syncolporate classes), 28% porate taxa (1, 2, 3 4, 5-porate, periporate and extraporate classes), 18% colpate (monocolpate, stephanocolpate -3, 6, 12 colpi-, heterocolpate classes), 4% fenestrate and 4% inaperturate. Only one anemophilous taxon (contaminant) Pinus sp., had vesiculate pollen. Size was another distinctive feature of pollen grains. Mirabilis jalapa (Nyctaginaceae) exhibited the largest measure ca. 245 µm and the polyad of Pithecellobium sp. 225 µm, against Mimosa sp. (35) (Fabaceae-Caesalpinioideae) with 9 µm. However, most of the taxa reported ranged from 18 to 40 µm. Since pictures in Figures 3 to 15 were not in scale, the differences in size of pollen grains were poorly appreciated. However, each caption had its own scale. A proportion of 30% reticulate or psilate surfaces was observed on the taxa identified. 13% corresponded to echinate and similar proportion to scabrate 14% was distributed between striate, verrucate, clavate, baculate and rugulate sculptures.
Palynological descriptions were made for the dominant pollen Coffea arabica > 45% and the three secondary taxa > 3–15% of the pollen spectrum of Tetragonisca angustula honey in Table 1.
Coffea arabica L. (Rubiaceae) is a nectariferous/polleniferous shrub, see its tetralobate pollen in polar view Figure 11 (59). Grains monad, dimorphic, tricolporate and 4–5 colporate, sometimes exhibiting extra colpus, resembling pericolpate condition. When tri and tetracolporate condition they shape isopolar, radially symmetric; apertures conspicuous, colpus as long as grain, pores circular to slightly lalongate 3 µm diameter, exine fine 1.5–2.5 exine 2 µm thick, semitectate, sexine reticulate, homobrochate, sometimes resembling rugulate condition, amb circular, grains oblate-spheroidal 39 x 37. When tetra and penta aperturate condition, grains ambitus square with free colpus at poles resembling pericolpate condition, 40 µm in size.
Cassia sp. L. (Fabaceae-Caesalpinioideae) is a nectariferous/polleniferous tree, see its pollen in Figures 7, 8 (33). Grains isolated -monads- and tetrads. Isolate pollen grains are isopolar monads, radially symmetric, tricolporate; colpus long, contours not well defined, pores endexinic, circular ca. 10 µm diameter; exine semitectate 3 µm thick, sexine scabrate to micro-baculate, grouping in small patches resembling areolate-like condition almost as verrucae; ambitus circular; grains spheroidal 42 µm in size. Pollen grains of Cassia sp. may stick together forming a tetrahedral tetrad, measuring 72 µm as the largest diameter.
Paullinia sp. L (Sapindaceae) ia a nectariferous liana, see its triangular shaped pollen in polar view Figure 12 (63). Grains monad, shape isopolar, radially symmetric, triporate, apertures conspicuous, pores circular 3.0 µm diameter, slightly protruding; exine 2 µm thick, tectate, sexine reticulate, homobrochate; amb angular, grains oblate, 20 x 32 µm.
Vochysia sp. Aubl. (Vochysiaceae) is a nectariferous tree, see its subangular pollen in Figure 13 (69).
Monad, isopolar, radiosymmetric, tricolporate, colpi long, thin having margo ca. 4 µm thick, pores slightly protruding, club type, a lalongate 4 x 8 µm endoaperture, exine 1.5 µm thick, tectate, sexine psilate to slightly foveolate; angular perimeter of a pollen grain in polar view, amb angular, grains suboblate 21 x 25 µm.
Plant taxa identified in the pollen spectrum of T. angustula honey were explored in Table 1 for the floral resources they represented. From 79 taxa, 27 of them were nectariferous (34%) because they offer nectar, 25 were polleniferous (32%) because they offer pollen, 17 offer both nectar and pollen (22%) and the nutritional source they offer to bees was unknown in 10 (13%) of the taxa.
4.
Discussion
4.1. Significance of relative frequencies of pollen taxa in the T. angustula honey
Bees forage available resources. They are generalist if using all of them, or specialize on certain plant species for diverse reasons. For example, the sympatric Australian Tetragonula carbonaria and the smaller Austroplebeia australis share same resources but use them differently [21], this is a trait that may have a phylogeographic origin to reduce or to avoid competition of resource exploitation between these two species. Generalist T. carbonaria visited a wide offer of blooming plants, while the A. australis specialized on plants with nectars of higher sugar concentrations.
Pollen frequencies below 3% have low contribution for nutrition of the bee colony. They are possibly indicating contamination, admixture with other meliponaries of unknown origin or extraction, and further processing. This was not the case here. Therefore, the 74 taxa observed with pollen frequencies < 3% in the slide represent the 94.8% of presence of the plants in the habitat at flight range from the Tetragonisca angustula hive. For example, the Ammandra decasperma Arecaceae, strongly was probably reported for the first time in Costa Rica. There is no difference on nutritional implications between a rare pollen < 1% and a minor pollen (1-3%). However, only four of the 79 plant taxa reported here, exhibited frequencies greater than 3% representing 72% of total pollen counts: Coffea arabica (54.3%), Paullinia sp. (8.7%), Vochysia sp. (4.8%) and Cassia sp. (4.2%).
4.2. Ecological implications of the pollen assemblage of T. angustula honey
This small stingless bee has lower flight range than larger bees like Melipona spp. Therefore, it is important to have nectariferous and polleniferous flora surrounding Tetragonisca angustula meliponaries. This pollen assemblage indicated the presence of lowland tropical forest elements, probably small relicts of secondary forest surrounding open and cultivated areas where coffee pollen dominated in the honey pollen spectrum. Palynological techniques are fundamental to understand the ecology of the bee-plant relationships.
From the 88 palynological morphotypes detected in Figures 3 to 15, 79 were pollen grains and nine were spores, fungi and acari. The latter were low < 1% counts of 300 pollen grains and included the Lycopodium marker used in the acetolysis method. For this reason, the total count was 87 taxa.
Looking at the floral resources offered to bees by the plants of Table 1, either nectar, pollen or both, taxa offering only pollen were considered contaminants of honey because they did not provide nectar for honey formation. A high 32 % of polleniferous plants were present in this honey. The origin of that contamination is not immediate. Possibly attributed to the T. angustula foraging or inside the nest behavior. The low presence of anemophilous elements like Alnus sp., Corylus sp., Pinus sp. and Ulmus sp. showed the transitional lowland tropical floras with those from temperate latitudes.
The ecological roles of meliponine bees in tropical environments are multifactorial, considering diverse variables during foraging trips such as sheer number, morphological diversity, diversity in foraging strategies, generalist foraging habits (polylecty) and flower constancy [6]. An updated review on stingless bee ecology for 'tropical forest residents since the upper Cretaceous' [23]. The urban T. angustula singularly abundant in human environments [24] and a plethora of ethnic names [25] with the most peculiar cavity-nesting sites [26] is perhaps evolving since dinosaur scenarios. This docile tiny bee has an ecology of success in a distribution from Mexico to Northern Argentina, possibly of a T. angustula species complex to be deciphered (MS Engel, personal communication).
All the pollen morphological features were corroborating the richness in plant diversity visited by this small bee T. angustula, where the main assemblage corresponded to primary forest with scarce intervention. See few images illustrating the premontane tropical rainforest biome in Alajuela, Costa Rica in Figure 16. This vegetation included Café Coffea arabica, Botón de oro Tithonia diversifolia, Guarumo Cecropia peltata, Mango Mangifera indica. Despite the generalist habit of T. angustula, the presence of coffee cultivations surrounding this native forest provided the main temporary nectar source and caused and opportunistic foraging behaviour, as evidenced in the unifloral Coffea arabica pollen spectrum. Lists of bee flora like the Meso American melliferous native trees [27] so useful for meliponiculturists, were used to prepare a floral calendar with blooming seasons in Costa Rica [14].
Richness of T. angustula honey from a Colombian Andean premontane forest was high in the wet season with preference for Asteraceae herbs, trees and shrub species of Melastomataceae, Sapindaceae and Peraceae families [28]. Their vegetation consisted on secondary forests, sugar cane, banana and livestock grasslands agro systems. Floral selection varied according to seasonal availability for the Colombian maximum 40 species T. angustula pollen spectrum of honey in contrast to the 79 species for Costa Rica. In a coffee focal crop from Puerto Rico, high nectar sugar concentrations and high temperatures caused short floral visits (<15s) and increased numbers of bees in blooming coffee caused longer floral visits (16–180 seconds) [29]. Rising caffeine content of nectar was a driver for longer visits on C. arabica flowers and lesser on C. canephora flowers, whereas floral availability surrounding the coffee plantations and the type of plantation did not predict bee visits as pollinators in coffee cultivars from Puerto Rico. Prado et al. [29] also observed that bees carried pollen loads of Coffea sp., either C. arabica or C. canephora.
4.3. Nutritional implications of the pollen spectrum of T. angustula honey
Proximate analysis and phytochemicals of nectar are related to the botanical origin, and therefore they affect the chemical composition of honey regulated by honey standards [30] and broader components analyzed for nutritional and medicinal properties. Expectations of having distinctive chemical components in a coffee honey are valid, as for the unifloral European honeys [31]. However, the physicochemical properties did not characterize unifloral honeys according to their pollen spectra in the Brazilian study comparing Apis mellifera and Tetragonisca angustula honey [13]. Frequent Paullinia sp. and less frequent Bombax sp. and Gouania sp. characterized the pollen spectra of honey from the Peruvian Amazon with bioactive compounds of the nectar for their attributed medicinal properties [32].
In the Costa Rican pollen spectrum of T. angustula honey (See Table 1), the dominance of Coffea arabica pollen (54.3%) conferred the coffee unifloral attribute. Therefore, an important contribution to the chemical quality and bioactive properties of this T. angustula honey will derive from coffee nectar. Paullinia sp. (8.7%), Vochysia sp. (4.8%) and Cassia sp. (4.2%) were secondary pollen. There are 51 Paullinia spp. Sapindaceae liana species in Costa Rica [33]. From the Vochysiaceae family, Vochysia guatemalensis and Vochysia hondurensis are fast growing species and Vochysia ferruginea a slow growing species used in Costa Rican reforestation programs [34]. Carao Cassia grandis Fabaceae-Caesalpinioideae is an important resource of extrafloral nectar produced by extrafloral nectaries (EFNs) like Cassia fasciculate [35,36], it means lower counts of pollen in the spectrum representing higher nectar origin of these taxa. Nectar is the principal bee resource of Carao, which is known for the Holy Week harvest of an Apis mellifera dark honey with strong odor, aroma and flavor [37,38]. Floral nectar attracts bees for pollination, but not extrafloral nectar (EFN) which attracts predatory insects for plant protection. However, bees also use EFN to make honey. Cassia, Chamaecrista and Senna have EFN with similar EFN secretory morphologies [39] of specialized plant glands or secretory trichomes and vascularized parenchyma [40]. Honey from extrafloral nectaries have less pollen than floral honey because the resource is not collected as a reward for the pollination service. They have been studied less. Rubber Hevea brasiliensis Euphorbiaceae honey is made with EFN and is popular in India, Indonesia and Guatemala. The EFN botanical origin of rubber honey was identified by its principal pollen as [41]. It was compared with floral honey from Kerala, India. The phytochemicals were similar, but rubber honey was less antioxidant [42]. Rubber honey produced by A. mellifera, A. dorsata and T. itama from Indonesia also had similar phytochemicals [43] The A. mellifera honey was darker than A. dorsata and T. itama. Water content was higher in T. itama and A. dorsata honey than A. mellifera. The free acidity of A. dorsata honey duplicated that of A. mellifera, but T. itama honey was the highest.
Trigonelline is a bitter alkaloid in coffee, it was used as a marker of coffee honey. The trigonelline content was 2 to 2.5 times in Apis mellifera coffee honey compared to lemon and orange honey [44]. In a Brazilian study, Apis mellifera pollen frequencies of coffee honeys were 75–78%, ascorbic acid 295 mg/kg, total flavonoids 3.5 mg QE/kg, caffeine in nectar 1.6 mg/kg and in honey 12 mg/kg [45]. Coffea arabica pollen frequencies of 54.4 to 94.2% in Ethiopian coffee honey were positively correlated with caffeine contents 96 ± 20 mg/kg and 14 ± 2 invertase number [46]. This bitter honey moisture content was 17%, HMF 0.4 mg/kg and sugars were 36% fructose, 31% glucose, 1% sucrose, 0.1% turanose and 1% maltose. The content of trigonelline and caffeine in Apis mellifera coffee Coffea robusta honey samples from Vietnam ranged from 0.3–2.4 mg/kg and 9.0–38.0 mg/kg [47]. This was a brief coffee honey profiling.
5.
Conclusions and future developments
The pollen spectrum of this Tetragonisca angustula unifloral coffee honey was characterized by Coffea arabica (54.3%) with the frequencies of 79 identified pollen types, representing 37 families and 67 genera of flowering plants. These visited plants were mostly trees (51%) and herbs (19%). A surprisingly high 32% of the taxa in the pollen spectrum of this honey was from polleniferous flora, leaving more questions than answers on T. angustula behavior for such a biodiverse honey with 79 taxa, 75 < 3% and 25 of them are pollen fingerprints not conducing to nectariferous sources for honey making stingless bees, but polleniferous plants. Moreover, lower pollen frequencies are of less interest in food science −54.3% pollen explained the coffee nectar origin.
An expanded pot-honey sampling is recommended in the coffee lands of Costa Rica agro-systems with Tetragonisca angustula meliponiculture. Different harvest seasons related with Coffea arabica blooming would optimize timing for this unifloral honey production. It may deserve a protected designation of origin (PDO) for unifloral honeys with > 45% Coffea arabica frequencies in their pollen spectra, besides the entomological origin of Tetragonisca angustula. The guaranteed traditional specialty (GTS) protecting the artisanal production method would be an optional name suggested by the quality policy of the European Union (EU), applicable here for making the most of this unique honey to producers and consumers. More studies are needed to characterize and to investigate biofunctional benefits of unifloral coffee pot-honey produced by the stingless bee Tetragonisca angustula as informed before for Colombia [12], and here reported for Costa Rica. Accompanying pollen taxa will also have a role in the chemical composition, sensory characterization and bioactive properties derived by the corresponding assemblages of nectar composition.
Acknowledgments
Authors would like to thank MSc. Eduardo Herrera Gonzalez for collecting the pot-honey sample, T. angustula stingless bee keepers of Mariola from Costa Rica to protect this traditional practice, and for their skills to harvest this honey with culinary, nutritional and medicinal uses. To the team effort for the intercontinental post-harvest experiment networking scientific expertise from Brazil, Costa Rica, Ecuador, Germany, Malaysia, Panama, Spain, Thailand, the United States of America and Venezuela. Dr. David W Roubik kindly transported the T. angustula honey from the location of production to the palynological laboratory. The editorial support received was outstanding. To Universidad de Los Andes, Mérida, Venezuela. To Universitá Politecnica delle Marche, Ancona, Italy.
Conflict of interest
Authors declare no conflict of interest.










 DownLoad:
DownLoad: