1.
Introduction
Evolutionary algorithms (EAs) are a class of adaptive, global search algorithms inspired by natural evolutionary processes, mainly including genetic algorithms (GA), evolution strategy (ES), genetic programming (GP), and evolution programming (EP) [1]. EAs have been widely applied to the practical application domains, such as black box optimization and combinatorial optimization, yet a number of theoretical analysis results are relatively limited. As a commonly used indicator to measure the computational time, the first hitting time is the number of generations when EAs find the optimal solution or a satisfactory solution for the first time [2]. Moreover, the expected first hitting time is the average number of evaluations of the fitness function when EAs obtain the optimal or satisfactory solution for the first time, which evaluates the performance of EAs [3].
In the past few years, most theoretical approaches of the first hitting time have focused on discrete search spaces. Drift analysis, combined with Markov chains in the analysis of computation time complexity of EAs, was first introduced by He and Yao [4]. As drift analysis was being developed, multiplicative drift [5,6] and variable drift [7,8,9] have shown that the lower bound of the first hitting time is stronger than its upper bound. Sarker et al. [10] considered the first hitting time of EAs as a random variable and derived its time on a pseudo-Boolean function. Yu et al. [11] proposed a switch analysis method for estimating the time bound of EAs by combining two Markov chains, one of which served as a reference chain. Qian et al. [12] transformed the bit-by-bit noise into one-bit noise and discussed the first hitting time of EAs on the OneMax and LeadingOnes functions. Wegener et al. [13] analyzed the running time of EAs on the pseudo-Boolean function using tail inequalities. In these works, however, there have been few theoretical analyses in EAs for continuous optimization. Huang et al. [14] combined statistical methods with the average gain model to obtain an empirical distribution function for the expected gain and derived the upper bound closed expression. Feng et al. [15] established an equivalent relationship to analyze the effect of selection operators on the computation time of EAs. To generalize the drift analysis model, Morinaga et al. [16] introduced σ-algebraic flow stochastic process into the model. Jägersküpper [17] combined drift analysis with Markov chains, treating drift as a Markov chain, and analyzed the first hitting time of EAs on the linear function. Many important theoretical analysis results of them primarily focus on simplified versions rather than the (1 + 1) ES, which stems from the difficulties posed by population-based characteristics and the intricate adaptive selection strategies involved.
Agapie et al. [18] combined the transition kernel with the success region where each generation of (1 + 1) ES arrives and obtained the cumulative distribution function of success probability, which was estimated as the upper and lower bounds of the first hitting time for (1 + 1) ES with a uniform mutation operator on the sphere function. However, when the gap between the population fitness value and the optimal fitness value was substantial, they approximated the intersection of the fitness sphere and the mutation sphere as half of the mutation sphere. These approximations resulted in an inflated expected progress rate, ultimately causing significant looseness between the lower bound of the first hitting time of (1 + 1) ES on the sphere function and its actual running time. Morinaga et al. [19] proved that the expected hitting time of (1 + 1) ES on the convex quadratic functions was Θ(exp(−1/d)). Zhang et al. [20] analyzed the upper bound of the expected hitting time of (1 + 1) ES on the sphere function by combining martingale theory with the Lebesgue-dominated convergence theorem, but they did not provide a corresponding theoretical lower bound analysis. Agapie et al. [21] combined the reduction of distance from the t-1 generation population to the optimal solution with differential equations and analyzed the lower bound of the hitting time of (1 + 1) ES with a Gaussian mutation operator on the sphere function as Ω(n⋅log(R0ε)). Doerr et al. [22] established a dynamic drift model to analyze the relationship between the evolutionary strategy parameter selection and the first hitting time and obtained the expected first hitting time Θ(nλ/logλ+n/logn) on the OneMax function. Akimoto et al. [23] improved additive drift by treating the progress rate as a monotonic decreasing function, and analyzed that the convergence rate of the 1/5 success rule (1 + 1) ES solving sphere function was Θ(1/d). Jägersküpper [24] hypothesized that individuals were generated through anisotropic mutation and further obtained the asymptotical running time of (1 + 1) ES with a Gaussian mutation operator solving sphere function. Although many achievements have been made in the analysis of the first hitting time of (1 + 1) ES on the sphere function, few theoretical research results pay attention to its upper bound with a Gaussian mutation operator. Meanwhile, due to the simplified relationship between the sphere objective function and the mutation sphere, its lower bound with a uniform mutation operator is not tighter.
The main innovations and contributions of this paper can be outlined as follows:
1) The proposed method is based on a non-negative progress rate stochastic process, which is conducive to separating specific cases and algorithms, making the model more general.
2) The intersection of the fitness sphere and the mutation sphere is considered the success region where each generation of (1 + 1) ES arrives, and its lower bound with a uniform mutation operator is obtained for a tighter first hitting time.
3) The effectiveness of the 1/5 success rule of the (1 + 1) ES is verified, and its upper bound with a Gaussian mutation operator is obtained.
The structure of this paper is as follows. Some preliminary knowledge on the renewal theorem and stopping time is introduced, and then the renewal model is proposed in Section 2. The lower bound of the expected first hitting time of (1 + 1) ES with a uniform mutation operator is analyzed in Section 3. The upper bound of the expected first hitting time of (1 + 1) ES with a Gaussian mutation operator is analyzed in Section 4. Numerical experiments and results are reported in Section 5. Finally, Section 6 draws the conclusion.
2.
Preliminaries
In this section, we introduce the general process framework of (1 + 1) ES, renewal process, stopping time, and mathematical modeling of the algorithm.
2.1. Problem description and algorithm introduction
We consider minimizing the sphere function in this paper. Its corresponding mathematical expression is as follows:
where f(x) is the fitness function and Q is the search space. Let ξt={ξt1,ξt2,...,ξtn}∈Q be the t-generation population of EAs and n represents the problem size. The process description of (1 + 1) ES can be described as follows [23]:
In this paper, Algorithm 1 includes the use of mutation and selection. Δt uses a uniform mutation operator or Gaussian mutation operator; election is elite selection, that is, one individual is selected from the parent and offspring individuals as the population individual of the next generation. Within a certain range of iteration times G, the successful iteration times G′ is the iteration number that satisfies the condition of f(ξt)<f(ξt−1). Let ps=G′G, if ps>1/5, the mutation strength reduces, i.e., A=α; if ps<1/5, the mutation strength increases, i.e., A=α−1/4. Otherwise, it remains unchanged. Generally speaking, 0.85≤α<1 [25]. However, the main results presented in this paper, i.e., Theorem 3, are independent of such a specific implementation and can be applied to almost any stochastic search algorithm.
2.2. A renewal model of EAs
We consider the gradual process of EAs from their initial position to a satisfactory solution as a renewal process to establish a renewal model, which is different from the theoretical results on intelligent optimization algorithms [26,27]. Before establishing the model, the following theorem needs to be given.
Definition 1 (fitness difference function). Let d(ξtopt), t>0 be a random variable, then d(ξtopt )=f(ξtopt )−fopt is called the fitness difference function, where ξtopt represents the optimal individual of the t generation, and fopt represents the target fitness value, which measures the distance of the t generation population to the optimal solution.
Definition 2 (progress rate) [28]. During the running of EAs, the progress rate represents the decrease in the optimal distance between the t−1 to t generation populations, i.e., Xt=d(ξt−1opt )−d(ξtopt ),t=1,2,…, and quality gain represents the decrease in fitness between t−1 generation and t generation populations, which reflects the convergence time of EAs. The larger the progress rate, the faster the distance reduction from the optimal solution changes, and the faster the convergence time. It is obvious that {Xt}∞t=0 is a non-negative stochastic process, and the definition is as follows.
Definition 3 (renewal process of progress rate). Let {Xt}∞t=0 be a non-negative stochastic process. If there exists Yt=∑tn=1Xn=d(ξ0)−d(ξtopt) for any t=1,2,… then Yt is referred to as the renewal process of the progress rate of EAs in the t generation.
In stochastic algorithms, the first hitting time is an effective way to characterize its performance, i.e., the number of generations when EAs find a satisfactory solution for the first time. It can be described by the stopping time of the renewal process, and the definition of stopping time is defined.
Definition 4 (stopping time of renewal process). Let {Xt}∞t=0 be a non-negative stochastic process, if Tτ={τ|∑τ−1k=1Xk<d(ξ0)−ε,∑∞k=τXk⩾d(ξ0)−ε} is satisfied, then Tτ is described as a stopping time of Xt, where τ is a non-negative random variable.
The stopping time of the renewal process is an important concept in stochastic processes, which is described as independent of the state of the progress rate stochastic process {Xt}∞t=Tτ after time Tτ and related to the state of the progress rate stochastic process {Xt}t=Tτ0 before that time.
Theorem 1 (Wald's equation). If {Xt}∞t=0 are random variables with independent and identically distributed X having finite expectations E(X)<∞, and Tτ is a stopping time for {Xt}∞t=0 such that E(Tτ)<∞, then
Proof. Let: It = {1, if Tτ≤t;0, if Tτ>t.. Because {It=1}={Tτ⩽t}=∪tk=1{Tτ=k} and the progress rate stochastic process {Xt}∞t=Tτ are independent of each other, it can be concluded that {It=0} and {Xt}∞t=Tτ are also independent of each other. Therefore,
In Theorem 1, it holds true that the expectation of the renewal process of the progress rate is equal to the expected first hitting time multiplied by the expected progress rate.
Inference 1 (Wald's inequation). According to Theorem 1, in the running of EAs, if Tτ is the stopping time of {Xt}∞t=0 and there are two functions M1 and M2 that make M1<E(Xt)<M2 hold, then E(∑Tτt=1Xt) satisfies:
We can derive the renewal theory theorem for the expected first hitting time based on Inference 1, as shown in Theorem 2.
Theorem 2 (renewal theorem). If {Xt}∞t=0 are random variables with independent and identically distributed X having M1<E(X)<M2 and Tτ is a stopping time for {Xt}∞t=0 such that E(Tτ)<∞, then
Proof. For the lower bound proof, the stopping time Tτ={τ|∑τ−1k=1Xk<d(ξ0)−ε,∑∞k=τXk⩾ d(ξ0)−ε} in Definition 4 is equivalent to Tτ={τ|∑τk=1Xk>d(ξ0)−ε,∑τ−1k=1Xk⩽d(ξ0)−ε}, it follows from Inference 1 that the equation dTτ<E(∑Tτn=1Xn)<M2E(Tτ) holds. Thereby, limdTτ→∞infE(Tτ)dTτ>1M2. Now, we prove its upper bound. Let us fix a constant a and define another renewal process, i.e., Xrt={Xt,ifXt≤aa,ifXt>a,
μa=min{M1,infE(Xrt)}. Since 0<Xrt<Xt and 0<μa<E(Xrt) < M2, for all t, it follows that E(∑Trn=1Xn)<E(∑Ttn=1Xn), i.e., E(Tr)>E(Tt). Due to Inference 1, this yields μaE(Tt)<μaE(Tr) < E(∑Trn=1Xn)<dTτ+a, i.e., limdTτ→∞supE(Tτ)dTτ<1M1, thus 1M2<E(Tτ)dTτ<1M1.
In the running of EAs, due to the difficulty in finding the optimal solution, when the fitness difference function value of the parent individual to the optimal solution is equal to ε, the algorithm terminates, that is, it reaches a specific stopping distance of Yt=E(∑Tτt=1Xt)=d(ξ0)−ε, and then Theorem 3 represents the stochastic process model of the expected first hitting time analysis.
Theorem 3 (renewal model). According to Theorem 2, in the running of EAs, if Tτ is the stopping time of {Xt}∞t=0 and there exist two functions M1 and M2, such that M1<E(Xt)<M2, when EAs pass through the interval [ε,d(ξ0)], then it holds for Tτ that
Theorem 3 can be obtained from the proof of the additive drift theorem of Kötzing [29], which is a continuous space adaptation of the original discrete space drift result of He and Yao [30]. In Theorem 3, the upper and lower bounds on the expected progress rate vary as a function of M1 and M2, which result in tighter upper and lower bounds on the first hitting time. Sections 3 and 4 analyze the expected first hitting time on the sphere function using the uniform and Gaussian mutation operators as a basis.
3.
Sphere function and uniform distribution
In this section, we prove that there is an exponential lower bound on the expected first hitting time when the (1 + 1) ES with a uniform mutation operator is used to solve the sphere function minimization problem, which will be given in Theorem 4.
Theorem 4. In the running of the (1 + 1) ES with elitist selection, when the radius of the sphere function of the n-dimensional Euclidean space goes from fitness difference function value R/2 to ε, then the lower bound of the first hitting time Tτ is satisfied:
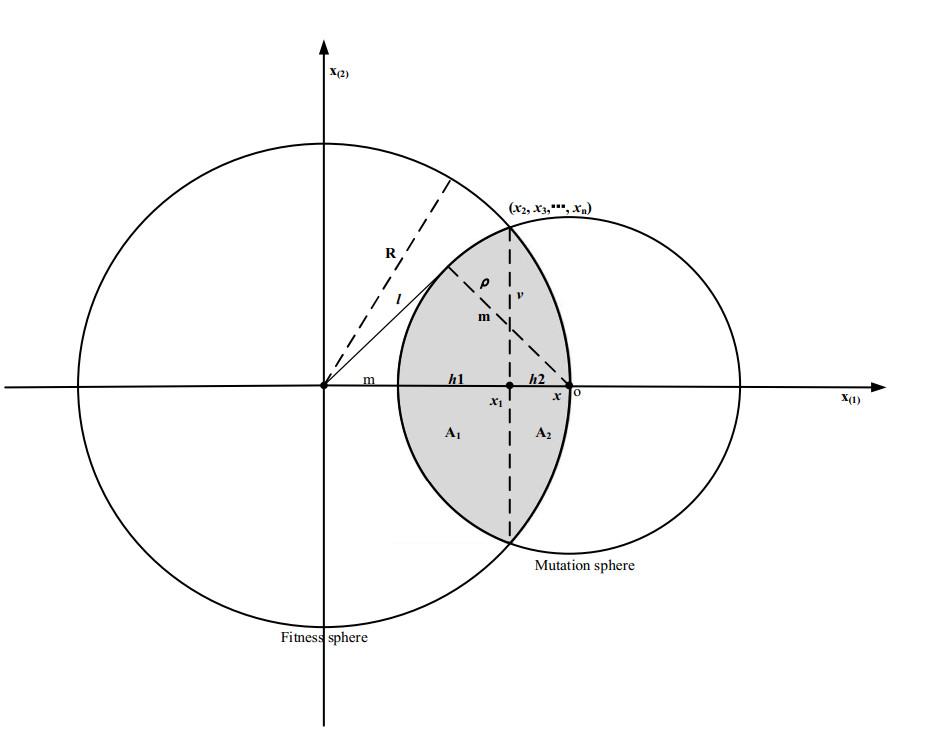
Due to the symmetry of the sphere, we assume that the current individual is located on the ox axis, the distance from the center of the fitness hypersphere is R, the state of the individual is o, and the n dimensional sphere with o as the center and ρ as the radius is the mutation sphere E1, which contains the next generation of individuals that are likely to reach the set. At the same time, fitness hypersphere E2 contains all possible solution space sets of the next-generation individual better than the current individual, as shown in Figure 1. However, during the running of (1 + 1) ES, not all the next-generation individuals generated by the mutation operator are superior to the previous-generation individuals. Therefore, we regard the fitness spherical cap A2 and mutation spherical cap A1 as the reached region S0=E1∩E2=A1∪A2 by the next generation individuals, and the two spherical caps can be regarded as the cut-off of the same hyperplane P, i.e., the success region. The region is irregular and the calculation of the volume is relatively complicated, so we will calculate the volume of the spherical cap by means of the spherical sector and the spherical cone. Next, we will give some important conclusions.
3.1. The uniform distribution inside the sphere
Suppose that in the n-dimensional sphere, the uniform mutation operator is uniformly distributed in the sphere with radius ρ, then, its corresponding volume is denoted as
and the probability density function of the sphere with radius ρ is
where IDn(ρ)(x) is the indicator function. When the uniform mutation operator is evenly distributed in the radius ρ sphere, the corresponding value is 1; otherwise, the value is 0. For more details, see [31].
Lemma 1. Let the radius of the hypersphere containing the spherical cap be r and its height be h. Then, the volume of the spherical sector is
where Scap is the area of the spherical cap and n represents the dimension of the hypersphere.
Lemma 2. Let the radius of the hypersphere containing the spherical cap be r and its height be h, n>3. Then, the area of the spherical cap is
Lemma 3. Let the radius of the bottom surface of the spherical cap be rcap and its height be h. Then, the volume of the spherical cone is
Theorem 5. Let the radius of the hypersphere containing the spherical cap be r, its radius of the bottom surface be rcap, and its height be h. Then, the volume of the spherical cap is
To calculate the volume of the fitness spherical cap, it is necessary to calculate not only the area Sfcap of the fitness spherical cap, but also the bottom radius rfcap, its heights h2 and h1, and the simultaneous equations:
We get it by solving
where x1 denotes the abscissa of the common hyperplane of the fitness and mutation spherical cap. Let the heights of the corresponding spherical caps be h2 and h1. The association with Eq (14) yields
From Eq (15), we can obtain h2 and h1. Next, we compute the bottom radius of the common hyperplane of the fitness and mutation spherical cap, and it is useful to assume that the height of the spherical cap is 0<h1,h2<R. Then, the bottom radius rfcap is
3.2. The volume of the fitness spherical cap
Before calculating the volume of the fitness spherical cap, its area is calculated without loss of generality. Assume that the radius of the mutation sphere where the fitness sphere cap intersects with the mutation sphere is ρ, the radius of the fitness sphere is R, its heights are h2<R and n>3, and the bottom radius is rcap; then the volume of the fitness spherical cap is discussed in two cases:
ⅰ) When n is odd:
We substitute Eqs (14)-(16) into Vol=1nSfcapR−1nπn−12Γ(n−12+1)(rcap)n−1(R−h2) to obtain the volume of the fitness spherical cap as:
ⅱ) When n is even:
Similarly, we substitute Eqs (14)-(16) into Eq (12) to obtain the volume of the fitness spherical cap as:
3.3. The volume of the mutation spherical cap
Assume that the radius of the fitness sphere where the mutation spherical cap intersects with the fitness sphere is R, the radius of the mutation sphere is ρ, its heights are h1<ρ and n>3, and the bottom radius is rcap. Then the volume of the mutation spherical cap is discussed in two cases:
ⅰ) When n is odd:
Inserting Eqs (15), (16), and (20) in Vol=1nSmcapρ−1nπn−12Γ(n−12+1)(rcap)n−1(ρ−h1), we obtain the volume of the mutation spherical cap as:
ⅱ) When n is even:
Inserting Eqs (15), (16), and (22) in Vol=1nSmcapρ−1nπn−12Γ(n−12+1)(rcap)n−1(ρ−h1), we obtain the volume of the mutation spherical cap as:
Since the expected progress rate probability density function is not easy to accurately calculate [32], it is difficult to calculate the expected first hitting time of the (1 + 1) ES on the sphere function. Therefore, we estimate by calculating the sum of the volume of the mutation spherical cap and the volume of the fitness spherical cap, which provides a theoretical basis for improving the estimation of the lower bound of the first hitting time of (1 + 1) ES on the sphere function.
3.4. Expected first hitting time of (1 + 1) ES
The position of the next generation of individuals generated by (1 + 1) ES during the running of the sphere function is the gray part of Figure 1, i.e., the intersection of the irregular successful regions is the union of spherical caps A1 and A2:
By Definition 2, we get the expected progress rate:
ⅰ) When n is even:
According to Eqs (24) and (25), we can obtain:
In order to calculate G1, we reduce the dimension of the integral to make w=‖v‖2. Thus, we obtain:
Because the integrand function of this integral contains the radical √(R−x)2+w, it is difficult to solve the integral. By taking into account the idea of substitution that regards (R−x)2 as the common factor of (R−x)2+w under the radical sign, where w=u(R−x)2, then dw=(R−x)2du, √(R−x)2+w=(R−x)√1+u and √1+u=1+12u+18u2+⋯ +12(−12)⋯(12−m+1)m!um+Rm(u). When w=0, u=0; when w=ρ2−x2, u=ρ2−x2(R−x)2. Hence, we obtain:
Similarly,
According to Eqs (26)-(29), we can draw the following conclusions:
ⅱ) When n is odd:
By Eqs (24) and (30), we can draw the following conclusions:
Also, from Eqs (27)-(29), the following asymptotic expressions can be approximated:
Obviously, when the dimension of the sphere function is odd or even, we find that the upper bound on the expected progress rate is exponential. By Theorem 3, the expected first hitting time E(Tτ) from the fitness difference function value R to R/2−ε in the running of the sphere function with a uniform mutation operator is:
Let c=ln(ρR), thus (ρR)=ec, then we can get that E(Tτ)>Ω(ecn) is the expected first hitting time of the elitist selection (1 + 1) ES with a uniform mutation operator solving sphere function. Therefore, Theorem 4 holds.
Theorem 4 has significantly improved the current lower bound Ω(n), which has a significant effect on reducing the time complexity of analyzing the 1/5 success rule of (1 + 1) ES.
4.
The sphere function and Gaussian mutation operator
Without loss of generality, the Gaussian mutation operator is different from the uniform mutation operator. It is assumed that independent offspring individuals are generated through the mutation vector m=σnN(0,I) and obey Gaussian distribution (see Figure 1).
Theorem 6. Let x=(x1,x2,⋅⋅⋅,xn) be an individual from the population σnN(0,I). Then
which obeys the chi-square distribution with degree of freedom n, and is denoted as k2∼χ2(n). The probability density function of k=√x21+x22+⋅⋅⋅x2n is
These results are a simplified form of [32]. For a more detailed proof, see [33]. Its mathematical expectations are as follows:
When n→∞, then
The validity of relation l2=k2−m2+(R−m)2 is evident based on the observations from Figure 1. Since offspring individuals ξtopt are generated by the mutation vector m=σnN(0,I) and d(ξt−1opt) is a constant, d(ξt−1opt)−d(ξtopt) is a random variable that depends on the mutation vector, and the specific form of d(ξtopt) is as follows [33]:
The d(ξt−1opt)−d(ξtopt) probability density function is
Thus, we can get the expected progress rate E(Xt):
where m1=k22R and m2=k=√nσ.
By normalizing the expected progress rate E(Xt) and the mutation strength σ [32]:
And we can get the normalized expected progress rate E∗(Xt):
Since (1 + 1) ES is adopted as the elitist selection strategy, R2−ε<E∗(Xt)<E∗(X0)<R holds for ∀t∈(0,τ). By Theorem 3, when running (1 + 1) ES on the sphere function, the first hitting time E(Tτ) from the fitness difference function value R2 to ε with a Gaussian mutation operator holds:
which implies that we obtain the upper bound of the first hitting time. The above analysis shows that we can consider that each individual follows an independent isotropic distribution. Jägersküpper [24] adopted a similar approach to analyzing the first hitting time of (1 + 1) ES on the sphere function and obtained the lower bound of the first hitting time, while the upper bound was not given the relevant theoretical analysis. It is shown that the proposed method is valuable for the first hitting time analysis of population-based algorithms.
5.
Numerical experiments and result analysis
The purpose of the experiments in this section is to verify the upper and lower bounds on the theoretical accuracy of the expected first hitting time for (1 + 1) ES with uniform and Gaussian mutation operators solving sphere functions.
5.1. Experimental parameter setting
In this section, we mainly set the following experimental parameters: R=d(ξ0)=(x1,x2,…,xn)=(5,0,…,0)=5,ρ=1,ε=0.001, and n∈[1,100]. For each given problem size n, we conduct 100 runs for Algorithm 1 on the sphere function. We define Tri to denote the i-th run first hitting time of Algorithm 1 and E(Tτ)=∑100i=1Tri100 to denote the actual running average first hitting time, i.e., E(Tτ)=t.
5.2. (1 + 1) ES with a uniform mutation operator
Theorem 4 gives the expected first hitting time of (1 + 1) ES with a uniform mutation operator from the previous Ω(n) to Ω(ecn). We arbitrarily take n∈[20,100] to verify that its lower bound is exponentially related to the problem size n. To verify the exponential time of the first hitting time, we only need to verify the linear relationship between logt and the problem size n, thus verifying our theoretical results. MATLAB simulation results are shown in Figure 2.
We can see from Figure 2 that logt increases with increasing problem size n, showing a linear relationship. Consequently, we have derived a tighter lower bound for the time complexity, which is consistent with the theoretical lower bound for the analysis time.
5.3. (1 + 1) ES with a Gaussian mutation operator
In Section 4, O(n2√n) is given as the upper bound of the expected first hitting time of (1 + 1) ES with a Gaussian mutation operator. The first hitting time of a polynomial is acceptable in real-world optimization problems. MATLAB simulation results are shown in Figure 3.
We can see from Figure 3 that when about n<20, the first hitting time increases as problem size n increases, which is faster than that of about n>20. We think that the first hitting time is a polynomial when n is large enough.
6.
Conclusions
In this paper, it is difficult to estimate the upper and lower bounds of (1 + 1) ES in the first time-solving sphere function, and the renewal model is proposed to solve it. The proposed method does not aim to directly determine the first hitting time, but views the individual population as a special renewal process, by introducing the stopping time of the special renewal process and combining Wald's inequality with the renewal theorem. The model is independent of the specific implementation of the algorithm and presents a gradual convergence process of EAs on a continuous search space, showing the gradual convergence process of (1 + 1) ES in a continuous search space. To verify the validity of the proposed method, we analyze the expected first hitting time of (1 + 1) ES on the sphere function. We obtain the lower bound of exponential time Ω(dm) with a uniform operator (1 + 1) ES and the upper bound of polynomial time O(n2√n) with a uniform operator (1 + 1) ES. Furthermore, the proposed method can be applicable to other intelligent optimization algorithms, such as differential evolution algorithm and particle swarm optimization.
This will also be further investigated in our future work. Based on the progress rate, statistical methods will be used to estimate the first hitting time of EAs, especially in the running time analysis with recombination, which will be very challenging. In addition, based on the discussed upper bound on the running time of (1 + 1) ES with a Gaussian mutation operator, another direction for further research is to analyze the lower bound on the running time of (1 + 1) ES with a Gaussian mutation operator. A closed interval can be constructed by upper and lower bounds to estimate the first hitting time of EAs, and then the theoretical results can be extended to the practical application of EAs.
Use of AI tools declaration
The authors declare they have not used artificial intelligence (AI) tools in the creation of this article.
Acknowledgments
The authors extend their sincere gratitude to the anonymous reviewers for their helpful comments and insightful suggestions. This work was supported by the Science and Technology Plan Project of Guizhou Province (QKH-Foundation-ZK[2022] General 550, QKH-Platform Talent-ZCKJ[2021]007), the Youth Science and Technology Talent Growth Project of the Guizhou Provincial Education Department (QJH-KY[2021]115, QJH-KY[2022]177), the Open Project of the Guizhou Key Laboratory of Pattern Recognition and Intelligent System (GZMUKL[2022]KF05), the Ministry of Education's Industry-University Collaborative Education Project (221001766110209), and the Research Fund Project of the Guiyang Institute of Humanities and Technology (2022RWJS034).
Conflict of interest
The authors declare that there are no conflicts of interest.









 DownLoad:
DownLoad:




