Dynamics and density function for a stochastic anthrax epidemic model

1.   Introduction

Anthrax is a contagious disease caused by bacteria produced by gram-positive endospores and can be spread between animals and humans ^[1]. The disease can infect all warm-blooded animals, especially herbivores such as cattle, sheep, goats, and horses ^[2,3,4,5]. When herbivores ingest a sufficient number of spores from soil and plants, they are usually infected with anthrax. Once infected, the animal will die within 24–48 hours ^[6,7]. Humans are infected with anthrax primarily through contact with diseased animals. Once the bacteria enters the human body, it can cause symptoms such as fever, skin lesions and breathing difficulties ^[7]. Anthrax spores have a strong ability to survive, which can result in contaminated soil and water becoming long-lasting sources of infection ^[9]. Anthrax occurs worldwide in 2004, a massive outbreak of anthrax killed up to 500 animals in Zimbabwe, and 109 animal anthrax deaths were reported in North Dakota in 2005. Between August 2009 and October 2010, there was an outbreak of 273 human cutaneous anthrax cases and 140 animal anthrax deaths in Bangladesh ^{[10,11,12,13,14]}. In a limited resource environment, anthrax has caused great harm to the development of animal husbandry and human health. As a result, anthrax has attracted widespread attention, and some progress has been made in disease control and vaccine research. In order to efficiently control the spread of anthrax, it is imperative to investigate the dynamics of the disease.

In the past few decades, various mathematical models have been intensively studied on anthrax dynamics. In previous studies, Hahn and Furniss analyzed how anthrax spreads and determined the threshold of the disease ^[15]. In relation to animal migration, Friedman and Yakubu addressed the basic reproduction number of the model. They examined the sufficient conditions for the presence of an endemic equilibrium point in the diffusion model ^[16]. Mushayabasa et al. investigated the global asymptotic stability of the endemic equilibrium point by analyzing a model that considers the vectorial impacts of anthrax transmission ^[17]. In fact, the spread of the virus is linked to climate, season, temperature and humidity. Due to the complexity of the environment system, the parameters of the system inevitably change randomly due to perturbations, thus making it random. Incorporating randomness into mathematical models of biological and biochemical processes is essential for gaining a deeper comprehension of the mechanisms that regulate biological systems ^[18]. From ^[19,20], Cai and Wang examined how changes in the environment affect the spread of diseases by analyzing the random fluctuations in a susceptible-infected-susceptible (SIS) model that includes media coverage. However, few studies have constructed stochastic processes into anthrax models, which facilitates the study in this paper.

Soil renovation, heavy rains, and flash floods can lead to a rise in spore levels in the surroundings, heightening the likelihood of infection ^[21]. It is crucial to take into account environmental disturbances when studying anthrax. Based on the existing research ^[7], we present a stochastic model of anthrax to explore the impact of stochastic disturbances on threshold dynamics. The stability of the new model and the probability density function in the case of disease persistence are worth studying. It is well known that the endemic equilibrium point and the basic reproduction number can reflect the persistence of the disease for identified systems. However, environmental perturbations are unpredictable, so there is no positive equilibrium in the stochastic system ^[22]. In this way, a stochastic anthrax model is investigated for the stationary distribution of disease persistence. In practice, the statistical nature of the model can lead to prevention and control the disease easier ^[22,23]. However, the resolution of the high-dimensional Fokker-Planck equation presents a challenging task, and only a limited number of research endeavors have been dedicated to addressing the computation of the probability density function. To close this gap, in this paper we employ the four-dimensional Fokker-Planck equation to investigate the probability density function for the stochastic anthrax model. Our article has the following contributions:

● On the basis of existing research ^[7], we propose a stochastic anthrax model. Sufficient conditions for the existence of an ergodic stationary distribution of globally positive solutions are established.

● The probability density function expression has been explored by few studies due to the difficulty of solving the high-dimensional Fokker-Planck equation. Therefore, this study investigates the precise representation of the probability density function in the vicinity of the quasi-equilibrium point of the model when a persistent disease is present.

The rest of our paper is arranged as follows. Section 2 introduces the mathematical models and gives the relevant notation and lemma. Section 3 proves the unique ergodic stationary distribution existence when $R^s > 1$. In Section 4, when $R^s > 1$, the probability density function is obtained by solving the Fokker-Planck equation in four dimensions. Section 5 provides the numerical simulations for our results of the analysis. The main results are discussed in Section 6.

2.   Model formulation and preliminaries

2.1.   Anthrax model formulation

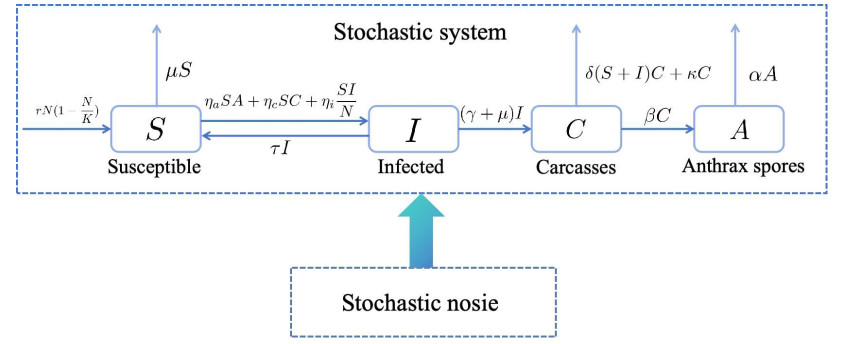
Understanding the transmission mechanisms of anthrax epidemics requires the use of mathematical models as an important tool. As it is known that there are different forms of anthrax models, here we consider the following anthrax model ^[7]:

where $S(t)$ and $I(t)$ are the number of susceptible and infected animals at time t, respectively. $N(t) = S(t)+I(t)$ denotes the total live animal population at time t, $A$ denotes grams of spores in the environment, and $C$ denotes the number of infected carcasses. The birth rate of animals is $r > 0$, $K$ is the animal carrying capacity, and $rN(1-\frac{N}{K})$ is born into the susceptible class per unit time. $\eta_a$ is the transmission rate of environment to susceptible animals, $\eta_c$ is the transmission rate of infected carcasses to susceptible animals, and $\eta_i$ is the transmission rate of infected animals to susceptible animals, so $\eta_a > 0, \eta_c > 0, \eta_i > 0$. $\mu$ is the death rate, $\gamma$ is the disease death rate, $\alpha$ is the spore decay rate, $\beta$ is the spore growth rate, $\delta$ the is carcass consumption rate, $\kappa$ is the carcass decay rate, and $\tau$ denotes the recovery rate of infected animals.

Assume that $\frac{\eta_i}{\gamma+\mu+\tau} < 1$, otherwise the anthrax increase is unbounded. On account of the total live animal population as $N(t) = S(t)+I(t)$, adding the equation $S(t)$ and $I(t)$ results in

and if $r > \mu$, this implies that $\limsup_{t\to \infty }N(t) \leqslant K(1-\frac{\mu}{r}) = S_0$.

Assuming $0 < N(0)\leqslant S_0$, the positive invariant is

The disease-free equilibrium point $E_0$ and the endemic equilibrium point $E^*$ are obtained by solving the equation. $E_0 = (S_0, 0, 0, 0), E^* = (S^*, I^*, A^*, C^*)$, where

$N^* = S_0-\frac{K\gamma}{r}(1-\frac{1}{D})$ with $D = \frac{\eta_i}{\gamma+\mu+\tau}+\frac{\gamma+\mu}{\gamma+\mu+\tau}\frac{\eta_cN^*}{\delta N^*+\kappa}+\frac{\gamma+\mu}{\gamma+\mu+\tau}\frac{\beta\eta_aN^*}{\alpha(\delta N^*+\kappa)}$, and the basic reproduction number of Model (2.1) is

According to Saad-Roy et al. ^[7], the main results about the stability of the equilibrium point are as follows:

(i) If $\mathit{R_0} < 1$, the disease-free eqilibrium $E_0 = (S_0, 0, 0, 0)$ is globally asymptotically stable; thus a small outbreak of anthrax is eradicated. If $\mathit{R_0} > 1$, the disease-free equilibrium is unstable; thus, anthrax persists.

(ii) If $\mathit{R_0} > 1$, there has a unique endemic equilibrium with $E^* = (S^*, I^*, A^*, C^*)$, which is globally asymptotically stable in $\Gamma$.

In real life, the dynamic behaviors of anthrax are disturbed by random factors in nature. In this paper, we consider random noise on the basis of the Model (2.1) and adopt the method used by Imhof et al. ^[24]. Our hypothesis posits a direct correlation between stochastic fluctuations and $S(t), I(t), A(t), C(t)$. Thus, the stochastic model for anthrax transmission is to be described in the following form:

where $\sigma_i$ $(i = 1, 2, 3, 4)$ represents the intensities of the white noises and the definition of $B_i(t)$ $(i = 1, 2, 3, 4)$ is based on complete probability space and is independent of standard Brownian motions. The transmission diagram illustrating the dynamics of anthrax transmission is shown in Figure 1. After giving the basic information of the anthrax model, the relevant lemma is given in the following section.

2.2.   Notations and lemmas

Throughout this paper, we use $X(t) = (S(t), I(t), A(t), C(t))$ as the solution of Model (2.2) with the initial value $X(0) = (S(0), I(0), A(0), C(0))$. Let $(\Omega, \mathcal{F}, \{\mathcal{F}_t\}_{t\geqslant0}, \mathbb{P})$ be the probability space with the filtration $\{\mathcal{F}_t\}_{t\geqslant0}$ satisfying the usual conditions that are right continuous, and $\mathcal{F}_0$ contains all $\mathbb{P}$-null sets. Let $\mathbb{R}_+^4$ be an-dimensional Euclidean space and $U_n = [\frac{1}{n}\cdot n]\times[\frac{1}{n}\cdot n]\times[\frac{1}{n}\cdot n]\times[\frac{1}{n}\cdot n]$.

Our focus in this section is on the existence and uniqueness of a globally positive solution. In order to achieve this goal, Lemma 2.1 is introduced to demonstrate the existence of a positive solution to the Model ($2.2$). The proof of the existence theorem for positive solution can be obtained in terms of Mao and Bahar ^[25,26], so the proof is omitted here.

Lemma 2.1. For any initial value ${X(0) = (S(0), I(0), A(0), C(0))} \subseteq \mathbb{R}_+^4$, Model ($2.2$) has a unique global positive solution ${X(t) = (S(t), I(t), A(t), C(t)), t\geqslant0 }$, and the solution will remain in $\mathbb{R}_+^4$ with probability one.

Based on the existence of the positive solution, the next step we will concentrate on is the asymptotic estimate of the Model (2.2).

Lemma 2.2. If for all $\epsilon > 1$, the following inequalities hold

there exists a positive constant $\hat{T}(\epsilon)$ such that the solution ${X(t) = (S(t), I(t), A(t), C(t)) }$ with initial value $X(0)\subseteq\mathbb{R}_+^4$ has the following property $\limsup_{t\to \infty }\mathbb{E}|X(t)|\leqslant \hat{T}(\epsilon)$. For this expression, the solution $X(t)$ is stochastically ultimately bounded.

The proof of Lemma 2.2 is shown in the Appendix.

Let $X(t)$ be a regular time-homogeneous Markov process in $\mathbb{R}^l$ described by the following stochastic differential eqaution: $\mbox{d}X(t) = b(X)\mbox{d}t+\sum_{r = 1}^kg_r(X)\mbox{d}B_r(t)$. The diffusion matrix is defined as follows: $B(X) = ((b_{i, j}(X))), b_{i, j}(X) = \sum_{r = 1}^{k}g^i_rg^j_r(X)$, where $X(t)$ is nonsingular ^[27], then we have the following lemma.

Lemma 2.3. (Khasminskii ^[27]). The Markov process $X(t)$ has a unique ergodic stationary distribution $v(\cdot)$ if there exists a bounded open domain $U\subset\mathbb{R}^l$ with regular boundary $\Gamma$ and if it has the following properties:

(i) There exists a positive $\bar{E}$ such that $\sum_{i, j = 1}^{n}b_{ij}(X)\xi_i\xi_j \geqslant\bar{E}|\xi|^2$, $X\in U$, $\bar{E}\in \mathbb{R}^l$;

(ii) There exists a nonnegative $C^2$-function $V$ such that $LV$ is negative for any $X\in \mathbb{R}^l\backslash U$.

Thus the Markov process $X(t)$ has a stationary distribution $v(\cdot)$. Let $f(x)$ be a function integrable with respect to the measure $\pi$, for all $x\in \mathbb{R}^l$. We can get

According to the Routh-Hurwitz stability principle and Zhou et al. ^[28], the following algebraic equation solving theory is given.

Lemma 2.4 (Zhou et al. ^[28]). For the four-dimensional real matrix $D = diag(\sigma_1, \sigma_2, \sigma_3, \sigma_4)$, $Z = (a_{ij})_{4\times4}$, the characteristic polynomial of $Z$ is $\omega_Z(\zeta) = \zeta^4+s_1\zeta^3+s_2\zeta^2+s_3\zeta+s_4$. Assuming that $\Lambda = (\nu_{ij})_{4\times4}$ is a symmetric matrix, we have the following algebraic equation

If $Z$ has all negative real part eigenvaues, that is,

then $\Lambda$ is a positive definite matrix.

Using Lemmas 2.5–2.7, we will develop solutions for the four dimensions as described by Tan et al. ^[23] and Zhou et al. ^[29].

Lemma 2.5 (Zhou et al. ^[29]). For the algebraic equation $G_0^2+B_1X_1+X_1B_1^T = 0$ and $G_0 = \mathit{\mbox{diag}}(1, 0, 0, 0)$,

where $r_{22} = \frac{a_3}{2(a_1(a_2a_3-a_1a_4)-a_3^2)}, r_{13} = -r_{22}, r_{33} = \frac{a_1}{a_3}r_{22}, r_{11} = \frac{a_2a_3-a_1a_4}{a_3}r_{22}, r_{24} = -r_{33}, r_{44} = \frac{a_1a_2-a_3}{a_3a_4}r_{22}$. If $a_1 > 0$, $a_3 > 0, a_4 > 0$ and $a_1a_2-a_3 > 0, a_1(a_2a_3-a_1a_4)-a_3^2 > 0$, then the matrix $X_1$ is postive definite.

Lemma 2.6 (Tan et al. ^[23]). For the algebraic equation $G_0^2+B_2X_2+X_2B_2^T = 0$ and $G_0 = \mathit{\mbox{diag}}(1, 0, 0, 0)$,

where $\widetilde{r}_{22} = \frac{1}{2(b_1b_2-b_3)}, \widetilde{r}_{13} = -\widetilde{r}_{22}, \widetilde{r}_{11} = b_2\widetilde{r}_{22}, \widetilde{r}_{33} = \frac{b_1}{b_3}\widetilde{r}_{22}$. If $b_1 > 0, b_3 > 0$ and $b_1b_2-b_3 > 0$, then the matrix $X_2$ is semi-postive definite.

Lemma 2.7 (Tan et al. ^[23]). For the algebraic equation $G_0^2+B_2X_2+X_2B_2^T = 0$ and $G_0 = diag(1, 0, 0, 0)$,

where $\widetilde{r}_{11} = \frac{1}{2c_1}, \widetilde{r}_{22} = \frac{1}{2c_1c_2}$. If $c_1 > 0$ and $c_2 > 0$, then the matrix $X_3$ is semi-postive definite.

For a stochastic model, stability is the basis for studying other properties, so the stationary distribution is an important research content. Thus, the ergodic stationary distribution of the Model (2.2) is studied in the following section.

3.   Stationary distribution

Due to the complex structure of nonlinear systems, it is generally difficult to solve their state equations. Therefore, the Lyapunov method has been widely applied ^{[30,31,32,33,34,35]}. In this section, within the framework of the stochastic Lyapunov method, we will provide sufficient conditions for the ergodicity of the global positive solution and the existence of a stationary distribution.

Define

where $\mathit{R^s}$ is a stochastic threshold for Model (2.2). Next, its ergodicity is discussed using threshold.

Theorem 3.1. If ${R}^s > 1$, for any initial value $(S(0), I(0), A(0), C(0))\in \mathbb{R}^4_+$, then Model ($2.2$) has a unique stationary distribution v(·) and it follows the ergodic property.

Proof. The diffusion matrix of Model ($2.2$) is given by

where $X = (S, I, A, C)$. Choose $\bar{E} = \min_{(SI, A, C)\in\bar{U}\subset\mathbb{R}_+^4}\{\sigma_1^2S^2, \sigma_2^2I^2, \sigma_3^2A^2, \sigma_4^2C^2\}$, then we have $\bar{E} > 0$, where $\bar{U} = [\frac{1}{n}\cdot n]\times[\frac{1}{n}\cdot n]\times[\frac{1}{n}\cdot n]\times[\frac{1}{n}\cdot n]$. For any $(S, I, A, C)\in \bar{U}$ and $(\xi_1, \xi_2, \xi_3, \xi_4)\in\mathbb{R}^4_+$, from (3.1), we have

where $|\xi| = (\xi_1^2+\xi_2^2+\xi_3^2+\xi_4^2)^\frac{1}{2}$, then the condition (i) in Lemma 2.3 holds.

Construct the following function:

and the positive constants $m_i$ $(i = 1, 2, 3, 4)$ will be determined at a later stage. By It$\hat{o}$'s fomular, it can be obtained that

Let

then we can get

Thus,

Define the function

where $W_2 = S+I, W_3 = -\ln S, W_4 = -\ln I, W_5 = -\ln A$, and $W_6 = \frac{1}{p+1}(S+I)^{p+1}$. Select a suitable constant $M > 0$ satisfying the following condiction

where

It is easy to check that

where $U_n = [\frac{1}{n}\cdot n]\times[\frac{1}{n}\cdot n]\times[\frac{1}{n}\cdot n]\times[\frac{1}{n}\cdot n]$. Furthermore, $W(S, I, A, C)$ is a continuous function. Hence, $(S, I, A, C)$ must have a minimum point $(\bar{S}_0, \bar{I}_0, \bar{A}_0, \bar{C}_0)$ in the interior of $\mathbb{R}^4_+$, then we define a nonnegative function $\bar{W}:\mathbb{R}^4_+\to\mathbb{R}$ as follows

By utilizing It$\hat{o}$'s formula, we can derive the following result

and

Choose $0 < p < \min\{1, \frac{\mu}{\sigma_1^2}\land\frac{\mu+\gamma}{\sigma_2^2}\}$, then we can see that

hence,

Next, we form a condensed subset D in order to satisfy the condition (ii) as outlined in Lemma 2.3. Define the bounded closed set

where $\xi$ is a suffciently small constant. Choose $\xi$ satisfying the following conditions

where

Divide $\mathbb{R}_+^4\setminus D$ into six domains:

We aim to demonstrate that the inequality $L\bar{W}(S, I, A, C)\leqslant -1$ holds true on the domain $\mathbb{R}_+^4\setminus D$. This is equivalent to establishing its validity on the six specified domains.

Case 1: If $(S, I, A, C)\in D_1$, one can see that

Case 2: If $(S, I, A, C)\in D_2$, one can see that

Case 3: If $(S, I, A, C)\in D_3$, one can see that

Case 4: If $(S, I, A, C)\in D_4$, one can see that

Case 5: If $(S, I, A, C)\in D_5$, one can see that

Case 6: If $(S, I, A, C)\in D_6$, one can see that

Hence, we obtain $L\bar{W}\leqslant-1$ for all $(S, I, A, C)\in\mathbb{R}_+^4\setminus D$. According to Lemma 2.3, it can be deduced that the Model ($2.2$) possesses a unique stationary distribution denoted as v(·). This serves to conclude the proof.

Remark 1. As we know, a deterministic system disease persistence is measured according to the basic reproduction number $\mathit{R_0}$ and the endemic equilibrium point $E^*$. However, in a stochastic model, there is no positive equilibrium due to unpredictable noise perturbations. Therefore, the persistence of the disease in a stochastic system is reflected by the presence of an ergodicity stationary distribution. According to Theorem 3.1, Model (2.2) has a unique stationary distribution when $R^s > 1$. Comparing the expressions for $R_0$ and $R^s$, we find that $R^s\leqslant R_0$ and the presence of disease in both the model and the stochastic model can be assessed using a consistent measure of $R^s > 1$.

Remark 2. Model (2.2) characterizes the impact of random noise on the spread of anthrax, which is an extension of Model (2.1). When random noise is absent, i.e., $\sigma_i = 0$ $(i = 1, 2, 3, 4)$, Model (2.2) degenerates into Model (2.1).

4.   Probability density function

This section aims to derive the precise formulation of the density function for Model (2.2) at a quasi-equilibrium point. It is important to emphasize that the probability density function serves as a representation of the dynamic attributes of a stochastic system with statistical relevance. Our main goal is to ascertain the probability density function for the purpose of examining the dynamics of the model from a statistical perspective.

Before proving the probability density function, two equivalent differential equation forms for Model ($2.2$) are given. Let $x_1 = \ln S, x_2 = \ln I, x_3 = \ln A, x_4 = \ln C$. By It$\hat{o}$'s formula, an equivalent model can be obtained:

Let $b_1 = \mu+\frac{\sigma_1^2}{2}, b_2 = \gamma+\mu+\tau+\frac{\sigma_2^2}{2}, b_3 = \alpha+\frac{\sigma_3^2}{2}, b_4 = \kappa+\frac{\sigma_4^2}{2}$. If

holds, Model ($2.2$) admits a quasi-steady $\bar{E}_1 = (\bar{S}_1, \bar{I}_1, \bar{A}_1, \bar{C}_1) = (e^{x_1^*}, e^{x_2^*}, e^{x_3^*}, e^{x_4^*})$, where $\bar{I}_1$ is the positive root of the equtaion

and

In addition, assume if $R^s > 1$, then $\bar{R}^s > 1$, which means that Model ($2.2$) admits a quasi-steady $\bar{E}_1$ under the condition $R^s > 1$. Let

where $x_1^* = \ln \bar{S}_1, x_2^* = \ln \bar{I}_1, x_3^* = \ln \bar{A}_1, x_4^* = \ln \bar{C}_1$, then the linearized system of ($4.1$) is as follows:

where

By employing the above lemmas, we will demonstrate the probability density function of the Model ($2.2$) near the quasi-steady equilibrium $\bar{E}_1$.

Let $Y = (y_1, y_2, y_3, y_4)^T, D = \mbox{diag}(\sigma_1, \sigma_2, \sigma_3, \sigma_4)$, and $B(t) = (B_1(t), B_2(t), B_3(t), B_4(t))^T$. We can rewrite Model ($4.3$) as the following form:

where

then the linearized Model (4.3) can be simiplified to $\mbox{d}Y = ZY\mbox{d}t+D\mbox{d}B(t)$. Based on the pertinent theory proposed by Zhou et al., it is postulated that there is a probability density function denoted as $\Phi(y_1, y_2, y_3, y_4)$ in the vicinity of the quasi-endemic equilibrium $\bar{E}_1$.

Theorem 4.1. [Zhou et al. ^[22]] Assuming that $R^s > 1$ for any initial value $(S(0), I(0), A(0), C(0)\in\mathbb{R}_+^4$, the solution $(S(t), I(t), A(t), C(t))$ of the Model (2.2) follows the unique log-normal probability density function $\Phi(S, I, A, C)$ around the quasi-endemic equilibrium $\bar{E}_1$, which is described by

where $\Lambda$ is a positive definite matrix.

From Gardiner ^[36], the density function $U(Y) = U(y_1, y_2, y_3, y_4)$ of the quasi-stationary distribution of Model ($4.3$) at the origin $Y^* = (0, 0, 0, 0)$ can be described by the four-dimensional Fokker-Planck equation as follows:

which can be approximated by a Gaussian distribution

$\bar{M}$ is a real symmetric matrix, which is described by $\bar{M}D^2\bar{M}+Z^T\bar{M}+\bar{M}Z = 0$. If $\bar{M}$ is positive definite, let $\bar{M}^{-1} = \Lambda$, then

According to Tian et al. ^[37], ($4.4$) can be rewriten as the sum of the four equations as follows:

where $D_1 = (\sigma_1, 0, 0, 0), D_2 = (0, \sigma_2, 0, 0), D_3 = (0, 0, \sigma_3, 0), D_4 = (0, 0, 0, \sigma_4), \Lambda = \Lambda_1+\Lambda_2+\Lambda_3+\Lambda_4$, $D^2 = D_1^2+D_2^2+D_3^2+D_4^2$. Consider the corresponding characteristic equation of $Z$ as follows:

where

In $s_2$, the following formula can be calculated

In $s_3$, the following formula can be calculated

In $s_4$, the following formula can be calculated

where $\tau-\frac{\eta_i\bar{S}_1^2}{\bar{N}_1^2} > 0$ and

while $s_1 > 0$, $s_2 > 0$, and $s_3 > 0$. We can calculate $s_1s_2-s_3 > 0$ and $s_1(s_2s_3-s_1s_4)-s_3^2 > 0$. As per the Routh-Hurwitz stability criterion ^[38], it can be deduced that the matrix $Z$ possesses eigenvalues with negative real parts. According to the theory of matrix similar transformations, it is evident that $\omega_Z(\zeta)$ is a similarity invariant, indicating that $s_1, s_2, s_3$, and $s_4$ are also similarity invariants.

Next, the corresponding proof for the positive definiteness of $\Lambda$ is divided into four steps.

Proof. Step 1. Consider the algebraic equation

Let $Z_1 = U_1ZU_1^{-1}$, where

and

where $w_1 = -\frac{a_{33}a_{41}}{a_{21}}, w_2 = -a_{41}-a_{42}+\frac{a_{41}a_{44}}{a_{21}}-\frac{a_{24}a_{41}^2}{a_{21}^2}$.

Case 1: When $w_1\neq0$ and $w_2\neq0$, there exists the elimination matrix $U_{11}$ such that $Z_{11} = U_{11}Z_{1}U_{11}^{-1}$, where

then there is

where $w_3 = \frac{w_2}{w_1}\frac{a_{33}w_1-a_{33}w_2}{w_1}+\frac{w_2}{w_1}\frac{a_{24}a_{41}-a_{21}a_{44}}{a_{21}}+\frac{a_{23}a_{41}}{a_{21}}$.

Case 1-1: If $w_3\neq0$, in order to find the standard transformation matrix $Q_{111}$ such that $T_{111} = Q_{111}Z_{11}Q_{111}^{-1}$, where

with

Thus, we can get

Meanwhile, ($4.6$) has the following form:

That is, $D_0^2+T_{111}\Theta_1+\Theta _1T_{111}^T = 0$, where $\Theta_1 = \frac{1}{\rho_{111}^2}(Q_{111}U_{11}U_1)\Lambda_1(Q_{111}U_{11}U_1)^T$, $\rho_{111} = a_{21}w_1w_3\sigma_1$.

According to Lemma 2.5, we can obtain the semipositive definite matrix

Therefore, it can be calculated that

is positive definite.

Case 1-2: If $w_3 = 0$, we can find the standard transformation matrix $Q_{112}$ such that $T_{112} = Q_{112}Z_{11}Q_{112}^{-1}$, where

with

We have

where $b_i (i = 1, 2, 3, 4)$ are marks, and we only care about their traits. According to the uniqueness of $\omega_Z(\zeta)$, it can be obtained that

The following results can be obtained that $b_1b_2-b_3 > 0$, then ($4.6$) can be transformed into the following form:

That is, $D_0^2+T_{112}\Theta_2+\Theta _2T_{112}^T = 0$, where $\Theta_2 = \frac{1}{\rho_{112}^2}(Q_{112}U_{11}U_1)\Lambda_1(Q_{112}U_{11}U_1)^T$, $\rho_{112} = a_{21}w_1\sigma_1$.

According to the Lemma 2.6, we can obtain the semipositive definite matrix

Therefore, by calculation,

is semi-postive definite.

Case 2: When $w_1\neq0$ and $w_2 = 0$, the objective is to determine the standard transformation matrix $Q_{12}$ that satisfies the equation $T_{12} = Q_{12}Z_{1}Q_{12}^{-1}$, where

with

We can obtain that $T_{12} = T_{111}$, and ($4.6$) can be transformed into

where $\Theta_1 = \frac{1}{\rho_{12}^2}(Q_{12}U_1)\Lambda_1(Q_{12}U_1)^T$, $\rho_{12} = -\frac{a_{23}a_{33}a_{41}^2}{a_{21}}\sigma_1$. Consequently,

is a positive definite matrix.

Case 3: When $w_1 = 0$ and $w_2\neq0$, there exists the transformation matrix $U_{13}$ such that $Z_{13} = U_{13}Z_{1}U_{13}^{-1}$, where

then we have

we are able to find the standard transformation matrix $Q_{13}$ such that $T_{13} = Q_{13}Z_{13}Q_{13}^{-1}$, where

with

We can obtain that $T_{13} = T_{111}$, and ($4.6$) can be transformed into

where $\Theta_1 = \frac{1}{\rho_{13}^2}(Q_{13}U_{13}U_1)\Lambda_1(Q_{13}U_{13}U_1)^T$, $\rho_{13} = -a_{21}w_2\sigma_1$. Consequently,

is a positive definite matrix.

Case 4: When $w_1 = 0$ and $w_2 = 0$, there exists the transformation matrix $U_{14}$ such that $T_{14} = Q_{14}Z_{1}Q_{14}^{-1}$, where

with

We then have

$c_1 = a_{11}+a_{21}+\frac{a_{24}a_{41}}{a_{21}} > 0$, $c_2 = (a_{11}+a_{12})a_{21}+(a_{41}+a_{42})a_{24}-a_{14}a_{41}+\frac{a_{11}a_{24}a_{41}}{a_{21}}+\frac{a_{23}a_{33}a_{41}}{a_{21}}+\frac{a_{24}^2a_{41}^2}{a_{21}^2} > 0$. Thus, ($4.6$) can be transformed into

where $\Theta_3 = \frac{1}{\rho_{14}^2}(Q_{14}U_1)\Lambda_1(Q_{14}U_1)^T$, $\rho_{14} = a_{21}\sigma_1$. With Lemma 2.7, we can obtain the semi-postive definite matrix

Therefore, by calculation,

is semi-postive definite.

Step 2. For the following algebraic equation

consider the corresponding order matrix $J_2$ and elimination matrix $U_2$:

Let $Z_2 = (U_2J_2)Z(U_2J_2)^{-1}$, then we can obtain that

where $r_1 = -a_{41}+\frac{a_{14}a_{44}+a_{42}a_{44}}{a_{33}}$, $r_2 = -a_{11}+\frac{a_{13}a_{14}+a_{12}a_{44}+a_{14}^2}{a_{33}}$.

Case 1: When $r_1\neq0, r_2\neq0$, there exists the elimination matrix $U_{21}$ such that $Z_{21} = U_{21}Z_2U_{21}^{-1}$, where

then we have

where $r_3 = (a_{42}+\frac{a_{44}r_2}{r_1})\frac{r_2}{r_1}-a_{12}-\frac{(a_{13}+a_{14})r_2}{r_1}$.

Case 1-1: If $r_3\neq0$, the standard transformation matrix $Q_{211}$ can be determined in order to obtain the transformation $T_{211}$ as $T_{211} = Q_{211}Z_{21}Q_{211}^{-1}$, where

with

As a result, we have $T_{211} = T_{111}$, and ($4.12$) has the following form:

That is, $D_0^2+T_{211}\tilde{\Theta}_1+\tilde{\Theta}_1T_{211} = 0$, where $\tilde{\Theta}_1 = \frac{1}{\rho_{211}^2}(Q_{211}U_{21}U_2J_2)\Lambda_2(Q_{211}U_{21}U_2J_2)^T$, $\rho_{211} = a_{33}r_1r_3\sigma_2$. According to Lemma 2.5, we can obtain the semipositive definite matrix

Therefore, it can be obtained by calculation that

Case 1-2: If $r_3 = 0$, we can find the standard transformation matrix $Q_{212}$ such that $T_{212} = Q_{212}Z_{21}Q_{212}^{-1}$, where

then we have

where

We can obtain $\tilde{b}_1\tilde{b}_2-\tilde{b}_3 > 0$, then ($4.12$) can be transformed into the following form:

That is, $D_0^2+T_{212}\tilde{\Theta}_2+\tilde{\Theta}_2T_{212}^T = 0$, where $\tilde{\Theta}_2 = \frac{1}{\rho_{212}^2}(Q_{212}U_{21}U_2J_2)\Lambda_2(Q_{212}U_{21}U_2J_2)^T$, $\rho_{212} = a_{33}r_1\sigma_2$. According to Lemma 2.6, we can obtain the semipositive definite matrix

Therefore, it can be obtained by calculation that

is semi-postive definite.

Case 2: When $r_1\neq0$ and $r_2 = 0$, there exists the transformation matrix $Q_{22}$ such that $T_{22} = Q_{22}Z_{2}Q_{22}^{-1}$, where

with

It can be obtained that $T_{22} = T_{111}$, and ($4.12$) can be transformed into

where $\tilde{\Theta}_1 = \frac{1}{\rho_{22}^2}(Q_{22}U_2J_2)\Lambda_2(Q_{22}U_2J_2)^T$, $\rho_{22} = -a_{21}a_{33}r_1\sigma_2$. Consequently,

is a positive definite matrix.

Case 3: When $r_1 = 0$ and $r_2\neq0$, there exists the transformation matrix $U_{23}$ such that $Z_{23} = U_{23}Z_{2}U_{23}^{-1}$

then we have

We can find the standard transformation matrix $Q_{23}$ such that $T_{23} = Q_{23}Z_{23}Q_{23}^{-1}$, where

with

It can be obtained by calculation that $T_{23} = T_{111}$, and ($4.12$) can be transformed into

where $\tilde{\Theta}_1 = \frac{1}{\rho_{23}^2}(Q_{23}U_{23}U_2J_2)\Lambda_2(Q_{23}U_{23}U_2J_2)^T$, $\rho_{23} = -a_{33}a_{44}r_2\sigma_2$. Consequently,

is a positive definite matrix.

Case 4: When $r_1 = 0$ and $r_2 = 0$, there exists the transformation matrix $Q_{24}$ such that $T_{24} = Q_{24}Z_{2}Q_{24}^{-1}$, where

then we have

where $c_1 = a_{11}+a_{21}+a_{33}+a_{44}-a_{13}-a_{14}-a_{42} > 0$, $c_2 = \frac{s_4}{a_{13}a_{42}+a_{14}a_{42}-a_{12}a_{44}} > 0$. Thus, ($4.12$) can be transformed into

where $\tilde{\Theta}_3 = \frac{1}{\rho_{24}^2}(Q_{24}U_2J_2)\Lambda_2(Q_{24}U_2J_2)^T$, $\rho_{24} = a_{33}\sigma_2$. With Lemma 2.7, we can obtain the positive semidefinite matrix

Therefore, it can be obtained by calculation that

is semi-postive definite.

Step 3. For the following algebraic equation

consider the corresponding order matrix $J_3$ and elimination matrix $U_3$ :

Let $Z_3 = (U_3J_3)Z(U_3J_3)^{-1}$. It can be obtained by calculation that

where $k_1 = a_{21}+\frac{a_{21}a_{23}-a_{11}a_{23}}{a_{13}}+\frac{a_{12}a_{23}^2}{a_{13}^2}$, $k_2 = a_{24}-\frac{a_{14}a_{23}}{a_{13}}$.

Case 1: When $k_1 = 0$ and $k_2\neq0$, there exists the standard transformation matrix $Q_{31}$ such that $T_{31} = Q_{31}Z_3Q_{31}^{-1}$, where

with

We can obtain that $T_{31} = T_{111}$, and ($4.18$) can be transformed into

where $\bar{\Theta}_1 = \frac{1}{\rho_{31}^2}(Q_{31}U_3J_3)\Lambda_3(Q_{31}U_3J_3)^T$, $\rho_{31} = (a_{13}a_{41}-a_{23}a_{42})k_2\sigma_3$, and $\bar{\Theta}_1 = \Theta_1$. Consequently,

is positive definite matrix.

Case 2: When $k_1\neq0$, $k_2 = 0$, there exists the transformation matrix $U_{32}$ such that $Z_{32} = U_{32}Z_3U_{32}^{-1}$, where

then we have

where $k_3 = \frac{(a_{13}a_{44}+a_{12}a_{23}+a_{13}a_{21})k_1}{a_{23}a_{42}-a_{13}a_{41}}-\frac{a_{13}^2a_{42}k_1^2}{(a_{23}a_{42}-a_{13}a_{41})^2}$.

Case 2-1: If $k_3\neq0$, we can find the standard transformation matrix $Q_{321}$ such that $T_{321} = Q_{321}Z_{32}T_{321}^{-1}$, where

with

It can be obtained by calculation that $T_{321} = T_{111}$, and ($4.18$) can be transformed into

where $\bar{\Theta}_1 = \frac{1}{\rho_{321}^2}(Q_{321}U_{32}U_3J_3)\Lambda_3(Q_{321}U_{32}U_3J_3)^T$, $\rho_{321} = (a_{13}a_{41}-a_{23}a_{42})k_3\sigma_3$. Consequently,

is positive definite matrix.

Case 2-2: If $k_3 = 0$, we can find the standard transformation matrix $Q_{322}$ such that $T_{322} = Q_{322}Z_{32}Q_{322}^{-1}$, where

with

We can find

which means that

we can find that $\bar{b}_1\bar{b}_2-\bar{b}_3 > 0$, and ($4.18$) can be transformed into the following form :

That is, $D_0^2+T_{322}\bar{\Theta}_2+\bar{\Theta}_2T_{322}^T = 0$, where $\bar{\Theta}_2 = \frac{1}{\rho_{322}^2}(Q_{322}U_{32}U_3J_3)\Lambda_3(Q_{322}U_{32}U_3J_3)^T$, $\rho_{322} = (a_{13}a_{41}-a_{23}a_{42})\sigma_3$. According to Lemma 2.6, we are able to obtain the semipositive definite matrix

Therefore, it can be obtained by calculation that

is semi-postive definite.

Case 3: When $k_1 = 0$ and $k_2 = 0$, there exists the transformation matrix $Q_{33}$ such that $T_{33} = Q_{33}Z_3Q_{33}^{-1}$, where

with $n_3^* = -a_{13}a_{33}+a_{14}(a_{11}+a_{44}-\frac{a_{12}a_{23}}{a_{13}})$ and $n_4^* = a_{12}(a_{11}+\frac{a_{13}a_{21}}{a_{13}})+a_{14}a_{42}$, then we can find

where

Thus, ($4.18$) can be transformed into

where $\bar{\Theta}_3 = \frac{1}{\rho_{33}^2}(Q_{33}U_3J_3)\Lambda_3(Q_{33}U_3J_3)^T$, $\rho_{33} = -a_{13}\sigma_3$. With Lemma 2.7, we can obtain the positive semi-definite matrix

Therefore, it can be obtained by calculation that

is semi-postive definite.

Step 4. For the following algebraic equation

consider the corresponding order matrix $J_4$ and elimination matrix $U_4$:

Let $Z_4 = (U_4J_4)Z(U_4J_4)^{-1}$. It can be obtained that

where $p_1 = -a_{33}+\frac{a_{21}a_{33}}{a_{12}}$, $p_2 = a_{33}$.

Case 1: When $p_1 = 0$ and $p_2\neq0$, it is possible to determine the standard transformation matrix $Q_{41}$ in order to satisfy the equation $T_{41} = Q_{41}Z_4Q_{41}^{-1}$, where

with

then it can be obtained by calculation that $T_{41} = T_{111}$, and ($4.23$) can be transformed into

where $\hat{\Theta}_1 = \frac{1}{\rho_{41}^2}(Q_{41}U_4J_4)\Lambda_4(Q_{41}U_4J_4)^T$, $\rho_{41} = (a_{13}a_{21}-\frac{a_{14}a_{21}^2}{a_{12}})a_{33}\sigma_4$, and $\hat{\Theta}_1 = \Theta_1$. Consequently,

is positive definite matrix.

Case 2: When $p_1\neq0$ and $p_2 = 0$, there exists the transformation matrix $U_{42}$, then $Z_{42} = U_{42}Z_4U_{42}^{-1}$, where

then we can find

where $p_3 = a_{33}+\frac{a_{33}(a_{12}-a_{21})(a_{12}a_{24}+a_{21}a_{41})}{a_{12}a_{13}+a_{14}a_{21}}-\frac{a_{12}a_{33}^2(a_{11}+a_{12})(a_{12}-a_{21})^2}{a_{21}(a_{12}a_{13}+a_{14}a_{21})^2}$.

Case 2-1: If $p_3\neq0$, we can find the standard transformation matrix $Q_{421}$ such that $T_{421} = Q_{421}Z_{42}Q_{421}^{-1}$, where

with

then we can obtain that $T_{421} = T_{111}$, and ($4.23$) can be transformed into

where $\hat{\Theta}_1 = \frac{1}{\rho_{421}^2}(Q_{421}U_{42}U_4J_4)\Lambda_4(Q_{421}U_{42}U_4J_4)^T$, $\rho_{421} = \frac{-a_{21}(a_{12}a_{13}+a_{14}a_{21})}{a_{12}}\sigma_4$. Consequently,

is positive definite matrix.

Case 2-2: If $p_3 = 0$, we are able to find the standard transformation matrix $Q_{422}$ such that $T_{422} = Q_{422}Z_{42}Q_{422}^{-1}$, where

with

We then have

which means that

$\hat{b}_1\hat{b}_2-\hat{b}_3 > 0$, and ($4.23$) can be transformed into the following form :

That is, $D_0^2+T_{422}\hat{\Theta}_2+\hat{\Theta}_2T_{422}^T = 0$, where $\hat{\Theta}_2 = \frac{1}{\rho_{422}^2}(Q_{422}U_{42}U_4J_4)\Lambda_4(Q_{422}U_{42}U_4J_4)^T$, $\rho_{422} = \frac{-a_{21}(a_{12}a_{13}+a_{14}a_{21})}{a_{21}}\sigma_4$. According to Lemma 2.6, we can find the semipositive definite matrix

Therefore, we can obtain that

is semi-postive definite.

Case 3: When $p_1 = 0$ and $p_2 = 0$, there exists the transformation matrix $Q_{42}$ such that $T_{43} = Q_{42}Z_{4}Q_{42}$, where

with

We then have

where

Thus, ($4.23$) can be transformed into

where $\hat{\Theta}_3 = \frac{1}{\rho_{43}^2}(Q_{43}U_4J_4)\Lambda_4(Q_{43}U_4J_4)^T$, $\rho_{43} = -a_{12}\sigma_4$. With Lemma 2.7, we can obtain the positive semidefinite matrix $\hat{\Theta}_3$

Therefore, it can be obtained by calculation that

is semi-postive definite.

In summary, $\Lambda_3$, $\Lambda_4$ are positive definite and $\Lambda_1, \Lambda_1$ are at least semi-positive definite. Hence, $\Lambda = \Lambda_1+\Lambda_2+\Lambda_3+\Lambda_4$ is a positive definite matrix, and there is a unique and precise density function surrounding the quasi-endemic equilibrium $\bar{E}$ when $R^s > 1$. Considering the transformation of $(y_1, y_2, y_3, y_4) = (\ln{\frac{S}{\bar{S}_1}}, \ln{\frac{I}{\bar{I}_1}}, \ln{\frac{A}{\bar{A}_1}}, \ln{\frac{C}{\bar{C}_1}})$ and $(S, I, A, C)$, the unique ergodic stationary distribution $v(\cdot)$ of Model $(2.2)$ approximately follows a unique log-normal probability density function

This completes the proof of Theorem 4.1.

Remark 3. By combining Theorems 3.1 and 4.1, it is possible to find evidence that the stationary distribution of Model (2.2) around the equilibrium $\bar {E} _1$ is compatible with the probability density function $\Phi(S, I, A, C)$. Hence, a reasonable stochastic criterion for disease persistence can be achieved when $R^s > 1$. From this we can see that accurately representing the density function can be an efficient method for preventing and managing numerous epidemics.

5.   Numerical simulations

In this section, we apply theoretical findings to analyze the dynamics of anthrax and investigate the impact of environmental disturbance on the transmission of the disease. Using by Milstein's method ^[], the discretization equation of Model (2.2) is given by

where the time increment is $\Delta t > 0$, and $\chi_k, \pi_k, \omega_k, \zeta_k\:(k = 1, ..., n)$ are the independent Gaussian random variables following the distribution $N(0, 1)$. As stated by Saad-Roy et al. ^[7] and Mushayabasa et al. ^[17], Table 1 displays the relevant biological parameters and the initial value of Model (2.2). Next, our objective is to perform empirical examples to concentrate on the following three aspects:

1. If $R^s > 1$, there is a unique ergodicity property stationary distribution.

2. Stochastic fluctuations have an impact on disease persistence in the Model (2.2).

3. Focus on the probability density function of Model (2.2).

5.1.   Dynamical behaviors of Model (2.2) under $R^s > 1$

The main parameters are given in Table 1. Let the stochastic perturbations be $(\sigma_1, \sigma_2, \sigma_3, \sigma_4) = (0.005, 0.005, 0.005, 0.005)$ in Model (2.2) then we can calculate that

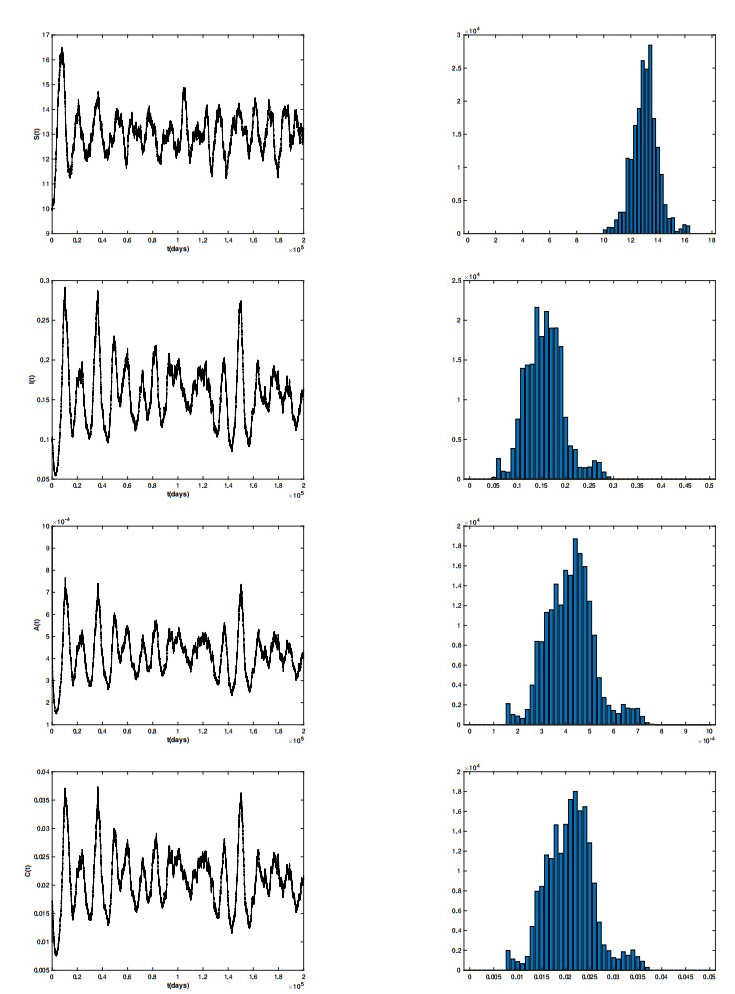
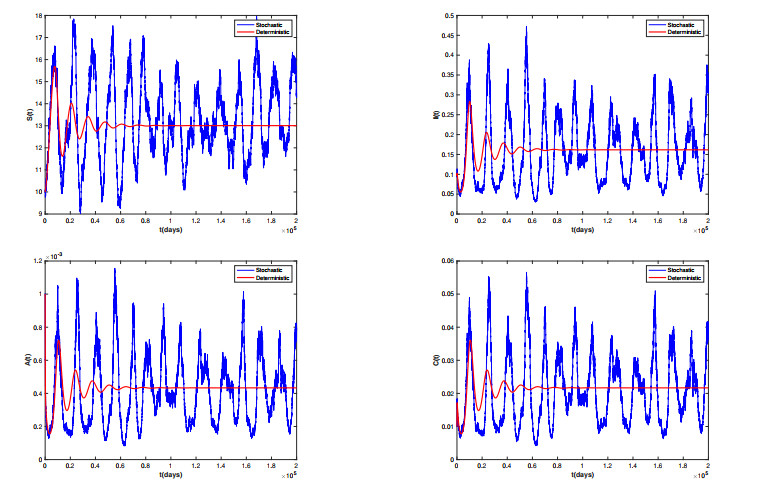
The disease has a tendency to persist in both deterministic and stochastic models according to Theorem 3.1. It can be inferred that Model (2.2) has a stationary distribution $v(\cdot)$. In Figure 2, we give the time series diagram of the model solution and its corresponding histogram. In the time series diagram in Figure 2, the curve fluctuates up and down, but the overall trend is stable. The corresponding interval of frequency can be seen in the histogram on the right. It is shown that the Model (2.2) has a unique ergodic stationary distribution, which is consistent with the result of Theorem 3.1. This indicates that the disease will endure. In real life, anthrax is not easy to be completely eradicated, but in a relatively stable state. Next, the dynamical behavior is observed when the parameters of the stochastic and deterministic models are identical. It is shown that the stochastic path fluctuates around the deterministic path, which indicates that the stochastic Model (2.2) has an ergodic stationary distribution. Figure 3 confirms this.

5.2.   Impact of random noises $\sigma_1, \sigma_2, \sigma_3, \sigma_4$ on the disease persistence

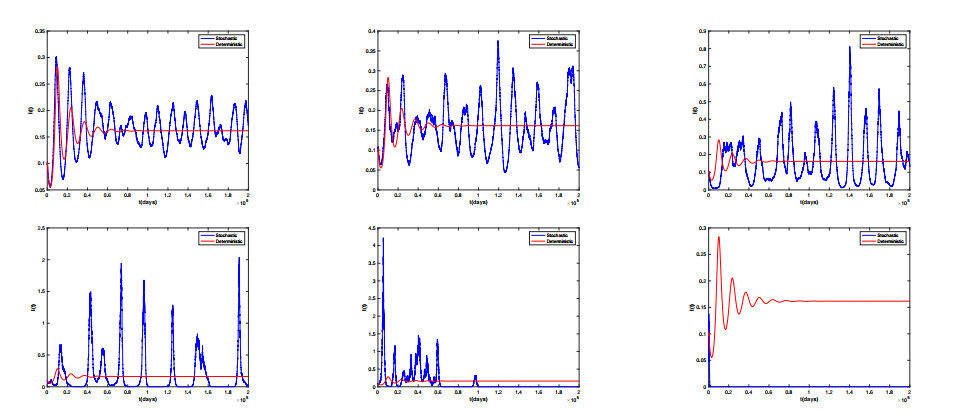
Mathematical limitations make it tough to establish sufficient conditions for disease extinction in the stochastic anthrax model ^[42,43]. Therefore, for a comprehensive discussion, we present numerical simulation of disease elimination with high noise. For example, to prevent the spread of anthrax, people can increase the culling rate or vaccination rate, which will effectively eliminate the spread of anthrax.

We use numerical simulations to prove that excessive environmental noise can lead to the extinction of anthrax. Let $\sigma = \sigma_1 = \sigma_2 = \sigma_3 = \sigma_4$, $\sigma$ be taken as 0.002, 0.005, and 0.01, respectively. The other parameters and initial value are identical to those in Table 1 and the simple calculations show that $\mathit{R^s} > 1$. It can be concluded that the disease persists; if we let $\sigma = 0.02, 0.05, 0.1$, studies have shown that large enough environment noise will eradicate the disease, and the numerical simulation clearly shows our conclusion in Figure 4.

5.3.   The probability density function of Model (2.2)

In this part, the numerical representation of the probability density function of Model (2.2) will be our focus. From Theorem 3.1, we can calculate that if $(\sigma_1, \sigma_2, \sigma_3, \sigma_4) = (0.005, 0.005, 0.005, 0.005)$, the Model (2.2) has a unique stationary distribution. Moreover, through meticulous computation, it is determined that the variables' values in Table 2 are all positive. By the definition of $\bar{E}_1$, we obtain that $(\bar{S}_1, \bar{I}_1, \bar{A}_1, \bar{C}_1) = (24.8194, 0.4094, 0.00044, 0.02852)$. According to Theorem 4.1, we know that the distribution has a probability density function around the quasi-steady state $\bar{E}_1$, and the stationary distribution $v(\cdot)$ obeys a log-normal density function $\Phi(S, I, A, C)$. Its function expression is:

and the corresponding marginal density functions are :

By constructing frequency histograms and fitting curves for the variables $S, I, A,$ and $C$, the marginal density functions $F(S)$, $F(I)$, $F(A)$, and $F(C)$ were plotted. The numerical findings depicted in Figure 5 validate the assertion that the fitting curves closely align with the corresponding theoretical marginal density functions.

6.   Conclusions and discussion

To explore the possibility of an ergodic stationary distribution and a representation of the probability density function, we propose the stochastic anthrax model in this study. We will discuss our primary contributions in the two areas.

By considering the effect of external environmental perturbations, we focus on the stochastic anthrax model. First, we calculate the basic reproduction number of the deterministic model $\mathit{R}_0$, if $\mathit{R_0} < 1$, which means that the anthrax will be extinct in the animal population, while $\mathit{R_0} > 1$ implies that anthrax will persistence. For stochastic Model (2.2), the uniform boundedness of the model is presented. Second, we demonstrate that the stochastic anthrax model has a unique ergodic stationary distribution at the threshold $R_s > 1$ in Lemma 2.3 and Theorem 3.1 by building appropriate Lyapunov functions and applying ergodic theory. From the similar threshold and basic reproduction number, $\mathit{R}^s > 1$ can be seen as a unified criterion to ensure the persistence of disease in deterministic and stochastic models. Comparing the expressions for $R_0$ and $R^s$, we find that $R^s\leqslant R_0$, so $R^s > 1$ can be viewed as a uniform measure to determine the persistence of the disease in both the model and the stochastic model. In addition, by setting up noise perturbations of different intensity, we found that the higher the noise level, the faster the disease extinction. That is, external disturbances play an important role in disease development, such as environmental elimination, culling of infected animals, and vaccination.

Understanding the statistical characteristics is crucial for managing infectious diseases, but it is challenging to ascertain the statistical properties of disease persistence within an ergodic stationary distribution. To study the dynamic behavior of disease, we construct the endemic equilibrium point, through the equivalence between the Model (4.1) and the corresponding linear Model (4.3) and deduced the log-normal accurate expression of $\Phi(S, I, A, C)$ four-dimensional density function. Furthermore, the covariance matrix $\Lambda$ is determined through the use of an algebraic equation $D^2+Z\Lambda+\Lambda Z^T = 0$. The precision of $\Lambda$ can be verified by applying the stability theory to the zero solution of the linear equation, as discussed in the previous research ^[39]. Furthermore, our method and theory can demonstrate that $\Lambda$ is positive definite, even in cases where $D$ is a semi-definite matrix.

Finally, there are several important themes that deserve further study. To begin, the stochastic model established in this paper only considers the effect of white noise. However, L$\acute{e}$vy noise can describe the model more accurately when there is a sudden change in the environment. On the other hand, time delay is an important factor affecting the stability of ecological dynamic systems, as time delay may alter the stability of the system and lead to system fluctuations ^[43,44]. Therefore, considering L$\acute{e}$vy noise and delay effects has theoretical value and practical significance. We leave these for future work.

Use of AI tools declaration

The authors declare they have not used Artificial Intelligence (AI) tools in the creation of this article.

Acknowledgments

The research was supported by the Ningxia Natural Science Foundation (No. 2022AAC03265), and Natural Science Foundation of China (No. 12161068).

Conflict of interest

The authors declare there is no conflicts of interest.

Appendix 1 : The proof of Lemma 2.1

Proof. Denote the Lyapunov function : $V(S, I, A, C) = S^\epsilon+\epsilon I^\epsilon+A^\epsilon+C^\epsilon$, for $\epsilon > 1$, applying It$\hat{o}$'s formula

where

Let

It follows from ($2.3$) that there exists the positive constant $\hat{T}_2$ such that $F(S, I, A, C)\leqslant\hat{T}_2$. Hence, we can obtain that

which yields that $\mbox{d}V(S, I, A, C)\leqslant[\hat{T}_2-V(S, I, A, C)]\mbox{d}t +\epsilon\sigma_1 S^\epsilon \mbox{d}B_1(t)+\epsilon \sigma_2I^v \mbox{d}B_2(t)+\epsilon\sigma_3 A^\epsilon \mbox{d}B_3(t)+\epsilon \sigma_4 C^\epsilon \mbox{d}B_4(t)$. Integrating both sides of the equation $\rm{d[e^tV(S, I, A, C)]}$ and taking expectations leads to the following

Thus, $\limsup_{t\to \infty }\mathbb{E}V(S, I, A, C)\leqslant\hat{T}_2$, as a result, $\limsup_{t\to \infty }\mathbb{E}|X(t)|^\epsilon\leqslant\frac{\hat{T}^2}{4^{(1-\frac{\epsilon}{2})\wedge0}}: = \hat{T}(\epsilon).$ In addition, when $\epsilon = 2$, we have $\limsup_{t\to \infty }\mathbb{E}|X(t)|^2\leqslant\hat{T}_2$, which is the second moment of the solution of Model ($2.2$). Now, for any $\varepsilon > 0$, let $\Psi = \sqrt{\frac{\hat{T}_2}{\varepsilon}}$. By Chebyshev's inequality, $\mathbb{P}\{|X(t)| > \Psi\}\leqslant\frac{\mathbb{E}|X(t)|^2}{\Psi^2}$, which yields that $\limsup_{t\to \infty }\mathbb{P}\{|X(t)| > \Psi\}\leqslant\frac{\hat{T}_2}{\Psi^2} = \varepsilon$. Therefore, we have $\limsup_{t\to \infty }\mathbb{P}\{|X(t)|\leqslant\Psi\}\geqslant 1-\varepsilon$. In other words, the solution of Model ($2.2$) is stochastically ultimately bounded.

Appendix 2 : Theory in obtaining standardized transformation matrix

Through the use of invertible linear transformations, we will derive the corresponding standardized transformation matrices of standard $B_1$. The matrix of $B_1$: For the algebraic equation $D_1^2+Z\Lambda_1+\Lambda_1 Z^T = 0$, where $D = \mbox{diag}(\sigma_1, 0, 0, 0)$ and

We assume that $a_{21}\neq0$, $a_{32}\neq0$ and $a_{43}\neq0$. Define $X = (x_1, x_2, x_3, x_4)$, which follows $\mbox{d}X = ZX\mbox{d}t$. Considering the following vector $Y = (y_1, y_2, y_3, y_4)^T$,

then the corresponding strandardized transformation matrix is given by

We derive that $Y = NX$, which means $\mbox{d}Y = N\mbox{d}X = NZX\mbox{d}t = (NAN^{-1})Y\mbox{d}t$, then we have

Therefore, we can obtain that the corresponding standard $B_1$ matrix is $NZN^{-1}: = Z_1$, which refers to Lemma 2.5. Let $\rho = a_{21}a_{32}a_{43}\sigma$ and $\Theta = \rho^{-2}N\Lambda N^T$.