Stress-strength reliability estimation for the inverted exponentiated Rayleigh distribution under unified progressive hybrid censoring with application

1.   Introduction

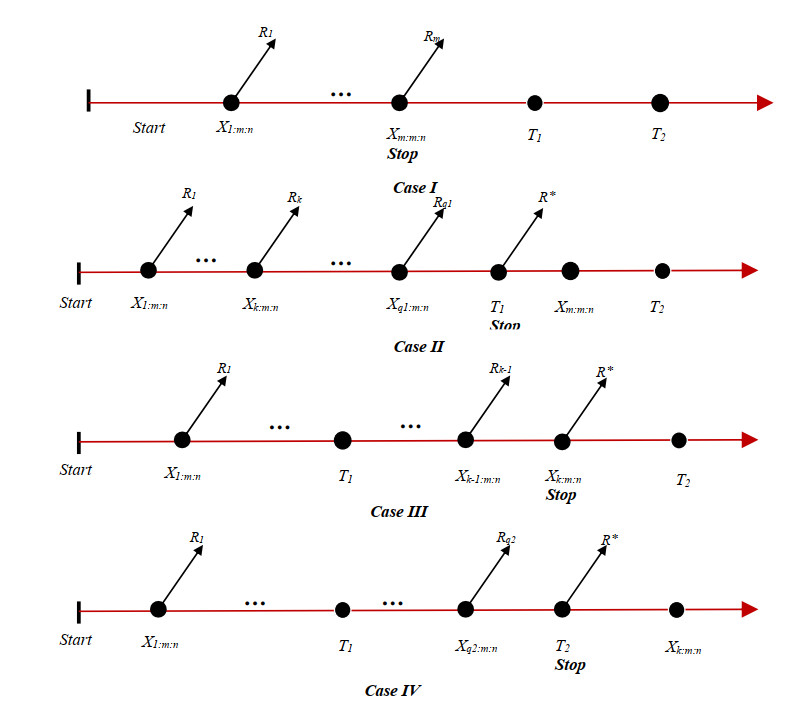
In reliability study under an ideal state, a set of the complete sample can be observed, and experimenters make statistical inferences using the entire data. However, in real life, due to substantial improvement of science and technology, we cannot get the adequate number of failure times of some units which are put on the life testing experiment. Therefore, censoring schemes are put forward for practical significance. The forms of censoring schemes are varied. Type-I and Type-II schemes are the two fundamental censoring schemes. Type-I censoring refers to the removal of units that have not failed after a preset time T. The Type-II censoring is to discard the remaining units when the number of failed units reaches a preset number m. Furthermore, if Type-I and Type-II are combined together (see ^[1]), it is hybrid censoring scheme. The main limitation of the hybrid censoring scheme and its generalizations is that a small effective sample size may be acquired. Therefore, Balakrishnan et al. ^[2] proposed Type-I and Type-II unified hybrid (unified Hy) censoring schemes. However, none of these censoring schemes (CSs) allows the removal of the units while in a life-test experiment. The progressive censoring (PrC) scheme allows the removal of units and observing a certain number of failures during the experiment, which makes life testing efficient; see ^[3]. Later, a generalization of the PrC known as the progressive hybrid was proposed in ^[4]. Needless to say, there has been a great deal of research done on estimation problems of different distributions under the above censoring schemes. Panahi ^[5] studied the ML and Bayesian statistical inference problems of unified Hy censored model for the Burr Type III distribution. Lee and Seo ^[6] considered the estimates for the Gompertz parameters under PrC sample. Similar tests were considered in ^[7] for Weibull distribution when right CS is available. Starling et al. ^[8] for improving Weibull distribution using generalized Type-I CS. Also, for accelerated life-time reliability model (ALTM), Wang et al. ^[9] considered estimation methods under PrC. In ^[10] and ^[11] presented statistical inferences of the ALTM under adaptive type-I progressively hybrid and unified Hy censoring schemes respectively. Further, Lone et al. ^[12] considered a reliability model based on a unified hybrid censoring scheme. The other developments on censoring schemes can be seen in ^[13,14]. Moreover, the developments and needs in engineering, manufacturing and technology inspire more improved censoring schemes (CS). Recently, Gorny and Cramer ^[15] introduced a novel CS called the unified PHCS, which is used in reliability studies as follows: An experiment starts with n identical items. The effective number of failures $k$ and $m; (k < m)$ are predetermined, and the Prg $R = ({R}_{1}, {R}_{2}, ..., {R}_{m})$ with ${\sum }_{i = 1}^{m}{R}_{i} = n-m$ is also fixed in advance. Let ${T}_{1}$ and ${T}_{2}({T}_{1} < {T}_{2})$ be the two time points. This experiment will be stopped at ${T}^{*} = max\left\{min\left\{{X}_{k:m:n}, {T}_{2}\right\}, min\left\{{X}_{m:m:n}, {T}_{1}\right\}\right\}$. So, the joint likelihood function of the three forms of failure times is defined as

where $(Q, T)$ is $(m, {x}_{i:m:n})$, $({d}_{1}, {T}_{1})$, $(k, {x}_{k:m:n})$ and $({d}_{2}, {T}_{2})$ for cases I, II, III and IV, respectively. Figure 1 shows the structure of the unified PHCS.

The problem of estimating the stress-strength reliability model has received significant interest in reliability theory. This reliability system is introduced in ^[16] and is defined as the probability of the strength component (X) overcoming the stress (Y) imposed on it, namely, $R = P(X > Y)$. Therefore, if the stress exceeds the strength, system component will fail, and the probability of not failing of the system component is proposed as a measure of system reliability. The reliability model has wide applications in different areas of scientific study, such as engineering, medicine, physics, quality control and clinical trials. In engineering studies, R gives the probability that the strength of a system component exceeds the stress on the system from external factors. In medical studies, if X represents control, and Y represents treatment outcomes, then $R = P(X > Y)$ can be interpreted as the effectiveness of treatment. In addition to usages in engineering and clinical studies, the probability R comes up in various fields of study, such as bioequivalence assessment ^[17], heritability of a genetic trait ^[18], etc.

Many researchers have considered the problem of estimating R with complete and censored samples. Bhattacharyya and Johnson ^[19] estimated the multicomponent S-S reliability model. Rao et al. ^[20] considered independent inverse Rayleigh random variables as stress and strength and estimated the $R = P(X > Y)$. Ghitany et al. ^[21] investigated the S-S reliability model using power Lindley distributions. Akgul and Senoglu ^[22] assumed that stress and strength are random variables following Weibull distributions and estimated R using ranked set sampling. Bai et al. ^[23] investigated a reliability model using progressively interval censored samples from finite mixture distributions. Demiray and Kizilaslan ^[24] estimated an S-S model of a consecutive k-out-of-n system with proportional hazard rate family. Asadi and Panahi ^[25] discussed reliability estimation and presented the application of this model in coating processes. Zhang et al. ^[26] investigated the multicomponent reliability model using Marshall-Olkin Weibull distribution. De La Cruz ^[27] and Wang et al. ^[28] considered the reliability estimation under unit-half-normal and generalized exponential distributions, respectively, and Zhuang et al. ^[29] studied the reliability based on Bayesian deep learning.

This paper discusses the problem of reliability parameters estimation using the inverted exponentiated Rayleigh (IERayleigh) distribution under Unified PHCS. The probability density function PDF $\mathrm{f}(.)$ and CDF $\mathrm{F}(.)$, of the IERayleigh distribution are given by

and

The IERayleigh distribution is a widely used life distribution in reliability and life test research, especially in analyzing the data of life-testing experiments in physics, medicine, biological sciences and engineering sciences. The hazard functions ($H\left(x\right) = 2\alpha \beta {x}^{-3}\mathit{exp}(-\beta /{x}^{2})/(1-\mathit{exp}(-\beta /{x}^{2}\left)\right)$) have non-monotonic forms (see Figure 2), which are quite suitable for data sets with a non-monotonic failure rate in actual production. For example, this model can be used in evaluating data of survival after successful surgery. In this case, the initial risk increases immediately postoperatively for possible reasons, and then the risk decreases steadily as the patient recovers. Due to the non-monotonic form of the hazard rate, this distribution behaves similarly to some well-known models: namely, the log-normal distribution, the inverse Weibull distribution and the generalized inverse exponential distribution.

Since then, IERayleigh has been widely used in many fields. For example, Kayal et al. ^[30] showed that the IERayleigh distribution can be considered in modeling the endurance of deep groove ball bearings data. Gao and Gui ^[31] applied this distribution to carbon fibers data. Panahi and Moradi ^[32] found that the IERayleigh distribution provided a good model for engineering problems, such as the maximum spreading diameter of nano-droplet impact on hydrophobic surface. Fan and Gui ^[33] showed that this distribution can be applied in the African aluminum industry.

Let the model consist of strength variable with $IERayleigh(\alpha, \beta)$ and independent stress variable with $IERayleigh(\gamma, \beta)$. Then, the S-S reliability model can be written as

where, ${f}_{X}\left(.\right)$ and ${F}_{Y}\left(.\right)$ are defined in Eqs (2) and (3), respectively. This model is widely utilized in reliability engineering to determine the probability of the system working properly.

Also, the use of different types of data in reliability encourages researchers to study the application of reliability models in different sciences. In this study, we try to expand the applications of the reliability model in the engineering field. Hence, this study aims to look into the reliability model through different estimation methods based on Unified PHCS and consider its application in the splashing data.

To the best of our knowledge, no one has applied the IERayleigh distribution to S-S reliability model under unified PHCS. That is why we consider the estimation of the reliability model, in the case of each component having an IERayleigh distribution with common shape parameter $\mathrm{\beta }$, and both are exposed to unified PHCS. Another importance is the implementation of the obtained methods to the splashing diameter data under two pressures. So, this study has novelty with regard to the considered S-S reliability model under unified PHCS as well as real data application of the obtained estimates.

The S-S reliability model parameters are acquired using MLEs. The stochastic EMA is applied to attain the MLE of the S-S model. Using the normal approximation, approximate confidence intervals for the reliability model's parameters are obtained. Under the squared error and Linex and generalized entropy loss functions, the Bayesian estimates are calculated by Gibbs sampler together with the MeHa algorithm. This algorithm is considered to compute the associated credible intervals. The droplet splashing data under two nozzle pressures are compared by using the considered S-S reliability model.

The rest of this paper is organized as follows. The stochastic EMA and ApCIs estimates for the reliability model are derived in Section 2. In Section 3, the Bayesian estimates by the Gibbs sampler together with the MeHa algorithm under three loss functions are proposed. In Section 4, we offer a simulation study, under which the above estimation methods are comparatively analyzed. In Section 5, an illustration of how the proposed model and methods may be utilized in engineering problems is presented. A summary and some conclusions are given in Section 6.

1.1.   Nomenclature and Acronyms

2.   Maximum likelihood estimation

In this section, MLEs of the unknown parameters of reliability model are evaluated based on the unified PHC sample. Let $\underset{⎴}{X} = ({X}_{1:{m}_{1}:{n}_{1}}, ..., {X}_{{Q}_{1}:{m}_{1}:{n}_{1}})$ and $\underset{⎴}{Y} = ({Y}_{1:{m}_{2}:{n}_{2}}, ..., {Y}_{{Q}_{2}:{m}_{2}:{n}_{2}})$ be unified PHCS samples from $IERayleigh(\alpha, \beta)$ and $IERayleigh(\gamma, \beta)$, respectively. Then, the likelihood function of the observed sample is attained as

where ${\xi }_{{x}_{i:{m}_{1}:{n}_{1}}} = \beta /{x}_{i:{m}_{1}:{n}_{1}}^{2}$, ${\xi }_{{y}_{i:{m}_{2}:{n}_{2}}} = \beta /{y}_{i:{m}_{2}:{n}_{2}}^{2}$, ${\xi }_{{T}_{x}} = \beta /{T}_{x}^{2}$, ${\xi }_{{T}_{y}} = \beta /{T}_{y}^{2}$, and

Therefore, $\mathit{ln}L\left(\alpha, \beta, \gamma |data\right)$ can be written as

The MLEs can be obtained by taking derivatives of $\alpha$, $\beta$ and $\gamma$ and making them equal to 0. Using the invariance property of the MLE helps us to obtain MLE of R, denoted by $\widehat{R}$, replacing the parameters in Eq (4) with their estimates to be found by using $\widehat{\alpha }$ and $\widehat{\gamma }$. That is, $\widehat{R}$ can be written as

Theorem 2.1. Suppose the failure times come from IERayleigh distribution. The MLEs of $\alpha$ and $\gamma$, given $\beta$, exist and have the following expressions.

and

Proof. See Appendix.

It is observed that the MLEs of parameters cannot be solved explicitly. Therefore, we propose to use stochastic EMA, which is an appropriate method for the censored data sets.

2.1.   Stochastic EMA

The Newton-Raphson algorithm is a frequently used method to derive the MLE of model parameters. In this method, the second derivatives of the log-likelihood function are needed, which may be complicated in some situations. Therefore, the EM algorithm is employed for comparison purposes. The EM algorithm has two steps: the expectation (E) step and the maximization (M) step. The E-step involves computation of the pseudo log-likelihood function. The M-step involves maximization of the pseudo log-likelihood function. The sample collected from unified PHCS may be viewed as incomplete data, and thus we proceed to explore the EM algorithm to obtain the MLEs of model parameters. Let $\underset{⎴}{X} = ({X}_{1:{m}_{1}:{n}_{1}}, ..., {X}_{{Q}_{1}:{m}_{1}:{n}_{1}})$ and $\underset{⎴}{Y} = ({Y}_{1:{m}_{2}:{n}_{2}}, ..., {Y}_{{Q}_{2}:{m}_{2}:{n}_{2}})$ denote the observed data, and the censored data are symbolized by $Z = ({Z}_{1}, ..., {Z}_{{Q}_{1}})$ and $V = ({V}_{1}, ..., {V}_{{Q}_{2}})$, where ${Z}_{r} = ({Z}_{r1}, ..., {Z}_{r{R}_{r}}); r = \left\{\mathrm{1, 2}, ...{Q}_{1}\right\}$ and ${V}_{r} = ({V}_{r1}, ..., {V}_{r{R}_{r}}); r = \left\{\mathrm{1, 2}, ...{Q}_{2}\right\}$ are $1\times {R}_{r}$ vectors. Thus, ${W}_{1} = (X, Z, {Z}^{\text{'}})$ and ${W}_{2} = (Y, V, {V}^{\text{'}})$ denote the complete data sets for strength and stress variables, respectively. Here, ${Z}^{\text{'}} = ({Z}_{1}^{\text{'}}, ..., {Z}_{{R}_{x}^{*}}^{\text{'}})$ and ${V}^{\text{'}} = ({V}_{1}^{\text{'}}, ..., {V}_{{R}_{y}^{*}}^{\text{'}})$ indicate the censored samples. The log-likelihood function based on complete data (${l}_{compelet}\left(\underline{W}\right|data)$) can be attained as

Based on E-step of the EM algorithm, we replace the missing information data with the conditional expectations of corresponding random variables. Then, the ${l}_{complete}\left(\underline{W}\right|data)$ can be shown as follows:

It is observed that the calculations of the conditional expectations of Eq (8) are more complicated and take a long time. So, by borrowing the idea of Diebolt and Celeux ^[34], we apply the stochastic EM algorithm (stochastic EMA), in which the E-step has been replaced by the stochastic step. This algorithm is a more suitable approximate idea and less computationally expensive than the EM algorithm. To calculate the stochastic EMA, we consider

Therefore, the MLEs of the parameters can be obtained by differentiating the following log-likelihood function partially with respect to the parameters:

2.2.   Asymptotic confidence intervals

In this subsection, we derive the approximate asymptotic distribution of MLE to construct approximate confidence intervals for $\widehat{R}$. Theoretically speaking, the variance-covariance of $\widehat{\theta } = (\widehat{\alpha }, \widehat{\beta }, \widehat{\gamma })$ can be derived from the Fisher matrix $I(\alpha, \beta, \gamma)$, whose elements are shown as

The detailed derivations are omitted to maintain brevity. It is worth mentioning that the expected values in the Fisher information matrix cannot be obtained explicitly since the distribution of the MLEs under the unified PHCS cannot be obtained explicitly. Therefore, the observed information matrix $I(\alpha, \beta, \gamma)$ is applied in the asymptotic normality of the MLE. Based on regularity conditions, the estimator $\widehat{R}$ asymptotically is normal with mean $R$ and variance ${\xi }_{R}$.

where $\frac{\partial R}{\partial \alpha } = -\frac{\gamma }{(\alpha +\gamma {)}^{2}}~~ \text{and}~~ \frac{\partial R}{\partial \gamma } = \frac{\alpha }{(\alpha +\gamma {)}^{2}}$. Thus, the $100(1-\varpi)\%$ asymptotic confidence interval of R can be created by

where ${z}_{\varpi }$ is ${z}_{\varpi /2}100{\varpi }^{th}$ percentile of normal distribution ($N\left(\mathrm{0, 1}\right)$).

3.   Bayesian estimation

In contrast to frequentist methods, the Bayesian approaches take advantage of available data and incorporate prior information of model parameters, thereby attracting much attention in statistical inference. So, in this section, the approximate BEs of R model are attained when all the parameters $\alpha, \gamma$ and $\beta$ have independent gamma distributions with parameters $({a}_{i}, {b}_{i}); i = \mathrm{1, 2}, 3$, respectively, as prior distributions. The gamma distribution is very flexible, and the Jeffreys prior, which is one of the commonly used non-informative priors, is a special case of it. Further, in the case of non-informative priors, very small non-negative values of the hyper-parameters, i.e., ${a}_{i} = {b}_{i} = 0.0001$, are used, which are almost like Jeffreys priors, but they are proper, inversely.

Using the likelihood function (5) and the joint prior distributions, the joint posterior distribution of unknown parameters $\alpha, \gamma$ and $\beta$ is defined as follows:

Now, the Bayesian estimators are motivated by three loss functions, which are SqE, Linex and GeE. The Bayesian estimator for R under the SqE loss function is the posterior mean and determined by

Based on the Linex loss function, the Bayesian estimator for R is given by

Under the GeE loss function, the Bayesian estimator for R is expressed as follows:

The integrals (11)–(13) are very hard to solved analytically, so we will utilize the MCMC method. Important sampling (ImS) and Metropolis-Hastings (MeHa) are two approaches of the MCMC. It is easy to calculate the BEs based on the ImS method, which is important in practice. However, if the form of the PDF becomes complicated, the conditional posterior distribution of the parameters cannot be easily attained, so the MeHa algorithm is a more appropriate choice for calculating the BEs. This algorithm is an efficient method to calculate the BEs. It can be easily conducted and help to reduce the operational complexity of high dimensional distributions. So, the BEs and the corresponding CrIs of R based on unified PHCS are computed by using the Gibbs sampler together with MeHa in ^[35,36] the algorithm. To apply this method, the marginal posterior PDFs of $\alpha, \gamma$ and $\beta$ can be re-expressed as

and

and also,

Therefore, the conditional posterior probability for α and γ are, respectively, expressed as follows:

and

It is clearly seen that Eq (16) does not show standard forms, and therefore it is not possible to sample directly by standard process. In that case, if the posterior density function is roughly symmetric, a normal distribution can be used to approximate it. So, we will use the Gibbs sampler together with MeHa technique to calculate the BE of R. The conditional posterior distributions $\alpha, \gamma$ and $\beta$ are generated using Algorithm 1. We borrow the idea of Ren and Gui ^[37] and use the trace plots for an MCMC chain to assess the convergence of the iteration process. If the MCMC chain is mixing adequately, the trace plot will fluctuate randomly around the true value as the lag value increases. The trace plot for n = 30, m = 15, ${T}_{1} = 0.7, {T}_{2} = 1.5$ is displayed in Figure 3. From Figure 3, it can be seen that the estimation results are reasonable.

4.   Simulation study

This section is devoted to the comparative study of the proposed estimates under different unified PHCS. Different estimation methods of reliability parameters are applied using frequency and Bayesian estimations. For comparison and analysis, 10, 000 cycles of simulations are repeated for the whole process. The performance of the estimates is compared based on the following criteria:

■ Mean square error ($MSE = \frac{1}{M}{\sum }_{I = 1}^{M}{\left({\widehat{\theta }}_{i}-{\theta }_{i}\right)}^{2}$): The smaller value of MSE indicates the better performance of the estimates. Here, ${\theta }_{i}$ denotes the obtained estimate at the i^th sample of the unknown parameter $\theta$, and M is the number of generated sequence data.

■ Average coverage probabilities

the probability of containing the true values of the parameters in between the interval estimates. Here, $1(.)$ is the indicator function, and $L(.)$ and $U(.)$ denote the lower and upper bounds of intervals, respectively.

■ Average lengths ($A{L}_{(1-\varpi)\%} = \frac{1}{M}{\sum }_{i = 1}^{M}\left({U}_{{\widehat{\theta }}_{i}}\right((1-\varpi)\%)-{L}_{{\widehat{\theta }}_{i}}((1-\varpi)\%\left)\right)$): Average length of the interval estimates with $\varpi$ significance level has been evaluated. Smaller length corresponds to better performance of the interval estimates. Here, $L(.)$ and $U\left(.\right)$ denote the lower and upper bounds.

We consider values ($\alpha, \beta, \gamma$) as (3.5, 2, 4) to provide values of R as 0.533. Two different ${T}_{i}; i = \mathrm{1, 2}$ values ${T}_{1} = 0.7, {T}_{2} = 1.5$ and ${T}_{1} = 1.5, {T}_{2} = 2.8$ are taken for both S-S variables. We have formulated three systematic CSs and determined the removals by providing fast failure, moderate failure and late failure, respectively. The MLEs are computed by applying the stochastic EMA. To make the iteration converge easily, the true values of the parameters are set for the initial values in simulation experiments. In the Bayesian estimations, very small values of the hyper-parameters, i.e., a_i = b_i = 0.0001 for i = 1, 2, 3 can be considered. However, due to the closeness of the BEs to the MLEs under this prior distribution, we also consider informative priors as ${a}_{1} = 7, {b}_{1} = 2, {a}_{3} = 2, {b}_{3} = 1, {a}_{2} = 8, {b}_{2} = 2$. The informative priors' parameters are chosen such that their mean is equal to the true parameter values. On both assumptions of informative and non-informative priors, the Bayes estimates under three loss functions are calculated based on the Gibbs sampler within the MeHa algorithm.

We propose four different sets of (m, n) as (30, 15), (30, 24), (50, 25) and (50, 40). For the MeHa algorithm, we take M = 10, 000 and NB = 1000. The significance level was taken as $\varpi = 0.05$. The MSEs and average lengths (ALs) of R are presented in Tables 1–4. According to the results shown in Tables 1–4, we can get some conclusions.

Tables 1 and 2 reflect that the MSE becomes smaller as the sample size increases, which shows the consistency of the estimators. The performances of the estimators are better when m increases. The values of ${T}_{i}; i = 1, 2$ for the stress-strength variables are assumed to be the same for both components to account for the simultaneous testing time. We can see that the increasing of T₁ and T₂ for other fixed values causes smaller MSE values in all cases since it provides more testing time to let more failure be observed. From the censoring scheme, it is observed that the CS III always has the worst performance. In parallel to increasing sample sizes, all estimates provide closer results to each other. The Bayesian method performs better than the frequency method obviously, and its estimates have smaller MSEs. The MSEs of the estimations based on the informative prior are smaller than the non-informative cases. The performances of the ML and Bayesian estimators are observed close to each other under non-informative prior.

Moreover, it is noted from Tables 3 and 4 that the average lengths of the ApCIs and CrIs are decreasing with larger sample sizes. The CrIs have also smaller average length than ApCIs. The coverage probabilities (CP) of interval estimates under different censoring schemes show no apparent difference. Also, the CPs of the ApCIs are closer to the significance level (0.95) than the CrIs.

From the above analysis of the results, we present the conclusion that the results of the BEs, especially under the Linex loss function, perform better than ML estimates in the proposed model environment.

5.   Real data analysis

One of the engineering applications of reliability modeling is to consider the diameter of the splashing droplets under two different atomizing pressures. The data sets are taken from Planche et al. ^[38], which represents the splashing degree under different atomizing pressures (MPa). We consider splashing degree for atomizing pressures of 1.0 MPa (dataset 1) and 1.5 MPa (dataset 2). The splashing droplets under 1.5 and 1.0 MPa pressures are considered as stress data X and strength data Y, respectively. If the S-S reliability is greater than 0.50, we can say that the 1.5 pressure will increase the splashing phenomenon. Moreover, if the system reliability is less than 0.50, we will think of the reverse result of the aforementioned scenario. In order to find the fitting performance of the IERayleigh distribution, we adopt the Kolmogorov-Smirnov statistic (KoSm) with the p-value. The KoSm statistics and corresponding p-values (given in brackets) are computed based on the MLEs of the model parameters. The KoSm values (p-values) for dataset I and dataset II are 0.077004 (0.8287) and 0.077926 (0.7162), respectively. Furthermore, PP and histogram plots for observations under dataset I and dataset II samples have been drawn in Figures 4 and 5, which present the same law as the numerical results. We assumed that this distribution has the same shape parameter to illustrate the proposed method. For testing that ${H}_{0} = {\beta }_{1} = {\beta }_{2} = \beta$, we perform a likelihood ratio test, and the respective value is 1.786. This value cannot get the critical point ${\chi }_{0.95}^{2}\left(1\right) = 3.84$. Thus, both stress and strength variables can be modeled by using the IERayleigh with equal $\beta$ parameter.

It is observed that since all the estimates of $R = P(X > Y)$ values are greater than 0.50, the 1.5 MPa pressure should be used for decreasing the splashing phenomenon on the considered scenario. We assume different unified PHCS censoring plans as

By applying the model established above and the proposed methods, the MLEs based on stochastic EMA, Bayesian point estimation based on Gibbs sampler together with MeHa method, approximate confidence intervals and HPD credible intervals can be acquired and constructed. The prior beliefs of the parameters are unavailable. So, we chose non-informative priors with hyper-parameter values (a_i, b_i) = (0.0001, 0.0001), i = 1, 2, 3, for Bayesian computation.

The point estimation results along with 95% ApCI and CrI are reported in Table 5 for this real data study. We observed close estimates to each other for both estimation methods. Moreover, both approximate Bayes estimates of R are similar. The CrI lengths (CrILs) are obtained smaller than ApCI lengths (ApCILs). It is observed that since all the estimates of R values are greater than 0.50, the 1.5 MPa increases the splashing phenomenon.

We also consider the diagnostic plot for showing the convergence of the simulated Markov chains. We consider the trace plot which is a plot of the iteration number i against the value of Rⁱ at each iteration. We present the trace plot of the stress-strength reliability in MCMC chains with 14, 000 iterations and first 5000 time being burn-in time in Figure 6. The trace plot shows that the Markov chain fluctuates around estimation with a similar variation. Further, as we see from Figure 7, the density plot seems to have asymmetrical and unimodal shape. It has a unique peak, and it determines the mode of the distribution. We present the diagnostic plots for SCII. The plots of the other censoring schemes are similar.

6.   Conclusions

The issue of a stress-strength reliability model for IERayleigh distribution under unified PHCS was examined in this study. The unified PHCS is a flexible progressive censoring that can be used to reduce cost and time. It provides many different options for reliability studies and helps to overcome many problems in reliability engineering. We used classical and Bayesian methods for the estimation procedures, and we observed consistent results. Since MLE of R cannot be obtained in a closed form, the stochastic EMA is proposed to estimate the unknown parameters. The asymptotic intervals are created based on the Fisher matrix. The Bayesian estimates are calculated using the Gibbs sampler together with the MeHa algorithm with three loss functions and gamma priors. In addition, the constriction of the HPD credible intervals is provided based on MCMC samples. An extensive simulation study is implemented to validate the accuracy of the produced estimators. We found that, for point and interval estimations, the Bayes estimators using MCMC method outperformed MLEs. Therefore, if previous knowledge about the data is available, one may consider employing the Bayesian approach using the Gibbs sampler together with the MeHa algorithm for all practical purposes when analyzing data; otherwise, one may turn to MLEs or Bayesian estimation based on non-informative prior. Finally, we consider a real engineering example to show the potential application of our reliability model problem. The results show that increasing the pressure reduces the splashing phenomenon and thus improves the surface quality. Finally, the considered problem in this study can be extended in different ways such as considering the correlation between the stress and strength random variables and multicomponent stress-strength reliability model.

Acknowledgements

The authors extend their appreciation to the Deputyship for Research & Innovation, Ministry of Education in Saudi Arabia for funding this research work through the project number (IF2/PSAU/2022/01/21551).

Conflict of interest

The authors declare that there is no conflict of interest.

Appendix

Proof of Theorem 2.1

Fix ${Q}_{1}$, $\gamma$ and $\beta$. Since $\mathit{ln}t\le t-1, t > 0$ holds, let $t = \frac{\alpha }{\widehat{\alpha }}$, and then

By putting $\widehat{\alpha } = -\frac{{Q}_{1}}{{Ą}_{x}}; \text{}{\mathrm{Ą}}_{x} = {\sum }_{i = 1}^{{Q}_{1}}\mathit{ln}(1-\mathit{exp}(-{\xi }_{{x}_{i:{m}_{1}:{n}_{1}}}\left)\right)+{\sum }_{i = 1}^{{Q}_{1}}{R}_{i}\mathit{ln}(1-\mathit{exp}(-{\xi }_{{x}_{i:{m}_{1}:{n}_{1}}}\left)\right)+{R}_{x}^{*}\mathit{ln}(1-\mathit{exp}(-{\xi }_{{T}_{x}}\left)\right)$ in the Eq (A.1), we have

This implies that

where ${Ą}_{y} = {\sum }_{i = 1}^{{Q}_{2}}\mathit{ln}(1-\mathit{exp}(-{\xi }_{{y}_{i:{m}_{2}:{n}_{2}}}\left)\right)+{\sum }_{i = 1}^{{Q}_{2}}{R}_{i}\mathit{ln}(1-\mathit{exp}(-{\xi }_{{y}_{i:{m}_{2}:{n}_{2}}}\left)\right)+{R}_{y}^{*}\mathit{ln}(1-\mathit{exp}(-{\xi }_{{T}_{y}}\left)\right)$ and

Using the transformation $-\widehat{\alpha }{Ą}_{x} = {Q}_{1}$, we have

Equality holds if and only if $\alpha = \hat{\alpha}$. Now, we want to show the MLE of γ, given α and β, exists and has the following expression.

Using a similar procedure, we consider $t = \frac{\gamma }{\widehat{\gamma }}$, and so by taking $\widehat{\gamma }$ from Eq (A.2), we have

Then,

So, the existence of $\widehat{\gamma }$ makes $l\left(\alpha, \beta, \gamma |data\right)\le l\left(\alpha, \beta, \widehat{\gamma }|data\right)$, and when $\widehat{\gamma } = \gamma$, the equal sign holds. This proves that the function $l\left(\alpha, \beta, \gamma |data\right)$ reaches its maximum value at the point $\left(\widehat{\alpha }, \beta, \widehat{\gamma }\right)$, where $\beta$ is given.