Barycentric rational interpolation method for solving time-dependent fractional convection-diffusion equation

1.   Introduction

Air pollution reduction has been the core solution to facilitate several Sustainable Development Goals (SDGs), such as sustainable cities and communities, responsible consumption and production and climate action ^[1]. The conflict between air pollution reduction and economic growth needs to be resolved by establishing a comprehensive model for describing the pollution life cycle ^[2]. However, the focus of existing research has been placed on pollution apportionment and PM_2.5 concentration forecast. The analysis of the patterns of emerging pollutions and the variations of PM_2.5 concentration at different places and times has been overlooked in the literature ^[3]. It is thus critical to develop a spatiotemporal analysis platform where the user can be positively involved in the process and able to express the intention to reach the analysis goals. This kind of user-interactive platform is very useful to generate insightful implications by combining the knowledge of domain experts and artificial intelligence.

Modeling PM_2.5 concentrations is a challenging task because we need to apportion the sources which emit the aerosols and analyze the transportation pathways the aerosols follow. The PM_2.5 sources could be generated from nature (dust soiling, volcanic eruptions, sea salt, etc.), anthropogenic activities (vehicle emissions, burning activities, coal and gasoline combustion, etc.) or photochemical transformation of precursor emissions such as sulfur dioxide (SO₂) and nitrogen oxides (NO_x). Several models of PM_2.5 source apportionment have been proposed. The most prevalent ones are the receptor model and the tracer model. The receptor model follows the principle of pollutant mass conservation, stipulating that the measured density of a pollutant element conforms to that for all nearby sources that contain the pollutant element ^[4,5]. The tracer model, on the other hand, directly captures pollutant samples at potential sources and analyzes the chemical characteristics of the samples. By using the metal elements and ions as tracers or markers, the tracer model can provide evidence for the sources contributing to the PM_2.5 compositions ^[6].

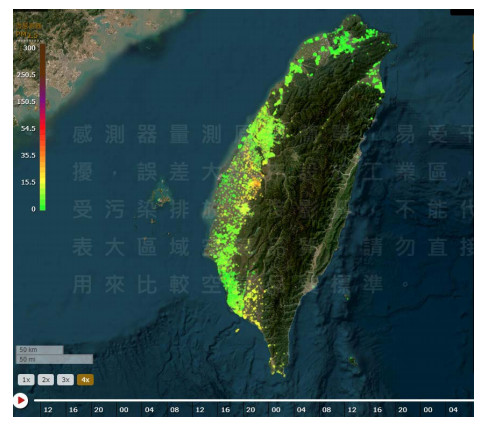
Both the receptor model and the tracer model require expensive particulate sensors to identify the elements in the captured pollutants. Government agencies can only afford to establish air quality monitoring supersites at hot-spot places such as industrial complexes or metropolises. However, the pollution sources could happen anywhere and anytime. Moreover, the transportation of the emitted particulates is influenced by cyclone conditions and geographical landscape, which are also location- and time-dependent ^[7]. Hence, spatiotemporal analyses are critical for developing a robust and reliable model explaining the PM_2.5 pollution episodes. Thanks to the government-executed Digital Construction Design Project for construction of the Internet-of-Things (IoT) of low-cost sensors, more than 9,600 microsites have been set up nationwide as of June 20, 2023 (see Figure 1). Although the low-cost sensor IoT cannot work with the receptor model or the tracer model to identify the chemical elements contained in the pollution, it does open a door for conducting spatiotemporal pollution analysis with fruitful image analysis techniques.

Figure 1.  Air quality IoT of low-cost sensors (image from Taiwan EPA, https://wot.epa.gov.tw/).

DownLoad: Full-Size Img PowerPoint

In this paper, we propose a visualization-based spatiotemporal analysis approach which enables the user to actively specify the spatial relationships between pollution objects and land objects to retrieve the most similar pollution episodes observed in history. The user can click on a retrieved episode and call up a pollution feature detection function to further examine the spatiotemporal characteristics of the pollution features. Our analysis method is novel in terms of not only offering a visualization platform for analyzing pollution episodes but also saving a lot of human effort to search and extract the pollution features from the big volume of monitored air-quality data.

1.1.   Spatiotemporal pollution analysis

The characteristics of existing studies can be compared according to the methodologies applied to the spatiotemporal analysis. From the literature review, the articles of spatiotemporal pollution analysis mainly adopt five approaches, as chronicled in Table 1.

Table 1.  Comparison of recent works on spatiotemporal pollution analysis.

	Probability based	Classic statistics	Regression	Time series analysis	Machine learning
Yu and Wang [8] (2010)	●
Habermann et al. [13] (2015)			●
Song et al. [10] (2019)		●
Lung et al. [11] (2020)		●	●
Yang et al. [12] (2020)		●	●
Liu et al. [14] (2020)			●
Jiang et al. [9] (2020)	●
Kersey et al. [16] (2020)		●	●	●
Kalo et al. [17] (2020)		●	●
Dzhambov et al. [15] (2023)				●
Zareba et al. [18] (2023)					●
Li et al. [19] (2023)			●		●
Chicas et al. [20] (2023)		●		●	●

---

 | Show Table

DownLoad: CSV

Probability distributions are employed to model the spatiotemporal variations of PM_2.5 concentrations. Both parametric and non-parametric probability distributions can be used depending on the approximation method. It is assumed in Yu and Wang ^[8] that the PM_2.5/PM₁₀ ratio is invariant at the same location during the same period of a year. They used the historical data of PM_2.5/PM₁₀ ratios to construct a non-parametric probability distribution for predicting PM_2.5 given the PM₁₀ concentration. Jiang et al. ^[9] applied a parametric probability distribution which used two parameters to describe the shape and the phase characteristics of the probability density functions (PDFs) of the hourly PM_2.5 concentrations in each city over seasonal time frames. The optimal values of the two parameters are determined by fitting the historical data. The number of articles applying probability-based approaches is small, as compared to those using other approaches. The reason is the difficulty of explaining the result of probability distributions.

Classic statistics is a more popular approach in early studies. In particular, the correlation coefficient (CC) and coefficient of variance (CV) are broadly employed statistical indices for conducting spatiotemporal analysis of air pollutions monitored at different sites along a given time span. The spatiotemporal distribution of air pollution characteristics in Jiangsu Province, China, was studied in Song et al. ^[10], which elaborately examined the spatial and temporal CCs between air quality index and meteorology and between major pollutant variations. Lung et al. ^[11] showed that the CV among ten community locations exceeds 20% in more than one fifth of the days in July and December. The largest variations typically appear on weekends, mainly yielded by traffic, restaurants and temples. Lung et al. ^[11] also investigated the CC between microsites and the nearest supersite to validate the consistence of pollution patterns at highly correlated sites. Yang et al. ^[12] investigated the CC between PM_2.5 concentrations/variations and the urbanization level of the city. Their result was a positive/negative correlation between urbanization and PM_2.5 concentrations/variations.

The third group of articles use the regression methodology. The regression technique is useful in finding the relationships between a set of independent variables and the responsive variable. Regression has been applied to estimate the pollution concentrations from meteorological or socioeconomic factors. Habermann et al. ^[13] chose five independent factors, namely, the altitude, distance to industrial land use, distance to expressways, traffic flow and demographics. They applied linear regression to model NO₂ concentration in these factors. Similarly, Lung et al. ^[11] and Liu et al. ^[14] applied spatial linear regression on neighboring monitoring sites and economic variables in a particular time period. Yang et al. ^[12] used spatial regression with a quadratic expression to reveal the contribution of urbanization, industrialization and green land area to the accumulation of PM_2.5 concentrations. The next category of articles applied time series analysis to find the trends of PM_2.5 concentrations and related factors, such as atmospheric conditions, land observations, human activities and diseases. Dzhambov et al. ^[15] aimed to investigate the short-term effects of air pollution on hospital admission for asthma in Sofia during the period of January 1, 2009, to December 31, 2018. Negative binomial regressions were analyzed to reveal associations between air pollution and daily hospital admission for asthma.

More recently, several advanced studies have been conducted in various countries, such as the United States, Poland, South Korea and Japan. These studies applied hybrid or machine learning approaches to boost the performance of air-pollution spatiotemporal analysis. The studies in the United States ^[16,17] hybridized statistics, regression and time-series analysis to reveal the relationship between air pollution and public health. A spatiotemporal interpolation and visualization of real-time air pollution data for the contiguous United States was also provided. For the study conducted in Krakow, Poland ^[18], unsupervised clustering algorithms were applied to analyze spatiotemporal patterns of air pollution over one-year hourly PM₁₀ data. It revealed that a "bagel" pattern is found in the case of maximum concentrations, due to pollution produced in Krakow's surrounding counties and the city of Krakow form a separate cluster. For the case of average concentrations, Krakow city and its southeastern counties were grouped in one cluster, separate from the northwest part, due to the topography of the terrain. The study in Seoul, South Korea ^[19], showed that 64.9% of the premature mortality cases in 2019 are due to PM_2.5, while the remaining are attributed to NO₂. The study integrated a random forest approach into land-use regression modeling to predict daily and diurnal PM_2.5 and NO₂ and evaluate the significance of contributing factors. Finally, in the study in Nagasaki Prefecture, Japan ^[20], a hybrid method combining statistical correlation, time series analysis and machine learning techniques was proposed to make the interpretation of the pollution dynamics more complete. The study offered a holistic perspective of the spatiotemporal distribution, trend, forecast and contributing factors.

Most of the existing methods conduct analyses separately on the spatial and temporal domains due to the high complexity of computations incurred by enormous combinations in spatiotemporal scenarios. However, the higher-level correlation existing in the spatiotemporal domain can only be revealed from a holistic view of both dimensions. The classic approaches rely on probability, statistics and regression, and their numerical results are hard to interpret and lack a visualization facility to show the implications. In this paper, we propose to use image processing techniques to facilitate air-pollution spatiotemporal analysis. The benefits of our method are two-fold. First, the analysis result obtained by applying image processing technique is visualizable and is intrinsic to interpreting the implications. People prefer to see images rather than numeric values to infer insightful knowledge. Second, image processing is a well-established discipline, and there exist many available algorithms for elaborate analyses.

1.2.   Spatial image retrieval

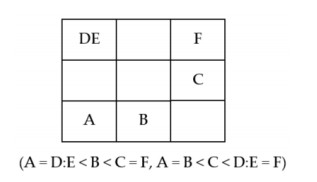
Most image retrieval methods focus on similarity matching with colors, textures and contours, without paying too much attention to the spatial relationships between the objects in the image. However, in the applications of some domains, such as geographic information systems and urban planning, the object spatial relationships are particularly important. To this end, Chang et al. ^[21] proposed the 2D string data structure, which tallies the sequences of object projections along the x and y axes, respectively. Figure 2 shows an example of the 2D string for an image whose objects have been represented by alphabetical symbols. The 2D string containing the projection sequences of the objects along the x and y axes is (A = D:E < B < C = F, A = B < C < D:E = F), where the indicator " < " denotes "left of" for the x projection sequence or "below" for the y projection sequence, the separator "=" means "at the same location along the referred axis, " and the indicator ":" corresponds to "at the same location along both axes."

Figure 2.  An example of the 2D string.

DownLoad: Full-Size Img PowerPoint

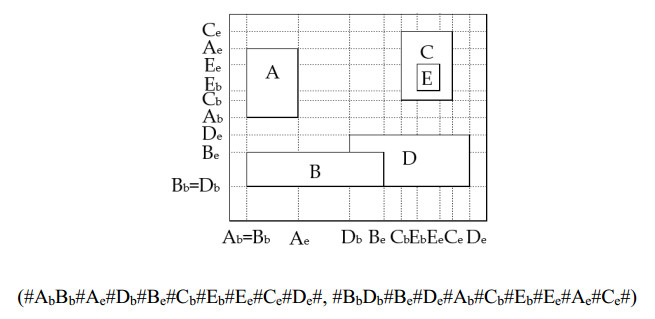
However, the 2D string cannot describe complex spatial relationships between objects such as "contained" and "overlapped." Many improved versions of the 2D string exist. A notable one is the 2D Be-string ^[22] which removes all of the indicators and is hence more efficient than the 2D string. The 2D Be-string representation is as follows. For each axis, every object has two projection lines, at the beginning and ending boundaries of the object along that axis. A dummy object projection line "#" is inserted between two consecutive projection lines if they are not coinciding. Figure 3 illustrates the construction of the 2D Be-string for an image containing five objects. For each of the five objects, two projection lines with the subscripts "b" and "e, " respectively, intersect the object at the beginning and ending boundaries. It is noted that a dummy object projection line "#" is placed at the beginning and the end of the string for each axis because the objects are not aligned with the image boundaries. Therefore, the complete 2D Be-string of the image in Figure 3 is (#A_bB_b#A_e#D_b#B_e#C_b#E_b#E_e#C_e#D_e#, #B_bD_b#B_e#D_e#A_b#C_b#E_b#E_e#A_e#C_e#). It is seen in this example that the 2D Be-string can describe complex spatial relationships such as "contained" and "overlapped, " and the location of the objects does not have to be constrained within a grid.

Figure 3.  The 2D Be-string of an iconic picture.

DownLoad: Full-Size Img PowerPoint

The next step is to estimate the similarity between two images already represented by the 2D Be-string representation scheme. Wang ^[22] proposed to compute the similarity based on the longest common subsequence (LCS) between the 2D Be-strings of the two images. The LCS is the one which possesses the greatest number of characters among all common subsequences of two strings. Apparently, the LCS focuses on how similar the subsequences of two strings are, but it ignores the differences between them. That is, longer strings tend to have longer LCSs. The measure needs to be normalized by the string length.

The application of computing the 2D Be-string similarity proceeds as follows. Assume that the user submits a query image Q containing N objects, and Q is to be matched with every database image D. Let the 2D Be-string representations for Q and D be Q = (Q_x, Q_y) and D = (D_x, D_y). The LCS between Q_x and D_x is derived, and let it be denoted by C_x and the LCS excluding the dummy objects be denoted by M_x. Let L(S) denote the function that returns the length of string S. The similarity between Q_x and D_x can be derived as follows.

The similarity Sim_y between Q_y and D_y can be computed similarly.

Next, we can derive the overall similarity between Q and D as the mean of Sim_x and Sim_y as follows.

With Eq (1) and Eq (2), one is able to compute the similarities between the query and every database image. The retrieved images are ranked in the order of decreasing value of similarity to the query.

1.3.   Convolutional feature detector

There exist many convolutional feature detectors in the field of image processing and analysis. The probability of a pixel being an element of a particular feature, such as a line, an edge, a corner point or an isolated point, can be estimated by examining the intensities of its neighboring pixels. Convolutional filters can be designed to estimate the feature probability. In the literature, various convolutional filters have been proposed, such as the line detector, corner-point detector and edge detector. We briefly review two examples in the following.

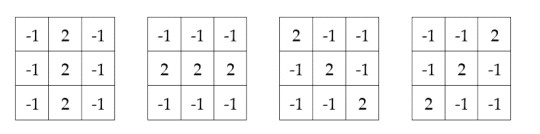
A line is a sequence of contiguous pixels which have high-contrasting intensity compared to those pixels residing at both sides. The convolutional filters shown in Figure 4 can be applied to detect the presence of vertical, horizontal and oblique-orientation lines in an image.

Figure 4.  Line filters for detecting vertical, horizontal and two oblique-orientation lines.

DownLoad: Full-Size Img PowerPoint

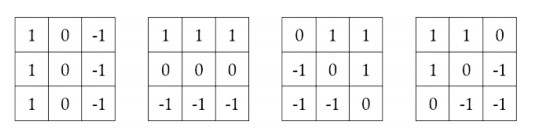
Edges exist at boundaries between adjacent heterogeneous regions which share a common side. Noise removal usually precedes the edge detection process to avoid the presence of false edges. The Prewitt operator suggests the edge filters shown in Figure 5 to detect the presence of vertical, horizontal and oblique edges in an image. There exist other edge detectors, such as the Roberts operator and Sobel operator. We introduce these operators in the Supplement to save space.

Figure 5.  Prewitt edge filters for detecting vertical, horizontal and two oblique edges.

DownLoad: Full-Size Img PowerPoint

These convolutional feature detectors are simple yet powerful operations which can automatically extract the air pollution features revealing important clues, such as furnace combustion point pollution, a linear emission source from road traffic or a large pollution region from a dust storm, resulting in different pollution episodes. Moreover, the fast computational nature of convolution operations facilitates the application of analysis on both spatial and temporal domains, overcoming the computational difficulty suffered by existing methods.

2.   Proposed Methods

2.1.   Framework architecture

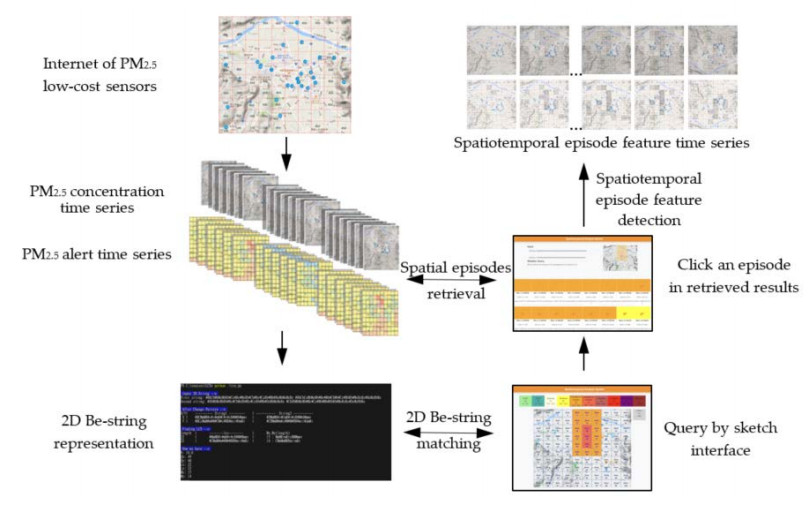
The framework architecture of our proposed methods is shown in Figure. 6. We resolve the monitored field as an n×n image and consider the measured PM_2.5 concentrations as the gray intensities in the image. By deploying an IoT of PM_2.5 low-cost sensors, we are able to acquire the time series data of PM_2.5 concentrations and corresponding air-quality alert categories. For each image in the PM_2.5 alert time series, the connected component with the homogeneous alert category form an object in the image. Every object is labeled with a unique ID, and the boundaries of its minimum bounding rectangle are recorded. The object information is used to generate the 2D Be-string representation of the image. To facilitate the pollution episode retrieval, a query-by-sketch interface is developed where the user can sketch the alert objects of interest and the spatial relationships between them. The 2D Be-string of the query is generated and is compared to that of each database image in the alert time series. The retrieved result shows the alert database images in the order of decreasing similarity score to the query. To further explore the pollution episode, the user can click the retrieved image of interest and is led to the episode feature detection interface. Various convolutional filters can be employed to explore the changes of the detected features in the short-term PM_2.5 concentration time series containing the episode. Our proposed methods are novel given the fact that this research is the first proposal for applying image processing techniques to facilitate the air pollution spatiotemporal analysis. The analysis result is visualizable and is intrinsic to interpreting the implications.

Figure 6.  Framework architecture of the proposed methods.

DownLoad: Full-Size Img PowerPoint

2.2.   Pollution map time series generation

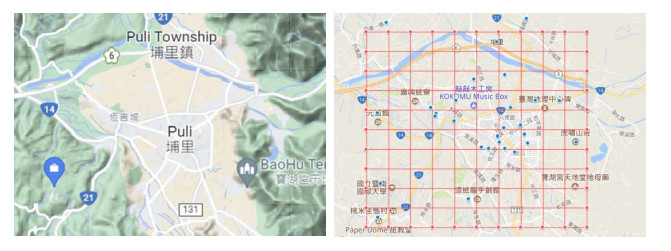
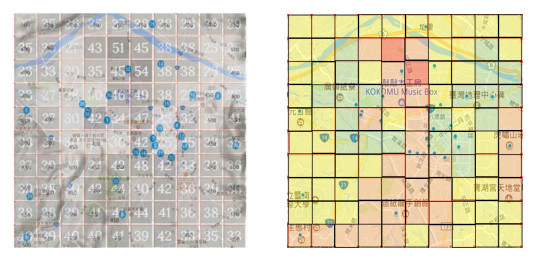
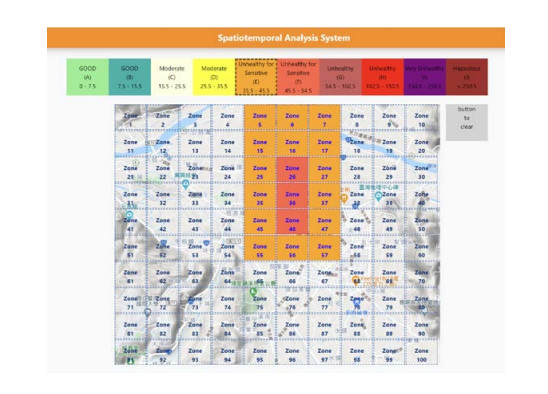
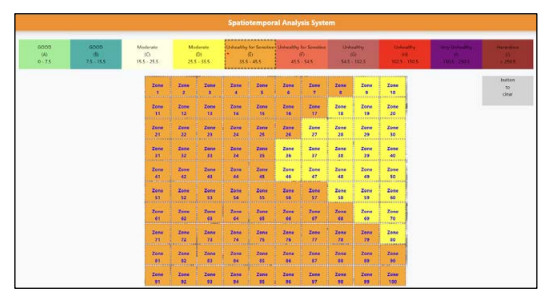
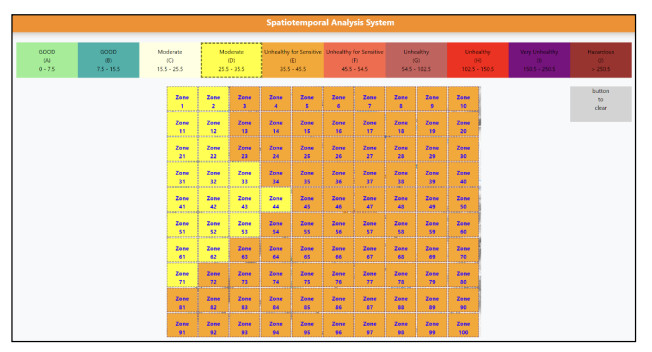
In this paper, we chose Puli Basin as our study field, as shown in Figure 7(a), located in the central Taiwan area. It is seen that the center of Puli Basin is surrounded by mountains. To the north of Puli downtown, there is a highway and a river, and there are several streams at the southern side of Puli. The highway is the main commuting line for labor workers, and the river valley is the passage of external air pollution emitting from the western metropolis. The basin geography is a good choice for conducting a pilot study because the quantity of daily inbound and outbound vehicles is not as large as that observed in western metropolis, and the citizen living styles are stable, resulting in several frequently seen pollution patterns in the basin. Since 2016, Yin et al. ^[23] has built a network of 32 low-cost PM_2.5 sensors in an 8×8 km² area within the Puli basin. The sensors, model G7 PMS7003, use a laser beam to illuminate the particles. The scattered light is then analyzed to estimate the particle size and the number of particles. As the residential communities and the business district are near the basin center, more sensors were deployed in the center than the suburban area to monitor the plausible pollutants with a finer resolution. Figure 7(b) shows the deployed sensor sites marked by blue points. We model the studied field by 10×10 grids. The hourly PM_2.5 concentration of each grid is estimated by applying Gaussian smoothing with the measured intensity of neighboring PM_2.5 sensors. So, for every hour, we obtain a PM_2.5 concentration map image of 10×10 pixels, and the estimated PM_2.5 concentrations in the grids are considered as the gray values of the image. Another version of the map image is produced by converting the PM_2.5 concentrations to those with 10 air-quality alert levels (see Figure 8) modified from the alert categories defined by the Taiwan Environmental Protection Administration (EPA). This alert image is for depicting the concept conceiving the pollution region as an image object. Figure 9 shows an example converting a PM_2.5 concentration map image (the gray value is superimposed in the grid for reference) to a corresponding PM_2.5 alert map image. If we continuously monitor the PM_2.5 concentrations for 365 straight days, we will produce a time series of 365 × 24 = 8,760 PM_2.5 concentration map images and another time series of 8,760 PM_2.5 alert map images. The first time series will be used for pollution episode feature analysis, and the second time series will be used for pollution episode retrieval, as will be described in the following sections.

Figure 7.  Studied field in this paper. (a) Basin geography of Puli Township. (b) Deployed PM_2.5 sensors and the 10×10 grid sampling.

DownLoad: Full-Size Img PowerPoint

Figure 8.  10 air-quality alert levels by reference to the range of PM_2.5 concentration.

DownLoad: Full-Size Img PowerPoint

Figure 9.  An example of converting a PM_2.5 concentration map image to a corresponding PM_2.5 alert map image.

DownLoad: Full-Size Img PowerPoint

2.3.   Pollution spatiotemporal episode retrieval

After converting the PM_2.5 concentration image to a corresponding PM_2.5 alert image, we can render the spatial relationships between the pollution alert objects. This will reveal important clues for understanding the spatial context of pollution objects and land objects. For example, we may see a pollution alert level-6 object frequently appears at the southern bank of the river, which indicates a plausible anthropogenic pollution source such as crop burning or garbage combustion. By representing the pollution alert objects and land objects with the 2D Be-strings, the user can sketch a query like "show me the hourly alert images in summer where a pollution alert level-6 object appears at the southern bank of the river." The retrieved result would alleviate the effort to reveal anthropogenic activities that cause the pollution.

To facilitate this, we need to align the PM_2.5 alert objects and the land objects into a single image. The PM_2.5 alert objects can be automatically labeled by the region-growing technique ^[24]. The minimum bounding rectangle for each alert object is found. For the land objects, they need to be manually labeled. Fortunately, the land objects are seldom changed, and we can carefully label these objects one time and use the result for a long period. After we combine the PM_2.5 alert objects and the land objects into a single image, the corresponding 2D Be-strings of the PM_2.5 alert image are generated for spatiotemporal retrieval of pollution episodes.

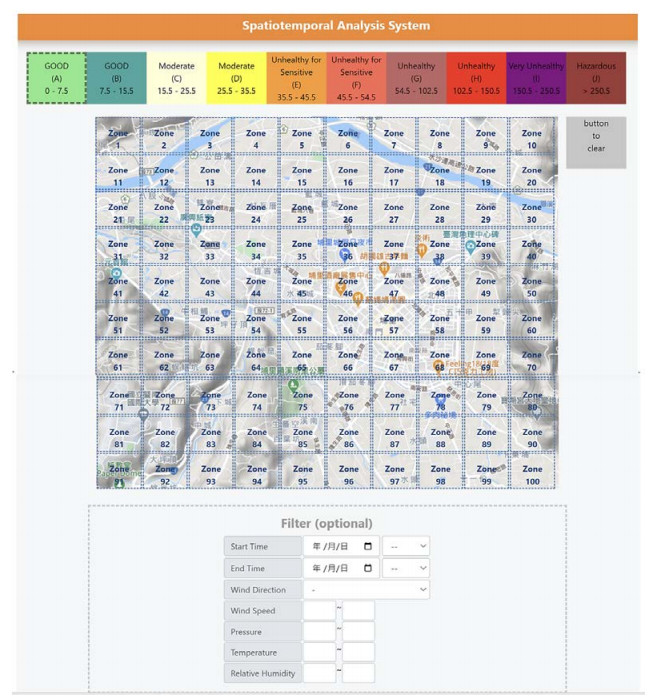
In order to retrieve the interesting pollution episode images in the PM_2.5 alert time series, a query interface needs to be developed. The Query-by-Sketch (QBS) interface is a broadly adopted scheme in the literature for facilitating the query interface for spatial relationship image retrieval. For example, Giangreco et al. ^[25] proposed a QBS interface for image retrieval with color sketches. The angular radial partitioning (ARP) for the sketch edges and the color moments were used as the features, and a distance metric was designed for computation of similarity ranking. Wang et al. ^[26] developed a free-hand sketch interface to graphically portray the spatial ideas of objects for image retrieval. The nearest images stored in the database to the sketch query are ranked and displayed. In this study, we developed a QBS interface that is customized to the grid-location and alert-color representation. Figure 10 shows the layout of our QBS interface. The upper half contains the pallet and the map in grid structures. The pallet offers 10 colors corresponding to the 10 air-quality alert categories with which the user can sketch alert regions and the spatial relationships among them on the map. The map is formatted as 10×10 grid structures with a grid square as the minimal unit for an alert region. The lower half offers a filter function where the user can limit the retrieved episode maps in the specified time and weather criteria. The filter function is useful when the user intends to deeply exploit the relationships between the retrieved pollution episodes and the seasonal and weather factors. Figure 11 shows a QBS example where the user intends to see if there exist any alert images containing a pollution source along the main road towards the southern bank of the river. So, the user sketches a line pollution source coinciding with the main road at the southern bank of the river. The center of the pollution source is an alert level-6 object, and it is contained in a level-5 object, indicating that the pollution is mitigated as the location is away from the main road.

Figure 10.  Layout and functions of our QBS query interface.

DownLoad: Full-Size Img PowerPoint

Figure 11.  A QBS example where the user sketches an iconic query.

DownLoad: Full-Size Img PowerPoint

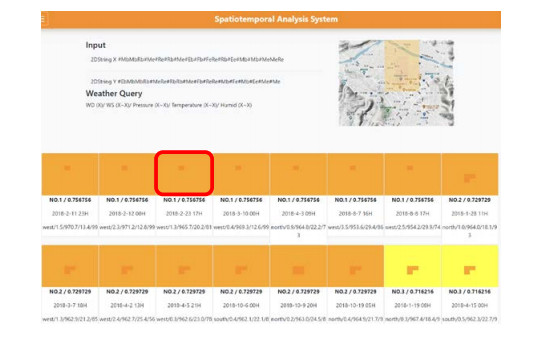
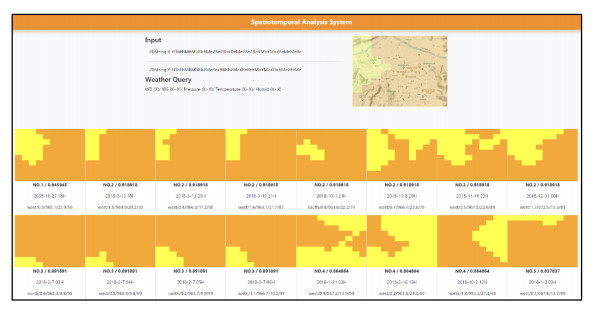
When the user submits the QBS query for retrieval, the thumbnail image of the sketch query is shown in the retrieval page for reference (see the upper right of Figure 12), and the 2D Be-strings of the query are automatically generated (see the upper left of Figure 12) as follows.

Figure 12.  The produced 2D Be-strings of the query and the retrieved episodes.

DownLoad: Full-Size Img PowerPoint

X string: MbMbRb#Me#Re#Rb#Me#Eb#Fb#FeRe#Rb#Ee#Mb#Mb#MeMeRe

Y string: EbMbMbRb#MeRe#RbRb#Me#Fb#ReRe#Mb#Fe#Mb#Ee#Me#Me

As previously noted, the land objects of mountains and rivers have been manually labeled by experts as M and R objects, respectively. The user-sketched level-5 and level-6 alert objects are automatically labeled as E and F objects by the region-growing algorithm. By using the 2D Be-string representation, the spatial relationships between the pollution alert objects and the land objects can be rendered. The similarity score between the query and each image in the PM_2.5 alert time series is calculated based on the LCS. The retrieved pollution episodes are then shown in the order of decreasing similarity score to the query (see the lower half of Figure 12). Multiple episodes may share the same similarity score. As seen in the figure, the first seven episodes have the highest similarity score of 0.756756, followed by the next seven episodes which have a similarity score of 0.729729. The last two episodes have the third rank similarity score of 0.716216. The remaining retrieved episodes can be displayed by clicking the "next page" button on the user interface, and we present these retrievals in the Supplement to save space. It is noted that the first-rank and the second-rank episodes have similar appearances of alert objects. However, their spatial relationships to the implicit land objects are different. It is seen that the position of the level-6 alert object contained in the first-rank episodes is nearer to the upper side of the image than that in the second-rank episodes, resulting in different spatial relationships to the land objects of mountains and rivers. For the episodes contained in the third-rank group, the outer alert object is of level 4, while in the query the outer alert object is of level 5. Another interesting fact is that although multiple episodes share the same similarity score, they may appear at different times and dates. For example, the first-rank retrievals contain the episodes recorded in the morning and evening on different dates in February, March, April and August. This phenomenon validates our anticipation that some particular pollution episodes frequently occur in a year, and the cause of these patterns must be related to local factors which need to be explored. The user can click the retrieved episode of interest (for example, the third retrieved episode in Figure 12) to activate our episode feature detection interface for conducting more focused analyses as described in the next section.

2.4.   Pollution spatiotemporal episode feature analysis

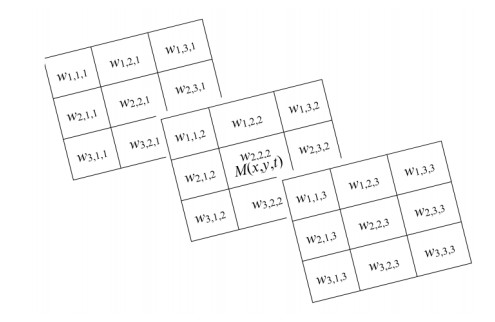
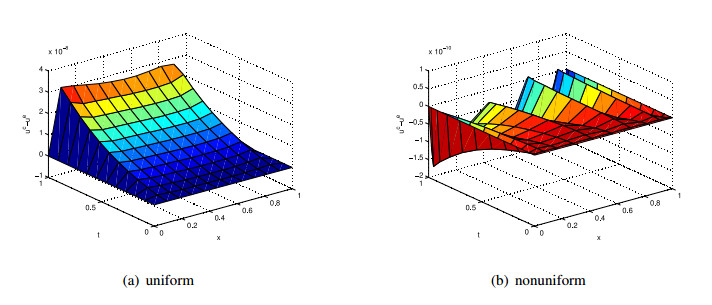
The spatiotemporal feature detection analysis is designed for automatic detection of various emerging pollution patterns in the time series. There are three commonly seen PM_2.5 pollution patterns, i.e., point source, line source and region source. The point source is a single pollutant emission spot, such as a combustion furnace. Vehicles on roadways are typical examples of pollution line sources. Region sources have larger coverage on the surface than the point and line sources. For example, the PM_2.5 purple alert has a large area of serious concentrations because it is usually caused by climate phenomena such as dust storms, cyclones or temperature inversions. We adopt several spatiotemporal masks to detect various pollution patterns. In addition to the classic 2-dimensional convolutional feature detectors (see Section 2.3), we further propose 3-dimensional convolutional filters by including the time domain as the third dimension. A structure of a 3×3×3 spatiotemporal filter is illustrated in Fig. 13. It is seen that the center of the filter is aligned with a grid position (x, y) at time t, and the filter consists of three masks for times t − 1, t and t + 1, respectively. There are, in total, 27 weight values in the 3-dimensional convolutional filter. So, the change of pollution in both the spatial and time domains can be detected. The 3-dimensional convolutional filter can be generalized to an n×m×k mask where n and m are the mask widths in the two spatial axes, and k is the mask depth in the temporal axis. The values of n, m and k are odd numbers to enable us to align the filter center at M(x, y, t), the value of grid (x, y) at time t in the time series maps. We define the convolution operation on M(x, y, t) with an n×m×k mask as follows.

Figure 13.  The weight values in a 3×3×3 convolutional filter centered at M(x, y, t).

DownLoad: Full-Size Img PowerPoint

The convolution operation is performed by aligning the filter through the entire image to obtain a response map R(x, y, t). The pollution pattern is declared to be detected at a spatiotemporal location if the absolute response value at that location is higher than a threshold, i.e.,

where δ is the specified feature response threshold.

The automatic episode feature detection is critical when the government agent intends to send technical staff and instruments to the PM_2.5 pollution hot spot. Figure 14 shows the example for detecting horizontal and vertical line features of pollutants by clicking the third retrieved episode in Figure 12. The left image shows the original PM_2.5 concentration map, while the right image is the sum of absolute response maps of line features obtained by applying the convolution process. It is seen that there are two major line pollution sources. One is horizontal (at the second row from the top) and is near the exit of the highway, and the other is vertical (at the sixth column from the left) and is along the main road connecting the highway exit to downtown. Both line sources are automatically detected by using the 3×3×1 mask as previously noted. These are typical pollution patterns incurred by rush-hour traffic on a business weekday. The episode feature detection can be continuously performed within a specified time span such as from 5 AM to 8 PM such that the dynamic changes of spatiotemporal features are displayed for insightful visualization. More complex analyses can be conducted by using appropriate 3-dimensional convolutional filters of an arbitrary size of n×m×k to further detect the episode feature differences in the temporal axis. More illustrative examples will be presented in Section 4.

Figure 14.  The detected horizontal and vertical line features by clicking the third retrieved episode in Figure 12.

DownLoad: Full-Size Img PowerPoint

3.   Results

3.1.   Pollution episode retrieval

In addition to the line pollution source emitted from the main road, the pollutants yielded by the western metropolis seep into Puli through the northern river valley and the southern streams. The user can visualize this by sketching a pollution map example as shown in Figure 15. From the left end of Puli, the pollutants drifting through the northern river valley and the southern streams form a particular shape of an alert-level-5 object and a cleaner level-4 triangle object to the right end of Puli. When the user submits the sketch example, the 2D Be-strings of the query are automatically generated (as shown in the upper left of Figure 16), and the retrieved most similar images are shown in decreasing order of their similarity to the query (see the lower half of Figure 16). It is seen that several retrieved images have exactly the same object shapes and spatial relationships among them. Some other retrievals have strip-shape level-4 object rather than triangle objects. This is because the resulting spatial relationship between the two alert objects is the same as that in the query. They do have differences in the spatial relationship between the level-4 object and the mountains. From this illustrative QBS example, it is highly possible that the river valley and streams are the main passages of external air pollution emitted from the western metropolis.

Figure 15.  The user sketches a QBS query indicating the search intention.

DownLoad: Full-Size Img PowerPoint

Figure 16.  The retrieved most similar episodes for the submitted QBS query in Figure 15.

DownLoad: Full-Size Img PowerPoint

As a validation of our QBS methodology, we sketch another pollution map (as shown in Figure 17) where the spatial relationship of the two alert objects is opposite to that in the previous QBS example. The retrieved images responding to the query are shown at the bottom of Figure 18. As seen in the first twelve most similar retrievals, the level-4 object appears at the left end of the image, agreeing with the query sketch. The remaining four images are retrieved because they have the same objects as in the query but less similar in their mutual spatial relationships. The QBS interface and the 2D Be-string matching are effective in realizing the air pollution image map retrieval in accordance with the user's intention.

Figure 17.  The user sketches a QBS query opposite to that in Figure 15.

DownLoad: Full-Size Img PowerPoint

Figure 18.  The retrieved most similar episodes for the submitted QBS query in Figure 17.

DownLoad: Full-Size Img PowerPoint

3.2.   Pollution episode feature detection

The QBS searches for results with most similar spatial object relationships to the query but without detecting the object shape features and giving no information about the feature temporal changes. In practicing the QBS component, if the user sees any retrieval of interest and would like to perform more insightful analyses, he/she can click the particular result and will activate the spatiotemporal feature detection component with the clicked result as the middle of a 24-hour time series (the length of the time window is amendable by the user) to prepare the episode feature detection. Both 2-dimensional and 3-dimensional convolutional filters are applicable to the specified time series.

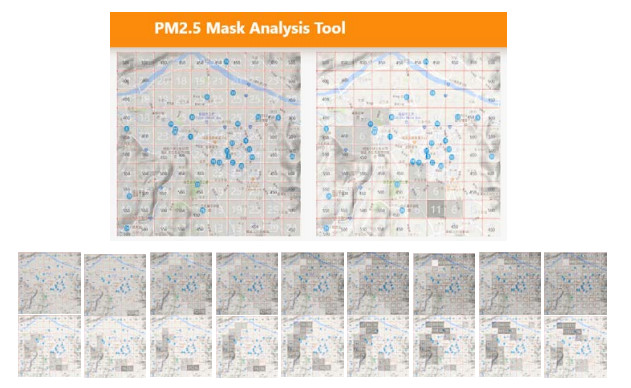
As shown in the upper half of Figure 19, the left image is the original PM_2.5 concentration map corresponding to the clicked retrieval indicated in the QBS results in Figure 12, and the right image is a snapshot of the feature map for detecting line features by applying the 2-dimensional line filters. It is at a morning commuting hour, and a line pollution episode is detected at the main street from the northern highway exit to Puli downtown. By specifying a length of time window, the video of the paired images (the PM_2.5 concentration map and the feature map) is displayed along the time span. As shown in the lower half, a nine-hour time window (from 4 AM to 12 AM) is specified, and the corresponding video is displayed for visualization. The first row shows the consecutive PM_2.5 concentration maps, and the second row displays the real-time detected features. As such, the user can inspect when and where the detected pollution features emerge and when they diminish. Automatic detection of various emerging pollution patterns in the time series can be also conducted by setting a threshold on the response feature value to produce a binary feature map such that further actions can be activated automatically at the place if its response feature value exceeds the threshold.

Figure 19.  The detected horizontal and vertical line features in a specified time window.

DownLoad: Full-Size Img PowerPoint

Figure 20 illustrates the edge feature detection for a pollution episode. A large region pollution source emerges from the downtown. The edge responses start intensifying during the first four hours and reach the peak responses afterward. The edge profile of the region pollution is articulated by the filter. The government agent, such as the Taiwan EPA, can issue a pollution alert in time for the residential area which is affected by the region pollution source.

Figure 20.  The detected edge features in a specified time window.

DownLoad: Full-Size Img PowerPoint

An example of applying both 2- and 3-dimensional filters is illustrated in Figure 21. The upper half shows three images which are the original PM_2.5 concentration map, the feature map produced by the 2-dimensional edge filter and the feature map obtained by the 3-dimensional filter. A time window of the video is displayed at the lower half of Figure 21 to show the variations in the three types of images. In the first row of PM_2.5 concentration maps, we observe an event where a large region of pollution is emitted at the center of the map, and concentrations start to accumulate quickly in a few hours. In the second row of edge feature maps, the edge outlining the pollution region is clearly articulated, and this information is useful for alerting the influenced residents. However, it is not known whether the pollution event is worsening or improving in the time span. In the third row of feature maps obtained by the 3-dimensional filter, we see the remarkable concentration variations in the time domain. In the first two hours, though the region pollution has appeared (see the detected edges in the second row), the PM_2.5 concentration remains constant without being more severe. As can be seen in the first two images in the third row, most grid squares have insignificant responses. Since the third hour, the size of the pollution region is not changed, but the third image in the third row indicates that the PM_2.5 concentration quantity is higher than that in this region observed in previous hours. During the fourth hour and the seventh hour, the PM_2.5 concentration increases significantly in this region, as revealed in the third row where the image becomes darker (having stronger responses) in this period. At the eighth hour, the intensification rate of the pollution becomes slower, especially at the northern sites (see the white grids at the north). The pollution event finally stagnates without worsening at the ninth hour. As can be observed in the last image of the third row, almost all grids have insignificant responses. From this illustrative example, we see that the 2-dimensional filter is able to depict the locations and shapes of the detected features, while the 3-dimensional filter can indicate whether the detected pollution is intensifying, stagnating or diminishing.

Figure 21.  The detected edge features and temporal variations in response by applying both 2- and 3-dimensional filters.

DownLoad: Full-Size Img PowerPoint

4.   Conclusions

The purpose of this research was to develop a framework for air pollution spatiotemporal episode retrieval and feature analysis. The proposed method allows the user to probe into why particular pollution episodes are frequently observed in a place and how these pollution episodes are influenced by local terrain, meteorological conditions and anthropogenic activities. We propose a QBS interface enabling the user to sketch his/her contemplation of the episode and its spatial relationship to land objects. The user interacts with the QBS interface until an episode of interest is retrieved. Then, the user clicks the interesting episode to activate our spatiotemporal feature analysis interface. Various 2-dimensional and 3-dimensional convolutional feature detection filters are offered. By setting a threshold, the feature analysis interface is able to detect when and where the pollution episode emerges, stagnates and diminishes. The experimental results demonstrate the effectiveness of the proposed methods that traditional methods cannot reach. The benefit of this research is offering the user an interactive analysis platform for visual spatiotemporal retrieval and feature analysis of air-pollution episodes.

Use of AI tools declaration

The authors declare that we have not used artificial intelligence (AI) tools in the creation of this article.

Acknowledgments

The authors are grateful to Rong-Fuh Day for providing the dataset and Bin-Jiun Chen and Tsai-Jen Cheng for their code development of the proposed algorithms. This research was funded by the National Science and Technology Council of Taiwan, under Grant NSTC 110-2410-H-130 -055 -MY2.

Conflict of interest

The authors declare there is no conflict of interest.