EECHS-ARO: Energy-efficient cluster head selection mechanism for livestock industry using artificial rabbits optimization and wireless sensor networks

1.   Introduction

The agriculture and livestock industries are famous and have existed for over a century. Due to the increase in population, food demand is drastically growing every day ^[1,2]. Therefore, the agriculture and livestock industries must meet the food demands by enriching manufacturing efficiency. Most livestock industries have started utilizing wireless sensor networks (WSNs) to monitor the state and behaviors of various fauna ^[3,4]. Generally, a WSN contains an assortment of sensor nodes associated wirelessly and collects information about its surrounding environments. The sensors cope with less energy (power), less storage and minimal processing capabilities. Due to resource constraints, a routing task is a significant challenge in various applications like surveillance and monitoring, medical applications, agriculture and landslide detection. In recent years, the clustering approach has proved its efficacy in determining the best routing path by minimizing energy consumption and fast data delivery ^[5].

Generally, the fauna is monitored by sensors which allows it to move randomly from one position to another in the livestock industry. Due to its dynamic and mobile nature, the sensing information varies from time to time. Therefore, this leads to frequent topological fluctuations that distract the packet transmission and energy depletion. An efficient clustering approach has been introduced to minimize energy depletion and improve the data transfer rate ^[6]. In the clustering approach, the sensor with adequate resources is selected as the cluster head (CH) by the base station (BS); then, the CH gathers the sensing data from their cluster members and sends the data in aggregate format to the BS. Several traditional clustering approaches are introduced in the literature to address the clustering issues ^[7]. One of the famous clustering approaches is the LEACH protocol, which selects the CHs periodically. This protocol achieves a better network lifetime than other clustering approaches. However, the performance degrades in the later course due to increased network sizes ^[8].

In recent years, swarm intelligence (SI) optimization techniques have proved their efficacy in tackling various complex, high-dimensional and multi-modal problems ^[9]. Particle swarm optimization (PSO) mimics the behavior of birds flocking or fish schooling aspects ^[10]. Artificial bee colony (ABC) optimization determines the behavior of the honeybee's food foraging ^[11]. Grey wolf optimization (GWO) imitates the behavior of grey wolf hunting and leadership hierarchy ^[12]. Dragonfly optimization (DA) mimics the behavior of the hunting and migration activities of dragonflies ^[13]. The flashing behavior of fireflies inspires firefly optimization (FA) ^[14], the cuckoo search (CS) algorithm imitates the behavior of the cuckoo bird's obligate parasitic brood process ^[15] and sparrow search optimization mimics the behavior of foraging, predation and anti-predation of the sparrow population ^[16]. Most of the researchers in the literature have utilized an SI algorithm in the livestock industry to improve cluster formation by selecting the optimal CH, thereby achieving a better network lifetime even when the network size increases. Though several approaches are addressed in the literature, an energy-efficient clustering approach is necessary; it should consider several metrics together, like energy consumption, residual energy (RE), distance among members from CH to BS, node degree and node centrality to select the optimal CHs.

In 2022, Wang et al. created the artificial rabbits optimization (ARO) algorithm, a new SI-based optimization method ^[17]. ARO mimics rabbits' survival processes, including detour foraging and arbitrary hiding strategies. According to the "no free lunch" theorem, no optimization algorithm handles all optimization issues. A study conducted by Riad et al. ^[18] compared ARO with the whale optimization algorithm, circle search algorithm, enhanced transient search optimization, jellyfish search algorithm and grasshopper optimizer algorithm in terms of their ability to solve the proton exchange membrane fuel cell model, which is a challenging optimization problem in power systems. The results showed that ARO was the best algorithm in terms of convergence speed and quality of solutions. Another study by Elshahed et al. ^[19] compared ARO with differential evolution (DE) and golden search optimization (GSO) in terms of their ability to solve the energy issues in photovoltaic solar inverters. The results show that ARO could find better solutions than DE and GSO in less time.

Every metaheuristic algorithm should encompass the solution space with a globally optimal solution without being trapped in local optima. Stability between exploration and exploitation is required for the best outcomes ^[20]. Based on the investigation, we notice that ARO can handle complex and multi-modal optimization problems. It can also address issues with constraints and does not require prior knowledge about the problem domain. The pros of ARO mentioned above motivate us to select the ARO algorithm for the optimal selection of CHs. Here, we apply the ARO algorithm to solve the clustering formation issues in WSNs for livestock industries. This work has been processed by electing a cluster head and cluster construction. The optimal CH is determined by using the ARO technique. Later, the cluster formation is processed based on the adjacent nodes to CHs. Lastly, the fauna sensors transfer the sensed data to the CH and transmit the aggregate data to farmers or the BS through the internet.

The significant contributions of this proposed work are specified below.

1) The ARO algorithm is presented to solve the problem of lifetime improvement for a WSN by choosing the optimum CH.

2) ARO is used to process cluster formation after the appropriate CH selection. The cluster is then formed by utilizing the nearest node. Finally, the sensors installed in the fauna start sending information to the CH and the aggregate data to the BS.

3) The CH is chosen based on the fitness function, which incorporates characteristics such as RE, sensor-to-BS distance, node degree (ND) and node centrality (NC).

4) The experimentation is carried out on the MATLAB 2021a platform. The obtained EECHS-ARO results achieve a better outcome by enhancing the network lifespan by 15% and improving the packet transfer proportion by ~5–6%.

The rest of the paper is structured as follows. Section 2 discusses the recent studies on cluster formation in WSNs. The system model and an energy model are presented in Section 3. Section 4 provides insight into the proposed EECHS-ARO approach. Section 5 offers the experimental setup, parameter settings and a comparative study of the proposed model outcome with other existing techniques. Finally, Section 6 concludes the work with future directions.

2.   Related works

WSNs are widely utilized in the cattle industry to sense the activities of fauna. Sensors are applied to various body parts of the fauna to monitor their activities; the same can help the owner care for their fauna. The sensors often sense the various fauna activities and transfer the information to owners via the internet. Numerous sensors are applied to fauna and their hostile environment to ensure the health states and prevent the health and fauna from various disease attacks ^[21,22]. This section addresses the related works of numerous optimization-based clustering approaches in industrial WSNs. Generally, optimization algorithms are used widely in different problems to maximize or minimize fitness functions. The natural behaviors of animals, birds or humans are imitated or encouraged to introduce a diverse range of optimization techniques ^[9]. Researchers used some of the most renowned optimization algorithms, such as ABC, PSO, GWO, CS, FA and DA.

The ant lion optimizer (ALO) algorithm has been introduced for the livestock industry to select the best CH fauna among the various fauna in wireless body area networks ^[23]. The experimentation was processed on a MATLAB platform. The outcome of the ALO algorithm was contrasted with ACO, MFO and GHO approaches. However, it required more time for convergence and achieved poor exploration during CH selection. The authors of ^[24] addressed the CH selection problem by using the GWO technique. Later, Awan et al. ^[25] applied the GWO technique to select the best CH in the livestock industry. The experimentation was carried out on a MATLAB platform. The outcome of GWO was contrasted with comprehensive learning particle swarm optimizer (CLPSO) and Clustering algorithm based on ant colony optimization (ACO) for vehicular AD hoc networks (CACONET). However, GWO suffers from poor convergence and leads to local optima solutions. It fails to attain the best CH when the network size increases.

The authors of ^[26] introduced the energy-efficient cluster-tree-based data gathering (CTEEDG) mechanism for industrial WSNs. The presented tool addresses the issues of WSNs in two ways, i.e., CH selection and inter-cluster transmission. Initially, the CH election is processed with the aid of fuzzy logic and the packets are received from the adjacent nodes. Later, the inter-cluster information is processed based on tree topology among the CH and BS. The simulation results convey that the proposed model attained better outcomes than other techniques. However, the selected CH sensor was not guaranteed for the optimal solution. Hybrid FA with PSO was introduced in ^[27] to address the clustering issue to WSNs. The proposed model was integrated with the LEACH-C mechanism to determine the best CH. This hybrid mechanism enhances the search capabilities for attaining the optimal CH. The model's performance improved the network lifetime and enhanced the packet delivery ratio (PDR) compared to other algorithms. However, it required a considerable amount of time to converge while determining the optimal CH.

The authors of ^[28] introduced a hybrid whale with grey wolf optimization technique to address the clustering issue in WSNs. This mixed technique enhanced the search capability by balancing diversification and intensification and improved the convergence rate compared to other methods. The experimentation was carried out using NS2. The proposed model showed superior performance on the network lifetime. The hybrid GWO with crow search optimization technique was introduced in ^[29] for CH selection in WSNs. The proposed model achieved a better outcome in terms of the network lifetime and PDR. However, it drained the sensor energy during iterations. The hybrid glowworm swarm optimization with FA algorithm was introduced to select the best CH to improve the network lifetime ^[30]. The performance of the proposed model was contrasted with GA, ABC, FA and ALO techniques. However, it consumes more time to converge while selecting the optimal CH.

The authors of ^[31] introduced the seagull optimization algorithm (SOA)-based energy-aware cluster-routing protocol to improve the network lifetime in the livestock industry. The authors concentrated on enhancing the network lifetime, thereby reducing network latency. The SOA technique achieved a better outcome of a 20% network lifetime and improved the PDR rate. The hybrid elephant herding and artistic approach was proposed to handle the clustering issue and extend the network lifetime in WSNs ^[32]. This hybrid technique optimizes the search capability while selecting the best CH. The outcome of the hybrid technique improved the network lifetime relative to other existing algorithms. However, this technique reduces the data communication rate due to poor network stability.

Based on the literature review on optimization algorithms, some significant research gaps that need to be considered before solving the complex optimization problems are presented below.

● While many optimization algorithms exist, there is always room for improvement in terms of efficiency. Develop new algorithms that can solve optimization problems more quickly or with fewer iterations.

● Many optimization algorithms are designed to work with smooth and convex functions. However, there are many real-world problems that involve non-smooth and non-convex functions. Develop optimization algorithms that can effectively handle these types of functions.

● Many real-world problems involve multiple conflicting objectives that need to be optimized simultaneously. Develop optimization algorithms that can handle multiple objectives efficiently and effectively.

● Real-world problems often involve uncertainty and randomness. Develop optimization algorithms that can handle these factors and provide robust solutions.

Despite that, some shortcomings are noticed in the literature review. One shortcoming is that it requires a longer convergence period to select the CH. It also obtains the deprived network stability and drains the sensor energy during iterations. This work introduces a novel approach, namely, ARO algorithm-based energy-efficient cluster formation (EECHS-ARO), to enhance the network lifetime and improve the PDR. In addition, the EECHS-ARO technique optimizes the intensification and diversification search process while selecting the CH. Hence, it improves the network lifetime.

3.   Preliminaries

This section discusses the network paradigms utilized in this work. In addition, the energy depletion models are presented to state the energy utilization for each packet transmission and response. These two models aid the algorithm in determining the cluster head selection process, and adjacent neighbors can join the nearest cluster, termed cluster formation.

3.1.   Network paradigms

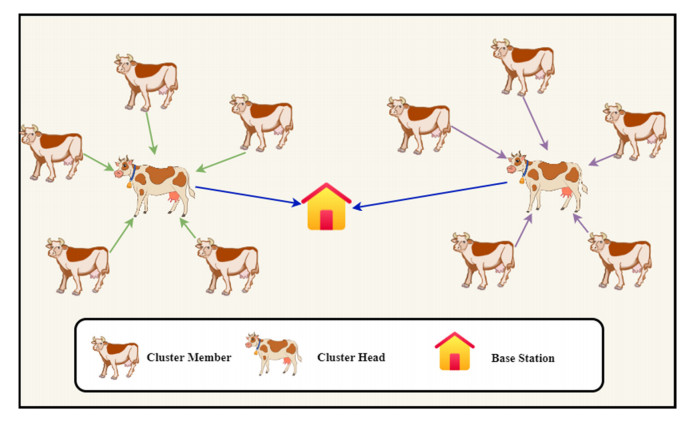
In this network model, we consider that the sensors are fixed with fauna in a livestock ranch. The fauna can move from one position to another within the farm. The BS is positioned at the mid-point of the network. The formulated EECHS-ARO technique is processed in the BS and elects the high-quality node as the optimal CH. Later, the adjacent node of the CH is forced to form clusters termed cluster members. The CH's responsibility is to collect its members' sensing data and transfer the aggregate data to the BS. The overview of the proposed EECHS-ARO network model is presented in Figure 1.

The proposed EECHS-ARO technique assumes the following network paradigms ^[23].

1) Initially, sensors are arbitrarily scattered in the network deployment area.

2) Each sensor fixed in fauna is mobile in nature and equal energy resources.

3) The BS is positioned at the mid-point of the livestock ranch.

4) The CH gathers the sensed information from its members and forwards the aggregate information to the BS.

5) Sensors hold a variable transmission design.

3.2.   Energy model

The EECHS-ARO algorithm utilizes traditional channel paradigms to communicate the information from sensors to the BS ^[33,34]. In our proposed algorithm, the distance parameter is represented as ${\mathit{\Delta}},$ which computes the distance among the nodes $\alpha$ and $\beta$ within the deployment area. Else, it processes the multipath channel fading mechanism to determine the span. The energy dissipation of node $\alpha$ communicates $\gamma$ bits of information to node $\beta$ concerning the span ${\mathit{\Delta}} \left(\alpha, \beta \right)$ and receives $\delta$ bits of information from node $\beta$ to $\alpha$. The mathematical formulation of overall energy depletion ${\varpi }_{total}$ for transmission (${\varpi }_{tr}$) and receiving (${\varpi }_{re}$) is presented as follows.

The energy depletion for data transmission is represented below.

where ${\varpi }_{tr}\left(\gamma \right)$ represents the energy depleted for the transmission of $\gamma$ bits from node $\alpha$ to $\beta$, ${\varpi }_{Elec}$ denotes the energy depleted per bit to operate the transmitter device, ${\chi }_{fs}$ and ${\chi }_{mp}$ determine the energy for the free space amplifying process and multipath model and ${{\mathit{\Delta}} }_{0}$ specifies the threshold transmission boundary (i.e., ${{\mathit{\Delta}} }_{0} = \sqrt{\frac{{\chi }_{fs}}{{\chi }_{mp}}}$).

where ${\varpi }_{re}\left(\delta \right)$ determines the energy depletion for receiving $\delta$ bits from node $\alpha$ to $\beta$.

4.   ARO

ARO is a recently proposed SI algorithm which mimics rabbits' foraging and hiding schemes ^[17]. In addition, the energy-shrinking process incorporated changeover among both methods. The mathematical formulation of ARO is presented below.

4.1.   Detour foraging process (Diversification)

The detour foraging process is utilized to diversify the search space. Generally, rabbits are herbivores that mainly focus on grass, forbs and leafy weeds. They prefer to find food sources far away from their region than its region. In the detour foraging process, we consider that each individual (rabbit) in the swarm holds its territory with grass and d number of tunnels. The rabbit arbitrarily visits the other region's food sources to obtain enough food, termed detour foraging. In contrast, each individual in the swarm needs to update its position concerning arbitrarily selected individuals, and it incorporates a perturbation. The mathematical formulation of the detour foraging process is represented in Eq (4).

where ${\overrightarrow{\delta }}_{a}\left(k+1\right)$ denotes the ${a}^{th}$ rabbit position at iteration $k+1$, ${\overrightarrow{{\mathit{\Psi}} }}_{a}\left(k\right)$ and ${\overrightarrow{{\mathit{\Psi}} }}_{b}\left(k\right)$ specify the ${a}^{th}$ and ${b}^{th}$ rabbit position at iteration $k$. The population size of ARO is represented as $N,$ and the dimension of the problem is defined as $D$. $M$ determines the maximum number of iterations, and $round$ specifies the round-off value near the next integer. The symbol ($\times$) specifies the ceiling function, $\chi$ denotes the traditional normal distribution within [0, 1] and the random vectors are ${\rho }_{1}, {\rho }_{2}$ and ${\rho }_{3}$ within the range of [0, 1]; ${\mathit{\Phi}}$ represents the jump length to diversify the search space and eradicate the local extrema. ${\mathit{\Upsilon}}$ denotes the random walk length that indicates the movement length at the detour foraging process. ${\mathit{\Psi}}$ represents the mapping vector that aids in selecting the individuals randomly for the foraging process.

4.2.   Arbitrary hiding (Intensification)

The arbitrary hiding process is the generic activity of real rabbits that dig a few holes near their region to hide from predators. In ARO, the search individuals generate a random spot around each dimension of the search space, frequently hiding in any holes to minimize the probability of becoming prey. The arbitrary hiding process is mathematically formulated and given in Eq (5).

where H represents the hiding parameter linearly reduced from 1 to $1/M$ with an arbitrary perturbation over the iterations. In this process, the holes are dug within leading rabbit neighborhood positions, whereas the neighborhood gets minimized during iterations. According to this, rabbits are exposed to hunting and attack from predators. To escape, rabbits need to find safe holes in which to hide. Hence, they neglect to arbitrarily select a hole from their holes in which to hide to eliminate the trap. The mathematical arbitrary hiding process is given in Eq (6).

where ${\overrightarrow{h}}_{a, r}\left(k\right)$ denotes an arbitrarily selected hole for hiding from all holes, and ${\rho }_{4}$ and ${\rho }_{5}$ are two random values within the range [0, 1]. According to Eq (6), the ${a}^{th}$ individual updates its position toward the arbitrarily chosen hole. Once the detour foraging or arbitrary hiding is attained, then the role of the ${a}^{th}$ rabbit is updated as below.

The above Eq (7) conveys that, if the fitness of the individual position of the ${a}^{th}$ rabbit is improved over the current position, then the current situation will be eliminated and the updated position will be retained as per Eq (1) or Eq (6).

4.3.   Energy shrink phase (Trade-off between intensification and diversification)

This phase balances the intensification and diversification process in the ARO algorithm by providing energy factors. Initially, the rabbits start to perform the detour foraging, whereas the individual conducts an arbitrary hiding process throughout the iterations. The energy factor of ARO is introduced to switch from diversification to intensification, and its mathematical formulation is given in Eq (8).

where r denotes the arbitrary value within the range of [0, 1]. If $E\left(k\right)$ is higher than 1 (i.e., $E\left(k\right) > 1$), the individual starts to diversify the regions arbitrarily among the different individuals. Otherwise, if $E\left(k\right)\le 1$, then the individual inclined to intensify its search regions arbitrarily. This energy factor E aids the algorithm in balancing the search process and moves the individual near optimality.

4.4.   Objective function

The optimal selection of the CH is determined according to the formulated objective function. The solution's fitness is computed based on the best positions of the rabbit. In EECHS-ARO, we utilized various parameters for cluster head selection, such as RE, the distance between the sensor and CH (DSCH), the distance between the CH and BS (DCBS), ND and NC.

Fitness 1 (f1) – RE:

The RE is used to specify the remaining energy held in the sensors ^[30]. It is computed as the difference between the sensors' initial and consumed energy. The RE measurement is given in Eq (9).

where $RE\left(i\right)$ denotes the remaining energy of sensor $i$, ${\varpi }_{spent}$ specifies the energy spent on data transmission and ${\varpi }_{Initial}$ illustrates the initial energy of the sensor.

Fitness 2 (f2) – DSCH:

The DSCH parameter is used to measure the span of the sensor node ${\eta }_{i}$ and CH by using the Euclidean distance mechanism. This parameter must be minimized to diminish network energy practice. The DSCH can be mathematically formulated and is given in Eq (10).

Fitness 3 (f3) – DCBS:

The DCBS fitness measures the span of the BS and CH by focusing on the number of adjacent nodes in the respective CH. Distance plays a vital role in energy depletion; therefore, this fitness is quite significant. The mathematical formulation of DCBS is given in Eq (11).

Fitness 4 (f4) – CH balancing factor (CBF):

The CBF fitness aids in balancing the $m$ cluster head and cluster members by considering energy balance; there is a possibility that some clusters with many members and some with fewer members will form a cluster as an outcome of the arbitrary clustering of sensor nodes. The CBF calculation is given in Eq (12)

The current position of the rabbit search individual's objective function ${\overrightarrow{{\mathit{\Psi}} }}_{a}\left(fit\right)$ is computed, and it is represented in Eq (13).

where $\vartheta$, $\zeta$, $\lambda$ and $\mu$ denote the constant parameters, and the cumulative value of these parameters is equal to 1 (i.e., $\vartheta +\zeta +\lambda +\mu = 1$). In this process, the rabbit attains the best position; the particular sensor will be selected as the CH for that corresponding network iteration. The cluster head selection mechanism of ARO is presented in Algorithm 1.

4.5.   Cluster formation framework using ARO

Cluster formation is a process of clustering the adjacent similar sensors to their corresponding CH in the network. Once the CH is selected, the EECHS-ARO decides on the cluster members to join their respective CH by using the nearest neighbor concepts. The adjacent sensors of CH and ${\eta }_{i}$ are measured by using the Euclidian distance formula given in Eq (10). Furthermore, efficient cluster formation reduces energy depletion in the network. Thus, it improves the network lifetime. Therefore, the CH gathers the sensed information of their respective members and forwards the aggregated information to the BS. The proposed model's outcome deliberates better by selecting the optimal CH and improves the network lifetime.

5.   Experimental results and analysis

In this experiment, all sensors were connected to fauna on a cattle farm to monitor and analyze the health status. The fauna are free to roam from one place to another at a speed of 4.5 km/hr within the farm boundary limit of 1, 2 and 3 km. In this work, the sensors cope with resource constraints, and energy depletion is a significant challenge in the wireless network. The experimentation was carried out on a MATLAB 2021a platform. The farm deployment area was 1500 m, with 150 various sensors, and the transmission range varied from 100 to 1000 m. The performance of the proposed model has been compared with other recent state-of-the-art algorithms such as QOBOA ^[35], ALO ^[23] and TLBO ^[36]. The network parameter settings for experimentation are presented in Table 1. The implementation of the proposed model with the number of nodes (NoNs) equal to 50 and 100 and a transmission range (TR) of 800 is shown in Figure 2.

5.1.   Analysis of TR vs number of clusters

The analysis of the number of clusters (NoC) is achieved by focusing on the TR to analyze the proposed system's efficacy in selecting the optimal CHs. We have validated the accuracy of the proposed method in six different node-size scenarios. In Scenario 1, an NoN of 25 with various transmission ranges between 100 and 1000 m are considered; the results are represented in Table 2 and Figure 3. Table 2 represents the transmission range for NoC with NoN equal to 25 and 50. At the same time, Figure 3 demonstrates that the proposed EECHS-ARO provides the better outcome as a result of selecting a reduced NoC for a transmission range of 100 to 900 compared to other algorithms such as QOBOA, ALO and TLBO. In addition, the reduced NoC values result into an increase in communication ranges.

In Scenario 2, the number of sensors applied is 50 and the transmission range was varied from 100 to 1000 m. The results of Scenario 2 were observed and are presented in Table 2. Table 2 indicates the NoCs formed for various transmission ranges given a network size of 50. The performance of the proposed method was compared with existing algorithms such as QOBOA, ALO and TLBO algorithms. The visual representation of the NoC formed is presented in Figure 4. Figure 4 conveys that the proposed EECHS-ARO algorithm provided a better outcome in terms of attaining the minimal number of cluster heads, as compared to QOBOA, ALO and TLBO. In addition, it is noticed that the NoC is minimized resulting into an increase in transmission range because of the ARO algorithm. It is also seen that all sensors are free to join with their respective cluster heads to transfer the sensed information of fauna.

In Scenarios 3 and 4, the network sizes are 75 and 100, respectively, with transmission ranges varying from 100 to 1000 m and a deployment area of 1500 × 1500 m. The results of Scenario 3 are provided in Table 3. Figure 5 conveys that the NoC was minimal for the proposed EECHS-ARO (3) compared to QOBOA, ALO and TLBO, which were 6, 6 and 5, respectively, for the 1000 m communication range. In addition, Figure 6 illustrates the outcome of the proposed method and compares the algorithm for a network size of 100. The results of the proposed model achieved an NoC of 4, whereas QOBOA, ALO and TLBO attained NoCs of 7, 7 and 5, respectively. The outcome specifies that the proposed algorithm boosts the CH selection mechanism's convergence. It is also noted that the NoC decreases resulting into an increase in transmission range. Thus, the outcome of the proposed model specifies that the EECHS-ARO technique achieves better balance during the exploration and exploitation search process.

The network size of 125 and 150 nodes with a transmission range of 100 to 1000 m and a deployment area of 1500 × 1500 m are considered in Scenarios 5 and 6. The results of Scenarios 5 and 6 are presented in Table 4 and Figures 7 and 8. Table 4 indicates that the outcome of the proposed model is better than those of QOBOA, ALO and TLBO. Figure 7 presents the NoC versus the TR for a given network size of 125. It is observed that the NoCs for the proposed EECHS-ARO, QOBOA, ALO and TLBO were 9, 8, 6 and 5, respectively, for a TR of 1000 m. Figure 8 illustrates the outcomes of the proposed model and three existing algorithms for the NoC with varied TRs given a network size of 150. The NoCs for the proposed algorithm, QOBOA, ALO and TLBO were 7, 7, 6 and 5, respectively, at 1000 m. The NoC of the proposed algorithm was minimal compared to those of the QOBOA, ALO and TLBO resulting into an increase in the transmission range.

5.2.   Analysis of PDR

This section aids in determining the efficacy of the proposed model in terms of the PDR from the perspective of varying the number of sensor nodes. The PDR was computed based on the successful transmission of packets from the generated source node to the BS. The PDR outcome for different NoNs is tabulated in Table 5. Table 5 conveys that the proposed algorithms achieved a better PDR outcome than QOBOA, ALO and TLBO. Given network sizes of 25 and 50, the PDR achieved a PDR of 97%. Furthermore, QOBOA, ALO, and TLBO achieved 90, 93 and 95%, respectively, for a transmission range of 1000 m. Though the TR increased, the existing algorithm failed to attain a better PDR because of an improper search balance of the exploration and exploitation process.

Figure 9 presents a graphical presentation of the proposed method and existing algorithms' PDR results for different numbers of sensor nodes. The proposed method achieved a better PDR for all network sizes of 25, 50, 75,100,125 and 150 nodes. The TLBO algorithm can compete with the proposed model in terms of ability to attain minimal cluster head selection. However, it suffers during iterations due to optimal local strikes. Therefore, as compared to the other algorithms, the proposed model achieved a better outcome in terms of obtaining the optimal CHs and minimized the count of control communications while improving the PDR.

5.3.   Analysis of latency

Latency aids in determining the amount of time spent to transmit the information from the source to the BS. Figure 10 shows the latency for different numbers of rounds. The obtained results indicate that the latency in QOBOA, ALO, TLBO and EECHS-ARO were 495,465,430 and 380 ms, respectively. It depicts that the proposed model reduced latency by 115, 85 and 48 ms compared to QOBOA, ALO and TLBO. This achievement is due to the optimal selection of the CH in the network and eradicating the bottleneck issues near the BS. Table 6 shows the latency values with respect to the number of rounds. It is observed that the latency value increases as the number of rounds increases. The latency analysis shows that the proposed model finds the best CH by considering the load balance between the CH and the BS.

5.4.   Analysis of network lifetime

Table 7 depicts the number of alive nodes (NoAN) for different numbers of rounds. It is noticed that the NoAN for the proposed EECHS-ARO, TLBO, ALO and QOBOA were 18, 10, 0 and 0, respectively, for 1800 rounds. The NoAN was relatively high for EECHS-ARO compared to TLBO, ALO and QOBOA. The proposed model maintained the alive nodes for all iterations up to 1950 rounds. In contrast, in the case of the TLBO and ALO algorithms, all nodes were dead within 1900 and 1820 rounds, respectively.

Figure 11 shows the outcome of the NoAN for different numbers of rounds for a network size of 150. The effect of the proposed model conveys that it improved the NoAN by reducing the energy consumption in the network. In addition, the results indicate that 50% of the network nodes were active up to approximately 1100 rounds.

5.5.   Analysis and discussion

The experimentation shows that the proposed EECHS-ARO algorithm achieved a better outcome in terms of the NoC, PDR and network lifetime. The investigation was conducted for different scenarios of with different transmission ranges and numbers of sensor nodes in a cattle farm network. The outcomes of the other techniques convey that the proposed method improves the network performance when the network size increases. In addition, the proposed EECHS-ARO achieved better performance than the algorithms of TLBO, ALO and QOBOA. The performance improvement is because EECHS-ARO selects the optimal CH by considering various objectives and allows the members to join with their corresponding CHs. Furthermore, it reduced the energy consumption rate by 15%, as well as the network path establishment cost, to transmit the data from the CH to the BS.

In addition, the time complexity of the proposed EECHS-ARO resides in three significant factors, namely, the population size $\left(P\right)$, the dimensionality of the problem $\left(D\right)$ and the total number of iterations. For the initial phase, the population initialization takes $O(P\times D)$. Second, in the detour foraging phase, all solutions undergo computation, taking $O(P\times D)$. Third, in the arbitrary hiding phase, the selected individuals will perform the calculation, averaging $O\left(P*D\right)/2$. In the energy-shrinking phase, the unimproved solutions are subjected to improve their states. The balancing phenomena of intensification and diversification are handled at every iteration. Since every time the quantity of solution gets divided into two halves, we can define $T\left(F*S\right)$ as $\frac{T\left(F*S\right)}{2}$; the computational time analysis at every run of the rabbit phase is $\left(F*S\right)log\left(F*S\right)$ and the final statement for rabbit phase is $\frac{T\left(F*S\right)}{2}+\left(F*S\right)log\left(F*S\right)$, which will result in $O$. Finally, the fitness evaluation takes the complexity of O(P).

The overall computation time of the proposed EECHS-ARO can be measured as $T\left(P*D\right) = O\left(P*D\right)+O\left(P*D\right)+O\left(P*D\right)+O$. Based on the asymptotic notations considering upper-bound time complexity, it can be determined to be $T\left(P*D\right) = O$.

6.   Conclusions

Energy depletion in WSNs is considered to be one of the major issues since the sensors are connected to resource constraints. So, the clustering approach has been introduced to eradicate the energy conservation issue. The sensors are merged with fauna that are capable of moving from one location to another because they are dynamic creatures. This paper presents a novel algorithm, i.e., the EECHS-ARO algorithm, to address energy conservation as a result of selecting the optimal CHs, thereby improving the network performance. The proposed EECHS-ARO provided better outcomes for selecting optimal CHs, improved the PDR by ~5% and enhanced the network lifetime by ~15%. The performance of the proposed method was compared with that of the TLBO, ALO and QOBOA algorithms. Further, the work can be extended by utilizing a hybrid optimization technique to decrease the CH selection's convergence period. Moreover, the proposed approach will focus on an objective function that uses adequate network constraints to select the optimal CH in vehicular ad hoc network (VANET), mobile Ad hoc network (MANET), and heterogeneous networks.

Acknowledgments

This research is supported by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R195), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflict of interest

The authors declare that there is no conflict of interest.