Oscillatory dynamics of p53 pathway in etoposide sensitive and resistant cell lines

Fang Yan; Changyong Dai; Haihong Liu; Fang Yan; Changyong Dai; Haihong Liu

doi:10.3934/era.2022105

Electronic Research Archive

2022, Volume 30, Issue 6: 2075-2108. doi: 10.3934/era.2022105

Previous Article Next Article

Research article

Oscillatory dynamics of p53 pathway in etoposide sensitive and resistant cell lines

1.
Department of Mathematics, Yunnan Normal University, Kunming, 650500, China
2.
Key Laboratory of Complex System Modeling and Application for Universities in Yunnan, Kunming, 650500, China

Received: 30 September 2021 Revised: 02 January 2022 Accepted: 06 January 2022 Published: 14 April 2022

In this paper, the kinetics of p53 in two cell lines with different degrees of sensitivity to chemotherapeutic drugs is studied. There is much research that has explored the p53 oscillation, but there are few comparisons between cells that are sensitive to drug treatment and those that are not. Here, the kinetics of the p53 system between etoposide-sensitive and etoposide-resistant cell lines in response to different drug doses and different protein synthesis time delays are studied and compared. First, the results showed that time delay is an important condition for p53 oscillation by producing Hopf bifurcation in both the etoposide-sensitive and etoposide-resistant cells. If the protein synthesis time delays are zero, the system cannot oscillate even the dose of the drug increases. Second, the time delay required for producing sustained oscillation in sensitive cells is shorter than the drug-resistant cells. In addition, the p53-Wip1 negative feedback loop in drug-resistant cells is relatively highly strengthened than the drug-sensitive cells. To sum up, p53 oscillation is controlled by time delay, drug dose, and the coupled negative feedback network including p53-mdm2 and p53-wip1. Moreover, in the two different types of cells, the control mechanisms are similar, but there are also differences.

Keywords:

Citation: Fang Yan, Changyong Dai, Haihong Liu. Oscillatory dynamics of p53 pathway in etoposide sensitive and resistant cell lines[J]. Electronic Research Archive, 2022, 30(6): 2075-2108. doi: 10.3934/era.2022105

Related Papers:

[1]	Latifah Hanum, Dwi Ertiningsih, Nanang Susyanto . Sensitivity analysis unveils the interplay of drug-sensitive and drug-resistant Glioma cells: Implications of chemotherapy and anti-angiogenic therapy. Electronic Research Archive, 2024, 32(1): 72-89. doi: 10.3934/era.2024004
[2]	Jianmin Hou, Quansheng Liu, Hongwei Yang, Lixin Wang, Yuanhong Bi . Stability and bifurcation analyses of p53 gene regulatory network with time delay. Electronic Research Archive, 2022, 30(3): 850-873. doi: 10.3934/era.2022045
[3]	Xin Du, Quansheng Liu, Yuanhong Bi . Bifurcation analysis of a two–dimensional p53 gene regulatory network without and with time delay. Electronic Research Archive, 2024, 32(1): 293-316. doi: 10.3934/era.2024014
[4]	Rina Su . Dynamic analysis for a class of hydrological model with time delay under fire disturbance. Electronic Research Archive, 2022, 30(9): 3290-3319. doi: 10.3934/era.2022167
[5]	Xiaowen Zhang, Wufei Huang, Jiaxin Ma, Ruizhi Yang . Hopf bifurcation analysis in a delayed diffusive predator-prey system with nonlocal competition and schooling behavior. Electronic Research Archive, 2022, 30(7): 2510-2523. doi: 10.3934/era.2022128
[6]	Fengrong Zhang, Ruining Chen . Spatiotemporal patterns of a delayed diffusive prey-predator model with prey-taxis. Electronic Research Archive, 2024, 32(7): 4723-4740. doi: 10.3934/era.2024215
[7]	San-Xing Wu, Xin-You Meng . Hopf bifurcation analysis of a multiple delays stage-structure predator-prey model with refuge and cooperation. Electronic Research Archive, 2025, 33(2): 995-1036. doi: 10.3934/era.2025045
[8]	Mengting Sui, Yanfei Du . Bifurcations, stability switches and chaos in a diffusive predator-prey model with fear response delay. Electronic Research Archive, 2023, 31(9): 5124-5150. doi: 10.3934/era.2023262
[9]	Miao Peng, Rui Lin, Zhengdi Zhang, Lei Huang . The dynamics of a delayed predator-prey model with square root functional response and stage structure. Electronic Research Archive, 2024, 32(5): 3275-3298. doi: 10.3934/era.2024150
[10]	Li Li, Zhiguo Zhao . Inhibitory autapse with time delay induces mixed-mode oscillations related to unstable dynamical behaviors near subcritical Hopf bifurcation. Electronic Research Archive, 2022, 30(5): 1898-1917. doi: 10.3934/era.2022096

Abstract

1. Introduction

Tumor cells can be divided into drug-sensitive cells and drug-resistant cells. For sensitive tumor cells, drug resistance (such as gene mutation) is usually produced during chemotherapy, which makes the life of the tumor cells more tenacious and is not conducive to drug-induced apoptosis. In order to better treat tumors, we need to understand their inherent resistance mechanisms. For example, when a tumor cell is sensitive, it is easy to change from sensitive to resistant under what circumstances. Problems like these are worthy of our study. It is well known that more than 50 $\%$ of cancer patients have mutations in the p53 gene clinically ^[1]. As an important tumor suppressor, it acts as a transcription factor to regulate the expression of downstream target genes to induce cell survival or death in response to acute stress ^[2,3]. Zhang et al. showed that under stress, cell survival or apoptosis is related to the number of pulses of p53 ^[4,5]. When subjected to a large enough damage or stimulation, a higher level p53 or sustained p53 pulse will be induced, which then triggers cell apoptosis. When the stimulus is weak or mild, a few p53 pulses will be produced, which then causes cell cycle arrest ^[6], thereby repairing the damaged gene and preventing it from being inherited to the next generation by means of cell division. Based on the importance of p53 in tumor therapy and cell fate decision making, the medical and academic community have made many efforts to develop new and effective p53-based anticancer therapies ^[7,8,9,10].

Based on the above analysis, it is reasonable to study cells that are sensitive and resistant to drugs from the perspective of the expressive character of the p53 transcription factor. There is a great deal of research that has shown that the expression level of p53 is regulated by Mdm2 (a p53-specific E3 ubiquitin ligase) and there is a negative regulatory loop between them. More specifically, p53 can promote the transcription and translation of Mdm2 which in turn can degrade p53 protein by promoting ubiquitination ^[11,12]. Furthermore, the p53-Mdm2 negative feedback loop is considered as the basis of p53 oscillation ^[13], and the functional mechanism of this feedback loop in p53 networks has been studied by many researchers ^[14,15]. In addition, Wip1 (wild-type p53-induced phosphatase 1) as a member of the PP2C and p53 target gene families is also important for the expression level of p53, which forms the second negative feedback loop with p53. In particular, similar to Mdm2, p53 also promotes transcription and translation of Wip1 that can, in turn, lead to dephosphorylation of its downstream target proteins including p53, Mdm2, ATM, and so on ^[16,17,18]. ATM (ataxia telangiectasia mutated kinase) is usually maintained at a basal level in normal cells. When exposed to external stimuli (such as DNA damage, radiation, and chemical drugs), the dimeric or multimeric form of ATM is rapidly converted to the active form of ATM by autophosphorylation ^[19]. The phosphorylated/activated ATM can directly bind to MDM2 and promote its phosphorylation so that blocks degradation of p53 and maintains the activity and stability of p53 through such an indirect action ^[20]. Research has shown that the ATM-p53-Wip1 negative feedback loop also contributes to the pulse of p53 ^[5,21]. Therefore, it is very necessary to understand the intrinsic mechanism of the coupled negative feedback loops of p53-Mdm2 and ATM-p53-Wip1 in sensitive cells and drug-resistant cells.

In recent years, there has been a tremendous amount of research on p53 tumor suppressor factor ^[22,23,24]. These results suggested that the negative feedback loop between p53 and Mdm2 has made a significant contribution to the occurrence of p53 oscillation that can decide the cell fate including survival and death in response to DNA damage or other stimulation ^{[4,13,14,25,26,27]}. In most of the above studies, protein synthesis including transcription and translation is regarded as an instantaneous process. However, it is well known that both of them are the basic steps of gene expression in cells, that is not only slow but also complex multi-stage reactions involving the sequential assembly of long molecules ^[28]. Therefore, transcription and translation are usually not completed in an instant, but need take a long time ^{[29,30,31,32,33]}. Therefore, pay attention to the impact of time delay needed in the important protein synthesis process on the p53 dynamic is necessary and meaningful.

In this paper, motivated by the above considerations, a new model including time delay needed in the protein synthesis process of Mdm2 and Wip1 is proposed based on the model established in ^[33]. The effects of time delay and parameters related to drug doses and the strength of the feedback loops in etoposide-sensitive (U-2 OS) and etoposide-resistant cell lines (MCF7) are studied via the analysis on the new model. The results indicated that different types and scales of time delay have different effects on the system and time delay corresponding to the transcriptional and translational of Mdm2 and Wip1 promoted by p53 is critical to the oscillation of p53. Moreover, the oscillation is a combinatorial result of time delay, drug dose and the strength of feedback loop involving p53.

2. Materials and methods

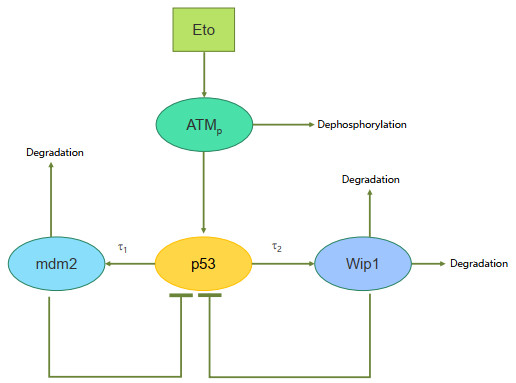
In , we present a schematic diagram of the network including p53, Mdm2, Wip1 and $ATM_p$ . When the cell is subjected to the chemotherapy drug Etoposide, a large amount of non-phosphorylated ATM is converted to phosphorylated $ATM$ denoted by $ATM_p$ . $ATM_p$ stabilizes p53 from an inactive state to an active state by phosphorylating p53 at Ser15 and Ser20 ^{[33,34,35,36]}. Furthermore, the activated p53 can promote the expression level of Mdm2 and Wip1 protein by promoting transcription and translation. In turn, Mdm2 accelerates the degradation of p53, and Wip1 can dephosphorylate p53 to reduce its activity. A mathematical model is proposed by Ruizhen Yang et al. to describe the relationship among these molecules ^[33]. However, it is worth noticing that there are necessary time delays during the transcription and translation process of Mdm2 and Wip1 protein. Typically, it needs a certain time between the action of the transcription factor on the gene promoter and the appearance of the corresponding mature mRNA in the cytoplasm ^[37,38]. Similarly, the synthesis of a typical protein from mRNA also requires a certain translation delay ^[37,39]. Meanwhile, from a theoretical view, the time delay can usually lead to oscillation and even more complex dynamic behaviors of gene regulatory networks ^{[40,41,42,43]}. Based on the above considerations, the synthesis time delays of protein Mdm2 and Wip1 protein are incorporated in the previous model, which yields the following ordinary differential equation model:

$\begin{equation} \left\{ \begin{split} & \dot x = {k_{p0}} - {k_{mp}}(u(t),z(t))xy - {\gamma _p}x,\\ & \dot y = {k_{m0}} + \frac{{{k_{pm}}{x^{{n_1}}}(t - {\tau _1})}}{{K_{pm}^{{n_1}}(u(t - {\tau _1}),z(t - {\tau _1})) + {x^{{n_1}}}(t - {\tau _1})}} - {\gamma _m}(u(t),z(t),{\gamma _{m0}},{\gamma _{m1}})y,\\ & \dot z = {k_{w0}} + \frac{{{k_{pw}}{x^{{n_2}}}(t - {\tau _2})}}{{K_{pw}^{{n_2}}(u(t - {\tau _2}),z(t - {\tau _2})) + {x^{{n_2}}}(t - {\tau _2})}} - {\gamma _w}z,\\ & \dot u = {S_{ea}}Eto(AT{M_t} - u) - {D_{a0}}u, \end{split} \right. \end{equation}$

(2.1)

Figure 1. Schematic diagram of the cell fate decision module including p53, Mdm2, Wip1, and

$ATM_p$ . Under the action of the chemotherapeutic drug Etoposide, ATM is activated quickly via phosphorylation. The activated ATM promotes the activation and accumulation of p53 by phosphorylation. Further, the phosphorylated p53 accelerates the synthesis of Mdm2 and Wip1 by promoting the transcription and translation of them. In turn, Mdm2 and Wip1 recede the activation of p53 by promoting degradation and dephosphorylation. Here, the phosphorylated ATM is denoted by

$ATM_p$ . The transcription and translation of Mdm2 and Wip1 accelerated by p53 is a time-consuming process, and the corresponding two time delays are denoted by

$\tau_1$ and

$\tau_2$ . Here, red arrows indicate promotion, black arrows represent degradation or dephosphorylation, and short horizontal lines refer to the inhibition.

DownLoad: Full-Size Img PowerPoint

where

$\begin{align*} &\ {k_{mp}}(u(t),z(t)) = {k_{mp0}}\frac{{{D_{p0}} + {D_{wp}}z}}{{{S_{p0}} + {D_{p0}} + {S_{ap}}u + {D_{wp}}z}},\\ &\ {K_{pm}}(u(t),z(t)) = {K_{pm0}}\frac{{{S_{p0}} + {D_{p0}} + {S_{ap}}u + {D_{wp}}z}}{{{S_{p0}} + {S_{ap}}u}},\\ &\ {K_{pw}}(u(t),z(t)) = {K_{pw0}}\frac{{{S_{p0}} + {D_{p0}} + {S_{ap}}u + {D_{wp}}z}}{{{S_{p0}} + {S_{ap}}u}},\\ &\ {\gamma _m}(u(t),z(t),{\gamma _{m0}},{\gamma _{m1}}) = \frac{{{\gamma _{m0}}({D_{m0}} + {D_{wm}}z) + {\gamma _{m1}}({S_{m0}} + {S_{am}}u)}}{{{S_{m0}} + {D_{m0}} + {S_{am}}u + {D_{wm}}z}}. \end{align*}$

In the above model, $x, y, z$ and $u$ represent the concentration of p53, Mdm2, Wip1 and $ATM_p$ respectively. The values and the specific biological meanings of the parameters in Eq (2.1) are given in Table 1 and Table 2 in the Supplementary Part. In this paper, we mainly focus on the effects of time delay and parameters related to drug doses and the strength of the feedback loops on the kinetic properties of p53, Mdm2, and Wip1 in the sensitive cells and drug-resistant cells under the action of Eto (Etoposide). The theoretical and analytical derivation is too tedious to read, so it is put in the Supplementary Part. Here, the numerical simulations are executed by using the software Mathematica 12.

3. Results

In this section, the kinetics of the p53 pathway between sensitive and resistant cell lines in response to etoposide chemotherapeutic drugs is compared. Some theoretical derivations are given, which are put in the Supplementary Section due to the formulas involved in the derivation process being too interminable to read. Here, the numerical simulations are shown, which agree highly with the theoretical results. The parameter values used are shown in Table 1 and Table 2 in the Supplementary Section. All of them were selected based on the literature ^[33], only three types are expected. First, the time delays are evaluated on the basis of biological fact. Based on the conclusion that each consecutive intron splicing in mammalian cells required about 0.4 to 7.5 minutes ^[44,45], the number of introns within the genes of Mdm2 and Wip1 can be calculated in order to achieve the desired length of Mdm2 and Wip1 protein synthesis time delay $\tau1$ and $\tau2$ . Second, drug dose is a human-driven changed parameter. Third, $k_{pm}$ and $k_{pw}$ is taken within small neighborhoods of the values in the literature ^[33].

3.1. Effect of time delays on drug-sensitive cells

Here, the effect of time delays on drug-sensitive cells when the Etoposide dose $Eto = 1$ . Firstly, it can be seen from () that as the value of $\tau_1$ increases, the system changes from a stable steady state to an oscillation state. Moreover, the amplitude and period of the oscillation increases as $\tau_1$ . In turn, as shown in (), the system barely changes and stays stable all the time although $\tau_2$ changes when $\tau_1 = 0$ . Secondly, when $\tau_1$ is fixed at 1.5 (as shown in ()), as $\tau_2$ continues to increase, the oscillation appears gradually and then disappears and goes back to the stable state again. Moreover, the amplitude of the oscillation climbs up and then declines with $\tau_2$ . In summary, $\tau_1$ can induce the system to oscillate separately, and $\tau_2$ cannot cause oscillation alone. If $\tau_1$ is fixed in a proper range, oscillations can occur with the increase of $\tau_2$ and then gradually vanished (). When $\tau_1$ is large, $\tau_2$ still has a similar effect, but it has little effect on the system (Figure 5). The results indicated that the time delay corresponding to the synthesis of Mdm2 protein promoted by p53 can used to produce p53 oscillation that can trigger cell apoptosis or cell cycle arrest to avoid the damage information inherited to the next generation cells. However, the time delay corresponding to the synthesis of Wip1 protein promoted by p53 only play a supporting role in this process.

Figure 2. Effects of

$\tau_1$ on the system in a sensitive cell system when the time delay

$\tau_2 = 0$ . (a)

$\tau_1 = 1.5$ . (b)

$\tau_1 = 2$ . (c)

$\tau_1 = 2.5$ . (d) Bifurcation diagram of the p53 concentration with regard to

$\tau_1$ .

DownLoad: Full-Size Img PowerPoint

Figure 3. Effects of

$\tau_2$ on the system in a sensitive cell system when the time delay

$\tau_1 = 0$ . (a)

$\tau_2 = 1$ . (b)

$\tau_2 = 2$ . (c)

$\tau_2 = 3$ .

DownLoad: Full-Size Img PowerPoint

Figure 4. Effects of

$\tau_2$ on the system in a sensitive cell system when the time delay

$\tau_1 = 1.5$ . (a)

$\tau_2 = 0$ . (b)

$\tau_2 = 1.5$ . (c)

$\tau_2 = 3$ .

DownLoad: Full-Size Img PowerPoint

Figure 5. Effects of

$\tau_2$ on the system in a sensitive cell system when the time delay

$\tau_1 = 2$ . (a)

$\tau_2 = 0$ . (b)

$\tau_2 = 1.5$ . (c)

$\tau_2 = 3$ .

DownLoad: Full-Size Img PowerPoint

3.2. Effects of drug dose of Etoposide on drug-sensitive cells

As shown in , we take two sets of fixed time delays for $\tau_1$ and $\tau_2$ . It is easy to observe from () that Eto can not cause oscillation when $\tau_1 = \tau_2 = 0$ . However, when $\tau_1 > 0$ is shown in Figure 7, we can conclude that the oscillation is strengthened as the Eto value increases from Figure 7(a–c). However, the oscillation disappears and the system goes back to a stable state as the Eto value continues to increase Figure 7(d–e). From another point of view, whether the drug dose of Eto can induce oscillation of the p53 pathway depends on the value of time delays. The importance of time delay to the oscillation of the system is proved once again. In summary, the system oscillates when the value of Eto is within an appropriate range (the closed region in Figure 7f), and stabilizes when the value is far away. It is suggested that the drug dose is not as bigger as better to the treatment, but needs to control at an appropriate range.

Figure 6. Effects of the drug dose Eto on sensitive cell systems when

$\tau_1 = \tau_2 = 0$ . (a)

$Eto = 1$ . (b)

$Eto = 2$ . (c)

$Eto = 3$ .

DownLoad: Full-Size Img PowerPoint

Figure 7. Effects of the drug dose Eto on sensitive cell systems when

$\tau_1 = 2, \tau_2 = 0$ . (a)

$Eto = 0$ . (b)

$Eto = 0.5$ . (c)

$Eto = 1$ . (d)

$Eto = 1.5$ . (e)

$Eto = 2$ . (f) Bifurcation diagram of the p53 concentration with regard to Eto.

DownLoad: Full-Size Img PowerPoint

3.3. Comparison of effects of $k_{pm}$ and $k_{pw}$ on drug-sensitive cells

Both Mdm2 and Wip1 form a negative feedback loop with p53 and can inhibit the p53 expression level. However, the combined inhibitory effect of the two is less clear. Below, we studied the effect of $k_{pm}$ (Rate constant of $p53_p$ -induced production of Mdm2) and $k_{pw}$ (Rate constant of $p53_p$ -induced production of Wip1) on the system to indirectly study the effect of the two feedback loops of p53-Mdm2 and p53-Wip1. Since $\tau_2$ has very little effect on the system in sensitive cell, it is treated as 0. For $k_{pm}$ and $k_{pw}$ , on the basis of the parameter value in ^[33], take the value of about one-tenth of them as the interval to obtain a series of images, where the range of $k_{pm}$ is from 0.7 to 1.174 and the range of $k_{pw}$ is from 0.1046 to 0.1796, respectively, as shown in Figure 8. On the one hand, comparing () and (), we can see that $k_{pm}$ has a significant impact on the system, and $k_{pw}$ has little effect on the system. On the other hand, and showed that both $k_{pm}$ and $k_{pw}$ have the ability to induce Hopf bifurcation thereby changing the qualitative behavior. However, the bifurcation point in Figure 8(d) falls in the range (0.7, 1.174) and the Figure 8(h) does not in the range (0.1046, 0.1796). Therefore, in practice, the p53-Mdm2 negative feedback loop in sensitive cell lines plays a major role in inducing oscillation, and Wip1 has the effect on its amplitude. Thus, to master the cell fate decision, it is needed to regulate the strength of the p53-Mdm2 and p53-Wip1 negative feedback loops to induce the p53 oscillation and control its amplitude so that treat diseases.

Figure 8. The effect of

$k_{pm}$ and

$k_{pw}$ on the system of sensitive cell when

$\tau_1$ = 1.8.

$k_{pw}$ is taken as 0.1496 in the top row (a)-(c) and

$k_{pm}$ is taken as 0.9172 in the bottom row (d)-(f). (a)

$k_{pm} = 0.7$ . (b)

$k_{pm} = 0.9172$ . (c)

$k_{pm} = 1.174$ . (d)

$k_{pw} = 0.1046$ . (e)

$k_{pw} = 0.1496$ . (f)

$k_{pw} = 0.1796$ .

DownLoad: Full-Size Img PowerPoint

3.4. Effect of time delays on drug-resistant cells

First we study the effect of $\tau_1$ on drug-resistant cells. Similar to sensitive cell lines, $\tau_1$ alone can induce system oscillation, while $\tau_2$ can not do it as shown in Figures 9 and 10. By comparing Figure 2() and (), it can be seen that the critical value of $\tau_1$ to induce sustained oscillation of p53 in the sensitive cells is smaller than in the drug-resistant cells. In addition, the amplitudes and periods of the oscillation in the drug-resistant cells were significantly lower than those in sensitive cells. More importantly, the levels of Mdm2 and Wip1, especially the latter, were significantly higher in the drug-resistant cells than the sensitive cells, which may be the reason why the p53 level of the drug-resistant cells is not easy to increase.

Figure 9. Effects of

$\tau_1$ on the drug-resistant cell system when the time delay

$\tau_2 = 0$ . (a)

$\tau_1 = 1.7$ . (b)

$\tau_1 = 2$ . (c)

$\tau_1 = 2.5$ . (d) Bifurcation diagram of the p53 concentration with regard to

$\tau_1$ .

DownLoad: Full-Size Img PowerPoint

Figure 10. Effects of

$\tau_2$ on the drug-resistant cell system when the time delay

$\tau_1 = 0$ . (a)

$\tau_2 = 1$ . (b)

$\tau_2 = 2$ . (c)

$\tau_2 = 3$ .

DownLoad: Full-Size Img PowerPoint

Next we study the effect of $\tau_2$ on the system. The results shown in and illuminated that the $\tau_2$ has a similar property in drug-resistant cells to drug-sensitive cells, that is properly sized $\tau_2$ is beneficial to the p53 oscillation, while too large $\tau_2$ can lead to the oscillation disappearing. By comparing Figures 4, 5 with Figures 11, 12, it is obvious that the amplitude of p53 oscillation is much smaller in drug-resistant cells than in the drug-sensitive cells, for Mdm2 and Wip1 oscillation, it is the opposite. This means that although the protein synthesis time delay of Wip1 plays a supporting role, it is crucial to the p53 oscillation and either too small or too big are not beneficial to it. Therefore, the protein synthesis time delay of Wip1 and the feedback loop of p53-Wip1 are of great significance to the cells. Maybe the sensitive switched to resistant is trigged via changes of the protein synthesis time delay of Wip1 and the feedback loop of p53-Wip1.

Figure 11. Effects of

$\tau_2$ on the drug-resistant cell system when the time delay

$\tau_1 = 2$ . (a)

$\tau_2 = 0$ . (b)

$\tau_2 = 2$ . (c)

$\tau_2 = 5$ .

DownLoad: Full-Size Img PowerPoint

Figure 12. Effects of

$\tau_2$ on the drug-resistant cell system when the time delay

$\tau_1 = 1.7$ . (a)

$\tau_2 = 0$ . (b)

$\tau_2 = 0.5$ . (c)

$\tau_2 = 2$ . (d)

$\tau_2 = 3$ . (e)

$\tau_2 = 3.5$ .

DownLoad: Full-Size Img PowerPoint

3.5. Effect of Etoposide on drug-resistant cells.

From , it can be found that when $\tau_1$ and $\tau_2$ are both set to 0, the system will not oscillate with the increase of the value of Eto. In other words, the time delay of protein synthesis is necessary to produce p53 oscillation. If the protein synthesis is too fast, no matter how much drug dose imports, it also can not produce oscillation and also can not play block the cell damage inherited by the next generation. However, once a certain time delay exists, the value of Eto can also make the system lose its stability and induce oscillation as shown in Figure 14. Moreover, neither too big nor too small of the Eto can lead to oscillation. This means that only appropriate dose of drug can have therapeutic effects under the time delay with a proper range. Therefore, the cell fate decision is a result of the combination of time delay and drug dose. Comparing Figures 7 and 14, we can see that in order for the system to produce oscillations, drug-resistant cells require a larger dose of drug than sensitive cells.

Figure 13. Effects of the drug dose Eto on drug-resistant cell systems when

$\tau_1 = \tau_2 = 0$ . (a)

$Eto = 5$ . (b)

$Eto = 10$ . (c)

$Eto = 15$ .

DownLoad: Full-Size Img PowerPoint

Figure 14. Effects of the drug dose Eto on drug-resistant cell systems when

$\tau_1 = 2, \tau_2 = 0$ . (a)

$Eto = 0$ . (b)

$Eto = 5$ . (c)

$Eto = 10$ . (d)

$Eto = 20$ . (e) Bifurcation diagram of the p53 concentration with regard to Eto.

DownLoad: Full-Size Img PowerPoint

3.6. Comparison of effects of $k_{pm}$ and $k_{pw}$ on drug-resistant cells.

When $Eto = 5$ and $\tau1 = 2$ , as shown in () and (), both $k_{pm}$ and $k_{pw}$ obviously influence the amplitude of the oscillation. Figure 15(d) and (h) showed that both of them also have the ability to induce Hopf bifurcation thereby changing the qualitative behavior. However, the bifurcation points in Figure 15(d) fall out of the range (1.92, 2.88) and the Figure 15(h) does not in the range (0.696, 0.957). Therefore, in practice of the drug-resistant cells, the p53-Mdm2 and p53-Wip1 negative feedback loops have an effect on the amplitude of the oscillation, but can not induce oscillation, which is different from the drug-sensitive cells. Thus, triggering the oscillation in drug-resistant cells is more difficult than drug-sensitive cells.

Figure 15. Effects of the drug dose Eto on drug-resistant cell systems when

$\tau_1 = 2, \tau_2 = 0$ . (a)

$Eto = 0$ . (b)

$Eto = 5$ . (c)

$Eto = 10$ . (d)

$Eto = 20$ . (e) Bifurcation diagram of the p53 concentration with regard to Eto.

DownLoad: Full-Size Img PowerPoint

4. Conclusions

Experiments suggested that the Mdm2-p53 negative feedback plays a primary role in producing oscillation, while wip1-p53 plays a secondary role ^[4,5]. In this paper, the dynamic effect of time delay within the coupled p53-Mdm2 and p53-wip1 negative feedback loop in two types of cells is compared. It is the first investigation to focus on the effects of time delays on the p53 pathway oscillation in drug-sensitive and drug-resistant cell lines. Here, the synergic effect of p53-Mdm2 and p53-wip1 negative feedback loop was also explained from the perspective of time delay. As shown in Figure 16, the time delay corresponding to the protein synthesis of Mdm2 induced by p53 is necessary to trigger oscillation. The critical value of bifurcation point is different between the drug-sensitive and drug-resistant cell lines, which demonstrated that to generation oscillation needed more time in drug-resistant cells than in drug-sensitive cells. Moreover, the period and amplitude of the p53 oscillation is smaller in drug-resistant cells than in drug-sensitive cells. However, the concentration of Mdm2 and Wip1 is much higher in drug-resistant cells than in drug-sensitive cells.

Figure 16. Bifurcation diagram of the p53 module with time delay

$\tau_1$ . (a) The concentration of p53 with regard to

$\tau_1$ . (b) The concentration of Mdm2 with regard to

$\tau_1$ . (c) The concentration of wip1 with regard to

$\tau_1$ .

DownLoad: Full-Size Img PowerPoint

In specific research, we find that the system gradually stabilizes when the time delays $\tau_1$ and $\tau_2$ are both zero. To facilitate the study, we first consider $\tau_2 = 0$ , and then use Hopf bifurcation theory to study the role of $\tau_1$ in the drug-sensitive cells (see the Supplementary Section). We find that the value of $\tau_1$ produces a Hopf bifurcation at $\tau_1^0$ , and the oscillation corresponding to the limit cycle of the system is consistent with the numerical simulation results (). Moreover, we studied the direction and period of Hopf bifurcation for sensitive cells. Theoretically, the amplitude and period of the oscillation became larger with the increase of time delay $\tau_1$ , which is consistent with the numerical simulation results (Figure 2).

The synergy between $\tau_1$ and $\tau_2$ and the effect of drug dose Eto on the system are also researched through numerical simulation. The results show that the system can oscillate only when the value of Eto is in a region. The oscillation region is larger for drug-resistant cells than the drug-sensitive cells, as shown in . This means that to produce oscillation it doesn't need too much drug in sensitive cells, but the resistant cells are on the contrary. Moreover, the time delay can cause the oscillation to happen in advance and also enhance it. Thus, the intensity of the oscillation can be adjusted by changing the value of Eto and the time delay $\tau_1$ .

Figure 17. Bifurcation diagram of the p53 module with a combinational effect of

$Eto$ and

$\tau_1$ . (a) The concentration of p53 with regard to

$Eto$ and

$\tau_1$ in the drug-sensitive cells. (b) The concentration of p53 with regard to

$Eto$ and

$\tau_1$ in the drug-resistant cells.

DownLoad: Full-Size Img PowerPoint

In addition, the two negative feedback loops of p53-Mdm2 and p53-Wip1 were studied indirectly by studying the effects of $k_{pm}$ and $k_{pw}$ on the system. In theory, both of the $k_{pm}$ and $k_{pw}$ can change the state of the cells between stable state and oscillation state, and the direction of them are opposite. However, in practice, in resistant cells, they can only regulate the amplitude of the oscillation. But in sensitive cells, $k_{pm}$ can not only regulate the amplitude but also can induce oscillation.

The research in this paper shows that time delay is crucial for producing oscillation of the coupled negative feedback loops including p53-Mdm2 and p53-Wip1. Time delay can regulate the system to generate oscillations and the period and amplitude of oscillations. And the oscillations can be controlled by time delay and Eto dose. This may provide a new perspective for the medical treatment of drug-resistant cells.

Acknowledgments

The authors express gratitude to the anonymous referee for his/her helpful suggestions and the partial supports of the National Natural Science Foundations of China (12062027 and 12162032), Cultivating Plan Program for the Leader in Science and Technology (2019HB015), Ten Thousand Talent Plans for Young Top-notch Talents, and Fundamental Research Projects (LS21005) of Yunnan Province.

Conflict of interest

The authors declare there is no conflicts of interest.

Supplementary

4.1. The information of Parameters

The parameter value and their biological significance used in the main body are given in Table S1 and Table S2.

Table S1. Model parameters and biological significance of drug-sensitive cells.

Parameter	Description	value	Reference
$k_{p0}$	Basal production rate of p53	1.3396/h	[33]
$k_{m0}$	Basal production rate of Mdm2	0.08/h	[33]
$k_{w0}$	Basal production rate of Wip1	0.105/h	[33]
${k_{pm}}$	Rate constant of $p53_p$ -induced production of Mdm2	0.9172/h	[33]
${k_{pw}}$	Rate constant of $p53_p$ -induced production of Wip1	0.1496/h	[33]
${n_{1}}$	Hill coefficient of $p53_p$ -induced production of Mdm2	4	[33]
${n_{2}}$	Hill coefficient of $p53_p$ -induced production of Wip1	4	[33]
${K_{pm0}}$	Michaelis constant for $p53_p$ -induced production of Mdm2	0.4025	[33]
${K_{pw0}}$	Michaelis constant for $p53_p$ -induced production of Wip1	0.4025	[33]
${k_{mp0}}$	Rate constant of Mdm2-induced degradation of $p53_u$	4.038/h	[33]
${\gamma _p}$	Mdm2-independent degradation rate constant of p53	0.1/h	[33]
${\gamma _{m0}}$	Degradation rate constant of $Mdm2_u$	0.2579/h	[33]
${\gamma _{m1}}$	Degradation rate constant of $Mdm2_p$	7.7362/h	[33]
${\gamma _{w}}$	Degradation rate constant of Wip1	0.4	[33]
${S_{ea}}$	Rate constant of etoposide-induced phosphorylation of ATM	1/ $\mu$ Mh	[33]
${D_{a0}}$	Rate constant of dephosphorylation of ATM	80/h	[14]
${S_{p0}}$	Rate constant of ATM-independent phosphorylation of p53	0.25	[33]
${S_{ap}}$	Rate constant of ATM-mediated phosphorylation of p53	0.8335/h	[33]
${D_{p0}}$	Rate constant of Wip1-independent dephosphorylation of p53	0.75/h	[33]
${D_{wp}}$	Rate constant of Wip1-mediated dephosphorylation of p53	0.25/h	[33]
${S_{m0}}$	Rate constant of ATM-independent phosphorylation of Mdm2	0.0153/h	[33]
${S_{am}}$	Rate constant of ATM-mediated phosphorylation of Mdm2	0.283	[33]
${D_{m0}}$	Rate constant of Wip1-independent dephosphorylation of Mdm2	0.5/h	[33]
${D_{wm}}$	Rate constant of Wip1-mediated dephosphorylation of Mdm2	0.5/h	[33]
${ATM_t}$	Total amount of ATM	16	[33]
${\tau_1}$	Time delay in production of Mdm2	0.5–3/h	Estimated
${\tau_2}$	Time delay in production of Wip1	0.5–3/h	Estimated

| Show Table

DownLoad: CSV

Table S2. Model parameters and biological significance of drug-resistant cells.

Parameter	Description	value	Reference
$k_{p0}$	Basal production rate of p53	2.4138/h	[33]
$k_{m0}$	Basal production rate of Mdm2	0.2/h	[33]
$k_{w0}$	Basal production rate of Wip1	0.35/h	[33]
${k_{pm}}$	Rate constant of $p53_p$ -induced production of Mdm2	2.3854/h	[33]
${k_{pw}}$	Rate constant of $p53_p$ -induced production of Wip1	0.8702/h	[33]
${n_{1}}$	Hill coefficient of $p53_p$ -induced production of Mdm2	4	[33]
${n_{2}}$	Hill coefficient of $p53_p$ -induced production of Wip1	4	[33]
${K_{pm0}}$	Michaelis constant for $p53_p$ -induced production of Mdm2	0.4025	[33]
${K_{pw0}}$	Michaelis constant for $p53_p$ -induced production of Wip1	0.4025	[33]
${k_{mp0}}$	Rate constant of Mdm2-induced degradation of $p53_u$	2.7048/h	[33]
${\gamma _p}$	Mdm2-independent degradation rate constant of p53	0.25/h	[33]
${\gamma _{m0}}$	Degradation rate constant of $Mdm2_u$	0.1804/h	[33]
${\gamma _{m1}}$	Degradation rate constant of $Mdm2_p$	3.6088/h	[33]
${\gamma _{w}}$	Degradation rate constant of Wip1	0.4	[33]
${S_{ea}}$	Rate constant of etoposide-induced phosphorylation of ATM	1/ $\mu$ Mh	[33]
${D_{a0}}$	Rate constant of dephosphorylation of ATM	30/h	[14]
${S_{p0}}$	Rate constant of ATM-independent phosphorylation of p53	0.25	[33]
${S_{ap}}$	Rate constant of ATM-mediated phosphorylation of p53	0.4335/h	[33]
${D_{p0}}$	Rate constant of Wip1-independent dephosphorylation of p53	0.75/h	[33]
${D_{wp}}$	Rate constant of Wip1-mediated dephosphorylation of p53	0.25/h	[33]
${S_{m0}}$	Rate constant of ATM-independent phosphorylation of Mdm2	0.0479/h	[33]
${S_{am}}$	Rate constant of ATM-mediated phosphorylation of Mdm2	0.2830	[33]
${D_{m0}}$	Rate constant of Wip1-independent dephosphorylation of Mdm2	0.5/h	[33]
${D_{wm}}$	Rate constant of Wip1-mediated dephosphorylation of Mdm2	0.5/h	[33]
${ATM_t}$	Total amount of ATM	3.5	[33]
${\tau_1}$	Time delay in production of Mdm2	0.5–3/h	Estimated
${\tau_2}$	Time delay in production of Wip1	0.5–3/h	Estimated

| Show Table

DownLoad: CSV

4.2. The existence of Hopf bifurcations

Without loss of generality, in this part, the parameters are chosen from Table 1 which corresponds to the drug-sensitive cells. For the drug-resistant cells, the approach is similar. All the calculation are performed via the software Mathematica 12.

Due to the high degree of nonlinearity in model (2.1), we only calculate the numerical equilibrium points. Submit the parameters in Table 1 into the model (2.1) and let all the right hands to zero, then we get a set of algebraic equations. Solving these linear equations by Mathematica Software, we can easily obtain the only positive equilibrium point (X, Y, Z, U) = (1.059, 0.4292, 0.3961, 0.1975).

Let's study the effects of $\tau_1$ first. For the sake of convenience, suppose $\tau_2 = 0$ . Obviously, all the functions in the right hand of model (2.1) are derivative at the neighborhood of the positive equilibrium point. Make Taylor expand for Eq (2.1) at the equilibrium point, which is a tedious and classic formula based process and is performed by Mathematica Software. Then neglecting the nonlinear part, the rest is linear equations, which is

$\begin{equation} \left\{ \begin{split} & \dot x = c_1x(t)+c_2y(t)+c_3z(t)+c_4u(t),\\ & \dot y = c_5 x(t - \tau_1)+c_6y(t)+c_7z(t - \tau_1)+c_8z(t)+c_9u(t - \tau_1) + c_{10}u(t),\\ & \dot z = c_{11}x(t)+c_{12}z(t)+c_{13}z(t)+c_{14}u(t) ,\\ & \dot u = c_{15}u(t), \end{split} \right. \end{equation}$

(4.1)

where

$\begin{align*} c_{1}& = -\frac{Y k_{{\rm{mp0}}} \left(D_{{\rm{p0}}}+Z D_{{\rm{wp}}}\right)}{U S_{{\rm{ap}}}+D_{{\rm{p0}}}+Z D_{{\rm{wp}}}+S_{{\rm{p0}}}}-\gamma _p,\ c_{2} = -\frac{X k_{{\rm{mp0}}} \left(D_{{\rm{p0}}}+Z D_{{\rm{wp}}}\right)}{U S_{{\rm{ap}}}+D_{{\rm{p0}}}+Z D_{{\rm{wp}}}+S_{{\rm{p0}}}},\\ c_{3}& = \frac{X Y D_{{\rm{wp}}} k_{{\rm{mp0}}} \left(D_{{\rm{p0}}}+Z D_{{\rm{wp}}}\right)}{\left(U S_{{\rm{ap}}}+D_{{\rm{p0}}}+Z D_{{\rm{wp}}}+S_{{\rm{p0}}}\right){}^2}-\frac{X Y D_{{\rm{wp}}} k_{{\rm{mp0}}}}{U S_{{\rm{ap}}}+D_{{\rm{p0}}}+Z D_{{\rm{wp}}}+S_{{\rm{p0}}}},\\ \ c_{4}& = \frac{X Y S_{{\rm{ap}}} k_{{\rm{mp0}}} \left(D_{{\rm{p0}}}+Z D_{{\rm{wp}}}\right)}{\left(U S_{{\rm{ap}}}+D_{{\rm{p0}}}+Z D_{{\rm{wp}}}+S_{{\rm{p0}}}\right){}^2},\\ c_{5}& = \frac{n_1 k_{{\rm{pm}}} X^{n_1-1}}{\left(\frac{K_{{\rm{pm0}}} \left(U S_{{\rm{ap}}}+D_{{\rm{p0}}}+Z D_{{\rm{wp}}}+S_{{\rm{p0}}}\right)}{U S_{{\rm{ap}}}+S_{{\rm{p0}}}}\right){}^{n_1}+X^{n_1}}-\frac{n_1 k_{{\rm{pm}}} X^{2 n_1-1}}{\left(\left(\frac{K_{{\rm{pm0}}} \left(U S_{{\rm{ap}}}+D_{{\rm{p0}}}+Z D_{{\rm{wp}}}+S_{{\rm{p0}}}\right)}{U S_{{\rm{ap}}}+S_{{\rm{p0}}}}\right){}^{n_1}+X^{n_1}\right){}^2},\\ \ c_{6}& = -\frac{\gamma _{{\rm{m1}}} \left(U S_{{\rm{am}}}+S_{{\rm{m0}}}\right)+\gamma _{{\rm{m0}}} \left(D_{{\rm{m0}}}+Z D_{{\rm{wm}}}\right)}{U S_{{\rm{am}}}+D_{{\rm{m0}}}+Z D_{{\rm{wm}}}+S_{{\rm{m0}}}},\\ \ c_{7}& = -\frac{n_1 D_{{\rm{wp}}} k_{{\rm{pm}}} K_{{\rm{pm0}}} X^{n_1} \left(\frac{K_{{\rm{pm0}}} \left(U S_{{\rm{ap}}}+D_{{\rm{p0}}}+Z D_{{\rm{wp}}}+S_{{\rm{p0}}}\right)}{U S_{{\rm{ap}}}+S_{{\rm{p0}}}}\right){}^{n_1-1}}{\left(U S_{{\rm{ap}}}+S_{{\rm{p0}}}\right) \left(\left(\frac{K_{{\rm{pm0}}} \left(U S_{{\rm{ap}}}+D_{{\rm{p0}}}+Z D_{{\rm{wp}}}+S_{{\rm{p0}}}\right)}{U S_{{\rm{ap}}}+S_{{\rm{p0}}}}\right){}^{n_1}+X^{n_1}\right){}^2},\\ \ c_{8}& = \frac{Y D_{{\rm{wm}}} \left(\gamma _{{\rm{m1}}} \left(U S_{{\rm{am}}}+S_{{\rm{m0}}}\right)+\gamma _{{\rm{m0}}} \left(D_{{\rm{m0}}}+Z D_{{\rm{wm}}}\right)\right)}{\left(U S_{{\rm{am}}}+D_{{\rm{m0}}}+Z D_{{\rm{wm}}}+S_{{\rm{m0}}}\right){}^2}-\frac{Y D_{{\rm{wm}}} \gamma _{{\rm{m0}}}}{U S_{{\rm{am}}}+D_{{\rm{m0}}}+Z D_{{\rm{wm}}}+S_{{\rm{m0}}}}, \end{align*}$

$\begin{align*} c_{9}& = -\frac{n_1 k_{{\rm{pm}}} X^{n_1} \left(\frac{S_{{\rm{ap}}} K_{{\rm{pm0}}}}{U S_{{\rm{ap}}}+S_{{\rm{p0}}}}-\frac{S_{{\rm{ap}}} K_{{\rm{pm0}}} \left(U S_{{\rm{ap}}}+D_{{\rm{p0}}}+Z D_{{\rm{wp}}}+S_{{\rm{p0}}}\right)}{\left(U S_{{\rm{ap}}}+S_{{\rm{p0}}}\right){}^2}\right) \left(\frac{K_{{\rm{pm0}}} \left(U S_{{\rm{ap}}}+D_{{\rm{p0}}}+Z D_{{\rm{wp}}}+S_{{\rm{p0}}}\right)}{U S_{{\rm{ap}}}+S_{{\rm{p0}}}}\right){}^{n_1-1}}{\left(\left(\frac{K_{{\rm{pm0}}} \left(U S_{{\rm{ap}}}+D_{{\rm{p0}}}+Z D_{{\rm{wp}}}+S_{{\rm{p0}}}\right)}{U S_{{\rm{ap}}}+S_{{\rm{p0}}}}\right){}^{n_1}+X^{n_1}\right){}^2},\\ \ c_{10}& = \frac{Y S_{{\rm{am}}} \left(\gamma _{{\rm{m1}}} \left(U S_{{\rm{am}}}+S_{{\rm{m0}}}\right)+\gamma _{{\rm{m0}}} \left(D_{{\rm{m0}}}+Z D_{{\rm{wm}}}\right)\right)}{\left(U S_{{\rm{am}}}+D_{{\rm{m0}}}+Z D_{{\rm{wm}}}+S_{{\rm{m0}}}\right){}^2}-\frac{Y S_{{\rm{am}}} \gamma _{{\rm{m1}}}}{U S_{{\rm{am}}}+D_{{\rm{m0}}}+Z D_{{\rm{wm}}}+S_{{\rm{m0}}}},\\ c_{11}& = \frac{n_2 k_{{\rm{pw}}} X^{n_2-1}}{\left(\frac{K_{{\rm{pw0}}} \left(U S_{{\rm{ap}}}+D_{{\rm{p0}}}+Z D_{{\rm{wp}}}+S_{{\rm{p0}}}\right)}{U S_{{\rm{ap}}}+S_{{\rm{p0}}}}\right){}^{n_2}+X^{n_2}}-\frac{n_2 k_{{\rm{pw}}} X^{2 n_2-1}}{\left(\left(\frac{K_{{\rm{pw0}}} \left(U S_{{\rm{ap}}}+D_{{\rm{p0}}}+Z D_{{\rm{wp}}}+S_{{\rm{p0}}}\right)}{U S_{{\rm{ap}}}+S_{{\rm{p0}}}}\right){}^{n_2}+X^{n_2}\right){}^2},\\ c_{12}& = -\frac{n_2 D_{{\rm{wp}}} k_{{\rm{pw}}} K_{{\rm{pw0}}} X^{n_2} \left(\frac{K_{{\rm{pw0}}} \left(U S_{{\rm{ap}}}+D_{{\rm{p0}}}+Z D_{{\rm{wp}}}+S_{{\rm{p0}}}\right)}{U S_{{\rm{ap}}}+S_{{\rm{p0}}}}\right){}^{n_2-1}}{\left(U S_{{\rm{ap}}}+S_{{\rm{p0}}}\right) \left(\left(\frac{K_{{\rm{pw0}}} \left(U S_{{\rm{ap}}}+D_{{\rm{p0}}}+Z D_{{\rm{wp}}}+S_{{\rm{p0}}}\right)}{U S_{{\rm{ap}}}+S_{{\rm{p0}}}}\right){}^{n_2}+X^{n_2}\right){}^2},\\ c_{13}& = -\gamma _w,\\ c_{14}& = -\frac{n_2 k_{{\rm{pw}}} X^{n_2} \left(\frac{S_{{\rm{ap}}} K_{{\rm{pw0}}}}{U S_{{\rm{ap}}}+S_{{\rm{p0}}}}-\frac{S_{{\rm{ap}}} K_{{\rm{pw0}}} \left(U S_{{\rm{ap}}}+D_{{\rm{p0}}}+Z D_{{\rm{wp}}}+S_{{\rm{p0}}}\right)}{\left(U S_{{\rm{ap}}}+S_{{\rm{p0}}}\right){}^2}\right) \left(\frac{K_{{\rm{pw0}}} \left(U S_{{\rm{ap}}}+D_{{\rm{p0}}}+Z D_{{\rm{wp}}}+S_{{\rm{p0}}}\right)}{U S_{{\rm{ap}}}+S_{{\rm{p0}}}}\right){}^{n_2-1}}{\left(\left(\frac{K_{{\rm{pw0}}} \left(U S_{{\rm{ap}}}+D_{{\rm{p0}}}+Z D_{{\rm{wp}}}+S_{{\rm{p0}}}\right)}{U S_{{\rm{ap}}}+S_{{\rm{p0}}}}\right){}^{n_2}+X^{n_2}\right){}^2},\\ c_{15}& = -D_{{\rm{a0}}}-{\rm{Eto}} S_{{\rm{ea}}}. \end{align*}$

Furthermore, we can get the characteristic equations of equations (2.1)

$\begin{equation} \begin{split} &(c_{15}-\lambda) e^{-\lambda \tau _1} ((c_{12}+c_{13}-\lambda )((c_1-\lambda )(\lambda -c_6)(-e^{\lambda \tau _1})-c_2 c_5)\\ &+c_{11}(-c_6 c_3 e^{\lambda \tau _1}+c_3 \lambda e^{\lambda \tau _1}+c_2 c_8 e^{\lambda \tau _1}+c_2 c_7)) = 0. \end{split} \end{equation}$

(4.2)

Simplify (4.2) to get:

$\begin{equation} \begin{split} \lambda ^4+\lambda ^3 m_1+\lambda ^2 m_2+\lambda m_3+m_4+e^{-\lambda \tau _1} \left(\lambda ^2 m_5+\lambda m_6+m_7\right) = 0, \end{split} \end{equation}$

(4.3)

where

$\begin{align*} &\ m_{1} = -c_1-c_6-c_{12}-c_{13}-c_{15},\\ &\ m_2 = c_1 c_6+c_{12} c_6+c_{13} c_6+c_{15} c_6-c_3 c_{11}+c_1 c_{12}+c_1 c_{13}+c_1 c_{15}+c_{12} c_{15}+c_{13} c_{15},\\ &\ m_3 = c_3 c_6 c_{11}-c_2 c_8 c_{11}+c_3 c_{15} c_{11}-c_1 c_6 c_{12}-c_1 c_6 c_{13}-c_1 c_6 c_{15}-c_1 c_{12} c_{15}\\ &-c_6 c_{12} c_{15}-c_1 c_{13} c_{15}-c_6 c_{13} c_{15},\\ &\ m_4 = -c_3 c_6 c_{11} c_{15}+c_2 c_8 c_{11} c_{15}+c_1 c_6 c_{12} c_{15}+c_1 c_6 c_{13} c_{15},\\ &\ m_5 = -c_2 c_5,\\ &\ m_6 = -c_2 c_7 c_{11}+c_2 c_5 c_{12}+c_2 c_5 c_{13}+c_2 c_5 c_{15},\\ &\ m_7 = c_2 c_7 c_{11} c_{15}-c_2 c_5 c_{12} c_{15}-c_2 c_5 c_{13} c_{15}.\\ \end{align*}$

In order to theoretically analyze the sufficient conditions for generating oscillations, we assume that $iw(w > 0)$ is a root of Eq (4.3). Then, bring $iw$ into Eq (4.3) to get:

$\begin{equation} \begin{split} &-i m_1 w^3-m_5 w^2 \left(\cos \left(\tau _1 w\right)-i \sin \left(\tau _1 w\right)\right)-m_2 w^2+i m_6 w \left(\cos \left(\tau _1 w\right)-i \sin \left(\tau _1 w\right)\right)\\ &+m_7 \left(\cos \left(\tau _1 w\right)-i \sin \left(\tau _1 w\right)\right)+i m_3 w+m_4+w^4 = 0. \end{split} \end{equation}$

(4.4)

Separating the real part and the imaginary part we can get

$\begin{equation} \left\{ \begin{split} &-m_5 w^2 \cos \left(\tau _1 w\right)-m_2 w^2+m_6 w \sin \left(\tau _1 w\right)+m_7 \cos \left(\tau _1 w\right)+m_4+w^4 = 0,\\ &-m_5 w^2 \cos \left(\tau _1 w\right)-m_2 w^2+m_6 w \sin \left(\tau _1 w\right)+m_7 \cos \left(\tau _1 w\right)+m_4+w^4 = 0. \end{split} \right. \end{equation}$

(4.5)

Then there will be

$\begin{equation} \left\{ \begin{split} &\cos(w\tau_1) = -\frac{m_7 w^4-m_1 m_6 w^4+m_3 m_6 w^2-m_2 m_7 w^2+m_4 m_7}{m_5 m_6 w^3+m_6^2 w^2-m_5 m_7 w^2+m_7^2}, \\ &\sin(w\tau_1) = -\frac{m_5 w^6-m_1 m_5 w^5+m_6 w^5-m_2 m_5 w^4+m_3 m_5 w^3+m_4 m_5 w^2}{m_5 m_6 w^3+m_6^2 w^2-m_5 m_7 w^2+m_7^2}\\ &+\frac{m_2 m_6 w^3-m_1 m_7 w^3-m_4 m_6 w+m_3 m_7 w}{m_5 m_6 w^3+m_6^2 w^2-m_5 m_7 w^2+m_7^2}. \end{split} \right. \end{equation}$

(4.6)

The above equations are squared and then the equations of the equal sign are added separately. Then, there will be

$\begin{equation} \begin{split} &r_1 w^{12}+r_2 w^{11}+r_3 w^{10}+r_4 w^9+r_5 w^8+r_6 w^7+r_7 w^6+r_8 w^5\\ &+r_9 w^4+r_{10} w^3+r_{11} w^2+r_{12} = 0, \end{split} \end{equation}$

(4.7)

where

$\begin{align*} &r_1 = m_5^2,\\ &r_2 = 2 m_5 m_6-2 m_1 m_5^2,\\ &r_3 = m_1^2 m_5^2-2 m_2 m_5^2-2 m_1 m_6 m_5+m_6^2,\\ &r_4 = 2 m_1 m_2 m_5^2+2 m_3 m_5^2-4 m_2 m_6 m_5+2 m_1 m_7 m_5,\\ &r_5 = m_6^2 m_1^2-2 m_5 m_7 m_1^2-2 m_3 m_5^2 m_1+2 m_2 m_5 m_6 m_1+m_2^2 m_5^2+2 m_4 m_5^2\\ &-2 m_2 m_6^2+m_7^2+2 m_3 m_5 m_6,\\ &r_6 = 2 m_5 m_6 m_2^2-2 m_3 m_5^2 m_2-2 m_1 m_5 m_7 m_2-2 m_1 m_4 m_5^2+4 m_4 m_5 m_6-2 m_3 m_5 m_7,\\ &r_7 = m_3^2 m_5^2-m_6^2 m_5^2-2 m_2 m_4 m_5^2-2 m_2 m_3 m_6 m_5-2 m_1 m_4 m_6 m_5+4 m_1 m_3 m_7 m_5\\ &+m_2^2 m_6^2-2 m_1 m_3 m_6^2+2 m_4 m_6^2+m_1^2 m_7^2-2 m_2 m_7^2,\\ &r_8 = -2 m_5 m_6^3-4 m_2 m_4 m_5 m_6+2 m_5^2 m_7 m_6+2 m_3 m_4 m_5^2+2 m_2 m_3 m_5 m_7+2 m_1 m_4 m_5 m_7,\\ &r_9 = -m_6^4+m_3^2 m_6^2-2 m_2 m_4 m_6^2+2 m_5 m_7 m_6^2+2 m_3 m_4 m_5 m_6+m_4^2 m_5^2+m_2^2 m_7^2-m_5^2 m_7^2\\ &-2 m_1 m_3 m_7^2+2 m_4 m_7^2-2 m_3^2 m_5 m_7,\\ &r_{10} = 2 m_5 m_6 m_4^2-2 m_3 m_5 m_7 m_4-2 m_5 m_6 m_7^2,\\ &r_{11} = 2 m_5 m_7^3+m_3^2 m_7^2-2 m_6^2 m_7^2-2 m_2 m_4 m_7^2+m_4^2 m_6^2,\\ &r_{12} = m_4^2 m_7^2-m_7^4. \end{align*}$

Let function $f(w) = r_1 w^{12}+r_2 w^{11}+r_3 w^{10}+r_4 w^9+r_5 w^8+r_6 w^7+r_7 w^6+r_8 w^5+r_9 w^4+r_{10} w^3+r_{11} w^2+r_{12}$ .\\

The carry-in parameters can be obtained by calculation $f(0) = r_{12} < 0$ , $f(2) > 0$ . Therefore, there exists a positive root $w_0 \approx1.056501$ of Eq (4.7). From (4.6) we can get

$\tau _1^{(j)} = \frac{\arccos\left(-\frac{-m_1 m_6 w_0^4+m_7 w_0^4+m_3 m_6 w_0^2-m_2 m_7 w_0^2+m_4 m_7}{m_5 m_6 w_0^3+m_6^2 w_0^2-m_5 m_7 w_0^2+m_7^2}\right)}{w_0}+ \frac{{2\pi j}}{{{w_0}}},$

where $j = 0, 1, 2, 3\cdots$ . And we define $\tau _1^0 = \min \left\{ {\tau _1^{(j)} > 0} \right\}_{j = 0}^{ + \infty }$ . Thus, when $\tau_1 = \tau_1^{0}$ , Eq (4.3) has a pair of pure imaginary roots $\pm i{w_0}$ .

Furthermore, we let $\lambda (\tau _1) = \alpha (\tau _1)+iw(\tau _1)$ is a root of (4.3), $\alpha (\tau _1^0) = 0$ and $iw(\tau _1^0) = w_0$ . We will get ${\left. {\frac{{d{\mathop{\rm Re}\nolimits} (\lambda ({\tau _1}))}}{{d{\tau _1}}}} \right|_{{\tau _1} = \tau _1^0}} > 0$ , and the specific derivation is as follows. Bring $\lambda (\tau _1)$ into (4.4) and then differentiate $\tau_1$ at both ends of the equation to get

$\begin{equation} \begin{split} \frac{1}{\lambda '\left(\tau _1\right)}& = \frac{e^{\tau _1 \lambda \left(\tau _1\right)} \left(4 \lambda^3 \left(\tau _1\right){}+3 m_1 \lambda^2 \left(\tau _1\right){}+2 m_2 \lambda \left(\tau _1\right)+m_3\right)}{m_5 \lambda^3 \left(\tau _1\right){}+m_6 \lambda^2 \left(\tau _1\right){}+m_7 \lambda \left(\tau _1\right)}\\ &+\frac{-m_5 \tau _1 \lambda^2 \left(\tau _1\right){}+2 m_2 \lambda \left(\tau _1\right)-m_6 \tau _1 \lambda \left(\tau _1\right)-m_7 \tau _1+m_6}{m_5 \lambda^3 \left(\tau _1\right){}+m_6 \lambda^2 \left(\tau _1\right){}+m_7 \lambda \left(\tau _1\right)}.\\ \end{split} \end{equation}$

(4.8)

Take $w = w_0, \tau_1 = \tau_1^0$ , then combining (4.6), (4.8) and $\lambda (\tau _1^0) = iw_0(\tau _1^0)$ we can get

$\begin{equation} \begin{split} {\left. {\Re \left( {\frac{1}{{\lambda '\left( {{\tau _1}} \right)}}} \right)} \right|_{{\tau _1} = \tau _1^0,w = {w_0}}} = \frac{{{D_2} - \frac{{{D_4}{D_5}}}{{{D_3}}} - \frac{{{D_6}{D_7}}}{{{D_3}}}}}{{{D_1}}} > 0, \end{split} \end{equation}$

(4.9)

where

$\begin{align*} &D_1 = m_5^2 w_0^6+m_6^2 w_0^4-2 m_5 m_7 w_0^4+m_7^2 w_0^2,\\ &D_2 = -2 m_5^2 w_0^4-m_6^2 w_0^2+2 m_5 m_7 w_0^2,\\ &D_3 = m_5 m_6 w_0^3+m_6^2 w_0^2-m_5 m_7 w_0^2+m_7^2\\ &D_4 = 3 m_1 m_5 w_0^5-4 m_6 w_0^5-m_3 m_5 w_0^3+2 m_2 m_6 w_0^3-3 m_1 m_7 w_0^3+m_3 m_7 w_0,\\ &D_5 = m_5 w_0^6-m_1 m_5 w_0^5+m_6 w_0^5-m_2 m_5 w_0^4+m_3 m_5 w_0^3-m_2 m_6 w_0^3+m_1 m_7 w_0^3\\ &+m_4 m_5 w_0^2+m_4 m_6 w_0-m_3 m_7 w_0,\\ &D_6 = -m_1 m_6 w_0^4+m_7 w_0^4+m_3 m_6 w_0^2-m_2 m_7 w_0^2+m_4 m_7,\\ &D_7 = 4 m_5 w_0^6-2 m_2 m_5 w_0^4+3 m_1 m_6 w_0^4-4 m_7 w_0^4-m_3 m_6 w_0^2+2 m_2 m_7 w_0^2.\\ \end{align*}$

Therefore, $sign\{ {\left. {\frac{{d\Re [\lambda (\tau)]}}{{d\tau }}} \right|_{{\tau _1} = \tau _1^0}}\} = sign\{ {\left. {\Re [\frac{1}{{\lambda '(\tau)}}]} \right|_{{\tau _1} = \tau _1^0}}\} > 0$ , which is that the root of characteristic equation (4.3) crosses the virtual axis from left to right as $\lambda (\tau _1^0) = \pm {{\rm{i}}}{w_0}$ . We can assert that the system experienced a Hopf bifurcation at $\tau_1 = \tau_1^0$ . Specifically, the system is progressively stable when $\tau_1 < \tau_1^0$ , and the system is oscillating when $\tau_1 > \tau_1^0$ . Therefore, for the system we studied, the dynamic properties of p53, Mdm2, and Wip1 can be theoretically predicted and adjusted by time delay.

4.3. Properties of Hopf bifurcations

In the previous section, we have obtained that the system (2.1) undergoes a Hopf bifurcation or Turing-Hopf bifurcation at the positive constant $({X}, {Y}, {Z}, {U})$ when ${\tau _1} = \tau _1^0$ and let $\tau_2 = 0$ for convenience. In this section, we will study the properties of Hopf bifurcation and the stability of bifurcated periodic solutions by using the normal form theory and central manifold theory due to Hassard, Kazarinoff and Wan ^[46].

Throughout this section, we always assume that system (2.1) undergoes Hopf bifurcation when ${\tau _1} = \tau _1^0$ at the positive equilibrium $({X}, {Y}, {Z}, {U})$ , and the corresponding purely imaginary roots of the characteristic equation are $\pm {{\rm{i}}}{w_0}$ . Subsequently, we let $\bar x = x(t) - X, \bar y = y(t)-Y, \bar z = z(t)-Z, \bar u = u(t)-U$ . And we still denote $\bar x, \bar y, \bar z, \bar u$ as $x, y, z, u$ . Moreover, let ${\tau _1} = \tau _1^0 + \gamma$ normalizing the time delay ${\tau _1}$ by the time-scaling $t \to {t / {{\tau _1}}}$ , and the system (2.1) transform to

$\begin{equation} \left\{ \begin{split} & \dot x = (\gamma +\tau_1^0)f_1(x,y,z,u),\\ & \dot y = (\gamma +\tau_1^0)(f_{21}(x,y,z,u)-f_{22}(x,y,z,u)),\\ & \dot z = (\gamma +\tau_1^0)f_3(x,y,z,u),\\ & \dot u = (\gamma +\tau_1^0)(Eto*Sea \left({\rm{ATM}}_t-u(t)\right)-D_{{\rm{a0}}} u(t)). \end{split} \right. \end{equation}$

(4.10)

$\begin{align*} &f_1(x,y,z,u) = {k_{p0}} - {k_{mp}}(u(t),z(t))xy - {\gamma _p}x,\\ &f_{21}(x,y,z,u) = {k_{m0}} + \frac{{{k_{pm}}{x^{{n_1}}}(t - 1)}}{{K_{pm}^{{n_1}}(u(t - 1),z(t - 1)) + {x^{{n_1}}}(t - 1)}},\\ &f_{22}(x,y,z,u) = {\gamma _m}(u(t),z(t),{\gamma _{m0}},{\gamma _{m1}})y,\\ &f_3(x,y,z,u) = {k_{w0}} + \frac{{{k_{pw}}{x^{{n_2}}}(t)}}{{K_{pw}^{{n_2}}(u(t),z(t)) + {x^{{n_2}}}(t)}} - {\gamma _w}z.\\ \end{align*}$

By expanding Taylor on the left end of Eq (4.10) at the equilibrium point (X, Y, Z, U), we can get

$\begin{align*} &x'(t) = (\tau_1^0+\gamma)(f_{1 r}+\frac{1}{2}(u^2 f_{1_{{\rm{uu}}}}+2 u x f_{1_{{\rm{ux}}}}+2 u y f_{1_{{\rm{uy}}}}+2 u z f_{1_{{\rm{uz}}}}\\ &+x^2 f_{1_{{\rm{xx}}}}+2 x y f_{1_{{\rm{xy}}}}+2 x z f_{1_{{\rm{xz}}}}+2 y z f_{1_{{\rm{yz}}}}+z^2 f_{1_{{\rm{zz}}}})+\frac{1}{6}(u^3 f_{1_{{\rm{uuu}}}}\\ &+3 u^2 x f_{1_{{\rm{uux}}}}+3 u^2 y f_{1_{{\rm{uuy}}}}+3 u^2 z f_{1_{{\rm{uuz}}}}+3 u x^2 f_{1_{{\rm{uxx}}}}+6 u x y f_{1_{{\rm{uxy}}}}\\ &+6 u y z f_{1_{{\rm{uyz}}}}+3 u z^2 f_{1_{{\rm{uzz}}}}+x^3 f_{1_{{\rm{xxx}}}}+3 x^2 y f_{1_{{\rm{xxy}}}}+3 x^2 z f_{1_{{\rm{xxz}}}}\\ &+6 x y z f_{1_{{\rm{xyz}}}}+3 x z^2 f_{1_{{\rm{xzz}}}}+3 y z^2 f_{1_{{\rm{yzz}}}}+z^3 f_{1_{{\rm{zzz}}}}+6 u x zf_{1_{{\rm{uxz}}}})+u f_{1 u}\\ &+x f_{1 x}+y f_{1 y}+z f_{1 z}),\\ &y'(t) = (\tau_1^0+\gamma)(f_{21 r}-f_{22 r}+\frac{1}{2}(f_{21_{{\rm{uu}}}} u(t-1)^2+2 f_{21_{{\rm{ux}}}} u(t-1) x(t-1)\\ &+2 f_{21_{{\rm{uz}}}} u(t-1) z(t-1)+f_{21_{{\rm{xx}}}} x(t-1)^2+2 f_{21_{{\rm{xz}}}} x(t-1) z(t-1)+f_{21_{{\rm{zz}}}} z(t-1)^2)\\ &+\frac{1}{6}(f_{21_{{\rm{uuu}}}} u(t-1)^3+3 f_{21_{{\rm{uux}}}} u(t-1)^2 x(t-1)+3 f_{21_{{\rm{uuz}}}} u(t-1)^2 z(t-1)\\ &+3 f_{21_{{\rm{uxx}}}} u(t-1) x(t-1)^2+6 f_{21_{{\rm{uxz}}}} u(t-1) x(t-1) z(t-1)+3 f_{21_{{\rm{uzz}}}} u(t-1) z(t-1)^2\\ &+f_{21_{{\rm{xxx}}}} x(t-1)^3+3 f_{21_{{\rm{xxz}}}} x(t-1)^2 z(t-1)+3 f_{21_{{\rm{xzz}}}} x(t-1) z(t-1)^2+f_{21_{{\rm{zzz}}}} z(t-1)^3)\\ &+f_{21 u} u(t-1)+f_{21 x} x(t-1)+f_{21 z} z(t-1)+\frac{1}{2}(-u^2 f_{22_{{\rm{uu}}}}-2 u y f_{22_{{\rm{uy}}}}-2 u z f_{22_{{\rm{uz}}}}\\ &-2 y z f_{22_{{\rm{yz}}}}-z^2 f_{22_{{\rm{zz}}}})+\frac{1}{6}(-u^3 f_{22_{{\rm{uuu}}}}-3 u^2 y f_{22_{{\rm{uuy}}}}-3 u^2 z f_{22_{{\rm{uuz}}}}-6 u y z f_{22_{{\rm{uyz}}}}-3 u z^2 f_{22_{{\rm{uzz}}}}\\ &-3 y z^2 f_{22_{{\rm{yzz}}}}-z^3 f_{22_{{\rm{zzz}}}})-u f_{22 u}-y f_{22 y}-z f_{22 z}), \end{align*}$

$\begin{align*} &z'(t) = (\tau_1^0+\gamma)(f_{3 r}+\frac{1}{2} \left(u^2 f_{3_{{\rm{uu}}}}+2 u x f_{3_{{\rm{ux}}}}+2 u z f_{3_{{\rm{uz}}}}+x^2 f_{3_{{\rm{xx}}}}+2 x z f_{3_{{\rm{xz}}}}+z^2 f_{3_{{\rm{zz}}}}\right)\\ &+\frac{1}{6}(u^3 f_{3_{{\rm{uuu}}}}+3 u^2 x f_{3_{{\rm{uux}}}}+3 u^2 z f_{3_{{\rm{uuz}}}}+3 u x^2 f_{3_{{\rm{uxx}}}}+3 u z^2 f_{3_{{\rm{uzz}}}}+x^3 f_{3_{{\rm{xxx}}}}+3 x^2 z f_{3_{{\rm{xxz}}}}\\ &+3 x z^2 f_{3_{{\rm{xzz}}}}+z^3 f_{3_{{\rm{zzz}}}}+6 u x z f_{3_{{\rm{uxz}}}})+u f_{3 u}+x f_{3 x}+z f_{3 z}),\\ &u'(t) = (\tau_1^0+\gamma)(u \left(-D_{{\rm{a0}}}-{\rm{Eto}}*{\rm{Sea}}\right)). \end{align*}$

where $f_{1r}, f_{21r}$ expand Taylor's remainder above third order on behalf of Taylor. $f_{1x}, f_{1xy}$ and $f_{1xyz}$ stands for the value of $\frac{\partial f_1}{\partial x}, \frac{\partial {}^{\wedge}2f_1}{\partial x\partial y}$ and $\frac{\partial {}^{\wedge}3f_1}{\partial x\partial y\partial z}$ at (X, Y, Z, U) respectively. The meaning of other symbols can be deduced by the same principle. Let

$\begin{align*} U &\ = {\left( {{u_1}(t),{u_2}(t),{u_3}(t),{u_4}(t)} \right)^T}\\ &\ = {\left( {x(t),y(t),z(t),u(t)} \right)^T}. \end{align*}$

And define $C = C\left({\left[ { - 1, 0} \right], {R^4}} \right)$ , then (4.10) becomes to

$\begin{equation} \begin{split} \dot U = {L_\gamma }\left( {{U_t}} \right) + f\left( {\gamma ,{U_t}} \right), \end{split} \end{equation}$

(4.11)

where ${L_\gamma }:C \to {R^4}, f:R \times C \to {R^4}$ whose specific form is as follows

$\begin{equation} \begin{split} &L_{\gamma }(\phi ) = (\gamma +{\rm{ \mathsf{ τ}_1^0 }}) \left( \begin{array}{c} \phi _1(0) \\ \phi _2(0) \\ \phi _3(0) \\ \phi _4(0) \\ \end{array} \right) \left( \begin{array}{cccc} f_{1 x} & f_{1 y} & f_{1 z} & f_{1 u} \\ 0 & -f_{22 y} & -f_{22 z} & -f_{22 u} \\ f_{3 x} & 0 & f_{3 z} & f_{3 u} \\ 0 & 0 & 0 & -D_{{\rm{a0}}}-{\rm{Eto}}*S_{{\rm{ea}}} \\ \end{array} \right)\\ &+(\gamma +{\rm{ \mathsf{ τ}_1^0 }}) \left( \begin{array}{c} \phi _1(-1) \\ \phi _2(-1) \\ \phi _3(-1) \\ \phi _4(-1) \\ \end{array} \right) \left( \begin{array}{cccc} 0 & 0 & 0 & 0 \\ f_{21 x} & 0 & f_{21 z} & f_{21 u} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \end{array} \right), \end{split} \end{equation}$

(4.12)

$\begin{equation} \begin{split} f(\gamma ,\phi ) = \left( {\begin{array}{*{20}{c}} E\\ F\\ R\\ 0 \end{array}} \right), \end{split} \end{equation}$

(4.13)

$\begin{align*} \begin{array}{l} E = {f_{1r}} + \frac{1}{2}\left( {{\phi _4}{{(0)}^2}{f_{{1_{{{\rm{uu}}}}}}} + 2{\phi _4}(0){\phi _1}(0){f_{{1_{{{\rm{ux}}}}}}} + 2{\phi _2}(0){\phi _4}(0){f_{{1_{{{\rm{uy}}}}}}} + 2{\phi _3}(0){\phi _4}(0){f_{{1_{{{\rm{uz}}}}}}}} \right.\\ \left. { + {\phi _1}{{(0)}^2}{f_{{1_{{{\rm{xx}}}}}}} + 2{\phi _2}(0){\phi _1}(0){f_{{1_{{{\rm{xy}}}}}}} + 2{\phi _3}(0){\phi _1}(0){f_{{1_{{{\rm{xz}}}}}}} + 2{\phi _2}(0){\phi _3}(0){f_{{1_{{{\rm{yz}}}}}}} + {\phi _3}{{(0)}^2}{f_{{1_{{{\rm{zz}}}}}}}} \right)\\ + \frac{1}{6}\left( {6{\phi _4}(0){\phi _1}(0){\phi _3}(0){f_{{1_{{{\rm{uxz}}}}}}} + {\phi _4}{{(0)}^3}{f_{{1_{{{\rm{uuu}}}}}}} + 3{\phi _4}{{(0)}^2}{\phi _1}(0){f_{{1_{{{\rm{uux}}}}}}} + 3{\phi _4}{{(0)}^2}{\phi _2}(0){f_{{1_{{{\rm{uuy}}}}}}}} \right.\\ + 3{\phi _4}{(0)^2}{\phi _3}(0){f_{{1_{{{\rm{uuz}}}}}}} + 3{\phi _4}(0){\phi _1}{(0)^2}{f_{{1_{{{\rm{uxx}}}}}}} + 6{\phi _4}(0){\phi _1}(0){\phi _2}(0){f_{{1_{{{\rm{uxy}}}}}}} + 6{\phi _4}(0){\phi _2}(0){\phi _3}(0){f_{{1_{{{\rm{uyz}}}}}}}\\ + 3{\phi _4}(0){\phi _3}{(0)^2}{f_{{1_{{{\rm{uzz}}}}}}} + {\phi _3}{(0)^3}{f_{{1_{{{\rm{xxx}}}}}}} + 3{\phi _2}(0){\phi _3}{(0)^2}{f_{{1_{{{\rm{xxy}}}}}}} + 3{\phi _2}{(0)^2}{\phi _3}(0){f_{{1_{{{\rm{xxz}}}}}}}\\ \left. { + 6{\phi _1}(0){\phi _2}(0){\phi _3}(0){f_{{1_{{{\rm{xyz}}}}}}} + 3{\phi _1}(0){\phi _3}{{(0)}^2}{f_{{1_{{{\rm{xzz}}}}}}} + 3{\phi _2}(0){\phi _3}{{(0)}^2}{f_{{1_{{{\rm{yzz}}}}}}} + {\phi _3}{{(0)}^3}{f_{{1_{{{\rm{zzz}}}}}}}} \right), \end{array} \end{align*}$

$\begin{align*} \begin{array}{l} F = {f_{21r}} - {f_{22r}} + \frac{1}{2}\left( { - {\phi _4}{{(0)}^2}{f_{{{22}_{{{\rm{uu}}}}}}} - 2{\phi _4}(0){\phi _2}(0){f_{{{22}_{{{\rm{uy}}}}}}} - 2{\phi _4}(0){\phi _3}(0){f_{{{22}_{{{\rm{uz}}}}}}}} \right.\\ \left. { - 2{\phi _2}(0){\phi _3}(0){f_{{{22}_{{{\rm{yz}}}}}}} - {f_{{{22}_{{{\rm{zz}}}}}}}{\phi _3}{{(0)}^2}} \right) + \frac{1}{6}\left( { - {\phi _4}{{(0)}^3}{f_{{{22}_{{{\rm{uuu}}}}}}} - 3{\phi _4}{{(0)}^2}{\phi _2}(0){f_{{{22}_{{{\rm{uuy}}}}}}}} \right.\\ - 3{\phi _4}{(0)^2}{\phi _3}(0){f_{{{22}_{{{\rm{uuz}}}}}}} - 6{\phi _4}(0){\phi _2}(0){\phi _3}(0){f_{{{22}_{{{\rm{uyz}}}}}}} - 3{\phi _4}(0){\phi _3}{(0)^2}{f_{{{22}_{{{\rm{uzz}}}}}}}\\ \left. { - 3{\phi _2}(0){\phi _3}{{(0)}^2}{f_{{{22}_{{{\rm{yzz}}}}}}} - {f_{{{22}_{{{\rm{zzz}}}}}}}{\phi _3}{{(0)}^3}} \right) + \frac{1}{2}\left( {{\phi _4}{{( - 1)}^2}{f_{{{21}_{{{\rm{uu}}}}}}} + 2{\phi _4}( - 1){\phi _1}( - 1){f_{{{21}_{{{\rm{ux}}}}}}}} \right.\\ + 2{\phi _3}( - 1){\phi _4}( - 1){f_{{{21}_{{{\rm{uz}}}}}}} + {\phi _1}{( - 1)^2}{f_{{{21}_{{{\rm{xx}}}}}}}\left. { + 2{\phi _1}( - 1){\phi _3}( - 1){f_{{{21}_{{{\rm{xz}}}}}}} + {\phi _3}{{( - 1)}^2}{f_{{{21}_{{{\rm{zz}}}}}}}} \right)\\ + \frac{1}{6}\left( {{\phi _4}{{( - 1)}^3}{f_{{{21}_{{{\rm{uuu}}}}}}} + 3{\phi _1}( - 1){\phi _4}{{( - 1)}^2}{f_{{{21}_{{{\rm{uux}}}}}}}} \right. + 3{\phi _3}( - 1){\phi _4}{( - 1)^2}{f_{{{21}_{{{\rm{uuz}}}}}}}\\ + 3{\phi _4}( - 1){\phi _1}{( - 1)^2}{f_{{{21}_{{{\rm{uxx}}}}}}} + {\phi _1}{( - 1)^3}{f_{{{21}_{{{\rm{xxx}}}}}}} + 6{\phi _3}( - 1){\phi _4}( - 1){\phi _1}( - 1){f_{{{21}_{{{\rm{uxz}}}}}}}\\ + 3{\phi _3}{( - 1)^2}{\phi _4}( - 1){f_{{{21}_{{{\rm{uzz}}}}}}} + 3{\phi _3}( - 1){\phi _1}{( - 1)^2}{f_{{{21}_{{{\rm{xxz}}}}}}} + 3{\phi _1}( - 1){\phi _3}{( - 1)^2}{f_{{{21}_{{{\rm{xzz}}}}}}}\\ \left. { + {\phi _3}{{( - 1)}^3}{f_{{{21}_{{{\rm{zzz}}}}}}}} \right), \end{array} \end{align*}$

$\begin{align*} \begin{array}{l} R = {f_{3r}} + \frac{1}{2}\left( {{\phi _4}{{(0)}^2}{f_{{3_{{{\rm{uu}}}}}}} + 2{\phi _4}(0){\phi _1}(0){f_{{3_{{{\rm{ux}}}}}}} + 2{\phi _3}(0){\phi _4}(0){f_{{3_{{{\rm{uz}}}}}}} + {\phi _1}{{(0)}^2}{f_{{3_{{{\rm{xx}}}}}}}} \right.\\ \left. { + 2{\phi _3}(0){\phi _1}(0){f_{{3_{{{\rm{xz}}}}}}} + {\phi _3}{{(0)}^2}{f_{{3_{{{\rm{zz}}}}}}}} \right) + \frac{1}{6}\left( {3{u^2}{\phi _1}(0){f_{{3_{{{\rm{uux}}}}}}} + {\phi _4}{{(0)}^3}{f_{{3_{{{\rm{uuu}}}}}}} + 3z{\phi _4}{{(0)}^2}} \right.\\ + 3{\phi _1}{(0)^2}{\phi _4}(0){f_{{3_{{{\rm{uxx}}}}}}} + 6{\phi _1}(0){\phi _4}(0){{\rm{z}}}{f_{{3_{{{\rm{uxz}}}}}}} + 3{\phi _3}{(0)^2}{\phi _4}(0){f_{{3_{{{\rm{uzz}}}}}}} + {\phi _1}{(0)^3}{f_{{3_{{{\rm{xxx}}}}}}}\\ \left. { + 3{\phi _3}(0){\phi _1}{{(0)}^2}{f_{{3_{{{\rm{xxz}}}}}}} + 3{\phi _3}{{(0)}^2}{\phi _1}(0){f_{{3_{{{\rm{xzz}}}}}}} + {\phi _3}{{(0)}^3}{f_{{3_{{{\rm{zzz}}}}}}}} \right), \end{array} \end{align*}$

where $\phi = {\left({{\phi _1}\left(t \right), {\phi _2}\left(t \right), {\phi _3}\left(t \right), {\phi _4}\left(t \right)} \right)^T} \in C$ . According to the Riesz representation theorem there exists a $4 \times 4$ matrix function $\eta (\theta, \gamma)$ , which is bounded variogram on $\theta \in \left[ { - 1, 0} \right]$ such that ${L_\gamma }\phi = \int_{ - 1}^0 d \eta \left({\theta, \gamma } \right)\phi \left(\theta \right)$ for $\phi \in C\left({\left[ { - 1, 0} \right], {R^4}} \right)$ .

In fact, we can choose

$\begin{equation} \begin{split} \begin{array}{l} \eta (\theta ,\gamma ) = (\gamma + \tau _{{\rm{1}}}^{{\rm{0}}})\left( {\begin{array}{*{20}{c}} {{f_{1x}}}&{{f_{1y}}}&{{f_{1z}}}&{{f_{1u}}}\\ 0&{ - {f_{22y}}}&{ - {f_{22z}}}&{ - {f_{22u}}}\\ {{f_{3x}}}&0&{{f_{3z}}}&{{f_{3u}}}\\ 0&0&0&{ - {D_{{{\rm{a0}}}}} - {{\rm{Eto}}}*{S_{{{\rm{ea}}}}}} \end{array}} \right)\delta \left( \theta \right)\\ + (\gamma + \tau _{{\rm{1}}}^{{\rm{0}}})\left( {\begin{array}{*{20}{c}} 0&0&0&0\\ {{f_{21x}}}&0&{{f_{21z}}}&{{f_{21u}}}\\ 0&0&0&0\\ 0&0&0&0 \end{array}} \right)\delta \left( {\theta + 1} \right), \end{array} \end{split} \end{equation}$

(4.14)

where $\delta \left(\theta \right)$ is Dirac delta function. And we define

$\begin{equation} \begin{split} {\Lambda _\gamma }\phi = \left\{ {\begin{array}{*{20}{c}} {\frac{{d\phi \left( \theta \right)}}{{d\theta }}{{\rm{ , }}}\theta \in \left[ { - 1,0} \right),}\\ {{{\rm{ }}}\int_{ - 1}^0 d \eta \left( {\theta ,\gamma } \right)\phi \left( \theta \right){{\rm{ , }}}\theta = 0,} \end{array}} \right.{{\rm{ and }}}\ {R_\gamma }\phi = \left\{ {\begin{array}{*{20}{c}} {{{\rm{0 , }}}\theta \in \left[ { - 1,0} \right),}\\ {f\left( {\gamma ,\phi } \right){{\rm{ , }}}\theta = 0.} \end{array}} \right. \end{split} \end{equation}$

(4.15)

Obviously, we can transform (4.11) to the following form

$\begin{equation} \begin{split} \dot U_t = {\Lambda _\gamma }{U_t} + {R_\gamma }{U_t}, \end{split} \end{equation}$

(4.16)

where ${U_t}\left(\theta \right) = U\left({t + \theta } \right)$ . For $\psi \in {C^1}\left({\left[ { - 1, 0} \right], {{\left({{R^4}} \right)}^*}} \right)$ , we define

$\begin{equation} \begin{split} &\ \Lambda _\gamma ^*\psi (s) = \left\{ {\begin{array}{*{20}{c}} {\frac{{ - d\psi \left( s \right)}}{{ds}}{{\rm{ , }}}\theta \in \left( {0, - 1} \right],}\\ {{{\rm{ }}}\int_{ - 1}^0 d {\eta ^T}\left( {t,\gamma } \right)\psi \left( { - t} \right){{\rm{ , }}}s = 0,} \end{array}} \right. \end{split} \end{equation}$

(4.17)

and

$\begin{equation} \begin{split} &\ \langle {\psi \left( s \right),\phi \left( \theta \right)} \rangle = \bar \psi \left( s \right)\phi \left( 0 \right) - \int_{ - 1}^0 {\int_{\xi = 0}^\theta {\bar \psi (\xi - \theta )} } d\eta \left( \theta \right)\phi \left( \xi \right)d\xi,\\ \end{split} \end{equation}$

(4.18)

which is a bilinear inner product. Obviously, ${\Lambda _0}$ and $\Lambda _0^*$ are adjoint operators for each other. In addition, $\pm {{\rm{i}}}{w_0}\tau _1^0$ are the eigenvalues of ${\Lambda _0}$ . Therefore, they are also eigenvalues of $\Lambda _0^*$ . We let $q\left(\theta \right)$ be the eigenvector of ${\Lambda _0}$ corresponding to ${{\rm{i}}}{w_0}\tau _1^0$ and ${q^*}\left(s \right)$ be the eigenvector of $\Lambda _0^*$ corresponding to $- {{\rm{i}}}{w_0}\tau _1^0$ , which meet the following conditions

$\begin{equation} \begin{split} &\ q\left( \theta \right) = {e^{{{\rm{i}}}{w_0}\tau _1^0\theta }}{\left( {1,{v_1},{v_2},{v_3}} \right)^T},\\ &\ {q^*}\left( s \right) = G{e^{{{\rm{i}}}{w_0}\tau _1^0s}}\left( {1,v_1^*,v_2^*,v_3^*} \right). \end{split} \end{equation}$

(4.19)

From ${\Lambda _0}q\left(0 \right) = {{\rm{i}}}{w_0}\tau _1^0q\left(0 \right)$ and $\Lambda _0^*{q^*}\left(0 \right) = - {{\rm{i}}}{w_0}\tau _1^0{q^*}\left(0 \right)$ , it is easy to deduce

$\begin{align*} &{v_1} = - \frac{{{e^{ - i{w_0}\tau _1^0}}\left( {{c_{{{\rm{11}}}}}{c_{{\rm{7}}}} + {c_{{{\rm{11}}}}}{c_{{\rm{8}}}}{e^{i{w_0}\tau _1^0}} - {c_{{{\rm{12}}}}}{c_{{\rm{5}}}} - {c_{{{\rm{13}}}}}{c_{{\rm{5}}}} + i{c_{{\rm{5}}}}{w_{{\rm{0}}}}} \right)}}{{({w_{{\rm{0}}}} + i{c_{{\rm{6}}}})(i{c_{{{\rm{12}}}}} + i{c_{{{\rm{13}}}}} + {w_{{\rm{0}}}})}},\\ &{v_2} = - \frac{{{c_{{{\rm{11}}}}}}}{{{c_{{{\rm{12}}}}} + {c_{{{\rm{13}}}}} - i{w_{{\rm{0}}}}}},\\ &{v_3} = 0,\\ &v_1^* = -\frac{c_2}{c_6+i w_0},\\ &v_2^* = \frac{V_{21}}{V_{22}},\\ &v_3^* = \frac{V_{31}}{V_{32}},\\ & V_{21} = i c_2 c_9 c_{14} e^{i \tau _1 w_0}-i c_{11} w_0^2-c_6 c_{11} w_0+c_4 c_{14} w_0-c_{11} c_{15} w_0-i c_4 c_6 c_{14}\\ &+i c_2 c_{10} c_{14}+i c_6 c_{11} c_{15},\\ & V_{22} = \left(w_0-i c_6\right) \left(-i c_{12} w_0-i c_{13} w_0-i c_{15} w_0+c_{14}^2-c_{12} c_{15}-c_{13} c_{15}+w_0^2\right),\\ & V_{31} = c_2 c_9 w_0 e^{i \tau _1^0 w_0}-i c_2 c_9 c_{12} e^{i \tau _1^0 w_0}-i c_2 c_9 c_{13} e^{i \tau _1^0 w_0}-i c_4 w_0^2-c_4 c_6 w_0\\ &+c_2 c_{10} w_0-c_4 c_{12} w_0-c_4 c_{13} w_0+c_{11} c_{14} w_0+i c_4 c_6 c_{12}-i c_2 c_{10} c_{12}+i c_4 c_6 c_{13}\\ &-i c_2 c_{10} c_{13}-i c_6 c_{11} c_{14},\\ & V_{32} = -\left(w_0-i c_6\right) \left(-i c_{12} w_0-i c_{13} w_0-i c_{15} w_0+c_{14}^2-c_{12} c_{15}-c_{13} c_{15}+w_0^2\right). \end{align*}$

From

$\begin{align*} \begin{array}{l} \langle {{q^*},q} \rangle = {{\bar q}^*}\left( 0 \right)q\left( 0 \right) - \int_{ - 1}^0 {\int_{\xi = 0}^\theta {{{\bar q}^*}(\xi - \theta )} } d\eta \left( \theta \right)q\left( \xi \right)d\xi \\ = {{\bar q}^*}\left( 0 \right)q\left( 0 \right) + {{\bar q}^*}\left( 0 \right)\tau _1^0\left( {\begin{array}{*{20}{c}} 0&0&0&0\\ {{f_{21x}}}&0&{{f_{21z}}}&{{f_{21u}}}\\ 0&0&0&0\\ 0&0&0&0 \end{array}} \right){e^{ - {{\rm{i}}}{w_0}\tau _1^0}}q\left( 0 \right)\\ = \bar G\left[ {\tau _1^0\overline {{v_1}^*} {e^{ - {{\rm{i}}}{w_0}\tau _1^0}}\left( {{f_{21u}}{v_{{\rm{3}}}} + {f_{21x}} + {f_{21z}}{v_2}} \right) + {v_1}\overline {{v_1}^*} + {v_2}\overline {{v_2}^*} + {v_3}\overline {{v_3}^*} + 1} \right], \end{array} \end{align*}$

and making $\langle {{q^*}, q} \rangle = 1$ , we let $\bar G = \frac{1}{{\tau _1^0\overline {{v_1}^*} {e^{ - {{\rm{i}}}{w_0}\tau _1^0}}\left({{f_{21u}}{v_{{\rm{3}}}} + {f_{21x}} + {f_{21z}}{v_2}} \right) + {v_1}\bar{v_1^*} + {v_2}\bar{v_2^*} + {v_3}\bar{v_3^*} + 1}}$ . And then $G = \begin{array}{l} \frac{1}{{\tau _1^0{v_1}^*{e^{{{\rm{i}}}{w_0}\tau _1^0}}\left({{f_{21u}}\overline {{v_{{\rm{3}}}}} + {f_{21x}} + {f_{21z}}\overline {{v_2}} } \right) + {v_1^*}\bar{v_1} + {v_2^*}\bar{v_2} + {v_3^*}\bar {v_3} + 1}}\\ \end{array}$ .

The above $\bar{v_1}$ and $\bar{v_1^*}$ represent the conjugate plural of ${v_1}$ and $v_1^*$ respectively and the other analogy. Next we will compute the coordinate to describe the center manifold ${C_0}$ at $\gamma = 0$ using the way of Hassard et al. ^[46].

We let ${U_t}$ be the solution of (4.11) at at $\gamma = 0$ and define

$\begin{equation} \begin{split} &\ z\left( t \right) = \langle {{q^*},{x_t}} \rangle\\ &\ W\left( {t,\theta } \right) = {U_t}\left( \theta \right) - 2{\mathop{\rm Re}\nolimits} \left\{ {z\left( t \right)q\left( \theta \right)} \right\}. \end{split} \end{equation}$

(4.20)

On the center manifold ${C_0}$ , we can regard $W\left({t, \theta } \right)$ as

$\begin{equation} \begin{split} W\left( {z,\bar z,\theta } \right) = {W_{20}}\left( \theta \right)\frac{{{z^2}}}{2} + {W_{11}}\left( \theta \right)z\bar z + {W_{02}}\left( \theta \right)\frac{{{{\bar z}^2}}}{2} + \cdots. \end{split} \end{equation}$

(4.21)

In fact, $z\left(t \right)$ and $\bar z\left(t \right)$ are local coordinates for center manifold $C_0$ in the direction of ${q^*}$ and ${\bar q^*}$ . It is easy to know that $W\left({t, \theta } \right)$ is real only when ${U_t}\left(\theta \right)$ is real. We just consider it is a real solution of (4.11), and then

$\begin{equation} \begin{split} \dot z\left( t \right) & = \langle {{q^*},{{\dot U}_t}} \rangle \\ & = \langle {{q^*},{\Lambda _0}{U_t} + {R_0}{U_t}} \rangle \\ & = {\langle {\Lambda _0^*{q^*},{U_t}} \rangle + \langle {{q^*},f\left( {0,{U_t}} \right)} \rangle }\\ & = {{{\rm{i}}}{w_0}\tau _1^0z + {{\bar q}^*}\left( 0 \right)f\left( {0,W\left( {z,\bar z,\theta } \right) + 2Re\left\{ {z\left( t \right)q\left( \theta \right)} \right\}} \right)}\\ & = {{\rm{i}}}{w_0}\tau _1^0z + {{\bar q}^*}\left( 0 \right){f_0}{{\rm{ }}}, \end{split} \end{equation}$

(4.22)

$\begin{equation} \begin{split} {f_0}{{\rm{ }}} = f\left( {0,W\left( {z,\bar z,\theta } \right) + 2Re\left\{ {z\left( t \right)q\left( \theta \right)} \right\}} \right){{\rm{ }}}, \end{split} \end{equation}$

(4.23)

$\begin{equation} \begin{split} \dot z\left( t \right) = {{\rm{i}}}{w_0}\tau _1^0z + g(z,\bar z), \end{split} \end{equation}$

(4.24)

where

$\begin{equation} \begin{split} g(z,\bar z) = {{{\rm{g}}}_{{{\rm{20}}}}}\frac{{{z^2}}}{2}{{\rm{ + }}}{{{\rm{g}}}_{{{\rm{11}}}}}z\bar z{{\rm{ + }}}{{{\rm{g}}}_{{{\rm{02}}}}}\frac{{{{\bar z}^2}}}{2}{{\rm{ + }}}{{{\rm{g}}}_{{{\rm{21}}}}}\frac{{{z^2}\bar z}}{2}{{\rm{ + }}} \cdots. \end{split} \end{equation}$

(4.25)

The following formula can be obtained from Eqs (4.21) and (4.22).

$\begin{equation} \begin{split} {U_t} & = W\left( {t,\theta } \right) + 2Re\left\{ {z\left( t \right)q\left( \theta \right)} \right\}\\ & = {W_{20}}\left( \theta \right)\frac{{{z^2}}}{2} + {W_{11}}\left( \theta \right)z\bar z + {W_{02}}\left( \theta \right)\frac{{{{\bar z}^2}}}{2} + zq + \bar z\bar q \cdots \\ & = {W_{20}}\left( \theta \right)\frac{{{z^2}}}{2} + {W_{11}}\left( \theta \right)z\bar z + {W_{02}}\left( \theta \right)\frac{{{{\bar z}^2}}}{2} + {e^{{{\rm{i}}}{w_0}\tau _1^0\theta }}{\left( {1,{v_1},{v_2},{v_3}} \right)}z\\ &+{e^{ - {{\rm{i}}}{w_0}\tau _1^0\theta }}{\left( {1,{{\bar v}_1},{{\bar v}_2},{{\bar v}_3}} \right)}\bar z + \cdots. \end{split} \end{equation}$

(4.26)

Combined with (4.23), (4.25) we have

$\begin{equation} \begin{split} g(z,\bar z)& = {{\rm{ }}}{\bar {q^*}}\left( 0 \right){f_0}\\ & = \bar{q^*}\left( 0 \right)f\left( {0,{U_t}} \right)\\ & = \bar G\tau _1^0\left( {1,\bar {v_1^*},\bar {v_2^*},\bar {v_3^*}} \right) \times \left( {\begin{array}{*{20}{c}} E\\ F\\ R\\ 0 \end{array}} \right). \end{split} \end{equation}$

(4.27)

Comparing the coefficients of (4.25) and (4.27), we obtain

$\begin{align*} {g_{20}} & = 2\tau _1^0\bar G\left( \frac{1}{2} v_3^2 \bar{v_1^*} f_{21_{{\rm{uu}}}} e^{-2 i w_0 \tau_1^0}+\frac{1}{2} v_3^2 \bar{v_2^*} f_{3_{{\rm{uu}}}}-\frac{1}{2} v_3^2 \bar{v_1^*} f_{22_{{\rm{uu}}}}+v_3 \bar{v_1^*} f_{21_{{\rm{ux}}}} e^{-2 i w_0 \tau_1^0}+v_3 \bar{v_2^*} f_{3_{{\rm{ux}}}}\right. \\ &-v_3 \bar{v_1^*} f_{22_{{\rm{ux}}}}+v_3 v_1 \bar{v_1^*} f_{21_{{\rm{uy}}}} e^{-2 i w_0 \tau_1^0}+v_3 v_1 \bar{v_2^*} f_{3_{{\rm{uy}}}}-v_3 v_1 \bar{v_1^*} f_{22_{{\rm{uy}}}}+v_2 v_3 \bar{v_1^*} f_{21_{{\rm{uz}}}} e^{-2 i w_0 \tau_1^0}\\ &+v_2 v_3 \bar{v_2^*} f_{3_{{\rm{uz}}}}-v_2 v_3 \bar{v_1^*} f_{22_{{\rm{uz}}}}+\frac{1}{2} \bar{v_1^*} f_{21_{{\rm{xx}}}} e^{-2 i w_0 \tau_1^0}+v_1 \bar{v_1^*} f_{21_{{\rm{xy}}}} e^{-2 i w_0 \tau_1^0}+v_2 \bar{v_1^*} f_{21_{{\rm{xz}}}} e^{-2 i w_0 \tau_1^0}\\ &+\frac{1}{2} v_1^2 \bar{v_1^*} f_{21_{{\rm{yy}}}} e^{-2 i w_0 \tau_1^0}+v_2 v_1 \bar{v_1^*} f_{21_{{\rm{yz}}}} e^{-2 i w_0 \tau_1^0}+\frac{1}{2} v_2^2 \bar{v_1^*} f_{21_{{\rm{zz}}}} e^{-2 i w_0 \tau_1^0}+\frac{1}{2} \bar{v_2^*} f_{3_{{\rm{xx}}}}-\frac{1}{2} \bar{v_1^*} f_{22_{{\rm{xx}}}}\\ &+v_1 \bar{v_2^*} f_{3_{{\rm{xy}}}}-v_1 \bar{v_1^*} f_{22_{{\rm{xy}}}}+v_2 \bar{v_2^*} f_{3_{{\rm{xz}}}}-v_2 \bar{v_1^*} f_{22_{{\rm{xz}}}}+\frac{1}{2} v_1^2 \bar{v_2^*} f_{3_{{\rm{yy}}}}-\frac{1}{2} v_1^2 \bar{v_1^*} f_{22_{{\rm{yy}}}}+v_2 v_1 \bar{v_2^*} f_{3_{{\rm{yz}}}}\\ &-v_2 v_1 \bar{v_1^*} f_{22_{{\rm{yz}}}}+\frac{1}{2} v_2^2 \bar{v_2^*} f_{3_{{\rm{zz}}}}-\frac{1}{2} v_2^2 \bar{v_1^*} f_{22_{{\rm{zz}}}}+\frac{1}{2} v_3^2 f_{1_{{\rm{uu}}}}+v_3 f_{1_{{\rm{ux}}}}+v_3 v_1 f_{1_{{\rm{uy}}}}+v_2 v_3 f_{1_{{\rm{uz}}}}+v_1 f_{1_{{\rm{xy}}}}\\ &\left. +v_2 f_{1_{{\rm{xz}}}}+\frac{1}{2} v_1^2 f_{1_{{\rm{yy}}}}+v_2 v_1 f_{1_{{\rm{yz}}}}+\frac{1}{2} v_2^2 f_{1_{{\rm{zz}}}}+\frac{f_{1_{{\rm{xx}}}}}{2}\right), \end{align*}$

$\begin{align*} {g_{11}} & = \tau _1^0\bar G\left(\bar{v_3} f_{1_{{\rm{ux}}}}+v_3 f_{1_{{\rm{ux}}}}+f_{1_{{\rm{xx}}}}+\bar{v_1} f_{1_{{\rm{xy}}}}+\bar{v_2} f_{1_{{\rm{xz}}}}+\bar{v_3} \bar{v_2^*} f_{3_{{\rm{ux}}}}+\bar{v_2^*} f_{3_{{\rm{xx}}}}+\bar{v_1} \bar{v_2^*} f_{3_{{\rm{xy}}}}+\bar{v_2} \bar{v_2^*} f_{3_{{\rm{xz}}}}\right.\\ &+\bar{v_3} \bar{v_1^*} f_{21_{{\rm{ux}}}}+\bar{v_1^*} f_{21_{{\rm{xx}}}}+\bar{v_1} \bar{v_1^*} f_{21_{{\rm{xy}}}}+\bar{v_2} \bar{v_1^*} f_{21_{{\rm{xz}}}}-\bar{v_3} \bar{v_1^*} f_{22_{{\rm{ux}}}}-\bar{v_1^*} f_{22_{{\rm{xx}}}}-\bar{v_1} \bar{v_1^*} f_{22_{{\rm{xy}}}}-\bar{v_2} \bar{v_1^*} f_{22_{{\rm{xz}}}}\\ &+\bar{v_3} f_{1_{{\rm{uy}}}} v_1+f_{1_{{\rm{xy}}}} v_1+\bar{v_1} f_{1_{{\rm{yy}}}} v_1+\bar{v_2} f_{1_{{\rm{yz}}}} v_1+\bar{v_3} \bar{v_2^*} f_{3_{{\rm{uy}}}} v_1+\bar{v_2^*} f_{3_{{\rm{xy}}}} v_1+\bar{v_1} \bar{v_2^*} f_{3_{{\rm{yy}}}} v_1+\bar{v_2} \bar{v_2^*} f_{3_{{\rm{yz}}}} v_1\\ &+\bar{v_3} \bar{v_1^*} f_{21_{{\rm{uy}}}} v_1+\bar{v_1^*} f_{21_{{\rm{xy}}}} v_1+\bar{v_1} \bar{v_1^*} f_{21_{{\rm{yy}}}} v_1+\bar{v_2} \bar{v_1^*} f_{21_{{\rm{yz}}}} v_1-\bar{v_3} \bar{v_1^*} f_{22_{{\rm{uy}}}} v_1-\bar{v_1^*} f_{22_{{\rm{xy}}}} v_1-\bar{v_1} \bar{v_1^*} f_{22_{{\rm{yy}}}} v_1\\ &-\bar{v_2} \bar{v_1^*} f_{22_{{\rm{yz}}}} v_1+\bar{v_3} f_{1_{{\rm{uz}}}} v_2+f_{1_{{\rm{xz}}}} v_2+\bar{v_1} f_{1_{{\rm{yz}}}} v_2+\bar{v_2} f_{1_{{\rm{zz}}}} v_2+\bar{v_3} \bar{v_2^*} f_{3_{{\rm{uz}}}} v_2+\bar{v_2^*} f_{3_{{\rm{xz}}}} v_2+\bar{v_1} \bar{v_2^*} f_{3_{{\rm{yz}}}} v_2\\ &+\bar{v_2} \bar{v_2^*} f_{3_{{\rm{zz}}}} v_2+\bar{v_3} \bar{v_1^*} f_{21_{{\rm{uz}}}} v_2+\bar{v_1^*} f_{21_{{\rm{xz}}}} v_2+\bar{v_1} \bar{v_1^*} f_{21_{{\rm{yz}}}} v_2+\bar{v_2} \bar{v_1^*} f_{21_{{\rm{zz}}}} v_2-\bar{v_3} \bar{v_1^*} f_{22_{{\rm{uz}}}} v_2-\bar{v_1^*} f_{22_{{\rm{xz}}}} v_2\\ &-\bar{v_1} \bar{v_1^*} f_{22_{{\rm{yz}}}} v_2-\bar{v_2} \bar{v_1^*} f_{22_{{\rm{zz}}}} v_2+\bar{v_3} f_{1_{{\rm{uu}}}} v_3+\bar{v_1} f_{1_{{\rm{uy}}}} v_3+\bar{v_2} f_{1_{{\rm{uz}}}} v_3+\bar{v_3} \bar{v_2^*} f_{3_{{\rm{uu}}}} v_3+\bar{v_2^*} f_{3_{{\rm{ux}}}} v_3\\ &+\bar{v_1} \bar{v_2^*} f_{3_{{\rm{uy}}}} v_3+\bar{v_2} \bar{v_2^*} f_{3_{{\rm{uz}}}} v_3+\bar{v_3} \bar{v_1^*} f_{21_{{\rm{uu}}}} v_3+\bar{v_1^*} f_{21_{{\rm{ux}}}} v_3+\bar{v_1} \bar{v_1^*} f_{21_{{\rm{uy}}}} v_3+\bar{v_2} \bar{v_1^*} f_{21_{{\rm{uz}}}} v_3\\ & \left.-\bar{v_3} \bar{v_1^*} f_{22_{{\rm{uu}}}} v_3-\bar{v_1^*} f_{22_{{\rm{ux}}}} v_3-\bar{v_1} \bar{v_1^*} f_{22_{{\rm{uy}}}} v_3-\bar{v_2} \bar{v_1^*} f_{22_{{\rm{uz}}}} v_3\right), \end{align*}$

$\begin{align*} {g_{02}}& = 2\tau _1^0\bar G\left(\frac{1}{2} f_{1_{{\rm{yy}}}} \bar{v_1}{}^2+\frac{1}{2} \bar{v_2^*} f_{3_{{\rm{yy}}}} \bar{v_1}{}^2+\frac{1}{2} e^{2 i w_0 \tau_1^0} \bar{v_1^*} f_{21_{{\rm{yy}}}} \bar{v_1}{}^2-\frac{1}{2} \bar{v_1^*} f_{22_{{\rm{yy}}}} \bar{v_1}{}^2+\bar{v_3} f_{1_{{\rm{uy}}}} \bar{v_1}+f_{1_{{\rm{xy}}}} \bar{v_1}+\bar{v_2} f_{1_{{\rm{yz}}}} \bar{v_1}\right.\\ &+\bar{v_3} \bar{v_2^*} f_{3_{{\rm{uy}}}} \bar{v_1}+\bar{v_2^*} f_{3_{{\rm{xy}}}} \bar{v_1}+\bar{v_2} \bar{v_2^*} f_{3_{{\rm{yz}}}} \bar{v_1}+e^{2 i w_0 \tau_1^0} \bar{v_3} \bar{v_1^*} f_{21_{{\rm{uy}}}} \bar{v_1}+e^{2 i w_0 \tau_1^0} \bar{v_1^*} f_{21_{{\rm{xy}}}} \bar{v_1}\\ &+e^{2 i w_0 \tau_1^0} \bar{v_2} \bar{v_1^*} f_{21_{{\rm{yz}}}} \bar{v_1}-\bar{v_3} \bar{v_1^*} f_{22_{{\rm{uy}}}} \bar{v_1}-\bar{v_1^*} f_{22_{{\rm{xy}}}} \bar{v_1}-\bar{v_2} \bar{v_1^*} f_{22_{{\rm{yz}}}} \bar{v_1}+\frac{1}{2} \bar{v_3}{}^2 f_{1_{{\rm{uu}}}}+\bar{v_3} f_{1_{{\rm{ux}}}}+\bar{v_2} \bar{v_3} f_{1_{{\rm{uz}}}}\\ &+\frac{f_{1_{{\rm{xx}}}}}{2}+\bar{v_2} f_{1_{{\rm{xz}}}}+\frac{1}{2} \bar{v_2}{}^2 f_{1_{{\rm{zz}}}}+\frac{1}{2} \bar{v_3}{}^2 \bar{v_2^*} f_{3_{{\rm{uu}}}}+\bar{v_3} \bar{v_2^*} f_{3_{{\rm{ux}}}}+\bar{v_2} \bar{v_3} \bar{v_2^*} f_{3_{{\rm{uz}}}}+\frac{1}{2} \bar{v_2^*} f_{3_{{\rm{xx}}}}+\bar{v_2} \bar{v_2^*} f_{3_{{\rm{xz}}}}\\ &+\frac{1}{2} \bar{v_2}{}^2 \bar{v_2^*} f_{3_{{\rm{zz}}}}+\frac{1}{2} e^{2 i w_0 \tau_1^0} \bar{v_3}{}^2 \bar{v_1^*} f_{21_{{\rm{uu}}}}+e^{2 i w_0 \tau_1^0} \bar{v_3} \bar{v_1^*} f_{21_{{\rm{ux}}}}+e^{2 i w_0 \tau_1^0} \bar{v_2} \bar{v_3} \bar{v_1^*} f_{21_{{\rm{uz}}}}+\frac{1}{2} e^{2 i w_0 \tau_1^0} \bar{v_1^*} f_{21_{{\rm{xx}}}}\\ &+e^{2 i w_0 \tau_1^0} \bar{v_2} \bar{v_1^*} f_{21_{{\rm{xz}}}}+\frac{1}{2} e^{2 i w_0 \tau_1^0} \bar{v_2}{}^2 \bar{v_1^*} f_{21_{{\rm{zz}}}}-\frac{1}{2} \bar{v_3}{}^2 \bar{v_1^*} f_{22_{{\rm{uu}}}}-\bar{v_3} \bar{v_1^*} f_{22_{{\rm{ux}}}}-\bar{v_2} \bar{v_3} \bar{v_1^*} f_{22_{{\rm{uz}}}}-\frac{1}{2} \bar{v_1^*} f_{22_{{\rm{xx}}}}\\ &\left.-\bar{v_2} \bar{v_1^*} f_{22_{{\rm{xz}}}}-\frac{1}{2} \bar{v_2}{}^2 \bar{v_1^*} f_{22_{{\rm{zz}}}}\right), \end{align*}$

$\begin{align*} {g_{21}}& = 2\tau _1^0\bar G\left(\frac{1}{2} W_{20}^4(0) \bar{v_3} f_{1_{{\rm{uu}}}}+W_{11}^4(0) f_{1_{{\rm{ux}}}}+\frac{W_{20}^4(0) f_{1_{{\rm{ux}}}}}{2}+\frac{1}{2} W_{20}^1(0) \bar{v_3} f_{1_{{\rm{ux}}}}+\frac{1}{2} \bar{v_3} f_{1_{{\rm{uxx}}}}+\frac{1}{2} W_{20}^4(0) \bar{v_1} f_{1_{{\rm{uy}}}}\right.\\ &+\frac{1}{2} W_{20}^2(0) \bar{v_3} f_{1_{{\rm{uy}}}}+\frac{1}{2} W_{20}^4(0) \bar{v_2} f_{1_{{\rm{uz}}}}+\frac{1}{2} W_{20}^3(0) \bar{v_3} f_{1_{{\rm{uz}}}}+W_{11}^1(0) f_{1_{{\rm{xx}}}}+\frac{W_{20}^1(0) f_{1_{{\rm{xx}}}}}{2}+\frac{f_{1_{{\rm{xxx}}}}}{2}\\ &+\frac{1}{2} \bar{v_1} f_{1_{{\rm{xxy}}}}+\frac{1}{2} \bar{v_2} f_{1_{{\rm{xxz}}}}+W_{11}^2(0) f_{1_{{\rm{xy}}}}+\frac{W_{20}^2(0) f_{1_{{\rm{xy}}}}}{2}+\frac{1}{2} W_{20}^1(0) \bar{v_1} f_{1_{{\rm{xy}}}}+W_{11}^3(0) f_{1_{{\rm{xz}}}}\\ &+\frac{W_{20}^3(0) f_{1_{{\rm{xz}}}}}{2}+\frac{1}{2} W_{20}^1(0) \bar{v_2} f_{1_{{\rm{xz}}}}+\frac{1}{2} W_{20}^2(0) \bar{v_1} f_{1_{{\rm{yy}}}}+\frac{1}{2} W_{20}^3(0) \bar{v_1} f_{1_{{\rm{yz}}}}+\frac{1}{2} W_{20}^2(0) \bar{v_2} f_{1_{{\rm{yz}}}}\\ &+\frac{1}{2} W_{20}^3(0) \bar{v_2} f_{1_{{\rm{zz}}}}+\frac{1}{2} W_{20}^4(0) \bar{v_3} \bar{v_2^*} f_{3_{{\rm{uu}}}}+W_{11}^4(0) \bar{v_2^*} f_{3_{{\rm{ux}}}}+\frac{1}{2} W_{20}^4(0) \bar{v_2^*} f_{3_{{\rm{ux}}}}+\frac{1}{2} W_{20}^1(0) \bar{v_3} \bar{v_2^*} f_{3_{{\rm{ux}}}}\\ &+\frac{1}{2} \bar{v_3} \bar{v_2^*} f_{3_{{\rm{uxx}}}}+\frac{1}{2} W_{20}^4(0) \bar{v_1} \bar{v_2^*} f_{3_{{\rm{uy}}}}+\frac{1}{2} W_{20}^2(0) \bar{v_3} \bar{v_2^*} f_{3_{{\rm{uy}}}}+\frac{1}{2} W_{20}^4(0) \bar{v_2} \bar{v_2^*} f_{3_{{\rm{uz}}}}+\frac{1}{2} W_{20}^3(0) \bar{v_3} \bar{v_2^*} f_{3_{{\rm{uz}}}}\\ &+W_{11}^1(0) \bar{v_2^*} f_{3_{{\rm{xx}}}}+\frac{1}{2} W_{20}^1(0) \bar{v_2^*} f_{3_{{\rm{xx}}}}+\frac{1}{2} \bar{v_2^*} f_{3_{{\rm{xxx}}}}+\frac{1}{2} \bar{v_1} \bar{v_2^*} f_{3_{{\rm{xxy}}}}+\frac{1}{2} \bar{v_2} \bar{v_2^*} f_{3_{{\rm{xxz}}}}+W_{11}^2(0) \bar{v_2^*} f_{3_{{\rm{xy}}}}\\ &+\frac{1}{2} W_{20}^2(0) \bar{v_2^*} f_{3_{{\rm{xy}}}}+\frac{1}{2} W_{20}^1(0) \bar{v_1} \bar{v_2^*} f_{3_{{\rm{xy}}}}+W_{11}^3(0) \bar{v_2^*} f_{3_{{\rm{xz}}}}+\frac{1}{2} W_{20}^3(0) \bar{v_2^*} f_{3_{{\rm{xz}}}}+\frac{1}{2} W_{20}^1(0) \bar{v_2} \bar{v_2^*} f_{3_{{\rm{xz}}}}\\ &+\frac{1}{2} W_{20}^2(0) \bar{v_1} \bar{v_2^*} f_{3_{{\rm{yy}}}}+\frac{1}{2} W_{20}^3(0) \bar{v_1} \bar{v_2^*} f_{3_{{\rm{yz}}}}+\frac{1}{2} W_{20}^2(0) \bar{v_2} \bar{v_2^*} f_{3_{{\rm{yz}}}}+\frac{1}{2} W_{20}^3(0) \bar{v_2} \bar{v_2^*} f_{3_{{\rm{zz}}}}\\ &+\frac{1}{2} e^{i w_0 \tau_1^0} W_{20}^4(-1) \bar{v_3} \bar{v_1^*} f_{21_{{\rm{uu}}}}+e^{-i w_0 \tau_1^0} W_{11}^4(-1) f_{21_{{\rm{ux}}}}+\frac{1}{2} e^{i w_0 \tau_1^0} W_{20}^4(-1) \bar{v_1^*} f_{21_{{\rm{ux}}}}\\ &+\frac{1}{2} e^{i w_0 \tau_1^0} W_{20}^1(-1) \bar{v_3} \bar{v_1^*} f_{21_{{\rm{ux}}}}+\frac{1}{2} e^{-i w_0 \tau_1^0} \bar{v_3} \bar{v_1^*} f_{21_{{\rm{uxx}}}}+\frac{1}{2} e^{i w_0 \tau_1^0} W_{20}^4(-1) \bar{v_1} \bar{v_1^*} f_{21_{{\rm{uy}}}}\\ &+\frac{1}{2} e^{i w_0 \tau_1^0} W_{20}^2(-1) \bar{v_3} \bar{v_1^*} f_{21_{{\rm{uy}}}}+\frac{1}{2} e^{i w_0 \tau_1^0} W_{20}^4(-1) \bar{v_2} \bar{v_1^*} f_{21_{{\rm{uz}}}}+\frac{1}{2} e^{i w_0 \tau_1^0} W_{20}^3(-1) \bar{v_3} \bar{v_1^*} f_{21_{{\rm{uz}}}}\\ &+e^{-i w_0 \tau_1^0} W_{11}^1(-1) \bar{v_1^*} f_{21_{{\rm{xx}}}}+\frac{1}{2} e^{i w_0 \tau_1^0} \bar{v_1^*} f_{21_{{\rm{xx}}}}+\frac{1}{2} e^{-i w_0 \tau_1^0} \bar{v_1^*} f_{21_{{\rm{xxx}}}}+\frac{1}{2} e^{-i w_0 \tau_1^0} \bar{v_1} \bar{v_1^*} f_{21_{{\rm{xxy}}}}\\ &+\frac{1}{2} e^{-i w_0 \tau_1^0} \bar{v_2} \bar{v_1^*} f_{21_{{\rm{xxz}}}}+e^{-i w_0 \tau_1^0} W_{11}^2(-1) \bar{v_1^*} f_{21_{{\rm{xy}}}}+\frac{1}{2} e^{i w_0 \tau_1^0} W_{20}^2(-1) \bar{v_1^*} f_{21_{{\rm{xy}}}}\\ &+\frac{1}{2} e^{i w_0 \tau_1^0} W_{20}^1(-1) \bar{v_1} \bar{v_1^*} f_{21_{{\rm{xy}}}}+e^{-i w_0 \tau_1^0} W_{11}^3(-1) \bar{v_1^*} f_{21_{{\rm{xz}}}}+\frac{1}{2} e^{i w_0 \tau_1^0} W_{20}^3(-1) \bar{v_1^*} f_{21_{{\rm{xz}}}}\\ &+\frac{1}{2} e^{i w_0 \tau_1^0} W_{20}^1(-1) \bar{v_2} f_{21_{{\rm{xz}}}}+\frac{1}{2} e^{i w_0 \tau_1^0} W_{20}^2(-1) \bar{v_1} \bar{v_1^*} f_{21_{{\rm{yy}}}}+\frac{1}{2} e^{i w_0 \tau_1^0} W_{20}^3(-1) \bar{v_1} \bar{v_1^*} f_{21_{{\rm{yz}}}}\\ &+\frac{1}{2} e^{i w_0 \tau_1^0} W_{20}^2(-1) \bar{v_2} \bar{v_1^*} f_{21_{{\rm{yz}}}}+\frac{1}{2} e^{i w_0 \tau_1^0} W_{20}^3(-1) \bar{v_2} \bar{v_1^*} f_{21_{{\rm{zz}}}}-\frac{1}{2} W_{20}^4(0) \bar{v_3} \bar{v_1^*} f_{22_{{\rm{uu}}}}-W_{11}^4(0) \bar{v_1^*} f_{22_{{\rm{ux}}}}\\ &-\frac{1}{2} W_{20}^4(0) \bar{v_1^*} f_{22_{{\rm{ux}}}}-\frac{1}{2} W_{20}^1(0) \bar{v_3} \bar{v_1^*} f_{22_{{\rm{ux}}}}-\frac{1}{2} \bar{v_3} \bar{v_1^*} f_{22_{{\rm{uxx}}}}-\frac{1}{2} W_{20}^4(0) \bar{v_1} \bar{v_1^*} f_{22_{{\rm{uy}}}}-\frac{1}{2} W_{20}^2(0) \bar{v_3} \bar{v_1^*} f_{22_{{\rm{uy}}}}\\ &-\frac{1}{2} W_{20}^4(0) \bar{v_2} \bar{v_1^*} f_{22_{{\rm{uz}}}}-\frac{1}{2} W_{20}^3(0) \bar{v_3} \bar{v_1^*} f_{22_{{\rm{uz}}}}-W_{11}^1(0) \bar{v_1^*} f_{22_{{\rm{xx}}}}-\frac{1}{2} W_{20}^1(0) \bar{v_1^*} f_{22_{{\rm{xx}}}}-\frac{1}{2} \bar{v_1^*} f_{22_{{\rm{xxx}}}}\\ &-\frac{1}{2} \bar{v_1} \bar{v_1^*} f_{22_{{\rm{xxy}}}}-\frac{1}{2} \bar{v_2} \bar{v_1^*} f_{22_{{\rm{xxz}}}}-W_{11}^2(0) \bar{v_1^*} f_{22_{{\rm{xy}}}}-\frac{1}{2} W_{20}^2(0) \bar{v_1^*} f_{22_{{\rm{xy}}}}-\frac{1}{2} W_{20}^1(0) \bar{v_1} \bar{v_1^*} f_{22_{{\rm{xy}}}}\\ &-W_{11}^3(0) \bar{v_1^*} f_{22_{{\rm{xz}}}}-\frac{1}{2} W_{20}^3(0) \bar{v_1^*} f_{22_{{\rm{xz}}}}-\frac{1}{2} W_{20}^1(0) \bar{v_2} \bar{v_1^*} f_{22_{{\rm{xz}}}}-\frac{1}{2} W_{20}^2(0) \bar{v_1} \bar{v_1^*} f_{22_{{\rm{yy}}}}-\frac{1}{2} W_{20}^3(0) \bar{v_1} \bar{v_1^*} f_{22_{{\rm{yz}}}}\\ &-\frac{1}{2} W_{20}^2(0) \bar{v_2} \bar{v_1^*} f_{22_{{\rm{yz}}}}-\frac{1}{2} W_{20}^3(0) \bar{v_2} \bar{v_1^*} f_{22_{{\rm{zz}}}}+\frac{1}{2} \bar{v_3} f_{1_{{\rm{uyy}}}} v_1^2+\frac{1}{2} f_{1_{{\rm{xyy}}}} v_1^2+\frac{1}{2} \bar{v_1} f_{1_{{\rm{yyy}}}} v_1^2+\frac{1}{2} \bar{v_2} f_{1_{{\rm{yyz}}}} v_1^2\\ &+\frac{1}{2} \bar{v_3} \bar{v_2^*} f_{3_{{\rm{uyy}}}} v_1^2+\frac{1}{2} \bar{v_2^*} f_{3_{{\rm{xyy}}}} v_1^2+\frac{1}{2} \bar{v_1} \bar{v_2^*} f_{3_{{\rm{yyy}}}} v_1^2+\frac{1}{2} \bar{v_2} \bar{v_2^*} f_{3_{{\rm{yyz}}}} v_1^2+\frac{1}{2} e^{-i w_0 \tau_1^0} \bar{v_3} \bar{v_1^*} f_{21_{{\rm{uyy}}}} v_1^2\\ &+\frac{1}{2} e^{-i w_0 \tau_1^0} \bar{v_1^*} f_{21_{{\rm{xyy}}}} v_1^2+\frac{1}{2} e^{-i w_0 \tau_1^0} \bar{v_1} \bar{v_1^*} f_{21_{{\rm{yyy}}}} v_1^2+\frac{1}{2} e^{-i w_0 \tau_1^0} \bar{v_2} \bar{v_1^*} f_{21_{{\rm{yyz}}}} v_1^2-\frac{1}{2} \bar{v_3} \bar{v_1^*} f_{22_{{\rm{uyy}}}} v_1^2\\ &-\frac{1}{2} \bar{v_1^*} f_{22_{{\rm{xyy}}}} v_1^2-\frac{1}{2} \bar{v_1} \bar{v_1^*} f_{22_{{\rm{yyy}}}} v_1^2-\frac{1}{2} \bar{v_2} \bar{v_1^*} f_{22_{{\rm{yyz}}}} v_1^2+\bar{v_3} f_{1_{{\rm{uxy}}}} v_1+W_{11}^4(0) f_{1_{{\rm{uy}}}} v_1+f_{1_{{\rm{xxy}}}} v_1\\ &+W_{11}^1(0) f_{1_{{\rm{xy}}}} v_1+\bar{v_1} f_{1_{{\rm{xyy}}}} v_1+\bar{v_2} f_{1_{{\rm{xyz}}}} v_1+W_{11}^2(0) f_{1_{{\rm{yy}}}} v_1+W_{11}^3(0) f_{1_{{\rm{yz}}}} v_1+\bar{v_3} \bar{v_2^*} f_{3_{{\rm{uxy}}}} v_1\\ &+W_{11}^4(0) \bar{v_2^*} f_{3_{{\rm{uy}}}} v_1+\bar{v_2^*} f_{3_{{\rm{xxy}}}} v_1+W_{11}^1(0) \bar{v_2^*} f_{3_{{\rm{xy}}}} v_1+\bar{v_1} \bar{v_2^*} f_{3_{{\rm{xyy}}}} v_1+\bar{v_2} \bar{v_2^*} f_{3_{{\rm{xyz}}}} v_1+W_{11}^2(0) \bar{v_2^*} f_{3_{{\rm{yy}}}} v_1\\ &+W_{11}^3(0) \bar{v_2^*} f_{3_{{\rm{yz}}}} v_1+e^{-i w_0 \tau_1^0} \bar{v_3} \bar{v_1^*} f_{21_{{\rm{uxy}}}} v_1+e^{-i w_0 \tau_1^0} W_{11}^4(-1) \bar{v_1^*} f_{21_{{\rm{uy}}}} v_1+e^{-i w_0 \tau_1^0} \bar{v_1^*} f_{21_{{\rm{xxy}}}} v_1\\ &+e^{-i w_0 \tau_1^0} W_{11}^1(-1) \bar{v_1^*} f_{21_{{\rm{xy}}}} v_1+e^{-i w_0 \tau_1^0} \bar{v_1} \bar{v_1^*} f_{21_{{\rm{xyy}}}} v_1+e^{-i w_0 \tau_1^0} \bar{v_2} \bar{v_1^*} f_{21_{{\rm{xyz}}}} v_1\\ &+e^{-i w_0 \tau_1^0} W_{11}^2(-1) \bar{v_1^*} f_{21_{{\rm{yy}}}} v_1+e^{-i w_0 \tau_1^0} W_{11}^3(-1) \bar{v_1^*} f_{21_{{\rm{yz}}}} v_1-\bar{v_3} \bar{v_1^*} f_{22_{{\rm{uxy}}}} v_1-W_{11}^4(0) \bar{v_1^*} f_{22_{{\rm{uy}}}} v_1\\ &-\bar{v_1^*} f_{22_{{\rm{xxy}}}} v_1-W_{11}^1(0) \bar{v_1^*} f_{22_{{\rm{xy}}}} v_1-\bar{v_1} \bar{v_1^*} f_{22_{{\rm{xyy}}}} v_1-\bar{v_2} \bar{v_1^*} f_{22_{{\rm{xyz}}}} v_1-W_{11}^2(0) \bar{v_1^*} f_{22_{{\rm{yy}}}} v_1\\ &-W_{11}^3(0) \bar{v_1^*} f_{22_{{\rm{yz}}}} v_1+\bar{v_3} f_{1_{{\rm{uyz}}}} v_2 v_1+f_{1_{{\rm{xyz}}}} v_2 v_1+\bar{v_1} f_{1_{{\rm{yyz}}}} v_2 v_1+\bar{v_2} f_{1_{{\rm{yzz}}}} v_2 v_1+\bar{v_3} \bar{v_2^*} f_{3_{{\rm{uyz}}}} v_2 v_1\\ &+\bar{v_2^*} f_{3_{{\rm{xyz}}}} v_2 v_1+\bar{v_1} \bar{v_2^*} f_{3_{{\rm{yyz}}}} v_2 v_1+\bar{v_2} \bar{v_2^*} f_{3_{{\rm{yzz}}}} v_2 v_1+e^{-i w_0 \tau_1^0} \bar{v_3} \bar{v_1^*} f_{21_{{\rm{uyz}}}} v_2 v_1+e^{-i w_0 \tau_1^0} \bar{v_1^*} f_{21_{{\rm{xyz}}}} v_2 v_1\\ &+e^{-i w_0 \tau_1^0} \bar{v_1} \bar{v_1^*} f_{21_{{\rm{yyz}}}} v_2 v_1+e^{-i w_0 \tau_1^0} \bar{v_2} \bar{v_1^*} f_{21_{{\rm{yzz}}}} v_2 v_1-\bar{v_3} \bar{v_1^*} f_{22_{{\rm{uyz}}}} v_2 v_1-\bar{v_1^*} f_{22_{{\rm{xyz}}}} v_2 v_1-\bar{v_1} \bar{v_1^*} f_{22_{{\rm{yyz}}}} v_2 v_1\\ &-\bar{v_2} \bar{v_1^*} f_{22_{{\rm{yzz}}}} v_2 v_1+\bar{v_3} f_{1_{{\rm{uuy}}}} v_3 v_1+f_{1_{{\rm{uxy}}}} v_3 v_1+\bar{v_1} f_{1_{{\rm{uyy}}}} v_3 v_1+\bar{v_2} f_{1_{{\rm{uyz}}}} v_3 v_1+\bar{v_3} \bar{v_2^*} f_{3_{{\rm{uuy}}}} v_3 v_1\\ &+\bar{v_2^*} f_{3_{{\rm{uxy}}}} v_3 v_1+\bar{v_1} \bar{v_2^*} f_{3_{{\rm{uyy}}}} v_3 v_1+\bar{v_2} \bar{v_2^*} f_{3_{{\rm{uyz}}}} v_3 v_1+e^{-i w_0 \tau_1^0} \bar{v_3} \bar{v_1^*} f_{21_{{\rm{uuy}}}} v_3 v_1+e^{-i w_0 \tau_1^0} \bar{v_1^*} f_{21_{{\rm{uxy}}}} v_3 v_1\\ &+e^{-i w_0 \tau_1^0} \bar{v_1} \bar{v_1^*} f_{21_{{\rm{uyy}}}} v_3 v_1+e^{-i w_0 \tau_1^0} \bar{v_2} \bar{v_1^*} f_{21_{{\rm{uyz}}}} v_3 v_1-\bar{v_3} \bar{v_1^*} f_{22_{{\rm{uuy}}}} v_3 v_1-\bar{v_1^*} f_{22_{{\rm{uxy}}}} v_3 v_1-\bar{v_1} \bar{v_1^*} f_{22_{{\rm{uyy}}}} v_3 v_1\\ &-\bar{v_2} \bar{v_1^*} f_{22_{{\rm{uyz}}}} v_3 v_1+\frac{1}{2} \bar{v_3} f_{1_{{\rm{uzz}}}} v_2^2+\frac{1}{2} f_{1_{{\rm{xzz}}}} v_2^2+\frac{1}{2} \bar{v_1} f_{1_{{\rm{yzz}}}} v_2^2+\frac{1}{2} \bar{v_2} f_{1_{{\rm{zzz}}}} v_2^2+\frac{1}{2} \bar{v_3} \bar{v_2^*} f_{3_{{\rm{uzz}}}} v_2^2+\frac{1}{2} \bar{v_2^*} f_{3_{{\rm{xzz}}}} v_2^2\\ &+\frac{1}{2} \bar{v_1} \bar{v_2^*} f_{3_{{\rm{yzz}}}} v_2^2+\frac{1}{2} \bar{v_2} \bar{v_2^*} f_{3_{{\rm{zzz}}}} v_2^2+\frac{1}{2} e^{-i w_0 \tau_1^0} \bar{v_3} \bar{v_1^*} f_{21_{{\rm{uzz}}}} v_2^2+\frac{1}{2} e^{-i w_0 \tau_1^0} \bar{v_1^*} f_{21_{{\rm{xzz}}}} v_2^2\\ &+\frac{1}{2} e^{-i w_0 \tau_1^0} \bar{v_1} \bar{v_1^*} f_{21_{{\rm{yzz}}}} v_2^2+\frac{1}{2} e^{-i w_0 \tau_1^0} \bar{v_2} \bar{v_1^*} f_{21_{{\rm{zzz}}}} v_2^2-\frac{1}{2} \bar{v_3} \bar{v_1^*} f_{22_{{\rm{uzz}}}} v_2^2-\frac{1}{2} \bar{v_1^*} f_{22_{{\rm{xzz}}}} v_2^2-\frac{1}{2} \bar{v_1} \bar{v_1^*} f_{22_{{\rm{yzz}}}} v_2^2\\ &-\frac{1}{2} \bar{v_2} \bar{v_1^*} f_{22_{{\rm{zzz}}}} v_2^2+\frac{1}{2} \bar{v_3} f_{1_{{\rm{uuu}}}} v_3^2+\frac{1}{2} f_{1_{{\rm{uux}}}} v_3^2+\frac{1}{2} \bar{v_1} f_{1_{{\rm{uuy}}}} v_3^2+\frac{1}{2} \bar{v_2} f_{1_{{\rm{uuz}}}} v_3^2+\frac{1}{2} \bar{v_3} \bar{v_2^*} f_{3_{{\rm{uuu}}}} v_3^2+\frac{1}{2} \bar{v_2^*} f_{3_{{\rm{uux}}}} v_3^2\\ &+\frac{1}{2} \bar{v_1} \bar{v_2^*} f_{3_{{\rm{uuy}}}} v_3^2+\frac{1}{2} \bar{v_2} \bar{v_2^*} f_{3_{{\rm{uuz}}}} v_3^2+\frac{1}{2} e^{-i w_0 \tau_1^0} \bar{v_3} \bar{v_1^*} f_{21_{{\rm{uuu}}}} v_3^2+\frac{1}{2} e^{-i w_0 \tau_1^0} \bar{v_1^*} f_{21_{{\rm{uux}}}} v_3^2\\ &+\frac{1}{2} e^{-i w_0 \tau_1^0} \bar{v_1} \bar{v_1^*} f_{21_{{\rm{uuy}}}} v_3^2+\frac{1}{2} e^{-i w_0 \tau_1^0} \bar{v_2} \bar{v_1^*} f_{21_{{\rm{uuz}}}} v_3^2-\frac{1}{2} \bar{v_3} \bar{v_1^*} f_{22_{{\rm{uuu}}}} v_3^2-\frac{1}{2} \bar{v_1^*} f_{22_{{\rm{uux}}}} v_3^2-\frac{1}{2} \bar{v_1} \bar{v_1^*} f_{22_{{\rm{uuy}}}} v_3^2\\ &-\frac{1}{2} \bar{v_2} \bar{v_1^*} f_{22_{{\rm{uuz}}}} v_3^2+W_{11}^4(0) f_{1_{{\rm{uz}}}} v_2+f_{1_{{\rm{xxz}}}} v_2+\bar{v_1} f_{1_{{\rm{xyz}}}} v_2+W_{11}^1(0) f_{1_{{\rm{xz}}}} v_2+\bar{v_2} f_{1_{{\rm{xzz}}}} v_2+W_{11}^2(0) f_{1_{{\rm{yz}}}} v_2\\ &+W_{11}^3(0) f_{1_{{\rm{zz}}}} v_2+W_{11}^4(0) \bar{v_2^*} f_{3_{{\rm{uz}}}} v_2+\bar{v_2^*} f_{3_{{\rm{xxz}}}} v_2+\bar{v_1} \bar{v_2^*} f_{3_{{\rm{xyz}}}} v_2+W_{11}^1(0) \bar{v_2^*} f_{3_{{\rm{xz}}}} v_2+\bar{v_2} \bar{v_2^*} f_{3_{{\rm{xzz}}}} v_2\\ &+W_{11}^2(0) \bar{v_2^*} f_{3_{{\rm{yz}}}} v_2+W_{11}^3(0) \bar{v_2^*} f_{3_{{\rm{zz}}}} v_2+e^{-i w_0 \tau_1^0} \bar{v_3} \bar{v_1^*} f_{21_{{\rm{uxz}}}} v_2+e^{-i w_0 \tau_1^0} W_{11}^4(-1) \bar{v_1^*} f_{21_{{\rm{uz}}}} v_2\\ &+e^{-i w_0 \tau_1^0} \bar{v_1^*} f_{21_{{\rm{xxz}}}} v_2+e^{-i w_0 \tau_1^0} \bar{v_1} \bar{v_1^*} f_{21_{{\rm{xyz}}}} v_2+e^{-i w_0 \tau_1^0} W_{11}^1(-1) \bar{v_1^*} f_{21_{{\rm{xz}}}} v_2+e^{-i w_0 \tau_1^0} \bar{v_2} \bar{v_1^*} f_{21_{{\rm{xzz}}}} v_2\\ &+e^{-i w_0 \tau_1^0} W_{11}^2(-1) \bar{v_1^*} f_{21_{{\rm{yz}}}} v_2+e^{-i w_0 \tau_1^0} W_{11}^3(-1) \bar{v_1^*} f_{21_{{\rm{zz}}}} v_2-W_{11}^4(0) \bar{v_1^*} f_{22_{{\rm{uz}}}} v_2-\bar{v_1^*} f_{22_{{\rm{xxz}}}} v_2\\ &-\bar{v_1} \bar{v_1^*} f_{22_{{\rm{xyz}}}} v_2-W_{11}^1(0) \bar{v_1^*} f_{22_{{\rm{xz}}}} v_2-\bar{v_2} \bar{v_1^*} f_{22_{{\rm{xzz}}}} v_2-W_{11}^2(0) \bar{v_1^*} f_{22_{{\rm{yz}}}} v_2-W_{11}^3(0) \bar{v_1^*} f_{22_{{\rm{zz}}}} v_2\\ &+W_{11}^4(0) f_{1_{{\rm{uu}}}} v_3+\bar{v_3} f_{1_{{\rm{uux}}}} v_3+W_{11}^1(0) f_{1_{{\rm{ux}}}} v_3+f_{1_{{\rm{uxx}}}} v_3+\bar{v_1} f_{1_{{\rm{uxy}}}} v_3+W_{11}^2(0) f_{1_{{\rm{uy}}}} v_3+W_{11}^3(0) f_{1_{{\rm{uz}}}} v_3\\ &+W_{11}^4(0) \bar{v_2^*} f_{3_{{\rm{uu}}}} v_3+\bar{v_3} \bar{v_2^*} f_{3_{{\rm{uux}}}} v_3+W_{11}^1(0) \bar{v_2^*} f_{3_{{\rm{ux}}}} v_3+\bar{v_2^*} f_{3_{{\rm{uxx}}}} v_3+\bar{v_1} \bar{v_2^*} f_{3_{{\rm{uxy}}}} v_3+W_{11}^2(0) \bar{v_2^*} f_{3_{{\rm{uy}}}} v_3\\ &+W_{11}^3(0) \bar{v_2^*} f_{3_{{\rm{uz}}}} v_3+e^{-i w_0 \tau_1^0} W_{11}^4(-1) \bar{v_1^*} f_{21_{{\rm{uu}}}} v_3+e^{-i w_0 \tau_1^0} \bar{v_3} \bar{v_1^*} f_{21_{{\rm{uux}}}} v_3+e^{-i w_0 \tau_1^0} W_{11}^1(-1) \bar{v_1^*} f_{21_{{\rm{ux}}}} v_3\\ &+e^{-i w_0 \tau_1^0} \bar{v_1^*} f_{21_{{\rm{uxx}}}} v_3+e^{-i w_0 \tau_1^0} \bar{v_1} \bar{v_1^*} f_{21_{{\rm{uxy}}}} v_3+e^{-i w_0 \tau_1^0} \bar{v_2} \bar{v_1^*} f_{21_{{\rm{uxz}}}} v_3+e^{-i w_0 \tau_1^0} W_{11}^2(-1) \bar{v_1^*} f_{21_{{\rm{uy}}}} v_3\\ &+e^{-i w_0 \tau_1^0} W_{11}^3(-1) \bar{v_1^*} f_{21_{{\rm{uz}}}} v_3-W_{11}^4(0) \bar{v_1^*} f_{22_{{\rm{uu}}}} v_3-\bar{v_3} \bar{v_1^*} f_{22_{{\rm{uux}}}} v_3-W_{11}^1(0) \bar{v_1^*} f_{22_{{\rm{ux}}}} v_3-\bar{v_1^*} f_{22_{{\rm{uxx}}}} v_3\\ &-\bar{v_1} \bar{v_1^*} f_{22_{{\rm{uxy}}}} v_3-W_{11}^2(0) \bar{v_1^*} f_{22_{{\rm{uy}}}} v_3-W_{11}^3(0) \bar{v_1^*} f_{22_{{\rm{uz}}}} v_3+\bar{v_3} f_{1_{{\rm{uuz}}}} v_2 v_3+\bar{v_1} f_{1_{{\rm{uyz}}}} v_2 v_3+\bar{v_2} f_{1_{{\rm{uzz}}}} v_2 v_3\\ &+\bar{v_3} \bar{v_2^*} f_{3_{{\rm{uuz}}}} v_2 v_3+\bar{v_1} \bar{v_2^*} f_{3_{{\rm{uyz}}}} v_2 v_3+\bar{v_2} \bar{v_2^*} f_{3_{{\rm{uzz}}}} v_2 v_3+e^{-i w_0 \tau_1^0} \bar{v_3} \bar{v_1^*} f_{21_{{\rm{uuz}}}} v_2 v_3+e^{-i w_0 \tau_1^0} \bar{v_1^*} f_{21_{{\rm{uxz}}}} v_2 v_3\\ &\left.+e^{-i w_0 \tau_1^0} \bar{v_1} \bar{v_1^*} f_{21_{{\rm{uyz}}}} v_2 v_3+e^{-i w_0 \tau_1^0} \bar{v_2} \bar{v_1^*} f_{21_{{\rm{uzz}}}} v_2 v_3-\bar{v_3} \bar{v_1^*} f_{22_{{\rm{uuz}}}} v_2 v_3-\bar{v_1} \bar{v_1^*} f_{22_{{\rm{uyz}}}} v_2 v_3-\bar{v_2} \bar{v_1^*} f_{22_{{\rm{uzz}}}} v_2 v_3\right). \end{align*}$

Since ${W_{20}}\left(\theta \right)$ and ${W_{11}}\left(\theta \right)$ are unknown in ${g_{21}}$ , we will continue to solve for ${W_{20}}\left(\theta \right)$ and ${W_{11}}\left(\theta \right)$ . From (4.17) and (4.21) we have

$\begin{equation} \begin{split} \dot W & = {{\dot U}_t} - \dot z\left( t \right)q\left( \theta \right) - \dot{\bar{z}}\bar q\left( \theta \right)\\ & = {\Lambda _0}{U_t} + {R_0}{U_t} - \left[ {{{\rm{i}}}{w_0}\tau _1^0z\left( t \right) + {{\bar q}^*}\left( 0 \right){f_0}\left( {z,\bar z} \right)} \right]q\left( \theta \right)\\ &- \left[ { - {{\rm{i}}}{w_0}\tau _1^0z\left( t \right) + {q^*}\left( 0 \right){{\bar f}_0}\left( {z,\bar z} \right)} \right]\bar q\left( \theta \right)\\ & = \left\{ \begin{array}{l} {\Lambda _0}W - 2\Re \left( {{{\bar q}^*}\left( 0 \right)q(\theta){f_0}\left( {z,\bar z} \right)} \right){{\rm{, }}}\theta \in \left[ { - 1,0} \right)\\ {\Lambda _0}W - 2\Re \left( {{{\bar q}^*}\left( 0 \right)q(\theta){f_0}\left( {z,\bar z}q(\theta \right)} \right){{\rm{ + }}}{f_0}{{\rm{, }}}\theta = 0 \end{array} \right.\\ & = {\Lambda _0}W + H\left( {z,\bar z,\theta } \right), \end{split} \end{equation}$

(4.28)

where

$\begin{equation} \begin{split} H\left( {z,\bar z,\theta } \right) = {H_{{{\rm{20}}}}}\left( \theta \right)\frac{{{z^2}}}{2}{{\rm{ + }}}{H_{{{\rm{11}}}}}\left( \theta \right)z\bar z{{\rm{ + }}}{H_{{{\rm{02}}}}}\left( \theta \right)\frac{{{{\bar z}^2}}}{2}{{\rm{ + }}} \cdots. \end{split} \end{equation}$

(4.29)

Differentiating formula (4.21) for $t$ we can have

$\begin{equation} \begin{split} \dot W & = {W_z}\dot z + {W_{\bar z}}\dot{\bar z}\\ & = \left( {{W_{20}}\left( \theta \right)z + {W_{11}}\left( \theta \right)\bar z \cdots } \right)\left( {{{\rm{i}}}{w_0}\tau _1^0z + g\left( {z,\bar z} \right)} \right)\\ & + \left( {{W_{11}}\left( \theta \right)z + {W_{02}}\left( \theta \right)\bar z \cdots } \right)\left( { - {{\rm{i}}}{w_0}\tau _1^0\bar z + \bar g\left( {z,\bar z} \right)} \right). \end{split} \end{equation}$

(4.30)

Bring (4.22) and (4.20) into (4.30), we obtain

$\begin{equation} \begin{split} \dot W & = {\Lambda _0}\left( {{W_{20}}\left( \theta \right)\frac{{{z^2}}}{2} + {W_{11}}\left( \theta \right)z\bar z + {W_{02}}\left( \theta \right)\frac{{{{\bar z}^2}}}{2} + \cdots } \right)\\ & + {H_{{{\rm{20}}}}}\left( \theta \right)\frac{{{z^2}}}{2}{{\rm{ + }}}{H_{{{\rm{11}}}}}\left( \theta \right)z\bar z{{\rm{ + }}}{H_{{{\rm{02}}}}}\left( \theta \right)\frac{{{{\bar z}^2}}}{2}{{\rm{ + }}} \cdots \\ & = \left( {{\Lambda _0}{W_{20}}\left( \theta \right) + {H_{{{\rm{20}}}}}\left( \theta \right)} \right)\frac{{{z^2}}}{2} + \left( {{\Lambda _0}{W_{11}}\left( \theta \right) + {H_{{{\rm{11}}}}}\left( \theta \right)} \right)z\bar z\\ & + \left( {{\Lambda _0}{W_{02}}\left( \theta \right) + {H_{02}}\left( \theta \right)} \right)\frac{{{{\bar z}^2}}}{2} + \cdots. \\ \end{split} \end{equation}$

(4.31)

Compare the coefficients of ${z^2}$ and $z\bar z$ in (4.30) and (4.31) to obtain the following equation

$\begin{equation} \begin{split} \left( {{\Lambda _0} - 2{{\rm{i}}}{w_0}\tau _1^0I} \right){W_{20}}\left( \theta \right) = - {H_{20}}\left( \theta \right), \end{split} \end{equation}$

(4.32)

and

$\begin{equation} \begin{split} {\Lambda _0}{W_{11}}\left( \theta \right) = - {H_{{{\rm{11}}}}}\left( \theta \right), \end{split} \end{equation}$

(4.33)

where $I$ is a identity matrix.

$\begin{equation} \begin{split} H\left( {z,\bar z,\theta } \right) & = - {{\bar q}^*}\left( 0 \right){f_0}q\left( \theta \right) - {q^*}\left( 0 \right){{\bar f}_0}\bar q\left( \theta \right)\\ & = - g\left( {z,\bar z} \right)q\left( \theta \right) - \bar g\left( {z,\bar z} \right)\bar q\left( \theta \right)\\ & = - \left( {{{{g}}_{{{\rm{20}}}}}\frac{{{z^2}}}{2}{{\rm{ + }}}{{{g}}_{{{\rm{11}}}}}z\bar z{{\rm{ + }}}{{{g}}_{{{\rm{02}}}}}\frac{{{{\bar z}^2}}}{2}{{\rm{ + }}} \cdots } \right)q\left( \theta \right)\\ & - \left( {{{{{\bar g}}}_{{{\rm{20}}}}}\frac{{{{\bar z}^2}}}{2}{{\rm{ + }}}{{{{\bar g}}}_{{{\rm{11}}}}}z\bar z{{\rm{ + }}}{{{{\bar g}}}_{{{\rm{02}}}}}\frac{{{z^2}}}{2}{{\rm{ + }}} \cdots } \right)\bar q\left( \theta \right), \end{split} \end{equation}$

(4.34)

for $\theta \in \left[ { - 1, 0} \right)$ .

Comparing the corresponding coefficients of (4.29)and (4.34), we can get the following equation

$\begin{equation} \begin{split} {H_{20}}\left( \theta \right) = - {g_{20}}q\left( \theta \right) - {{\bar g}_{02}}\bar q\left( \theta \right),\\ \end{split} \end{equation}$

(4.35)

$\begin{equation} \begin{split} {H_{11}}\left( \theta \right) = - {g_{11}}q\left( \theta \right) - {{\bar g}_{11}}\bar q\left( \theta \right).\\ \end{split} \end{equation}$

(4.36)

From (4.33) we can obtain

$\begin{equation} \begin{split} {\Lambda _0}{W_{20}}\left( \theta \right) = 2{{\rm{i}}}{w_0}\tau _1^0{W_{20}}\left( \theta \right) - {H_{20}}\left( \theta \right).\\ \end{split} \end{equation}$

(4.37)

According the definition of ${\Lambda _0}$ , $q\left(\theta \right) = q(0)e^{iw_0\tau_1^0\theta}$ and combining (4.35), (4.37) then

$\begin{equation} \begin{split} {{\dot W}_{20}}\left( \theta \right) = 2{{\rm{i}}}{w_0}\tau _1^0{W_{20}}\left( \theta \right) + {g_{20}}q\left( 0 \right){e^{{{\rm{i}}}{w_0}\tau _1^0\theta }} + {{\bar g}_{02}}\bar q\left( 0 \right){e^{ - {{\rm{i}}}{w_0}\tau _1^0\theta }}, \end{split} \end{equation}$

(4.38)

$\begin{equation} \begin{split} {W_{20}}\left( \theta \right) = \frac{{{{\rm{i}}}{g_{20}}}}{{{w_0}\tau _1^0}}q\left( 0 \right){e^{{{\rm{i}}}{w_0}\tau _1^0\theta }} + \frac{{{{\rm{i}}}{{\bar g}_{02}}}}{{3{w_0}\tau _1^0}}\bar q\left( 0 \right){e^{ - {{\rm{i}}}{w_0}\tau _1^0\theta }} + {N_1}{e^{{{\rm{2i}}}{w_0}\tau _1^0\theta }}, \end{split} \end{equation}$

(4.39)

where ${N_1} = {\left({N_1^{(1)}, N_1^{(2)}, N_1^{(3)}, N_1^{(4)}} \right)^T}$ is a constant vector.

Similarly, we can get

$\begin{equation} \begin{split} &{{\dot W}_{11}}\left( \theta \right) = {g_{11}}q\left( 0 \right){e^{{{\rm{i}}}{w_0}\tau _1^0\theta }} + {{\bar g}_{11}}\bar q\left( 0 \right){e^{ - {{\rm{i}}}{w_0}\tau _1^0\theta }},\\ &{W_{11}}\left( \theta \right) = - \frac{{{{\rm{i}}}{g_{11}}}}{{{w_0}\tau _1^0}}q\left( 0 \right){e^{{{\rm{i}}}{w_0}\tau _1^0\theta }} + \frac{{{{\rm{i}}}{{\bar g}_{11}}}}{{{w_0}\tau _1^0}}\bar q\left( 0 \right){e^{ - {{\rm{i}}}{w_0}\tau _1^0\theta }} + {N_2}, \end{split} \end{equation}$

(4.40)

where, ${N_2} = {\left({N_2^{(1)}, N_2^{(2)}, N_2^{(3)}, N_2^{(4)}} \right)^T}$ is also a constant vector. Next we just need to calculate ${N_1}$ and ${N_2}$ . From (4.33), (4.34) and the define of ${\Lambda _0}$ the following equations can be exported.

$\begin{equation} \begin{split} &{H_{20}}\left( 0 \right) = - {g_{20}}q\left( 0 \right) - {{\bar g}_{02}}\bar q\left( 0 \right)\\ &+ 2\tau _1^0\left( {\begin{array}{*{20}{c}} \begin{array}{l} \frac{1}{2}v_3^2{f_{{1_{{{\rm{uu}}}}}}} + {v_3}{f_{{1_{{{\rm{ux}}}}}}} + {v_3}{v_1}{f_{{1_{{{\rm{uy}}}}}}} + {v_2}{v_3}{f_{{1_{{{\rm{uz}}}}}}} + {v_1}{f_{{1_{{{\rm{xy}}}}}}} + {v_2}{f_{{1_{{{\rm{xz}}}}}}} + \frac{1}{2}v_1^2{f_{{1_{{{\rm{yy}}}}}}}\\ + {v_2}{v_1}{f_{{1_{{{\rm{yz}}}}}}} + \frac{1}{2}v_2^2{f_{{1_{{{\rm{zz}}}}}}} + \frac{{{f_{{1_{{{\rm{xx}}}}}}}}}{2} \end{array}\\ \begin{array}{l} {v_1}{f_{{{21}_{{{\rm{xy}}}}}}}{e^{ - 2i w_0 \tau_1^0}} + {v_2}{f_{{{21}_{{{\rm{xz}}}}}}}{e^{ - 2i w_0 \tau_1^0}} + \frac{1}{2}v_1^2{f_{{{21}_{{{\rm{yy}}}}}}}{e^{ - 2i w_0 \tau_1^0}} - {v_1}{f_{{{22}_{{{\rm{xy}}}}}}} - {v_2}{f_{{{22}_{{{\rm{xz}}}}}}}\\ - \frac{1}{2}v_1^2{f_{{{22}_{{{\rm{yy}}}}}}} + \frac{1}{2}{f_{{{21}_{{{\rm{xx}}}}}}}{e^{ - 2i w_0 \tau_1^0}} - \frac{{{f_{{{22}_{{{\rm{xx}}}}}}}}}{2} + {v_3}{f_{{{21}_{{{\rm{ux}}}}}}}{e^{ - 2i w_0 \tau_1^0}} - {v_3}{f_{{{22}_{{{\rm{ux}}}}}}}\\ + {v_1}{v_3}{f_{{{21}_{{{\rm{uy}}}}}}}{e^{ - 2i w_0 \tau_1^0}} + {v_1}{v_2}{f_{{{21}_{{{\rm{yz}}}}}}}{e^{ - 2i w_0 \tau_1^0}} + \frac{1}{2}v_2^2{f_{{{21}_{{{\rm{zz}}}}}}}{e^{ - 2i w_0 \tau_1^0}} - {v_1}{v_2}{f_{{{22}_{{{\rm{yz}}}}}}}\\ - \frac{1}{2}v_2^2{f_{{{22}_{{{\rm{zz}}}}}}} + \frac{1}{2}v_3^2{f_{{{21}_{{{\rm{uu}}}}}}}{e^{ - 2i w_0 \tau_1^0}} - \frac{1}{2}v_3^2{f_{{{22}_{{{\rm{uu}}}}}}} - {v_1}{v_3}{f_{{{22}_{{{\rm{uy}}}}}}} + {v_2}{v_3}{f_{{{21}_{{{\rm{uz}}}}}}}{e^{ - 2i w_0 \tau_1^0}}\\ - {v_2}{v_3}{f_{{{22}_{{{\rm{uz}}}}}}} \end{array}\\ \begin{array}{l} \frac{1}{2}v_3^2{f_{{3_{{{\rm{uu}}}}}}} + {v_3}{f_{{3_{{{\rm{ux}}}}}}} + {v_3}{v_1}{f_{{3_{{{\rm{uy}}}}}}} + {v_2}{v_3}{f_{{3_{{{\rm{uz}}}}}}} + {v_1}{f_{{3_{{{\rm{xy}}}}}}} + {v_2}{f_{{3_{{{\rm{xz}}}}}}} + \frac{1}{2}v_1^2{f_{{3_{{{\rm{yy}}}}}}}\\ + {v_2}{v_1}{f_{{3_{{{\rm{yz}}}}}}} + \frac{1}{2}v_2^2{f_{{3_{{{\rm{zz}}}}}}} + \frac{{{f_{{3_{{{\rm{xx}}}}}}}}}{2} \end{array}\\ 0 \end{array}} \right). \end{split} \end{equation}$

(4.41)

$\begin{equation} \begin{split} &{H_{11}}\left( 0 \right) = - {g_{11}}q\left( 0 \right) - {{\bar g}_{11}}\bar q\left( 0 \right)\\ & + \tau _1^0\left( {\begin{array}{*{20}{c}} \begin{array}{l} \bar {{v_3}} {f_{{1_{{{\rm{ux}}}}}}} + {v_1}\bar {{v_3}} {f_{{1_{{{\rm{uy}}}}}}} + {v_2}\bar {{v_3}} {f_{{1_{{{\rm{uz}}}}}}} + \bar {{v_1}} {f_{{1_{{{\rm{xy}}}}}}} + \bar {{v_2}} {f_{{1_{{{\rm{xz}}}}}}} + {v_1}\bar {{v_1}} {f_{{1_{{{\rm{yy}}}}}}} + {v_1}\bar {{v_2}} {f_{{1_{{{\rm{yz}}}}}}}\\ + {v_2}\bar {{v_1}} {f_{{1_{{{\rm{yz}}}}}}} + {v_1}{f_{{1_{{{\rm{xy}}}}}}} + {v_2}{f_{{1_{{{\rm{xz}}}}}}} + {f_{{1_{{{\rm{xx}}}}}}} + {v_3}\bar {{v_3}} {f_{{1_{{{\rm{uu}}}}}}} + {v_3}\bar {{v_1}} {f_{{1_{{{\rm{uy}}}}}}} + {v_3}\bar {{v_2}} {f_{{1_{{{\rm{uz}}}}}}}\\ + {v_2} + \bar {{v_2}} {f_{{1_{{{\rm{zz}}}}}}} + {v_3}{f_{{1_{{{\rm{ux}}}}}}} \end{array}\\ \begin{array}{l} \bar {{v_3}} {f_{{{21}_{{{\rm{ux}}}}}}} - \bar {{v_3}} {f_{{{22}_{{{\rm{ux}}}}}}} + {v_1}\bar {{v_3}} {f_{{{21}_{{{\rm{uy}}}}}}} + \bar {{v_1}} {f_{{{21}_{{{\rm{xy}}}}}}} - \bar {{v_1}} {f_{{{22}_{{{\rm{xy}}}}}}} + \bar {{v_2}} {f_{{{21}_{{{\rm{xz}}}}}}} - \bar {{v_2}} {f_{{{22}_{{{\rm{xz}}}}}}}\\ + {v_1}\bar {{v_1}} {f_{{{21}_{{{\rm{yy}}}}}}} + {v_1}{f_{{{21}_{{{\rm{xy}}}}}}} + {f_{{{21}_{{{\rm{xx}}}}}}} - {f_{{{22}_{{{\rm{xx}}}}}}} + - {v_1}\bar {{v_3}} {f_{{{22}_{{{\rm{uy}}}}}}} + {v_2}\bar {{v_3}} {f_{{{21}_{{{\rm{uz}}}}}}} - {v_1}\bar {{v_1}} {f_{{{22}_{{{\rm{yy}}}}}}}\\ + {v_1} + \bar {{v_2}} {f_{{{21}_{{{\rm{yz}}}}}}} - {v_1}\bar {{v_2}} {f_{{{22}_{{{\rm{yz}}}}}}} + {v_2}\bar {{v_1}} {f_{{{21}_{{{\rm{yz}}}}}}} - {v_1}{f_{{{22}_{{{\rm{xy}}}}}}} + {v_2}{f_{{{21}_{{{\rm{xz}}}}}}} + {v_3}\bar {{v_3}} {f_{{{21}_{{{\rm{uu}}}}}}}\\ - {v_3}\bar {{v_3}} {f_{{{22}_{{{\rm{uu}}}}}}} + {v_3}\bar {{v_1}} {f_{{{21}_{{{\rm{uy}}}}}}} - {v_2}\bar {{v_3}} {f_{{{22}_{{{\rm{uz}}}}}}} + {v_3}\bar {{v_2}} {f_{{{21}_{{{\rm{uz}}}}}}} - {v_2}\bar {{v_1}} {f_{{{22}_{{{\rm{yz}}}}}}} + {v_2} + \bar {{v_2}} {f_{{{21}_{{{\rm{zz}}}}}}}\\ - {v_2}\bar {{v_2}} {f_{{{22}_{{{\rm{zz}}}}}}} + {v_3}{f_{{{21}_{{{\rm{ux}}}}}}} - {v_2}{f_{{{22}_{{{\rm{xz}}}}}}} - {v_3}\bar {{v_1}} {f_{{{22}_{{{\rm{uy}}}}}}} - {v_3}\bar {{v_2}} {f_{{{22}_{{{\rm{uz}}}}}}} + {v_3}\left( { - {f_{{{22}_{{{\rm{ux}}}}}}}} \right) \end{array}\\ \begin{array}{l} \bar {{v_3}} {f_{{3_{{{\rm{ux}}}}}}} + {v_1}\bar {{v_3}} {f_{{3_{{{\rm{uy}}}}}}} + {v_2}\bar {{v_3}} {f_{{3_{{{\rm{uz}}}}}}} + \bar {{v_1}} {f_{{3_{{{\rm{xy}}}}}}} + \bar {{v_2}} {f_{{3_{{{\rm{xz}}}}}}} + {v_1}\bar {{v_1}} {f_{{3_{{{\rm{yy}}}}}}} + {v_1}\bar {{v_2}} {f_{{3_{{{\rm{yz}}}}}}} + {v_2}\bar {{v_1}} {f_{{3_{{{\rm{yz}}}}}}}\\ + {v_2}\bar {{v_2}} {f_{{3_{{{\rm{zz}}}}}}} + {v_1}{f_{{3_{{{\rm{xy}}}}}}} + {v_2}{f_{{3_{{{\rm{xz}}}}}}} + {f_{{3_{{{\rm{xx}}}}}}} + {v_3} + \bar {{v_3}} {f_{{3_{{{\rm{uu}}}}}}} + {v_3}\bar {{v_1}} {f_{{3_{{{\rm{uy}}}}}}} + {v_3}\bar {{v_2}} {f_{{3_{{{\rm{uz}}}}}}} + {v_3}{f_{{3_{{{\rm{ux}}}}}}} \end{array}\\ 0 \end{array}} \right). \end{split} \end{equation}$

(4.42)

Since $i\omega_0\tau_0$ is the eigenvalue of $A(0)$ and $q(0)$ is the corresponding eigenvector, there is

$\begin{equation} \left( i\omega_{0}\tau_0I-\int_{-1}^0 e^{i\omega_{0}\tau_0\theta}d\eta(\theta) \right) q(0) = 0, \end{equation}$

(4.43)

and

$\begin{equation} \left( -i\omega_{0}\tau_0I-\int_{-1}^0 e^{-i\omega_{0}\tau_0\theta}d\eta(\theta) \right) \bar{q}(0) = 0. \end{equation}$

(4.44)

So, we can get

$\begin{equation} \begin{split} \left( {\begin{array}{*{20}{c}} {2i{w_0} - {f_{1x}}}&{ - {f_{1y}}}&{ - {f_{1z}}}&{ - {f_{1u}}}\\ 0&{2i{w_0} + {f_{22y}}}&{{f_{22z}}}&{{f_{22u}}}\\ { - {f_{3x}}}&0&{2i{w_0} - {f_{3z}}}&{ - {f_{3u}}}\\ 0&0&0&{2i{w_0} + {D_{{{\rm{a0}}}}}{{\rm{ + Eto}}} \cdot {S_{{{\rm{ea}}}}}} \end{array}} \right) \times {N_1}\\ = 2\left( {\begin{array}{*{20}{c}} \begin{array}{l} \frac{1}{2}v_3^2{f_{{1_{{{\rm{uu}}}}}}} + {v_3}{f_{{1_{{{\rm{ux}}}}}}} + {v_3}{v_1}{f_{{1_{{{\rm{uy}}}}}}} + {v_2}{v_3}{f_{{1_{{{\rm{uz}}}}}}} + {v_1}{f_{{1_{{{\rm{xy}}}}}}} + {v_2}{f_{{1_{{{\rm{xz}}}}}}} + \frac{1}{2}v_1^2{f_{{1_{{{\rm{yy}}}}}}}\\ + {v_2}{v_1}{f_{{1_{{{\rm{yz}}}}}}} + \frac{1}{2}v_2^2{f_{{1_{{{\rm{zz}}}}}}} + \frac{{{f_{{1_{{{\rm{xx}}}}}}}}}{2} \end{array}\\ \begin{array}{l} {v_1}{f_{{{21}_{{{\rm{xy}}}}}}}{e^{ - 2i w_0 \tau_1^0}} + {v_2}{f_{{{21}_{{{\rm{xz}}}}}}}{e^{ - 2i w_0 \tau_1^0}} + \frac{1}{2}v_1^2{f_{{{21}_{{{\rm{yy}}}}}}}{e^{ - 2i w_0 \tau_1^0}} - {v_1}{f_{{{22}_{{{\rm{xy}}}}}}} - {v_2}{f_{{{22}_{{{\rm{xz}}}}}}}\\ - \frac{1}{2}v_1^2{f_{{{22}_{{{\rm{yy}}}}}}} + \frac{1}{2}{f_{{{21}_{{{\rm{xx}}}}}}}{e^{ - 2i w_0 \tau_1^0}} - \frac{{{f_{{{22}_{{{\rm{xx}}}}}}}}}{2} + {v_3}{f_{{{21}_{{{\rm{ux}}}}}}}{e^{ - 2i w_0 \tau_1^0}} - {v_3}{f_{{{22}_{{{\rm{ux}}}}}}}\\ + {v_1}{v_3}{f_{{{21}_{{{\rm{uy}}}}}}}{e^{ - 2i w_0 \tau_1^0}} + {v_1}{v_2}{f_{{{21}_{{{\rm{yz}}}}}}}{e^{ - 2i w_0 \tau_1^0}} + \frac{1}{2}v_2^2{f_{{{21}_{{{\rm{zz}}}}}}}{e^{ - 2i w_0 \tau_1^0}} - {v_1}{v_2}{f_{{{22}_{{{\rm{yz}}}}}}}\\ - \frac{1}{2}v_2^2{f_{{{22}_{{{\rm{zz}}}}}}} + \frac{1}{2}v_3^2{f_{{{21}_{{{\rm{uu}}}}}}}{e^{ - 2i w_0 \tau_1^0}} - \frac{1}{2}v_3^2{f_{{{22}_{{{\rm{uu}}}}}}} - {v_1}{v_3}{f_{{{22}_{{{\rm{uy}}}}}}} + {v_2}{v_3}{f_{{{21}_{{{\rm{uz}}}}}}}{e^{ - 2i w_0 \tau_1^0}}\\ - {v_2}{v_3}{f_{{{22}_{{{\rm{uz}}}}}}} \end{array}\\ \begin{array}{l} \frac{1}{2}v_3^2{f_{{3_{{{\rm{uu}}}}}}} + {v_3}{f_{{3_{{{\rm{ux}}}}}}} + {v_3}{v_1}{f_{{3_{{{\rm{uy}}}}}}} + {v_2}{v_3}{f_{{3_{{{\rm{uz}}}}}}} + {v_1}{f_{{3_{{{\rm{xy}}}}}}} + {v_2}{f_{{3_{{{\rm{xz}}}}}}} + \frac{1}{2}v_1^2{f_{{3_{{{\rm{yy}}}}}}}\\ + {v_2}{v_1}{f_{{3_{{{\rm{yz}}}}}}} + \frac{1}{2}v_2^2{f_{{3_{{{\rm{zz}}}}}}} + \frac{{{f_{{3_{{{\rm{xx}}}}}}}}}{2} \end{array}\\ 0 \end{array}} \right), \end{split} \end{equation}$

(4.45)

and

$\begin{equation} \begin{split} &\left( {\begin{array}{*{20}{c}} { - {f_{1x}}}&{ - {f_{1y}}}&{ - {f_{1z}}}&{ - {f_{1u}}}\\ 0&{{f_{22y}}}&{{f_{22z}}}&{{f_{22u}}}\\ { - {f_{3x}}}&0&{ - {f_{3z}}}&{ - {f_{3u}}}\\ 0&0&0&{{D_{{{\rm{a0}}}}}{{\rm{ + Eto}}} \cdot {S_{{{\rm{ea}}}}}} \end{array}} \right) \times {N_2}\\ & = \left( {\begin{array}{*{20}{c}} \begin{array}{l} \bar {{v_3}} {f_{{1_{{{\rm{ux}}}}}}} + {v_1}\bar {{v_3}} {f_{{1_{{{\rm{uy}}}}}}} + {v_2}\bar {{v_3}} {f_{{1_{{{\rm{uz}}}}}}} + \bar {{v_1}} {f_{{1_{{{\rm{xy}}}}}}} + \bar {{v_2}} {f_{{1_{{{\rm{xz}}}}}}} + {v_1}\bar {{v_1}} {f_{{1_{{{\rm{yy}}}}}}} + {v_1}\bar {{v_2}} {f_{{1_{{{\rm{yz}}}}}}}\\ + {v_2}\bar {{v_1}} {f_{{1_{{{\rm{yz}}}}}}} + {v_1}{f_{{1_{{{\rm{xy}}}}}}} + {v_2}{f_{{1_{{{\rm{xz}}}}}}} + {f_{{1_{{{\rm{xx}}}}}}} + {v_3}\bar {{v_3}} {f_{{1_{{{\rm{uu}}}}}}} + {v_3}\bar {{v_1}} {f_{{1_{{{\rm{uy}}}}}}} + {v_3}\bar {{v_2}} {f_{{1_{{{\rm{uz}}}}}}}\\ + {v_2} + \bar {{v_2}} {f_{{1_{{{\rm{zz}}}}}}} + {v_3}{f_{{1_{{{\rm{ux}}}}}}} \end{array}\\ \begin{array}{l} \bar {{v_3}} {f_{{{21}_{{{\rm{ux}}}}}}} - \bar {{v_3}} {f_{{{22}_{{{\rm{ux}}}}}}} + {v_1}\bar {{v_3}} {f_{{{21}_{{{\rm{uy}}}}}}} + \bar {{v_1}} {f_{{{21}_{{{\rm{xy}}}}}}} - \bar {{v_1}} {f_{{{22}_{{{\rm{xy}}}}}}} + \bar {{v_2}} {f_{{{21}_{{{\rm{xz}}}}}}} - \bar {{v_2}} {f_{{{22}_{{{\rm{xz}}}}}}}\\ + {v_1}\bar {{v_1}} {f_{{{21}_{{{\rm{yy}}}}}}} + {v_1}{f_{{{21}_{{{\rm{xy}}}}}}} + {f_{{{21}_{{{\rm{xx}}}}}}} - {f_{{{22}_{{{\rm{xx}}}}}}} + - {v_1}\bar {{v_3}} {f_{{{22}_{{{\rm{uy}}}}}}} + {v_2}\bar {{v_3}} {f_{{{21}_{{{\rm{uz}}}}}}} - {v_1}\bar {{v_1}} {f_{{{22}_{{{\rm{yy}}}}}}}\\ + {v_1} + \bar {{v_2}} {f_{{{21}_{{{\rm{yz}}}}}}} - {v_1}\bar {{v_2}} {f_{{{22}_{{{\rm{yz}}}}}}} + {v_2}\bar {{v_1}} {f_{{{21}_{{{\rm{yz}}}}}}} - {v_1}{f_{{{22}_{{{\rm{xy}}}}}}} + {v_2}{f_{{{21}_{{{\rm{xz}}}}}}} + {v_3}\bar {{v_3}} {f_{{{21}_{{{\rm{uu}}}}}}}\\ - {v_3}\bar {{v_3}} {f_{{{22}_{{{\rm{uu}}}}}}} + {v_3}\bar {{v_1}} {f_{{{21}_{{{\rm{uy}}}}}}} - {v_2}\bar {{v_3}} {f_{{{22}_{{{\rm{uz}}}}}}} + {v_3}\bar {{v_2}} {f_{{{21}_{{{\rm{uz}}}}}}} - {v_2}\bar {{v_1}} {f_{{{22}_{{{\rm{yz}}}}}}} + {v_2} + \bar {{v_2}} {f_{{{21}_{{{\rm{zz}}}}}}}\\ - {v_2}\bar {{v_2}} {f_{{{22}_{{{\rm{zz}}}}}}} + {v_3}{f_{{{21}_{{{\rm{ux}}}}}}} - {v_2}{f_{{{22}_{{{\rm{xz}}}}}}} - {v_3}\bar {{v_1}} {f_{{{22}_{{{\rm{uy}}}}}}} - {v_3}\bar {{v_2}} {f_{{{22}_{{{\rm{uz}}}}}}} + {v_3}\left( { - {f_{{{22}_{{{\rm{ux}}}}}}}} \right) \end{array}\\ \begin{array}{l} \bar {{v_3}} {f_{{3_{{{\rm{ux}}}}}}} + {v_1}\bar {{v_3}} {f_{{3_{{{\rm{uy}}}}}}} + {v_2}\bar {{v_3}} {f_{{3_{{{\rm{uz}}}}}}} + \bar {{v_1}} {f_{{3_{{{\rm{xy}}}}}}} + \bar {{v_2}} {f_{{3_{{{\rm{xz}}}}}}} + {v_1}\bar {{v_1}} {f_{{3_{{{\rm{yy}}}}}}} + {v_1}\bar {{v_2}} {f_{{3_{{{\rm{yz}}}}}}} + {v_2}\bar {{v_1}} {f_{{3_{{{\rm{yz}}}}}}}\\ + {v_2}\bar {{v_2}} {f_{{3_{{{\rm{zz}}}}}}} + {v_1}{f_{{3_{{{\rm{xy}}}}}}} + {v_2}{f_{{3_{{{\rm{xz}}}}}}} + {f_{{3_{{{\rm{xx}}}}}}} + {v_3} + \bar {{v_3}} {f_{{3_{{{\rm{uu}}}}}}} + {v_3}\bar {{v_1}} {f_{{3_{{{\rm{uy}}}}}}} + {v_3}\bar {{v_2}} {f_{{3_{{{\rm{uz}}}}}}} + {v_3}{f_{{3_{{{\rm{ux}}}}}}} \end{array}\\ 0 \end{array}} \right). \end{split} \end{equation}$

(4.46)

Finally, according to the definition of $\eta \left(\theta \right)$ , we can solve ${N_1}$ , ${N_2}$ and ${g_{21}}$ . Besides we can also get the following values

$\begin{array}{l} {C_1}\left( 0 \right) = \frac{{{\rm{i}}}}{{2{w_0}\tau _1^0}}\left( {{g_{11}}{g_{20}} - 2{{\left| {{g_{11}}} \right|}^2} - \frac{{{{\left| {{g_{02}}} \right|}^2}}}{3}} \right) + \frac{{{g_{21}}}}{2},\\ {\mu _2} = - \frac{{{\mathop{\rm Re}\nolimits} \left\{ {{C_1}\left( 0 \right)} \right\}}}{{{\mathop{\rm Re}\nolimits} \left\{ {\lambda '\left( {\tau _1^0} \right)} \right\}}},\\ {T_2} = - \frac{{Im\left\{ {{C_1}\left( 0 \right)} \right\} + {\mu _2}Im\left\{ {\lambda '\left( {\tau _1^0} \right)} \right\}}}{{{w_0}\tau _1^0}},\\ {\beta _2} = 2{\mathop{\rm Re}\nolimits} \left\{ {{C_1}\left( 0 \right)} \right\}. \end{array}$

From the above discussion we can get the following results:

(1) The direction of Hopf bifurcation is determined by ${\mu _2}$ : if ${\mu _2} > 0$ ( ${\mu _2} < 0$ ), then the Hopf bifurcation is supercritical (subcritical) and the bifurcating periodic solutions exist for $\tau > \tau _1^0$ ( $\tau < \tau _1^0$ );

(2) The stability of the bifurcating periodic solutions is depended on ${\beta _2}$ , the bifurcating periodic solutions in the center manifold are stable (unstable) for ${\beta _2} < 0$ ( ${\beta _2} > 0$ );

(3) The period of the bifurcating periodic solutions is determined by ${T_2}$ :the period increases if ${T_2} > 0$ (decreases ${T_2} < 0$ ).

References

[1]	K. Vahakangas, Molecular Epidemiology of Human Cancer Risk, Lung Cancer, 2003, 43–59. https://doi.org/10.1385/1-59259-323-2:43 doi: 10.1385/1-59259-323-2:43
[2]	F. Murray-Zmijewski, E. A. Slee, X. Lu, A complex barcode underlies the heterogeneous response of p53 to stress, Nat. Rev. Mol. Cell Biol., 9 (2008), 702–712. https://doi.org/10.1038/nrm2451 doi: 10.1038/nrm2451
[3]	K. H. Vousden, Outcomes of p53 activation-spoilt for choice, J. Cell Sci., 119 (2006), 5015–5020. https://doi.org/10.1242/jcs.03293 doi: 10.1242/jcs.03293
[4]	X. P. Zhang, F. Liu, Z, Cheng, W. Wang, Cell fate decision mediated by p53 pulses, Proc. Natl. Acad. Sci. U.S.A., 106 (2009), 12245–12250. https://doi.org/10.1073/pnas.0813088106 doi: 10.1073/pnas.0813088106
[5]	X. P. Zhang, F. Liu, W. Wang, Two-phase dynamics of p53 in the DNA damage response, Proc. Natl. Acad. Sci. U.S.A., 108 (2011), 8990–8995. https://doi.org/10.1073/pnas.1100600108 doi: 10.1073/pnas.1100600108
[6]	K. H. Vousden, D. P. Lane, p53 in health and disease, Nat. Rev. Mol. Cell Biol., 8 (2007), 275–283. https://doi.org/10.1038/nrm2147 doi: 10.1038/nrm2147
[7]	S. Shangary, S. Wang, Small-molecule inhibitors of the MDM2-p53 protein-protein interaction to reactivate p53 function: a novel approach for cancer therapy, Annu. Rev. Pharmacol., 49 (2009), 223–241. https://doi.org/10.1146/annurev.pharmtox.48.113006.094723 doi: 10.1146/annurev.pharmtox.48.113006.094723
[8]	M. J. Duffy, N. C. Synnott, J. Crown, Mutant p53 as a target for cancer treatment, Eur. J. Cancer., 83 (2017), 258–265. https://doi.org/10.1016/j.ejca.2017.06.023 doi: 10.1016/j.ejca.2017.06.023
[9]	V. J. N. Bykov, S. E. Eriksson, J. Bianchi, K. G. Wiman, Targeting mutant p53 for efficient cancer therapy, Nat. Rev. Cancer., 18 (2018), 89–102. https://doi.org/10.1038/nrc.2017.109 doi: 10.1038/nrc.2017.109
[10]	Y. Pan, Y. Yuan, G. Liu, Y. Wei, P53 and Ki-67 as prognostic markers in triple-negative breast cancer patients, Plos One, 12 (2017), e0172324. https://doi.org/10.1371/journal.pone.0172324 doi: 10.1371/journal.pone.0172324
[11]	D. Michael, M. Oren, The p53-Mdm2 module and the ubiquitin system, Semin. Cancer Biol., 13 (2003), 49–58. https://doi.org/10.1016/S1044-579X(02)00099-8 doi: 10.1016/S1044-579X(02)00099-8
[12]	Y. Haupt, R. Maya, A. Kazaz, M. Oren, Mdm2 promotes the rapid degradation of p53, Nature, 387 (1997), 296–299. https://doi.org/10.1038/387296a0 doi: 10.1038/387296a0
[13]	L. Ma, J. Wagner, J. J. Rice, W. Hu, A. J. Levine, G. A. Stolovitzky, A plausible model for the digital response of p53 to DNA damage, Proc. Natl. Acad. Sci. U.S.A., 102 (2005), 14266–14271. https://doi.org/10.1073/pnas.0501352102 doi: 10.1073/pnas.0501352102
[14]	R. L. Bar-Or, R, Maya, L. A. Segel, U. Alon, A. J. Levine, M. Oren, Generation of oscillations by the p53-Mdm2 feedback loop: a theoretical and experimental study, Proc. Natl. Acad. Sci. U.S.A., 97 (2000), 11250–11255. https://doi.org/10.1073/pnas.210171597 doi: 10.1073/pnas.210171597
[15]	J. H. Park, S. W. Yang, J. M. Park, S. H. Ka, J. Kim, Y. Kong, et al., Positive feedback regulation of p53 transactivity by DNA damage-induced ISG15 modification, Nat. Commun., 7 (2016), 12513. https://doi.org/10.1038/ncomms12513 doi: 10.1038/ncomms12513
[16]	H. Cha, J. M. Lowe, H. Li, J. Lee, G. I. Belova, D. V. Bulavin, et al., Wip1 directly dephosphorylates $\gamma$ -H2AX and attenuates the DNA damage response, Cancer Res., 70 (2010), 4112–4122. https://doi.org/10.1158/0008-5472.CAN-09-4244 doi: 10.1158/0008-5472.CAN-09-4244
[17]	H. Sakai, H. Fujigaki, S. Mazur, E. Appella, Wild-type p53-induced phosphatase 1 (Wip1) forestalls cellular premature senescence at physiological oxygen levels by regulating DNA damage response signaling during DNA replication, Cell Cycle, 13 (2014), 1015–1029. https://doi.org/10.4161/cc.27920 doi: 10.4161/cc.27920
[18]	S. Shreeram, O. N. Demidov, W. K. Hee, H. Yamaguchi, N. Onishi, C. Kek, et al., Wip1 phosphatase modulates ATM-dependent signaling pathways, Mol. Cell, 23 (2006), 757–764. https://doi.org/10.1016/j.molcel.2006.07.010 doi: 10.1016/j.molcel.2006.07.010
[19]	N. Geva-Zatorsky, N. Rosenfeld, S. Itzkovitz, R. Milo, A. Sigal, E. Dekel, et al., Oscillations and variability in the p53 system, Mol. Syst. Biol., 2 (2006), 0033. https://doi.org/10.1038/msb4100068 doi: 10.1038/msb4100068
[20]	A. M. Weber, A. J. Ryan, ATM and ATR as therapeutic targets in cancer, Pharmacol. Ther., 149 (2015), 124–138. https://doi.org/10.1016/j.pharmthera.2014.12.001 doi: 10.1016/j.pharmthera.2014.12.001
[21]	S. Banin, L. Moyal, S. Shieh, Y. Taya, C. W. Anderson, L. Chessa, et al., Enhanced phosphorylation of p53 by ATM in response to DNA damage, Science, 281 (1998), 1674–1677. https://doi.org/10.1126/science.281.5383.1674 doi: 10.1126/science.281.5383.1674
[22]	E. Haines, A. Zimmermann, F. Zenke, A. Blaukat, Selective DNA-PK inhibitor, M3814, boosts p53 apoptotic response to DNA double strand breaks and effectively kills acute leukemia cell: Implications for AML therapy, Cancer Res., 78 (2018), 4830–4830. https://doi.org/10.1158/1538-7445.AM2018-4830 doi: 10.1158/1538-7445.AM2018-4830
[23]	W. Freed-Pastor, C. Prives, Targeting mutant p53 through the mevalonate pathway, Nat. Cell Biol., 18 (2016), 1122–1124. https://doi.org/10.1038/ncb3435 doi: 10.1038/ncb3435
[24]	R. J. Ihry, K. A. Worringer, M. R. Salick, E. Frias, D. Ho, K. Theriault, et. al., p53 inhibits CRISPR–Cas9 engineering in human pluripotent stem cell, Nat. Med., 24 (2018), 939–946. https://doi.org/10.1101/168443 doi: 10.1101/168443
[25]	Q. Cheng, J. Chen, Mechanism of p53 stabilization by ATM after DNA damage, Cell Cycle, 9 (2010), 472–478. https://doi.org/10.4161/cc.9.3.10556 doi: 10.4161/cc.9.3.10556
[26]	C. Zhou, X. Zhang, F. Liu, W. Wang, Modeling the interplay between the HIF-1 and p53 pathways in hypoxia, Sci. Rep., 5 (2015), 13834. https://doi.org/10.1038/srep13834 doi: 10.1038/srep13834
[27]	X. Tian, B. Huang, X. Zhang, M. Liu, F. Liu, J. N. Onuchic, W. Wang, Modeling the response of a tumor-suppressive network to mitogenic and oncogenic signals, Proc. Natl. Acad. Sci. U.S.A., 114 (2017), 5337–5342. https://doi.org/10.1073/pnas.1702412114 doi: 10.1073/pnas.1702412114
[28]	D. Bratsun, D. Volfson, L. S. Tsimring, J. Hasty, Delay-induced stochastic oscillations in gene regulation, Proc. Natl. Acad. Sci. U.S.A., 102 (2005), 14593–14598. https://doi.org/10.1073/pnas.0503858102 doi: 10.1073/pnas.0503858102
[29]	B. Novák, J. J. Tyson, Design principles of biochemical oscillators, Nat. Rev. Mol. Cell Biol., 9 (2008), 981–991. https://doi.org/10.1038/nrm2530 doi: 10.1038/nrm2530
[30]	A. Honkela, J. Peltonen, H. Topa, I. Charapitsa, F. Matarese, K. Grote, et al., Genome-wide modeling of transcription kinetics reveals patterns of RNA production delays, Proc. Natl. Acad. Sci. U.S.A., 112 (2015), 13115–13120. https://doi.org/10.1073/pnas.1420404112 doi: 10.1073/pnas.1420404112
[31]	A. Prindle, J. Selimkhanov, H. Li, I. Razinkov, L. S. Tsimring, J. Hasty, Rapid and tunable post-translational coupling of genetic circuits, Nature, 508 (2014), 387–391. https://doi.org/10.1038/nature13238 doi: 10.1038/nature13238
[32]	H. K. Yalamanchili, B. Yan, J. Li, J. Qin, Z. Zhao, F. Y. L. Chin, et al., DDGni: dynamic delay gene-network inference from high-temporal data using gapped local alignment, Bioinformatics, 30 (2013), 377–383. https://doi.org/10.1093/bioinformatics/btt692 doi: 10.1093/bioinformatics/btt692
[33]	R. Yang, B. Huang, Y. Zhu, Y. Li, F. Liu, J. Shi, Cell type-dependent bimodal p53 activation engenders a dynamic mechanism of chemoresistance, Sci. Adv., 4 (2018), eaat5077. https://doi.org/10.1126/sciadv.aat5077 doi: 10.1126/sciadv.aat5077
[34]	C. Prives, Signaling to p53: breaking the MDM2–p53 circuit, Cell, 95 (1998), 5–8. https://doi.org/10.1016/S0092-8674(00)81774-2 doi: 10.1016/S0092-8674(00)81774-2
[35]	J. M. Stommel, G. M. Wahl, Accelerated MDM2 auto-degradation induced by DNA-damage kinases is required for p53 activation, The EMBO J., 23 (2004), 1547–1556. https://doi.org/10.1038/sj.emboj.7600145 doi: 10.1038/sj.emboj.7600145
[36]	E. Batchelor, C. S. Mock, I. Bhan, A. Loewer, G. Lahav, Recurrent initiation: a mechanism for triggering p53 pulses in response to DNA damage, Mol. cell., 30 (2008), 277–289. https://doi.org/10.1016/j.molcel.2008.03.016 doi: 10.1016/j.molcel.2008.03.016
[37]	N. A. M. Monk, Oscillatory expression of Hes1, p53, and NF-kappaB driven by transcriptional time delays, Curr. Biol., 13 (2003), 1409–1413. https://doi.org/10.1016/S0960-9822(03)00494-9 doi: 10.1016/S0960-9822(03)00494-9
[38]	Y. Zhang, H. Liu, F. Yan, J. Zhou, Oscillatory dynamics of p38 activity with transcriptional and translational time delays, Sci. Rep., 7 (2017), 11495. https://doi.org/10.1038/s41598-017-11149-5 doi: 10.1038/s41598-017-11149-5
[39]	D. M. Longo, J. Selimkhanov, J. D. Kearns, J. Hasty, A. Hoffmann, L. S. Tsimring, Dual Delayed Feedback Provides Sensitivity and Robustness to the NF- $\kappa$ B Signaling Module, PLoS Comput. Biol., 9 (2013), e1003112. https://doi.org/10.1371/journal.pcbi.1003112 doi: 10.1371/journal.pcbi.1003112
[40]	Q. Wang, M. Perc, Z. Duan, G. Chen, Synchronization transitions on scale-free neuronal networks due to finite information transmission delays, Phys. Rev. E., 80 (2009), 026206. https://doi.org/10.1103/PhysRevE.80.026206 doi: 10.1103/PhysRevE.80.026206
[41]	Q. Wang, H. Zhang, G. Chen, Stimulus-induced transition of clustering firings in neuronal networks with information transmission delay, Eur. Phys. J. B., 86 (2013), 301. https://doi.org/10.1140/epjb/e2013-40078-3 doi: 10.1140/epjb/e2013-40078-3
[42]	A. Roxin, N. Brunel, D. Hansel, Role of delays in shaping spatiotemporal dynamics of neuronal activity in large networks, Phys. Rev. Lett., 94 (2005), 238103. https://doi.org/10.1103/PhysRevLett.94.238103 doi: 10.1103/PhysRevLett.94.238103
[43]	E. Rossoni, Y. Chen, M. Ding, J. Feng, Stability of synchronous oscillations in a system of Hodgkin-Huxley neurons with delayed diffusive and pulsed coupling, Phys. Rev. E., 71 (2005), 061904. https://doi.org/10.1103/PhysRevE.71.061904 doi: 10.1103/PhysRevE.71.061904
[44]	J. Lewis, Autoinhibition with transcriptional delay: A simple mechanism for the zebrafish somitogenesis oscillator, Curr. Biol. Cb., 13 (2003), 1398–1408. https://doi.org/10.1016/s0960-9822(03)00534-7 doi: 10.1016/s0960-9822(03)00534-7
[45]	A. Audibert, D. Weil, F. Dautry, In vivo kinetics of mRNA splicing and transport in mammalian cells, Mol. Cell. Biol., 22 (2002), 6706–6718. https://doi.org/10.1128/MCB.22.19.6706–6718.2002 doi: 10.1128/MCB.22.19.6706–6718.2002
[46]	B. D. Hassard, N. D. Kazarinoff, Y. H. Wan, Theory and applications of Hopf bifurcation, Cambridge University Press, (1981). http://dx.doi.org/10.1090/conm/445

Reader Comments

Your name:*

Email:*
© 2022 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by/4.0)

通讯作者: 陈斌, bchen63@163.com

1.
沈阳化工大学材料科学与工程学院沈阳 110142

Electronic Research Archive

1 1.3

Metrics

Article views(1341) PDF downloads(45) Cited by(0)

Preview PDF

Download XML

Export Citation

Article outline

Show full outline

Figures and Tables

Figures(17) / Tables(2)

Electronic Research Archive

Oscillatory dynamics of p53 pathway in etoposide sensitive and resistant cell lines

Related Papers:

Abstract

1. Introduction

2. Materials and methods

3. Results

3.1. Effect of time delays on drug-sensitive cells

3.2. Effects of drug dose of Etoposide on drug-sensitive cells

3.3. Comparison of effects of kpm k_{pm} and kpw k_{pw} on drug-sensitive cells

3.4. Effect of time delays on drug-resistant cells

3.5. Effect of Etoposide on drug-resistant cells.

3.6. Comparison of effects of kpm k_{pm} and kpw k_{pw} on drug-resistant cells.

4. Conclusions

Acknowledgments

Conflict of interest

Supplementary

4.1. The information of Parameters

4.2. The existence of Hopf bifurcations

4.3. Properties of Hopf bifurcations

References

Reader Comments

通讯作者: 陈斌, bchen63@163.com

Metrics

Figures and Tables

Other Articles By Authors

Related pages

Tools

Export File

Citation

Format

Content

Catalog

Abstract

1. Introduction

2. Materials and methods

3. Results

3.1. Effect of time delays on drug-sensitive cells

3.2. Effects of drug dose of Etoposide on drug-sensitive cells

3.3. Comparison of effects of kpm k_{pm} and kpw k_{pw} on drug-sensitive cells

3.4. Effect of time delays on drug-resistant cells

3.5. Effect of Etoposide on drug-resistant cells.

3.6. Comparison of effects of kpm k_{pm} and kpw k_{pw} on drug-resistant cells.

4. Conclusions

Acknowledgments

Conflict of interest

Supplementary

4.1. The information of Parameters

4.2. The existence of Hopf bifurcations

4.3. Properties of Hopf bifurcations

References

3.3. Comparison of effects of $k_{pm}$ and $k_{pw}$ on drug-sensitive cells

3.6. Comparison of effects of $k_{pm}$ and $k_{pw}$ on drug-resistant cells.

3.3. Comparison of effects of $k_{pm}$ and $k_{pw}$ on drug-sensitive cells

3.6. Comparison of effects of $k_{pm}$ and $k_{pw}$ on drug-resistant cells.