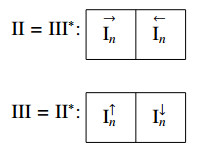Brauer configuration algebras and Kronecker modules to categorify integer sequences

1.   Introduction

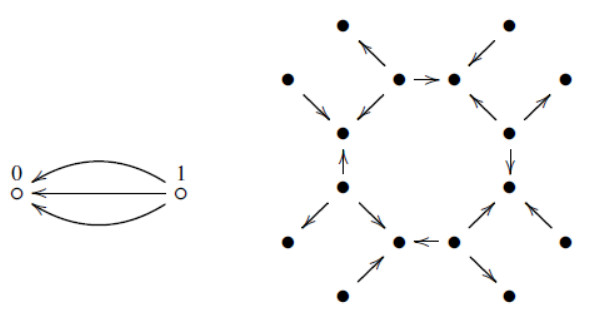
According to Ringel and Fahr ^[1], a categorification of a sequence of numbers means to consider instead of these numbers suitable objects in a category (for instance, representation of quivers) so that the numbers in question occur as invariants of the objects, equality of numbers may be visualized by isomorphisms of objects functional relations by functorial ties. The notion of this kind of categorification arose from the use of suitable arrays of numbers to obtain integer partitions of dimensions of indecomposable preprojective modules over the 3-Kronecker algebra (see Figure 1, where it is shown the 3-Kronecker quiver and a part of its associated oriented 3-regular tree or universal covering $(T, E, \Omega_{t})$ as described by Ringel and Fahr in ^[2]).

Firstly they noted that the vector dimension of these kinds of modules consists of even-index Fibonacci numbers (denoted $f_{i}$ and such that $f_{i} = f_{i-1}+f_{i-2}$, for $i\geq2$, $f_{0} = 0$, $f_1 = 1$) then they used results from the universal covering theory developed by Gabriel and his students to identify such Fibonacci numbers with dimensions of representations of the corresponding universal covering. In particular, preinjective and preprojective representations of the 3-Kronecker quiver were used in ^[2] by Ringel and Fahr to derive a partition formula for even-index Fibonacci numbers.

The categorification process of even-index Fibonacci numbers introduced in ^[2] allowed Ringel and Fahr to define an array of numbers $T = T_{(i, j)}$ called even-index Fibonacci partition triangle ^[3] with similar properties as the Pascal\textquotesingle s triangle and to include the integer sequence A132262 in the OEIS (On-Line Encyclopedia of Integer Sequences). In particular, some modules called Fibonacci modules, Auslander-Reiten sequences and suitable filtrations of these types of modules were used in ^[1] to categorify the following identities between Fibonacci numbers:

Entries in the array $T$ are categorified by Fibonacci modules provided that they give Jordan-Hölder multiplicities of these modules.

We point out that Ringel in ^[4] exhibits combinatorial data which can be derived from a category $\mathrm{mod} \; \Lambda$, where $\Lambda$ is a hereditary {Artin} algebra of Dynkin type $\Delta$. He comments that many enumeration problems give rise to categorification of different integer sequences. For instance, the number of some tilting modules and the number of antichains in $\mathrm{mod} \; \Lambda$ categorify the Catalan numbers if $\Lambda$ is an algebra of Dynkin type $\mathbb{A}_{n}$. Whereas, if $\Lambda$ is of Dynkin type $\mathbb{B}_{n}$ then such number of modules and antichains categorify the sequence $\binom{2n}{n}$. Results regarding the categorification of integer sequences encouraged Ringel to propose the creation of an On-Line Encyclopedia of Dynkin Functions (OEDF) with the same purposes as the OEIS. Such construction is currently an open problem (the number of indecomposable $\Lambda$-modules over an algebra $\Lambda$ of Dynkin type is an example of a Dynkin function).

1.1.   Contributions

In this work, to categorify integer sequences, we identify combinatorial information arising from the preprojective component of the 2-Kronecker algebra (or simply the Kronecker algebra) with combinatorial information arising from indecomposable projective modules over some Brauer configuration algebras introduced recently by Green and Schroll in ^[5]. In particular, we use these settings to define categorifications of the sequences encoded in the OEIS as A052558 and A052591. Configurations of some multisets called polygons define such Brauer configuration algebras.

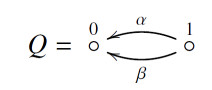
We recall here that the Kronecker problem is equivalent to the problem of determining the indecomposable representations over a field $k$ of the 2-Kronecker quiver $Q$ illustrated in Figure 2.

We will see that some invariants associated with indecomposable projective modules over some suitable Brauer configuration algebras allow categorify any counting function. Since polygons in Brauer configurations are multisets, we will assume that such polygons consists of words of the form

where for each $i$, $1\leq i\leq t$, $x_{i}$ is an element of the polygon called vertex and $s_{i}$ is the number of times that the vertex $x_{i}$ occurs in the polygon. In particular, if vertices $x_{i}$ in a polygon $V$ of a Brauer configuration are integer numbers then the corresponding word $w$ will be interpreted as a partition of an integer number $n_{V}$ associated with the polygon $V$ where it is assumed that each vertex $x_{i}$ is a part of the partition and $s_{i}$ is the number of times that the part $x_{i}$ occurs in the partition and $n_{V} = \underset{i = 1}{\overset{t}{\sum\limits}}s_{i}x_{i}$.

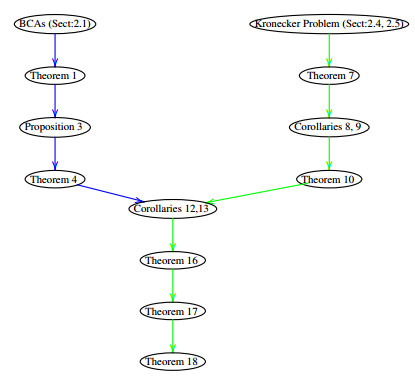
The following diagram (1.3) shows how the theory of Brauer configuration algebras (BCAs) and the Kronecker problem are related to the main results (targets of green arrows) presented in this paper.

This paper is distributed as follows: in Section 2, we recall main definitions and notation used throughout the document, in particular, in this section we define Brauer configuration algebras, and the Kronecker problem.

In Section 3, some directed graphs named helices are associated with preprojective Kronecker modules to categorify numbers in sequences A052558 and A052591. Besides, it is defined a sequence $\Lambda_{K^{n}}$ of Brauer configuration algebras whose indecomposable projective modules are in bijective correspondence with preprojective Kronecker modules via the number of summands in the heart of such indecomposable modules. Formulas for the dimension of this type of algebras and corresponding centers are also given. Section 4 describes how it is possible to use integer sequences to build Brauer configuration algebras, the process is applied to any counting function. Concluding remarks are given in Section 5. Examples of helices are shown in the Appendix.

2.   Preliminaries

In this section, we recall main definitions and notation to be used throughout the paper ^{[5,6,7,8,9,10]}.

2.1.   Brauer configuration algebras

Green and Schroll introduced in ^[5] Brauer configuration algebras as a generalization of Brauer graph algebras which are biserial algebras of tame representation type and whose representation theory is encoded by some combinatorial data based on graphs. According to them, underlying every Brauer graph algebra is a finite graph with a cyclic orientation of the edges at every vertex and a multiplicity function ^[6]. The construction of a Brauer graph algebra is a special case of the construction of a Brauer configuration algebra in the sense that every Brauer graph is a Brauer configuration with the restriction that every polygon is a set with two vertices. In the sequel, we remind Brauer configuration and Brauer configuration algebra definitions.

A Brauer configuration $\Gamma$ is a quadruple of the form $\Gamma = (\Gamma_{0}, \Gamma_{1}, \mu, \mathcal{O})$ where:

($B1$) $\Gamma_{0}$ is a finite set whose elements are called vertices.

($B2$) $\Gamma_{1}$ is a finite collection of multisets called polygons. In this case, if $V\in \Gamma_{1}$ then the elements of $V$ are vertices possibly with repetitions, $\mathrm{occ}(\alpha, V)$ denotes the frequency of the vertex $\alpha$ in the polygon $V$ and the valency of $\alpha$ denoted $val(\alpha)$ is defined in such a way that:

($B3$) $\mu$ is an integer valued function such that $\mu:\Gamma_{0}\rightarrow \mathbb{N}$ where $\mathbb{N}$ denotes the set of positive integers, it is called the multiplicity function.

($B4$) $\mathcal{O}$ denotes an orientation defined on $\Gamma_{1}$ which is a choice, for each vertex $\alpha \in \Gamma_0$, of a cyclic ordering of the polygons in which $\alpha$ occurs as a vertex, including repetitions, we denote $S_{\alpha}$ such collection of polygons. More specifically, if $S_{\alpha} = \{V^{(\alpha_{1})}_{1}, V^{(\alpha_{2})}_{2}, \dots, V^{(\alpha_t)}_{t}\}$ is the collection of polygons where the vertex $\alpha$ occurs with $\alpha_{i} = \mathrm{occ}(\alpha, V_{i})$ and $V^{(\alpha_{i})}_{i}$ meaning that $S_{\alpha}$ has $\alpha_{i}$ copies of $V_{i}$ then an orientation $\mathcal{O}$ is obtained by endowing a linear order $<$ to $S_{\alpha}$ and adding a relation $V_{t} < V_{1}$, if $V_{1} = \mathrm{min} \; S_{\alpha}$ and $V_{t} = \mathrm{max} \; S_{\alpha}$, the set $(S_{\alpha}, < )$ is called the successor sequence at the vertex $\alpha$. According to this order the $\alpha_{i}$ copies of $V_{i}$ can be ordered as $V_{1, i} < V_{2, i} < \dots < V_{(\alpha_{i}-1), i} < V_{\alpha_{i}, i}$ and $S_{\alpha}$ can be ordered in the form $V^{(\alpha_{1})}_{1} < V^{(\alpha_{2})}_{2} < \dots < V^{(\alpha_{(t-1)})}_{(t-1)} < V^{\alpha_{t}}_{t}$. It is worth noting that this ordering is kept without changes in the successor sequences containing all the polygons $V_{1}, V_{2}, \dots, V_{t}$,

($B5$) Every vertex in $\Gamma_{0}$ is a vertex in at least one polygon in $\Gamma_{1}$.

($B6$) Every polygon has at least two vertices.

($B7$) Every polygon in $\Gamma_{1}$ has at least one vertex $\alpha$ such that $\mu(\alpha)val(\alpha) > 1$.

A vertex $\alpha\in\Gamma_{0}$ is said to be truncated if $val(\alpha)\mu(\alpha) = 1$, that is, $\alpha$ is truncated if it occurs exactly once in exactly one $V\in\Gamma_{1}$ and $\mu(\alpha) = 1$. A vertex is nontruncated if it is not truncated.

2.2.   The quiver of a Brauer configuration algebra

The quiver $Q_{\Gamma} = ((Q_{\Gamma})_{0}, (Q_{\Gamma})_{1})$ of a Brauer configuration algebra is defined in such a way that the vertex set $(Q_{\Gamma})_{0} = \{v_{1}, v_{2}, \dots, v_{m}\}$ of $Q_{\Gamma}$ is in correspondence with the set of polygons $\{V_{1}, V_{2}, \dots, V_{m}\}$ in $\Gamma_{1}$, noting that there is one vertex in $(Q_{\Gamma})_{0}$ for every polygon in $\Gamma_{1}$.

Arrows in $Q_{\Gamma}$ are defined by the successor sequences. That is, there is an arrow $v_{i}\stackrel{s_{i}}{\longrightarrow}v_{i+1}\in (Q_{\Gamma})_{1}$ provided that $V_{i} < V_{i+1}$ in $(S_{\alpha}, < )\cup\{V_{t} < V_{1}\}$ for some nontruncated vertex $\alpha\in\Gamma_{0}$. In other words, for each nontruncated vertex $\alpha\in\Gamma_{0}$ and each successor $V'$ of $V$ at $\alpha$, there is an arrow from $v$ to $v'$ in $Q_{\Gamma}$ where $v$ and $v'$ are the vertices in $Q_{\Gamma}$ associated with the polygons $V$ and $V'$ in $\Gamma_{1}$, respectively.

2.3.   The ideal of relations and definition of a Brauer configuration algebra

Fix a polygon $V\in\Gamma_{1}$ and suppose that $\mathrm{occ}(\alpha, V) = t\geq1$ then there are $t$ indices $i_{1}, \dots, i_{t}$ such that $V = V_{i_{j}}$. Then the special $\alpha$-cycles at $v$ are the cycles $C_{i_{1}}, C_{i_{2}}, \dots, C_{i_{t}}$ where $v$ is the vertex in the quiver of $Q_{\Gamma}$ associated with the polygon $V$. If $\alpha$ occurs only once in $V$ and $\mu(\alpha) = 1$ then there is only one special $\alpha$-cycle at $v$.

Let $k$ be a field and $\Gamma$ a Brauer configuration. The Brauer configuration algebra associated with $\Gamma$ is defined to be the bound quiver algebra $\Lambda_{\Gamma} = kQ_{\Gamma}/I_{\Gamma}$, where $Q_{\Gamma}$ is the quiver associated with $\Gamma$ and $I_{\Gamma}$ is the ideal in $kQ_{\Gamma}$ generated by the following set of relations $\rho_{\Gamma}$ of type I, II and III.

1) Relations of type I. For each polygon $V = \{\alpha_{1}, \dots, \alpha_{m}\}\in \Gamma_{1}$ and each pair of nontruncated vertices $\alpha_{i}$ and $\alpha_{j}$ in $V$, the set of relations $\rho_{\Gamma}$ contains all relations of the form $C^{\mu(\alpha_{i})}-C'^{\mu(\alpha_{j})}$ where $C$ is a special $\alpha_{i}$-cycle and $C'$ is a special $\alpha_{j}$-cycle.

2) Relations of type II. Relations of type II are all paths of the form $C^{\mu(\alpha)}a$ where $C$ is a special $\alpha$-cycle and $a$ is the first arrow in $C$.

3) Relations of type III. These relations are quadratic monomial relations of the form $ab$ in $kQ_{\Gamma}$ where $ab$ is not a subpath of any special cycle unless $a = b$ and $a$ is a loop associated with a vertex of valency 1 and $\mu(\alpha) > 1$.

Henceforth, if there is no confusion, we will assume notations, $\Lambda$, $I$ and $\rho$ instead of $\Lambda_{\Gamma}$, $I_{\Gamma}$ and $\rho_{\Gamma}$ for a Brauer configuration algebra, the ideal and set of relations, respectively defined by a given Brauer configuration $\Gamma$.

The following results give some description of the structure of Brauer configuration algebras ^[5,7].

Theorem 1 (^[5], Theorem B, Proposition 2.7, Theorem 3.10, Corollary 3.12). Let $\Lambda$ be a Brauer configuration algebra with Brauer configuration $\Gamma$.

1) There is a bijective correspondence between the set of indecomposable projective $\Lambda$-modules and the polygons in $\Gamma$.

2) If $P$ is an indecomposable projective $\Lambda$-module corresponding to a polygon $V$ in $\Gamma$. Then $\mathrm{rad} \; P$ is a sum of $r$ indecomposable uniserial modules, where $r$ is the number of (nontruncated) vertices of $V$ and where the intersection of any two of the uniserial modules is a simple $\Lambda$-module.

3) A Brauer configuration algebra is a multiserial algebra.

4) The number of summands in the heart $ht(P) = \mathrm{rad} \; P/\mathrm{soc} \; P$ of an indecomposable projective $\Lambda$-module $P$ such that $\mathrm{rad}^{2} \; P\neq 0$ equals the number of nontruncated vertices of the polygons in $\Gamma$ corresponding to $P$ counting repetitions.

5) If $\Lambda'$ is a Brauer configuration algebra obtained from $\Lambda$ by removing a truncated vertex of a polygon in $\Gamma_{1}$ with $d\geq 3$ vertices then $\Lambda$ is isomorphic to $\Lambda'$.

Proposition 2 (^[5], Proposition 3.3). Let $\Lambda$ be the Brauer configuration algebra associated with the Brauer configuration $\Gamma$. For each $V\in\Gamma_{1}$ choose a nontruncated vertex $\alpha$ and exactly one special $\alpha$-cycle $C_{V}$ at $V$,

Then $A\cup B$ is a $k$-basis of $\Lambda$.

Proposition 3 (^[5], Proposition 3.13). Let $\Lambda$ be a Brauer configuration algebra associated with the Brauer configuration $\Gamma$ and let $\mathcal{C} = \{C_{1}, \dots, C_{t}\}$ be a full set of equivalence class representatives of special cycles. Assume that for $i = 1, \dots, t$, $C_{i}$ is a special $\alpha_{i}$-cycle where $\alpha_{i}$ is a nontruncated vertex in $\Gamma$. Then

where $|Q_{0}|$ denotes the number of vertices of $Q$, $|C_{i}|$ denotes the number of arrows in the $\alpha_{i}$-cycle $C_{i}$ and $n_{i} = \mu(\alpha_{i})$.

The following result regards the center of a Brauer configuration algebra.

Theorem 4 (^[7], Theorem 4.9). Let $\Gamma$ be a reduced and connected Brauer configuration and let $Q$ be its induced quiver and let $\Lambda$ be the induced Brauer configuration algebra such that $\mathrm{rad}^{2} \; \Lambda \neq 0$ then the dimension of the center of $\Lambda$ denoted $\mathrm{dim}_{k} \; Z(\Lambda)$ is given by the formula:

where $|\mathcal{C}_{\Gamma}| = \{\alpha\in\Gamma_{0}\mid val(\alpha) = 1, \; and \; \mu(\alpha) > 1\}$.

2.4.   The Kronecker problem

The classification of indecomposable Kronecker modules was solved by Weierstrass in 1867 for some particular cases and by Kronecker in 1890 for the complex number field case. This problem is equivalent to the problem of finding canonical Jordan form of pairs of matrices $(A, B)$ (with the same size) with respect to the following elementary transformations over a field $k$ (for the sake of brevity, it is assumed that $k$ is an algebraically closed field):

(i) All elementary transformations on rows of the block matrix $(A, B)$.

(ii) All elementary transformations made simultaneously on columns of $A$ and $B$ having the same index number.

If the matrix blocks $P = (A, B)$ and $P' = (A', B')$ can be transformed one into the other by means of elementary transformations, then they are said to be equivalent or isomorphic as Kronecker modules. Figure 3 shows the matrix form (up to isomorphism) of the non-regular Kronecker modules ^[8,9]:

In this case, $\overset{\rightarrow }{\mathrm{I}_{n}}$ ($\overset{\leftarrow}{\mathrm{I}_{n}}$, respectively) denotes an $n\times (n+1)$ matrix obtained from the identity $\mathrm{I}_{n}$ by adding a column of zeroes. In fact, the last column (the first column, respectively) in these matrices consists only of zeroes. Similarly, $I^{\uparrow}_{n}$ ($I^{\downarrow}_{n}$) denotes an $n+1\times n$ matrix obtained from an $n\times n$ identity matrix by adding at the top (at the bottom) a row of zeroes.

We recall that the solution of the Kronecker matrix problem allows classifying the indecomposable representations of the path algebra $kQ$ with $Q$ a quiver with the shape given in Figure 2.

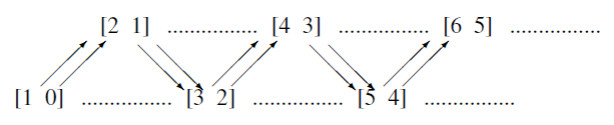
Figure 4 shows the preprojective component of the Auslander-Reiten quiver of the 2-Kronecker quiver which has as vertices isomorphism classes of indecomposable representations of type III ($[i+1 \; i]$ is a notation for the dimension vector of a preprojective representation (equivalently, preprojective module), whereas $[m \; m+1]$ is the dimension vector of a preinjective module). The preinjective component has isomorphism classes of indecomposable representations of type $\mathrm{III}^{*}$ as vertices.

Henceforth, we let $(n+1, n)$ ($(n, n+1)$) denote a representative of an isomorphism class of preprojective (preinjective) Kronecker modules obtained from a representation of type III (II) via elementary transformations. Actually, for the sake of simplicity, we will assume that such representatives have the form III (II).

2.5.   Helices

For $n\geq1$, let $P$ be an $(n+1)\times 2n$, $k$-matrix then $P$ can be partitioned into two $(n+1)\times n$ matrix blocks $A$ and $B$. In such a case we write $P = (P, A, B, n)$, where $A = (a_{i, j}) = [C^{A}_{i_{1}}, \dots, C^{A}_{i_{n}}]$, $B = (b_{i, j}) = [C^{B}_{j_{1}}, \dots, C^{B}_{j_{n}}]$, with $C^{A}_{i_{r}}$ ($C^{B}_{j_{s}}$) columns of $P$, if $I_{A}$ ($I_{B}$) is the set of indices $I_{A} = \{i_{r}\mid 1\leq r\leq n \}$ ($I_{B} = \{j_{s}\mid 1\leq s\leq n\}$) then $I_{A}\cap I_{B} = \varnothing$, and $|I_A| = |I_B| = n$. In this case, each column of the matrix $P$ belongs either to the matrix $A$ or to the matrix $B$ and a word $W_{P} = l_{m_{1}}\dots l_{m_{n}}\dots l_{m_{2n}}$, $l_{m_{h}}\in\{A, B\}$, $1\leq h\leq 2n$ is used to denote matrix $P$ by specifying the way that columns of $P$ have been assigned to the matrices $A$ and $B$.

A row $r_{P}$ of $P$ has the form $(r_{A}, r_{B})$ with $r_{A}$ ($r_{B}$) being a row of the matrix block $A$ ($B$). We let $R_{A}$ ($R_{B}$) denote the set of rows of the matrix block $A$ ($B$), whereas $\mathcal{H}_{n}$ denotes the set of all matrices $P$ with the aforementioned properties.

An helix associated with a matrix $P$ of type $\mathcal{H}_{n}$ is a connected directed graph $h$ whose construction goes as follows:

$(h1)$ (Vertices) Vertices of $h$ are entries of blocks $A$ and $B$. We let $h_{0}$ denote the set of vertices of $h$.

$(h2)$ Fix two different rows $i_{P} = (i_{A}, i_{B})$ and $j_{P} = (j_{A}, j_{B})$ of $P$.

$(h3)$ Choose sets $P_{A}$ and $P_{B}$ of pivoting entries also called pivoting vertices, $P_{A}\subset A$, $P_{B}\subset B$ such that $|P_{A}| = |P_{B}| = n$. Entries in $A\backslash P_{A}$ and $B\backslash P_{B}$ are said to be exterior entries or exterior vertices. In this case, if $x\in P_{A}$ ($x\in P_{B}$) then $x\notin i_{A}$ ($x\notin j_{B}$).

$P_{A}$ and $P_{B}$ are sets of the form:

where, $a_{i_{r}, j_{r}}\in R_{A}\backslash i_{A}$, $b_{t_{m}, h_{m}}\in R_{B}\backslash j_{B}$, $1\leq r, m\leq s$. It is chosen just only one entry $a_{i_{r}, j_{r}}$ ($b_{t_{m}, h_{m}}$) for each row in $R_{A}\backslash i_{A}$ ($R_{B}\backslash j_{B}$) and for each column $C_{A}$ ($C_{B}$) of $A$ ($B$).

$(h4)$ (Arrows) arrows in $h$ are defined in the following fashion:

$(a)$ Arrows in $h$ are either horizontal or vertical. We let $h_{1}$ denote the set of arrows of $h$.

$(b)$ Horizontal arrows connect a vertex of the matrix block $A$ ($B$) with a vertex of the matrix block $B$ ($A$). Vertical arrows only connect vertices in the same matrix block. Starting and ending vertices of horizontal (vertical) arrows are entries of the same row (column) of $P$.

$(c)$ The starting vertex of a horizontal (vertical) arrow is an exterior (pivoting) vertex. The ending point of a horizontal (vertical) arrow is a pivoting (exterior) vertex.

$(d)$ A pivoting vertex occurs as ending (starting) vertex just once. Thus, $h$ does not cross itself.

$(e)$ The first and last arrow of $h$ are horizontal and its starting vertex belongs to $i_{A}$.

$(f)$ Each vertical arrow is preceded by a unique horizontal arrow, and unless the first arrow, any horizontal arrow is preceded by a vertical arrow.

$(g)$ All the rows of $P$ are visited by $h$, and no row or column of $P$ is visited by arrows of $h$ more than once.

$(h)$ There are not horizontal arrows connecting exterior vertices of $j_{A}$ with vertices of $j_{B}$.

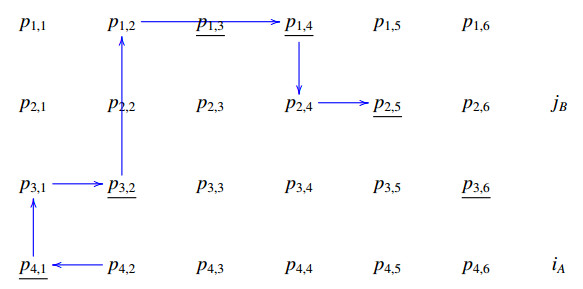
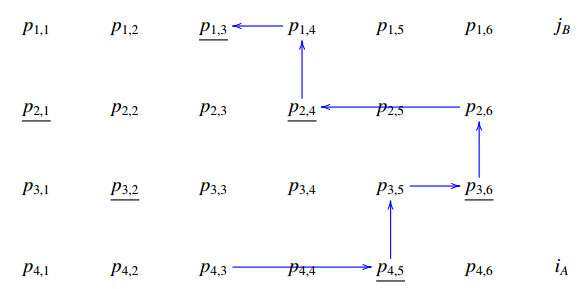
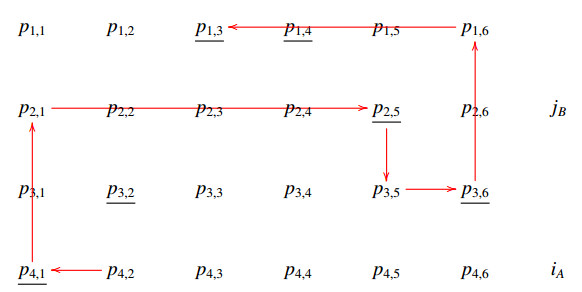
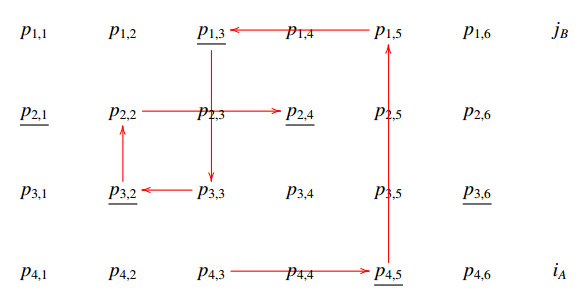
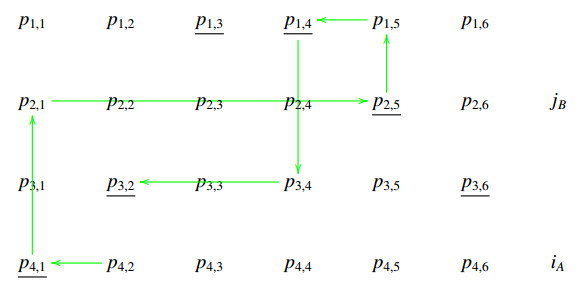
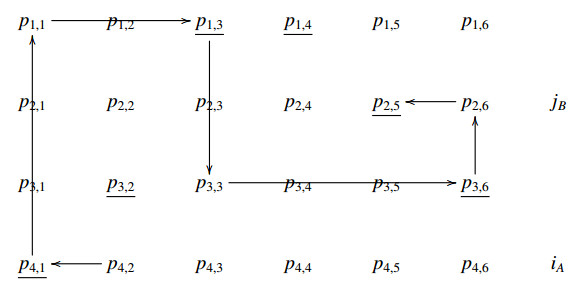
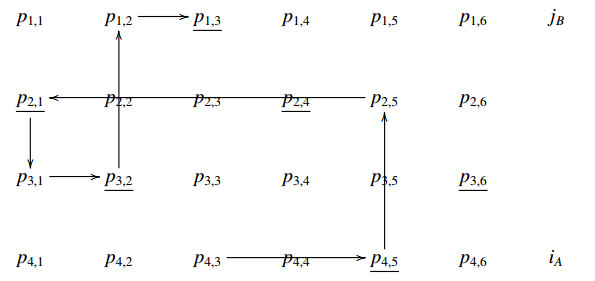
Remark 5. We let $(i_{P}, j_{P}, P_{A}, P_{B})$ denote the set of all helices which can be built by fixing these data associated with a matrix $P$ of type $\mathcal{H}_{n}$, $h^{P}_{n} = |(i_{P}, j_{P}, P_{A}, P_{B})|$ denotes the corresponding cardinality. See diagrams (A1)–(A8) in the Appendix where it is presented a set $(4_{P}, 2_{P}, P_{A}, P_{B})$ defined by the word $BAABAB$.

Matrix presentations of preprojective Kronecker modules $p$ of type III are of type $\mathcal{H}_{n}$, $n\geq1$ (In this case, $W_{p} = AA\dots ABB\dots B$). In ^[10], the authors studied sets of helices $(1_{p}, (n+1)_{p}, p_{A} = \{a_{i+1, i}\mid 1\leq i\leq n\}, p_{B} = \{b_{i, i}\mid 1\leq i\leq n\})$ associated with this kind of matrices.

Proposition 6. If $\mathcal{W}_{P}$ is the set of matrix words associated with a matrix $P$ of type $\mathcal{H}_{n}$ then $|\mathcal{W}_{P}|$ equals $\underset{m = 0}{\overset{n^{2}}{\sum\limits}}P(n, n, m) = (n+1)C_{n}$, where $P(n, n, m)$ denotes the number of partitions of $m$ into $n$ parts, each $\leq n$, $P(n, n, 0) = 1$, and $C_{n}$ denotes the $n$th Catalan number.

Proof. Each matrix word $W_{P}$ of the form $W_{P} = l_{m_{1}}\dots l_{m_{n}}\dots l_{m_{2n}}$, $l_{m_{h}}\in\{A, B\}$, $1\leq h\leq 2n$, gives rise to an integer partition $\lambda = (\lambda_{1}, \lambda_{2}, \dots, \lambda_{t})$, $\lambda_{i}, t\leq n$ of a nonnegative integer number $m\leq n^{2}$ by defining $\lambda_{1}$ as the number of $A$'s after the first occurrence of the letter $B$, $\lambda_{2}$ is the number of $A'$s after the second occurrence of the letter $B$ and so on. Since there are $n$ letters $A'$s and $n$ letters $B'$s in $W_{P}$ then the number of words associated with $P$ is $\binom{2n}{n}$. The result holds.

In Theorem 10 we prove that the number of helices $h^{p}_{n}$ associated with a preprojective Kronecker module, $p = (n+1, n)$ is $h^{p}_{n} = n!\lceil \frac{n}{2}\rceil$.

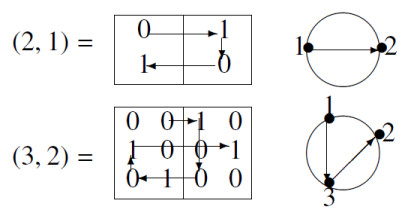
If we associate with a set of $n$ equidistant points on a circle the rows of a representation $p = (n+1, n)$ then the number of helices containing the fixed arrow $a_{1, 1}\rightarrow b_{1, 1}$ equals the number $a(n)$ of ways of connecting $n+1$ equally spaced points on a circle with a path of $n$ line segments ignoring reflections. In this case, vertical edges in a helix are in bijective correspondence with the edges of the path in the circle (Figure 5 shows examples of helices and these kinds of paths). Thus

Sequence $a(n)$ is recorded as A052558 in the OEIS.

3.   Categorification of the sequences A052558 and A052591

Results in this section can be interpreted as categorifications (see Remark 2) of the sequences $(n-1)!\lceil \frac{n}{2}\rceil$ and $n!\lceil \frac{n}{2}\rceil$ (A052558 and A052591 in the OEIS, respectively) via Kronecker modules and Brauer configuration algebras. Theorems 7 and 10 and Corollaries 8 and 9 prove that the number of helices associated with preprojective Kronecker modules is invariant with respect to admissible transformations.

The following results regard the number of helices associated with matrices of type $\mathcal{H}_{n}$ and in particular with preprojective Kronecker modules (see Figure 4), $k$ is an algebraically closed field.

Theorem 7. Let $(P, A, B, n)$, $(P', A', B', n)$, $H_{P}$ and $H_{P'}$ be two matrices of type $\mathcal{H}_{n}$ with corresponding sets of helices $H_{P}$ and $H_{P'}$ defined by systems of the form $(i_{P}, j_{P}, P_{A}, P_{B})$ and $(f_{P'}, g_{P'}, P'_{A'}, P'_{B'})$, respectively. Then $|H_{P}| = h^{P}_{n} = |H_{P'}| = h^{P'}_{n}$.

Proof. Firstly, we suppose without loss of generality that, $i_{P}\neq f_{P'}$ and $j_{P}\neq g_{P'}$. Then, we note that each helix $h\in (i_{P}, j_{P}, P_{A}, P_{B})$ gives rise to a unique helix $h'\in (i_{P}, g_{P}, P_{A''}, P_{B''})$, where $P_{A''}$ and $P_{B''}$ are suitable sets of pivoting entries in $P$. The process consists of copying helix $h$, in such a way that each occurrence of entries of $j_{P}$ is substituted by a corresponding occurrence of $g_{P}$ (taking into account the new sets of pivoting vertices, $P_{A''}$ and $P_{B''}$), conversely, each occurrence of $g_{P}$ is substituted by a corresponding occurrence of $j_{P}$, keeping without changes the remaining rows visited by the helix $h$. For example, if a vertical arrow $v\in h_{1}$ connects entries $p_{i, j}$ (starting vertex) and $p_{i', j}$ (ending vertex) in $P$ then the corresponding vertical arrow $v'\in h'_{1}$ connects entries of the rows $i$ and $i'$ if $i\in\{ j_{P}, g_{P}\}$ and $i'\notin \{j_{P}, g_{P}\}$ or if $i$ and $i'$ are such that $i, i'\notin\{j_{P}, g_{P}\}$, $v'$ connects rows $i$ and $j$ ($g$) if $i' = g$ ($i' = j$). We let $\sigma$ denote the bijection, $\sigma:(i_{P}, j_{P}, P_{A}, P_{B})\rightarrow (i_{P}, g_{P}, P_{A''}, P_{B''})$ defined by these substitutions. Thus, if a bijection $\delta:(i_{P}, g_{P}, P_{A''}, P_{B''})\rightarrow (f_{P}, g_{P}, P_{A'}, P_{B'})$ is defined as $\sigma$ where $P_{A'}$ and $P_{B'}$ are sets of pivoting entries of $P$ given by $P'_{A'}$ and $P'_{B'}$ respectively, then the maps composition $\delta\sigma$ is also a bijection from $(i_{P}, j_{P}, P_{A}, P_{B})$ to $(f_{P}, g_{P}, P_{A'}, P_{B'})$. Any helix $h'\in (f_{P}, g_{P}, P_{A'}, P_{B'})$ corresponds uniquely to an helix $h''\in(f_{P'}, g_{P'}, P'_{A'}, P'_{B'})$ via the identification $\tau: P\rightarrow P'$ such that $\tau(p_{i, j}) = p'_{i, j}$, in this case $p_{i, j}\in P_{A'}$ ($p_{i, j}\in P_{B'}$) if and only if $p'_{i, j}\in P'_{A'}$ ($p'_{i, j}\in P'_{B'}$). In general, a copy $h''\in (f_{P'}, g_{P'}, P'_{A'}, P'_{B'})$ of an helix $h'\in (f_{P}, g_{P}, P_{A}, P_{B})$ can be built taking into account that an initial exterior vertex $e_{f, j}\in h'$ has a vertex $e'_{f, j'}\in f_{A'}$ as its corresponding initial exterior copy and $h''$ visits the same rows in the same order as those visited previously by $h'$. We are done.

Examples of copies of elements of the set

associated with a matrix $P$ of type $\mathcal{H}_{3}$ and defined by the word $W_{P} = BAABAB$ are given in the Appendix (see A1–A8). In such a case, the corresponding copies belong to the set

and the matrix $P$ is partitioned according to the word $ABABBA$.

Corollary 8. Let $W_{P} = l_{m_{1}}\dots l_{m_{2n}}$ and $W'_{P} = l'_{m_{1}}\dots l'_{m_{2n}}$; $l_{m_{n}}, l'_{m_{n}}\in \{A, B\}$ be two words associated with a matrix $P$ of type $\mathcal{H}_{n}$ with corresponding sets of helices $H_{P} = (i_{P}, j_{P}, P_{A}, P_{B})$, and $H'_{P} = (f'_{P}, g'_{P}, P'_{A}, P'_{B})$. Then $|H_{P}| = |H'_{P}|$.

Proof. The result follows from Theorem 7 by replacing, $P', A', B', P'_{A'}, P'_{B'}, f_{P'}$ and $g_{P'}$ for $P, A, B, P'_{A}, P'_{B}, f'_{P}$ and $g'_{P}$, respectively.

Corollary 9. If for $n\geq 1$, $P$ and $P'$ are equivalent preprojective Kronecker modules with dimension vector of the form $[n+1 \; n]$ and corresponding sets of helices $H_{P}$ and $H_{P'}$ then $|H_{P}| = |H_{P'}|$.

Proof. Matrix presentations of preprojective Kronecker modules $P$ and $P'$ are both of type $\mathcal{H}_{n}$ defined by words of the form $AA\dots ABB\dots BB$.

Theorem 10. If for $n\geq1$, $P$ denotes a preprojective Kronecker module then the number of helices associated with $P$ is $h^{P}_{n} = n!\lceil\frac{n}{2}\rceil$ where $\lceil x \rceil$ denotes the smallest integer greatest than $x$.

Proof. According to Theorem 7 and Corollary 9, it suffices to determine the number of helices $|(1_{p}, (n+1)_{p}, p_{A} = \{a_{i+1, i}\mid 1\leq i\leq n\}, p_{B} = \{b_{i, i}\mid 1\leq i\leq n\})|$ associated with preprojective Kronecker modules $p = (n+1, n)$ of type III and words of the form $W_{p} = AA\dots ABB\dots B$.

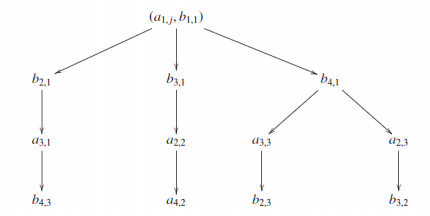
Firstly, we note that there is only one helix associated with the indecomposable preprojective modules $(2, 1)$ and $(3, 2)$. And the vertices sequence of helices associated with the indecomposable $(4, 3)$ with $a_{1, j}$ fixed are:

The number of helices is given by the number of vertices at the last level of the rooted tree showed in Figure 6:

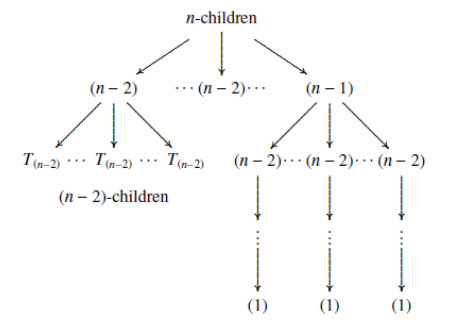
Suppose now that the result is true for any indecomposable preprojective Kronecker module $(t+1, t)$, $1\leq t < n$ then we can see that in general the rooted tree $T_{n}$ associated with the indecomposable preprojective Kronecker module $(n+1, n)$ has the following characteristics bearing in mind that vertex $b_{1, 1}$ gives the root node $a^{0}_{1}$:

$(a) \; a^{0}_{1}$ has $n$ children enumerated from the left to the right as $(a^{1}_{1}, a^{1}_{2}, \dots, a^{1}_{n})$,

$(b)$ For $1\leq i\leq n-1$ each vertex $a^{1}_{i}$ has $n-2$ children enumerated from the left to the right as $(a^{1}_{i, 1}, a^{1}_{i, 2}, \dots, a^{1}_{i, n-2})$ whereas vertex $a^{1}_{n}$ has $n-1$ children of the form $(a^{1}_{n, 1}, a^{1}_{n, 2}, \dots, a^{1}_{n, n-1})$, each children of a vertex $a^{1}_{n, l_{1}}$, $1\leq l_{1}\leq n-1$ has $n-2$ children $a^{1}_{n, l_{1}, l_{2}}$ with $1\leq l_{2}\leq n-2$, in general for this particular tree a vertex $a^{1}_{n, l_{1}, l_{2}, l_{3}, \dots, l_{t}}$ has $n-(t+1)$ children, $1\leq t\leq n-2$. Note that the number of vertices at the last level of the rooted tree $T'_{n}$ with $a^{1}_{n}$ as root node is $(n-1)!$,

$(c)$ For each $h$, $1\leq h\leq n-2$, vertex $a^{1}_{i, h}$ is a root node of the tree $T_{n-2}$.

Figure 7 shows the general structure of the rooted tree $T_{n}$.

According to the rules $(a)-(c)$ the number of vertices $L_{T_{n}}$ at the last level of the tree $T_{n}$ is given by the formula

We are done.

Remark 11. Sequence A052558 is categorified via the number of helices associated with preprojective Kronecker modules, if in the condition $(e)$ of its definition, it is assumed that the starting vertex is fixed. Without such fixing condition the number of helices associated with a preprojective Kronecker module is given by the sequence encoded as A052591 in the OEIS.

3.1.   Sequence A052591 Via Brauer configuration algebras

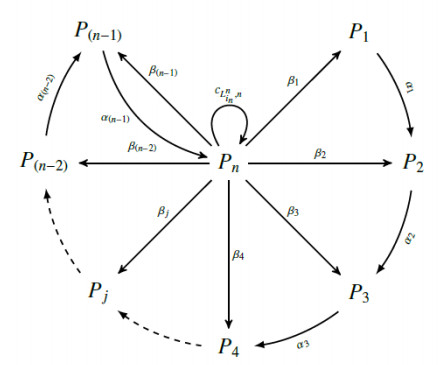
In this section, categorification of elements of the integer sequence A052591 is given via the number of summands in the heart of indecomposable projective modules over the Brauer configuration algebra $\Lambda_{K^n}$ defined by the Brauer configuration $K^{n} = (K^{n}_{0}, K^{n}_{1}, \mu, \mathcal{O})$ with the following properties for $n\geq3$ fixed:

1)

2) The orientation $\mathcal{O}$ is defined in such a way that for $t\geq1$

3) The multiplicity function $\mu$ is such that $\mu(x_{1}) = \mu(x_{2}) = 1$.

where the symbol $x^{(j)}_{i}$ in a given polygon $V_{t}$ means that $\mathrm{occ}(x_{i}, V_{t}) = j$. Note that, the specializations $x_{1} = 1$ and $x_{2} = 2$ allows describing polygons $V_{t}$ as integer partitions of numbers in the sequence A052591 (see Eq (1.2)).

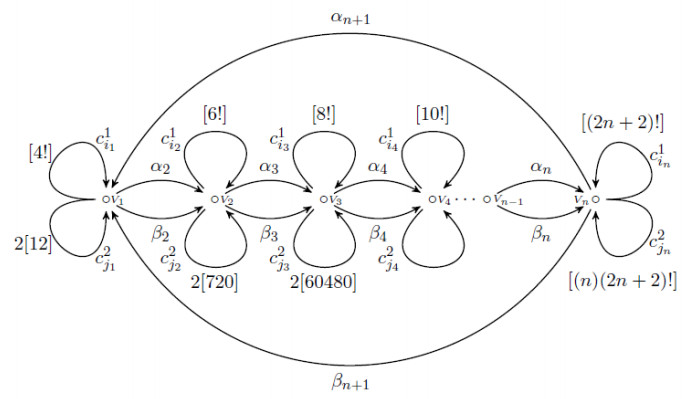
Figure 8 shows the Brauer quiver $Q_{K^{n}}$ associated with this configuration (numbers $n_{t_{1}} (n_{t_{2}})$ attached to the loops denote the occurrence of the vertex ($x_{1}$ above, $x_{2}$ below) in the corresponding polygon $V_{t}$, $1\leq t\leq n$), $c^{1}_{i_{t}} (c^{2}_{j_{t}})$ denotes a set of loops associated with the vertex $V_{t}$, $|c^{1}_{i_{t}}| = l^{1}_{t} = n_{t_{1}}-1$, $|c^{2}_{j_{t}}| = l^{2}_{t} = n_{t_{2}}-1$.

The admissible ideal ${I}$ is generated by the following relations (in this case, if there are associated $l^{1}_{t}$ ($l^{2}_{t}$) loops at the vertex $V_{t}$ associated with $x_{1}$ (associated with $x_{2}$) then we let $P^{j}_{t}$ denote the product of $j\leq l^{m}_{t}$ loops, $m\in\{1, 2\}$), $c^m_{h_s}$ is a notation for a set of cycles $\{c^m_{h_{s, 1}}, c^m_{h_{s, 2}}, \dots, c^m_{h_{s, l^{m}_{s}}}, m\in\{1, 2\}, h\in\{i, j\}, s\in\{1, 2, \dots, n\}\}$:

1) $c^{1}_{i_{s, x}}c^{1}_{i_{s, y}}-c^{1}_{i_{s, y}}c^{1}_{i_{s, x}}$, for all possible values of $i, s, x, y$,

2) $c^{2}_{j_{s, x}}c^{2}_{j_{s, y}}-c^{2}_{j_{s, y}}c^{2}_{j_{s, x}}$, for all possible values of $i, s, x, y$,

3) $c^{1}_{i_{s, x}}c^{2}_{j_{s, y}}$ and $c^{2}_{j_{s, x}}c^{1}_{i_{s, y}}$, for all possible values of $i, s, x, y$,

4) $c^{1}_{i_{s, x}}\beta_{s+1}$; $c^{2}_{j_{s, y}}\alpha_{s+1}$; $\beta_{s}c^{1}_{i_{s, x}}$; $\alpha_{s}c^{2}_{j_{s, x}}$, for all possible values of $i, s, x, y$,

5) $(c^{1}_{i_{s, x}})^2$; $(c^{2}_{j_{s, y}})^2$, for all possible values of $i, s, x, y$,

6) $\alpha_{t}\alpha_{t+1}$; $\alpha_{n+1}\alpha_{2}$; $\beta_{t}\beta_{t+1}$; $\beta_{n+1}\beta_{2}$$; \;\alpha_{t}\beta_{t+1}$; $\beta_{j}\alpha_{j+1}$; $\alpha_{n+1}\beta_{2}$; $\beta_{n+1}\alpha_{2}$, for all possible values of $j, t$,

7) $\alpha_{i}P^{j}_{i}\gamma_{i+1}$; $\alpha_{n+1}P^{j}_{1}\gamma_{2}$; $\beta_{t}P^{h}_{t}\gamma_{t+1}$; $\beta_{n+1}P^{h}_{1}\gamma_{2}$; $0 < j < l^{1}_{i}$, $0 < h < l^{2}_{t}$, $1\leq i, t\leq n$, $\gamma\in\{\alpha, \beta\}$,

8) For all the possible products (special cycles) of the form:

relations of the form $\varepsilon^{r}_{i}-\varepsilon^{s}_{j}$, $r, s\in\{1, 2, 3, 4\}$, $i, j\in\{1, 2\}$ take place. Note that, products of the form $P^0_{t-1}$ correspond to suitable orthogonal primitive idempotents $e_{t}$, $1\leq t\leq n$,

9) $\varepsilon^{1}_{1}\alpha_{t}$, $\varepsilon^{3}_{2}\beta_{t}$.

The following result holds for indecomposable projective modules over the algebra $\Lambda_{K^n}$.

Corollary 12. For $n\geq3$ fixed and $1\leq t\leq n$, the number of summands in the heart of the indecomposable projective representation $V_{t}$ over the Brauer configuration algebra $\Lambda_{K^n}$ equals the number of helices associated with the preprojective Kronecker module $(2t+3, 2t+2)$, $1\leq t\leq n$.

Proof. Firstly we note that for any $t$, $\mathrm{rad}^2 \; V_{t}\neq0$. Thus according to the Theorem 1 the number of summands in the heart of any of the indecomposable projective modules $V_{t}$ equals $\mathrm{occ}(x_{1}, V_{t})+\mathrm{occ}(x_{2}, V_{t}) = (2t+2)!+t(2t+2)! = h^{p}_{2t+2} = h^{(2t+3, 2t+2)}_{2t+2}$ which is the number of helices associated in a unique form to the indecomposable preprojective Kronecker module $(2t+3, 2t+2)$. We are done.

The following results regard the dimension of algebras of type $\Lambda_{K^n}$.

Corollary 13. For $n\geq3$ fixed, it holds that $\frac{1}{2}(\mathrm{dim}_{k} \; \Lambda_{K^{n}}) = n+t_{\gamma_{n}-1}+t_{\delta_{n}-1}$, where $\gamma_{n} = \underset{m = 1}{\overset{n}{\sum\limits}}m(2m+2)!$, $\delta_{n} = \underset{m = 1}{\overset{n}{\sum\limits}}(2m+2)!$, and $t_{h}$ denotes the $h$th triangular number.

Proof. Proposition 3 allows concluding that $\mathrm{dim}_{k} \; \Lambda_{K^n}/{I} = 2n+\underset{i = 1}{\overset{2}{\sum\limits}}|C_{i}|(|C_{i}|-1)$ where for each $i = 1, 2$, $|C_{i}| = val({x_{i}})$. The theorem holds taking into account that for any $j\geq 2$, $j(j-1) = 2t_{j-1}$.

Corollary 14. For $n\geq3$ fixed, it holds that $\mathrm{dim}_{k} \; Z(\Lambda_{K^{n}}) = -n+1+\underset{t = 1}{\overset{n}{\sum\limits}}h^{p}_{2t+2}$.

Proof. Since $\mathrm{rad}^2 \; \Lambda_{K^n}\neq0$, the result is a consequence of Theorem 4 with $\mu(x_{1}) = \mu(x_{2}) = 1$, $|K^{n}_{0}| = 2$, $|K^{n}_{1}| = n$ and $\mathrm{occ}(x_{1}, V_{t})+\mathrm{occ}(x_{2}, V_{t}) = h^{p}_{2t+2}$.

Remark 15. Similar results as those given in Corollaries 12-14 can be obtained for preprojective Kronecker modules of the form $(4t+2, 4t+1), t\geq1$ by considering in the original Brauer configuration that

keeping the relations in the quiver without changes (bearing in mind of course the new occurrences of the vertices for the different products). In particular, it holds that $\mathrm{dim}_{k} \; Z(\Lambda_{K^{n}}) = -n+1+\underset{t = 1}{\overset{n}{\sum\limits}}h^{p}_{4t+1}.$

4.   Brauer configuration algebras arising from counting Functions

In this section, we consider Brauer configurations arising from counting functions which are strictly increasing integer sequence whose elements count a given class of objects $\mathcal{D}_{n}$. For instance, $\mathcal{D}_{n}$ can be the set of linear extensions of a poset $(\mathcal{P}_{n}, \unlhd) = \{(i, j)\in\mathbb{N}^{2}\mid 0\leq i\leq j\leq n\}$, where $\unlhd$ is a partial order defined on $\mathcal{P}_{n}$ such that $(i, j)\unlhd (i', j')$ if and only if $i\leq i'$ and $j\leq j'$. According to Stanley ^[11], the number of linear extensions $e(\mathcal{P}_{n})$ of $\mathcal{P}_{n}$ is equal to the number of lattice paths from $(0, 0)$ to $(n, n)$ with steps $(1, 0)$ and $(0, 1)$, which never rise above the main diagonal $x = y$ of the plane $(x, y)$-plane. It can be shown that $e(\mathcal{P}_{n})$ is given by the $n$th Catalan number $C_{n} = \frac{1}{n+1}\binom{2n}{n}$.

We define now a family of Brauer configuration algebras $\Lambda_{D^{n}}$, $n > 1$ arisen from Brauer configurations $D^{n}$ whose nontruncated vertices are in correspondence with objects of type $\mathcal{D}_{n}$, polygons are obtained by choosing objects of type $\mathcal{D}_{s}$, for $1\leq s\leq n$. We assume the notation $L^{s}_{j, n}\in\mathcal{D}_{s}$ for the $j$th object of type $s$ in a given polygon. Without loss of generality, we assume that for the first polygon $P_{1}$, it holds that $|P_{1}| = u_{1} > 1$.

For $n\geq 2$ fixed, the definition of the Brauer configuration

goes as follows:

In $P^{h}_{(h-1)}$, it holds that, $1\leq i_{1}\leq u_{1}$ if $s = 1$, and $1\leq i_{s}\leq u_{s}-u_{(s-1)}$, if $s > 2$.

The orientation $\mathcal{O}^{n}$ is defined by the usual order of natural numbers. Thus, for a vertex $L^{i}_{j, n}\in D_{0}^{n}\backslash P^{n}_{n}$, the successor sequence has the form

For vertices $L^{(n-1)}_{r, n}$, the successor sequence has the form $P_{(n-1)} < P_{n}$, whereas for vertices of the form $L^{n}_{r, n}\in P^{n}_{n}$, the orientation is of the form $P_{n} < P_{n}$.

The following Figure 9 shows the shape of the Brauer quiver $Q_{D^{n}}$ defined by $D^{n}$.

$\alpha_{j}$, $\beta_{j}$ and $c_{L^{n}_{i_{n}}, n}$ denote $j\times 1$-matrices of the form:

where $\alpha^{j}_{L^{s}_{i_{s}}, n}$ ($\beta^{j}_{L^{s}_{i_{s}}, n}$) is a set of arrows defined by the successor sequence at vertex $L^{s}_{i_{s}, n}$ connecting the corresponding polygons (polygon $P_{n}$ with the corresponding $P_{j}$). And $c_{L^{n}_{i_{n}, n}}$ is a set of loops defined by vertices ${L^{n}_{i_{n}, n}}$, $1\leq i_{n}\leq u_{n}-u_{(n-1)}$.

The following relations generate the admissible ideal $J$ of the Brauer configuration algebra $\Lambda_{D^{n}} = kQ_{D^{n}}/J$, for all possible values of $i, i', j, j', r, r'$ and $n$.

1) $(c_{L^{n}_{{r}, n}})^{2}$, $c_{L^{n}_{{r}, n}}c_{L^{n}_{{r'}, n}}$, $r\neq r'$,

2) $\alpha^{j}_{L^{i}_{{r}}, n} \alpha^{j}_{L^{i'}_{{r'}}, n}$, $i\neq i'$,

3) $\alpha^{j}_{L^{i}_{{r}}, n} \alpha^{(j+1)}_{L^{i'}_{{r'}}, n}$,

4) $c_{L^{n}_{i_{n}, n}}\beta_{i}$,

5) $\alpha_{(n-1)}c_{L^{n}_{i_{n}, n}}$,

6) For $1\leq j\leq n$, fixed and $1\leq i\leq j$, $s_{L^{i}_{j, n}}-s_{L^{j}_{j', n}}$ where $s_{x}$ is a special cycle associated with the vertex $x$,

7) $\beta_{i}\alpha_{i}$,

products of the form; $\beta_{i}\alpha_{i}$, $\alpha_{(n-1)}c_{L^{n}_{i_{n}, n}}$, $c_{L^{n}_{i_{n}, n}}\beta_{i}$ means that relations of the form $xx'$, $y'y$ and $z'z$ take place where $x'$, $y'$ and $z'$ are entries of the corresponding matrices.

The following result categorifies numbers of a counting function $u_{t}$, for $t\geq1$.

Theorem 16. For $1\leq i\leq n$ and $n > 1$ fixed, the number of summands in the heart of the indecomposable projective module $P_{i}$ over the algebra $\Lambda_{D^{n}}$ is $u_{i}$.

Proof. Since $\mathrm{rad}^{2} \; P_{i}\neq0$, then the number of summands in the heart of the indecomposable projective module $P_{i}$ equals the number of its nontruncated vertices counting repetitions, which by definition is given by the sum $u_{1}+(u_{2}-u_{1})+\dots+(u_{(i-1)}-u_{(i-2)})+(u_{i}-u_{(i-1)}) = u_{i}$. We are done.

Theorem 17. For $n\geq 1$ fixed, $\mathrm{dim}_{k} \; \Lambda_{D^{n}} = 2n+n(n-1)u_{1}+2\underset{i = 2}{\overset{n}{\sum\limits}}t_{(n-i)}(u_{i}-u_{(i-1)})$.

Proof. It suffices to note that $val(L^{i}_{i_{s}, n}) = n-i+1$ and $\mu^{n}(L^{i}_{i_{s}, n}) = 1$ for any $L^{i}_{i_{s}, n}\in D_{0}^{n}\backslash P^{n}_{n}$, whereas for any $x\in P^{n}_{n}$, it holds that $val(x) = 1$ and $\mu^{n}(x) = 2$. We are done.

Since for any $n > 1$, $\mathrm{rad}^{2} \; \Lambda_{D^{n}}\neq0$, then we have the following result regarding the center of these algebras.

Theorem 18. For $n\geq 2$ fixed, $\mathrm{dim}_{k} \; Z(\Lambda_{D^{n}}) = (u_{n}-u_{(n-1)})+(n+1)$.

Proof. Note that $|D_{0}^{n}| = u_{n}$, $|D_{1}^{n}| = n$, $\underset{\alpha\in D_{0}^{n} }{\sum\limits}\mu^{n}(\alpha) = 2u_{n}-u_{(n-1)}$. Since $\#(Loops \; Q_{D^{(n-1)}}) = |\mathcal{C}_{\mathcal{D}^{n}}|$, the theorem holds.

Remark 19. Perhaps, the sequence $C_{n}$ of Catalan numbers is one of the most interesting counting functions, they count the number of plane binary trees with $n+1$ endpoints (or $2n+1$ vertices), the number of triangulations of an $(n+3)$ polygon, or the number of paths $L$ in the $(x, y)$-plane from $(0, 0)$ to $(2n, 0)$ with steps $(1, 1)$ and $(1, -1)$ that never pass below the $x$-axis, such paths are called Dyck paths ^[11]. Thus, if $u_{n} = C_{n+1}$, $n\geq 1$ then Theorem 4.1 categorifies numbers in this sequence $C_{n}$ via these enumeration problems.

Since the number of compositions (partitions in which the order of the summands is considered) of a positive integer $n$ in which no 1's appear is the Fibonacci number $f_{(n-1)}$ ^[12]. Then Theorem 4.1 categorifies these numbers by assuming that $u_{n} = f_{(n-1)}$ with $n\geq 4$. If $j > 4$, then $\mathrm{dim}_{k} \; (Z(\Lambda_{D^{j}})/C_{j})-1 = f_{(j-4)}$, where $C_{j}$ is a $k$-subspace of $Z(\Lambda_{D^{j}})$ isomorphic to $Z(\Lambda_{D^{j-1}})$.

Theorem 16 categorifies the sequence $p(n)$ which gives the number of partitions of a positive integer $n$, recall the Hardy-Ramanujan theorem which states that for large $n$, $p(n)\sim \frac{1}{4n\sqrt{3}}e^{\pi\sqrt{\frac{2n}{3}}}$ (see also the sequence A002865 whose numbers give the differences $p(n)-p(n-1)$). In this case, we use $u_{n} = p(n+1)$, $n\geq1$.

Another interesting sequence categorified by Theorem 4.1 is the sequence $M(n)$ encoded in the OEIS as A000372, which consists of Dedekind numbers, these numbers count the number of antichains in the powerset $2^{\boldsymbol{n}}$ (i.e., the set consisting of all the subsets of $\boldsymbol{n} = \{1, 2, 3, \dots, n\}$) ordered by inclusion or the number of elements in a free distributive lattice on $n$ generators. In this case $u_{n} = M(n)$, for $n\geq1$, worth noting that up to date only 8 numbers of this sequence are known.

5.   Concluding remarks

Any counting function (e.g., Fibonacci numbers, Catalan numbers, or Dedekind numbers) can be categorified in the sense of Ringel and Fahr via indecomposable projective modules over some Brauer configuration algebras. In particular, integer sequences encoded in the OEIS as A052558 and A052591 are categorified by preprojective Kronecker modules via some helices, which are suitable directed graphs associated with these modules.

Acknowledgments

This research has been supported by the Seminar Alexander Zavadskij on Representation of Algebras and Its Applications at Universidad Nacional de Colombia.

Conflict of interest

The authors declare there are no conflicts of interest.

Appendix

In this section, we present the set of helices

associated with a matrix $P$ of type $\mathcal{H}_{3}$ and defined by the word $W_{P} = BAABAB$. The corresponding copies (see Theorem 7) in

are also shown according with the associated word $ABABBA$.