Multi-step ahead ozone level forecasting using a component-based technique: A case study in Lima, Peru

1.   Introduction

Epidemics are widespread around the world, and always jeopardize public lives and health, such as COVID-19, malaria, severe acute respiratory syndrome (SARS), influenza and so on. The public has taken all kinds of measures to struggle against the different infectious epidemics. Various of mathematical models are established to research dynamics and influences of prevention and control for different epidemics [12,23,22,10,9,15]. Recently, both the popularization of knowledge about infectious diseases and the improvement of treatment have built a solid foundation for epidemics' prevention. This popularization can also lead to the strengthening in public self-protection. For instance, since Chinese had owned strongly self-protection and governments of China had taken efficient treatments, COVID-19 was first under effective control in China [11,17,13]. As a result, it is necessary to integrate self-protection and treatment into epidemic models. Because epidemics are always discovered at one location and then spread to other areas [21], reaction-diffusion models become essential to describe this spatial spread. Simultaneously, epidemic models with spatial spread usually can result in a development from a diseases-free state to an infective state, which can be predicted a wave for this evolution of epidemics. Consequently, traveling wave solution becomes critical to study the spatial spread of epidemics [7,8,18,20].

Many people have analyzed traveling wave solution and the asymptotic speed of propagation of classic compartmental epidemic models [16,26,1,4,30,28,32,25]. Ducrot and Magal [3] studied the existence and the non-existence of traveling wave solution satisfying a diffusive epidemic model with age-structure and constant recruitment, and constructed a suitable Lyapunov functional to discuss their asymptotic behavior at infinity. Li et al. [14] found that the existence and the non-existence of traveling wave solution for the system which is a nonlocal dispersal delayed SIR model with constant recruitment and Holling-slowromancapii@ incidence rate are determined via both the minimal wave speed and the basic reproduction number $R_0$ defined by the corresponding reaction system. Zhang et al.[29] considered the existence of traveling wave solution satisfying a influenza model with treatment for infectious individuals. Zhao et al. [31] proved the existence and non-existence of traveling wave solution for a SIR model with multiple parallel infectious stages which own same diffusion coefficients. Then Zhao et al. [33] established a two-groups reaction-diffusion epidemic model to research the influence of host heterogeneity in spread of disease by applying the traveling wave solution. However, human self-protection for susceptible individuals and treatment for infectious individuals were not considered together in a SEIR diffusion epidemic model.

In this paper, we firstly integrate self-protection into the classical reaction-diffusion SEIR model with constant recruitment, so susceptible individuals are divided into two groups: susceptible individuals $S_1$ without self-protection and susceptible people $S_2$ with self-protection. Next, the treatment for infectious individuals is considered such that $I_1$ represents the infectious with treatment and $I_2$ means the infectious without it. Therefore, a reaction-diffusion SEIR model is constructed as system (1), where $t\in\mathbb{R_+}$ and $x\in\mathbb{R}$. In this model, $S_i(x,\ t)$ and $I_i(x,\ t)$ $(i = 1,\ 2)$ represent the density of two groups of susceptible and infectious individuals above determined, respectively. $E(x,\ t)$ represents the density of individuals who are infected without infectivity. $R(x,\ t)$ represents the density of individuals who recover and own permanent immunity. $d_1,\ d_2,\ D_0,\ D_1,\ D_2,$ and $D$ represent diffusion coefficients of $S_1,\ S_2,\ E,\ I_1,\ I_2$ and $R,$ respectively. $\Lambda$ is constant recruitment. $\beta$ is bilinear incidence. $\mu$ is the sum of the mortality rate. $\alpha_i$ is the recovery rate of $I_i\ (i = 1,\ 2),$ respectively. $\gamma$ is the reciprocal of latency. $q_i$ is the proportion of individuals entering $I_i\ (i = 1,\ 2),$ respectively. $\rho$ is the migration rate from $S_1$ to $S_2.$ $\sigma$ is the rate which susceptible individuals with self-protection reduce contacts with infectious. $\theta$ represents the rate that the treatment for the infectious reduce their contacts with others.

Throughout this aritcle, we make the following assumption:

$\rm(A)$ $d_1 = d_2: = d,\ d>D_0>D_i>0,\ \Lambda,\ \beta,\ \theta,\ \rho,\ \mu,\ \sigma,\ \gamma,\ q_1,\ q_2,\ \alpha_i>0,\ q_1+q_2 = 1,\theta\in(0,\ 1],\ \sigma\in(0,1]$ for $i = 1,\ 2$.

In fact, for making a living, the susceptible has to move, and their diffusion is almost same without special cases. Especially, the susceptible with self-protection may take some methods, such as wearing masks, avoiding crowed public places and so on, to decrease the likelihood of connects with the infectious. The infectious could reduce going out owing to discomfort by disease. Thus, the assumption can better close to reality. In mathematical analysis of this model, the assumption (A) also can help us get an upper bound for the different susceptible and infected components to research the asymptotic behavior as $x\rightarrow+\infty.$

Since the equations $S_i(x,\ t),\ E(x,\ t)$ and $I_i(x,\ t)\ (i = 1,\ 2)$ are fully decoupled from $R(x,\ t)$, we only need to study the sub-system:

where $t\in\mathbb{R_+}$ and $x\in\mathbb{R}$.

The structure of this article is as follows. In Section 2, we firstly obtain the basic reproduction number $R_0$ and two non-negative constant equilibriums for the corresponding reaction system, and these equilibriums are also two non-negative constant equilibriums for system (2). Then, we find a $c^*>0$ called as the minimal spread speed. Next, as $R_0>1$ and the spread speed $c>c^*,$ we prove that system (2) admits non-trivial and non-negative traveling wave solution by applying the Schauder fixed point theorem. Meanwhile, a suitable Lyapunov functional is used to prove the asymptotic behavior of traveling wave solution at $x\rightarrow+\infty.$ At last, we obtain the existence of traveling wave solution connecting two non-negative constant equilibriums when $R_0>1$ and $c = c^*.$ In Section 3, we firstly prove the non-existence of non-trivial and non-negative traveling wave solution connecting two non-negative constant equilibriums as $R_0\leq1$. In particular, when $R_0>1$ and $c\in(0,\ c^*),$ we also study the non-existence via the two-sided Laplace transform. In Section 4, we take advantage of numerical simulations to display the existence of traveling wave solution connecting two non-negative constant equilibriums. Simultaneously, we also conclude that self-protection and treatment can decrease the spread speed for an epidemic via numerical simulations.

2.   Existence of traveling wave solution

In order to research traveling wave solution of system (2), the first step is to find what kind of constant equilibriums of system (2) exist. It is well known that there always exists an equilibrium $(S_1^0,\ S_2^0,\ 0,\ 0,\ 0) = (\frac{\Lambda}{\rho+\mu},\ \frac{\rho\Lambda}{\mu(\mu+\rho)},\ 0,\ 0,\ 0)$ named as the disease-free equilibrium of system (2). We can also find a positive equilibrium by the following system,

The point $(S_1^0,\ S_2^0,\ 0,\ 0,\ 0)$ is also the disease-free equilibrium of system (3). Via the next generation matrix method formulated in [24], the basic reproduction number for system (3) denoted by $R_0$ can be expressed as

Furthermore, taking advantage of the direct Lyapunov functional method, which is similar in [15], can claim the below theorem.

Theorem 2.1. If $R_0\leq1$, then there exists a unique constant equilibrium of system (3) which is the disease-free equilibrium $(S_1^0,\ S_2^0,\ 0,\ 0,\ 0),$ and it is globally asymptotically stable. If $R_0>1$, system (3) admits a positive equilibrium which is the endemic equilibrium $(S_1^*, S_2^*,\ E^*,\ I_1^*,\ I_2^*),$ and it is globally asymptotically stable.

In the rest of Section 2, we always assume $R_0>1$. Then system (2) exists two constant equilibriums: the disease-free equilibrium $(S_1^0,\ S_2^0,\ 0,\ 0,\ 0)$ and the endemic equilibrium $(S_1^*,\ S_2^*,\ E^*,\ I_1^*,\ I_2^*)$. So we research the existence of traveling wave solution satisfying system (2) and connecting $(S_1^0,\ S_2^0,\ 0,\ 0,\ 0)$ and $(S_1^*,\ S_2^*,\ E^*,\ I_1^*,\ I_2^*).$ Now, we show that traveling wave solution of system (2) is special solution with the form as

Substitute formula (4) into systmen (2), and we can obtain the wave form equations as follows:

for $\xi\in\mathbb{R}$, where $^{'}$ and $^{''}$ represent the first and the second derivative with respect to $\xi,$ respectively. Since we would like to find positive traveling wave solution connecting two equilibria, we need the positive solution $(S_1(\xi),\ S_2(\xi),\ E(\xi),\ I_1(\xi),\ I_2(\xi))$ of system (5) with following boundary conditions

Linearizing the $E$-th and $I_i$-th equations of (5) at the disease-free equilibrium $(S_1^0,\ S_2^0,\ 0,\ 0,\ 0)$ yields

Set $(E(\xi),\ I_1(\xi),\ I_2(\xi)) = (\eta_0,\ \eta_1,\ \eta_2)e^{\lambda\xi}$ and plug it into above equations, then we can obtain characteristic equations

Let

Denote $\Theta(\lambda,\ c) = \lambda^2\tilde{A}-\mu\tilde{B}-\tilde{V}+\tilde{F}$. Then system (7) can reduce to

And define $A = \tilde{V}^{-1}\tilde{A},\ B = \tilde{V}^{-1}\tilde{B},\ F = \tilde{V}^{-1}\tilde{F}$, then we yield that

and

where $\eta = (\eta_0,\ \eta_1,\ \eta_2)^\mathrm{T},\ m_0(\lambda,\ c) = -D_0\lambda^2+c\lambda+\mu+\gamma,\ m_1(\lambda,\ c) = -D_1\lambda^2+c\lambda+\mu+\alpha_1,\ m_2(\lambda,\ c) = -D_2\lambda^2+c\lambda+\mu+\alpha_2$. Let $\mathcal{M}(\lambda,\ c) = (-A\lambda^2+B\lambda+I)^{-1}F$, then equation (8) becomes

Let $\rho(\lambda,\ c)$ be the principal eigenvalue of $\mathcal{M}(\lambda,\ c)$ and define

For $c\geq0$ and $\lambda\in[0,\ \lambda_c),$ a direct calculation indicates that

Moreover, some properties of $\rho(\lambda,\ c)$ can be described as the following lemma:

Lemma 2.2. Below statements hold:

(ⅰ) $\lambda_c$ is strictly increasing in $c\in[0, +\infty)$, and $\lim_{c\rightarrow+\infty}\lambda_c = +\infty$,

(ⅱ) $\rho(0,\ c) = \sqrt{R_0}$ for any $c\in[0,\ +\infty)$, $\rho(\lambda,\ 0)$ is strictly increasing in $[0,\ \lambda_c),$ and $\rho(\lambda,\ c)\rightarrow+\infty$ as $\lambda\rightarrow{\lambda_c-0}$ for any $c\geq0,$ where $R_0$ is the basic reproduction number for system (3),

(ⅲ) for $\forall\lambda\in(0,\lambda_c)$, $\frac{\partial}{\partial c}\rho(\lambda,\ c)<0.$

Proof. It is well known that (ⅰ) is established, so we only prove (ⅱ) and (ⅲ). It follows from the definitions of both $R_0$ and $\rho(\lambda,\ c)$ that $\rho(0,\ c) = \sqrt{R_0}$ for any $c\in[0,\ +\infty)$. Due to $\rho(\lambda,\ 0)>0$ and $m_i(\lambda,\ 0)>0$ for $\lambda\in[0,\ \lambda_c)$ with $i = 0,\ 1,\ 2,$ it is the fact that

for $\lambda\in[0,\ \lambda_c)$. In addition, we can indicate $\lim_{\lambda\rightarrow{\lambda_c-0}}m_i(\lambda,\ c) = 0\ (i = 0,\ 1,\ 2),$ respectively, so the principal eigenvalue $\rho(\lambda,\ c)$ tends to $+\infty$ as $\lambda\rightarrow\lambda_c-0$. The direct derivative of the spread speed $c$ can show that

for $\forall\lambda\in[0,\ \lambda_c).$ The proof is complete.

According to Lemma 2.2, we define

Then we conclude $\hat\lambda(0) = \sqrt{R_0}$ and $\lim_{c\rightarrow+\infty}\hat\lambda(c) = 0.$ Meanwhile, $\hat\lambda(c)$ is continuous and strictly decreasing in $c\geq0$. Assume that $R_0>1$, then there exists a $c^*>0$ such that $\hat\lambda(c^*) = 1,\ \hat\lambda(c)>1$ for $c\in[0,\ c^*)$ and $\hat\lambda(c)<1$ for $c\in(c^*,\ +\infty).$ Let

it indicates that $\rho(\lambda_{*},\ c^*) = 1$ and $\rho(\lambda_{*},\ c)<1$ for any $c>c^*$. Define

Because of $\rho(\lambda_{*},\ c)<1$ for $c>c^*$, we claim that the following lemma is established.

Lemma 2.3. Assume that $R_0>1$, then there exist $c^*>0,$ named as the minimal spread speed, and $\lambda_*\in(0,\ \lambda_{c^*})$ such that

(ⅰ) $\rho(\lambda,\ c)>1$ for any $c\in[0,\ c^*)$ and $\lambda\in(0,\ \lambda_c),$

(ⅱ) $\rho(\lambda_*,\ c^*) = 1,\ \rho(\lambda,\ c^*)>1$ for any $\lambda\in(0,\ \lambda_*)$ and $\rho(\lambda,\ c^*)\geq1$ for any $\lambda\in(0,\ \lambda_{c^*}),$

(ⅲ) as $c>c^*$, there exists $\lambda_1(c)\in(0,\ \lambda_*)$ such that $\rho(\lambda_1(c),\ c) = 1,\ \rho(\lambda,\ c)\geq1$ for $\lambda\in(0,\ \lambda_1(c))$ and $\rho(\lambda_1(c)+\varepsilon_n(c),\ c)<1$ for some decreasing sequence $\{\varepsilon_n(c)\}$ satisfying $\lim_{n\rightarrow+\infty}\varepsilon_n = 0$ and $\lambda_1(c)+\varepsilon_n(c)<\lambda_*\ (n\in\mathbb{Z}).$ Especially, $\lambda_1(c)$ is strictly decreasing in $c>c^*$.

Since the $\mathcal{M}(\lambda,\ c)$ is non-negative and irreducible for $\lambda\in[0,\ \lambda_c)$, the bleow lemma holds with utilizing the Perron-Frobenius theorem.

Lemma 2.4. Assume that $R_0>1$, for $c>c^*$, there are positive unit vectors $\eta(c) = (\eta_0(c),\ \eta_1(c), \eta_2(c))^\mathrm{T}$ and $\zeta^n(c) = (\zeta_0^n(c),\ \zeta_1^n(c),\ \zeta_2^n(c))^\mathrm{T}$ for $n\in\mathbb{Z}$ such that

Fix $c>c^*$ and let $\lambda_1(c),\ \eta(c) = (\eta_0(c),\ \eta_1(c),\ \eta_2(c))^\mathrm{T}$ and $\zeta^n(c) = (\zeta_0^n(c),\ \zeta_1^n(c), \zeta_2^n(c))^\mathrm{T}$ $(n\in\mathbb{Z})$ own same definitions in Lemma 2.3 and Lemma 2.4. For convenience, we use $\lambda_1,\ \varepsilon_n,\ \eta = (\eta_0,\ \eta_1,\ \eta_2)^\mathrm{T}$ and $\zeta^n = (\zeta_0^n,\ \zeta_1^n,\ \zeta_2^n)^\mathrm{T}\ (n\in\mathbb{Z})$ instant of them, respectively. It follows from Lemma 2.4 and $\rho(\lambda_1+\varepsilon_n,\ c)<1$ that following equations and inequalities are established for $n\in\mathbb{Z}$

and

According to the above argument, we can construct suitable sub- and super-solutions which are defined in below lemmas. And then the local existence of solution for system (5) is proved via the Schauder fixed point theorem.

Lemma 2.5. Let the vector function $\mathcal{P}(\xi) = (p_0(\xi),\ p_1(\xi),\ p_2(\xi))^{\mathrm{T}}$ with $p_i(\xi) = \eta_i(\xi)e^{\lambda_1\xi}$ for $\xi\in\mathbb{R}$ and $i = 0,\ 1,\ 2,$ and it satisfies

Lemma 2.6. For each $\omega>0$ small enough with $\omega<\min\{\lambda_1,\frac{c}{d}\}$ and $M>1$ sufficiently large, the vector function $S^{-}(\xi) = (S_1^{-}(\xi),S_2^{-}(\xi))^{\mathrm{T}}$ defined by $S_i^{-}(\xi) = \max\{S_i^0(1-Me^{\omega\xi}),\ 0\}\ (i = 1,\ 2)$ satisfies

for $\xi\in\mathbb{R}$ and $\xi\neq-\frac{1}{\omega}\ln{M}$.

Proof. When $\xi>-\frac{1}{\omega}\ln{M},$ $S_i^{-}(\xi) = 0$ for $i = 1,\ 2,$ and inequalities (12)-(13) hold. When $\xi<-\frac{1}{\omega}\ln{M},$ it implies that $S_i^{-}(\xi) = S_i^0(1-Me^{\omega\xi}$ and $p_i(\xi) = \eta_ie^{\lambda_1\xi}.$ Due to $\omega<\frac{c}{d}$ and $e^{-\frac{\lambda_1-\omega}{\omega}\ln{M}}\rightarrow0$ as $M\rightarrow+\infty,$ it is shown that

so the inequality (12) is established. Furthermore,

and the inequality (13) is set up. The lemma is completely proved.

Lemma 2.7. Let $0<\epsilon<\frac{\omega}{2}$ with $\epsilon = \varepsilon_{n_0}$ for some $n_0\in\mathbb{Z},$ and the eigenvector $\zeta^{n_0} = (\zeta_0^{n_0},\ \zeta_1^{n_0},\ \zeta_2^{n_0})^{\mathrm{T}}$ is defined by $\zeta = (\zeta_0,\ \zeta_1,\ \zeta_2)^{\mathrm{T}}.$ We define the vector map $\mathcal{H}(\xi) = (h_0(\xi),\ h_1(\xi),\ h_2(\xi))^{\mathrm{T}}$ with $h_i(\xi) = \max\{\eta_ie^{\lambda_1\xi}-K\zeta_ie^{(\lambda_1+\epsilon)\xi},\ 0\},$ where $\eta_i$ and $\zeta_i$ are defined in Lemma 2.4 with $i = 0,\ 1,\ 2,$ respectively. For $K>0$ large enough such that

then the vector map $\mathcal{H}(\xi)$ satisfies

Proof. Firstly, we prove the inequality (14). For $\xi<\frac{1}{\epsilon}\ln{\frac{\eta_0}{K\zeta_0}},$ we yield $h_0(\xi) = \eta_0e^{\lambda_1\xi}-K\zeta_0e^{(\lambda_1+\epsilon)\xi},$ $S_1^{-}(\xi) = S_1^0(1-Me^{\omega\xi}),$ and $S_2^{-}(\xi) = S_2^0(1-Me^{\omega\xi}).$ To prove the inequality (14), it is sufficient to show the following inequality:

which is

According to equations (10), the proof of the inequality (17) can be replaced by proving

Because $S_i^0-S_i^{-}\leq S_i^0Me^{\omega\xi}$ and $\eta_ie^{\lambda_1\xi}-h_i(\xi)\leq K\zeta_ie^{(\lambda_1+\epsilon)\xi}$ for $i = 1,\ 2,$ it is obtained that

Thus, for the proof of the inequality (18), we only need to prove

which is

For $\xi<\frac{1}{\epsilon}\ln{\frac{\eta_0}{K\zeta_0}},$ it is the fact that $e^{(\omega-\epsilon)\xi}\rightarrow0$ as $K\rightarrow+\infty$. Thus, combining inequalities (11), the inequality (19) is obtained, and the inequality (14) is established. Finally, we can prove inequalities (15) and (16) via the similar way in the proof of the inequality (14). The proof is complete.

Now, we set $X>\max\left\{\frac{1}{\epsilon}\ln{\frac{\eta_0}{K\zeta_0}},\ \frac{1}{\epsilon}\ln{\frac{\eta_1}{K\zeta_1}},\ \frac{1}{\epsilon}\ln{\frac{\eta_2}{K\zeta_2}}\right\}.$ Define

where $i = 1,\ 2$ and $j = 0,\ 1,\ 2.$ And it is well known that $\Gamma_X$ is closed and convex.

For any

we consider the following boundary-value problem for $\xi\in(-X,\ X),$

satisfying the below boundary condition:

Applying the Gilbarg and Trudinger's Corollary 9.18 in [6], we can claim that there exists a unique solution

satisfying the problems (20)-(21), where

for $p>1.$ And it is shown that $(S_{1,X},\ S_{2,X},\ E_X,\ I_{1,X},\ I_{2,X})\in W^{2,p}((-X,\ X),\ \mathbb{R}^5)\ \hookrightarrow C^{1,\alpha}([-X,\ X],\ \mathbb{R}^5)$ for some $\alpha\in(0.\ 1)$ via the embedding theorem (see Gilbarg and Trudinger's Theorem 7.26 in [6]). Define the operator $\mathcal{T} = (\mathcal{T}_1,\ \mathcal{T}_2,\ \mathcal{T}_3,\ \mathcal{T}_4,\ \mathcal{T}_5)$ on $\Gamma_X$ such that

for any $(\chi_1,\ \chi_2,\ \varphi_0,\ \varphi_1,\ \varphi_2)\in\Gamma_X.$

Lemma 2.8. The operator $\mathcal{T}$ maps $\Gamma_X$ into $\Gamma_X.$

Proof. Firstly, we consider $S_i(\xi)\ (i = 1,\ 2).$ It is well known that $0$ is the sub-solution of the $S_i$-th equation in equation ({20}), respectively. $S_1^0$ and $S_2^0$ are super-solutions of $S_i$-th equations in equation ({20}), respectively. According to $0<S_{i,X}(X) = S_i^{-}(X)<S_i^0$ and $0 = S_{i,X}(-X) = S_i^{-}(-X)<S_i^0,$ while combining the maximum principle in [19], it is the fact that $0\leq S_{i,X}(\xi)\leq S_i^0$ for $\forall\xi\in[-X,\ X].$ Due to Lemma 2.6, it yields that $S_i^{-}(\xi)$ satisfies

and

for any $\xi\in[-X,\ X^{'}]$ with $X^{'} = -\frac{1}{\omega}\ln{M}.$ Because of $S_{i,X}(-X) = S_i^{-}(-X)$ and $S_{i,X}(X^{'})\geq S_i^{-}(X^{'}) = 0,$ it is concluded that $S_i^{-}(\xi)\leq S_{i,X}(\xi)$ for $\xi\in[-X,\ X^{'}]$ by the maximum principle. Therefore, we claim that $S_i^{-}(\xi)\leq S_{i,X}(\xi)\leq S_i^0$ for $\xi\in[-X,\ X].$

Secondly, we consider about $E_X,\ I_{1,X}$ and $I_{2,X}.$ It follows from the maximum principle that $E_X\geq0,\ I_{i,X}\geq0$ for any $\xi\in[-X,\ X].$ According to Lemma 2.5, it is obtained that

and

for any $\xi\in[-X,\ X].$ So the maximum principle shows that $E_X(\xi)\leq p_0(\xi),\ I_{1,X}(\xi)\ \leq p_1(\xi)$ and $I_{2,X}(\xi)\leq p_2(\xi).$ for $\xi\in[-X,\ X].$ Furthermore, Lemma 2.7 implies that

for $\xi\in[-X,X_0^{'}]$ with $X_0^{'} = \frac{1}{\epsilon}\ln{\frac{\eta_0}{K\zeta_0}},$

for $\xi\in[-X,X_1^{'}]$ with $X_1^{'} = \frac{1}{\epsilon}\ln{\frac{\eta_1}{K\zeta_1}},$ and

for $\xi\in[-X,X_2^{'}]$ with $X_2^{'} = \frac{1}{\epsilon}\ln{\frac{\eta_2}{K\zeta_2}}.$ Owing to $E_X(-X) = h_0(-X),\ I_{1,X}(-X) = h_1(-X)$ and $I_{2,X}(-X) = h_2(-X),$ while combining the fact $E_X(X_0^{'})\geq h_0(X_0^{'}) = 0,\ I_{1,X}(X_1^{'})\geq h_1(X_1^{'}) = 0$ and $I_{2,X}(X_2^{'})\geq h_2(X_2^{'}) = 0,$ we can implies that $h_0(\xi)\leq E_X(\xi),\ h_1(\xi)\leq I_{1,X}(\xi)$ and $h_2(\xi)\leq I_{2,X}(\xi)$ for $\xi\in[-X,\ X_i^{'}]\ (i = 0,\ 1,\ 2)$ by the maximum principle. Thus, one yields $h_0(\xi)\leq E_X(\xi)\leq p_0(\xi),\ h_1(\xi)\leq I_{1,X}(\xi)\leq p_1(\xi)$ and $h_2(\xi)\leq I_{2,X}(\xi)\leq p_2(\xi)$ for $\xi\in[-X,\ X].$ This completes the proof.

By taking advantage of the classic embedding theorem, $\mathcal{T}$ is a compact operator from $\Gamma_X$ to $\Gamma_X.$ In fact, $\mathcal{T}:\ \Gamma_X\rightarrow\Gamma_X$ is also a completely continuous operator (see [27]). Above all, the Schauder fixed point theorem implies that there exists a vector function $(S_{1,X},\ S_{2,X},\ E_{X},\ I_{1,X},\ I_{2,X})\in\Gamma_X$ satisfying

for $\xi\in[-X,\ X],$ which includes that $(S_{1,X},\ S_{2,X},\ E_{X},\ I_{1,X},\ I_{2,X})$ satisfies following equations for $i = 1,\ 2,$

We have proved the local existence of solution for system (5). In order to obtain the global existence, we need the following estimate.

Lemma 2.9. For a given $Y>0,$ there exist some positive constants $N_{S_i}(Y), N_{E}(Y)$ and $N_{I_i}(Y)$ such that

with $i = 1,\ 2,$ and these positive constants are independent of

Proof. We always set $i = 1,\ 2.$ The equation (22) can imply that $S_{i,X}(\xi)\leq S_i^0,\ E_{X}(\xi)\leq \eta_0e^{\lambda_1Y}\leq\widehat{N_{E}}(Y),$ and $I_{i,X}(\xi)\leq \eta_ie^{\lambda_1Y}\leq\widehat{N_{I_i}}(Y)$ for any $\xi\in[-Y,\ Y].$ And applying $L^p\ (p\geq2)$ estimates of linear elliptic differential equations to $S_{i,X}$, we can claim that

and

where $\Omega_i$ is a constant depending on $Y.$ $\phi_i$ can be considered as a linear function connecting points $(-Y,\ S_{i,X}(-Y))$ and $(Y,\ S_{i,X}(Y)),$ respectively. Therefore, there exists a constant $\widehat{Q_{S_i}}(Y)$ such that $\parallel S_{i,X}\parallel_{W^{2,p}(-Y,Y)}\leq\widehat{Q_{S_i}}(Y)$ for any $X>Y,$ respectively. Owing to $W^{2,p}(-Y,\ Y)\hookrightarrow C^{1,\alpha}[-Y,\ Y]$ for $\alpha = 1-\frac{1}{p},$ it is shown that $\parallel S_{i, X}\parallel_{C^{1,\alpha}[-Y,\ Y]}\leq\widetilde{N_{S_i}}(Y)\parallel S_{i, X}\parallel_{W^{p,\alpha}(-Y,\ Y)}$ where $\widetilde{N_{S_i}}(Y)$ is a constant depending on $Y,$ which can lead to $\parallel S_{i, X}\parallel_{C^{1,\alpha}[-Y,\ Y]}\leq\widehat{N_{S_i}}(Y)$ for $\widehat{N_{S_i}}(Y) = \widehat{Q_{S_i}}(Y)\widetilde{N_{S_i}}(Y)>0.$ According to the first and second equations in equations (22), we also obtain $\parallel S_{i, X}\parallel_{C^{2}[-Y,\ Y]}\leq\widehat{N_{S_i}}(Y)$ for $\widehat{N_{S_i}}(Y)>0,$ respectively. Via the similar way, we further yield that $\parallel E_{X}\parallel_{C^{2}[-Y,\ Y]}\leq\widehat{N_{E}}(Y)$ and $\parallel I_{i, X}\parallel_{C^{2}[-Y,\ Y]}\leq\widehat{N_{I_i}}(Y).$ Finally, the estimate (23) is established with differentiating two sides of the first five equations in equations (22). The proof is finished.

Set a sequence of positive numbers $\left\{X_m\right\}_{m>0}$ satisfying $X_m\rightarrow+\infty$ as $m\rightarrow+\infty.$ Thus, by Lemma 2.9, there exists a solution $(S_1,\ S_2,\ E,\ I_1,\ I_2)\in C^2(\mathbb{R},\ \mathbb{R}^5)$ of system (5) such that

with $\forall\xi\in\mathbb{R}.$ According to inequalities (24), we can gain

Now, we need to show some estimates about solution $(S_1(\xi),\ S_2(\xi),\ E(\xi),\ I_1(\xi),\ I_2(\xi))$ in order to research the asymptotic behavior as $\xi\rightarrow+\infty.$

Lemma 2.10. Let $r\leq\min\{\mu,\ \mu+\alpha_1,\ \mu+\alpha_2\},$ then we have

and

where $D_{min} = \min\{D_0,\ D_1,\ D_2\}$ and $\forall\xi\in\mathbb{R}.$

Proof. In this proof, we still set $i = 1,\ 2.$ As $E(\xi),\ I_1(\xi),\ I_2(\xi)$ are non-negative and not identically zero, the strong maximum principle implies that $E(\xi),\ I_1(\xi),\ I_2(\xi)>0$ for any $\xi\in\mathbb{R}$ and $E(\xi)+I_1(\xi)+I_2(\xi)>0.$ Define

and

Due to the define of $r$, it then follows that

So we need to consider the following Cauchy problems

for $\forall t>0,\ \forall\xi\in\mathbb{R}.$ Then, via the Theorem 12 and the Theorem 16 in [5], we can indicate

for $\forall t>0,\ \forall\xi\in\mathbb{R}.$ Applying the comparison principle in [19] concludes

Let $t\rightarrow+\infty,$ then one yields

for $\forall t>0,\ \forall\xi\in\mathbb{R},$ where

Owing to $d\geq D_0\geq D_i,$ we yield

and

for any $\xi\in\mathbb{R}.$ We also have $\sqrt{D_i}I_i(\xi)\leq\sqrt{D_i}g_i(\xi).$ Consequently, it is shown that

which implies

for $D_{min} = \min\{D_0,\ D_1,\ D_2\}$ and any $\xi\in\mathbb{R}.$

On the other hand, one has

for any $\xi\in\mathbb{R}.$ Then the maximum principle implies that

Via the similar argument on $S_1(\xi)$, we can indicate

This lemma is completely proved.

Since the system consisted by $E$-th and $I_i$-th equations in system (5) is cooperation and irreducible, the Theorem 2.2 in [2] and Lemma 2.10 can claim that there exists a positive constant $M_1$ such that

Furthermore, there exists a constant $\hat{M}>0$ such that

for $\forall\xi\in\mathbb{R}.$ Actually, $L^{p}$ interior estimate shows there exists a positive constant $M_2>0$ satisfying

for any $\xi\in\mathbb{R}$ and $p>1.$ The above inequality, combining the embedding theorem, can conclude that there exists a positive costant $M_3$ satisfying

Set $\hat{M} = M_1M_3$, then the inequality (29) is established via the estimate (30).

In order to take advantage of a suitable Lyapunov functional to research the asymptotic behavior of $(S_1(\xi),\ S_2(\xi),\ E(\xi),\ I_1(\xi),\ I_2(\xi))$ as $\xi\rightarrow+\infty,$ we define

Let $g(x) = x-1-\ln{x}$ and define a suitable Lyapunov functional

where

for each $(S_1(\cdot),\ S_2(\cdot),\ E(\cdot),\ I_1(\cdot),\ I_2(\cdot))\in\hat{E}.$ Then we claim the below lemma.

Lemma 2.11. Let (A) be satisfied and $(S_1(\cdot),\ S_2(\cdot),\ E(\cdot),\ I_1(\cdot),\ I_2(\cdot))$ be a positive solution of system (5) satisfying

and

for any $\xi\in\mathbb{R}$ and $i = 1,\ 2,$ where $\mathcal{N}$ is a positive constant. Then there exists a constant $m>0,$ depending on $\mathcal{N},$ such that

where the map $V(\xi)$ is defined as formula (31). Moreover, the map $V(\xi)$ is not increasing. In particular, $S_i(\xi) = S_i^*,\ E(\xi) = E^*,\ I_i(\xi) = I_i^*$ as the map $V(\xi)$ is a constant.

Proof. The previous description has shown $S_1$ and $S_2$ are bounded in $C^2(\mathbb{R}).$ Via inequalities (32)-(35), we can conclude that for any $\xi\in\mathbb{R}$

where $\hat{D} = \max\{D_0E^*,\ D_1I_1^*\ D_2I_2^*\},$ and $\hat{C} = \max\{1,\ C_1,\ C_2\}.$ Let

According to both the definition of $g(\cdot)$ and (32)-(34), it is shown that $0\leq\Phi(\xi)<+\infty, \forall\xi\in\mathbb{R}.$ Then, by combining the inequality (37), the inequality (36) holds.

Since a direct calculation with letting $x_1 = \frac{S_1(\xi)}{S_1^*},\ x_2 = \frac{S_2(\xi)}{S_2^*},\ x_3 = \frac{E(\xi)}{E^*},\ x_4 = \frac{I_1(\xi)}{I_1^*},\ x_5 = \frac{I_2(\xi)}{I_2^*}$ leads to

Therefore, via the mean inequality, we conclude that

which implies that the map $V(\xi)$ is non-increasing. Especially, when

the map $V(\xi)$ is a constant, which indicates that

This completes the proof.

Now, we gain the first theorem for existence of traveling wave solution for system (2) as below:

Theorem 2.12. If (A) and $R_0>1$ hold, system (2) admits a non-trivial and non-negative traveling wave solution $(S_1(\xi),\ S_2(\xi),\ E(\xi),\ I_1(\xi),\ I_2(\xi))$ satisfying the boundary condition (6) for each $c>c^*,$ where $c^*$ is the minimal spread speed and $R_0$ is the basic reproduction number for system (3).

Proof. We still set $i = 1,\ 2$ in this proof. It follows from the previous argument that there exists a vector function

satisfying system (5), and

for any $\xi\in\mathbb{R}.$ Therefore we only need to show that

Take an arbitrary increasing sequence $\{\xi_m\}$ with $\xi_m>0$ and $m\geq0$ such that $\xi_m\rightarrow+\infty$ as $m\rightarrow+\infty.$ Define

Via the elliptic estimate, it may assume that the sequence $(S_{1,m},\ S_{2,m},\ E_m,\ I_{1,m}, I_{2,m})$ converges towards $(S_{1,\infty},\ S_{2,\infty},\ E_{\infty},\ I_{1,\infty},\ I_{2,\infty})$ in $C_{loc}^{1}(\mathbb{R})\times\cdots\times C_{loc}^{1}(\mathbb{R}).$ As a result, $(S_{1,\infty},\ S_{2,\infty},\ E_{\infty},\ I_{1,\infty}, I_{2,\infty})$ is also a solution of system (5). In addition, the map $V(\xi)$ defined as the formula (31) is not increasing, then we yield

for any $\xi\in\mathbb{R}.$ Since the map $V(\xi)$ is bounded via Lemma 2.11, there exists a constant $\hat{G}\in\mathbb{R}$ such that

which implies that

in $C_{loc}^1(\mathbb{R}).$ Combining Lemma 2.11, we can claim that

Via the arbitrariness of the sequence $\{\xi_m\},$ we finally indicate

The proof is completed.

Furthermore, the second theorem of existence for traveling wave solution for system (2) is stated as below:

Theorem 2.13. Assume that (A) is satisfied and $R_0>1.$ Then for $c = c^*,$ system (2) also admits a non-trivial and non-negative traveling wave solution $(S_1(\xi),\ S_2(\xi),\ E(\xi),\ I_1(\xi),\ I_2(\xi))$ satisfying the boundary condition (6), where $c^*$ is the minimal spread speed and $R_0$ is the basic reproduction number for system (3).

Proof. Step 1. Take a decreasing sequence $\{c_m\}\in(c^*,\ c^*+1)$ with $\lim_{m\rightarrow+\infty}c_m = c^*.$ It follows from Theorem 2.12 that there exists a solution $(S_{1,m},\ S_{2,m},\ E_m,\ I_{1,m},\ I_{2,m})$ of system (5) for each $c_m$ satisfying conditions (6), (25), (26), (28) and (29). Since $(S_{1,m}(\cdot+a),\ S_{2,m}(\cdot+a),\ E_m(\cdot+a),\ I_{1,m}(\cdot+a),\ I_{2,m}(\cdot+a))$ is also the solution of system (5) satisfying equations (6) for any $a\in\mathbb{R},$ we can let

The interior elliptic estimates, Arzela-Ascoli theorem and a diagonalization argument can indicate a subsequence of $\{(S_{1,m},\ S_{2,m},\ E_m,\ I_{1,m}.\ I_{2,m})\}$ defined again by $\{(S_{1,m},\ S_{2,m},\ E_m,\ I_{1,m}.\ I_{2,m})\}$ satisfies

as $m\rightarrow+\infty$ in $C_{loc}^2(\mathbb{R},\ \mathbb{R}^5)$. And it is well known that $(S_{1},\ S_{2},\ E,\ I_{1}.\ I_{2})$ satisfies system (5) and

which implies that

Moreover, we yield $S_i>0,\ E>0,\ I_i>0.$ Above all, it is concluded that $(S_{1},\ S_{2},\ E,\ I_{1}.\ I_{2})$ satisfies estimates (25), (26), (28) and (29). Via Lemma 2.11, one gains

Next, we need to prove what the solution converges to as $\xi\rightarrow-\infty.$ Since Lemma 2.11 implies $V(\xi)$ defined as the formula (31) is non-increasing, then we can obtain either

or

If the formula (40) holds, via the similar way in Lemma 2.11, it can claim that

and then $L = 0,$ which implies that $V\equiv0$ for any $\xi\in\mathbb{R}.$ Consequently, applying Lemma 2.11 concludes that

which contradicts the equation (39). Thus, the equation (41) must be only workable. Due to the inequality (37), it is shown that

where $\Phi(\xi)$ is defined as the formula (38) in the proof of Lemma 2.11. Now, we firstly show that

On the contrary, if $E(\xi)>\delta$ in $\xi\in\mathbb{R}$ for some $\delta>0.$ According to $E(+\infty) = E^*,$ then it follows from the estimate (28) that there exists a constant $\hat\delta>0$ such that

which indicates that

and contradicts the equation (42). Therefore, the equation (43) holds. Secondly, we prove that

If

there exists a sequence $\{\xi_j\}$ satisfying

Via the estimate (28), we can have

Then, it is implied that

which contradicts the equation (41). Therefore,

In the similar way, we can also claim that

Finally, set $i = 1,\ 2$ and we show that

In order to hit the target, we firstly prove the existence of $\lim_{\xi\rightarrow-\infty}S_i(\xi).$ On the contrary, we assume that one of $\lim_{\xi\rightarrow-\infty}S_i(\xi)$ does not exist. Since $S_i(\xi)$ satisfies (26), we obtain

Take a sequence $\{\xi_n\}$ satisfies $\xi_n\rightarrow-\infty$ as $n\rightarrow+\infty$ and

Since $\lim_{n\rightarrow+\infty}I_i(\xi_n) = 0,$ adding the $S_1$-th equation and $S_2$-th equation implies that

which leads to a contradiction to inequalities (44). Thus, $\lim_{\xi\rightarrow-\infty}S_i(\xi)$ exists, respectively.

Step 2. This step is to prove $\lim_{\xi\rightarrow-\infty}S_i(\xi) = S_i^0$ Let $\lim_{\xi\rightarrow-\infty}S_i(\xi) = k_i.$ Utilizing the equation

we can obtain that

where

As $\xi\rightarrow-\infty,$ it follows from the Lebesgue dominated convergence theorem that

which leads to

Via the similar argument on $S_2(\xi)$, we can get

This completes the proof.

3.   Non-existence of traveling wave solution

The previous section has stated the existence of traveling wave solution connecting disease-free equilibrium and endemic equilibrium when $R_0>1$ and $c\geq c^*.$ In this section, we aim to prove the non-existence of this solution in three cases: (1) $R_0<1,$ (2) $R_0 = 1,$ (3) $R_0>1$ and $c\in(0,\ c^*).$

3.1.   Case(1): $R_0<1$

Theorem 3.1. If $R_0<1,$ there does not exist a non-negative and non-trivial traveling wave solution of system (5) satisfying the boundary condition (6), where $R_0$ is the basic reproduction number for system (3).

Proof. On the contrary, assume that there exists a solution $(S_1(\xi),\ S_2(\xi),\ E(\xi), I_1(\xi),\ I_2(\xi))$ satisfying system (5) and the boundary condition (6). Let $E_{sup} = \sup_{\xi\in\mathbb{R}}E(\xi)$ and take $i = 1,\ 2.$ We can yield from the $I_i$-th equation that

It follows from the comparison principle that

Next we research the following equation

where $\bar{\Lambda} = S_1^0+\sigma S_2^0.$ Via the comparison principle, we can show that

which indicates

and contradicts the fact $R_0<1.$ Above all, there exists no non-negative and non-trivial traveling wave solution as $R_0<1.$

3.2.   Case(2): $R_0=1$

Theorem 3.2. As $R_0 = 1,$ there does not exist a non-negative and non-trivial traveling wave solution of system (5) satisfying the boundary condition (6), where $R_0$ is the basic reproduction number for system (3).

Proof. Set a new sequence $\{\xi_m\}\subset\mathbb{R}$ such that

Now, we need to show $\hat{B} = 0$ by contradiction. Assume $\hat{B}>0,$ and we consider the function sequence $(S_{1,m}(\xi),\ S_{2,m}(\xi),\ E_{m}(\xi),\ I_{1,m}(\xi),\ I_{2,m}(\xi)) = (S_{1}(\xi+\xi_m),\ S_{2}(\xi+\xi_m),\ E_{m}(\xi+\xi_m),\ I_{1}(\xi+\xi_m),\ I_{2}(\xi+\xi_m)).$ We take a function subsequence denoted again by $(S_{1,m}(\xi),\ S_{2,m}(\xi),\ E_{m}(\xi),\ I_{1,m}(\xi),\\ I_{2,m}(\xi)),$ and utilizing elliptic estimates shows that

as $m\rightarrow+\infty$ in $C_{loc}^2(\mathbb{E})$ with $(\tilde{S_1}(\xi),\ \tilde{S_2}(\xi),\ \tilde{E}(\xi),\ \tilde{I_1}(\xi),\ \tilde{I_2}(\xi))$ satisfying

The maximum principle implies that

Moreover, we can yields

Owing to $\tilde{E}^{''}(0)\leq0$, $\beta[\tilde{S_1}(0)+\sigma\tilde{S_1}(0)]\left(\theta\frac{q_1\gamma}{\mu+\alpha_1}+\frac{q_2\gamma}{\mu+\alpha_2}\right)\hat{B}-(\mu+\gamma)\hat{B}\geq0$ and $\tilde{S_i}\leq S_i^0,$ we must claim $\beta[\tilde{S_1}(0)+\sigma\tilde{S_1}(0)]\left(\theta\frac{q_1\gamma}{\mu+\alpha_1}+\frac{q_2\gamma}{\mu+\alpha_2}\right)\hat{B}-(\mu+\gamma)\hat{B} = 0,$ which implies that $\tilde{S_i}(0) = S_i^0.$ The minimal principle with combining the $\tilde{S_i}$-th equation can lead to $\tilde{S_i}(\xi)\equiv S_i^0,\ \tilde{E}(\xi)\equiv0,\ \tilde{I_i}(\xi)\equiv 0,\ \forall\xi\in\mathbb{R}.$ Consequently, we have $\hat{B} = 0$ that contradicts $\hat{B}>0.$ This case is completely proved.

3.3.   Case(3): $R_0>1$ and $c\in(0,\ c^*)$

In this case, we attempt to utilize the two-sides Laplace transform to gain the non-existence of traveling wave solution for system (2). Therefore, we firstly need to imply the exponential boundedness for traveling wave solution via next two lemmas.

Lemma 3.3. Assume that $R_0>1,$ where $R_0$ is the basic reproduction number for system (3). For any $c>0,$ if system (5) admits a non-trivial and non-negative solution $(S_1(\xi),\ S_2(\xi),\ E(\xi),\ I_1(\xi), I_2(\xi))$ satisfying the boundary condition (6), then there exist two constants $\mathcal{J}>0$ and $G>0$ large enough such that

for $\xi<-2G.$

Proof. Set $i = 1,\ 2.$ Let $c>0$ and $(S_1(\xi),\ S_2(\xi),\ E(\xi),\ I_1(\xi),\ I_2(\xi))$ be traveling wave solution of system (5) satisfying the boundary condition (6). Thus, we can claim there exist $G>0$ large enough and small $\varepsilon\in(0,\ 1)$ such that

For any $\xi<-2G$, we can yield

For $y<\xi<-2G,$ let

Integrate both sides of inequalities (45) from $y$ to $\xi,$ with $y<\xi<-2G,$ and we can yield

It follows from Lemma 2.10 and inequality (29) that

and

where $\hat{P}$ is a positive constant. Due to inequalities (47)-(48), we have

In the following, we aim to prove that there exists a constant $\mathcal{J}>0$ such that

Let

and we conclude $|A|<0$ for $\varepsilon>0$ small enough on the basis of assumption $R_0>1.$ Add

to both sides of the inequality (46) multiplied by $-(\mu+\alpha_1)(\mu+\alpha_2),$ and it is obtained that

for $y<\xi<-2G.$ As $y\rightarrow-\infty$, the inequality (51), combining equations (49) and (50), leads to

In the similar way, we also can claim that

The proof is completed.

Lemma 3.4. Assume that $R_0>1,$ where $R_0$ is the basic reproduction number for system (3). For any $c>0,$ if there exists a non-trivial and non-negative traveling wave solution $(S_1(\xi),\ S_2(\xi),\ E(\xi), I_1(\xi),\ I_2(\xi))$ of system (5) satisfying the boundary condition (6), a positive constant $\mu_0$ can be found and satisfies

Proof. Fix $c>0.$ According to $\varepsilon>0$ and $G>0$ defined in Lemma 3.3, it is also shown that

And $R_0>1$ implies that

Thus, for any $\xi<-2G,$ we yield that

Set $i = 1,\ 2$ and remain in what follows. According to Lemma 3.3, it is indicated that

for any $\xi<-2G.$ Moreover, we integrate tow sides of the inequality (54) from $-\infty$ to $\xi$ and can obtain that

Integrating two sides of the inequality (57) from $-\infty$ to $\xi$ with $\xi<-2G$ indicates that

Via the similar way in equations (55) and (56), we can yield

and

which reduces to

and

Next, we need to claim there exist two positive constants $a$ and $b$ such that

Substituting equations (61) and (62) into the equation (59) has

which implies

Because $E(\xi)$ and $I_i(\xi)$ are non-negative, the above inequality reduces to

According to the inequality (53), we can claim that there exist two positive constants $\bar{a_0}$ and $\bar{b_0}$ such that

Plug the inequality (64) into the inequality (58), and it is shown that there are two constants $\bar{a}$ and $\bar{b}$ satisfying

Hence, for any $\xi<-2G,$ the inequality (3.3) is established by adding the inequality (64) and the inequality (65). Let

then we gain that

that is

Because $\mathcal{J}(\cdot)$ is increasing, it is implied that $a\eta\mathcal{J}(\xi-\eta)\leq b\mathcal{J}(\xi)$ for any $\xi<-2G$ and $\eta>0.$ Therefore, there exist a large enough $\xi_0>0$ and a small $\omega_0\in(0,\ 1)$ such that

Let $\Psi(\xi) = \mathcal{J}(\xi)e^{-\mu_0\xi}$ with $0<\mu_0 = \frac{1}{\xi_0}\ln\frac{1}{\omega_0}<\lambda_1,$ and then it is concluded that

for any $\xi<-2G.$ According to $\mathcal{J}(\xi)<\infty$ for any $\xi<-2G,$ we can find a constant $k_0>0$ such that $\Psi(\xi)\leq k_0$ for $\forall\xi<-2G,$ that is $\mathcal{J}(\xi)\leq k_0e^{\mu_0\xi}$ for any $\xi<-2G.$ Therefore, there exists a constant $q_0>0$ such that $\int_{-\infty}^{\xi}\bar{J}(x)\mathrm{d}x\leq q_0e^{\mu_0\xi}$ in $\xi\in(-\infty,\ -2G).$ Combining equations (59)-(60), we can also find a constant $p_0>0$ satisfying

Since $E(\xi)$ and $I_i(\xi)$ are bounded in $\mathbb{R}$, we obtain that

According to estimates (29) and (57), it yields

Via the $E$-th equation in system (5) and the inequality (54), we can conclude that

Finally, applying the similar argument on $I_i(\xi)$ shows that

This completes the proof.

According to above two theorems, we can obtain the following non-existence theorem.

Theorem 3.5. If $R_0>1,$ for $c\in(0,\ c^*),$ there exists no non-trivial and non-negative traveling wave solution $(S_1(\xi),\ S_2(\xi),\ E(\xi),\ I_1(\xi),\ I_2(\xi))$ of system (5) satisfying the boundary condition (6), where $c^*$ is the minimal spread speed and $R_0$ is the basic reproduction number for system (3).

Proof. We intend to prove this theorem by contradiction. Fix $c\in(0,\ c^*).$ On the contrary, we assume there exists a non-trivial and non-negative $(S_1(\xi),\ S_2(\xi),\ E(\xi),\\ I_1(\xi),\ I_2(\xi))$ of system (5) satisfying the boundary condition (6). Via Lemma 3.4, then there exists a positive constant $\mu_0$ defined in the proof of Lemma 3.4 such that inequalities (52) are established. Set $K_1(\xi) = S_1^0-S_1(\xi)$ and $K_2(\xi) = S_2^0-S_2(\xi)$ in $\mathbb{R}.$ Plugging $K_1(\xi)$ and $K_2(\xi)$ into $S_1$-th and $S_2$-th equations yields

According to the inequality

and the fact that

we can claim

for $i = 1,\ 2.$ In addition, since $K_i(\xi)$ is bounded and satisfies equations (68)-(69), integrating both sides of the sum of equations (66) and (67) from $-\infty$ to $\xi\leq0$ can show that

Let $f(\xi) = \int_{-\infty}^{\xi}\beta[S_1(x)+\sigma S_2(x)][\theta I_1(x)+I_2(x)]\mathrm{d}x,$ and $K_{\mu}(\xi) = \mu\int_{-\infty}^{\xi}[K_1(x)+K_2(x)]\mathrm{d}x$ for any $\xi\leq0.$ It follows from Lemma 3.4 that $f(\xi)\leq C_{f}e^{\mu_0\xi}$ on $\xi\in\mathbb{R},$ where $C_{f}$ is a positive constant. Hence, a direct calculation indicates that

for $\xi\leq0.$ Owing to $f(\xi) = O(e^{\mu_0\xi})$ as $\xi\rightarrow-\infty,$ we can claim that $K_1(\xi)+K_2(\xi) = O(e^{\mu_0^{'}\xi})$ as $\xi\rightarrow-\infty,$ where $\mu_0^{'} = \min\left\{\mu_0,\ \frac{c}{d}\right\}.$ Combining $0\leq K_1(\xi)+K(\xi)\leq\frac{\lambda}{\mu},$ we can conclude that

which implies

On the basis of the above discussion, we define the one-sided Laplace transforms for $E(\xi),$ $I_1(\xi)$ and $I_2(\xi)$ by

Next, we only consider $\hat{\lambda}\in\mathbb{R}_{+}.$ Since $E(\xi)>0$, $I_1(\xi)>0,$ $I_2(\xi)>0$ for any $\xi\in\mathbb{R},$ and $L_i(\cdot)$ is increasing for $\hat{\lambda}\in\mathbb{R}_{+},$ respectively, there exist two possibilities: (ⅰ) a positive constant $v_i>\mu_0$ can be found such that $L_i(\cdot)<\infty$ for any $0\leq\hat{\lambda}<v_i$ and $\lim_{\hat{\lambda}\rightarrow v_i-0}L_i(\hat{\lambda}) = \infty.$ (ⅱ) $L_i(\cdot)<\infty$ for any $\hat{\lambda}\geq0,$ where $i = 0,\ 1,\ 2.$ Therefore, we define two-sided Laplace transforms for $E(\cdot),\ I_1(\cdot)$ and $I_2(\cdot)$ by

and we also only research $\hat{\lambda}>0.$ Because $E(\cdot),\ I_1(\cdot)$ and $I_2(\cdot)$ are bounded in $\mathbb{R},$ respectively, it is the fact that

for any $\hat{\lambda}>0,$ which implies $\mathcal{L}_I(\cdot)$ owns the same property as $L_i(\cdot)$ in $\mathbb{R}_{+}$ with $i = 0,\ 1,\ 2,$ respectively.

In the following, we indicate that there indeed exists a $v_i = +\infty$ such that $\mathcal{L}_i(\hat{\lambda})<\infty$ for any $\hat{\lambda}\geq0$ with $i = 0,\ 1,\ 2,$ respectively. The first step is to prove $v_0 = v_1 = v_2$. According to

it is implied that

In the same way, we can obtain

and

Thus, it follows from equations (73) and (74) that $v_0 = v_1 = v_2.$ Let $v = v_0 = v_1 = v_2.$ The second step is to prove $v = +\infty$ via a contradiction. We assume that $v<+\infty$ and $\mathcal{L}_i(\hat{\lambda})<\infty\ (i = 0,\ 1,\ 2)$ for any $\hat{\lambda}\in[0,\ v)$ and $\lim_{\hat{\lambda}\rightarrow v-0}\mathcal{L}_i(\hat{\lambda}) = \infty.$ Equations (72)-(74) can show that $-D_1v^2+cv+(\mu+\alpha_1)>0$ and $-D_2v^2+cv+(\mu+\alpha_2)>0.$ If $D_0v^2-cv-(\mu+\gamma)\geq0$ and let $\hat{\lambda}\rightarrow v-0$ in both sides of (72), the right side shows

However, the left side tends to $\infty,$ which leads to a contraction. If $D_0v^2-cv-(\mu+\gamma)<0,$ plugging equations (73) and (74) into the equation (72) can obtain that

and $0<v<\lambda_c.$ As $\hat{\lambda}\rightarrow v-0,$ the right side is bounded, but the left side tends to $\infty.$ As a result, the case (ⅰ) is impossible.

If the case (ⅱ) is established, similarly, let $\hat{\lambda}\rightarrow+\infty$ in both sides of the equation (72). The right side is bounded but the left side tends to $\infty$ owing to $D_0\hat{\lambda}^2-c\hat{\lambda}-(\mu+\gamma)\rightarrow\infty,$ which also leads to a contraction. Above all, the non-existence is completely proved.

4.   Numerical simulations and discussion

Section 2 and Section 3 have proved the existence and non-existence of traveling wave solution for system (2) satisfying the boundary condition (6). In this section, we aim to visually display the existence of traveling wave solution for system (2) connecting disease-free equilibrium and endemic equilibrium. Now, we firstly take a set of parameters for system (2) as follows:

As a result, we can obtain the disease-free equilibrium $(S_1^0,\ S_2^0,\ E^0,\ I_1^0,\ I_2^0,\ R^0) = (8,\ 18.6667,\ 0,\ 0,\ 0,\ 0),$ the endemic equilibrium $(S_1^*,\ S_2^*,\ E^*,\ I_1^*,\ I_2^*,\ R^*)\approx(3.3762,\ 2.3999,\ 5.9687,\ 2.8274,\ 2.2383,\ 9.8565)$ and the basic reproduction number $R_0\approx3.2821>1.$ For simulations, we further intercept $[-200,\ 200]$ from spatial domain and $[0,\ 200]$ from time domain. Moreover, we take the Neumann boundary condition and the below piecewise functions as initial conditions for system (2):

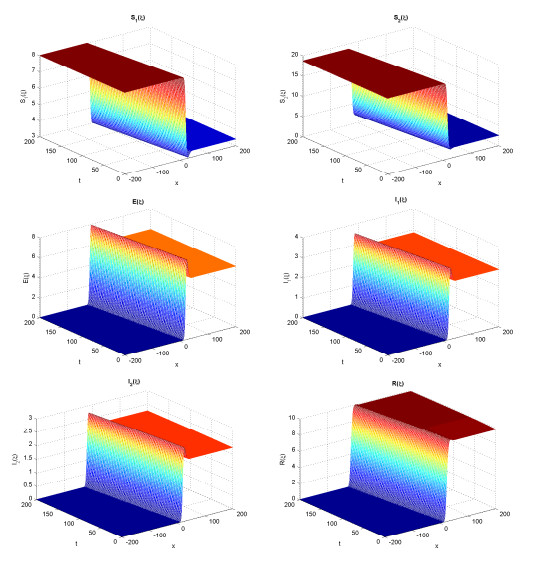
The figure 1, simulations with applying above conditions, indicate that there exists a traveling wave solution of system (2) connecting disease-free equilibrium and endemic equilibrium. Meanwhile, we cross section curves of traveling wave solution in figure 1 as $t = 200$ (see figure 2). And we can find that traveling waves for system (2) are not monotonic in figure 2.

Since we pay more attention to influences of self-protection and treatment in the spatial spread for an epidemic, it is critical to research the change of the minimal spread speed $c^*$ while self-protection $\sigma$ and treatment $\theta$ changing. The direct derivations of $\rho(\lambda,\ c)$ with respect to $\sigma$ and $\theta$ show that

respectively, where $\rho(\lambda,\ c)$ is defined as the formula (9). The inequality (76) means that the numerical increase in $\sigma$ and $\theta$ could lead to increasing of the minimal spread speed $c^*$ with applying Lemma 2.3. The figures (a) and (b) in figure 3 also display that the minimal spread speed $c^*$ is increasing with respect to $\sigma$ and $\theta$ for $\sigma,\ \theta\in[0.05,\ 1],$ respectively. In fact, measures about the enhancement of self-protection and treatment can lead to numerical reductions about both $\sigma$ and $\theta$, which implies the minimal spread speed $c^*$ will decrease via the inequality (76) and figure 3. Above all, the effective self-protection and treatment can reduce the spread speed for an epidemic.

In this paper, we mainly construct a non-monotonic reaction diffusion SEIR model with effects of self-protection and treatment in incident rate, and determine the existence and non-existence of traveling wave solution connecting disease-free equilibrium and endemic equilibrium. We prove the existence as $R_0>1$ and $c\geq c^*$. And when $R_0\leq1$ or $R_0>1$ with $c\in(0,\ c^*),$ there exists no non-trivial and non-negative traveling wave solution satisfying the boundary condition (6). Finally, the numerical simulations show the existence and indicate that self-protection and treatment can reduce the spread speed of an epidemic. However, self-protection and treatment may affect the movement of different individuals in various times and spaces. Some individuals may even choose or be forcibly quarantined. These factors are worthy being researched in the future.

Acknowledgments

We would like to thank you for following the instructions above very closely in advance. It will definitely save us lot of time and expedite the process of your paper's publication.